Non-Minimally Coupled Electromagnetic Fields and Observable Implications for Primordial Black Holes

Abstract

General relativity (GR) postulates have been verified with high precision, yet our understanding of how gravity interacts with matter fields remains incomplete. Various modifications to GR have been proposed in both classical and quantum realms to address these interactions within the strong gravity regime. One such approach is non-minimal coupling (NMC), where the space-time curvature (scalar and tensor) interacts with matter fields, resulting in matter fields not following the geodesics. To probe the astrophysical implications of NMC, in this work, we investigate non-minimally coupled electromagnetic (EM) fields in the presence of black holes. Specifically, we show that primordial black holes (PBHs) provide a possible tool to constrain the NMC parameter. PBHs represent an intriguing cosmological black hole class that does not conform to the no-hair theorem. We model the PBH as a Sultana–Dyer black hole and compare it with Schwarzschild. We examine observables such as the radius of the photon sphere, critical impact parameter, and total deflection angles for non-minimally coupled photons for Schwarzschild and Sultana–Dyer black holes. Both the black hole space-times lead to similar constraints on the NMC parameter. For a PBH of mass $M={10}^{-5} M_{\odot }$, the photon sphere will not be formed for one mode. Hence, the photons forming the photon sphere will be highly polarized, potentially leading to observable implications.

1. Introduction

General relativity (GR) describes the interaction of matter fields and gravity and manifests as a background geometry, quantified by the metric tensor $g_{\mu \nu }$ and the covariant derivative ${\nabla }_{\mu }$ associated with curved space-time. This influence, often termed minimal coupling between matter fields and gravity, can be nullified by constructing a freely falling frame. In such a frame, the laws of physics in GR mirror those described in the special theory of relativity, constituting the key postulate of GR known as Einstein’s equivalence principle (EEP) [1,2]. The EEP encompasses three sub-principles: the weak EEP (or the universality of free fall), local Lorentz invariance, and local position invariance. Observable signatures of the EEP have undergone rigorous testing through various astrophysical phenomena, including the perihelion motion of Mercury, lunar-laser ranging, and more, with high precision [3]. Recent discoveries, such as the detection of gravitational waves by LIGO-VIRGO-KAGRA [4] and the imaging of supermassive black holes at the centers of galaxies [5], have further strengthened the fundamental principles of GR.

Indeed, while astrophysical observations and experiments have provided robust validation of these postulates, their applicability is typically confined to the weak gravity limit [6,7,8]. However, the need for dark matter and dark energy to explain the current Universe, the elusive quantum theory of gravity, and its unification with the standard model of particle physics indicate the potential need for modifications to GR, particularly in the strong gravity regime [3]. The semiclassical theory of gravity has revealed that the quantum corrections of matter fields in curved space-time lead to effective actions featuring non-minimal coupling (NMC) to the geometry. More specifically, such couplings manifest as higher-order curvature invariants [9,10]. Recently, Ruhdorfer et al. did a systematic analysis and obtained an effective field theory of gravity coupled to the standard model of particle physics [11]. Their investigation showed the existence of non-minimal coupling of the standard model bosons with Riemann/Weyl curvature tensors leading to operators with mass dimension 6. Intriguingly, the terms derived by these authors resemble the non-minimal coupling terms proposed by Prasanna [12].

While classical and quantum theories of electrodynamics (ED) have demonstrated remarkable success, they are tested in the weak-gravity regime. Recent laboratory experiments, such as those involving X-rays, have tested quantum electrodynamics (QED) [13], yet these do not include gravity effects. Over the past four decades, numerous terrestrial and astrophysical tests have been devised to examine corrections to ED in the presence of gravitational fields [14,15,16,17,18,19,20,21,22,23,24,25,26,27]. For instance, the initial study on the effects of non-minimal coupling focused on a Schwarzschild background [14]. Subsequent studies extended these investigations to include scenarios involving a static black hole with non-zero electric charge described by the Reissner–Nordström metric and a neutral rotating black hole described by the Kerr metric [15,16]. See also Refs. [17,18]. Various models of non-minimal coupling have been proposed by different authors [19,20,21,22,23,24,25]. Recent studies have highlighted the potential of such coupling terms to address two unresolved issues in early Universe cosmology: the origin of primordial magnetic fields and the mechanism of baryogenesis [26,27]. These findings suggest that the non-minimal coupling of Maxwell’s theory with gravity may offer a promising avenue for resolving longstanding challenges in particle physics, gravity, and cosmology.

This leads us to the question: Will it be possible to constrain the NMC of EM fields? If yes, can such constraint be better than the current lower bounds from various astrophysical observations [28,29,30,31,32,33,34]? In this work, we show that the primordial black holes (PBHs) provide a possible tool to constrain the NMC parameter [35,36]. Specifically, we show that a PBH of mass around ${10}^{-5}{M}_{\odot }$ can provide a stringent constraint on the NMC parameter $\lambda$. We compare the constraints on the NMC parameter from the next-generation Event Horizon Telescope (EHT). Using these constraints, we evaluate the deflection angle of an NMC photon in the vicinity of a dynamical, spherically symmetric black hole described by the Sultana–Dyer metric [37] and a static black hole described by Schwarzschild space-time. To our knowledge, the detailed evaluation of the deflection angle in a black hole space-time to constrain the non-minimal coupling parameter is new. In Ref. [38], the authors used photon dispersion relation and computed the photon’s arrival time in Schwarzschild space-time. Considering signals from radar ranging past the Sun, the authors found $\lambda \sim 1.1\times {10}^{20}{\mathrm{cm}}^2$, which is about three orders of magnitude more stringent than the one obtained in Ref. [28]. We show that deflection angle analysis improves the bound on $\lambda$ by 10 orders of magnitude for a stellar mass black hole and is consistent with the constraint obtained from a binary pulsar.

Cosmological dark matter is thought to be a complex mixture of currently hypothetical entities such as primordial black holes (PBHs) and predominantly unknown weakly interacting massive particles (WIMPs) like neutrinos and axions [39]. In the past few years, after LIGO detected black holes in previously unexplored mass ranges, there has been a renewed interest in PBHs [35,40]. The PBH was introduced by Hawking half a century ago [41], with subsequent recognition that these BHs could constitute the majority of matter in the Universe [42,43,44]. PBHs are not subject to the constraints of big bang nucleosynthesis, so they are effectively non-baryonic DM [35]; while conclusive evidence remains elusive, diverse and accurate observations have revealed at least four mass windows potentially accommodating primordial black holes: the ${10}^{-16}$–${10}^{-10}$ $M_{\odot }$ range and the ${10}^{-6}$–${10}^{-5}$ $M_{\odot }$ range for small black holes, the 10–${10}^3$$M_{\odot }$ range for medium-sized black holes, and the hyper-massive range beyond [35]. It has recently been suggested that the outer Solar System harbors a PBH of mass $\sim {10}^{-6}{M}_{\odot }$ [45].

A curious reader will then wonder why PBHs can provide stringent constraints for the NMC parameter compared to astrophysical BHs of around 10–10²$M_{\odot }$. For a gravitating object of mass M and size (or radius) L, two parameters $(ϵ,\mathcal{K})$ serve as useful indicators to categorize gravitational fields [8,46]. $ϵ$ is a dimensionless parameter, while $\mathcal{K}$ is the square root of the Kretschmann scalar:

$$ϵ\sim GM/\left(L{c}^2\right),\mathcal{K}={\left(R_{\mu \nu \sigma \rho }{R}^{\mu \nu \sigma \rho }\right)}^{1/2},$$

where $R_{abcd}$ is the Riemann curvature tensor. Thus, $ϵ$ indicates the gravitational strength, helping to distinguish between the weak and strong gravity regimes. For instance, the Solar System, characterized by very small $ϵ$ values, clearly operates within the weak gravity regime, while BHs, where $ϵ$ approaches or equals one near the event horizon, imply a strong gravity regime. Using the definition of the tidal tensor ${\Phi }_{\mu \nu }\equiv R_{\mu 0\nu 0}$, we see that the Kretschmann scalar K measures the tidal intensity. The Kretschmann scalar ($\mathcal{K}$) remains finite everywhere outside the event horizon of a BH. Specifically, $\mathcal{K}\propto L^{-2}$ at the event horizon of a Schwarzschild BH. For a solar mass BH, $\mathcal{K}\sim {10}^{-6}{\mathrm{m}}^{-2}$, while for a PBH of ${10}^{-3} M_{\odot }$, $\mathcal{K}\sim 1{\mathrm{m}}^{-2}$. This implies that smaller BHs exhibit increasingly strong curvature near their horizons. Hence, NMC will have a significant impact on PBHs. In other words, PBHs can provide stringent constraints for the NMC parameter.

PBHs, as potential dark matter candidates, represent an intriguing class of cosmological BHs that emerge from density fluctuations in the early Universe. One of the distinguishing characteristics of PBHs is that they may not be stationary or asymptotically flat.1 This differentiates them from the isolated BH solutions in general relativity, such as the Schwarzschild or Kerr black holes, defined under stationarity and asymptotic flatness. Instead, PBHs could be dynamic and evolving, interacting with the expanding Universe and other matter, influenced by accretion and possibly emitting Hawking radiation [35,47].

This implies that PBHs do not necessarily conform to the no-hair theorem, which states that black holes in equilibrium states are fully described by just three externally observable parameters: mass, electric charge, and angular momentum. The theorem presumes a stationary and isolated black hole, conditions not typically applicable to cosmological black holes like PBHs. In cosmological contexts, black holes could have additional characteristics derived from their interactions and evolution in a non-flat space-time [48].

The possible deviation from the no-hair theorem in cosmological settings like those involving PBHs suggests complexities in their properties and behaviors, reflecting interactions with the cosmic environment and potentially making them distinct in terms of observational signatures from black holes that are purely described by general relativity. Sultana and Dyer (SD) obtained an exact spherically symmetric black hole solution in expanding cosmological space-time [37]. An SD black hole is asymptotically Friedmann–Lemaitre–Robertson–Walker (FLRW) [49,50]. Thus, the SD black hole can mimic a PBH in cosmological scenarios [50].

As mentioned earlier, we study the propagation of photons that are non-minimally coupled to gravity. We show that the two dispersion relations corresponding to the two polarizations differ from Schwarzschild and Kerr (photon confined in equatorial plane) [cf. Equation (34)]. In the case of Schwarzschild and Kerr, the two dispersions are quadratic, and the modifications to the dispersion relation occur in the $p_{\left(3\right)}$ component of the momentum. However, in the case of Sultana–Dyer, the modification to the dispersion relation [cf. Equations (44), (50), and (51)] occurs in all the components of the momentum. Further, one of the dispersion relations is quadratic, and the other is quartic. Interestingly, the quartic dispersion relation reduces to two quadratic dispersion relations for small values of $\tilde{\lambda }:=\lambda /r_{\mathrm{H}}^2$. We show that the radius of photon sphere $\left(r_0\right)$ and the corresponding value of impact parameter $\left(b_0\right)$ are different in SD and Schwarzschild space-times for a fixed value of $\tilde{\lambda }$. Even these values differ for different dispersion relations in the same space-time.

Then, from the dispersion relations, we derive the expressions for deflection angle $(d\varphi /dr)$ and evaluate total deflection angle $(\Delta \varphi )$ for every mode of polarization in a particular space-time (SD or Schwarzschild) and compare the results. We show that $\Delta \varphi$ behaves differently as a function of r, the radial distance from the black hole in the SD and Schwarzschild cases. We compute the total deflection angle for non-minimally coupled photons near Schwarzschild and Sultana–Dyer black holes and show that both these black holes have similar signatures with regard to the total deflection angle as well as the radius of the photon sphere. Interestingly, for a PBH of mass $M={10}^{-5}{M}_{\odot }$, the photon sphere will not be formed for one mode. Thus, the total deflection angle $\Delta \varphi$ of NMC photons near Schwarzschild and SD space-times will have a contribution only from the other modes. In other words, the photons forming the photon sphere will be highly polarized, potentially leading to observable implications.

This paper is organized as follows: In Section 2, we discuss the non-minimal coupling model of the electromagnetic fields with gravity and briefly discuss the procedure to obtain the photon dispersion relation in arbitrary 4D space-time. In Section 3, we briefly discuss the properties of the Sultana–Dyer black hole and the conserved quantities in this space-time. In Section 4, we obtain the modified dispersion relations in the local inertial frame for the Schwarzschild and Sultana–Dyer black holes. In Section 5, we evaluate the expressions for the deflection angles and total deflection angles for all polarization modes as a function of distance from the Schwarzschild (two polarization modes) and Sultana–Dyer (three polarization modes) black holes. We also obtain the constraint on the non-minimal coupling parameter $\lambda$. In Section 6, we obtain the quantitative difference in the total deflection angle for the Sultana–Dyer black hole from the Schwarzschild. In Section 7, we conclude by discussing the implications of our work for future observations. Appendix A, Appendix B and Appendix C contain calculation details.

In this work, we use the $(-,+,+,+)$ signature for the 4D space-time metric. Greek alphabets denote the four-dimensional space-time coordinates, and Latin alphabets denote the three-dimensional spatial coordinates.

2. The Model

The most general action of non-minimal coupling of electromagnetic (EM) fields [22] is

$$\begin{array}{c}\hfill {\mathcal{S}}_{NC}=\int d^{4}x\sqrt{-g}\left[\frac{R}{\kappa }-\frac{1}{4}{F}_{\mu \nu }{F}^{\mu \nu }+{\chi }^{\mu \nu \alpha \beta }{F}_{\mu \nu }{F}_{\alpha \beta }\right]\end{array}$$

(1)

where

$$\begin{array}{c}\hfill {\chi }^{\mu \nu \alpha \beta }=\frac{q_{1}R}{2}\left(g^{\mu \alpha }{g}^{\nu \beta }-g^{\mu \beta }{g}^{\nu \alpha }\right)+\frac{q_2}{2}\left(R^{\mu \alpha }{g}^{\nu \beta }-R^{\mu \beta }{g}^{\nu \alpha }+R^{\nu \beta }{g}^{\mu \alpha }-R^{\nu \alpha }{g}^{\mu \beta }\right)+\frac{q_3}{2}{R}^{\mu \nu \alpha \beta }.\end{array}$$

(2)

and consists of coupling between the EM field tensor, the Riemann and Ricci tensors, and the Ricci scalar. $q_1,q_2$, and $q_3$ are the coupling parameters. The above action is invariant under CPT and general coordinate transformations; however, it violates Einstein’s equivalence principle [38]. In our work, we assume $q_1\simeq q_2\simeq q_3\equiv \lambda$.

In Ref. [14], Drummond and Hathrell used Schwinger and de Witt’s effective action approach to obtain the non-minimal coupling terms. To obtain the effective action, one separates the degrees of freedom into two parts—heavy (h) and light (l)—corresponding to their field modes in the momentum space. The influence of heavy fields on light-particle scattering at low energies leads to the following effective Lagrangian:

$$exp\left[i\int d^{4}x{\mathcal{L}}_{\mathrm{eff}}(\ell )\right]=\int \mathcal{D}hexp\left[i\int d^{4}x\mathcal{L}(\ell ,h)\right],$$

(3)

where $\mathcal{D}$ is the measure in the field space and integration is over the heavy field. It is important to note that this is a low-energy effective action obtained by integrating out the heavy fields. In the case of Drummond and Hathrell, this corresponds to photon energies that are small compared to the electron mass, i.e., $\hslash \omega \ll m_e{c}^2$. In this limit, they found that the non-minimal coupling parameters are of the same order, i.e., $q_1\simeq q_2\simeq q_3\equiv \lambda$ [14]. It is important to note that Drummond and Hathrell’s analysis is suitable for electromagnetic waves with energies much less than $0.5\mathrm{MeV}$, and their analysis is not trustable for high-energy photons (hard X-rays).

Varying the action (1) with respect to the gauge field $A_{\mu }$ and taking the three coupling parameters to be the same ($q_1=q_2=q_3=\lambda$), we obtain:

$$\begin{array}{cc}\hfill (1-4\lambda R){\nabla }_{\nu }{F}^{\mu \nu }=& 6\lambda \left({\nabla }_{\nu }R\right)F^{\mu \nu }-8\lambda \left({\nabla }_{\alpha }{R^{\mu }}_{\beta }\right)F^{\alpha \beta }\hfill \\ \hfill & +4\lambda \left[{R^{\mu }}_{\alpha }\left({\nabla }_{\nu }{F}^{\alpha \nu }\right)+{R^{\nu }}_{\alpha }\left({\nabla }_{\nu }{F}^{\alpha \mu }\right)\right]+2\lambda {R^{\mu \nu }}_{\alpha \beta }\left({\nabla }_{\nu }{F}^{\alpha \beta }\right).\hfill \end{array}$$

(4)

The RHS of the above equation is a coordinate-dependent quantity and leads to a modified dispersion relation. In the case of Maxwell’s theory, we have the same dispersion relation ($p^{\mu }{p}_{\mu }=0$) for both polarization modes. The first two terms in the RHS act as the mass term, while the last two terms in the RHS modify the kinetic term. As the coupling terms are linearly related to EM fields, the non-minimal coupling leads to mixing of the two polarization modes.

For isolated, static black holes, like the Schwarzschild (de Sitter) or Kerr (de Sitter) metrics, that satisfy $R_{\mu \nu }\propto g_{\mu \nu }$, only the last term in the RHS of the above expression is non-zero. However, for black holes in an expanding universe, like the Sultana–Dyer metric, $R_{\mu \nu }\ne \Lambda g_{\mu \nu }$. Hence, we retain all terms in the RHS of the above expression. As mentioned in the Introduction, since $\mathcal{K}\propto L^{-2}$ at the event horizon of a Schwarzschild BH, the NMC term will have significant effect on a PBH.

Photon Dispersion Relation

To obtain the photon trajectory, it is advantageous to use the tetrad basis of four linearly independent vector fields (${e^{\mu }}_{\left(\nu \right)}$ where $\mu =0,1,2,3$). The enclosure in the parentheses distinguishes tetrad indices from the tensor indices. The tetrads ${e^{\mu }}_{\left(\nu \right)}$ or their inverse ${e_{\mu }}^{\left(\nu \right)}$ satisfy the relation, ${e^{\mu }}_{\left(\alpha \right)}{e^{\nu }}_{\left(\beta \right)}{g}_{\mu \nu }={\tilde{\eta }}_{\left(\alpha \right)\left(\beta \right)}$. As in the literature, we assume that ${e^{\mu }}_{\left(\nu \right)}$ are orthonormal, and hence, ${\tilde{\eta }}_{\left(\alpha \right)\left(\beta \right)}$ represents a metric corresponding to flat space-time with the diagonal elements $\left(-1,+1,+1,+1\right)$, and $g_{\mu \nu }$ denotes the metric tensor describing an arbitrary curved space-time [51]. The tetrads and their inverse are related as follows: ${e^{\mu }}_{\left(\alpha \right)}{e_{\nu }}^{\left(\alpha \right)}={\delta }_{\nu }^{\mu }$, where ${\delta }_{\nu }^{\mu }$ is the Kronecker delta function. If $p_{\left(\mu \right)}$ corresponds to the photon momentum in the local inertial frame, this is related to momentum in the non-inertial frame, $p_{\nu }$, by the relation $p_{\left(\nu \right)}={e^{\mu }}_{\left(\nu \right)}{p}_{\mu }$.

In the case of time-dependent black holes, we consider the variations of the curvature ($\mathcal{K})$ along the radial coordinate, and the time (T) is long compared to the EM waves’ reduced wavelength and period, i.e.,

$$\mathcal{K}\gg \lambda =1/k,T\gg 1/\omega .$$

Under the Eikonal approximation, we can locally treat the EM waves as planar and monochromatic [38]:

$$\begin{array}{c}\hfill {\nabla }_{\left(\mu \right)}{F}^{\left(\mu \right)\left(\nu \right)}=p_{\left(\mu \right)}{F}^{\left(\mu \right)\left(\nu \right)}.\end{array}$$

(5)

Thus, in the local inertial frame, the Bianchi identity of the EM field tensor and Equation (4) reduces to

$$\begin{array}{c}{p}_{\left(\alpha \right)}{F}_{\left(\mu \right)\left(\nu \right)}+p_{\left(\mu \right)}{F}_{\left(\nu \right)\left(\alpha \right)}+p_{\left(\nu \right)}{F}_{\left(\alpha \right)\left(\mu \right)}=0\hfill \end{array}$$

(6)

and

$$\begin{array}{cc}\hfill & (1-4\lambda R)p_{\left(\nu \right)}{F}^{\left(\mu \right)\left(\nu \right)}=2\lambda p_{\left(\nu \right)}{F}^{\left(\alpha \right)\left(\beta \right)}{R^{\left(\mu \right)\left(\nu \right)}}_{\left(\alpha \right)\left(\beta \right)}-8\lambda F^{\left(\alpha \right)\left(\beta \right)}{\nabla }_{\left(\alpha \right)}{R^{\left(\mu \right)}}_{\left(\beta \right)}\hfill \\ \hfill & +4\lambda \left[p_{\left(\nu \right)}{F}^{\left(\alpha \right)\left(\nu \right)}{R^{\left(\mu \right)}}_{\left(\alpha \right)}+p_{\left(\nu \right)}{F}^{\left(\alpha \right)\left(\mu \right)}{R^{\left(\nu \right)}}_{\left(\alpha \right)}\right]+6\lambda F^{\left(\mu \right)\left(\nu \right)}{\nabla }_{\left(\nu \right)}R\hfill \end{array}$$

(7)

Note that the second and the last terms in RHS are independent of the 4-momentum, $p_{\left(\nu \right)}$. For high-momentum photons, the contribution of these terms can be neglected compared to the other two terms that are linear in order. Thus, the above expression reduces to

$$\begin{array}{c}\hfill (1-4\lambda R)p_{\left(\nu \right)}{F}^{\left(\mu \right)\left(\nu \right)}\simeq 2\lambda {R^{\left(\mu \right)\left(\nu \right)}}_{\left(\alpha \right)\left(\beta \right)}\left(p_{\left(\nu \right)}{F}^{\left(\alpha \right)\left(\beta \right)}\right)+4\lambda \left[{R^{\left(\mu \right)}}_{\left(\alpha \right)}\left(p_{\left(\nu \right)}{F}^{\left(\alpha \right)\left(\nu \right)}\right)+{R^{\left(\nu \right)}}_{\left(\alpha \right)}\left(p_{\left(\nu \right)}{F}^{\left(\alpha \right)\left(\mu \right)}\right)\right]\end{array}$$

(8)

Setting the space-time indices $(\mu ,\nu )$ to 3-space index $(j,k)$, respectively, and setting $\alpha =0$ (the time index), the Bianchi identity in the local inertial frame (6) becomes

$$\begin{array}{c}\hfill p_{\left(0\right)}{F}_{\left(k\right)\left(j\right)}=p_{\left(k\right)}{F}_{\left(0\right)\left(j\right)}-p_{\left(j\right)}{F}_{\left(0\right)\left(k\right)}\end{array}$$

(9)

In Equation (8), we split the dummy index into time (0) and spatial parts (k), and fixing the space-time index $\mu$ to the 3-space index j and combining Equation (9) with them leads to the respective equations:

$$\begin{array}{cc}\hfill & [(1-4\lambda R)p_{\left(k\right)}{p}^{\left(0\right)}-4\lambda \left({R^{\left(0\right)}}_{\left(\alpha \right)}{p}_{\left(k\right)}{p}^{\left(\alpha \right)}-{R^{\left(0\right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}^{\left(\nu \right)}-{R^{\left(\nu \right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}^{\left(0\right)}\right)\hfill \\ \hfill & -4\lambda {R^{\left(0\right)\left(\nu \right)\left(\alpha \right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}_{\left(\alpha \right)}]F^{\left(k\right)\left(0\right)}=0\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & [(1-4\lambda R)\left(p_{\left(\nu \right)}{p}^{\left(\nu \right)}{\delta }_{\left(k\right)}^{\left(j\right)}-p_{\left(k\right)}{p}^{\left(j\right)}\right)+4\lambda (R^{\left(j\right)\left(\alpha \right)}{p}_{\left(k\right)}{p}_{\left(\alpha \right)}+R^{\left(\nu \right)\left(\alpha \right)}{p}_{\left(\nu \right)}{p}_{\left(\alpha \right)}{\delta }_{\left(k\right)}^{\left(j\right)}-{R^{\left(j\right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}^{\left(\nu \right)}\hfill \\ \hfill & -{R^{\left(\nu \right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}^{\left(j\right)})+4\lambda {R^{\left(j\right)\left(\nu \right)\left(\alpha \right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}_{\left(\alpha \right)}]F^{\left(k\right)\left(0\right)}=0\hfill \end{array}$$

(11)

Combining Equations (9) and (10), this leads to the following equation of motion:

$$\begin{array}{cc}\hfill & [(1-4\lambda R)p_{\left(\nu \right)}{p}^{\left(\nu \right)}{\delta }_{\left(k\right)}^{\left(j\right)}+4\lambda (R^{\left(j\right)\left(\alpha \right)}{p}_{\left(k\right)}{p}_{\left(\alpha \right)}+R^{\left(\nu \right)\left(\alpha \right)}{p}_{\left(\nu \right)}{p}_{\left(\alpha \right)}{\delta }_{\left(k\right)}^{\left(j\right)}-{R^{\left(j\right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}^{\left(\nu \right)}-{R^{\left(\nu \right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}^{\left(j\right)}\hfill \\ \hfill & +{{ϵ}^{\left(j\right)}}_{\left(k\right)})+\frac{p^{\left(j\right)}}{p_{\left(0\right)}}4\lambda ({R^{\left(0\right)}}_{\left(\alpha \right)}{p}_{\left(k\right)}{p}^{\left(\alpha \right)}-{R^{\left(0\right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}^{\left(\nu \right)}-{R^{\left(\nu \right)}}_{\left(k\right)}{p}_{\left(\nu \right)}{p}^{\left(0\right)}+{{ϵ}^{\left(0\right)}}_{\left(k\right)}\left)\right]F^{\left(k\right)\left(0\right)}=0\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill {{ϵ}^{\left(\alpha \right)}}_{\left(\beta \right)}& \equiv {R^{\left(\alpha \right)\left(\mu \right)\left(\nu \right)}}_{\left(\beta \right)}{p}_{\left(\mu \right)}{p}_{\left(\nu \right)}.\hfill \end{array}$$

(13)

The above equation of motion is for an arbitrary space-time. By choosing a coordinate system, it is always possible to obtain the dynamical and the constraint equations. Interestingly, we see that the terms containing $p^{\left(j\right)}/p^{\left(0\right)}$ can potentially lead to higher-order dispersion relations. As we will see, this is the case for the Sultana–Dyer black hole. Thus, for different space-times, the above equation of motion (12) will yield different dispersion relations and potentially provide constraints on $\lambda$ for that particular space-time.

The constraints on $\lambda$ are obtained in the literature by considering static black hole space-times, like Schwarzschild and slowly rotating Kerr [14,38,52]. In this work, we obtain constraints on $\lambda$ by considering a spherically symmetric black hole in cosmological space-time, commonly referred to as the Sultana–Dyer (SD) metric [37]. To our knowledge, such an analysis has not been performed, and we show that this provides a stringent constraint on the non-minimal coupling parameter $\lambda$, specifically for PBHs. We also show that the radius of the photon sphere and the corresponding critical impact parameter have similar values in both SD and Schwarzschild space-times for a fixed value of $\lambda$. We discuss the implications on these quantities for PBHs also.

3. Sultana–Dyer Black Hole

Sultana and Dyer obtained an exact spherically symmetric black hole solution in expanding cosmological space-time [37]:

$$\begin{array}{c}\hfill d{s}^2={\left(\frac{\eta }{{\eta }_0}\right)}^4\left[-\left(1-\frac{2GM}{r}\right)d{\eta }^2+\frac{4GM}{r}d\eta dr+\left(1+\frac{2GM}{r}\right)d{r}^2+r^{2}d{\Omega }^2\right]\end{array}$$

(14)

where M is the mass of the non-rotating black hole and ${\eta }_0$ is the conformal time in the current epoch, $t_0\sim 1/H_0$, and $H_0$ is the Hubble constant. The conformal time $\eta$ is related to the comoving or cosmic time t via the relation $dt=d\eta a\left(\eta \right)$, where the conformal scale factor for the above metric is $a\left(\eta \right)={\left(\eta /{\eta }_0\right)}^2$. Integrating the relation connecting conformal time and cosmic time, we obtain $t={\eta }^3/\left(3{\eta }_0^2\right)$, and $t_0={\eta }_0/3$. We list below some of the properties of the Sultana–Dyer space-time:

• The above line element corresponds to a black hole of mass M in a spatially flat FLRW universe with scale factor $a\left(t\right)\propto t^{2/3}$. This corresponds to black holes in the matter-dominated epoch.
• Sultana–Dyer is sourced by two non-interacting perfect fluids—null dust and normal dust. The stress–energy tensor is $T_{\mu \nu }=T_{\mu \nu }^{\left(1\right)}+T_{\mu \nu }^{\left(2\right)}$, where $T_{\mu \nu }^{\left(1\right)}={\rho }_0{u}_{\mu }{u}_{\nu }$ describes the normal dust with density ${\rho }_0$ and $u^{\alpha }{u}_{\alpha }=-1$ and $T_{\mu \nu }^{\left(2\right)}={\rho }_n{k}_{\mu }{k}_{\nu }$ describes a null dust with density ${\rho }_n$ and $k^{\alpha }{k}_{\alpha }=0$.
• The Kretschmann scalar for the line element (14) is

  $$\begin{array}{c}\hfill R^{\mu \nu \alpha \beta }{R}_{\mu \nu \alpha \beta }\equiv \mathcal{K}=48{\eta }_0^8\left(\frac{8M^2}{r^4{\eta }^{10}}+\frac{M^2}{r^6{\eta }^8}-\frac{4M(4M+r)}{r^3{\eta }^{11}}+\frac{5{(2M+r)}^2}{r^2{\eta }^{12}}\right).\end{array}$$

  (15)
  It implies that curvature singularities occur at $\eta =0$ and $r=0$. The singularity at $\eta =0$ is spacelike for $r>2GM\equiv r_{\mathrm{H}}$, timelike for $r<r_{\mathrm{H}}$, and null for $r=r_{\mathrm{H}}$ [53]. The singularity at $r=0$ is spacelike and surrounded by the event horizon.
• The energy density of the dust is positive only in the region

  $$\eta <\frac{r(r+r_{\mathrm{H}})}{r_{\mathrm{H}}}$$

  (16)
  At $r=r_{\mathrm{H}}$, the energy conditions for $\eta <2r_{\mathrm{H}}$ are satisfied everywhere. In other words, after this time $\eta$, those particles closest to the event horizon become superluminal [37]. As we will see, this condition translates to a constraint on $\lambda$.
• To understand the properties of the horizons, we rewrite the time coordinate $\eta$ as

  $$\begin{array}{c}\hfill \eta =\overline{t}+2Mln\left(\frac{r}{2GM}-1\right)\end{array}$$

  (17)

  in the line element (14). This leads to

  $$\begin{array}{c}\hfill d{\overline{s}}^2=a{(\overline{t},r)}^2\left[-\left(1-\frac{2GM}{r}\right)d{\overline{t}}^2+{\left(1-\frac{2GM}{r}\right)}^{-1}d{r}^2+r^{2}d{\Omega }^2\right]\end{array}$$

  (18)
  From the above line element, it is evident that the Sultana–Dyer metric is a black hole obtained by the conformal transformation of the Schwarzschild black hole. As the conformal transformation preserves the causal structure, $r=2GM\equiv r_{\mathrm{H}}$ remains the event horizon. Interestingly, since the line element is conformally invariant, there exists a conformal Killing vector $\zeta ={\partial }_t$, which is the Killing vector on Schwarzschild space-time and satisfies the following relation [54],

  $$\begin{array}{c}\hfill {\mathcal{L}}_{\zeta }{g}_{\mu \nu }=\left({\mathcal{L}}_{\zeta }ln{a}^2\right)g_{\mu \nu }\end{array}$$

  (19)

  where ${\mathcal{L}}_{\zeta }ln{a}^2=4/\eta$. The apparent horizon is given by [49,54]

  $$\begin{array}{cc}\hfill r_1& =-GM+\frac{-\eta +\sqrt{{\eta }^2+24GM\eta +16{\left(GM\right)}^2}}{4}\hfill \end{array}$$

  (20)

  $$\begin{array}{cc}\hfill r_2& =\frac{\eta }{2}\hfill \end{array}$$

  (21)

  where $r_1<r_2$. From the energy condition (16), it is clear that $r_1<r_2<r_{\mathrm{H}}$, implying that the apparent horizon lies inside the event horizon and asymptotically tends to the event horizon.
• Writing the line element (14) in non-geometrized units leads to

  $$\begin{array}{c}\hfill d{s}^2={\left(\frac{\eta }{{\eta }_0}\right)}^4\left[-\left(1-\frac{r_{\mathrm{H}}}{r}\right)c^{2}d{\eta }^2+\frac{2r_{\mathrm{H}}}{r}cd\eta dr+\left(1+\frac{r_{\mathrm{H}}}{r}\right)d{r}^2+r^{2}d{\Omega }^2\right].\end{array}$$

  (22)
  Substituting the following dimensionless variables:

  $$\begin{array}{c}\hfill \tilde{r}=\frac{r}{r_{\mathrm{H}}};\tilde{\eta }\equiv c\eta /r_{\mathrm{H}};{\tilde{\eta }}_0\equiv c{\eta }_0/r_{\mathrm{H}}\end{array}$$

  (23)

  in the Sultana–Dyer metric (22), we have

  $$d{s}^2=r_{\mathrm{H}}^2{\tilde{\eta }}^4\left[-\left(1-\frac{1}{\tilde{r}}\right)d{\tilde{\eta }}^2+\frac{2}{\tilde{r}}d\tilde{\eta }d\tilde{r}+\left(1+\frac{1}{\tilde{r}}\right)d{\tilde{r}}^2+{\tilde{r}}^{2}d{\Omega }^2\right]=r_{\mathrm{H}}^{2}d{\tilde{s}}^2$$

  (24)

  where

  $$\begin{array}{ccc}\hfill d{\tilde{s}}^2& =& {\tilde{\eta }}^4\left[-\left(1-\frac{1}{\tilde{r}}\right)d{\tilde{\eta }}^2+\frac{2}{\tilde{r}}d\tilde{\eta }d\tilde{r}+\left(1+\frac{1}{\tilde{r}}\right)d{\tilde{r}}^2+{\tilde{r}}^{2}d{\Omega }^2\right]\hfill \end{array}$$

  (25)

In the rest of this work, we use the dimensionless line element $d\tilde{s}$ defined in Equation (25). This choice is suitable because the affine parameter ($\tau$) and conserved quantities are dimensionless.

Conserved Quantities from Symmetries of the Metric

Although the Sultana–Dyer metric (25) is time-dependent, the space-time has conserved quantities. Besides the spherical symmetry, the metric is invariant under conformal transformations. Taking into account of the conformal symmetry, the following quantity is conserved with regard to dimensionless affine parameter $\tau$ [37,53]:

$$\begin{array}{cc}\hfill p_0\equiv -{\tilde{E}}_{\mathrm{SD}}& ={\tilde{\eta }}^4\left(-\left(1-\frac{1}{\tilde{r}}\right)\frac{d\tilde{\eta }}{d\tau }+\frac{1}{\tilde{r}}\frac{d\tilde{r}}{d\tau }\right).\hfill \end{array}$$

(26)

Due to the azimuthal symmetry, the following quantity is conserved [37]:

$$\begin{array}{c}\hfill p_3\equiv \tilde{L}={\tilde{\eta }}^4{\tilde{r}}^2\frac{d\varphi }{d\tau }.\end{array}$$

(27)

In Section 5, we show that the dispersion relation depends on the value of $b=\tilde{L}/\tilde{E}$, which is a dimensionless impact parameter. In the rest of this work, we obtain the change in photon propagation in the Sultana–Dyer space-time due to non-minimal coupling (1). We also compare our results with Schwarzschild space-time.

4. Modified Dispersion Relations

In this section, from the equation of motion (12), we obtain the modified photon dispersion relation for the non-minimally coupled electromagnetic fields. We also show that the modification in the dispersion relation will be significant near strongly gravitating objects like black holes. Interestingly, we show that the nature of the dispersion relation is different for time-independent (like Schwarzschild, Kerr) and time-dependent black hole (like Sultana–Dyer) space-times.

To derive the photon dispersion relation, we fix the photon momentum: $p^{\left(\mu \right)}=(p^{\left(0\right)},p^{\left(1\right)},0,p^{\left(3\right)})$—confined in the orbital plane of the gravitating object. We choose a more generic electric field form than Ref. [38]. Specifically, we choose $E^{\left(i\right)}=\left[E^{\left(1\right)},E^{\left(2\right)},E^{\left(3\right)}\right]$.

4.1. Time-Independent Black Hole Space-Times

For the Schwarzschild space-time,

$$\begin{array}{c}\hfill d{s}^2=-\left(1-\frac{r_{\mathrm{H}}}{r}\right)d{t}^2+{\left(1-\frac{r_{\mathrm{H}}}{r}\right)}^{-1}d{r}^2+r^{2}d{\Omega }^2,\end{array}$$

(28)

and using dimensionless coordinates $\tilde{r}=r/r_{\mathrm{H}},\tilde{t}=ct/r_{\mathrm{H}}$, we obtain,

$$\begin{array}{c}\hfill d{s}^2=r_{\mathrm{H}}^{2}d{\tilde{s}}_{\mathrm{Sch}}^2\end{array}$$

(29)

where

$$\begin{array}{c}\hfill d{\tilde{s}}_{\mathrm{Sch}}^2=\left[-\left(1-\frac{1}{\tilde{r}}\right)d{\tilde{t}}^2+{\left(1-\frac{1}{\tilde{r}}\right)}^{-1}d{\tilde{r}}^2+{\tilde{r}}^{2}d{\Omega }^2\right].\end{array}$$

(30)

Since the line element is independent of $\tilde{t}$ and $\varphi$, we have the following invariant quantities (with regard to $\tau$):

$$\begin{array}{c}\hfill {\tilde{E}}_{\mathrm{Sch}}=-\left(1-\frac{1}{\tilde{r}}\right)\frac{d\tilde{t}}{d\tau };{\tilde{L}}_{\mathrm{Sch}}={\tilde{r}}^2\frac{d\varphi }{d\tau }.\end{array}$$

(31)

The equation of motion (12) for the electric field $E^{\left(i\right)}=\left[E^{\left(1\right)},E^{\left(2\right)},E^{\left(3\right)}\right]$ in the line element (30) are:

$$\begin{array}{c}\hfill {{ϵ}^{\left(i\right)}}_{\left(j\right)}{E}^{\left(j\right)}=0.\end{array}$$

(32)

where the polarization tensor ${{ϵ}^{\left(i\right)}}_{\left(j\right)}$ is

$$\begin{array}{c}\hfill {{ϵ}^{\left(i\right)}}_{\left(j\right)}=\left[\begin{array}{ccc}-p_{\left(0\right)}^2+p_{\left(1\right)}^2+p_{\left(3\right)}^2+\frac{2\left(2p_{\left(0\right)}^2-2p_{\left(1\right)}^2+p_{\left(3\right)}^2\right)\lambda }{r^3}& 0& 0\\ 0& -p_{\left(0\right)}^2+p_{\left(1\right)}^2+p_{\left(3\right)}^2+\frac{2\left(-p_{\left(0\right)}^2+p_{\left(1\right)}^2-2p_{\left(3\right)}^2\right)\lambda }{r^3}& 0\\ -\frac{6p_{\left(1\right)}{p}_{\left(3\right)}\lambda }{r^3}& 0& -p_{\left(0\right)}^2+p_{\left(1\right)}^2+p_{\left(3\right)}^2+\frac{2\left(-p_{\left(0\right)}^2+p_{\left(1\right)}^2+p_{\left(3\right)}^2\right)\lambda }{r^3}\end{array}\right]\end{array}$$

(33)

For the Schwarzschild space-time, the Ricci tensor is zero; hence, those terms in the LHS of Equation (12) vanish. In order for the above Equation (32) to satisfy for arbitrary values of $[E^{\left(1\right)},E^{\left(2\right)},E^{\left(3\right)}]$, the determinant of the polarization tensor ${{ϵ}^{\left(i\right)}}_{\left(j\right)}$ must vanish. Demanding this leads to the following dispersion relation

$$\begin{array}{cc}\hfill & p^2={\mathcal{C}}_{\pm }{p}_{\left(3\right)}^2,p^2=0\hfill \end{array}$$

(34)

where

$$\begin{array}{c}{\mathcal{C}}_{+}=\frac{6\tilde{\lambda }}{2\tilde{\lambda }+{\tilde{r}}^3};{\mathcal{C}}_{-}=\frac{6\tilde{\lambda }}{4\tilde{\lambda }-{\tilde{r}}^3};\tilde{\lambda }\equiv \lambda /r_{\mathrm{H}}^2.\hfill \end{array}$$

(35)

Note that $\tilde{\lambda }$ is the dimensionless NMC parameter. It is important to note that the above dispersion relation differs from the one derived in Ref. [38]. From the above expression (34), we infer that one of the dispersion relations is the same as the dispersion relation for minimally coupled photons. The modified photon dispersion relations are quadratic with $\tilde{r},\tilde{\lambda }$- or $r,\lambda$-dependent corrections. Interestingly, the photon dispersion relation in the tetrad frame constructed in Kerr space-time (photons confined in the equatorial plane) is identical to Equation (34). Appendix A contains the detailed calculation for the Kerr space-time in the orthonormal basis [55]. Thus, the modified dispersion relation remains quadratic for the time-independent black hole space-times, like Schwarzschild and Kerr. In Ref. [52], we obtained the explicit form of the modified dispersion relation in a slowly rotating Kerr BH. There we discussed the shadow formation by NMC photons in Schwarzschild and slowly rotating Kerr BHs and their impact on BH observations.

4.2. Sultana–Dyer Black Hole

In this section, we show that the modified dispersion relation of the photons does not remain quadratic in the Sultana–Dyer black hole. We show it provides a key distinguishing feature between time-independent and Sultana–Dyer black hole space-times.

To do that, we construct a local inertial frame corresponding to the Sultana–Dyer metric (25). Appendix B contains the details of the tetrads and the components of the Riemann tensor in the local inertial frame. Unlike the Schwarzschild and Kerr black holes, the Ricci tensor is non-zero for the Sultana–Dyer black hole. Hence, in principle, all terms of Equation (12) will contribute to the dispersion relation.

Substituting the components of the Riemann tensor, Ricci tensor, and scalar in the local frame, as mentioned in (A9), into Equation (12), the equations of motion for the electric field $E^{\left(i\right)}=\left[E^{\left(1\right)},E^{\left(2\right)},E^{\left(3\right)}\right]$ are

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}{M}_{11}& 0& M_{13}\\ 0& M_{22}& 0\\ M_{31}& 0& M_{33}\end{array}\right]\left[\begin{array}{c}{E}^{\left(1\right)}\\ E^{\left(2\right)}\\ E^{\left(3\right)}\end{array}\right]=0\end{array}$$

(36)

where

$$\begin{array}{cc}\hfill M_{11}& =p_{\left(0\right)}^2\left(\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}-\frac{8{\tilde{\eta }}_0^4\tilde{\lambda }(3\tilde{r}+5)}{{\tilde{\eta }}^5{\tilde{r}}^2(\tilde{r}+1)}+\frac{88{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}-1\right)+\frac{p_{\left(1\right)}{p}_{\left(3\right)}^2}{p_{\left(0\right)}}\frac{12{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)}-p_{\left(0\right)}{p}_{\left(1\right)}\frac{32{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)}\hfill \\ \hfill & +p_{\left(1\right)}^2\left(-\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}+\frac{8{\tilde{\eta }}_0^4\tilde{\lambda }(7\tilde{r}+5)}{{\tilde{\eta }}^5{\tilde{r}}^2(\tilde{r}+1)}+\frac{8{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}+1\right)+p_{\left(3\right)}^2\left(\frac{2{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}+\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }(4\tilde{r}+7)}{{\tilde{\eta }}^5{\tilde{r}}^2(\tilde{r}+1)}-\frac{64{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}+1\right)\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill M_{13}& =-\frac{p_{\left(1\right)}^2{p}_{\left(3\right)}}{p_{\left(0\right)}}\frac{{12}^4\tilde{\lambda }}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)}-p_{\left(0\right)}{p}_{\left(3\right)}\frac{12{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)}+p_{\left(1\right)}{p}_{\left(3\right)}\frac{12{\tilde{\eta }}_0^4\tilde{\lambda }\left(2\tilde{\eta }+6{(\tilde{r}+1)}^2\right)}{{\tilde{\eta }}^6\tilde{r}(\tilde{r}+1)}\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill M_{22}& =p_{\left(0\right)}^2\left(-\frac{2{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}-\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }(18\tilde{r}+19)}{{\tilde{\eta }}^5{\tilde{r}}^2(\tilde{r}+1)}+\frac{88{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}-1\right)-p_{\left(0\right)}{p}_{\left(1\right)}\frac{8{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)}\hfill \\ \hfill & +p_{\left(1\right)}^2\left(\frac{2{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}+\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }(20\tilde{r}+19)}{{\tilde{\eta }}^5{\tilde{r}}^2(\tilde{r}+1)}-\frac{64{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}+1\right)+p_{\left(3\right)}^2\left(-\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}+\frac{64{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^5{\tilde{r}}^2}-\frac{64{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}+1\right)\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill M_{31}& =\frac{12{\tilde{\eta }}_0^4\tilde{\lambda }{p}_{\left(3\right)}^3}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)p_{\left(0\right)}}-\frac{12{\tilde{\eta }}_0^4\tilde{\lambda }{p}_{\left(0\right)}{p}_{\left(3\right)}}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)}+\frac{6{\tilde{\eta }}_0^4\tilde{\lambda }{p}_{\left(1\right)}{p}_{\left(3\right)}\left({\tilde{\eta }}^2(-\tilde{r}-1)-2\tilde{\eta }\tilde{r}(2\tilde{r}+3)+12{\left({\tilde{r}}^2+\tilde{r}\right)}^2\right)}{{\tilde{\eta }}^6{\tilde{r}}^3(\tilde{r}+1)}\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill M_{33}& =p_{\left(0\right)}^2\left(-\frac{2{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}-\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }(18\tilde{r}+19)}{{\tilde{\eta }}^5{\tilde{r}}^2(\tilde{r}+1)}+\frac{88{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}-1\right)-\frac{12{\tilde{\eta }}_0^4\tilde{\lambda }{p}_{\left(1\right)}{p}_{\left(3\right)}^2}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)p_{\left(0\right)}}-\frac{8{\tilde{\eta }}_0^4\tilde{\lambda }{p}_{\left(0\right)}{p}_{\left(1\right)}}{{\tilde{\eta }}^5\tilde{r}(\tilde{r}+1)}\hfill \\ \hfill & +p_{\left(1\right)}^2\left(\frac{2{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}+\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }(20\tilde{r}+19)}{{\tilde{\eta }}^5{\tilde{r}}^2(\tilde{r}+1)}-\frac{64{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}+1\right)+p_{\left(3\right)}^2\left(\frac{2{\tilde{\eta }}_0^4\tilde{\lambda }}{{\tilde{\eta }}^4{\tilde{r}}^3}+\frac{4{\tilde{\eta }}_0^4\tilde{\lambda }(10\tilde{r}+7)}{{\tilde{\eta }}^5{\tilde{r}}^2(\tilde{r}+1)}+\frac{8{\tilde{\eta }}_0^4\tilde{\lambda }(\tilde{r}+1)}{{\tilde{\eta }}^6\tilde{r}}+1\right)\hfill \end{array}$$

(41)

To satisfy Equation (36) for arbitrary values of $[E^{\left(1\right)},E^{\left(2\right)},E^{\left(3\right)}]$, the determinant of the first matrix at the LHS of Equation (36) has to be zero, which is nothing but the dispersion relation. The SD BH is a time-dependent BH, so the dispersion relations differ from the Schwarzschild BH. Specifically, we have two sets of dispersion relations—one quadratic and another quartic.

4.2.1. Quadratic Dispersion Relation in an SD BH (SD-I)

The quadratic dispersion relation, which we refer as SD-I, in the local inertial frame is

$$\begin{array}{cc}\hfill f_1{p}_{\left(0\right)}^2+f_2{p}_{\left(1\right)}^2+f_3{p}_{\left(3\right)}^2+f_4{p}_{\left(1\right)}{p}_{\left(0\right)}& =0\hfill \end{array}$$

(42)

where

$$\begin{array}{cc}\hfill f_1(\tilde{r},\tilde{\eta })& =-{\tilde{r}}^3{\tilde{\eta }}^6\left(\tilde{r}+1\right)+\tilde{\lambda }{\tilde{\eta }}_0^4\left[88{\tilde{r}}^2{(\tilde{r}+1)}^2-2{\tilde{\eta }}^2(\tilde{r}+1)-4\tilde{\eta }\tilde{r}(18\tilde{r}+19)\right]\hfill \end{array}$$

(43a)

$$\begin{array}{cc}\hfill f_2(\tilde{r},\tilde{\eta })& ={\tilde{\eta }}^6{\tilde{r}}^3(\tilde{r}+1)+\tilde{\lambda }{\tilde{\eta }}_0^4\left[2{\tilde{\eta }}^2(\tilde{r}+1)+4\tilde{\eta }\tilde{r}(20\tilde{r}+19)-64{\tilde{r}}^2{(\tilde{r}+1)}^2\right]\hfill \end{array}$$

(43b)

$$\begin{array}{cc}\hfill f_3(\tilde{r},\tilde{\eta })& ={\tilde{\eta }}^6{\tilde{r}}^3(\tilde{r}+1)+\tilde{\lambda }{\tilde{\eta }}_0^4\left[-4{\tilde{\eta }}^2(\tilde{r}+1)+64\tilde{\eta }\tilde{r}(\tilde{r}+1)-64{\tilde{r}}^2{(\tilde{r}+1)}^2\right]\hfill \end{array}$$

(43c)

$$\begin{array}{cc}\hfill f_4(\tilde{r},\tilde{\eta })& =-\tilde{\lambda }{\tilde{\eta }}_0^4\left(8\tilde{\eta }{\tilde{r}}^2\right)\hfill \end{array}$$

(43d)

Using the tetrad relations in Equation (A7), we obtain the following dispersion relation in the non-inertial frame:

$$\begin{array}{cc}\hfill f_1^{\prime }{p}_0^2+f_2^{\prime }{p}_1^2+f_3^{\prime }{p}_3^2+f_4^{\prime }{p}_1{p}_0& =0\hfill \end{array}$$

(44)

where

$$\begin{array}{cc}\hfill f_1^{\prime }& =\frac{{\tilde{\eta }}_0^4(\tilde{r}+1)}{{\tilde{\eta }}^4\tilde{r}}\left[-{\tilde{\eta }}^6{\tilde{r}}^3(\tilde{r}+1)+2\tilde{\lambda }{\tilde{\eta }}_0^4\left(-{\tilde{\eta }}^2+(44-36\tilde{\eta }){\tilde{r}}^2-\tilde{\eta }(\tilde{\eta }+38)\tilde{r}+44{\tilde{r}}^4+88{\tilde{r}}^3\right)\right]\hfill \end{array}$$

(45a)

$$\begin{array}{cc}\hfill f_2^{\prime }& =\frac{{\tilde{\eta }}_0^4(\tilde{r}+1)}{{\tilde{\eta }}^4\tilde{r}}\left[{\tilde{\eta }}^6(\tilde{r}-1){\tilde{r}}^3-2\tilde{\lambda }{\tilde{\eta }}_0^4\left({\tilde{\eta }}^2-4(10\tilde{\eta }+11){\tilde{r}}^2-(\tilde{\eta }-38)\tilde{\eta }\tilde{r}+32{\tilde{r}}^4\right)\right]\hfill \end{array}$$

(45b)

$$\begin{array}{cc}\hfill f_3^{\prime }& =\frac{{\tilde{\eta }}_0^4(\tilde{r}+1)}{{\tilde{\eta }}^4{\tilde{r}}^2}\left[{\tilde{\eta }}^6{\tilde{r}}^3-4\tilde{\lambda }{\tilde{\eta }}_0^4\left({\tilde{\eta }}^2-16\tilde{\eta }\tilde{r}+16{\tilde{r}}^3+16{\tilde{r}}^2\right)\right]\hfill \end{array}$$

(45c)

$$\begin{array}{cc}\hfill f_4^{\prime }& =\frac{2{\tilde{\eta }}_0^4(\tilde{r}+1)}{{\tilde{\eta }}^4\tilde{r}}\left[{\tilde{\eta }}^6{\tilde{r}}^3+2\tilde{\lambda }{\tilde{\eta }}_0^4\left({\tilde{\eta }}^2-2(\tilde{\eta }+22){\tilde{r}}^2+38\tilde{\eta }\tilde{r}-44{\tilde{r}}^3\right)\right]\hfill \end{array}$$

(45d)

4.2.2. Quartic Dispersion Relation in an SD BH (SD-II and SD-III)

The quartic dispersion relation in the local inertial frame is

$$\begin{array}{c}\hfill f_5{p}_{\left(0\right)}^4-f_6{p}_{\left(0\right)}{p}_{\left(1\right)}^3-f_7{p}_{\left(1\right)}{p}_{\left(0\right)}^3+f_8{p}_{\left(1\right)}^2{p}_{\left(0\right)}^2+f_9\left(-p_{\left(0\right)}^2+p_{\left(1\right)}^2+p_{\left(3\right)}^2\right)+f_{10}{\left(-p_{\left(0\right)}^2+p_{\left(1\right)}^2+p_{\left(3\right)}^2\right)}^2=0\end{array}$$

(46)

where

$$\begin{array}{cc}{f}_5\hfill & =32{\lambda }^2{\tilde{\eta }}_0^8\tilde{r}\left(6\tilde{r}{(\tilde{r}+1)}^2-\tilde{\eta }(2\tilde{r}+3)\right)\left(3{\tilde{\eta }}^2(\tilde{r}+1)-2\tilde{\eta }\tilde{r}(2\tilde{r}+3)+12{\tilde{r}}^2{(\tilde{r}+1)}^2\right)\hfill \end{array}$$

(47a)

$$\begin{array}{cc}{f}_6\hfill & =64{\lambda }^2{\tilde{\eta }}^2{\tilde{\eta }}_0^8{\tilde{r}}^2\left[4\tilde{r}(4\tilde{r}+3)-3\tilde{\eta }(\tilde{r}+1)\right]\hfill \end{array}$$

(47b)

$$\begin{array}{cc}{f}_7\hfill & =64{\lambda }^2\tilde{\eta }{\tilde{\eta }}_0^8{\tilde{r}}^2\left[3{\tilde{\eta }}^2(\tilde{r}+1)-4\tilde{\eta }\tilde{r}(2\tilde{r}+3)+24{\tilde{r}}^2{(\tilde{r}+1)}^2\right]\hfill \end{array}$$

(47c)

$$\begin{array}{cc}{f}_8\hfill & =192{\lambda }^2\tilde{\eta }{\tilde{\eta }}_0^8\tilde{r}\left[3{\tilde{\eta }}^2{(\tilde{r}+1)}^2-\tilde{\eta }\tilde{r}(\tilde{r}(\tilde{r}(3\tilde{r}+13)+21)+9)+4{\tilde{r}}^2(4\tilde{r}+3){(\tilde{r}+1)}^2\right]\hfill \end{array}$$

(47d)

$$\begin{array}{cc}\hfill f_9& =2\lambda {\tilde{\eta }}_0^4(\tilde{r}+1)p_{\left(0\right)}^2\left[2{\tilde{\eta }}_0^4\lambda \right(16\tilde{\eta }(\tilde{r}+1)(70\tilde{r}+99){\tilde{r}}^3+4{\tilde{\eta }}^2(\tilde{r}(18\tilde{r}-7)-87){\tilde{r}}^2\hfill \\ \hfill & +4{\tilde{\eta }}^3(10\tilde{r}+3)\tilde{r}+3{\tilde{\eta }}^4(\tilde{r}+1)-1488{(\tilde{r}+1)}^3{\tilde{r}}^4)+{\tilde{\eta }}^6{\tilde{r}}^3(3{\tilde{\eta }}^2(\tilde{r}+1)-10\tilde{\eta }\tilde{r}(2\tilde{r}+3)\hfill \\ \hfill & +60{\tilde{r}}^2{(\tilde{r}+1)}^2\left)\right]-8\lambda \tilde{\eta }{\tilde{\eta }}_0^4{p}_{\left(0\right)}{p}_{\left(1\right)}{\tilde{r}}^2(\tilde{r}+1)\left[5{\tilde{\eta }}^6{\tilde{r}}^3-4{\tilde{\eta }}_0^4\lambda \left(-7{\tilde{\eta }}^2-62\tilde{\eta }\tilde{r}+62(\tilde{r}+1){\tilde{r}}^2\right)\right]\hfill \\ \hfill & +2\lambda \tilde{\eta }{\tilde{\eta }}_0^4{p}_{\left(1\right)}^2(\tilde{r}+1)\left[2{\tilde{\eta }}_0^4\lambda \right(4\tilde{\eta }(\tilde{r}(24\tilde{r}+215)+129){\tilde{r}}^2+4{\tilde{\eta }}^2(4\tilde{r}-3)\tilde{r}-3{\tilde{\eta }}^3(\tilde{r}+1)\hfill \\ \hfill & -32(\tilde{r}+1)(4\tilde{r}+3){\tilde{r}}^3)+{\tilde{\eta }}^6{\tilde{r}}^3(10\tilde{r}(4\tilde{r}+3)-3\tilde{\eta }(\tilde{r}+1))]\hfill \end{array}$$

(47e)

$$\begin{array}{cc}\hfill f_{10}& ={(\tilde{r}+1)}^2[{\tilde{\eta }}^{12}{\tilde{r}}^6+4\lambda {\tilde{\eta }}^6{\tilde{\eta }}_0^4{\tilde{r}}^3\left({\tilde{\eta }}^2+14\tilde{\eta }\tilde{r}-14(\tilde{r}+1){\tilde{r}}^2\right)\hfill \\ \hfill & -4{\tilde{\eta }}_0^8{\lambda }^2\left(-{\tilde{\eta }}^4+8\tilde{\eta }(76\tilde{r}+49){\tilde{r}}^3+28{\tilde{\eta }}^2(\tilde{r}-6){\tilde{r}}^2-28{\tilde{\eta }}^3\tilde{r}+128{(\tilde{r}+1)}^2{\tilde{r}}^4\right)]\hfill \end{array}$$

(47f)

It is important to note that $f_5-f_8$ and $f_{10}$ do not include any component of momentum, but $f_9$ does, as all the terms in Equation (46) are quartic in $p_{\left(\mu \right)}$. As the dispersion relation in the local frame is very complicated, the quartic dispersion in the non-inertial frame is mathematically more complicated. To proceed with the rest of the mathematical derivation, we exclude all the terms with ${\tilde{\lambda }}^2$ in Equation (46). This assumption is justified, as we show later that $\tilde{\lambda }<1$. Omitting terms with ${\tilde{\lambda }}^2$ in Equation (46), we split the quartic dispersion relation and obtain two quadratic dispersion relations in the local inertial frame as follows:

$$\begin{array}{cc}\hfill & p_{\left(0\right)}^2\left(\frac{24\tilde{\lambda }(r+1)}{{\tilde{\eta }}_0^{2}r}-\frac{12\tilde{\lambda }}{{\tilde{\eta }}_0{r}^2(r+1)}-\frac{8\tilde{\lambda }}{{\tilde{\eta }}_{0}r(r+1)}+\frac{6\tilde{\lambda }}{r^3}-1\right)+p_{\left(0\right)}{p}_{\left(1\right)}\frac{8\tilde{\lambda }}{{\tilde{\eta }}_{0}r(r+1)}\hfill \\ \hfill & +p_{\left(1\right)}^2\left(\frac{12\tilde{\lambda }}{{\tilde{\eta }}_0{r}^2(r+1)}+\frac{16\tilde{\lambda }}{{\tilde{\eta }}_{0}r(r+1)}-\frac{6\tilde{\lambda }}{r^3}+1\right)+p_{\left(3\right)}^2=0\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill & p_{\left(0\right)}^2\left(\frac{96\tilde{\lambda }(r+1)}{{\tilde{\eta }}_0^{2}r}-\frac{48\tilde{\lambda }}{{\tilde{\eta }}_0{r}^2(r+1)}-\frac{32\tilde{\lambda }}{{\tilde{\eta }}_{0}r(r+1)}-1\right)+p_{\left(0\right)}{p}_{\left(1\right)}\frac{32\tilde{\lambda }}{{\tilde{\eta }}_{0}r(r+1)}\hfill \\ \hfill & +p_{\left(1\right)}^2\left(\frac{48\tilde{\lambda }}{{\tilde{\eta }}_0{r}^2(r+1)}+\frac{64\tilde{\lambda }}{{\tilde{\eta }}_{0}r(r+1)}+1\right)+p_{\left(3\right)}^2=0\hfill \end{array}$$

(49)

Using the tetrads defined in Appendix B, the above two dispersion relations in the non-inertial frame reduce to

$$\begin{array}{ccc}\hfill a_{22}{p}_1^2+a_{12}{p}_1+a_{02}& =& 0\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill a_{23}{p}_1^2+a_{13}{p}_1+a_{03}& =& 0\hfill \end{array}$$

(51)

where

$$\begin{array}{cc}\hfill a_{02}& =-\frac{{\tilde{E}}_{\mathrm{SD}}^2{\tilde{\eta }}_0^2}{{\tilde{\eta }}^4{\tilde{r}}^4}\left[+{\tilde{\eta }}_0^2(\tilde{r}+1){\tilde{r}}^3+\tilde{\lambda }\left(4{\tilde{\eta }}_0(2r+3)r-24{(r+1)}^2{r}^2-6{\tilde{\eta }}_0^2(r+1)\right)\right]+\frac{{\tilde{L}}_{\mathrm{SD}}^2{\tilde{\eta }}_0^4}{{\tilde{\eta }}^4{\tilde{r}}^2}\hfill \end{array}$$

(52a)

$$\begin{array}{cc}\hfill a_{12}& =-\frac{2{\tilde{E}}_{\mathrm{SD}}{\tilde{\eta }}_0^2}{{\tilde{\eta }}^4{\tilde{r}}^4(r+1)}\left[r^4\left({\tilde{\eta }}_0^2-24\tilde{\lambda }\right)+r^3\left({\tilde{\eta }}_0^2-48\tilde{\lambda }\right)-6{\tilde{\eta }}_0^2\tilde{\lambda }-6({\tilde{\eta }}_0-2){\tilde{\eta }}_0\tilde{\lambda }r-4\tilde{\lambda }{r}^2({\tilde{\eta }}_0(\tilde{r}-2)+6\right]\hfill \end{array}$$

(52b)

$$\begin{array}{cc}{a}_{22}\hfill & =\frac{{\tilde{\eta }}_0^2}{{\tilde{\eta }}^4{\tilde{r}}^4{(\tilde{r}+1)}^2}[\left({\tilde{\eta }}_0^2\left({\tilde{r}}^2-1\right)r^4+{\tilde{\eta }}_0^2\left({\tilde{r}}^2-1\right)r^3\right)+\tilde{\lambda }(-6{\tilde{\eta }}_0^2\left({\tilde{r}}^2-1\right)+8r^2\left({\tilde{\eta }}_0\left(2{\tilde{r}}^2+\tilde{r}-1\right)+3\right)\hfill \\ & -6({\tilde{\eta }}_0-2){\tilde{\eta }}_0\left({\tilde{r}}^2-1\right)r+24r^4+48r^3\left)\right]\hfill \end{array}$$

(52c)

$$\begin{array}{cc}{a}_{03}\hfill & =-\frac{{\tilde{E}}_{\mathrm{SD}}^2{\tilde{\eta }}_0^2}{{\tilde{\eta }}^4{\tilde{r}}^3}\left[\tilde{\eta }{0}^2{\tilde{r}}^2(\tilde{r}+1)+16\tilde{\lambda }\left({\tilde{\eta }}_0(2r+3)-6\tilde{r}{(\tilde{r}+1)}^2\right)\right]+\frac{{\tilde{L}}_{\mathrm{SD}}^2{\tilde{\eta }}_0^4}{{\tilde{\eta }}^4{\tilde{r}}^2}\hfill \end{array}$$

(52d)

$$\begin{array}{cc}{a}_{13}\hfill & =-\frac{2{\tilde{E}}_{\mathrm{SD}}{\tilde{\eta }}_0^2}{{\tilde{\eta }}^4{\tilde{r}}^3(\tilde{r}+1)}\left[r^3\left({\tilde{\eta }}_0^2-96\tilde{\lambda }\right)+r^2\left({\tilde{\eta }}_0^2-192\tilde{\lambda }\right)+48{\tilde{\eta }}_0\tilde{\lambda }-16\tilde{\lambda }r({\tilde{\eta }}_0(\tilde{r}-2)+6\right]\hfill \end{array}$$

(52e)

$$\begin{array}{cc}{a}_{23}\hfill & =\frac{{\tilde{\eta }}_0^2}{{\tilde{\eta }}^4{\tilde{r}}^4{(\tilde{r}+1)}^2}[\left({\tilde{\eta }}_0^2\left({\tilde{r}}^2-1\right)r^3+{\tilde{\eta }}_0^2\left({\tilde{r}}^2-1\right)r^2\right)+\tilde{\lambda }(32r\left({\tilde{\eta }}_0\left(2{\tilde{r}}^2+\tilde{r}-1\right)+3\right)+48{\tilde{\eta }}_0\left({\tilde{r}}^2-1\right)\hfill \\ \hfill & +96r^3+192r^2\left)\right]\hfill \end{array}$$

(52f)

${\tilde{E}}_{\mathrm{SD}}$ and ${\tilde{L}}_{\mathrm{SD}}$ are related to the covariant form of momentum components as

$$\begin{array}{c}\hfill p_0=\frac{{\tilde{\eta }}^4}{{\tilde{\eta }}_0^4}\left(-A\frac{d\tilde{\eta }}{d\tau }+C_1\frac{d\tilde{r}}{d\tau }\right)=-{\tilde{E}}_{\mathrm{SD}}\end{array}$$

(53a)

$$\begin{array}{c}\hfill p_1=\frac{C_1}{A}{\tilde{E}}_{\mathrm{SD}}+\frac{{\tilde{\eta }}^4}{{\tilde{\eta }}_0^4}\left(\frac{C_1^2}{A}+B\right)\frac{d\tilde{r}}{d\tau }\end{array}$$

(53b)

$$\begin{array}{c}\hfill p_3=\frac{{\tilde{\eta }}^4}{{\tilde{\eta }}_0^4}{C}_2\frac{d\varphi }{d\tau }={\tilde{L}}_{\mathrm{SD}}\end{array}$$

(53c)

where ${\tilde{E}}_{\mathrm{SD}},{\tilde{L}}_{\mathrm{SD}}$ are the energy and angular momentum of the photon in the SD space-time. The contravariant form of momentum $P^{\mu }$ is $p^0=d\tilde{\eta }/d\tau ,p^1=d\tilde{r}/d\tau ,p^2=d\theta /d\tau ,p^3=d\varphi /d\tau$; $A,B,C_1,C_2$ are defined in Appendix B, and $f_i,f_i^{\prime }$’s are defined above in Equations (43), (45), and (47).

This is the first important key result that we would like to highlight. The dispersion relations (44), (50), and (51), for the SD space-time, are very different than the dispersion relations in the Schwarzschild BH (34). In the case of Schwarzschild, the two dispersion relations (34) are quadratic, and the third one ($p^2=0$) is identical to the minimal coupling. However, in the SD space-time, one of the dispersion relations is quadratic (SD-I), and another is quartic (SD-II and SD-III). The quadratic dispersion (SD-I) has a different form (compared to Schwarzschild) as it contains the cross-term $p_0{p}_1$. As mentioned earlier, assuming $\tilde{\lambda }$ to be small and ignoring ${\tilde{\lambda }}^2$ terms reduces the quartic dispersion to two quadratic dispersion relations (50) (SD-II) and (51) (SD-III). Interestingly, both the quadratic dispersion relations contain the cross-terms $p_0{p}_1$. This indicates that the total deflection angle might differ for the two black hole space-times.

In the next section, we calculate the expression for the deflection angle, followed by the total deflection angle of the photon near the black hole. We compare the time-independent (Schwarzschild) and time-dependent (SD) BH results. As the total deflection angle depends on $\tilde{\lambda }$, we also obtain a constraint on the NMC parameter.

5. Deflection Angle

Potentially, the modification to the path taken by the photon leads to a change in the following two observable quantities:

• Photon arrival time at the detector.
• Photon deflection angle at the detector.

In Ref. [38], the authors used the photon dispersion relation and computed the photon’s arrival time in Schwarzschild space-time. Since we consider time-dependent black hole space-times, the photon deflection angle is more suitable. Hence, in this work, we obtain the total deflection angle of the non-minimally coupled photon in both Schwarzschild and Sultana–Dyer space-times and compare the results.

5.1. Schwarzschild Space-Time

To obtain the photon deflection angle, we need to rewrite the dispersion relation (34) in the non-inertial frame. To do this, substituting the tetrads for the line element (30) in the dispersion relation (34) leads to

$$\begin{array}{c}\hfill \left(1-\frac{1}{\tilde{r}}\right)p_1^2={\beta }_0^{-2}{\left(1-\frac{1}{\tilde{r}}\right)}^{-1}{p}_0^2-\frac{1}{{\tilde{r}}^2}\left(1-\mathcal{C}\pm \right)p_3^2\end{array}$$

(54)

where

$$\begin{array}{cc}\hfill p_0=-\left(1-\frac{1}{\tilde{r}}\right)\frac{d\tilde{t}}{d\tau }:={\tilde{E}}_{\mathrm{Sch}};& p_1={\left(1-\frac{1}{\tilde{r}}\right)}^{-1}\frac{d\tilde{r}}{d\tau };\hfill \end{array}$$

(55a)

$$\begin{array}{c}\hfill p_3={\tilde{r}}^2\frac{d\varphi }{d\tau }:={\tilde{L}}_{\mathrm{Sch}}\end{array}$$

(55b)

Substituting $p_0,p_3$ in Equation (54) and solving the resultant equation, we obtain

$$\begin{array}{c}\hfill \left(1-\frac{1}{\tilde{r}}\right)p_1^2={\left(1-\frac{1}{\tilde{r}}\right)}^{-1}{\tilde{E}}_{\mathrm{Sch}}^2-\frac{1}{{\tilde{r}}^2}\left(1-{\mathcal{C}}_{\pm }\right){\tilde{L}}_{\mathrm{Sch}}^2.\end{array}$$

Substituting the form of $p_1$ from Equation (55a) in the above equation, we obtain

$$\begin{array}{c}\hfill \frac{d\tilde{r}}{d\tau }={\tilde{L}}_{\mathrm{Sch}}{\left[\frac{1}{b^2}-\frac{\left(1-\frac{1}{\tilde{r}}\right)}{{\tilde{r}}^2}\left(1-{\mathcal{C}}_{\pm }\right)\right]}^{1/2}\end{array}$$

(56)

where $b\equiv {\tilde{L}}_{\mathrm{Sch}}/{\tilde{E}}_{\mathrm{Sch}}$ is the impact parameter. To obtain the deflection angle, we need to rewrite the above differential equation in terms of $\varphi$. Thus, dividing Equation (56) by $d\varphi /d\tau ={\tilde{L}}_{\mathrm{Sch}}/{\tilde{r}}^2$, the deflection angle $d\varphi /d\tilde{r}$ is

$$\begin{array}{c}\hfill \frac{d\varphi }{d\tilde{r}}=\frac{1}{{\tilde{r}}^2}{\left[\frac{1}{b^2}-\frac{\left(1-\frac{1}{\tilde{r}}\right)}{{\tilde{r}}^2}\left(1-{\mathcal{C}}_{\pm }\right)\right]}^{-1/2}.\end{array}$$

(57)

Note that the $-(+)$ sign corresponds to the deflection angle for the $+(-)$ polarization mode. In the $\tilde{\lambda }=0$ limit, the above expression reduces to the standard deflection angle for minimally coupled photons, cf. Equation (6.3.35) in Ref. [56], which provides a cut-off on the impact parameter for the photon.

From the above expression, we see that the impact parameter (b) and NMC parameter ($\tilde{\lambda }$) cannot be arbitrary for all values of $\tilde{r}$. In the limit of $\tilde{r}\to \infty$, the second term inside the RHS bracket vanishes, suggesting no constraints on b and $\tilde{\lambda }$. However, close to the horizon, the second term inside the bracket in the RHS is finite. Thus, we see that the modification to the dispersion relation is the most significant close to the horizon and is negligible very far from the horizon. This implies that b and $\tilde{\lambda }$ are constrained by the value of the horizon radius (which is in the dimensionless units in unity).

To go about this, we need to determine the radius of the photon sphere $r_0$ and its corresponding impact parameter $b_0$. At $r=r_0$, we have the following conditions:

$$\begin{array}{cc}\hfill \frac{d\tilde{r}}{d\tau }{|}_{r=r_0}=0;& \frac{d^2\tilde{r}}{d{\tau }^2}{|}_{r=r_0}=0\hfill \end{array}$$

(58)

From Equation (56) and the conditions (58), we can obtain ${\tilde{r}}_0$ (or $r_0$) and the corresponding impact parameter $b_0$. As mentioned above, the set $({\tilde{r}}_0,b_0)$ depends on the value of $\tilde{\lambda }$, as the photon dispersion relation depends on $\tilde{\lambda }$. In a recent work [52], we showed that the value of ${\tilde{r}}_0,b_0$ increases with $\tilde{\lambda }$ for the dispersion relation (54) with ${\mathcal{C}}_{+}$. Similarly, we showed that the value of ${\tilde{r}}_0,b_0$ decreases with $\tilde{\lambda }$ for the dispersion relation with ${\mathcal{C}}_{-}$. In other words, the value of ${\tilde{r}}_0,b_0$ depends on the type of polarization. To see this transparently, let us return to the condition (58). From the first condition, the impact parameter can be written as

$$\begin{array}{c}\hfill b_0=\frac{{\tilde{r}}_0}{\sqrt{\left(1-{\frac{1}{\tilde{r}}}_0\right)(1-{\mathcal{C}}_{\pm })}}\end{array}$$

(59)

Given that $b_0$ is a real positive number, we obtain the condition that the RHS of the above expression must be positive. This leads to the following constraint:

$$\begin{array}{c}\hfill 1-{\mathcal{C}}_{\pm }>0\end{array}$$

(60)

Using the definition of ${\mathcal{C}}_{\pm }$ from Equation (35) in the above expression, we obtain the following condition on $\tilde{\lambda }$:

$$\begin{array}{c}\hfill -1.688<\tilde{\lambda }<0.844.\end{array}$$

(61)

It is important to note that the above condition is valid for both the dispersion relations.

Having obtained the constraint on $\tilde{\lambda }$, we can obtain the deflection angles for the two polarization modes:

$$\begin{array}{cc}\hfill \frac{d\varphi }{d\tilde{r}}{|}_{+}^{\mathrm{Sch}}& =\frac{1}{{\tilde{r}}^2}{\left[\frac{1}{b^2}-\frac{\left(1-\frac{1}{\tilde{r}}\right)}{{\tilde{r}}^2}\left(1-\frac{6\tilde{\lambda }}{2\tilde{\lambda }+{\tilde{r}}^3}\right)\right]}^{-1/2}.\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill \frac{d\varphi }{d\tilde{r}}{|}_{-}^{\mathrm{Sch}}& =\frac{1}{{\tilde{r}}^2}{\left[\frac{1}{b^2}-\frac{\left(1-\frac{1}{\tilde{r}}\right)}{{\tilde{r}}^2}\left(1-\frac{6\tilde{\lambda }}{4\tilde{\lambda }-{\tilde{r}}^3}\right)\right]}^{-1/2}.\hfill \end{array}$$

(63)

In the above two equations, the subscript $+,-$ corresponds to the deflection for the dispersion relation with ${\mathcal{C}}_{+}$ and ${\mathcal{C}}_{-}$, respectively. From the expression of $d\varphi /d\tilde{r}$, we evaluate the total deflection angle for the two dispersion relations,

$$\begin{array}{c}\hfill {(\Delta \varphi )}^{\mathrm{Sch}}=2\pi -{\int }_{{\tilde{r}}_0}^{\infty }d\tilde{r}\left(\frac{d\varphi }{d\tilde{r}}{|}_{\pm }^{\mathrm{Sch}}\right)\end{array}$$

(64)

Next, in Section 6, we obtain the total deflection angle for Schwarzschild and compare it with the total deflection angle for SD space-time.

5.2. Sultana–Dyer Black Hole

In Section 4.2, we obtained two distinct—quadratic (42) and quartic (46)—dispersion relations for the NMC electromagnetic field in Sultana–Dyer space-time. In the previous subsection, for the Schwarzschild, $\tilde{\lambda }$, we obtained a constraint on $\lambda$ (see Equation (61)). In Appendix C, demanding the energy density of NMC EM fields or photons in Sultana–Dyer space-time be positive, we obtain a similar constraint on $\tilde{\lambda }$. Since these constraints are consistent for small values of $\tilde{\lambda }$, assuming $\tilde{\lambda }$ to be small, we can rewrite the quartic dispersion relation (46) as two quadratic relations (50) and (51). In the rest of this section, we use these three dispersion relations to obtain the total deflection angle.

To go about this, we first obtain a general expression for deflection angle in terms of $p_1$ and the conserved quantities ${\tilde{E}}_{\mathrm{SD}},{\tilde{L}}_{\mathrm{SD}}$. Rewriting the general expressions (53b) and (53c), we have

$$\begin{array}{cc}\hfill \frac{d\tilde{r}}{d\tau }& =\frac{\frac{{\tilde{\eta }}_0^4}{{\tilde{\eta }}^4}\left(p_1-\frac{C_1{\tilde{E}}_{\mathrm{SD}}}{A}\right)}{\left(\frac{C_1^2}{A}+B\right)}\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill \frac{d\varphi }{d\tau }& =\left(\frac{{\tilde{\eta }}_0^4}{{\tilde{\eta }}^4}\right)\frac{{\tilde{L}}_{\mathrm{SD}}}{C_2}.\hfill \end{array}$$

(66)

Dividing Equation (66) by Equation (65) leads to the following general expression for deflection angle in SD space-time:

$$\begin{array}{c}\hfill \frac{d\varphi }{d\tilde{r}}=\frac{{\tilde{L}}_{SD}\left(\frac{C_1^2}{A}+B\right)}{C_2\left[p_1-\frac{C_1}{A}{\tilde{E}}_{\mathrm{SD}}\right]}\end{array}$$

(67)

Note that $p_1$ in the above expression depends on the choice of the dispersion relation. In the previous section, we obtained three dispersion relations, (44) and (50) and (51). Once we obtain $p_1$, we will obtain the total deflection angle. To go about that, we first rewrite the quadratic dispersion relation (44) in the non-inertial frame as

$$\begin{array}{c}\hfill a_{21}{p}_1^2+a_{11}{p}_1+a_{01}=0,\end{array}$$

(68)

where

$$\begin{array}{cc}\hfill & a_{01}={f_1}^{\prime }{\tilde{E}}_{\mathrm{SD}}^2+{f_3}^{\prime }{\tilde{L}}_{\mathrm{SD}}^2;a_{11}=-{f_4}^{\prime }{\tilde{E}}_{\mathrm{SD}},a_{21}={f_2}^{\prime }\hfill \end{array}$$

(69)

Solving the above equation, we obtain

$$\begin{array}{c}\hfill p_1=\frac{-a_{11}\pm D_1}{2a_{21}},\mathrm{where}{D}_1={\left(a_{11}^2-4a_{21}{a}_{01}\right)}^{1/2}.\end{array}$$

(70)

Substituting the above form of $p_1$ in Equation (67), we obtain

$$\begin{array}{cc}\hfill \frac{d\varphi }{d\tilde{r}}{|}_{\mathrm{SD}\text{-}\mathrm{I}}& =\frac{\tilde{L}\left(\frac{C_1^2}{A}+B\right)}{C_2\left[\frac{-a_{11}\pm D_1}{2a_{21}}-\frac{C_1}{A}\tilde{E}\right]}\hfill \end{array}$$

(71)

Similarly, from the quadratic dispersion relations (50), (51) we obtain $p_1$. Substituting those in Equation (67), we obtain

$$\begin{array}{cc}\hfill \frac{d\varphi }{d\tilde{r}}{|}_{\mathrm{SD}\text{-}\mathrm{II}}& =\frac{\tilde{L}\left(\frac{C_1^2}{A}+B\right)}{C_2\left[\frac{-a_{12}\pm D_2}{2a_{22}}-\frac{C_1}{A}\tilde{E}\right]}\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill \frac{d\varphi }{d\tilde{r}}{|}_{\mathrm{SD}\text{-}\mathrm{III}}& =\frac{\tilde{L}\left(\frac{C_1^2}{A}+B\right)}{C_2\left[\frac{-a_{13}\pm D_3}{2a_{23}}-\frac{C_1}{A}\tilde{E}\right]}\hfill \end{array}$$

(73)

where $D_2={\left(a_{12}^2-4a_{22}{a}_{02}\right)}^{1/2}$ and $D_3={\left(a_{13}^2-4a_{23}{a}_{03}\right)}^{1/2}$. Note that here the subscripts SD-I, SD-II, SD-III in the LHS of the above equations correspond to the deflection angle for dispersion relations (44), (50), and (51), respectively. From Equations (71), (72), and (73), we can obtain the total deflection angle $\Delta \varphi$, i.e.,

$$\begin{array}{c}\hfill {(\Delta \varphi )}^{\mathrm{SD}}=2\pi -{\int }_{{\tilde{r}}_0}^{\infty }d\tilde{r}{\left(\frac{d\varphi }{d\tilde{r}}\right)}^{\mathrm{SD}}.\end{array}$$

(74)

The above expression measures how much a photon has been deflected from a straight line while passing a compact object and reaching the observer on Earth. Physically, it informs us about the effect of the gravitational attraction of the compact object on the passing photon close to it.

For a faraway observer, it is only possible to decipher whether the compact object is a Schwarzschild black hole or SD black hole by measuring the total deflection angle. In principle, given the same black hole mass M and NMC parameter $\tilde{\lambda }$, the total deflection angle from these two black hole space-times must be different. As mentioned earlier, starting from the energy–momentum tensor (A11), we obtain the following constraint:

$$-\frac{r_{\mathrm{H}}^2}{2}<\lambda <r_{\mathrm{H}}^2⟹-\frac{1}{2}<\tilde{\lambda }<1$$

(75)

Details are in Appendix C.

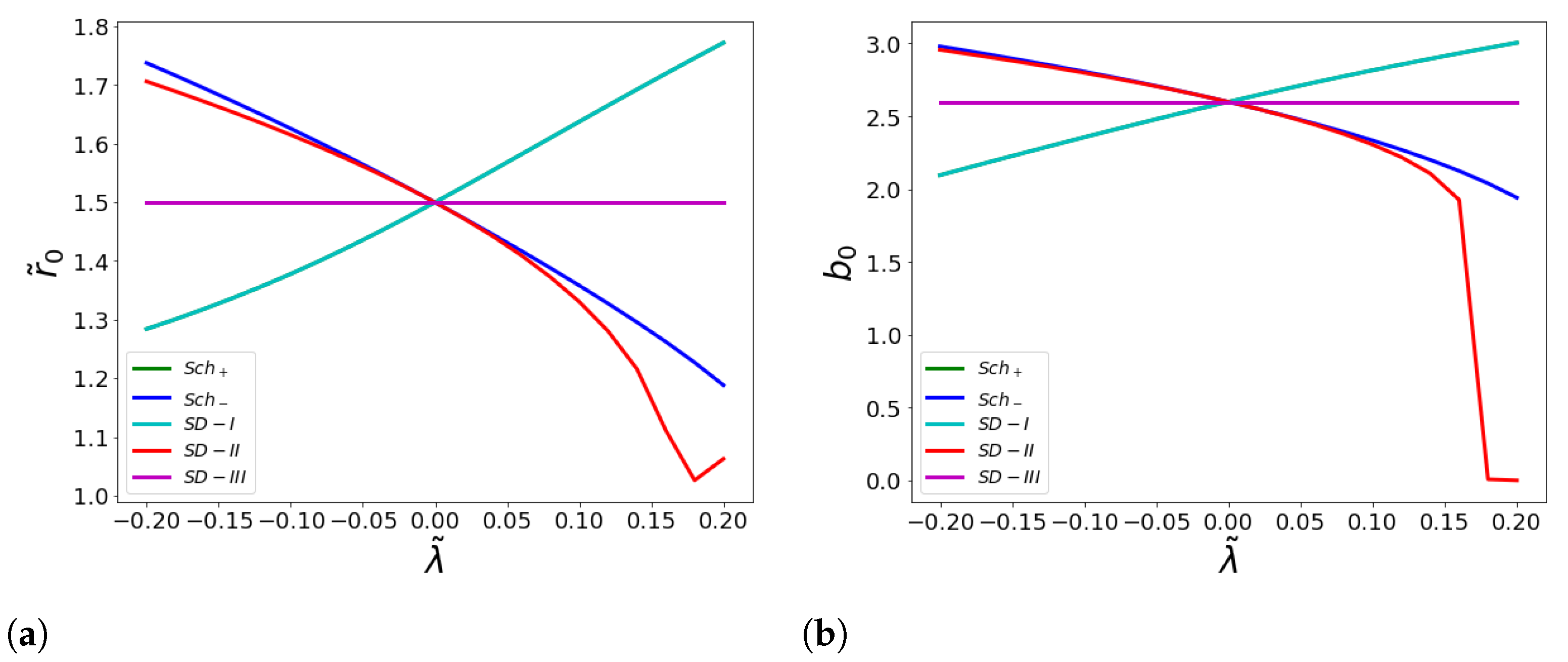
5.3. Bounds on $\lambda$

This section compares the constraint on $\lambda$ we obtained with the literature. In Refs. [14,29,31,32,33,34], several authors studied the effect of vacuum polarization on photon propagation in the gravitational field. In these, they obtained $\lambda \sim \alpha /\left(90\pi m_e^2\right)$ by considering the case where the photon energies are small compared to the electron mass, i.e., $\hslash \omega \ll m_e{c}^2$ ($m_e$ is the mass of an electron). However, their analysis is valid up to the Compton wavelength of electron ${\lambda }_e$, corresponding to photons of energy that are small compared to the electron mass. They showed that the constraint on the NMC parameter could be expressed as $\lambda \sim 1/{\Lambda }^2$ (in $\hslash =c=1$ unit) where $\Lambda$ is the cutoff of the theory, and further, they showed that $\lambda \sim 1/M_{\mathrm{Pl}}^2$ for a Planck-sized black hole. Drummond and Hathrell’s analysis only applies in a weak gravity limit [57,58,59].

Interestingly, the above constraint is consistent with the results derived in the previous subsection. We obtained $\lambda <r_{\mathrm{H}}^2$ for both the black hole space-times. For a Planck mass BH $\left(M_{\mathrm{Pl}}\right)$, the Schwarzschild radius can formally be written as $r_{\mathrm{H}}^{\mathrm{Pl}}\sim 2/M_{\mathrm{Pl}}$. Thus, $\lambda <r_{\mathrm{H}}^2$ leads to the same constraint $\lambda \sim 1/M_{\mathrm{Pl}}^2$ mentioned in the literature.

Table 1. Upper limit on $\lambda$ for different mass ranges: ${\lambda }_{\mathrm{SD}}$ and ${\lambda }_{\mathrm{Sch}}$ correspond to $\lambda$ determined in Sultana–Dyer and Schwarzschild space-times, respectively.

Black Hole Mass	${\mathit{r}}_{\mathbf{H}}$ (cm)	${\mathit{\lambda }}_{\mathbf{SD}}$ (cm2)	${\mathit{\lambda }}_{\mathbf{Sch}}$ (cm2)
Supermassive	∼${10}^{11}$	∼${10}^{22}$	∼${10}^{22}$
Solar-mass	$2.9\times {10}^5$	$8.41\times {10}^{10}$	$7.01\times {10}^{10}$
${10}^{-3}{M}_{\odot }$	$2.9\times {10}^2$	$8.41\times {10}^4$	$7.01\times {10}^4$
${10}^{-5}{M}_{\odot }$	$2.9$	$8.41$	$7.01$
${10}^{-10}{M}_{\odot }$	$2.9\times {10}^{-5}$	$8.41\times {10}^{-10}$	$7.01\times {10}^{-10}$

lists the upper limit of $\lambda$ for different black hole masses. From the table, we infer that the smaller black hole mass will provide stringent constraints on the NMC parameter compared to supermassive black holes. This is consistent with the discussion in the Introduction. As mentioned in the Introduction, the square root of the Kretschmann scalar ($\mathcal{K}$) measures the intensity of the gravitational field. From Table 1, we see that the strong gravity regime provides a stringent constraint on the NMC parameter. For instance, in Refs. [52,60], the observable photon ring does not form for $\lambda <-4.2\times {10}^{22}$ cm² for the $(+)$ mode and for $\lambda >2.1\times {10}^{22}$ cm² for the $(-)$ mode.

In Ref. [38], the authors obtained constraints on $\lambda$ considering photons in Schwarzschild space-time, and by considering signals from radar ranging past the Sun, they found $\lambda \sim 1.1\times {10}^{20}{\mathrm{cm}}^2$, which is about three orders of magnitude more stringent than the one obtained in Ref. [28]. Thus, compared to Ref. [38], the bound obtained here is more stringent—by over ten orders of magnitude. Note that in the case of signals coming from binary pulsar PSR B1534 + 12, the bound on $\lambda \sim 0.6\times {10}^{11}$ cm² [61,62]. It matches the bound on $\lambda$ we obtained for the Schwarzschild and Sultana–Dyer black holes.

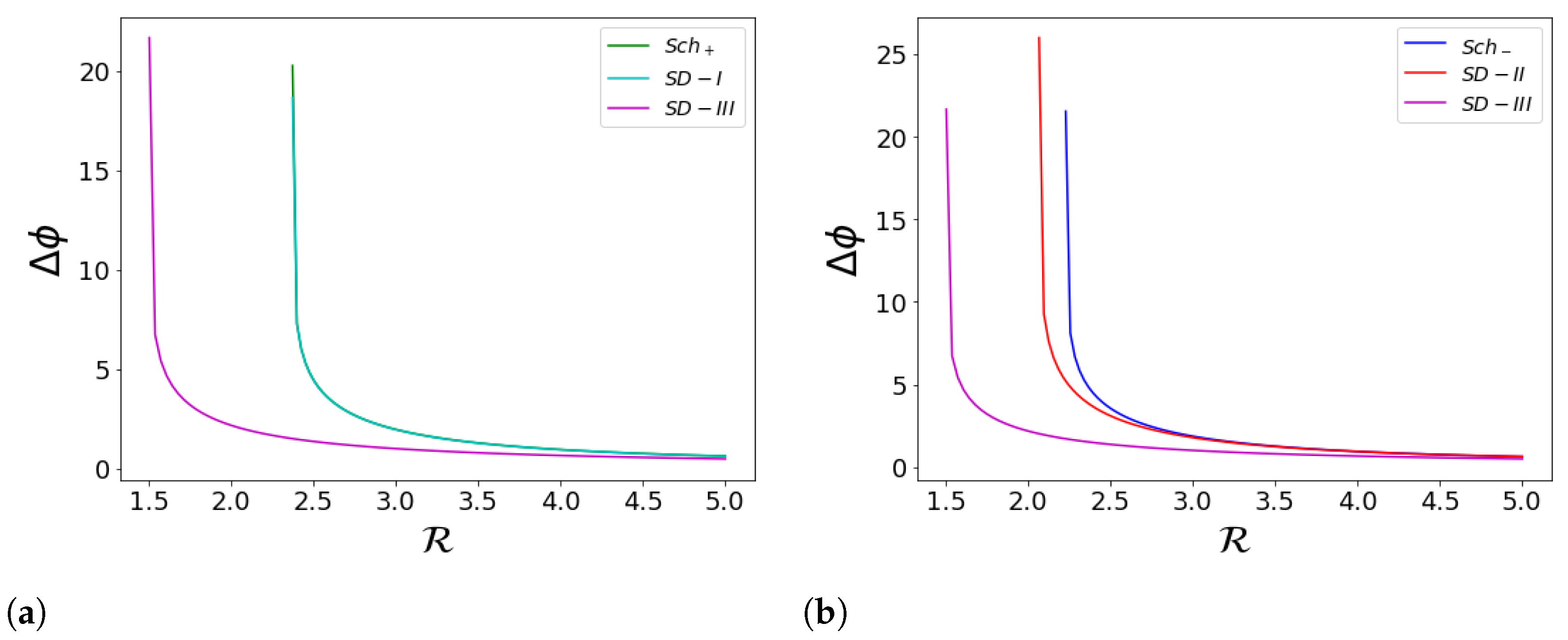
6. Comparing Total Deflection Angles in Schwarzschild and Sultana–Dyer Black Holes

In this section, we present the final results of this work, comparing the total deflection angle of NMC photons near time-independent (Schwarzschild) and time-dependent (Sultana–Dyer) black holes.

As mentioned earlier, the total deflection angle depends on the radius of the photon sphere $\left(r_0\right)$ and the NMC parameter $(\lambda$). To go about this, we demand the following conditions:

$$\begin{array}{cc}\hfill \frac{d\tilde{r}}{d\tau }{|}_{r=r_0}=0;& \frac{d^2\tilde{r}}{d{\tau }^2}{|}_{r=r_0}=0\hfill \end{array}$$

(76)

For SD space-time, using the expression (65) and the above conditions, we can obtain ${\tilde{r}}_0\equiv r_0/r_H$ (radius of the photon sphere scaled with the horizon radius $r_H$) and the corresponding impact parameter $b_0$. Unlike Schwarzschild, the three dispersion relations (71)–(73) for SD space-time are more involved. Hence, it is not possible to obtain analytical expressions for the same. Figure 1 contains $({\tilde{r}}_0,b_0)$ for the two dispersion relations for Schwarzschild and three dispersion relations for SD.

From Figure 1, we infer the following: First, for the dispersion relation-I (SD-I), which is the quadratic dispersion relation, the value of ${\tilde{r}}_0,b_0$ increases with the increase in $\tilde{\lambda }$. It is interesting to see that for $-0.2\le \tilde{\lambda }\le 0.2$, $({\tilde{r}}_0,b_0)$ for SD-I and $(+)$ polarization mode (Schwarzschild space-time) are identical (the green and cyan curves overlap in Figure 1a,b). However, $({\tilde{r}}_0,b_0)$ differs for other dispersion relations in SD and Schwarzschild space-time values. Second, for dispersion relation SD-II, these values decrease as $\tilde{\lambda }$ increases. Interestingly, for $\tilde{\lambda }=0.2$, ${\tilde{r}}_0$ is close to 1, implying that the radius of the photon sphere is close to the horizon radius. For the same $\tilde{\lambda }$, the impact parameter $b_0=0.0088$, which is less than the horizon radius and implies that for $\tilde{\lambda }=0.2$ no photon sphere can be formed for SD-II mode. We have verified that the photon sphere will not be formed for the SD-II mode when $\tilde{\lambda }\ge 0.168$. This is similar to the Schwarzschild space-time. In this case, the photon sphere will not be formed at $\tilde{\lambda }\le -0.5$ for the ${\mathcal{C}}_{+}$ mode and $\tilde{\lambda }\ge 0.25$ for the ${\mathcal{C}}_{-}$ mode of polarizations [52]. Lastly, for the dispersion relation III (SD-III), ${\tilde{r}}_0,b_0$ are constants irrespective of any value of $\tilde{\lambda }$.

For the three dispersion relations of Sultana–Dyer and the two dispersion relations of Schwarzschild, we can calculate the total deflection angle $\Delta \varphi$ numerically for different $\tilde{\lambda }$ values:

$$\begin{array}{c}\hfill (\Delta \varphi )=2\pi -{\int }_{{\tilde{r}}_0}^{\mathcal{R}}d\tilde{r}\left(\frac{d\varphi }{d\tilde{r}}\right).\end{array}$$

(77)

Here, ${\tilde{r}}_0$ is the radius of the photon sphere, scaled with BH horizon radius $r_{\mathrm{H}}$, and $\mathcal{R}$ is in multiples of $r_{\mathrm{H}}$. Figure 2 and Figure 3 contain the total deflection angle as a function of $\mathcal{R}$ for all the dispersion relations and for different values of $\tilde{\lambda }$; while Figure 2 is the plot of the deflection angle with $\mathcal{R}$ for stellar-mass black holes, Figure 3 is the plot of the deflection angle with $\mathcal{R}$ for PBHs of mass ${10}^{-5}{M}_{\odot }$. As mentioned earlier, the event horizon near PBHs of this mass exhibits strong curvature.

From the figures, we infer the following: First, as $\mathcal{R}$ increases, $\Delta \varphi$ saturates to a finite value. This is expected because the deflection angle must be large close to the horizon and will be negligible as we go away from the horizon. This trend is seen for all the dispersion relations for both the space-times. Second, for $\tilde{\lambda }=-0.2$, $\Delta \varphi$ is highest for SD-II and lowest for the (+)-polarization mode in Schwarzschild BH. Third, for $\tilde{\lambda }=0.1$, $\Delta \varphi$ is highest for both SD-I and the (+)-polarization mode in Schwarzschild space-time.

From Table 1, the upper limit of the NMC parameter is $\sim 8$ for a PBH of mass $M={10}^{-5}{M}_{\odot }$. This implies $\tilde{\lambda }\sim 0.8$. Figure 3 contains the plot of the total deflection angle $\Delta \varphi$ angle of NMC photons for Schwarzschild and SD space-times for this specific value of $\tilde{\lambda }$. For Schwarzschild, the photon sphere exists only for one mode (± polarization for $\pm 0.8$). For SD-I and SD-III modes, the photon sphere exists for $\tilde{\lambda }=0.8$, while for SD-II and SD-III modes, the photon sphere exists for $\tilde{\lambda }=-0.8$. Thus, the total deflection angle $\Delta \varphi$ of NMC photons near Schwarzschild and SD space-times will have a contribution only from the other modes. In other words, the photons forming the photon sphere are highly polarized, which can potentially lead to observable implications.

7. Conclusions and Discussions

In this work, we carried out a detailed analysis of the propagation of non-minimally coupled photons to gravity. To obtain a constraint on the coupling parameter, we calculated the deflection angle of a photon in the vicinity of a dynamical, spherically symmetric black hole described by the Sultana–Dyer space-time. To our knowledge, the detailed evaluation of the deflection angle in a black hole space-time to constrain the non-minimal coupling parameter is new.

Using the Eikonal approximation, we obtained the dispersion relations for the two polarization modes of electromagnetic fields in Schwarzschild and Sultana–Dyer space-times. We showed that the two dispersion relations corresponding to the two polarizations differ from Schwarzschild and Kerr [cf. Equation (34)]. In the case of Schwarzschild and Kerr, the two dispersions are quadratic, and the modifications to the dispersion relation occur in the $p_{\left(3\right)}$ component of the momentum. However, in the case of Sultana–Dyer, the modification to the dispersion relation [cf. Equations (44), (50) and (51)] occurs in all the components of the momentum. The key difference between the dispersion relations in these two space-times is that for Schwarzschild, both are quadratic, whereas for Sultana–Dyer, one is quartic. In the small $\tilde{\lambda }$ limit, the quartic dispersion relation reduces to two quadratic dispersion relations.

We compute the total deflection angle for non-minimally coupled photons near Schwarzschild and Sultana–Dyer black holes and show that both these black holes have similar signatures regarding the total deflection angle and radius of the photon sphere. Interestingly, our analysis shows that a PBH provides a stringent constraint on the NMC parameter. Thus, we conclude that irrespective of whether the PBH can be described as an isolated or cosmological black hole, the constraint on the NMC parameter is similar.

The constraint on $\lambda$ for the stellar-mass black holes is better than that obtained by Prasanna and Mohanty [38]. In Ref. [38], the authors used the photon dispersion relation to compute the photon’s arrival time and obtained $\lambda \sim 1.1\times {10}^{20}{\mathrm{cm}}^2$. The constraint we obtained is ten orders of magnitude more stringent compared to Ref. [38] and 13 orders of magnitude better than Ref. [28]. Interestingly, the bound we obtained matches with the bound obtained from the binary pulsar PSR B1534 + 12, which is $\lambda \sim 0.6\times {10}^{11}$ cm² [61,62]. This suggests looking for constraints on $\lambda$ in the next-generation EHT/VLBI measurement [5,63]. With increased sensitivity, such as ngVLA, $1\mu as$ astrometry can be achieved, which can potentially detect the deflection angle from PBHs of mass ${10}^{-5}{M}_{\odot }$, which are of the same size as Jovian-mass planets [64].

In the current analysis, we did not consider the frequency dependence of the polarization modes. However, the frequency dependence of the deflection angle can provide a helpful way to test the non-minimal coupling strength and can potentially be measured in radio frequencies [65]. The entire analysis is focused on the spherically symmetric space-times, as a PBH does not have spin. However, in the NS-NS and NS-BH mergers, the final black hole is expected to be axially symmetric (like Kerr). Therefore, we need to extend the analysis for the rotating black hole space-times. This is currently under investigation.