Predicting Solar Cycles with a Parametric Time Series Model
Abstract
:1. Introduction
2. Data and Methods
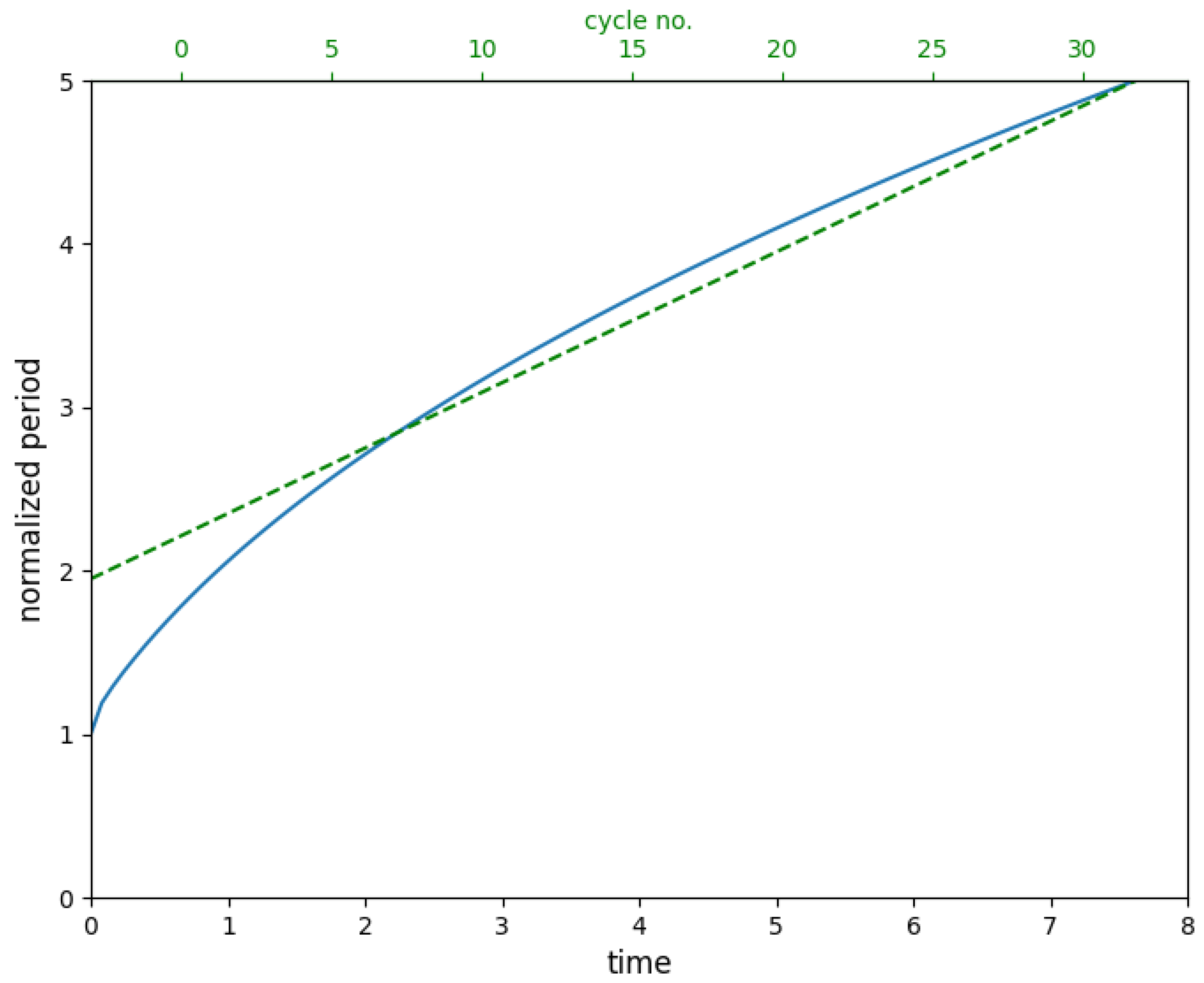
3. Analysis and Results
4. Discussion
4.1. Gleissberg Oscillation
4.2. Odd–Even Alternation
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ludendorff, H. Untersuchungen über die Häufigkeitskurve der Sonnenflecke. Mit 2 Abbildungen. Z. f. Astrophysik 1931, 2, 370. [Google Scholar]
- Gleissberg, W. A long-periodic fluctuation of the sun-spot numbers. Observatory 1939, 62, 158–159. [Google Scholar]
- Beer, J.; Vonmoos, M.; Muscheler, R. Solar Variability Over the Past Several Millennia. Space Sci. Rev. 2006, 125, 67–79. [Google Scholar] [CrossRef]
- Usoskin, I.G. A history of solar activity over millennia. Living Rev. Sol. Phys. 2017, 14, 3. [Google Scholar] [CrossRef]
- Petrovay, K. Solar cycle prediction. Living Rev. Sol. Phys. 2020, 17, 2. [Google Scholar] [CrossRef]
- Gleissberg, W. Eine Gleichung für die Sonnenfleckenkurve. Z. Astrophys. 1939, 18, 199. [Google Scholar]
- Mursula, K.; Usoskin, I.G.; Kovaltsov, G.A. Persistent 22-year cycle in sunspot activity: Evidence for a relic solar magnetic field. Sol. Phys. 2001, 198, 51–56. [Google Scholar] [CrossRef]
- Forgács-Dajka, E.; Major, B.; Borkovits, T. Long-term variation in distribution of sunspot groups. Astron. Astrophys. 2004, 424, 311–315. [Google Scholar] [CrossRef]
- Oláh, K.; Kolláth, Z.; Granzer, T.; Strassmeier, K.G.; Lanza, A.F.; Järvinen, S.; Korhonen, H.; Baliunas, S.L.; Soon, W.; Messina, S.; et al. Multiple and changing cycles of active stars. II. Results. Astron. Astrophys. 2009, 501, 703–713. [Google Scholar] [CrossRef]
- SILSO World Data Center. The International Sunspot Number. Available online: http://www.sidc.be/silso/ (accessed on 9 June 2024).
- Gleissberg, W. Secularly Smoothed Data on the Minima and Maxima of Sunspot Frequency. Sol. Phys. 1967, 2, 231–233. [Google Scholar] [CrossRef]
- Tripathi, B.; Nandy, D.; Banerjee, S. Stellar mid-life crisis: Subcritical magnetic dynamos of solar-like stars and the breakdown of gyrochronology. Mon. Not. R. Astron. Soc. Lett. 2021, 506, L50–L54. [Google Scholar] [CrossRef]
- Muñoz-Jaramillo, A.; Vaquero, J.M. Visualization of the challenges and limitations of the long-term sunspot number record. Nat. Astron. 2019, 3, 205–211. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Mursula, K.; Kovaltsov, G.A. Was one sunspot cycle lost in late XVIII century? Astron. Astrophys. 2001, 370, L31–L34. [Google Scholar] [CrossRef]
- Benson, B.; Pan, W.D.; Prasad, A.; Gary, G.A.; Hu, Q. Forecasting Solar Cycle 25 Using Deep Neural Networks. Sol. Phys. 2020, 295, 65. [Google Scholar] [CrossRef]
- Aparicio, A.J.P.; Carrasco, V.M.S.; Vaquero, J.M. Prediction of the Maximum Amplitude of Solar Cycle 25 Using the Ascending Inflection Point. Sol. Phys. 2023, 298, 100. [Google Scholar] [CrossRef]
- Chowdhury, P.; Jain, R.; Ray, P.C.; Burud, D.; Chakrabarti, A. Prediction of Amplitude and Timing of Solar Cycle 25. Sol. Phys. 2021, 296, 69. [Google Scholar] [CrossRef]
- Du, Z. Predicting the Maximum Amplitude of Solar Cycle 25 Using the Early Value of the Rising Phase. Sol. Phys. 2022, 297, 61. [Google Scholar] [CrossRef]
- Asikainen, T.; Mantere, J. Prediction of even and odd sunspot cycles. J. Space Weather Space Clim. 2023, 13, 25. [Google Scholar] [CrossRef]
- Nagovitsyn, Y.A.; Osipova, A.A.; Ivanov, V.G. Gnevyshev-Ohl Rule: Current Status. Astron. Rep. 2024, 68, 89–96. [Google Scholar] [CrossRef]
- Feynman, J.; Ruzmaikin, A. The Centennial Gleissberg Cycle and its association with extended minima. J. Geophys. Res. Space Phys. 2014, 119, 6027–6041. [Google Scholar] [CrossRef]
- Ruzmaikin, A.; Feynman, J. The Centennial Gleissberg Cycle: Origin and Forcing of Climate. In Astronomical Society of the Pacific Conference Series, Proceedings of the Outstanding Problems in Heliophysics: From Coronal Heating to the Edge of the Heliosphere; Hu, Q., Zank, G.P., Eds.; ASP: Appleton, WI, USA, 2014; Volume 484, p. 189. [Google Scholar]
- Biswas, A.; Karak, B.B.; Usoskin, I.; Weisshaar, E. Long-Term Modulation of Solar Cycles. Space Sci. Rev. 2023, 219, 19. [Google Scholar] [CrossRef]
- Karak, B.B. Models for the long-term variations of solar activity. Living Rev. Sol. Phys. 2023, 20, 3. [Google Scholar] [CrossRef]
- Pipin, V.V. The Gleissberg cycle by a nonlinear α–ω dynamo. Astron. Astrophys. 1999, 346, 295–302. [Google Scholar]
- Kleeorin, N.I.; Ruzmaikin, A.A. Mean-field dynamo with cubic non-linearity. Astron. Nachrichten 1984, 305, 265–275. [Google Scholar] [CrossRef]
- Schüssler, M.; Cameron, R.H. Origin of the hemispheric asymmetry of solar activity. Astron. Astrophys. 2018, 618, A89. [Google Scholar] [CrossRef]
- Charbonneau, P.; St-Jean, C.; Zacharias, P. Fluctuations in Babcock-Leighton Dynamos. I. Period Doubling and Transition to Chaos. Astrophys. J. 2005, 619, 613–622. [Google Scholar] [CrossRef]
- Charbonneau, P.; Beaubien, G.; St-Jean, C. Fluctuations in Babcock-Leighton Dynamos. II. Revisiting the Gnevyshev-Ohl Rule. Astrophys. J. 2007, 658, 657–662. [Google Scholar] [CrossRef]
- Charbonneau, P. Dynamo models of the solar cycle. Living Rev. Sol. Phys. 2020, 17, 4. [Google Scholar] [CrossRef]
- Durney, B.R. On the Differences Between Odd and Even Solar Cycles. Sol. Phys. 2000, 196, 421–426. [Google Scholar] [CrossRef]
- Charbonneau, P. Multiperiodicity, Chaos, and Intermittency in a Reduced Model of the Solar Cycle. Sol. Phys. 2001, 199, 385–404. [Google Scholar] [CrossRef]
- Thibeault, C.; Miara, L.; Charbonneau, P. Nonlinearity, time delay, and Grand Maxima in supercritical Babcock-Leighton dynamos. J. Space Weather Space Clim. 2023, 13, 32. [Google Scholar] [CrossRef]
- Nagy, M.; Lemerle, A.; Labonville, F.; Petrovay, K.; Charbonneau, P. The Effect of “Rogue” Active Regions on the Solar Cycle. Sol. Phys. 2017, 292, 167. [Google Scholar] [CrossRef]
- Nagy, M.; Petrovay, K.; Lemerle, A.; Charbonneau, P. Towards an algebraic method of solar cycle prediction. II. Reducing the need for detailed input data with ARDoR. J. Space Weather Space Clim. 2020, 10, 46. [Google Scholar] [CrossRef]
- Sonett, C.P. Sunspot time series: Spectrum from square law modulation of the Hale cycle. Geophys. Res. Lett. 1982, 9, 1313–1316. [Google Scholar] [CrossRef]
- Mursula, K. Hale cycle in solar hemispheric radio flux and sunspots: Evidence for a northward-shifted relic field. Astron. Astrophys. 2023, 674, A182. [Google Scholar] [CrossRef]
- Luo, P.X.; Tan, B.L. Long-term Evolution of Solar Activity and Prediction of the Following Solar Cycles. Res. Astron. Astrophys. 2024, 24, 035016. [Google Scholar] [CrossRef]

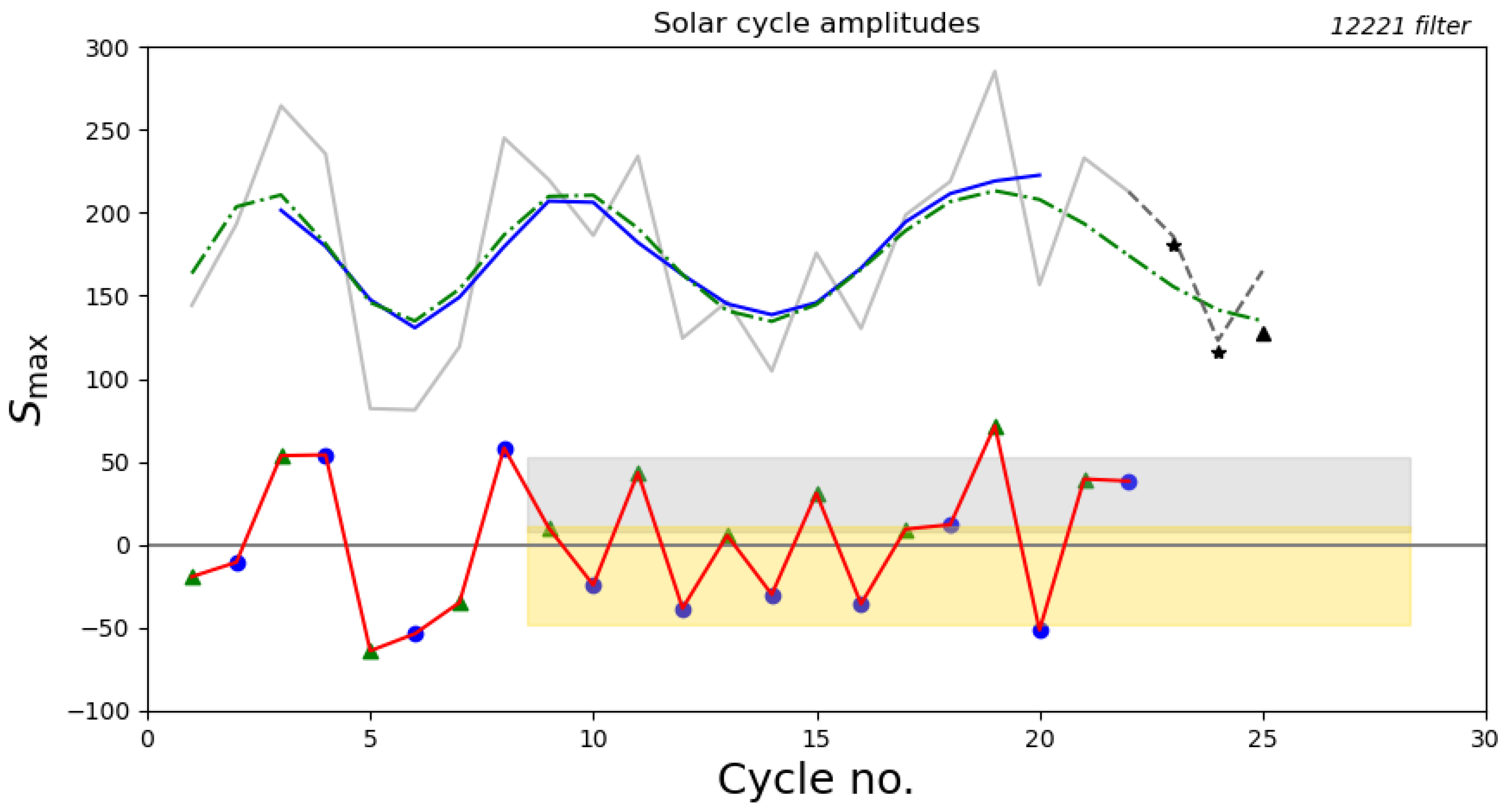
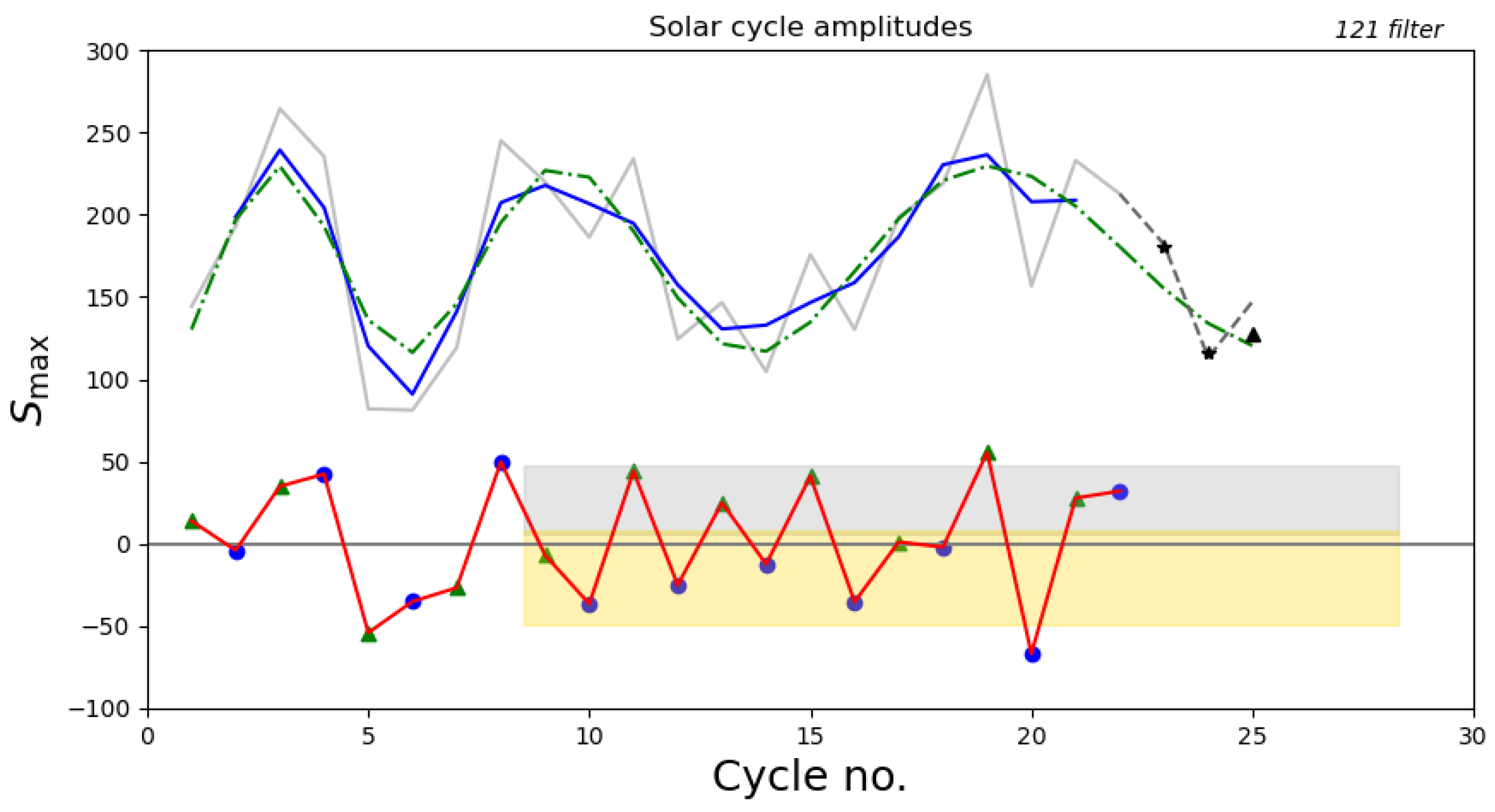
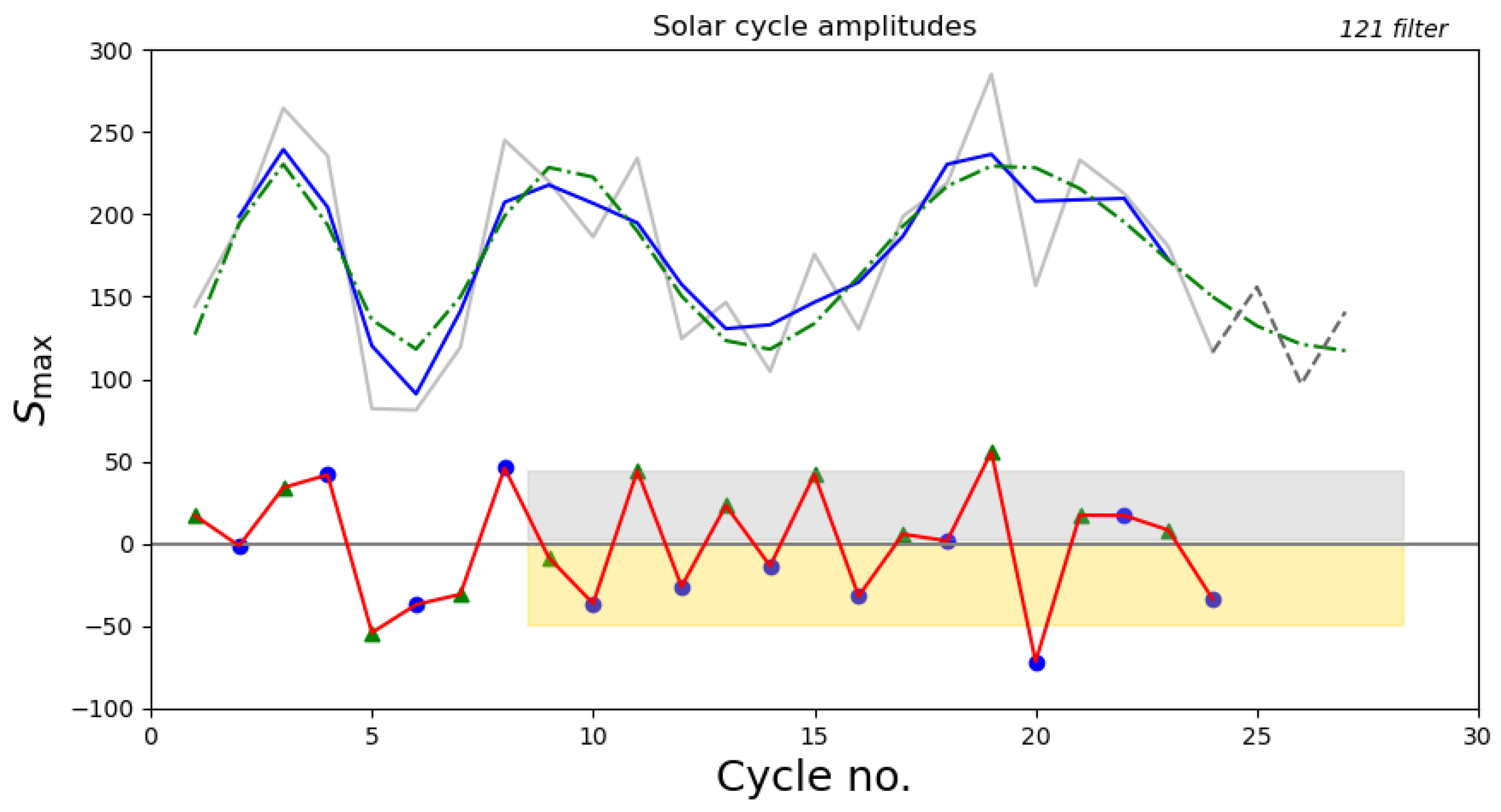
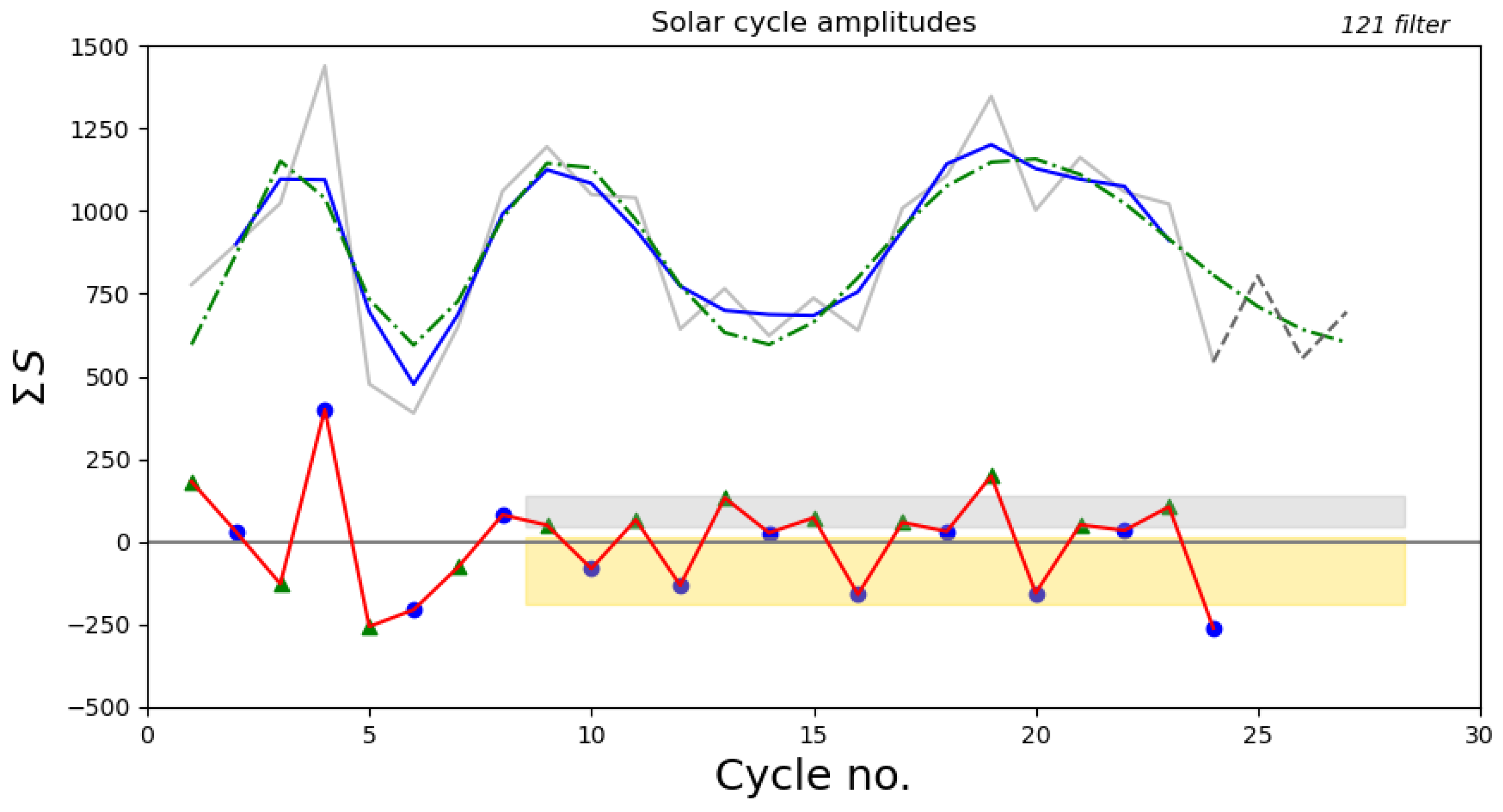
| Input Data | Last Cycle | Filter | Predictions | |||||
|---|---|---|---|---|---|---|---|---|
| in Input | SC23 | SC24 | SC25 | SC26 | SC27 | SC28 | ||
| 22 | 121 | |||||||
| 24 | 121 | 180 | 116 | |||||
| 25 | 121 | 180 | 116 | 127 | ||||
| 22 | 12221 | |||||||
| 24 | 12221 | 180 | 116 | |||||
| 25 | 12221 | 180 | 116 | 127 | ||||
| 22 | 121 | |||||||
| 24 | 121 | 1020 | 544 | |||||
| 25 | 121 | 1020 | 544 | 700 | ||||
| 22 | 12221 | |||||||
| 24 | 12221 | 1020 | 544 | |||||
| 25 | 12221 | 1020 | 544 | 700 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrovay, K. Predicting Solar Cycles with a Parametric Time Series Model. Universe 2024, 10, 364. https://doi.org/10.3390/universe10090364
Petrovay K. Predicting Solar Cycles with a Parametric Time Series Model. Universe. 2024; 10(9):364. https://doi.org/10.3390/universe10090364
Chicago/Turabian StylePetrovay, Kristof. 2024. "Predicting Solar Cycles with a Parametric Time Series Model" Universe 10, no. 9: 364. https://doi.org/10.3390/universe10090364






