Influence of Solar Wind Driving and Geomagnetic Activity on the Variability of Sub-Relativistic Electrons in the Inner Magnetosphere
Abstract
1. Introduction
2. Data and Methods
2.1. Datasets
- The interplanetary magnetic field IMF along with its component and its tangential component in geocentric solar magnetospheric coordinates (GSM).
- The southward magnetic field (), which corresponds to the absolute negative values of when all positive values have been set to zero, and the azimuthal electric field at the magnetopause ().
- The solar wind flow speed (), dynamic pressure (), and numerical density ().
- The geomagnetic indices Dst, SMR, SME, AL, SML, AE, AU, SMU, Kp, and Ap.
- The coupling functions1:
2.2. Processing
2.3. Presentation and Selection
3. Correlation Analysis
3.1. Results with Time Lag Set to Zero
3.2. Results with Time Lag
3.2.1. Solar Wind Velocity
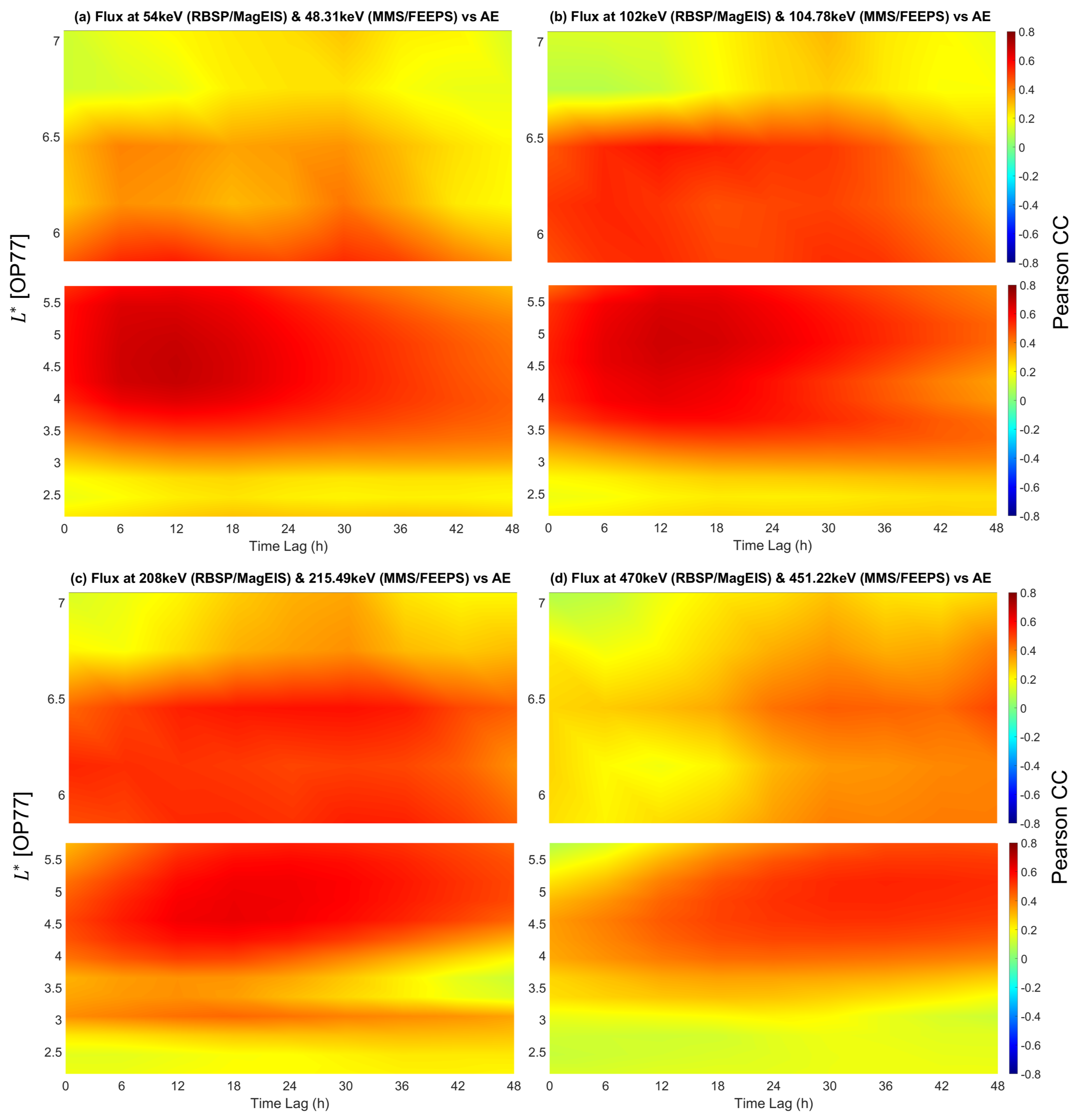
3.2.2. AE Index
4. Discussion
5. Conclusions
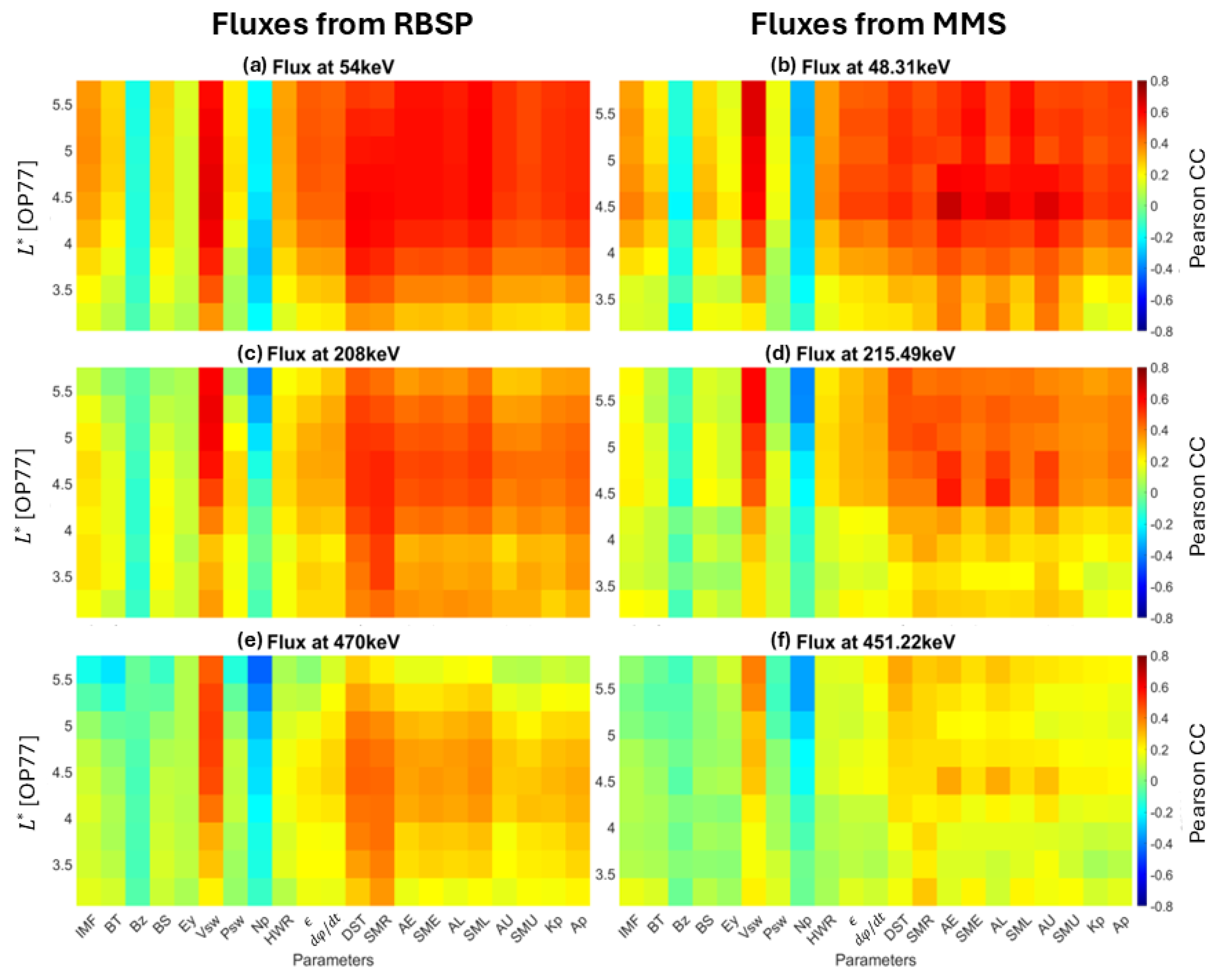
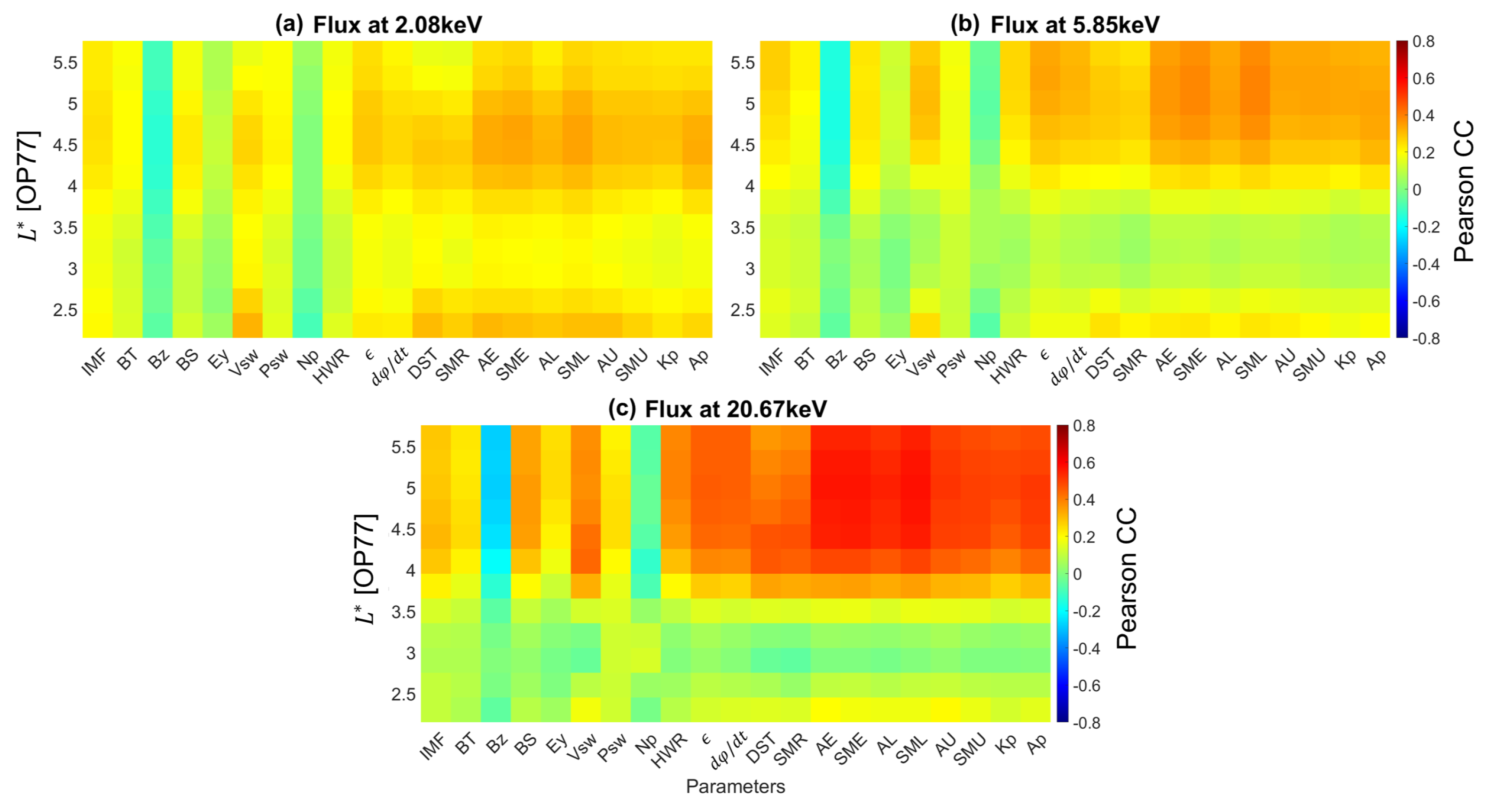
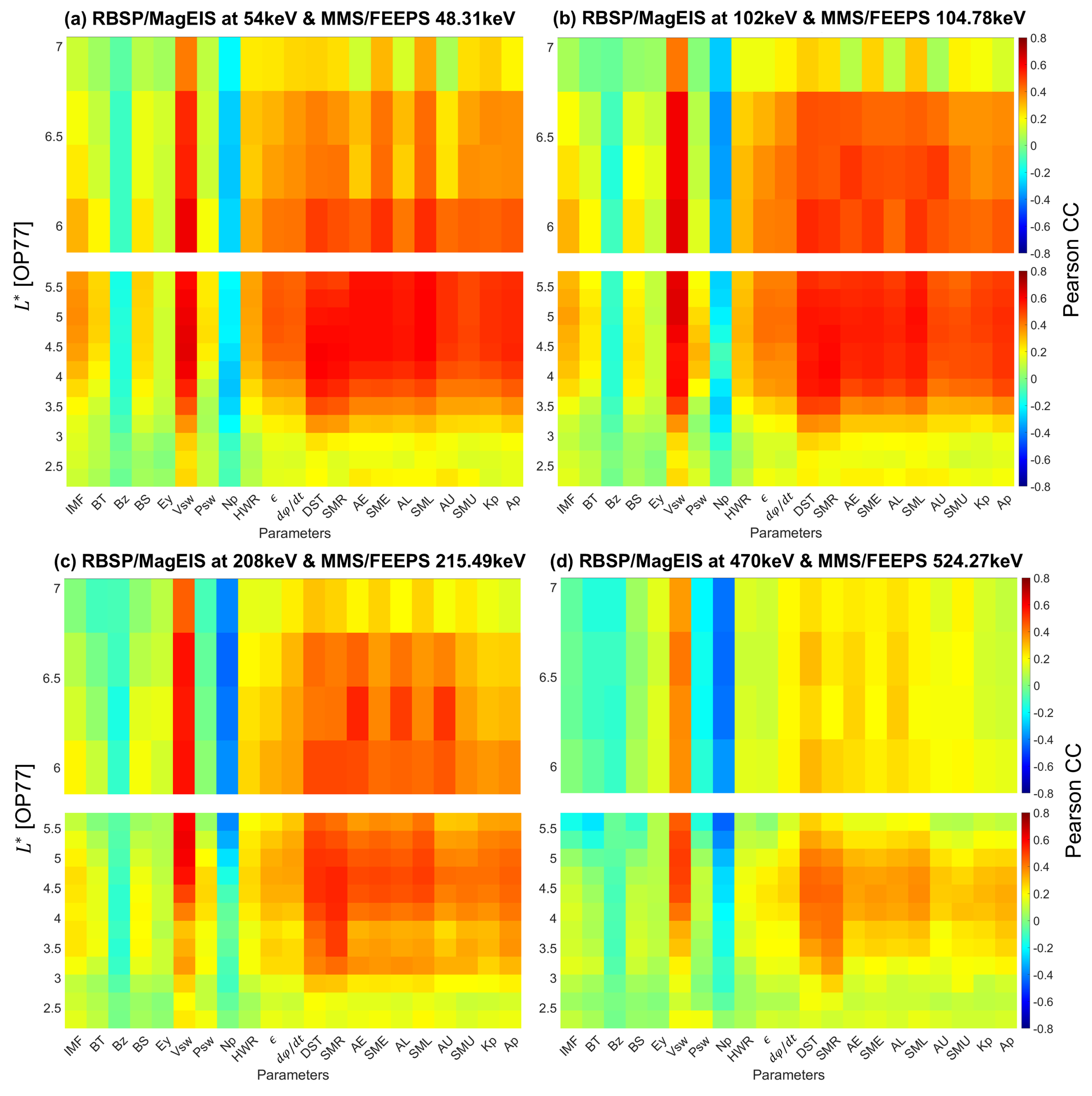
- Electron fluxes are well correlated with and the AE index across most energy channels, indicating that the variability of 1–500 keV electrons is the result of a delicate interplay between mechanisms for which these parameters are proxies. Additionally, these mechanisms require progressively longer timescales to influence electron fluxes as energy increases.
- Significant space weather parameters, i.e., , the coupling functions, and the geomagnetic indices, exhibit significant correlation with electrons at energies below 100 keV for , with correlation coefficients increasing as energy rises. Furthermore, this strong correlation extends to lower values as the energy increases, suggesting broader spatial influence, possibly because higher-energy electrons penetrate and get trapped in lower L-shells more effectively than lower-energy electrons. However, the correlation between the seed electron population (100–500 keV) and the parameters decreases and is confined in a smaller range, except for , where correlation remains consistently high.
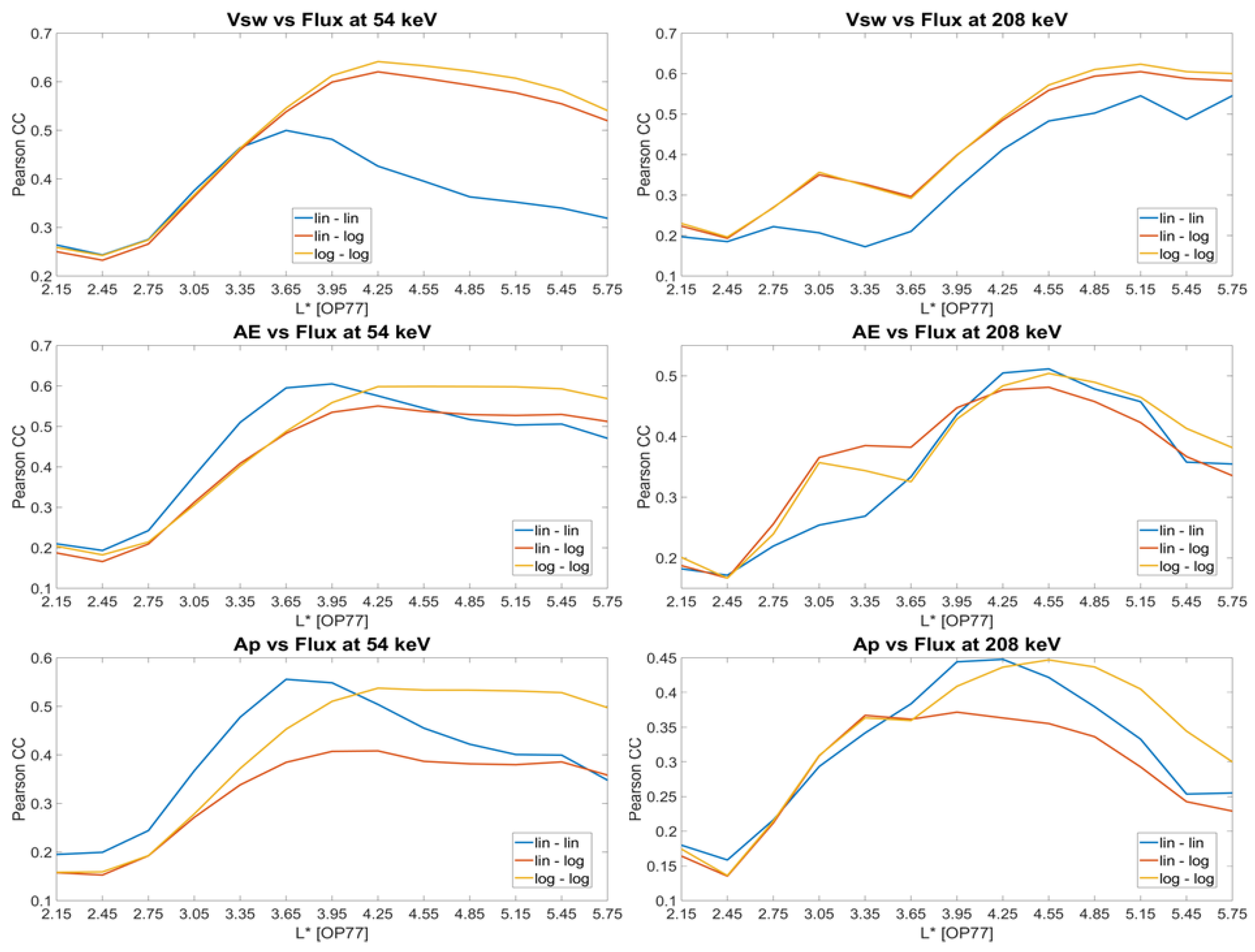
- is one of the most influential driving parameters for fluxes above 50 keV. The correlation strengthens with increasing energy, and peaks for electrons in the 100–250 keV energy range, suggesting that solar wind speed plays a crucial role in the behavior of seed electrons. Electrons of energies higher than 200 keV correlate stronger with after a lag of a few hours and until 48 h, indicating the importance of enhanced convection and/or radial diffusion.
- At the heart of the outer radiation belt, the response of the seed electron flux to solar wind speed variations is almost simultaneous, while the time lag values associated with the maximum correlation inwards and outwards of 4 suggest further diffusion. Moreover, the rate that the time lag increases at the inward transport of electrons indicates that it takes longer for electrons to fill the slot region than to diffuse outwards.
- Electron fluxes correlate strongly with the AE index in a wide energy range, particularly for energies above 20 keV, highlighting the significant role of substorm activity in influencing the source and seed populations (local acceleration). Fluxes above 50 keV correlate well with AE across the entire time lag range. Seed electrons correlate stronger with the index after a few hours, suggesting a delay in the results of substorm activity on electron fluxes. This delay is also longer with increasing energy, starting from 5 h at 50 keV and reaching 1 day for energies above 200 keV.
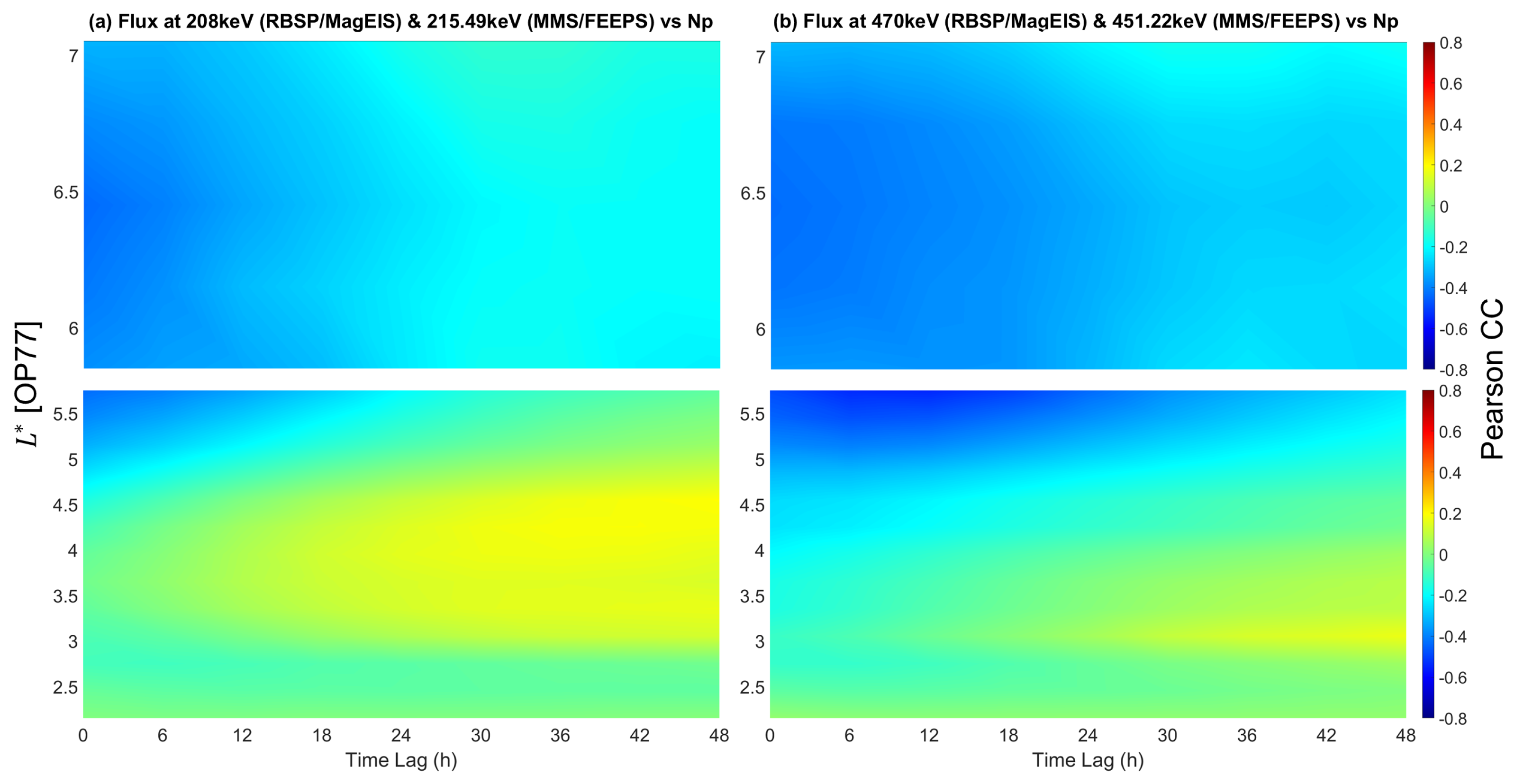
- reveals strong anti-correlation with electron fluxes of energies 200–500 keV for . With increasing energy, the correlation decreases further (stronger anti-correlation), indicating losses due to direct and/or indirect magnetopause shadowing.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AE | Auroral Electrojet (Index) |
| AL | Auroral Lower (Index) |
| Ap | Planetary A (Index) |
| AU | Auroral Upper (Index) |
| Dst | Disturbance Storm Time (Index) |
| ECT | Energetic Particle Composition and Thermal Suite |
| GEO | Geosynchronous Orbit |
| GOES | Geostationary Orbiting Environmental Satellites |
| HOPE | Helium Oxygen Proton Electron |
| HWR | Half-Wave Rectifier |
| IMF | Interplanetary Magnetic Field |
| Kp | Kennziffer Planetarisch (Index) |
| LANL | Los Alamos National Laboratory |
| MAGED | Magnetospheric Electron Detector |
| MagEIS | Magnetic Electron Ion Spectrometer |
| MMS | Magnetospheric Multiscale |
| RBSP | Radiation Belt Storm Probes |
| SME | SuperMAG Electrojet (Index) |
| SML | SuperMAG Lower (Index) |
| SMR | Substorm Magnetic Range (Index) |
| SMU | SuperMAG Upper (Index) |
| ULF | Ultra-Low Frequency |
| VLF | Very-Low Frequency |
Appendix A. Data Processing
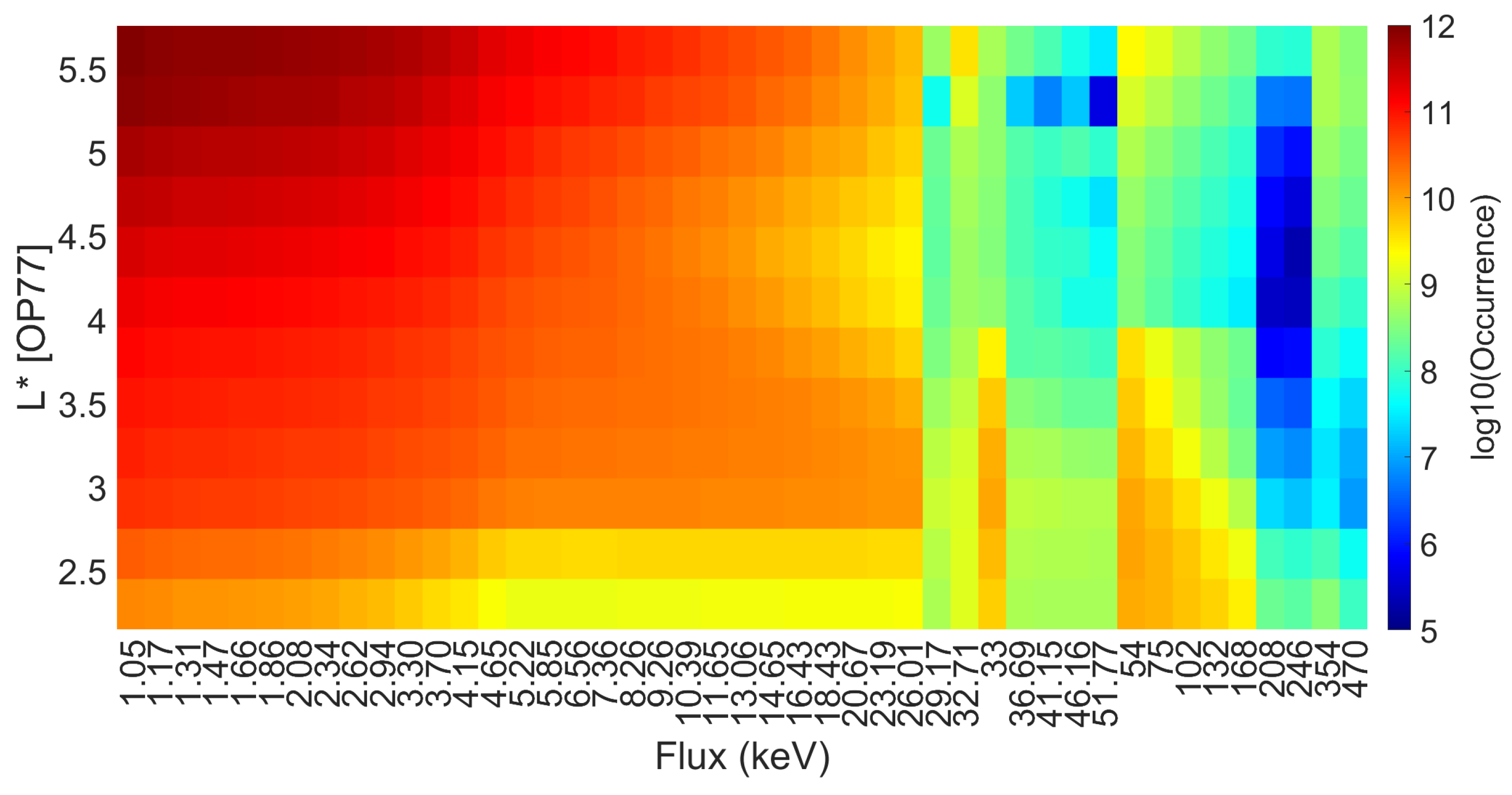
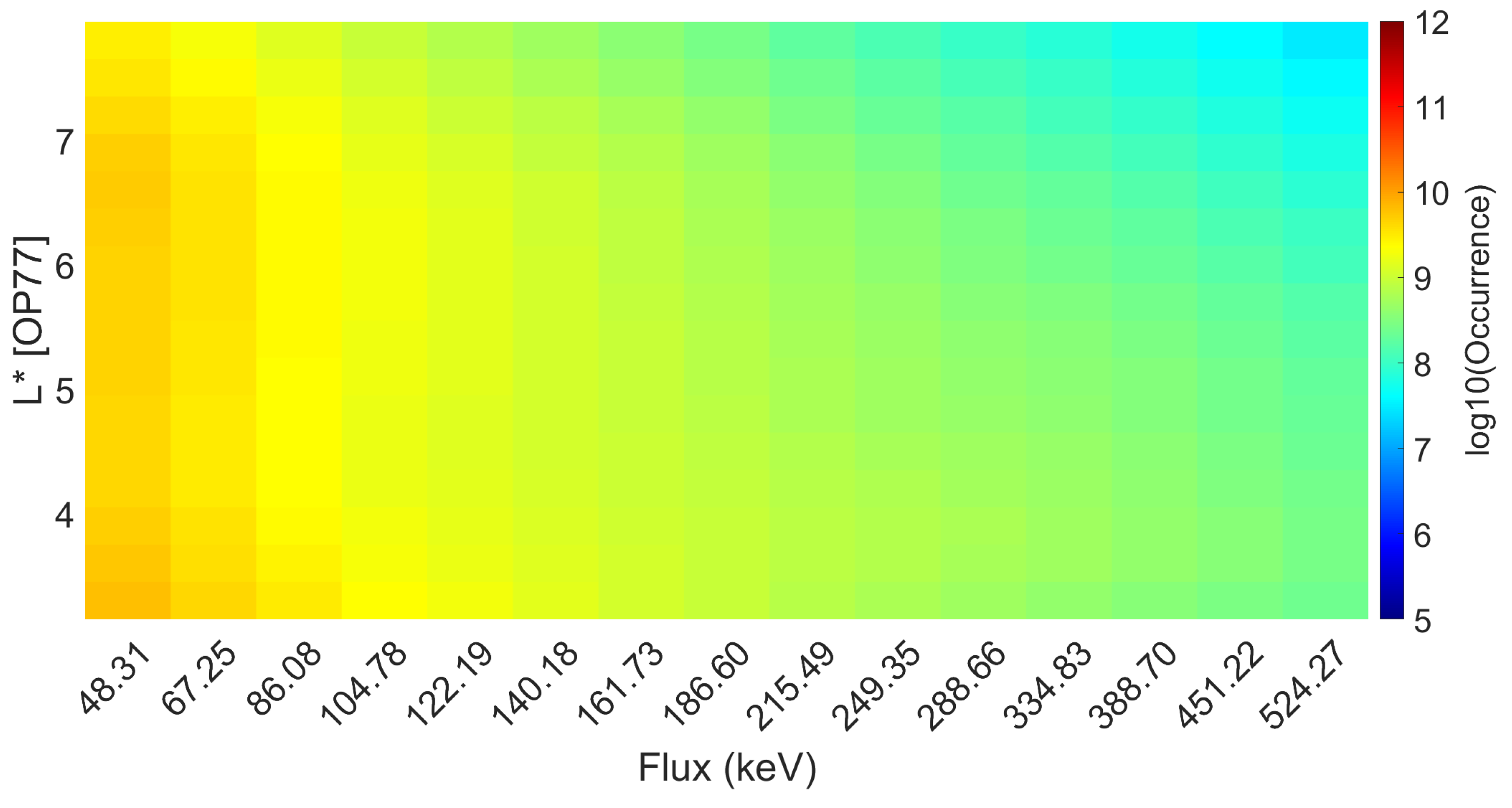
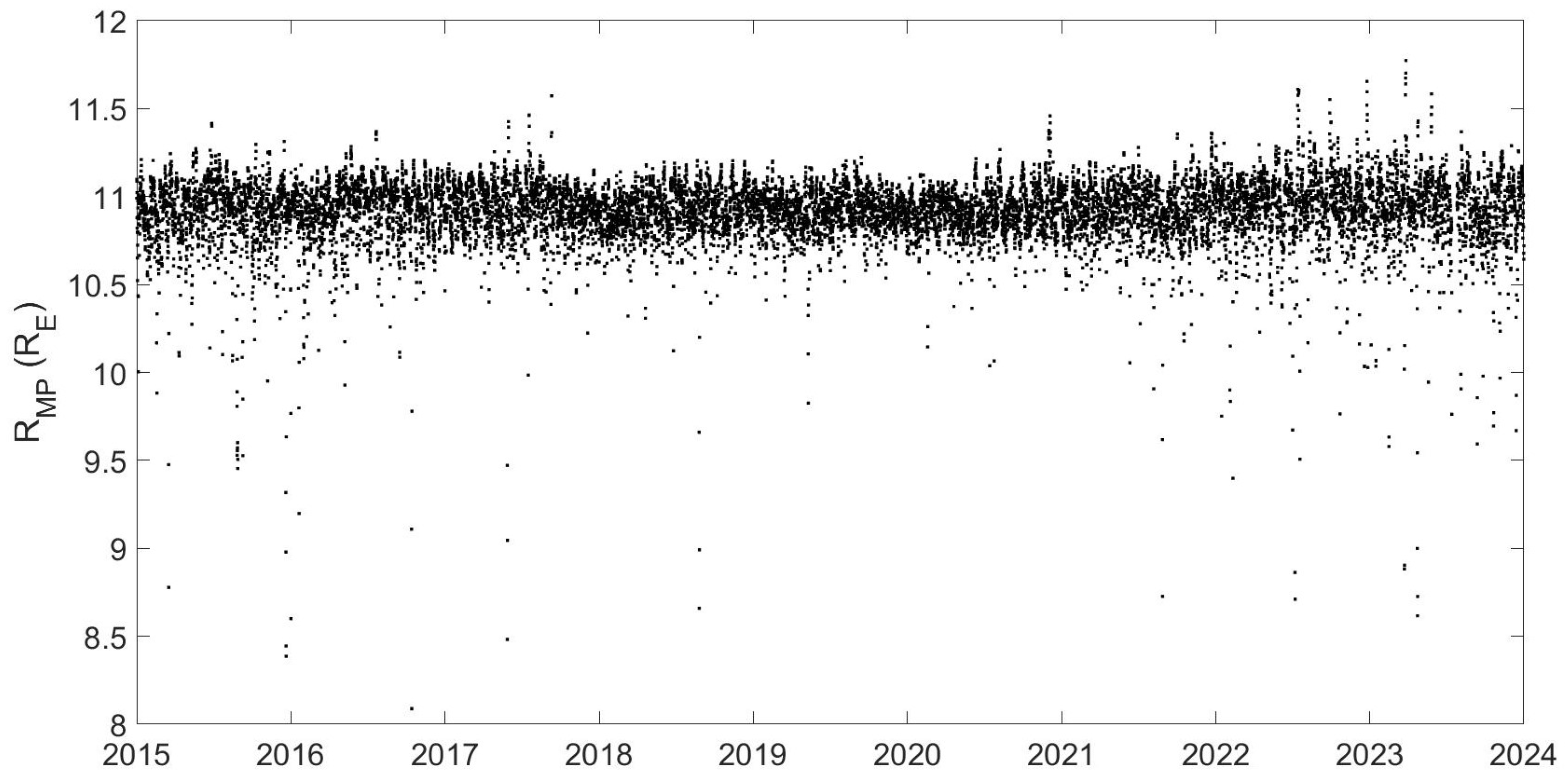
Appendix B. Correlation Analysis
Appendix C. Correlation Coefficients Between Flux and Np with Time Lag
| 1 | These coupling functions have demonstrated the ability to reproduce how the solar wind could interact with the magnetosphere in terms of correlating with geomagnetic indices. |
References
- Daglis, I.A.; Katsavrias, C.; Georgiou, M. From solar sneezing to killer electrons: Outer radiation belt response to solar eruptions. Philos. Trans. R. Soc. A 2019, 377, 20180097. [Google Scholar] [CrossRef]
- Reeves, G.D.; McAdams, K.L.; Friedel, R.H.W.; O’Brien, T.P. Acceleration and loss of relativistic electrons during geomagnetic storms. Geophys. Res. Lett. 2003, 30, 1529. [Google Scholar] [CrossRef]
- Katsavrias, C.; Daglis, I.A.; Li, W. On the statistics of acceleration and loss of relativistic electrons in the outer radiation belt: A superposed epoch analysis. J. Geophys. Res. Space Phys. 2019, 124, 2755–2768. [Google Scholar] [CrossRef]
- Katsavrias, C.; Sandberg, I.; Li, W.; Podladchikova, O.; Daglis, I.A.; Papadimitriou, C.; Aminalragia-Giamini, S. Highly relativistic electron flux enhancement during the weak geomagnetic storm of April-May 2017. J. Geophys. Res. Space Phys. 2019, 124, 4402–4413. [Google Scholar] [CrossRef]
- Li, W.; Thorne, R.M.; Ma, Q.; Ni, B.; Bortnik, J.; Baker, D.N.; Spence, H.E.; Reeves, G.; Kanekal, S.G.; Green, J.C.; et al. Radiation belt electron acceleration by chorus waves during the 17 March 2013 storm. J. Geophys. Res. Space Phys. 2014, 119, 4681–4693. [Google Scholar] [CrossRef]
- Nasi, A.; Daglis, I.A.; Katsavrias, C.; Li, W. Interplay of source/seed electrons and wave-particle interactions in producing relativistic electron psd enhancements in the outer van allen belt. J. Atmos. Sol.-Terr. Phys. 2020, 210, 105405. [Google Scholar] [CrossRef]
- Baker, D.N. The occurrence of operational anomalies in spacecraft and their relationship to space weather. IEEE Trans. Plasma Sci. 2000, 28, 2007–2016. [Google Scholar] [CrossRef]
- Horne, R.B.; Glauert, S.A.; Meredith, N.P.; Boscher, D.; Maget, V.; Heynderickx, D.; Pitchford, D. Space weather impacts on satellites and forecasting the Earth’s electron radiation belts with SPACECAST. Space Weather 2013, 11, 169–186. [Google Scholar] [CrossRef]
- O’Brien, T.P.; Lemon, C.L. Reanalysis of plasma measurements at geosynchronous orbit. Space Weather 2007, 5, S03007. [Google Scholar] [CrossRef]
- Thomsen, M.F.; Henderson, M.G.; Jordanova, V.K. Statistical properties of the surface-charging environment at geosynchronous orbit. Space Weather 2013, 11, 237–244. [Google Scholar] [CrossRef]
- Zheng, Y.; Ganushkina, N.Y.; Jiggens, P.; Jun, I.; Meier, M.; Minow, J.I.; O’Brien, T.P.; Pitchford, D.; Shprits, Y.; Tobiska, W.K.; et al. Space radiation and plasma effects on satellites and aviation: Quantities and metrics for tracking performance of space weather environment models. Space Weather 2019, 17, 1384–1403. [Google Scholar] [CrossRef] [PubMed]
- Katsavrias, C.; Aminalragia–Giamini, S.; Papadimitriou, C.; Sandberg, I.; Jiggens, P.; Daglis, I.A.; Evans, H. On the interplanetary parameter schemes which drive the variability of the source/seed electron population at GEO. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028939. [Google Scholar] [CrossRef]
- Smirnov, A.G.; Kronberg, E.A.; Latallerie, F.; Daly, P.W.; Aseev, N.; Shprits, Y.Y.; Kellerman, A.; Kasahara, S.; Turner, D.; Taylor, M.G.G.T. Electron intensity measurements by the cluster/ RAPID/IES instrument in Earth’s radiation belts and ring current. Space Weather 2019, 17, 553–566. [Google Scholar] [CrossRef]
- Sillanpää, I.; Ganushkina, N.Y.; Dubyagin, S.; Rodriguez, J.V. Electron fluxes at geostationary orbit from GOES MAGED data. Space Weather 2017, 15, 1602–1614. [Google Scholar] [CrossRef]
- Kellerman, A.C.; Shprits, Y.Y. On the influence of solar wind conditions on the outer-electron radiation belt. J. Geophys. Res. Space Phys. 2012, 117, A05217. [Google Scholar] [CrossRef]
- Shi, Y.; Zesta, E.; Lyons, L.R. Features of energetic particle radial profiles inferred from geosynchronous responses to solar wind dynamic pressure enhancements. Ann. Geophys. 2009, 27, 851–859. [Google Scholar] [CrossRef]
- Paulikas, G.A.; Blake, J.B. Effects of the Solar Wind on Magnetospheric Dynamics: Energetic Electrons at the Synchronous Orbit. In Quantitative Modeling of Magnetospheric Processes; Geophysical Monograph Series; Olson, W.P., Ed.; American Geophysical Union: Washington, DC, USA, 1979; Volume 21, pp. 180–202. [Google Scholar] [CrossRef]
- Reeves, G.D.; Morley, S.K.; Friedel, R.H.W.; Henderson, M.G.; Cayton, T.E.; Cunningham, G.; Blake, J.B.; Christensen, R.A.; Thomsen, D. On the relationship between relativistic electron flux, solar wind velocity: Paulikas and Blake revisited. J. Geophys. Res. Space Phys. 2011, 116, A02213. [Google Scholar] [CrossRef]
- Li, X.; Baker, D.N.; Temerin, M.; Reeves, G.; Friedel, R.; Shen, C. Energetic electrons, 50 keV to 6 MeV, at geosynchronous orbit: Their responses to solar wind variations. Space Weather 2005, 3, S04001. [Google Scholar] [CrossRef]
- Burton, R.K.; McPherron, R.L.; Russell, C.T. An empirical relationship between interplanetary conditions and Dst. J. Geophys. Res. Space Phys. 1975, 80, 4204–4214. [Google Scholar] [CrossRef]
- Akasofu, S.-I. Energy coupling between the solar wind and the magnetosphere. Space Sci. Rev. 1981, 28, 121–190. [Google Scholar] [CrossRef]
- Newell, P.T.; Sotirelis, T.; Liou, K.; Meng, C.-I.; Rich, F.J. A nearly universal solar wind-magnetosphere coupling function inferred from 10 magnetospheric state variables. J. Geophys. Res. Space Phys. 2007, 112, A01206. [Google Scholar] [CrossRef]
- Burch, J.L.; Moore, T.E.; Torbert, R.B.; Giles, B.L. Magnetospheric Multiscale Overview and Science Objectives. Space Sci. Rev. 2015, 199, 5–21. [Google Scholar] [CrossRef]
- Blake, J.B.; Mauk, B.H.; Baker, D.N.; Carranza, P.; Clemmons, J.H.; Craft, J.; Crain, W.R.; Crew, A.; Dotan, Y.; Fennell, J.F.; et al. The Fly’s Eye Energetic Particle Spectrometer (FEEPS) Sensors for the Magnetospheric Multiscale (MMS) Mission. Space Sci. Rev. 2016, 199, 309–329. [Google Scholar] [CrossRef]
- Boyd, A.J.; Reeves, G.D.; Spence, H.E.; Funsten, H.O.; Larsen, B.A.; Skoug, R.M.; Blake, J.B.; Fennell, J.F.; Claudepierre, S.G.; Baker, D.N.; et al. RBSP-ECT Combined Spin-Averaged Electron Flux Data Product. J. Geophys. Res. Space Phys. 2019, 124, 9124–9136. [Google Scholar] [CrossRef] [PubMed]
- Olson, W.P.; Pfitzer, K.A. Magnetospheric Magnetic Field Modeling. Annual Scientific Report. United States. 1977. Available online: https://www.osti.gov/biblio/7212748 (accessed on 4 December 2024).
- Shue, J.-H.; Song, P.; Russell, C.T.; Steinberg, J.T.; Chao, J.K.; Zastenker, G.; Vaisberg, O.L.; Kokubun, S.; Singer, H.J.; Detman, T.R.; et al. Magnetopause location under extreme solar wind conditions. J. Geophys. Res. Space Phys. 1998, 103, 17691–17700. [Google Scholar] [CrossRef]
- Johnson, J.R.; Wing, S. A solar cycle dependence of nonlinearity in magnetospheric activity. J. Geophys. Res. Space Phys. 2005, 110, A04211. [Google Scholar] [CrossRef]
- Wing, S.; Johnson, J.R.; Camporeale, E.; Reeves, G.D. Information theoretical approach to discovering solar wind drivers of the outer radiation belt. J. Geophys. Res. Space Phys. 2016, 121, 9378–9399. [Google Scholar] [CrossRef]
- Manshour, P.; Papadimitriou, C.; Balasis, G.; Paluš, M. Causal inference inthe outer radiation belt: Evidence for localacceleration. Geophys. Res. 2024, 51, e2023GL107166. [Google Scholar] [CrossRef]
- Turner, D.L.; Fennell, J.F.; Blake, J.B.; Claudepierre, S.G.; Clemmons, J.H.; Jaynes, A.N.; Leonard, T.; Baker, D.N.; Cohen, I.J.; Gkioulidou, M.; et al. Multipoint Observations of Energetic Particle Injections and Substorm Activity During a Conjunction Between Magnetospheric Multiscale (MMS) and Van Allen Probes. J. Geophys. Res. Space Phys. 2017, 122, 11481–11504. [Google Scholar] [CrossRef]
- Miyoshi, Y.; Kataoka, R.; Kasahara, Y.; Kumamoto, A.; Nagai, T.; Thomsen, M.F. High-speed solar wind with southward interplanetary magnetic field causes relativistic electron flux enhancement of the outer radiation belt via enhanced condition of whistler waves. Geophys. Res. Lett. 2013, 40, 4520–4525. [Google Scholar] [CrossRef]
- Claudepierre, S.G.; Elkington, S.R.; Wiltberger, M. Solar wind driving of magnetospheric ULF waves: Pulsations driven by velocity shear at the magnetopause. J. Geophys. Res. Space Phys. 2008, 113, A05218. [Google Scholar] [CrossRef]
- Shprits, Y.Y.; Subbotin, D.A.; Meredith, N.P.; Elkington, S.R. Review of modeling of losses and sources of relativistic electrons in the outer radiation belt II: Local acceleration and loss. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1694–1713. [Google Scholar] [CrossRef]
- Thorne, R.M.; Li, W.; Ni, B.; Ma, Q.; Bortnik, J.; Chen, L.; Baker, D.N.; Spence, H.E.; Reeves, G.D.; Henderson, M.G.; et al. Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 2013, 504, 411–414. [Google Scholar] [CrossRef]
- Bortnik, J.; Thorne, R.M.; Li, W.; Tao, X. Chorus waves in geospace and their influence on radiation belt dynamics. In Waves, Particles, and Storms in Geospace: A Complex Interplay; Balasis, G., Daglis, I.A., Mann, I.R., Eds.; Oxford University Press: Oxford, UK, 2016; pp. 193–212. ISBN 9780198705246. [Google Scholar]
- Li, W.; Ma, Q.; Thorne, R.M.; Bortnik, J.; Zhang, X.J.; Li, J.; Baker, D.N.; Reeves, G.D.; Spence, H.E.; Kletzing, C.A.; et al. Radiation belt electron acceleration during the 17 March 2015 geomagnetic storm: Observations and simulations. J. Geophys. Res. Space Phys. 2016, 121, 5520–5536. [Google Scholar] [CrossRef]
- Horne, R.B.; Thorne, R.M.; Glauert, S.A.; Meredith, N.P.; Pokhotelov, D.; Santolík, O. Electron acceleration in the Van Allen radiation belts by fast magnetosonic waves. Geophys. Res. Lett. 2007, 34, L17107. [Google Scholar] [CrossRef]
- Reeves, G.D.; Friedel, R.H.; Larsen, B.A.; Skoug, R.M.; Funsten, H.O.; Claudepierre, S.G.; Fennell, J.F.; Turner, D.L.; Denton, M.H.; Spence, H.E.; et al. Energy-dependent dynamics of keV to MeV electrons in the inner zone, outer zone, and slot regions. J. Geophys. Res. Space Phys. 2016, 121, 397–412. [Google Scholar] [CrossRef]
- Turner, D.L.; Shprits, Y.; Hartinger, M.; Angelopoulos, V. Explaining sudden losses of outer radiation belt electrons during geomagnetic storms. Nature 2012, 8, 208–212. [Google Scholar] [CrossRef]
- Katsavrias, C.; Daglis, I.A.; Turner, D.L.; Sandberg, I.; Papadimitriou, C.; Georgiou, M.; Balasis, G. Nonstorm loss of relativistic electrons in the outer radiation belt. Geophys. Res. Lett. 2015, 42, 10521–10530. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christodoulou, E.; Katsavrias, C.; Kordakis, P.; Daglis, I.A. Influence of Solar Wind Driving and Geomagnetic Activity on the Variability of Sub-Relativistic Electrons in the Inner Magnetosphere. Universe 2025, 11, 101. https://doi.org/10.3390/universe11030101
Christodoulou E, Katsavrias C, Kordakis P, Daglis IA. Influence of Solar Wind Driving and Geomagnetic Activity on the Variability of Sub-Relativistic Electrons in the Inner Magnetosphere. Universe. 2025; 11(3):101. https://doi.org/10.3390/universe11030101
Chicago/Turabian StyleChristodoulou, Evangelia, Christos Katsavrias, Panayotis Kordakis, and Ioannis A. Daglis. 2025. "Influence of Solar Wind Driving and Geomagnetic Activity on the Variability of Sub-Relativistic Electrons in the Inner Magnetosphere" Universe 11, no. 3: 101. https://doi.org/10.3390/universe11030101
APA StyleChristodoulou, E., Katsavrias, C., Kordakis, P., & Daglis, I. A. (2025). Influence of Solar Wind Driving and Geomagnetic Activity on the Variability of Sub-Relativistic Electrons in the Inner Magnetosphere. Universe, 11(3), 101. https://doi.org/10.3390/universe11030101





