From Known to Unknown: Cosmic Ray Transitions from the Sun, the Galaxy, and Extra-Galactic Systems
Abstract
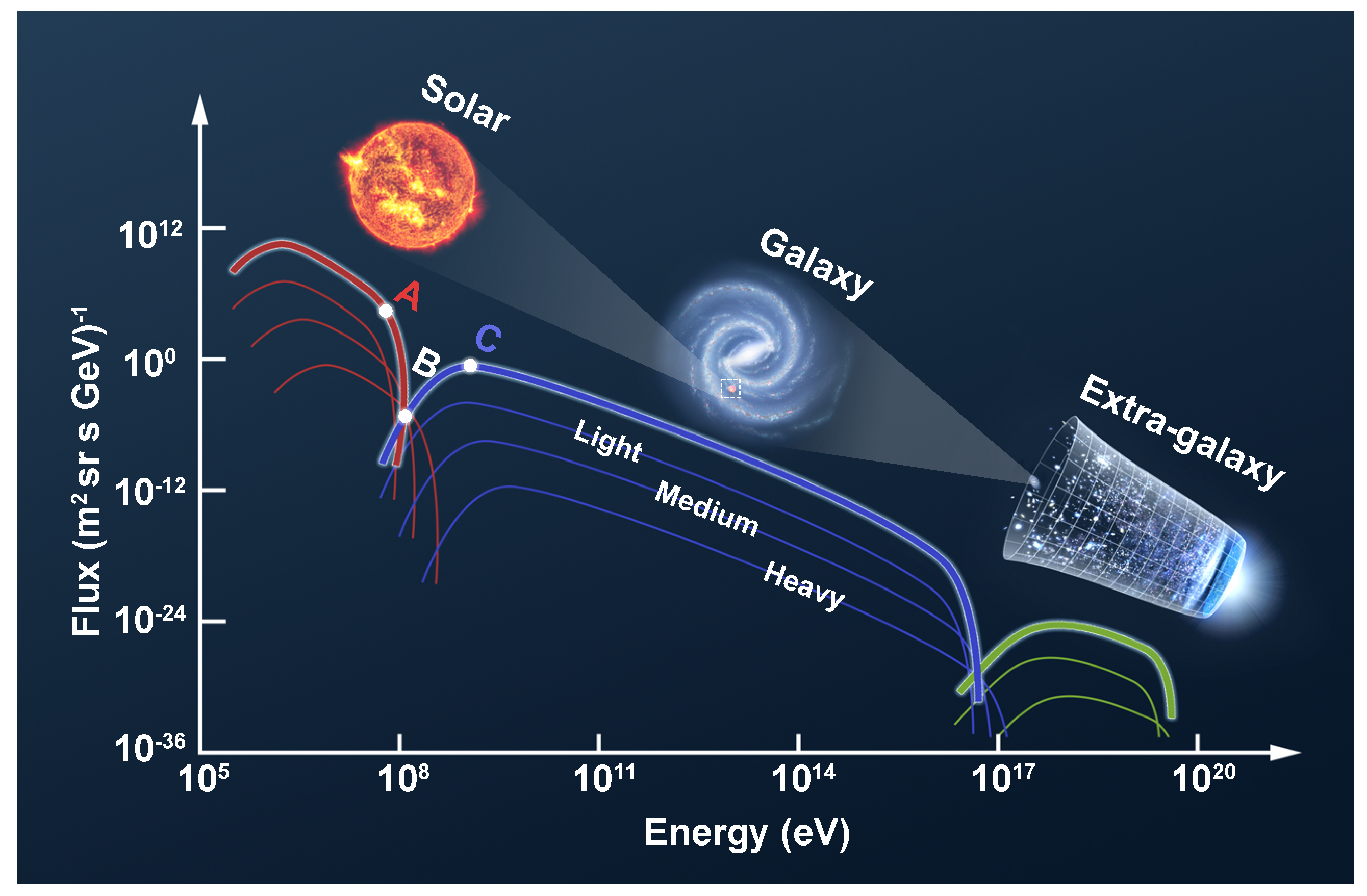
1. Introduction
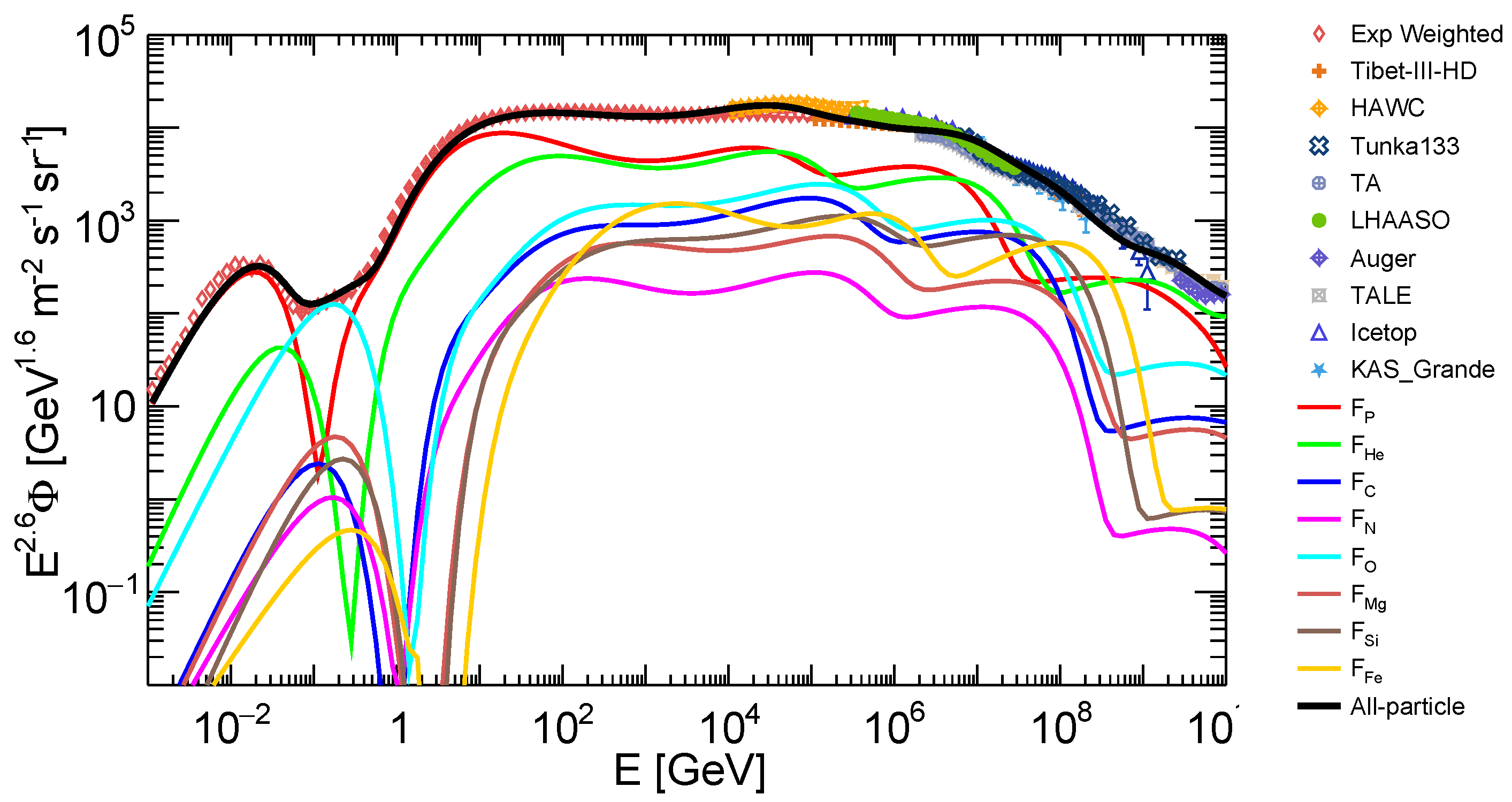
2. Dataset and Method

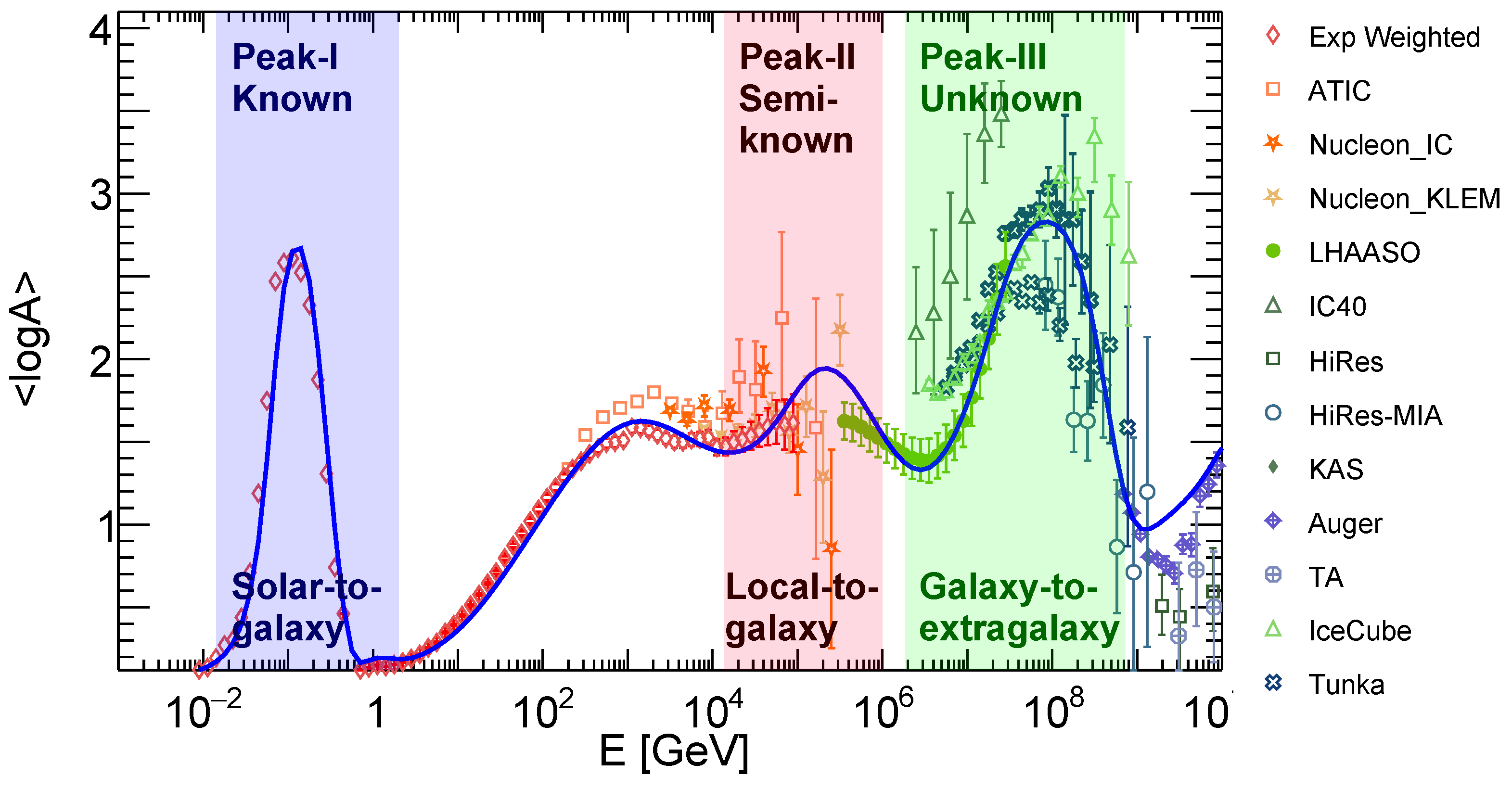
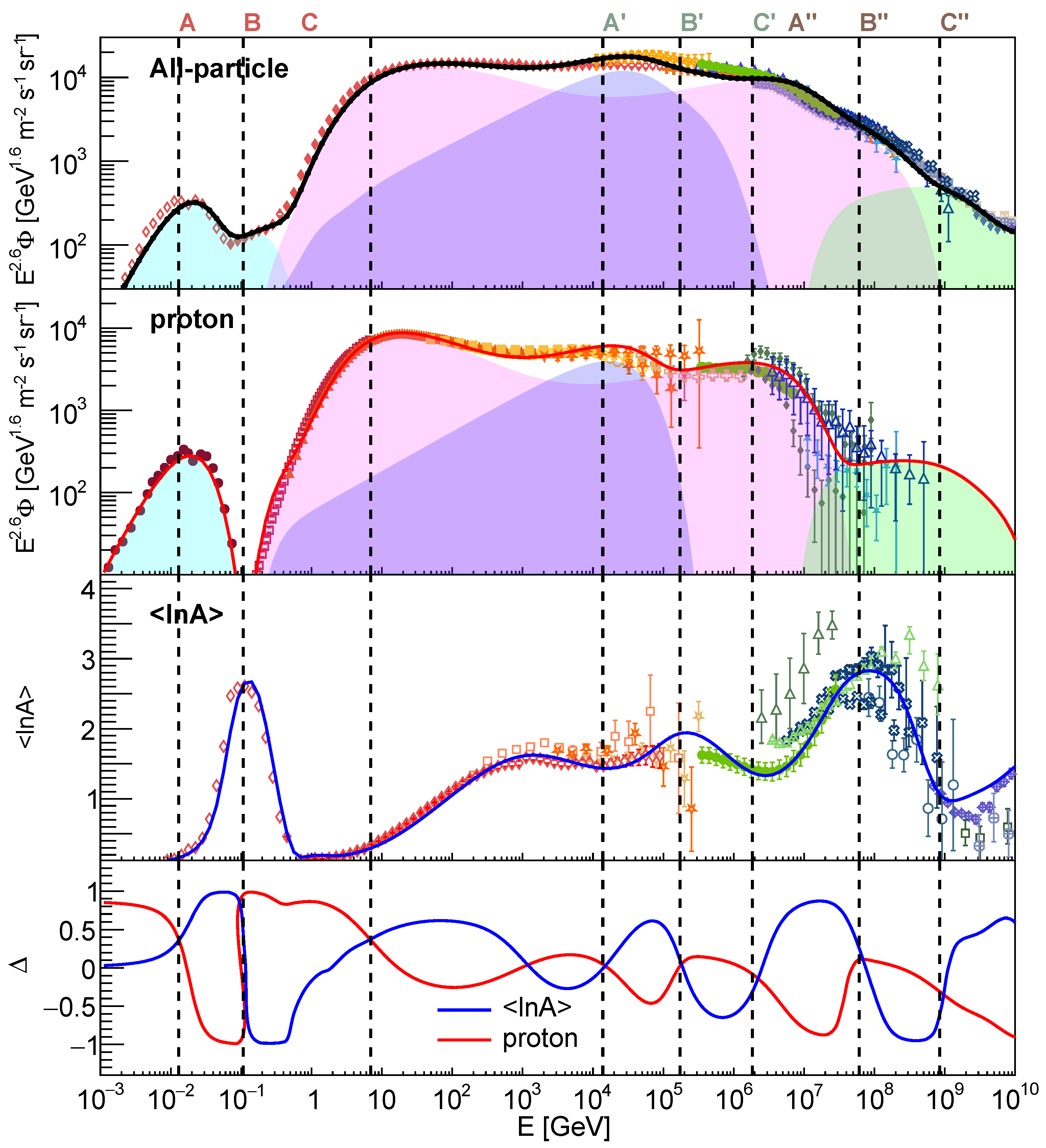
3. Results
4. Conclusions
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Fitting Results

References
- Owen, E.R.; Wu, K.; Inoue, Y.; Yang, H.Y.K.; Mitchell, A.M.W. Cosmic Ray Processes in Galactic Ecosystems. Galaxies 2023, 11, 86. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.A.; An, Q.; Axikegu, L.X.B.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, H.; et al. Ultrahigh-energy photons up to 1.4 petaelectronvolts from 12 γ-ray Galactic sources. Nature 2021, 594, 33–36. [Google Scholar] [CrossRef]
- Cao, Z. et al. [Lhaaso Collaboration] An ultrahigh-energy γ-ray bubble powered by a super PeVatron. Sci. Bull. 2024, 69, 449–457. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.; An, Q.; Axikegu; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, J.T.; et al. The First LHAASO Catalog of Gamma-Ray Sources. Astrophys. J. Suppl. Ser. 2024, 271, 25. [Google Scholar] [CrossRef]
- Alfaro, R.; Alvarez, C.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Babu, R.; Belmont-Moreno, E.; Caballero-Mora, K.S.; Capistrán, T.; Carramiñana, A.; et al. Ultra-high-energy gamma-ray bubble around microquasar V4641 Sgr. Nature 2024, 634, 557–560. [Google Scholar] [CrossRef]
- Liu, R. et al. [LHAASO Collaboration] Ultrahigh-Energy Gamma-ray Emission Associated with Black Hole-Jet Systems. arXiv 2024, arXiv:2410.08988. [Google Scholar] [CrossRef]
- Aharonian, F.; Bykov, A.; Parizot, E.; Ptuskin, V.; Watson, A. Cosmic Rays in Galactic and Extragalactic Magnetic Fields. Space Sci. Rev. 2012, 166, 97–132. [Google Scholar] [CrossRef]
- Aloisio, R.; Berezinsky, V.; Blasi, P.; Ostapchenko, S. Signatures of the transition from galactic to extragalactic cosmic rays. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2008, 77, 025007. [Google Scholar] [CrossRef]
- Giacinti, G.; Kachelrieß, M.; Semikoz, D.V.; Sigl, G. Cosmic ray anisotropy as signature for the transition from galactic to extragalactic cosmic rays. J. Cosmol. Astropart. Phys. 2012, 2012, 031. [Google Scholar] [CrossRef]
- Aloisio, R.; Berezinsky, V.; Gazizov, A. Transition from galactic to extragalactic cosmic rays. Astropart. Phys. 2012, 39, 129–143. [Google Scholar] [CrossRef]
- Berezinsky, V.; Gazizov, A.Z.; Grigorieva, S.I. Dip in UHECR spectrum as signature of proton interaction with CMB [rapid communication]. Phys. Lett. B 2005, 612, 147–153. [Google Scholar] [CrossRef]
- Berezinsky, V.; Gazizov, A.; Grigorieva, S. On astrophysical solution to ultrahigh energy cosmic rays. Phys. Rev.—Part Fields Gravit. Cosmol. 2006, 74, 043005. [Google Scholar] [CrossRef]
- Deligny, O. Cosmic rays around 1018 eV: Implications of contemporary measurements on the origin of the ankle feature. C. R. Phys. 2014, 15, 367–375. [Google Scholar] [CrossRef]
- Aloisio, R.; Berezinsky, V.; Blasi, P.; Gazizov, A.; Grigorieva, S.; Hnatyk, B. A dip in the UHECR spectrum and the transition from galactic to extragalactic cosmic rays. Astropart. Phys. 2007, 27, 76–91. [Google Scholar] [CrossRef]
- Kachelrieß, M.; Semikoz, D.V. Cosmic ray models. Prog. Part. Nucl. Phys. 2019, 109, 103710. [Google Scholar] [CrossRef]
- Cristofari, P. The transition from Galactic to extragalactic cosmic rays: The high-energy end of the Galactic spectrum. Eur. Phys. J. Web Conf. 2023, 283, 04002. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.; Axikegu; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Bian, W.; Bukevich,, A.V.; et al. Measurements of All-Particle Energy Spectrum and Mean Logarithmic Mass of Cosmic Rays from 0.3 to 30 PeV with LHAASO-KM2A. Phys. Rev. Lett. 2024, 132, 131002. [Google Scholar] [CrossRef]
- Giacalone, J.; Fahr, H.; Fichtner, H.; Florinski, V.; Heber, B.; Hill, M.E.; Kóta, J.; Leske, R.A.; Potgieter, M.S.; Rankin, J.S. Anomalous Cosmic Rays and Heliospheric Energetic Particles. Space Sci. Rev. 2022, 218, 22. [Google Scholar] [CrossRef]
- Ptuskin, V.S. Propagation, Confinement Models, and Large-Scale Dynamical Effects of Galactic Cosmic Rays. In The Astrophysics of Galactic Cosmic Rays; Diehl, R., Parizot, E., Kallenbach, R., Von Steiger, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 13, pp. 281–293. [Google Scholar] [CrossRef]
- Lipari, P.; Vernetto, S. The shape of the cosmic ray proton spectrum. Astropart. Phys. 2020, 120, 102441. [Google Scholar] [CrossRef]
- von Rosenvinge, T.; Cane, H.V. Solar Energetic Particles: An Overview. Geophys. Monogr. Ser. 2006, 165, 103–114. [Google Scholar] [CrossRef]
- Mewaldt, R.; Cohen, C.; Mason, G.; Desai, M.; Labrador, A.; Lee, M.; Li, G. Solar Energetic Particle Spectral Breaks. In Proceedings of the AGU Spring Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2008; Volume 2008, p. SH41A-10. [Google Scholar]
- Mewaldt, R.A. Solar Energetic Particle Composition, Energy Spectra, and Space Weather. In Solar Dynamics and Its Effects on the Heliosphere and Earth; Series: Space Sciences Series of ISSI; Baker, D.N., Klecker, B., Schwartz, S.J., Schwenn, R., von Steiger, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 22, pp. 303–316. [Google Scholar] [CrossRef]
- Peron, G.; Casanova, S.; Gabici, S.; Baghmanyan, V.; Aharonian, F. The contribution of winds from star clusters to the Galactic cosmic-ray population. Nat. Astron. 2024, 8, 530–537. [Google Scholar] [CrossRef]
- Corti, C.; Bindi, V.; Consolandi, C.; Whitman, K. Solar Modulation of the Local Interstellar Spectrum with Voyager 1, AMS-02, PAMELA, and BESS. Astrophys. J. 2016, 829, 8. [Google Scholar] [CrossRef]
- An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; Chen, J.L.; et al. Measurement of the cosmic ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Sci. Adv. 2019, 5, eaax3793. [Google Scholar] [CrossRef]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bongi, M.; Brogi, P.; Bruno, A.; et al. Observation of Spectral Structures in the Flux of Cosmic-Ray Protons from 50 GeV to 60 TeV with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2022, 129, 101102. [Google Scholar] [CrossRef]
- Alemanno, F.; An, Q.; Azzarello, P.; Barbato, F.C.T.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Catanzani, E.; Chang, J.; Chen, D.Y.; et al. Measurement of the Cosmic Ray Helium Energy Spectrum from 70 GeV to 80 TeV with the DAMPE Space Mission. Phys. Rev. Lett. 2021, 126, 201102. [Google Scholar] [CrossRef]
- Qiao, B.Q.; Guo, Y.Q.; Liu, W.; Bi, X.J. Nearby SNR: A Possible Common Origin of Multi-messenger Anomalies in the Spectra, Ratios, and Anisotropy of Cosmic Rays. Astrophys. J. 2023, 956, 75. [Google Scholar] [CrossRef]
- Mollerach, S.; Roulet, E. Extragalactic cosmic rays diffusing from two populations of sources. Phys. Rev. D 2020, 101, 103024. [Google Scholar] [CrossRef]
- Das, S.; Razzaque, S.; Gupta, N. Modeling the spectrum and composition of ultrahigh-energy cosmic rays with two populations of extragalactic sources. Eur. Phys. J. C 2021, 81, 59. [Google Scholar] [CrossRef]
- Blandford, R.; Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 1987, 154, 1–75. [Google Scholar] [CrossRef]
- Amenomori, M.; Bi, X.J.; Chen, D.; Cui, S.W.; Danzengluobu; Ding, L.K.; Ding, X.H.; Fan, C.; Feng, C.F.; Feng, Z.; et al. The All-Particle Spectrum of Primary Cosmic Rays in the Wide Energy Range from 1014 to 1017 eV Observed with the Tibet-III Air-Shower Array. Astrophys. J. 2008, 678, 1165–1179. [Google Scholar] [CrossRef]
- Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Barber, A.S.; Becerril, A.; Belmont-Moreno, E.; et al. All-particle cosmic ray energy spectrum measured by the HAWC experiment from 10 to 500 TeV. Phys. Rev. D 2017, 96, 122001. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Amin, N.M.; Andeen, K.; et al. Cosmic ray spectrum from 250 TeV to 10 PeV using IceTop. Phys. Rev. D 2020, 102, 122001. [Google Scholar] [CrossRef]
- Abbasi, R.U.; Abe, M.; Abu-Zayyad, T.; Allen, M.; Azuma, R.; Barcikowski, E.; Belz, J.W.; Bergman, D.R.; Blake, S.A.; Cady, R.; et al. The Cosmic Ray Energy Spectrum between 2 PeV and 2 EeV Observed with the TALE Detector in Monocular Mode. Astrophys. J. 2018, 865, 74. [Google Scholar] [CrossRef]
- Antoni, T.; Apel, W.D.; Badea, A.F.; Bekk, K.; Bercuci, A.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Chilingarian, A.; Daumiller, K.; et al. KASCADE measurements of energy spectra for elemental groups of cosmic rays: Results and open problems. Astropart. Phys. 2005, 24, 1–25. [Google Scholar] [CrossRef]
- Apel, W.D.; Arteaga-Velázquez, J.C.; Bekk, K.; Bertaina, M.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Cantoni, E.; Chiavassa, A.; Cossavella, F.; et al. KASCADE-Grande measurements of energy spectra for elemental groups of cosmic rays. Astropart. Phys. 2013, 47, 54–66. [Google Scholar] [CrossRef]
- Aab, A.; Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almela, A.; Alvarez Castillo, J.; Alvarez-Muñiz, J.; Alves Batista, R.; Anastasi, G.A.; et al. Measurement of the cosmic-ray energy spectrum above 2.5 × 10 18 eV using the Pierre Auger Observatory. Phys. Rev. D 2020, 102, 062005. [Google Scholar] [CrossRef]
- Budnev, N.M.; Chiavassa, A.; Gress, O.A.; Gress, T.I.; Dyachok, A.N.; Karpov, N.I.; Kalmykov, N.N.; Korosteleva, E.E.; Kozhin, V.A.; Kuzmichev, L.A.; et al. The primary cosmic-ray energy spectrum measured with the Tunka-133 array. Astropart. Phys. 2020, 117, 102406. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Barao, F.; Barrin, L.; Bartoloni, A.; Başeğmez-du Pree, S.; Bates, J.; et al. The Alpha Magnetic Spectrometer (AMS) on the international space station: Part II—Results from the first seven years. Phys. Rep. 2021, 894, 1–116. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Anderson, T.; Barrau, A.; Conklin, N.B.; Coutu, S.; Derome, L.; Han, J.H.; Jeon, J.A.; Kim, K.C.; Kim, M.H.; et al. Proton and Helium Spectra from the CREAM-III Flight. Astrophys. J. 2017, 839, 5. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Borisov, S.; et al. PAMELA Measurements of Cosmic-Ray Proton and Helium Spectra. Science 2011, 332, 69. [Google Scholar] [CrossRef]
- Varsi, F.; Ahmad, S.; Chakraborty, M.; Chandra, A.; Dugad, S.R.; Goswami, U.D.; Gupta, S.K.; Hariharan, B.; Hayashi, Y.; Jagadeesan, P.; et al. Evidence of a Hardening in the Cosmic Ray Proton Spectrum at around 166 TeV Observed by the GRAPES-3 Experiment. Phys. Rev. Lett. 2024, 132, 051002. [Google Scholar] [CrossRef] [PubMed]
- Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; Panov, A.; Podorozhny, D.; Tkachenko, A.; Tkachev, L.; Turundaevskiy, A.; et al. Energy spectra of abundant cosmic-ray nuclei in the NUCLEON experiment. Adv. Space Res. 2019, 64, 2546–2558. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Andeen, K.; Anderson, T.; Ansseau, I.; et al. Cosmic ray spectrum and composition from PeV to EeV using 3 years of data from IceTop and IceCube. Phys. Rev. D 2019, 100, 082002. [Google Scholar] [CrossRef]
- Kuznetsov, M.Y.; Petrov, N.A.; Plokhikh, I.A.; Sotnikov, V.V. Energy spectra of elemental groups of cosmic rays with the KASCADE experiment data and machine learning. J. Cosmol. Astropart. Phys. 2024, 2024, 125. [Google Scholar] [CrossRef]
- Ahn, H.S.; Allison, P.; Bagliesi, M.G.; Barbier, L.; Beatty, J.J.; Bigongiari, G.; Brandt, T.J.; Childers, J.T.; Conklin, N.B.; Coutu, S.; et al. Energy Spectra of Cosmic-ray Nuclei at High Energies. Astrophys. J. 2009, 707, 593–603. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Barao, F.; Barrin, L.; Bartoloni, A.; Başeǧmez-du Pree, S.; Battiston, R.; et al. Properties of Neon, Magnesium, and Silicon Primary Cosmic Rays Results from the Alpha Magnetic Spectrometer. Phys. Rev. Lett. 2020, 124, 211102. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Allen, M.S.; Alpat, B.; Ambrosi, G.; Arruda, L.; Attig, N.; Barao, F.; Barrin, L.; Bartoloni, A.; et al. Properties of Iron Primary Cosmic Rays: Results from the Alpha Magnetic Spectrometer. Phys. Rev. Lett. 2021, 126, 041104. [Google Scholar] [CrossRef]
- Qiao, B.Q.; Liu, W.; Guo, Y.Q.; Yuan, Q. Anisotropies of different mass compositions of cosmic rays. J. Cosmol. Astropart. Phys. 2019, 2019, 007. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, W.; Yuan, Q.; Hu, H.B.; Bi, X.J.; Wu, H.R.; Zhou, X.X.; Guo, Y.Q. Geminga SNR: Possible Candidate of the Local Cosmic-Ray Factory. Astrophys. J. 2022, 926, 41. [Google Scholar] [CrossRef]
- Panov, A.D.; Adams, J.H.; Ahn, H.S.; Bashinzhagyan, G.L.; Watts, J.W.; Wefel, J.P.; Wu, J.; Ganel, O.; Guzik, T.G.; Zatsepin, V.I.; et al. Energy spectra of abundant nuclei of primary cosmic rays from the data of ATIC-2 experiment: Final results. Bull. Russ. Acad. Sci. Phys. 2009, 73, 564–567. [Google Scholar] [CrossRef]
- Fitoussi, T. et al. [Pierre Auger Collaboration] Depth of Maximum of Air-Shower Profiles above 1017.8 eV Measured with the Fluorescence Detector of the Pierre Auger Observatory and Mass Composition Implications. In Proceedings of the 38th International Cosmic Ray Conference (ICRC2023)—Outreach & Education (O&E), Nagoya, Japan, 26 July–3 August 2023; p. 319. [Google Scholar] [CrossRef]
- Abu-Zayyad, T.; Belov, K.; Bird, D.J.; Boyer, J.; Cao, Z.; Catanese, M.; Chen, G.F.; Clay, R.W.; Covault, C.E.; Dai, H.Y.; et al. A measurement of the average longitudinal development profile of cosmic ray air showers between 10 17 and 10 18 eV. Astropart. Phys. 2001, 16, 1–11. [Google Scholar] [CrossRef]
- Berezhnev, S.F.; Besson, D.; Budnev, N.M.; Chiavassa, A.; Chvalaev, O.A.; Gress, O.A.; Dyachok, A.N.; Epimakhov, S.N.; Haungs, A.; Karpov, N.I.; et al. The Tunka-133 EAS Cherenkov light array: Status of 2011. Nucl. Instrum. Methods Phys. Res. A 2012, 692, 98–105. [Google Scholar] [CrossRef]
- Haungs, A. A Scintillator and Radio Enhancement of the IceCube Surface Detector Array. Eur. Phys. J. Web Conf. 2019, 210, 06009. [Google Scholar] [CrossRef]
- Cagnoli, I.; Kyratzis, D.; Serini, D. HERD space mission: Probing the Galactic Cosmic Ray frontier. Nucl. Instrum. Methods Phys. Res. A 2024, 1068, 169788. [Google Scholar] [CrossRef]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Cao, Z.; Catalanotti, S.; Chen, S.Z.; Chen, T.L.; Cui, S.W.; Dai, B.Z.; D’Amone, A.; et al. Cosmic ray proton plus helium energy spectrum measured by the ARGO-YBJ experiment in the energy range 3–300 TeV. Phys. Rev. D 2015, 91, 112017. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bongi, M.; Bonvicini, V.; Borisov, S.; Bottai, S.; et al. Time Dependence of the Proton Flux Measured by PAMELA during the 2006 July–2009 December Solar Minimum. Astrophys. J. 2013, 765, 91. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Ahn, H.S.; Allison, P.S.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Boyle, P.J.; Childers, J.T.; Conklin, N.B.; Coutu, S.; et al. Cosmic-ray Proton and Helium Spectra from the First CREAM Flight. Astrophys. J. 2011, 728, 122. [Google Scholar] [CrossRef]
| SCR | GCR | EGCR | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | 0.87 | −5.58 | 1.57 | 3.20 | 60 | 2.12 | 205 | 2.38 | 3 | 2.4 | 20 | 2.5 | ||
| He | 0.60 | −3.32 | 2.20 | 3.53 | 95 | 2.19 | 100 | 2.36 | 0.6 | 2.3 | 0.04 | 2.26 | ||
| C | 1000 | 0.7 | 36.64 | −4.07 | 1.90 | 3.26 | 15 | 2.19 | 20 | 2.36 | 0.01 | 2.3 | 0.002 | 2.26 |
| N | 90 | 1 | 10.72 | −3.90 | 1.9 | 3.45 | 4 | 2.19 | 3 | 2.36 | 0.001 | 2.3 | 2.26 | |
| O | 0.8 | 7.54 | −4.09 | 1.91 | 3.24 | 25 | 2.19 | 25 | 2.36 | 0.05 | 2.3 | 0.003 | 2.26 | |
| Mg | 800 | 0.7 | 0.27 | −4.08 | 1.91 | 3.25 | 6 | 2.19 | 5 | 2.36 | 0.01 | 2.3 | 2.26 | |
| Si | 400 | 0.6 | 0.048 | −4.15 | 1.91 | 3.18 | 8 | 2.19 | 15 | 2.36 | 0.001 | 2.3 | 2.26 | |
| Fe | 10 | 1.25 | 12.67 | −3.5 | 3.2 | 3.89 | 0.7 | 2 | 0.1 | 2.1 | 0.01 | 2.4 | 2.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Guo, Y.; Liu, W. From Known to Unknown: Cosmic Ray Transitions from the Sun, the Galaxy, and Extra-Galactic Systems. Universe 2025, 11, 96. https://doi.org/10.3390/universe11030096
Yao Y, Guo Y, Liu W. From Known to Unknown: Cosmic Ray Transitions from the Sun, the Galaxy, and Extra-Galactic Systems. Universe. 2025; 11(3):96. https://doi.org/10.3390/universe11030096
Chicago/Turabian StyleYao, Yuhua, Yiqing Guo, and Wei Liu. 2025. "From Known to Unknown: Cosmic Ray Transitions from the Sun, the Galaxy, and Extra-Galactic Systems" Universe 11, no. 3: 96. https://doi.org/10.3390/universe11030096
APA StyleYao, Y., Guo, Y., & Liu, W. (2025). From Known to Unknown: Cosmic Ray Transitions from the Sun, the Galaxy, and Extra-Galactic Systems. Universe, 11(3), 96. https://doi.org/10.3390/universe11030096






