Inflection Point Dynamics of Minimally Coupled Tachyonic Scalar Fields
Abstract
:1. Introduction
Dynamical Setup
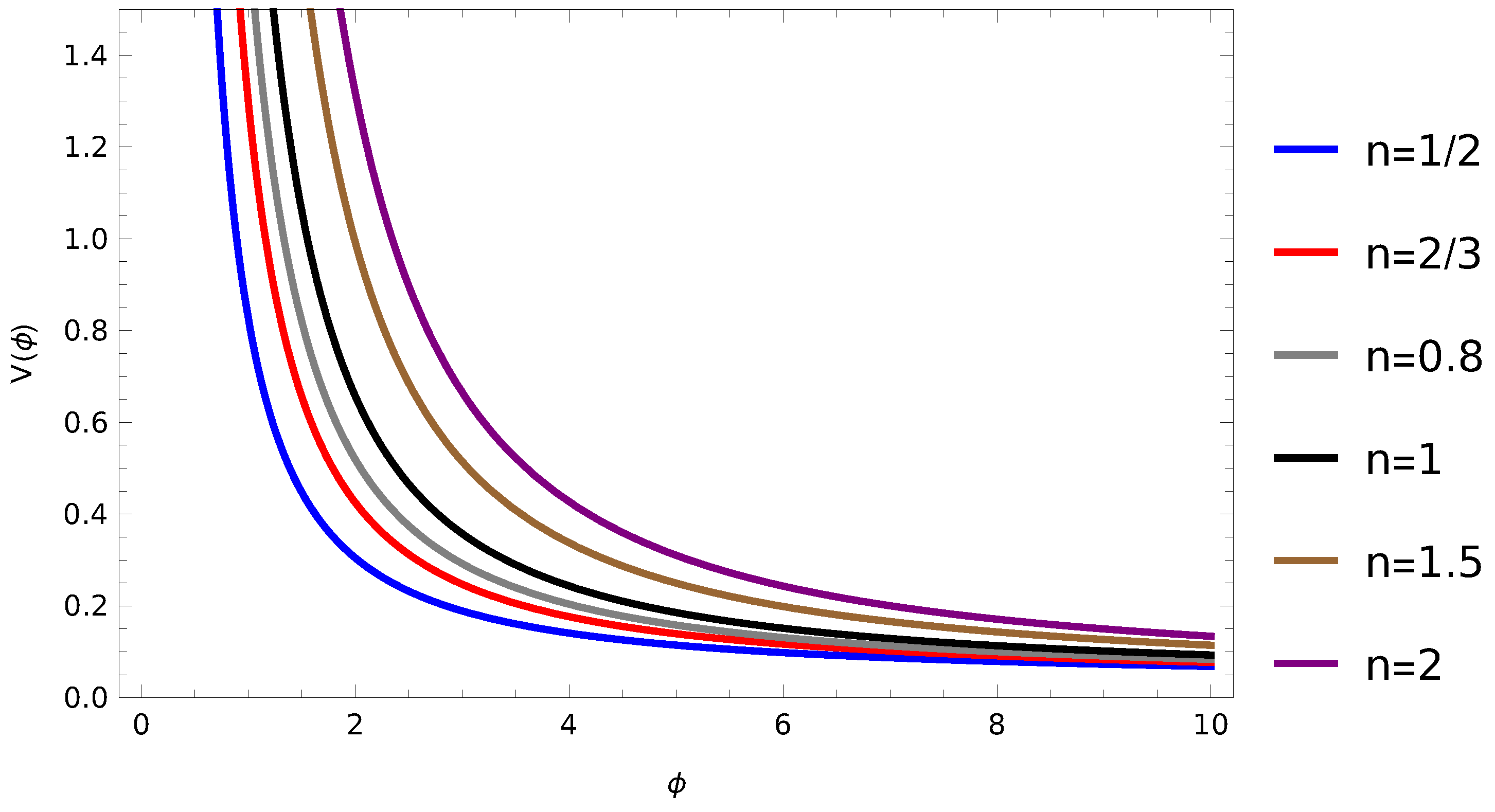
2. Inflection Point of Tachyonic Scalar Field
2.1. For Case I:
2.2. For Case II:
2.3. For Case III:
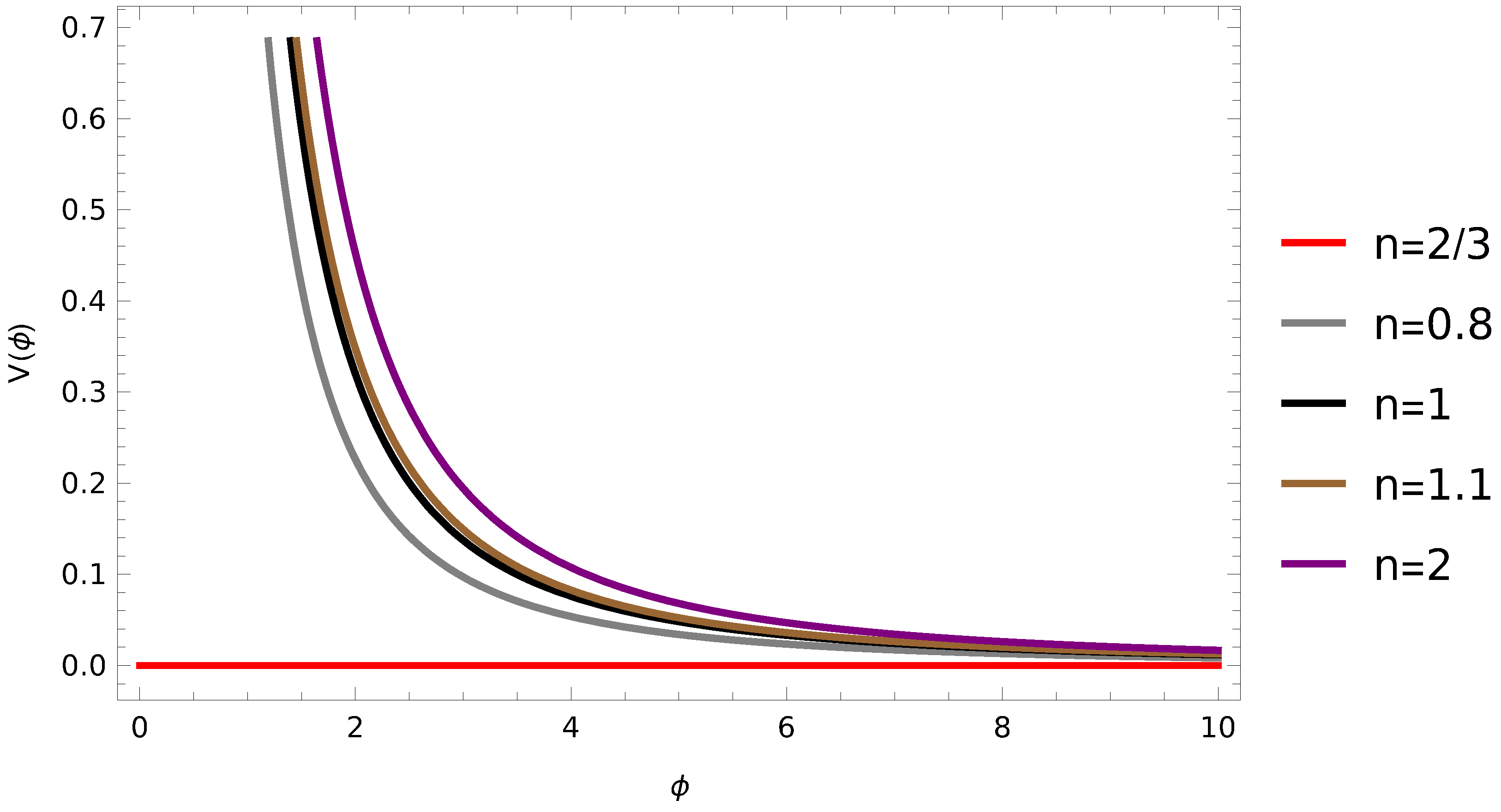
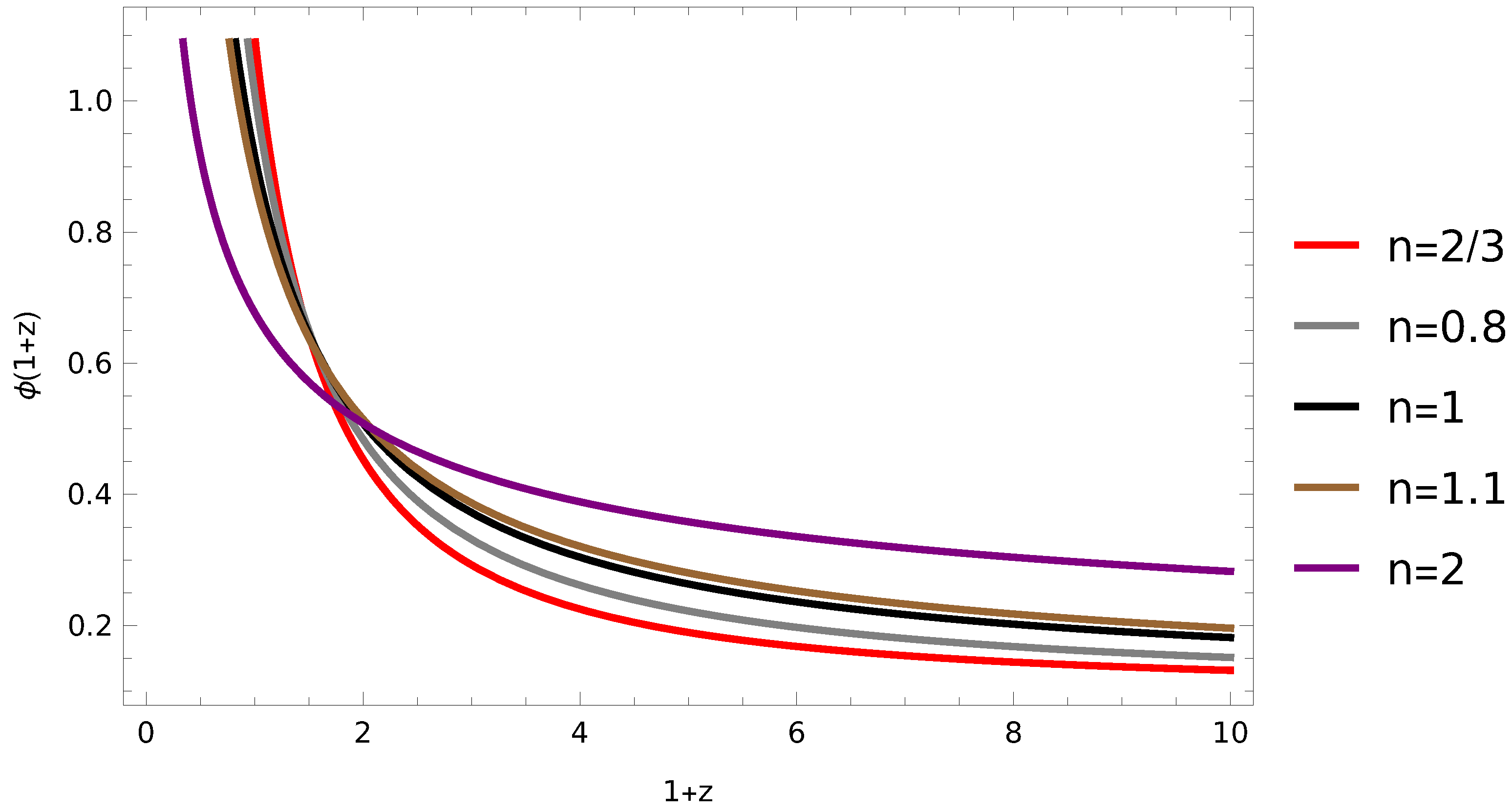
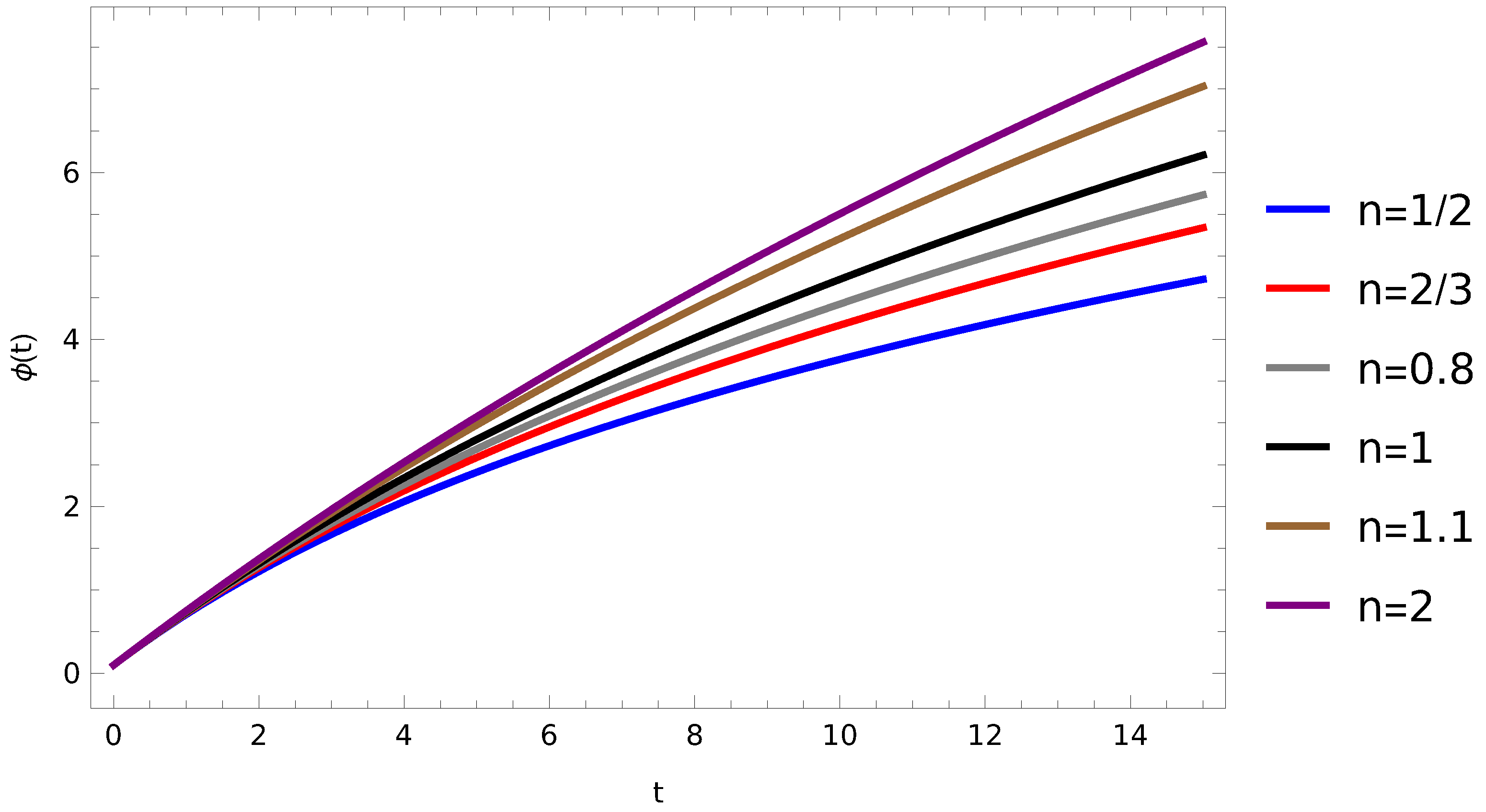
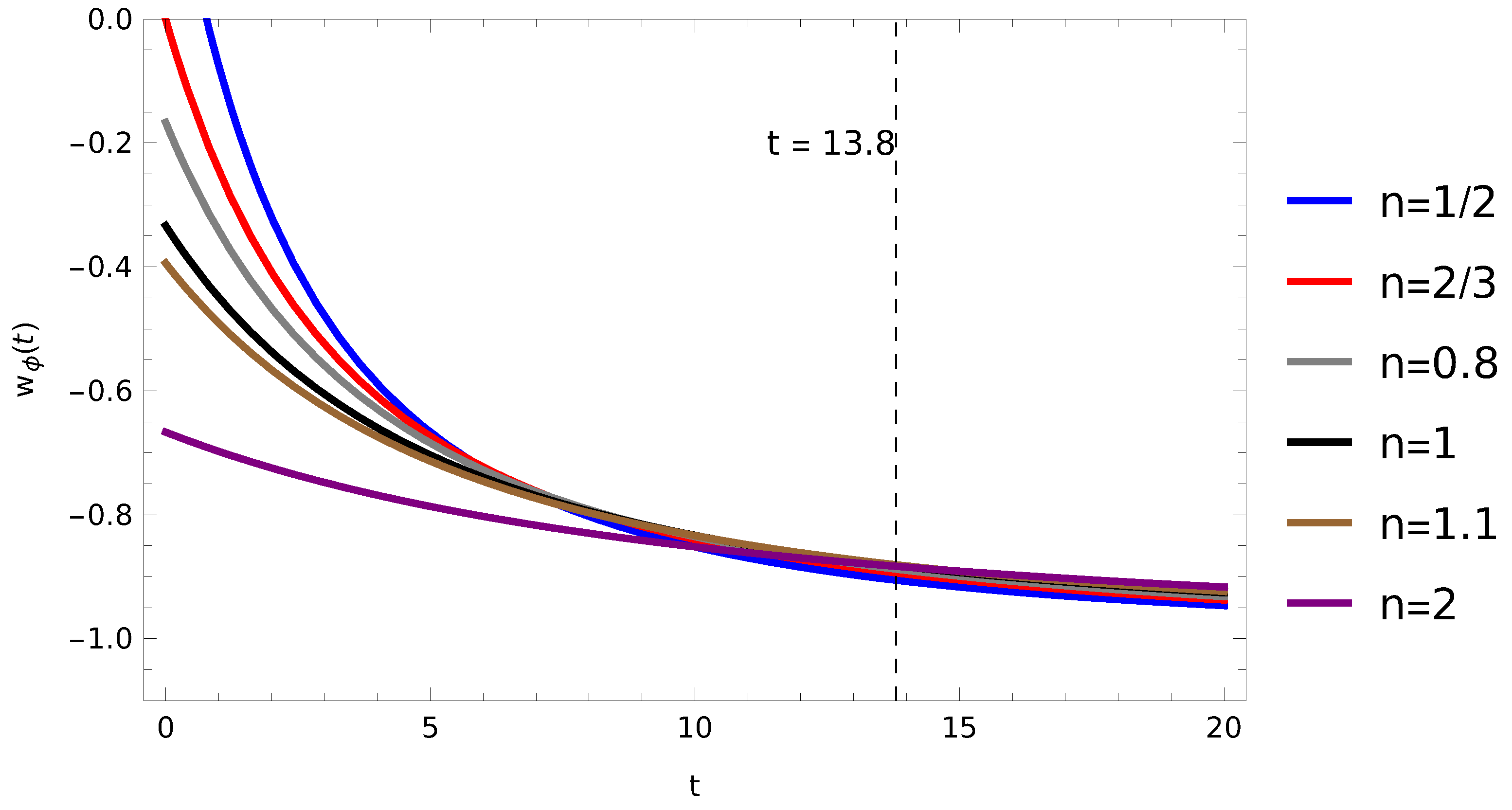
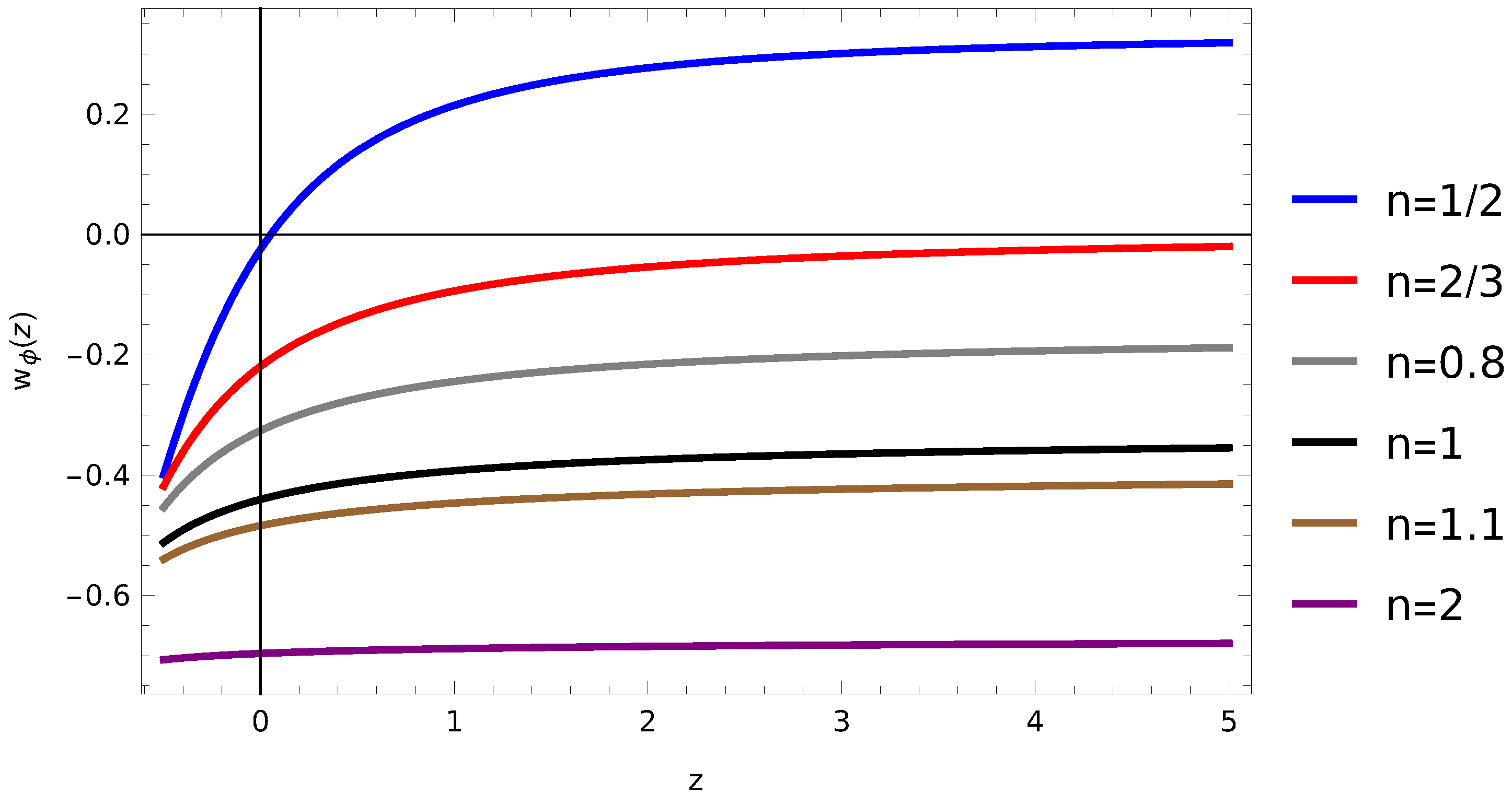
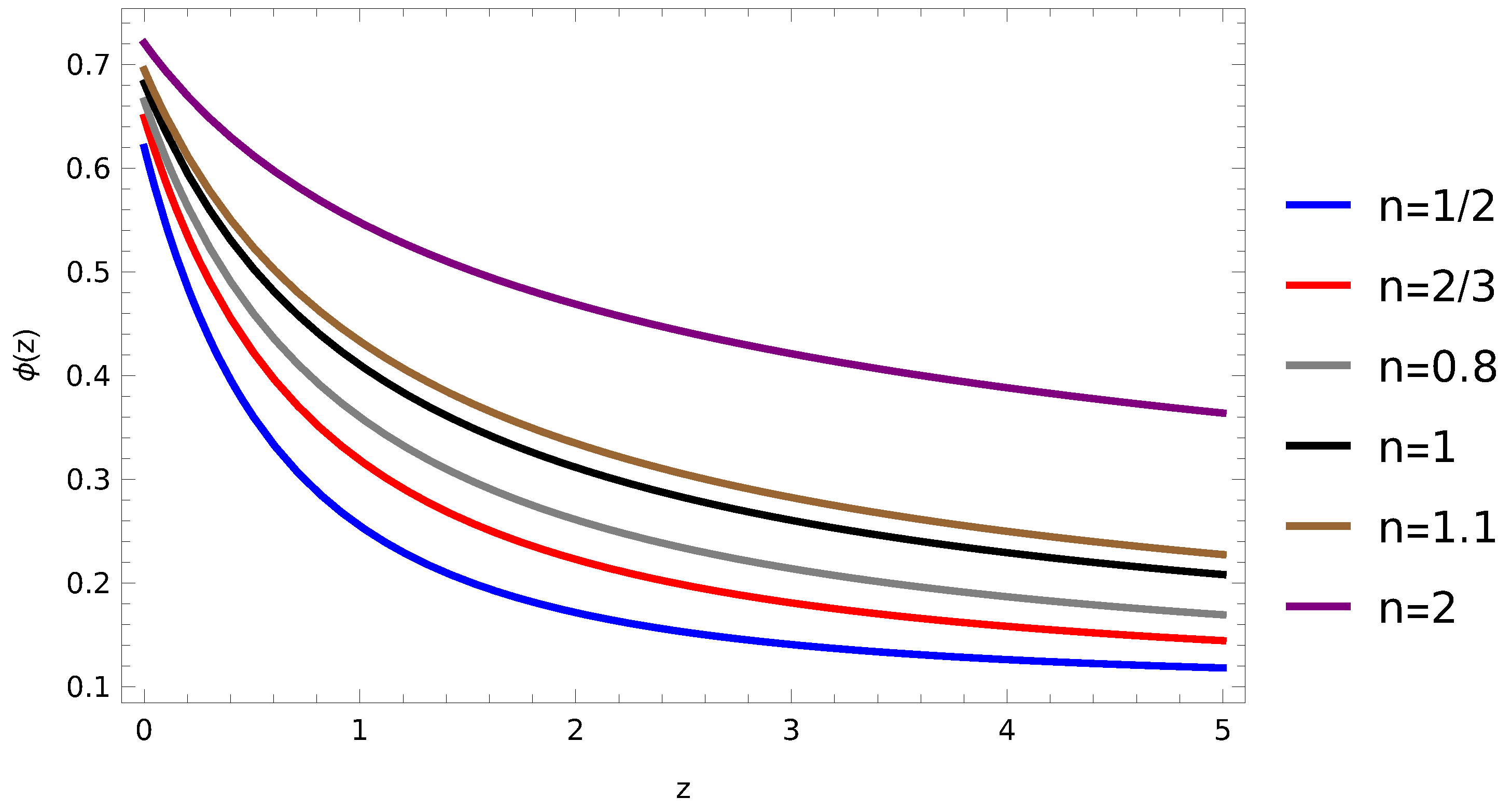
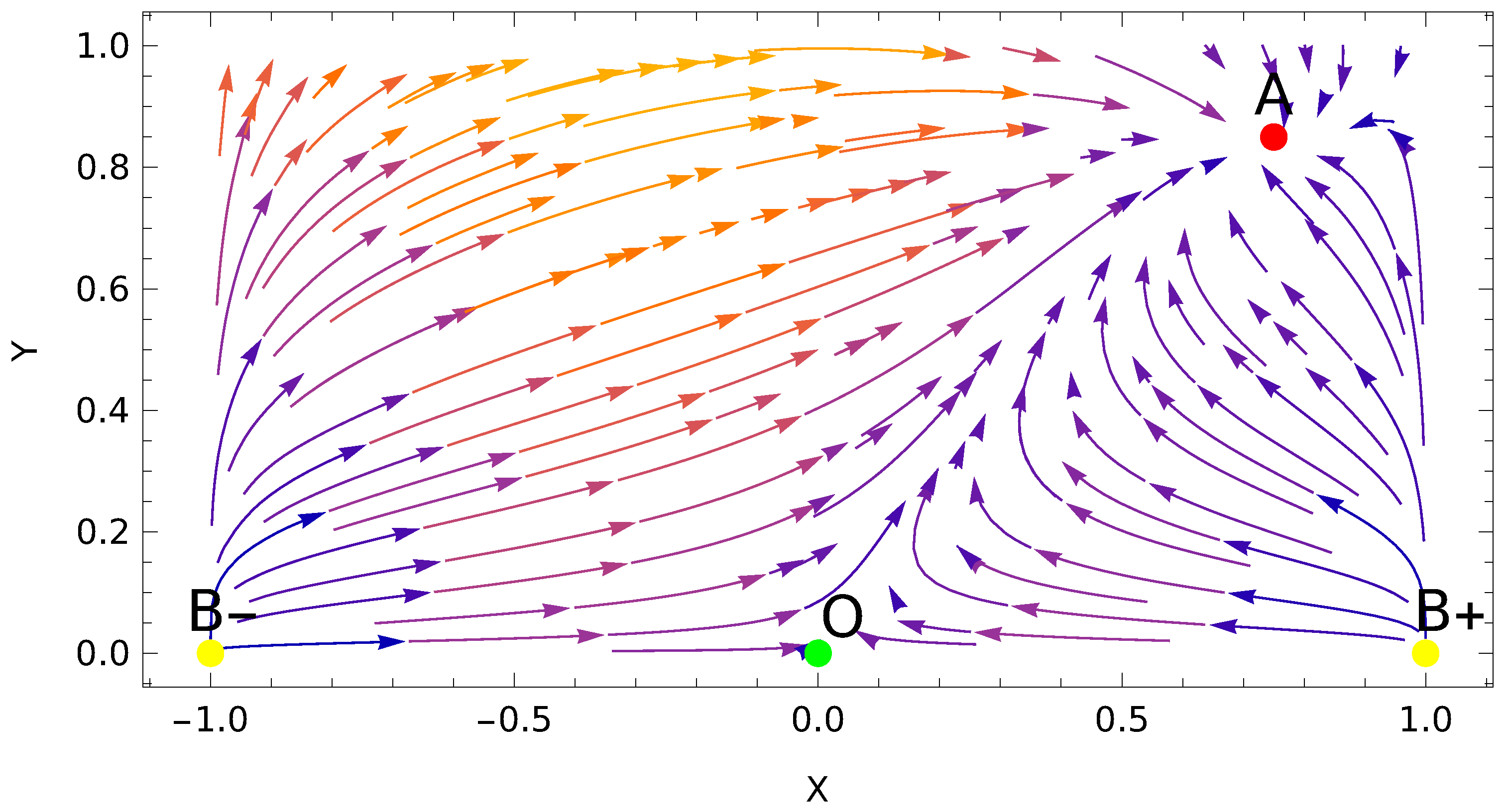
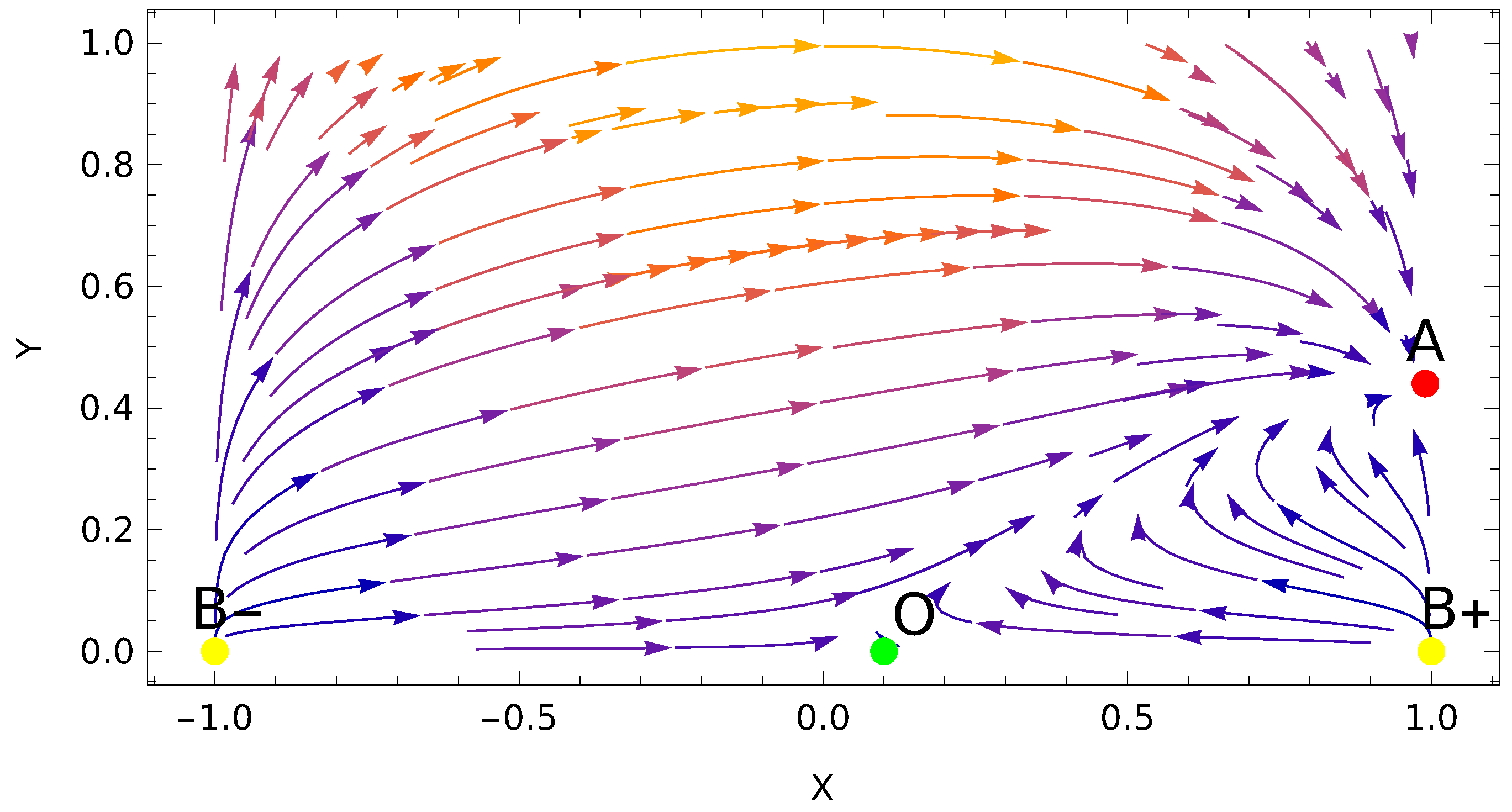
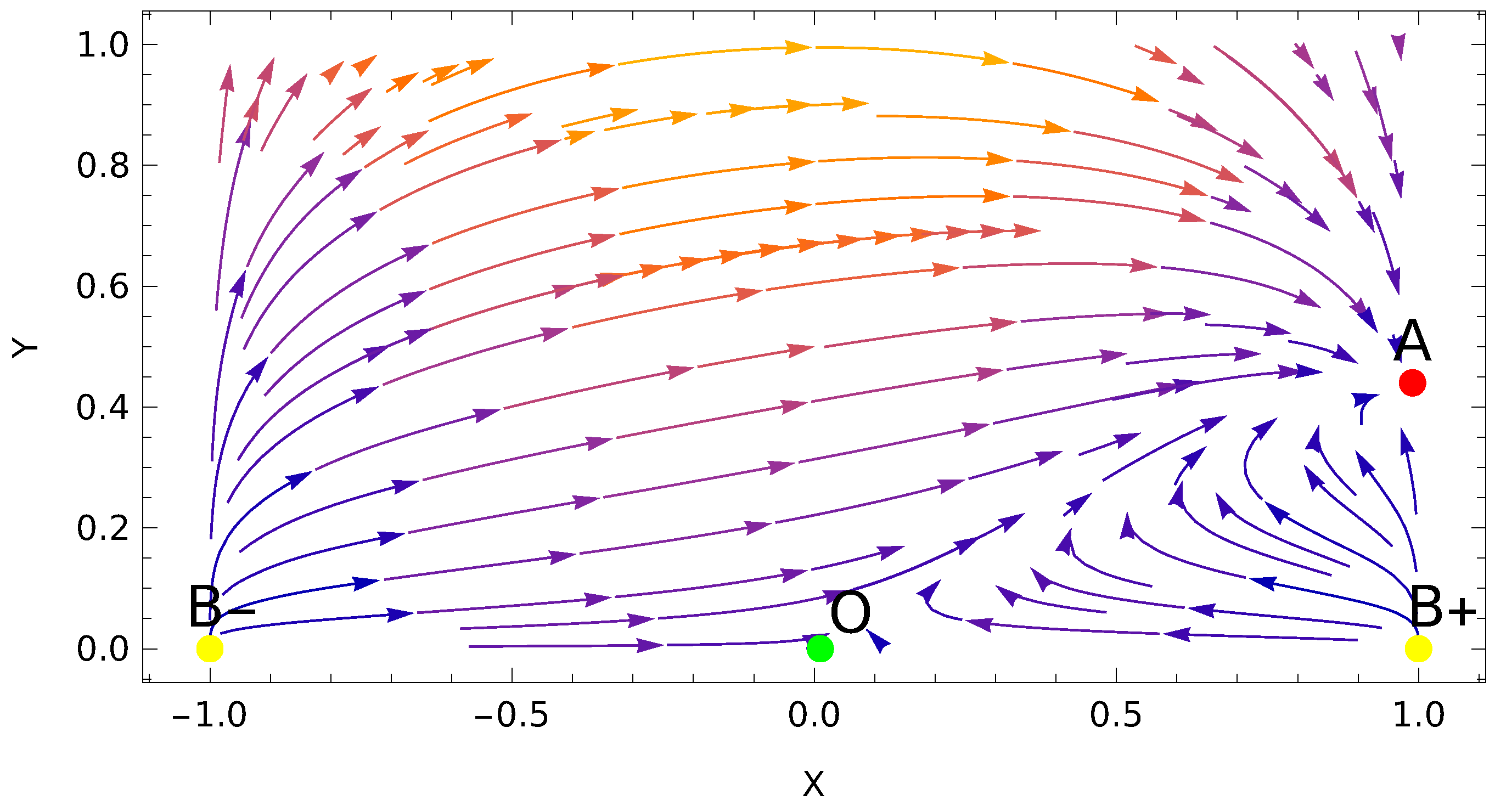
3. Dynamical Analysis at Inflection Point
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. [The Supernova Cosmology Project] Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-year Wilkinson Microwave Anisotropy Probe (WMAP)* observations: Determination of cosmological parameters. Astrophys. J. 2003, 148, 175. [Google Scholar] [CrossRef]
- Seo, H.; Eisenstein, D.J. Probing dark energy with baryonic acoustic oscillations from future large galaxy redshift surveys. Astrophys. J. 2003, 598, 720. [Google Scholar] [CrossRef]
- Blake, C.; Glazebrook, K. Probing dark energy using baryonic oscillations in the galaxy power spectrum as a cosmological ruler. Astrophys. J. 2003, 594, 665. [Google Scholar] [CrossRef]
- Jarosik, N.; Bennett, C.L.; Dunkley, J.; Gold, B.; Greason, M.R.; Halpern, M.; Hill, R.S.; Hinshaw, G.; Kogut, A.; Komatsu, E.; et al. Seven-year wilkinson microwave anisotropy probe (WMAP*) observations: Sky maps, systematic errors. and basic results, Astrophys. J. 2011, 192, 18. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration] Planck 2018 results VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration] Planck 2018 results I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, A1. [Google Scholar]
- Knop, R.A.; Aldering, G.; Amanullah, R.; Astier, P.; Blanc, G.; Burns, M.S.; Conley, A.; Deustua, S.E.; Doi, M.; Ellis, R.; et al. [The Supernova Cosmology Project] New constraints on Ωm, ΩΛ, and w from an independent set of 11 high-redshift supernovae observed with the Hubble Space Telescope. Astrophys. J. 2003, 598, 102. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia supernova discoveries at z>1 from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Platts, E.; Sloan, D.; Weltman, A. Current observations with a decaying cosmological constant allow for chaotic cyclic cosmology. J. Cosmol. Astropart. Phys. 2016, 4, 026. [Google Scholar] [CrossRef]
- Patil, T.; Panda, S.; Sharma, M. Dynamics of interacting scalar field model in the realm of chiral cosmology. Eur. Phys. J. C 2023, 83, 131. [Google Scholar] [CrossRef]
- Szydłowski, M.S.; Stachowski, A. Cosmology with decaying cosmological constant—Exact solutions and model testing. J. Cosmol. Astropart. Phys. 2015, 10, 066. [Google Scholar] [CrossRef]
- Bisabr, Y.; Salehi, H. Mechanism for a decaying cosmological constant. Class. Quantum Grav. 2002, 19, 2369. [Google Scholar] [CrossRef]
- Fujii, Y.; Nishioka, T. Model of a decaying cosmological constant. Phys. Rev. D 1990, 42, 361. [Google Scholar] [CrossRef]
- Bull, P.; Akrami, Y.; Adamek, J.; Baker, T.; Bellini, E.; Jiménez, J.B.; Bentivegna, E.; Camera, S.; Clesse, S.; Davis, J.H.; et al. Beyond ΛCDM: Problems, solutions, and the road ahead. Phys. Dark Universe 2016, 12, 56. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Popolo, A.D.; Delliou, M.L. Small scale problems of the ΛCDM model: A short review. Galaxies 2017, 5, 17. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Popolo, A.D. Cosmological measure with volume averaging and the vacuum energy problem. Class. Quantum Gravity 2012, 29, 085014. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J.E. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef] [PubMed]
- Escamilla-Rivera, C.; Najera, A. Dynamical dark energy models in the light of gravitational-wave transient catalogues. J. Cosmol. Astropart. Phys. 2022, 3, 060. [Google Scholar] [CrossRef]
- Zhao, G.B.; Raveri, M.; Pogosian, L.; Wang, Y.; Crittenden, R.G.; Handley, W.J.; Percival, W.J.; Beutler, F.; Brinkmann, J.; Chuang, C.H.; et al. Dynamical dark energy in light of the latest observations. Nat. Astron. 2017, 1, 627. [Google Scholar] [CrossRef]
- Mainini, R.; Macciò, A.V.; Bonometto, S.A.; Klypin, A. Modeling dynamical dark energy. Astrophys. J. 2003, 599, 24. [Google Scholar] [CrossRef]
- Brax, P.; Burrage, C.; Englert, C.; Spannowsky, M. LHC signatures of scalar dark energy. Phys. Rev. D 2016, 94, 084054. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef]
- Adame, A.G. et al. [The DESI collaboration] DESI 2024 VI: Cosmological constraints from the measurements of baryon acoustic oscillations. J. Cosmol. Astropart. Phys. 2025, 2025, 021. [Google Scholar] [CrossRef]
- Lodha, K. et al. [DESI Collaboration] DESI 2024: Constraints on physics-focused aspects of dark energy using DESI DR1 BAO data. Phys. Rev. D. 2025, 111, 023532. [Google Scholar] [CrossRef]
- Giarè, W.; Sabogal, M.A.; Nunes, R.C.; Valentino, E.D. Interacting dark energy after DESI baryon acoustic oscillation measurements. Phys. Rev. D. 2024, 133, 251003. [Google Scholar] [CrossRef]
- Alestas, G.; Caldarola, M.; Kuroyanagi, S.; Nesseris, S. DESI constraints on α-attractor inflationary models. arXiv 2024, arXiv:2410.00827. [Google Scholar] [CrossRef]
- Andriot, D. Quintessence: An analytical study, with theoretical and observational applications. arXiv 2024, arXiv:2410.17182. [Google Scholar]
- Andriot, D. Exponential quintessence: Curved, steep and stringy? J. High Energy Phys. 2024, 2024, 1–60. [Google Scholar] [CrossRef]
- Bhattacharya, S. Cosmological constraints on curved quintessence. J. Cosmol. Astropart. Phys. 2024, 2024, 073. [Google Scholar] [CrossRef]
- Verma, M.M.; Pathak, S.D. Cosmic expansion driven by real scalar field for different forms of potential. Astrophys. Space Sci. 2014, 350, 381. [Google Scholar] [CrossRef]
- Verma, M.M.; Pathak, S.D. The BICEP2 data and a single Higgs-like interacting scalar field. Anisotropic bouncing scenario in F (X)- V (ϕ) F(X)-V(ϕ) model. Int. J. Mod. Phys. D 2014, 23, 1450075. [Google Scholar] [CrossRef]
- Panda, S.; Sharma, M. Gauging universe expansion via scalar fields. Astrophys. Space Sci. 2016, 361, 1–8. [Google Scholar]
- Kumar, S.; Pathak, S.D.; Khlopov, M. Dynamics of Quasi-Exponential Expansion: Scalar Field Potential Insights. Int. J. Theor. Phys. 2024, 63, 238. [Google Scholar] [CrossRef]
- Verma, M.M.; Pathak, S.D. Shifted cosmological parameter and shifted dust matter in a two-phase tachyonic field universe. Astrophys. Space Sci. 2013, 344, 505. [Google Scholar] [CrossRef]
- Kumar, D.R.; Pathak, S.D.; Ojha, V.K. Gauging universe expansion via scalar fields. Chin. Phys. C 2023, 47, 055102. [Google Scholar] [CrossRef]
- Johri, V.B. Phantom cosmologies. Phys. Rev. D 2004, 70, 041303R. [Google Scholar] [CrossRef]
- Johri, V.B. Search for tracker potentials in quintessence theory. Class. Quantum Gravity 2002, 19, 5959. [Google Scholar] [CrossRef]
- Johri, V.B. Genesis of cosmological tracker fields. Phys. Rev. D 2001, 63, 103504. [Google Scholar] [CrossRef]
- Kumar, S.; Pathak, S.D.; Zhang, X. Deciphering star formation dynamics with coupled ϕCDM. Europhys. Lett. 2025, 149. [Google Scholar]
- Gialamas, I.D.; Hütsi, G.; Kannike, K.; Racioppi, A.; Raidal, M.; Vasar, M.; Veermäe, H. Interpreting DESI 2024 BAO: Late-time dynamical dark energy or a local effect? Phys. Rev. D. 2025, 111, 043540. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 64, 043511. [Google Scholar] [CrossRef]
- Park, C.G.; Ratra, B. Is excess smoothing of Planck CMB ansiotropy data partially responsible for evidence for dark energy dynamics in other w(z)CDM parametrizations? arXiv 2025, arXiv:2501.03480. [Google Scholar]
- Bhattacharya, S.; Borghetto, G.; Malhotra, A.; Parameswaran, S.; Tasinato, G.; Zavala, I. Cosmological tests of quintessence in quantum gravity. arXiv 2024, arXiv:2410.21243. [Google Scholar]
- Bagla, J.S.; Jassal, H.K.; Padmanabhan, T. Cosmology with tachyon field as dark energy. Phys. Rev. D. 2003, 67, 063504. [Google Scholar] [CrossRef]
- Copeland, E.J.; Garousi, M.R.; Sami, M.; Tsujikawa, S. What is needed of a tachyon if it is to be the dark energy? Phys. Rev. D. 2005, 71, 043003. [Google Scholar] [CrossRef]
- Padmanabhan, T. Accelerated expansion of the universe driven by tachyonic matter. Phys. Rev. D. 2002, 66, 021301. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A. An accurate bound on tensor-to-scalar ratio and the scale of inflation. Nucl. Phys. B 2014, 9, 386. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L. Einstein, Planck and Vera Rubin: Relevant encounters between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 603190. [Google Scholar] [CrossRef]
- Allahverdi, R.; Dutta, B.; Mazumdar, A. Attraction towards an inflection point inflation. Phys. Rev. D 2008, 78, 063507. [Google Scholar] [CrossRef]
- Battista, E. Nonsingular bouncing cosmology in general relativity: Physical analysis of the spacetime defect. Class. Quantum Grav. 2021, 19, 195007. [Google Scholar] [CrossRef]
- Bai, Y.; Stolarski, D. Dynamical inflection point inflation. J. Prof. Assoc. Cactus Dev. 2021, 3, 091. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A.; Pukartas, E. Constraining N=1 supergravity inflationary framework with non-minimal Kähler operators. J. High Energy Phys. 2014, 4, 1–27. [Google Scholar] [CrossRef]
- Enqvist, K.; Mazumdar, A. Cosmological consequences of MSSM flat directions. Phys. Rep. 2003, 380, 99–234. [Google Scholar] [CrossRef]
- Enqvist, K.; Jokinen, A.; Mazumdar, A. Dynamics of minimal supersymmetric standard model flat directions consisting of multiple scalar fields. J. Cosmol. Astropart. Phys. 2004, 1, 008. [Google Scholar] [CrossRef]
- Enqvist, K.; Mazumdar, A.; Stephens, P. Inflection point inflation within supersymmetry. J. Cosmol. Astropart. Phys. 2010, 2010, 020. [Google Scholar] [CrossRef]
- Allahverdi, R.; Enqvist, K.; Garcia-Bellido, J.; Jokinen, A.; Mazumdar, A. MSSM flat direction inflation: Slow roll, stability, fine-tuning and reheating. J. Cosmol. Astropart. Phys. 2007, 2007, 019. [Google Scholar] [CrossRef]
- Mazumdar, A.; Rocher, J. Particle physics models of inflation and curvaton scenarios. Phys. Reps. 2011, 497, 85–215. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A. Primordial blackholes and gravitational waves for an inflection-point model of inflation. Phys. Lett. B 2014, 733, 270–275. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A. Reconstructing inflationary potential from BICEP2 and running of tensor modes. arXiv 2014, arXiv:1403.5549. [Google Scholar]
- Allahverdi, R.; Enqvist, K.; Garcia-Bellido, J.; Mazumdar, A. Gauge-invariant inflaton in the minimal supersymmetric standard model. Phys. Rev. Lett. 2006, 97, 191304. [Google Scholar] [CrossRef]
- Choi, S.M.; Lee, H.M. Inflection point inflation and reheating. Eur. Phys. J. C 2016, 76, 1–15. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Owen, C.; Racioppi, A. Loop inflection-point inflation. Astropart. Phys. 2018, 103, 16–20. [Google Scholar] [CrossRef]
- Kaur, J.; Pathak, S.D.; Khlopov, M.Y. Inflection point of coupled quintessence. Astropart. Phys. 2024, 157, 102926. [Google Scholar] [CrossRef]
- Iacconi, L.; Assadullahi, H.; Fasiello, M.; Wands, D. Revisiting small-scale fluctuations in α-attractor models of inflation. J. Cosmol. Astropart. Phys. 2022, 6, 007. [Google Scholar] [CrossRef]
- Blanco-Pillado, J.J.; Gomez-Reino, M.; Metallinos, K. Accidental inflation in the landscape. J. Cosmol. Astropart. Phys. 2013, 2, 034. [Google Scholar] [CrossRef]
- Kefala, K.; Kodaxis, G.P.; Stamou, I.D.; Tetradis, N. Features of the inflaton potential and the power spectrum of cosmological perturbations. Phys. Rev. D 2021, 104, 023506. [Google Scholar] [CrossRef]
- Storm, S.D.; Scherrer, R.J. Observational constraints on inflection point quintessence with a cubic potential. Phys. Lett. B 2022, 829, 137126. [Google Scholar] [CrossRef]
- Cerezo, R.; Rosa, J.G. Warm inflection. J. High Energy Phys. 2013, 2013, 24. [Google Scholar] [CrossRef]
- Hotchkiss, S.; Mazumdar, A.; Nadathur, S. Inflection point inflation: WMAP constraints and a solution to the fine tuning problem. J. Cosmol. Astropart. Phys. 2011, 6, 002. [Google Scholar] [CrossRef]
- Chang, H.Y.; Scherrer, R.J. Inflection point quintessence. Phys. Rev. D 2013, 88, 083003. [Google Scholar] [CrossRef]
- Gorini, V.; Kamenshchik, A.; Moschella, U.; Pasquier, V. Tachyons, scalar fields, and cosmology. Phys. Rev. D. 2004, 69, 123512. [Google Scholar] [CrossRef]
- Singh, A.; Jassal, H.K.; Harma, M.S. Perturbations in tachyon dark energy and their effect on matter clustering. J. Cosmol. Astropart. Phys. 2020, 2020, 008. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Piao, Y.S.; Huang, Q.G.; Zhang, X.; Zhang, Y.Z. Non-minimally coupled tachyon and inflation. Phys. Lett. B. 2003, 570, 1. [Google Scholar] [CrossRef]
- Mezo, I. The Lambert W Function: Its Generalizations and Applications, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Kalugin, G.A. Analytical Properties of the Lambert W Function. Doctoral Thesis, Western University, London, ON, Canada, 2011. [Google Scholar]
- Thompson, R.I. Non-Canonical Dark Energy Parameter Evolution in a Canonical Quintessence Cosmology. Universe 2024, 10, 356. [Google Scholar] [CrossRef]
- Bahamonde, S.; Böhmer, C.G.; Carloni, S.; Copeland, E.J.; Fang, W.; Tamanini, N. Dynamical systems applied to cosmology: Dark energy and modified gravity. Phys. Rep. 2018, 775, 1–122. [Google Scholar] [CrossRef]
- Pathak, S.D.; Mishra, S.S.; Kaur, J.; Khlopov, M. Chapter 3—Application of Dynamical System Analysis in Cosmology, Advances in Computational Methods and Modeling for Science and Engineering; Morgan Kaufmann: Burlington, MA, USA, 2025; pp. 37–47. ISBN 9780443300127. [Google Scholar]
- Coley, A.A. Dynamical Systems and Cosmology; Springer Science Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Arrowsmith, D.K. An Introduction to Dynamical Systems; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Sharma, M.; Shahalam, M.; Wu, Q.; Wang, A. Preinflationary dynamics in loop quantum cosmology: Monodromy Potential. J. Cosmol. Astropart. Phys. 2018, 2018, 003. [Google Scholar] [CrossRef]
- Shahalam, M.; Shahalam, M.; Wu, Q.; Wang, A. Preinflationary dynamics in loop quantum cosmology: Power-law potentials. Phys. Rev. D 2017, 96, 123533. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaur, J.; Pathak, S.D.; Khlopov, M.; Sharma, M. Inflection Point Dynamics of Minimally Coupled Tachyonic Scalar Fields. Universe 2025, 11, 131. https://doi.org/10.3390/universe11040131
Kaur J, Pathak SD, Khlopov M, Sharma M. Inflection Point Dynamics of Minimally Coupled Tachyonic Scalar Fields. Universe. 2025; 11(4):131. https://doi.org/10.3390/universe11040131
Chicago/Turabian StyleKaur, Jaskirat, S. D. Pathak, Maxim Khlopov, and Manabendra Sharma. 2025. "Inflection Point Dynamics of Minimally Coupled Tachyonic Scalar Fields" Universe 11, no. 4: 131. https://doi.org/10.3390/universe11040131
APA StyleKaur, J., Pathak, S. D., Khlopov, M., & Sharma, M. (2025). Inflection Point Dynamics of Minimally Coupled Tachyonic Scalar Fields. Universe, 11(4), 131. https://doi.org/10.3390/universe11040131













