Determining the Scale Length and Height of the Milky Way’s Thick Disc Using RR Lyrae
Abstract
:1. Introduction
2. Observational Data
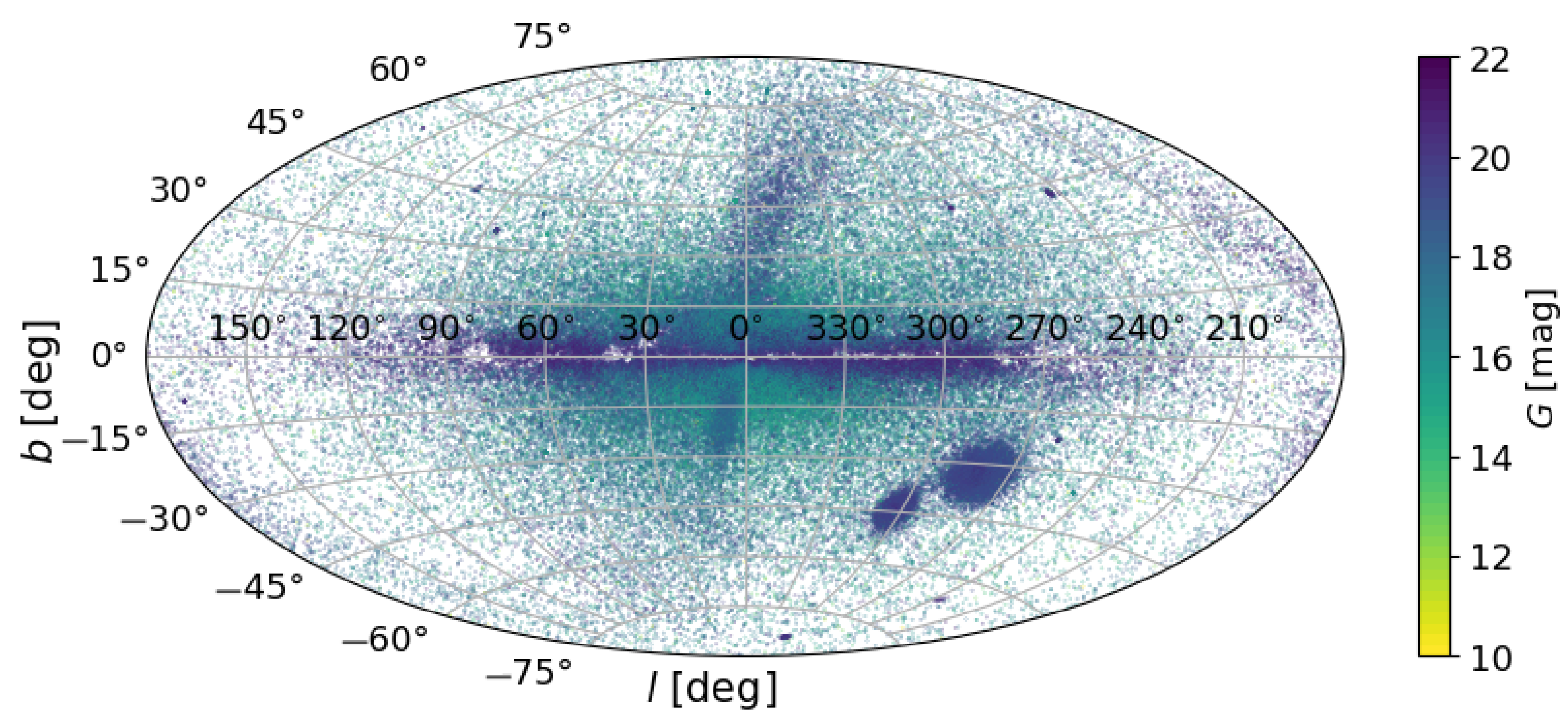
2.1. The Sample
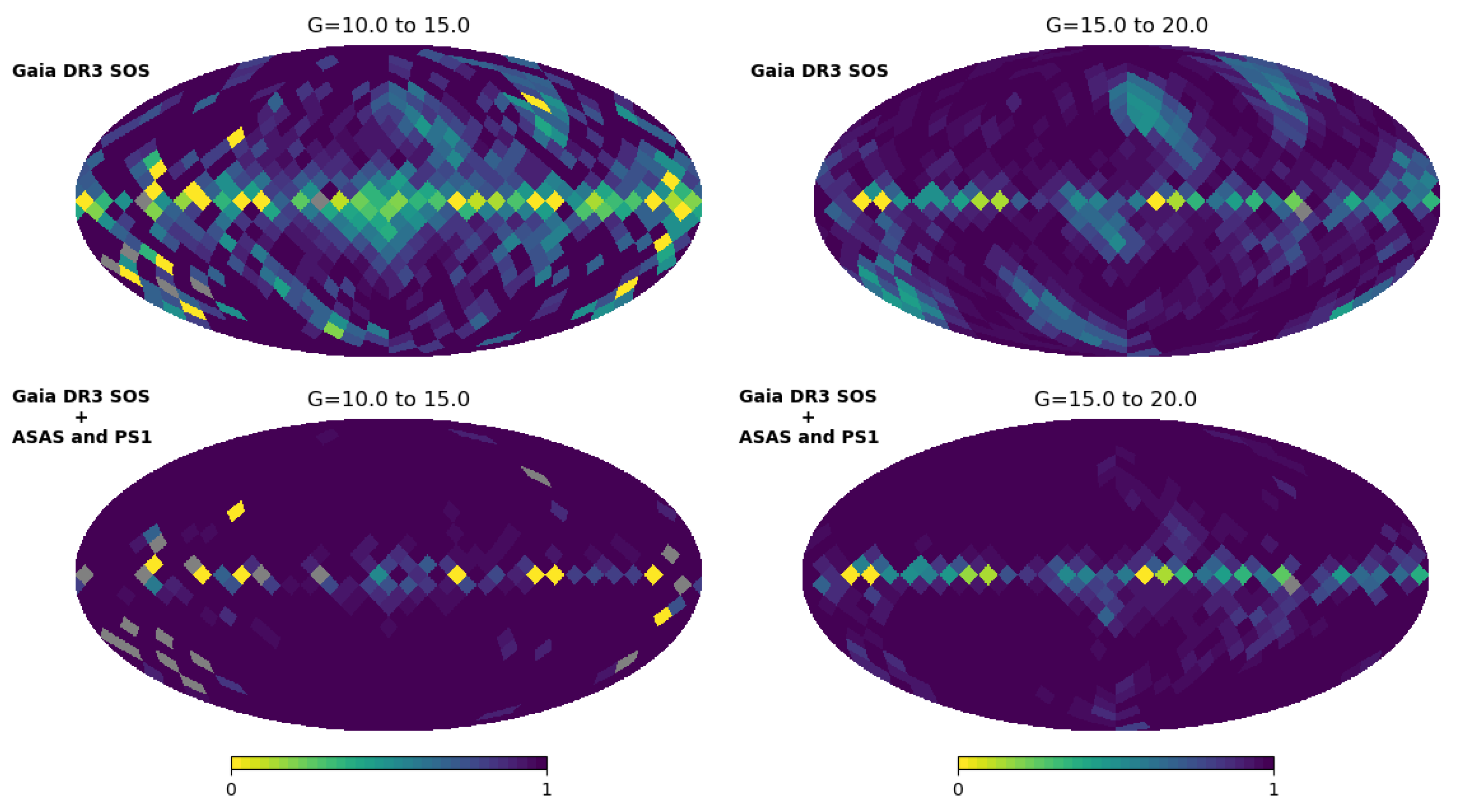
2.2. Selection Function
- ruwe.
- phot_bp_rp_excess_factor
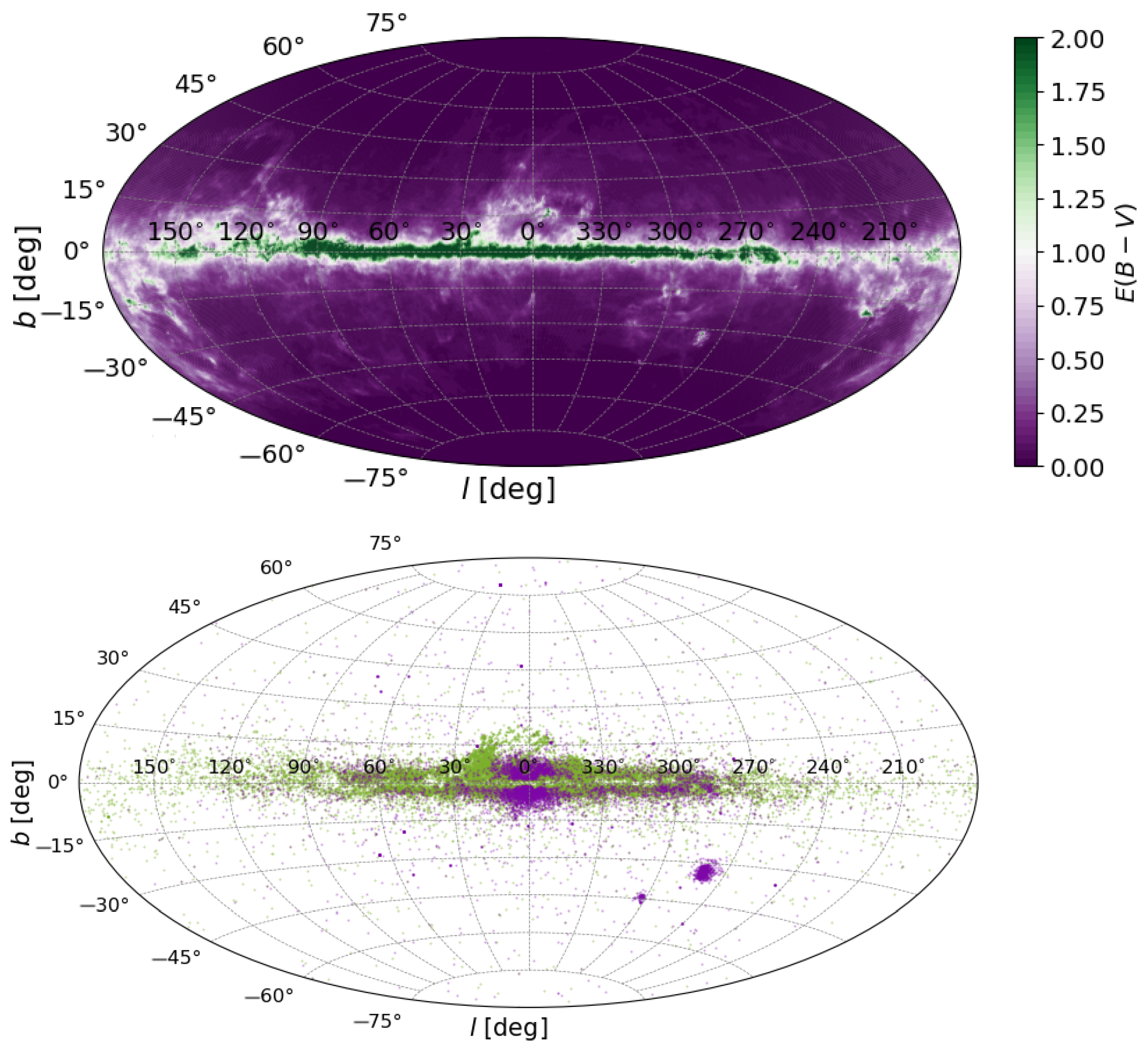
2.3. Distance Estimation
3. Thick Disc and Halo Fitting Model
3.1. Density Profile Models
3.1.1. The Thick Disc
3.1.2. The Halo
3.2. Fitting Procedure
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SDSS | Sloan Digital Sky Survey |
| RRLs | RR Lyrae stars |
| CMD | Color–magnitude diagrams |
| MCMC | Markov chain Monte Carlo |
| INS | Omportance nested sampling |
| SOS | Specific Objects Study |
| ASAS | ASAS-SN-II |
| PS1 | PanSTARRS1 |
Appendix A. Five Parameter Fitting
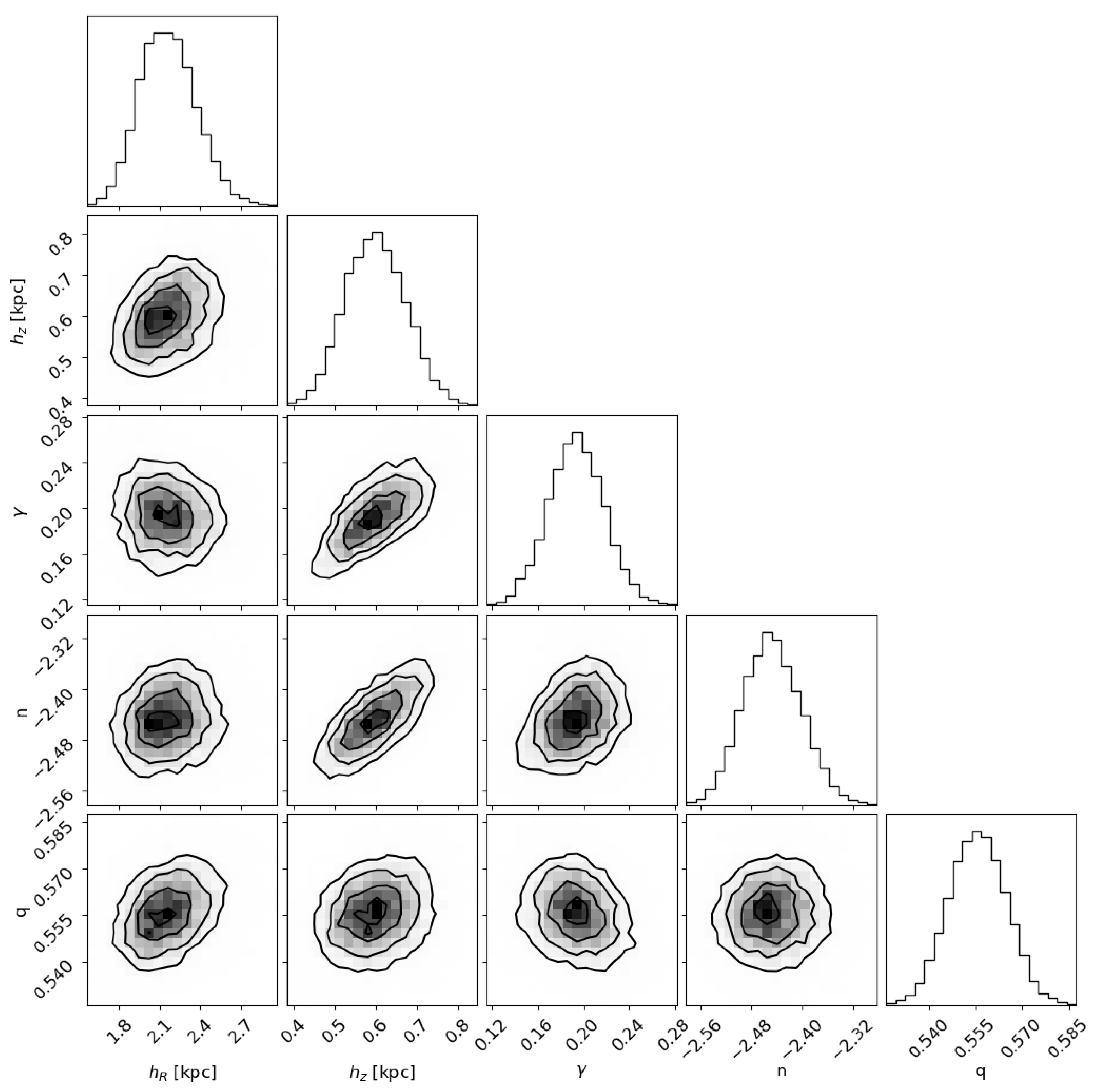
| Thick disc with exponential vertical profile and halo | |||||
| n | q | ||||
| median±range | |||||
| mean | |||||
| Thick disc with vertical profile and halo | |||||
| n | q | ||||
| median±range | |||||
| mean | |||||

| 1 | Data publicly available in the online archive at: https://github.com/cmateu/rrl_completeness/tree/main/data/. This sample was used in [32,40]. |
References
- Burstein, D. Structure and origin of S0 galaxies. III. The luminosity distribution perpendicular to the plane of the disks in S0’s. Astrophys. J. 1979, 234, 829–836. [Google Scholar] [CrossRef]
- Gilmore, G.; Reid, N. New light on faint stars-III. Galactic structure towards the South Pole and the Galactic thick disc. Mon. Not. R. Astron. Soc. 1983, 202, 1025–1047. [Google Scholar] [CrossRef]
- Bensby, T.; Alves-Brito, A.; Oey, M.S.; Yong, D.; Meléndez, J. A First Constraint on the Thick Disk Scale Length: Differential Radial Abundances in K Giants at Galactocentric Radii 4, 8, and 12 kpc. Astrophys. J. Lett. 2011, 735, L46. [Google Scholar] [CrossRef]
- Wyse, R.F.G.; Gilmore, G. Chemistry and Kinematics in the Solar Neighborhood: Implications for Stellar Populations and for Galaxy Evolution. Astron. J. 1995, 110, 2771. [Google Scholar] [CrossRef]
- Bensby, T.; Zenn, A.R.; Oey, M.S.; Feltzing, S. Tracing the Galactic Thick Disk to Solar Metallicities. Astrophys. J. Lett. 2007, 663, L13–L16. [Google Scholar] [CrossRef]
- Fuhrmann, K. Nearby stars of the Galactic disc and halo-IV. Mon. Not. R. Astron. Soc. 2008, 384, 173–224. [Google Scholar] [CrossRef]
- Reddy, B.E.; Lambert, D.L.; Allende Prieto, C. Elemental abundance survey of the Galactic thick disc. Mon. Not. R. Astron. Soc. 2006, 367, 1329–1366. [Google Scholar] [CrossRef]
- Robin, A.C.; Haywood, M.; Creze, M.; Ojha, D.K.; Bienayme, O. The thick disc of the Galaxy: Sequel of a merging event. Astron. Astrophys. 1996, 305, 125. [Google Scholar] [CrossRef]
- Robin, A.C.; Reylé, C.; Fliri, J.; Czekaj, M.; Robert, C.P.; Martins, A.M.M. Constraining the thick disc formation scenario of the Milky Way. Astron. Astrophys. 2014, 569, A13. [Google Scholar] [CrossRef]
- Jurić, M.; Ivezić, Ž.; Brooks, A.; Lupton, R.H.; Schlegel, D.; Finkbeiner, D.; Padmanabhan, N.; Bond, N.; Sesar, B.; Rockosi, C.M.; et al. The Milky Way Tomography with SDSS. I. Stellar Number Density Distribution. Astrophys. J. 2008, 673, 864–914. [Google Scholar] [CrossRef]
- Bovy, J.; Rix, H.W.; Hogg, D.W.; Beers, T.C.; Lee, Y.S.; Zhang, L. The Vertical Motions of Mono-abundance Sub-populations in the Milky Way Disk. Astrophys. J. 2012, 755, 115. [Google Scholar] [CrossRef]
- Larsen, J.A.; Humphreys, R.M. Fitting a Galactic Model to an All-Sky Survey. Astron. J. 2003, 125, 1958–1979. [Google Scholar] [CrossRef]
- Carollo, D.; Beers, T.C.; Chiba, M.; Norris, J.E.; Freeman, K.C.; Lee, Y.S.; Ivezić, Ž.; Rockosi, C.M.; Yanny, B. Structure and Kinematics of the Stellar Halos and Thick Disks of the Milky Way Based on Calibration Stars from Sloan Digital Sky Survey DR7. Astrophys. J. 2010, 712, 692–727. [Google Scholar] [CrossRef]
- Mateu, C.; Vivas, A.K. The Galactic thick disc density profile traced with RR Lyrae stars. Mon. Not. R. Astron. Soc. 2018, 479, 211–227. [Google Scholar] [CrossRef]
- Vieira, K.; Korchagin, V.; Carraro, G.; Lutsenko, A. Vertical Structure of the Milky Way Disk with Gaia DR3. Galaxies 2023, 11, 77. [Google Scholar] [CrossRef]
- Clementini, G.; Ripepi, V.; Garofalo, A.; Molinaro, R.; Muraveva, T.; Leccia, S.; Rimoldini, L.; Holl, B.; Jevardat de Fombelle, G.; Sartoretti, P.; et al. Gaia Data Release 3. Specific processing and validation of all-sky RR Lyrae and Cepheid stars: The RR Lyrae sample. Astron. Astrophys. 2023, 674, A18. [Google Scholar] [CrossRef]
- Cabrera Garcia, J.; Beers, T.C.; Huang, Y.; Li, X.Y.; Liu, G.; Zhang, H.; Hong, J.; Lee, Y.S.; Shank, D.; Gudin, D.; et al. Probing the Galactic halo with RR Lyrae stars-V. Chemistry, kinematics, and dynamically tagged groups. Mon. Not. R. Astron. Soc. 2024, 527, 8973–8990. [Google Scholar] [CrossRef]
- Smith, H.A. RR Lyrae stars. Camb. Astrophys. Ser. 1995, 27. [Google Scholar]
- Muraveva, T.; Delgado, H.E.; Clementini, G.; Sarro, L.M.; Garofalo, A. RR Lyrae stars as standard candles in the Gaia Data Release 2 Era. Mon. Not. R. Astron. Soc. 2018, 481, 1195–1211. [Google Scholar] [CrossRef]
- Layden, A.C. The Metallicities and Kinematics of RR Lyrae Variables.II. Galactic Structure and Formation from Local Stars. Astron. J. 1995, 110, 2288. [Google Scholar] [CrossRef]
- Kinemuchi, K. et al. [ROTSE Collaboration] Analysis of RR Lyrae Stars in the Northern Sky Variability Survey. Astron. J. 2006, 132, 1202–1220. [Google Scholar] [CrossRef]
- Mateu, C.; Vivas, K.; Downes, J.J.; Briceño, C.; Cruz, G. Gauging the Galactic thick disk with RR Lyrae stars. Eur. Phys. J. Web Conf. 2012, 19, 04006. [Google Scholar] [CrossRef]
- Sesar, B.; Ivezić, Ž.; Stuart, J.S.; Morgan, D.M.; Becker, A.C.; Sharma, S.; Palaversa, L.; Jurić, M.; Wozniak, P.; Oluseyi, H. Exploring the Variable Sky with LINEAR. II. Halo Structure and Substructure Traced by RR Lyrae Stars to 30 kpc. Astron. J. 2013, 146, 21. [Google Scholar] [CrossRef]
- Sesar, B.; Jurić, M.; Ivezić, Ž. The Shape and Profile of the Milky Way Halo as Seen by the Canada-France-Hawaii Telescope Legacy Survey. Astrophys. J. 2011, 731, 4. [Google Scholar] [CrossRef]
- Watkins, L.L.; Evans, N.W.; Belokurov, V.; Smith, M.C.; Hewett, P.C.; Bramich, D.M.; Gilmore, G.F.; Irwin, M.J.; Vidrih, S.; Wyrzykowski, Ł.; et al. Substructure revealed by RRLyraes in SDSS Stripe 82. Mon. Not. R. Astron. Soc. 2009, 398, 1757–1770. [Google Scholar] [CrossRef]
- Zinn, R.; Horowitz, B.; Vivas, A.K.; Baltay, C.; Ellman, N.; Hadjiyska, E.; Rabinowitz, D.; Miller, L. La Silla QUEST RR Lyrae Star Survey: Region I. Astrophys. J. 2014, 781, 22. [Google Scholar] [CrossRef]
- Tkachenko, R.V.; Bryndina, A.P.; Zhmailova, A.B.; Korchagin, V.I. Rotation of the Milky Way Halo in the Solar Vicinity Based on GAIA DR3 Catalog. Astron. Rep. 2024, 68, 664–671. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. PASP 2013, 125, 306. [Google Scholar] [CrossRef]
- Lange, J.U. nautilus: Boosting Bayesian importance nested sampling with deep learning. Mon. Not. R. Astron. Soc. 2023, 525, 3181–3194. [Google Scholar] [CrossRef]
- Jayasinghe, T.; Stanek, K.Z.; Kochanek, C.S.; Shappee, B.J.; Holoien, T.W.S.; Thompson, T.A.; Prieto, J.L.; Dong, S.; Pawlak, M.; Pejcha, O.; et al. The ASAS-SN catalogue of variable stars III: Variables in the southern TESS continuous viewing zone. Mon. Not. R. Astron. Soc. 2019, 485, 961–971. [Google Scholar] [CrossRef]
- Sesar, B.; Hernitschek, N.; Mitrović, S.; Ivezić, Ž.; Rix, H.W.; Cohen, J.G.; Bernard, E.J.; Grebel, E.K.; Martin, N.F.; Schlafly, E.F.; et al. Machine-learned Identification of RR Lyrae Stars from Sparse, Multi-band Data: The PS1 Sample. Astron. J. 2017, 153, 204. [Google Scholar] [CrossRef]
- Mateu, C.; Holl, B.; De Ridder, J.; Rimoldini, L. Empirical completeness assessment of the Gaia DR2, Pan-STARRS 1, and ASAS-SN-II RR Lyrae catalogues. Mon. Not. R. Astron. Soc. 2020, 496, 3291–3307. [Google Scholar] [CrossRef]
- Jayasinghe, T.; Stanek, K.Z.; Kochanek, C.S.; Shappee, B.J.; Holoien, T.W.S.; Thompson, T.A.; Prieto, J.L.; Dong, S.; Pawlak, M.; Pejcha, O.; et al. The ASAS-SN catalogue of variable stars-II. Uniform classification of 412 000 known variables. Mon. Not. R. Astron. Soc. 2019, 486, 1907–1943. [Google Scholar] [CrossRef]
- Robitaille, T.P. et al. [Astropy Collaboration] Astropy: A community Python package for astronomy. Astron. Astrophys. 2013, 558, A33. [Google Scholar] [CrossRef]
- Price-Whelan, A.M. et al. [Astropy Collaboration] The Astropy Project: Building an Open-science Project and Status of the v2.0 Core Package. Astron. J. 2018, 156, 123. [Google Scholar] [CrossRef]
- Price-Whelan, A.M. et al. [Astropy Collaboration] The Astropy Project: Sustaining and Growing a Community-oriented Open-source Project and the Latest Major Release (v5.0) of the Core Package. Astrophys. J. 2022, 935, 167. [Google Scholar] [CrossRef]
- Abuter, R. et al. [GRAVITY Collaboration] Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar] [CrossRef]
- Bennett, M.; Bovy, J. Vertical waves in the solar neighbourhood in Gaia DR2. Mon. Not. R. Astron. Soc. 2019, 482, 1417–1425. [Google Scholar] [CrossRef]
- Rybizki, J.; Drimmel, R. gdr2_Completeness: GaiaDR2 Data Retrieval and Manipulation; Astrophysics Source Code Library: Online, 2018; p. ascl–1811. [Google Scholar]
- Mateu, C. The Selection Function of Gaia DR3 RR Lyrae. Res. Notes Am. Astron. Soc. 2024, 8, 85. [Google Scholar] [CrossRef]
- Cantat-Gaudin, T.; Fouesneau, M.; Rix, H.W.; Brown, A.G.A.; Drimmel, R.; Castro-Ginard, A.; Khanna, S.; Belokurov, V.; Casey, A.R. Uniting Gaia and APOGEE to unveil the cosmic chemistry of the Milky Way disc. Astron. Astrophys. 2024, 683, A128. [Google Scholar] [CrossRef]
- Górski, K.M.; Hivon, E.; Banday, A.J.; Wandelt, B.D.; Hansen, F.K.; Reinecke, M.; Bartelmann, M. HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere. Astrophys. J. 2005, 622, 759–771. [Google Scholar] [CrossRef]
- Zonca, A.; Singer, L.; Lenz, D.; Reinecke, M.; Rosset, C.; Hivon, E.; Gorski, K. healpy: Equal area pixelization and spherical harmonics transforms for data on the sphere in Python. J. Open Source Softw. 2019, 4, 1298. [Google Scholar] [CrossRef]
- Rimoldini, L.; Holl, B.; Audard, M.; Mowlavi, N.; Nienartowicz, K.; Evans, D.W.; Guy, L.P.; Lecoeur-Taïbi, I.; Jevardat de Fombelle, G.; Marchal, O.; et al. Gaia Data Release 2. All-sky classification of high-amplitude pulsating stars. Astron. Astrophys. 2019, 625, A97. [Google Scholar] [CrossRef]
- Holl, B.; Audard, M.; Nienartowicz, K.; Jevardat de Fombelle, G.; Marchal, O.; Mowlavi, N.; Clementini, G.; De Ridder, J.; Evans, D.W.; Guy, L.P.; et al. Gaia Data Release 2: Summary of the variability processing and analysis results. arXiv 2018, arXiv:1804.09373. [Google Scholar] [CrossRef]
- Iorio, G.; Belokurov, V. Chemo-kinematics of the Gaia RR Lyrae: The halo and the disc. Mon. Not. R. Astron. Soc. 2021, 502, 5686–5710. [Google Scholar] [CrossRef]
- Lindegren, L.; Hernández, J.; Bombrun, A.; Klioner, S.; Bastian, U.; Ramos-Lerate, M.; de Torres, A.; Steidelmüller, H.; Stephenson, C.; Hobbs, D.; et al. Gaia Data Release 2. The astrometric solution. Astron. Astrophys. 2018, 616, A2. [Google Scholar] [CrossRef]
- Belokurov, V.; Penoyre, Z.; Oh, S.; Iorio, G.; Hodgkin, S.; Evans, N.W.; Everall, A.; Koposov, S.E.; Tout, C.A.; Izzard, R.; et al. Unresolved stellar companions with Gaia DR2 astrometry. Mon. Not. R. Astron. Soc. 2020, 496, 1922–1940. [Google Scholar] [CrossRef]
- Evans, D.W.; Riello, M.; De Angeli, F.; Carrasco, J.M.; Montegriffo, P.; Fabricius, C.; Jordi, C.; Palaversa, L.; Diener, C.; Busso, G.; et al. Gaia Data Release 2: Photometric content and validation. arXiv 2018, arXiv:1804.09368. [Google Scholar] [CrossRef]
- Schlegel, D.J.; Finkbeiner, D.P.; Davis, M. Maps of Dust Infrared Emission for Use in Estimation of Reddening and Cosmic Microwave Background Radiation Foregrounds. Astrophys. J. 1998, 500, 525–553. [Google Scholar] [CrossRef]
- Schlafly, E.F.; Finkbeiner, D.P.; Schlegel, D.J.; Jurić, M.; Ivezić, Ž.; Gibson, R.R.; Knapp, G.R.; Weaver, B.A. The Blue Tip of the Stellar Locus: Measuring Reddening with the Sloan Digital Sky Survey. Astrophys. J. 2010, 725, 1175–1191. [Google Scholar] [CrossRef]
- Yuan, H.B.; Liu, X.W.; Xiang, M.S. Empirical extinction coefficients for the GALEX, SDSS, 2MASS and WISE passbands. Mon. Not. R. Astron. Soc. 2013, 430, 2188–2199. [Google Scholar] [CrossRef]
- Li, X.Y.; Huang, Y.; Liu, G.C.; Beers, T.C.; Zhang, H.W. Photometric Metallicity and Distance Estimates for 136,000 RR Lyrae Stars from Gaia Data Release 3. Astrophys. J. 2023, 944, 88. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, H.; Li, C.; Wolf, C.; Onken, C.A.; Beers, T.C.; Casagrande, L.; Mackey, D.; Da Costa, G.S.; Bland-Hawthorn, J.; et al. Milky Way Tomography with the SkyMapper Southern Survey. II. Photometric Recalibration of SMSS DR2. Astrophys. J. 2021, 907, 68. [Google Scholar] [CrossRef]
- Harris, W.E. A New Catalog of Globular Clusters in the Milky Way. arXiv 2010, arXiv:1012.3224. [Google Scholar] [CrossRef]
- Ramos, P.; Mateu, C.; Antoja, T.; Helmi, A.; Castro-Ginard, A.; Balbinot, E.; Carrasco, J.M. Full 5D characterisation of the Sagittarius stream with Gaia DR2 RR Lyrae. Astron. Astrophys. 2020, 638, A104. [Google Scholar] [CrossRef]
- Helmi, A. et al. [Gaia Collaboration] Gaia Data Release 2. Kinematics of globular clusters and dwarf galaxies around the Milky Way. Astron. Astrophys. 2018, 616, A12. [Google Scholar] [CrossRef]
- Minniti, D.; Dékány, I.; Majaess, D.; Palma, T.; Pullen, J.; Rejkuba, M.; Alonso-García, J.; Catelan, M.; Contreras Ramos, R.; Gonzalez, O.A.; et al. Characterization of the VVV Survey RR Lyrae Population across the Southern Galactic Plane. Astron. J. 2017, 153, 179. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Hammersley, P.L.; López-Corredoira, M. Modelling star counts in the Monoceros stream and the Galactic anti-centre. Astron. Astrophys. 2011, 527, A6. [Google Scholar] [CrossRef]
- Carollo, D.; Beers, T.C.; Lee, Y.S.; Chiba, M.; Norris, J.E.; Wilhelm, R.; Sivarani, T.; Marsteller, B.; Munn, J.A.; Bailer-Jones, C.A.L.; et al. Two stellar components in the halo of the Milky Way. Nature 2008, 451, 216. [Google Scholar] [CrossRef]
- Liu, G.; Huang, Y.; Bird, S.A.; Zhang, H.; Wang, F.; Tian, H. Probing the Galactic halo with RR lyrae stars - III. The chemical and kinematic properties of the stellar halo. Mon. Not. R. Astron. Soc. 2022, 517, 2787–2800. [Google Scholar] [CrossRef]
- Wegg, C.; Gerhard, O.; Portail, M. The structure of the Milky Way’s bar outside the bulge. Mon. Not. R. Astron. Soc. 2015, 450, 4050–4069. [Google Scholar] [CrossRef]
- Tremmel, M.; Fragos, T.; Lehmer, B.D.; Tzanavaris, P.; Belczynski, K.; Kalogera, V.; Basu-Zych, A.R.; Farr, W.M.; Hornschemeier, A.; Jenkins, L.; et al. Modeling the Redshift Evolution of the Normal Galaxy X-Ray Luminosity Function. Astrophys. J. 2013, 766, 19. [Google Scholar] [CrossRef]
- Tkachenko, R.; Korchagin, V.; Jmailova, A.; Carraro, G.; Jmailov, B. The Influence of the Galactic Bar on the Dynamics of Globular Clusters. Galaxies 2023, 11, 26. [Google Scholar] [CrossRef]
- Naidu, R.P.; Conroy, C.; Bonaca, A.; Zaritsky, D.; Weinberger, R.; Ting, Y.S.; Caldwell, N.; Tacchella, S.; Han, J.J.; Speagle, J.S.; et al. Reconstructing the Last Major Merger of the Milky Way with the H3 Survey. Astrophys. J. 2021, 923, 92. [Google Scholar] [CrossRef]
- Belokurov, V.; Erkal, D.; Evans, N.W.; Koposov, S.E.; Deason, A.J. Co-formation of the disc and the stellar halo. Mon. Not. R. Astron. Soc. 2018, 478, 611–619. [Google Scholar] [CrossRef]
- Spitzer, L., Jr.; Schwarzschild, M. The Possible Influence of Interstellar Clouds on Stellar Velocities. Astrophys. J. 1951, 114, 385. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Carlberg, R.G. Spiral instabilities provoked by accretion and star formation. Astrophys. J. 1984, 282, 61–74. [Google Scholar] [CrossRef]
- Quinn, P.J.; Hernquist, L.; Fullagar, D.P. Heating of Galactic Disks by Mergers. Astrophys. J. 1993, 403, 74. [Google Scholar] [CrossRef]
- Schönrich, R.; Binney, J. Chemical evolution with radial mixing. Mon. Not. R. Astron. Soc. 2009, 396, 203–222. [Google Scholar] [CrossRef]
- Abadi, M.G.; Navarro, J.F.; Steinmetz, M.; Eke, V.R. Simulations of Galaxy Formation in a Λ Cold Dark Matter Universe. I. Dynamical and Photometric Properties of a Simulated Disk Galaxy. Astrophys. J. 2003, 591, 499–514. [Google Scholar] [CrossRef]
- Grand, R.J.J.; Kawata, D.; Belokurov, V.; Deason, A.J.; Fattahi, A.; Fragkoudi, F.; Gómez, F.A.; Marinacci, F.; Pakmor, R. The dual origin of the Galactic thick disc and halo from the gas-rich Gaia-Enceladus Sausage merger. Mon. Not. R. Astron. Soc. 2020, 497, 1603–1618. [Google Scholar] [CrossRef]
- Park, M.J.; Yi, S.K.; Peirani, S.; Pichon, C.; Dubois, Y.; Choi, H.; Devriendt, J.; Kaviraj, S.; Kimm, T.; Kraljic, K.; et al. Exploring the Origin of Thick Disks Using the NewHorizon and Galactica Simulations. Astrophys. J. Suppl. Ser. 2021, 254, 2. [Google Scholar] [CrossRef]
- Vieira, K.; Carraro, G.; Korchagin, V.; Lutsenko, A.; Girard, T.M.; van Altena, W. Milky Way Thin and Thick Disk Kinematics with Gaia EDR3 and RAVE DR5. Astrophys. J. 2022, 932, 28. [Google Scholar] [CrossRef]
- Bovy, J.; Rix, H.W.; Liu, C.; Hogg, D.W.; Beers, T.C.; Lee, Y.S. The Spatial Structure of Mono-abundance Sub-populations of the Milky Way Disk. Astrophys. J. 2012, 753, 148. [Google Scholar] [CrossRef]
- Mackereth, J.T.; Bovy, J.; Schiavon, R.P.; Zasowski, G.; Cunha, K.; Frinchaboy, P.M.; García Perez, A.E.; Hayden, M.R.; Holtzman, J.; Majewski, S.R.; et al. The age-metallicity structure of the Milky Way disc using APOGEE. Mon. Not. R. Astron. Soc. 2017, 471, 3057–3078. [Google Scholar] [CrossRef]
- Cabrera-Lavers, A.; Garzón, F.; Hammersley, P.L. The thick disc component of the Galaxy from near infrared colour-magnitude diagrams. Astron. Astrophys. 2005, 433, 173–183. [Google Scholar] [CrossRef]
- Iorio, G.; Belokurov, V. The shape of the Galactic halo with Gaia DR2 RR Lyrae. Anatomy of an ancient major merger. Mon. Not. R. Astron. Soc. 2019, 482, 3868–3879. [Google Scholar] [CrossRef]
- Smith, M.C.; Evans, N.W.; Belokurov, V.; Hewett, P.C.; Bramich, D.M.; Gilmore, G.; Irwin, M.J.; Vidrih, S.; Zucker, D.B. Kinematics of SDSS subdwarfs: Structure and substructure of the Milky Way halo. Mon. Not. R. Astron. Soc. 2009, 399, 1223–1237. [Google Scholar] [CrossRef]
- Deason, A.J.; Belokurov, V.; Evans, N.W. The Milky Way stellar halo out to 40 kpc: Squashed, broken but smooth. Mon. Not. R. Astron. Soc. 2011, 416, 2903–2915. [Google Scholar] [CrossRef]
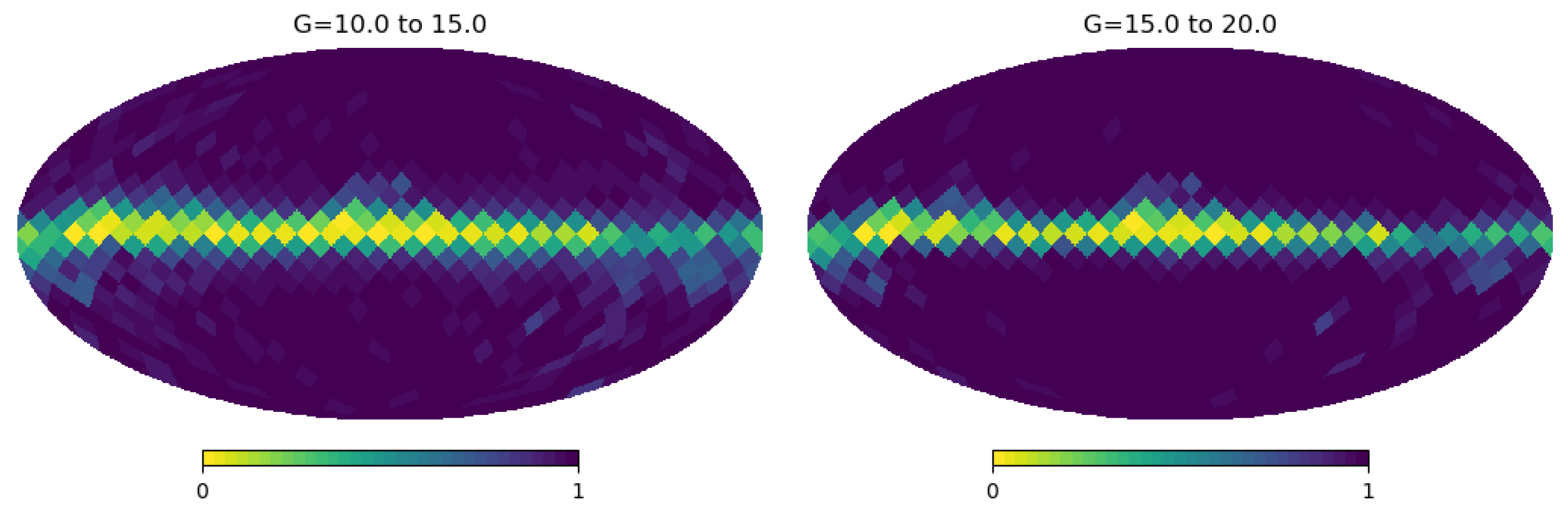
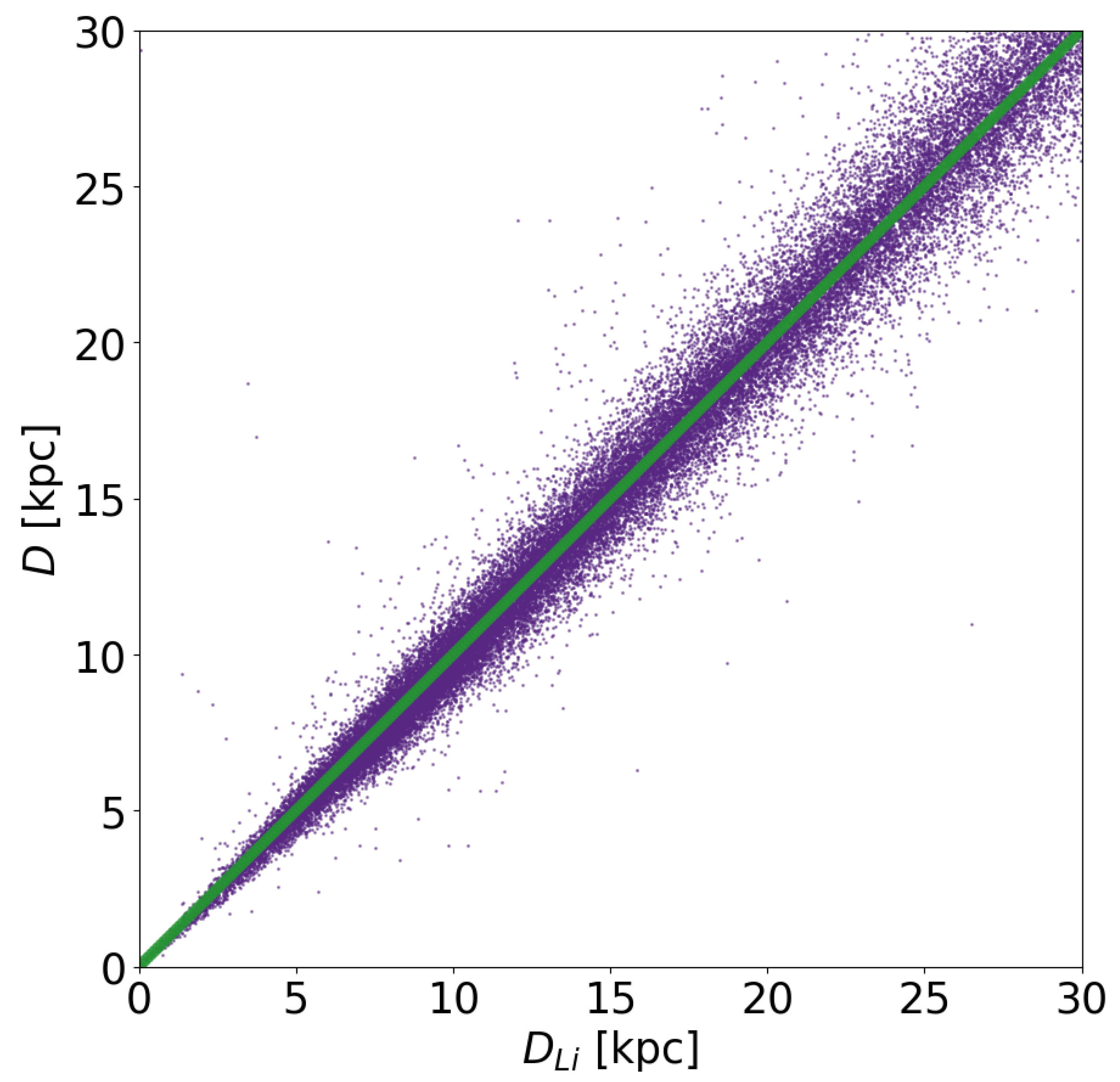
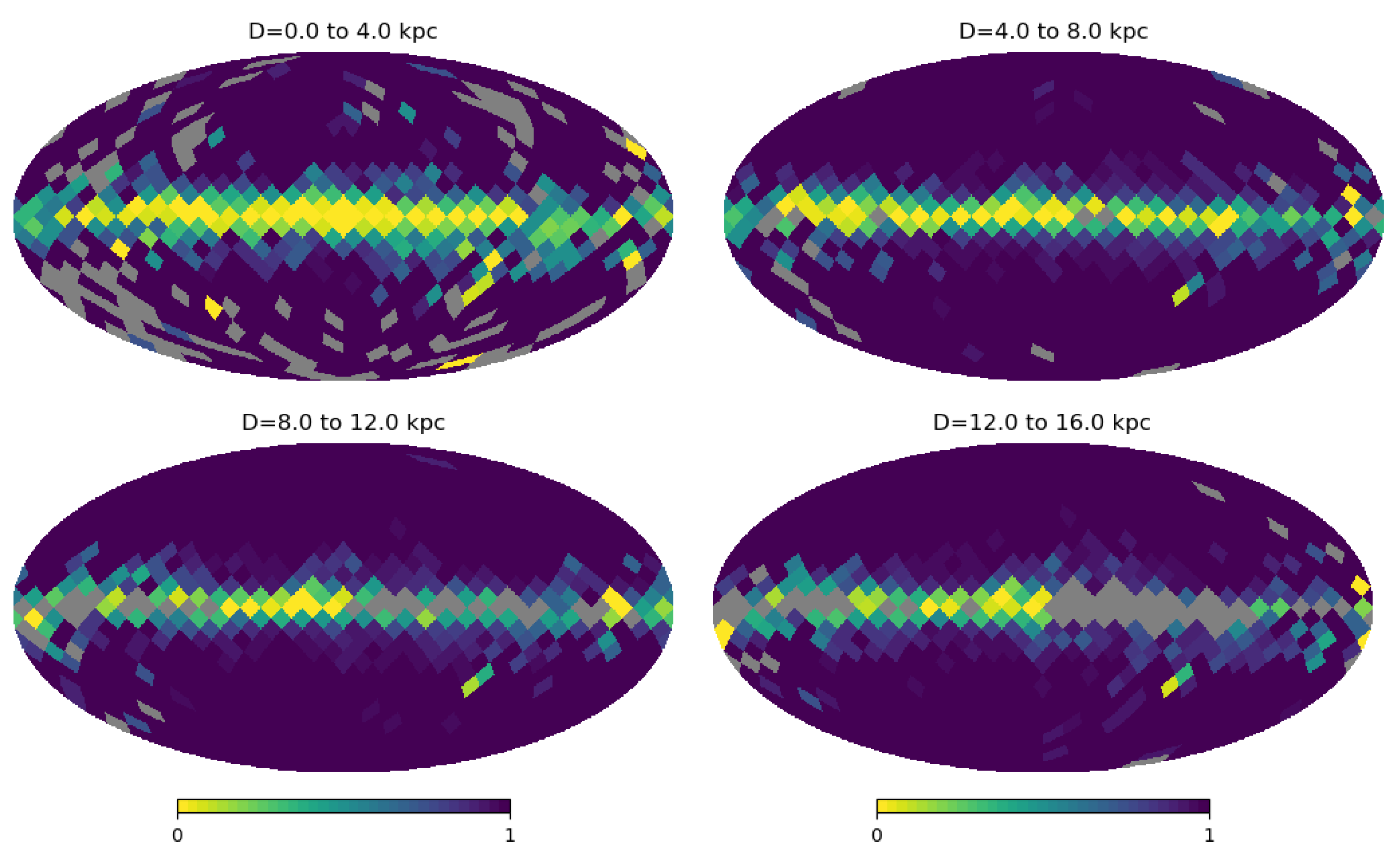
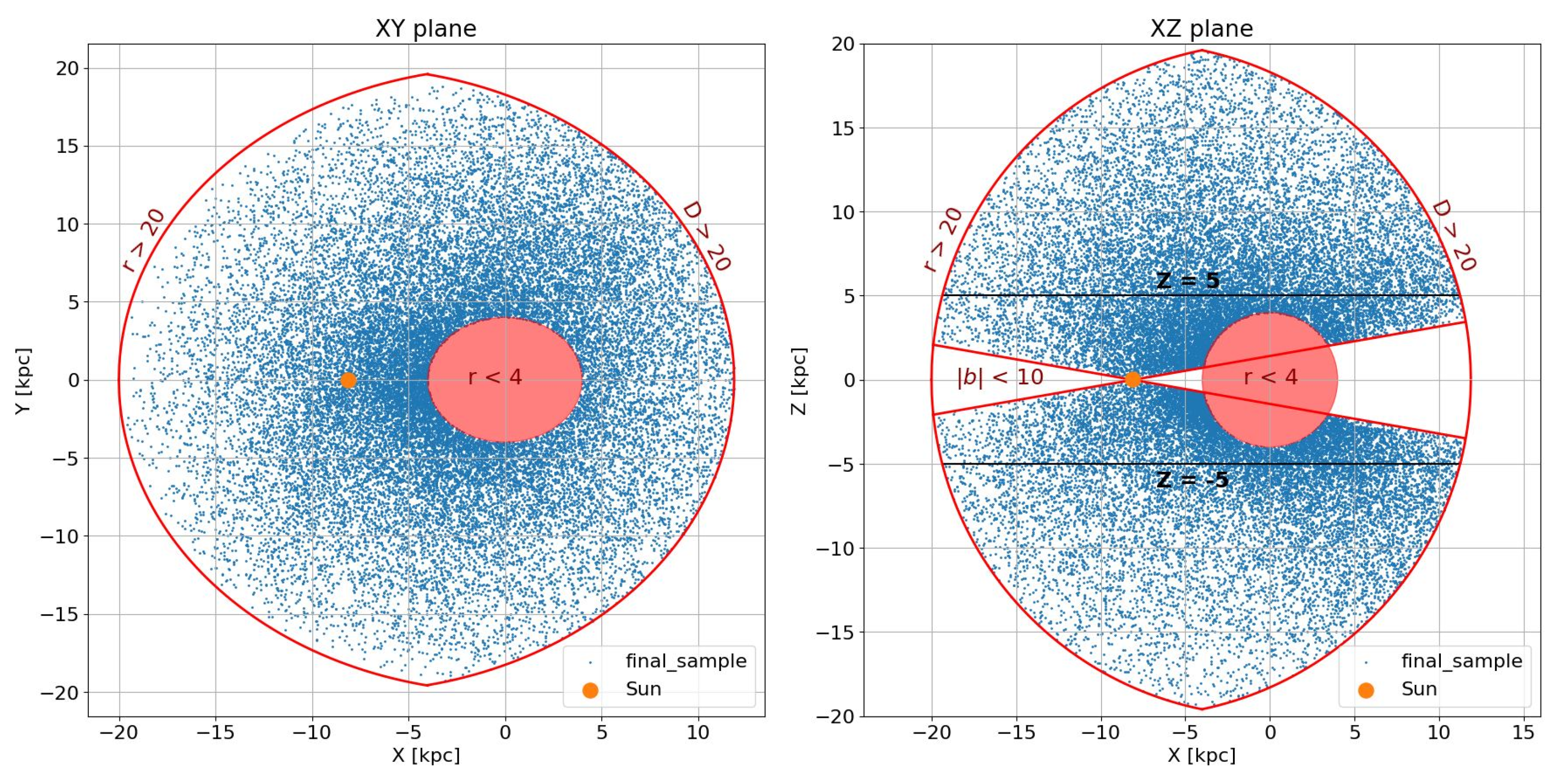
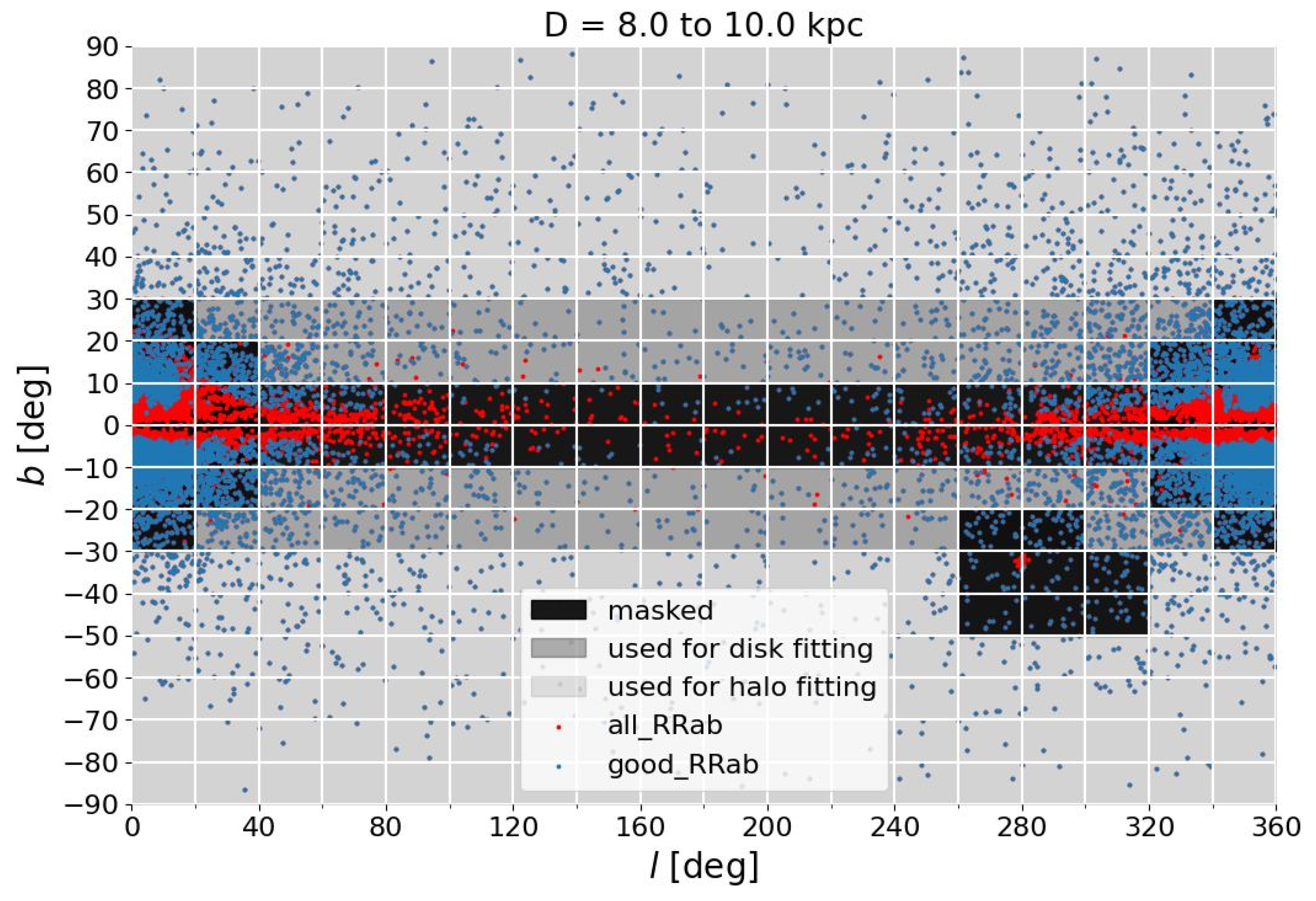
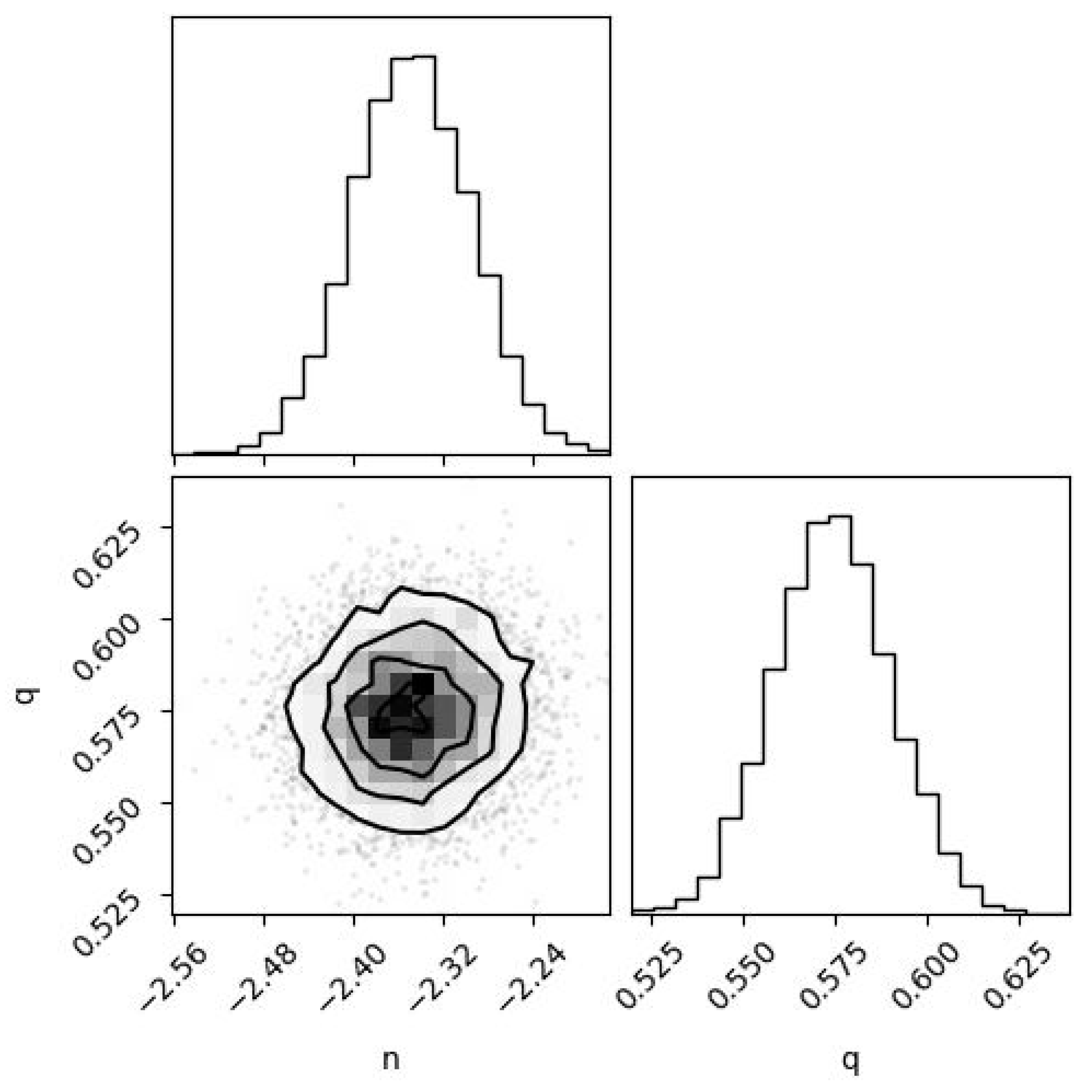

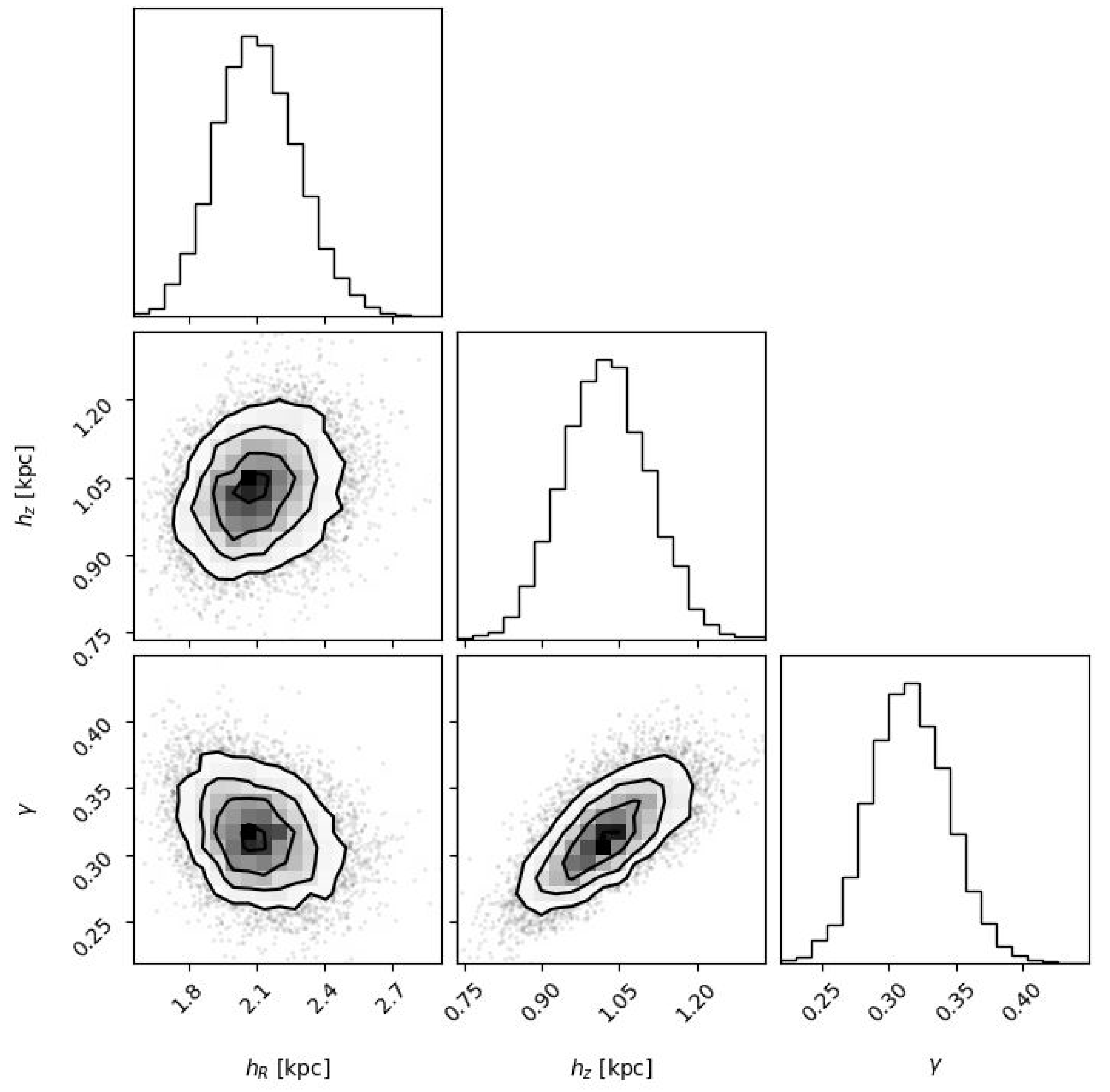
| Halo | |||
|---|---|---|---|
| n | q | ||
| median±range | |||
| mean±1 | |||
| Thick disc with exponential vertical profile | |||
| median±range | kpc | kpc | |
| mean±1 | kpc | kpc | |
| Thick disc with vertical profile | |||
| median±range | kpc | kpc | |
| mean±1 | kpc | kpc | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tkachenko, R.; Vieira, K.; Lutsenko, A.; Korchagin, V.; Carraro, G. Determining the Scale Length and Height of the Milky Way’s Thick Disc Using RR Lyrae. Universe 2025, 11, 132. https://doi.org/10.3390/universe11040132
Tkachenko R, Vieira K, Lutsenko A, Korchagin V, Carraro G. Determining the Scale Length and Height of the Milky Way’s Thick Disc Using RR Lyrae. Universe. 2025; 11(4):132. https://doi.org/10.3390/universe11040132
Chicago/Turabian StyleTkachenko, Roman, Katherine Vieira, Artem Lutsenko, Vladimir Korchagin, and Giovanni Carraro. 2025. "Determining the Scale Length and Height of the Milky Way’s Thick Disc Using RR Lyrae" Universe 11, no. 4: 132. https://doi.org/10.3390/universe11040132
APA StyleTkachenko, R., Vieira, K., Lutsenko, A., Korchagin, V., & Carraro, G. (2025). Determining the Scale Length and Height of the Milky Way’s Thick Disc Using RR Lyrae. Universe, 11(4), 132. https://doi.org/10.3390/universe11040132






