Correlating the 0νββ-Decay Amplitudes of 136Xe with the Ordinary Muon Capture (OMC) Rates of 136Ba
Abstract
:1. Introduction
2. Theory
2.1. Nuclear-Model Calculations
2.2. Ordinary Muon Capture (OMC)
2.3. Decay
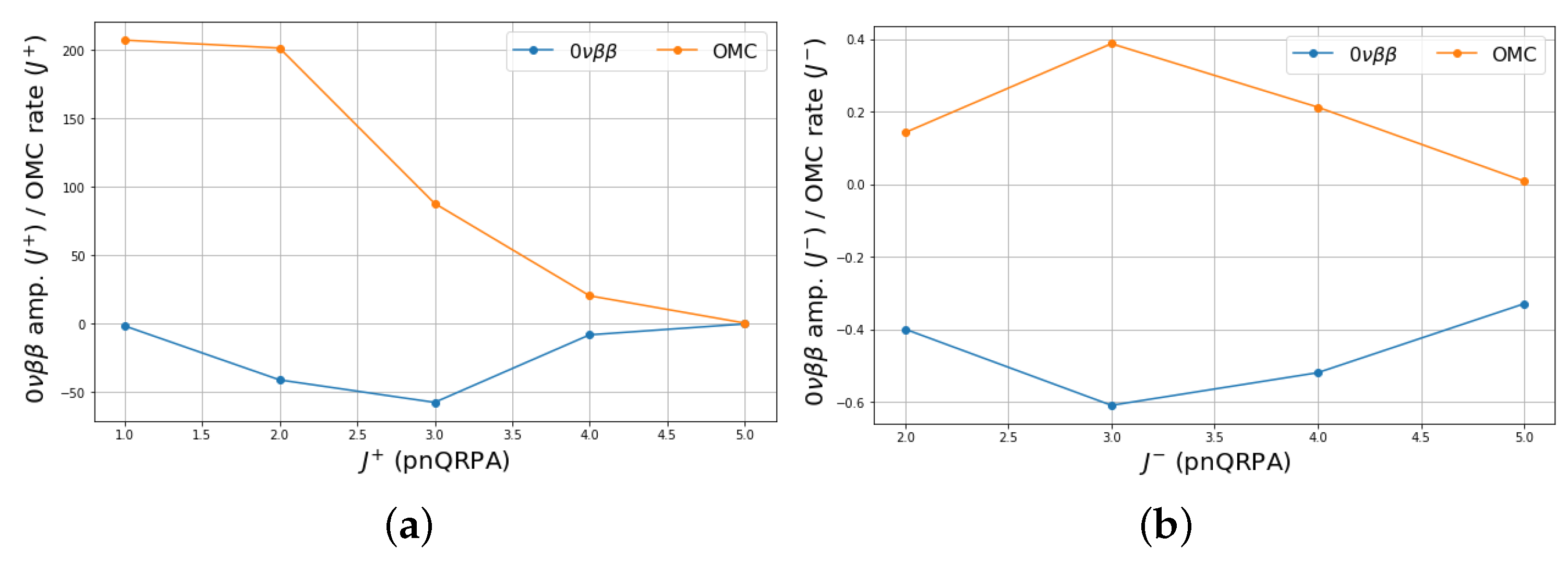
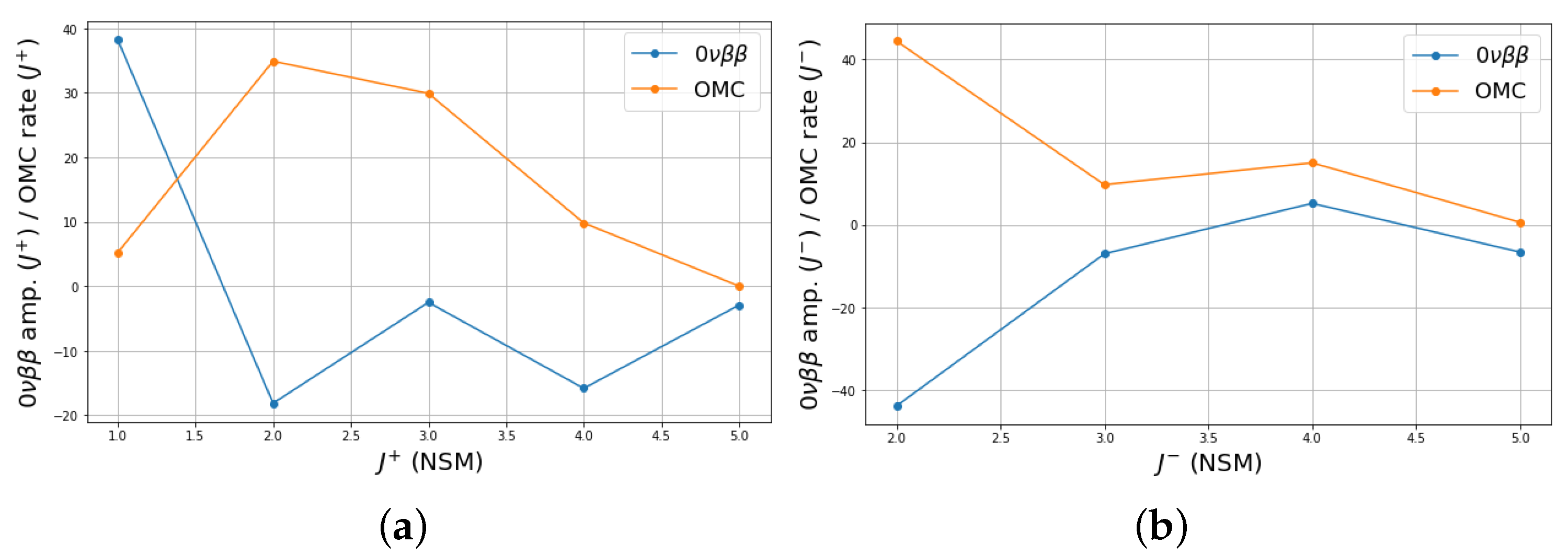
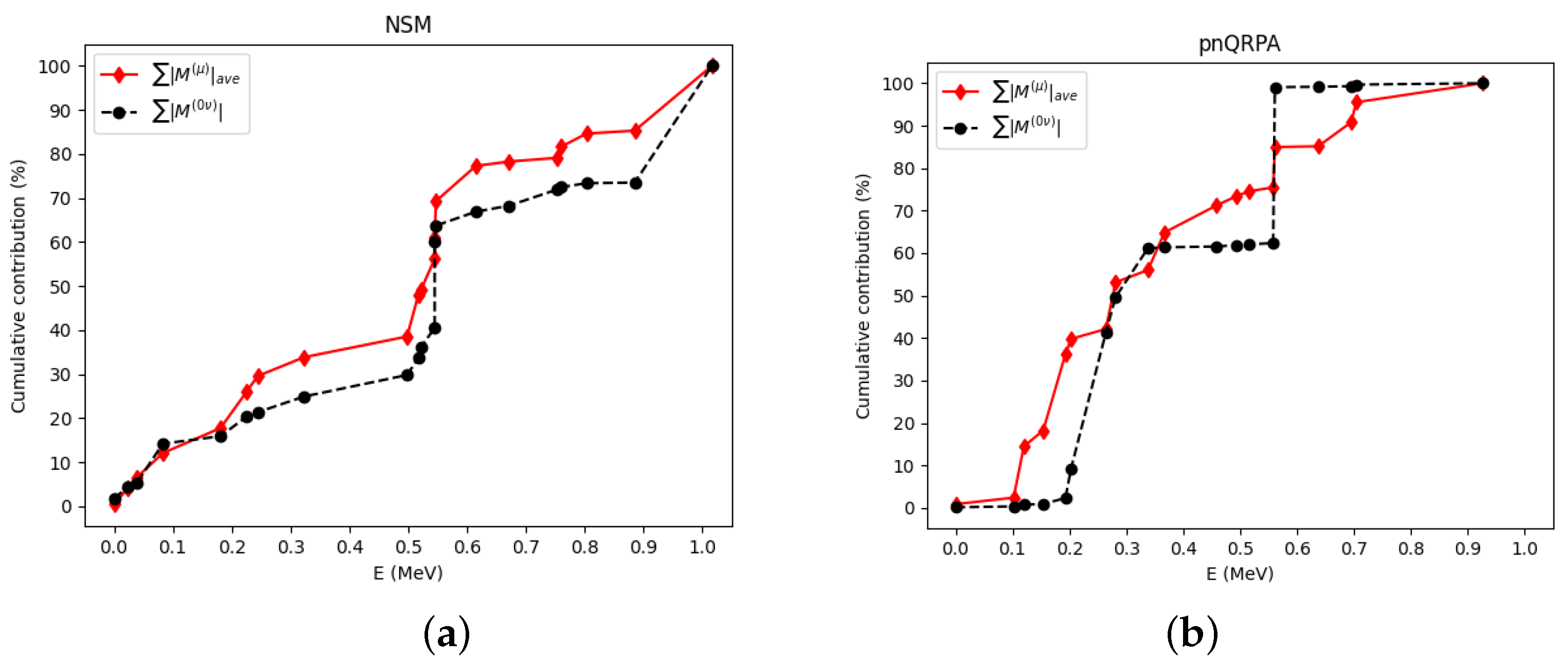
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agostini, M.; Benato, G.; Detwiler, J.A.; Menéndez, J.; Vissani, F. Toward the discovery of matter creation with neutrinoless ββ decay. Rev. Mod. Phys. 2023, 95, 025002. [Google Scholar] [CrossRef]
- Blaum, K.; Eliseev, S.; Danevich, F.A.; Tretyak, V.I.; Kovalenko, S.; Krivoruchenko, M.I.; Novikov, Y.N.; Suhonen, J. Neutrinoless double-electron capture. Rev. Mod. Phys. 2020, 92, 045007. [Google Scholar] [CrossRef]
- Engel, J.; Menéndez, J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: A review. Rep. Prog. Phys. 2017, 80, 046301. [Google Scholar] [CrossRef] [PubMed]
- Suhonen, J.; Civitarese, O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys. Rep. 1998, 300, 123–214. [Google Scholar] [CrossRef]
- Ejiri, H.; Suhonen, J.; Zuber, K. Neutrino–nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys. Rep. 2019, 797, 1. [Google Scholar] [CrossRef]
- Suhonen, J. Impact of the quenching of gA on the sensitivity of 0νββ experiments. Phys. Rev. C 2017, 96, 055501. [Google Scholar] [CrossRef]
- Suhonen, J.T. Value of the Axial-Vector Coupling Strength in β and ββ Decays: A Review. Front. Phys. 2017, 5, 55. [Google Scholar] [CrossRef]
- Suhonen, J.; Kostensalo, J. Double β Decay and the Axial Strength. Front. Phys. 2019, 7, 29. [Google Scholar] [CrossRef]
- Measday, D. The nuclear physics of muon capture. Phys. Rep. 2001, 354, 243–409. [Google Scholar] [CrossRef]
- Kortelainen, M.; Suhonen, J. Ordinary muon capture as a probe of virtual transitions of ββ decay. Europhys. Lett. 2002, 58, 666. [Google Scholar] [CrossRef]
- Kortelainen, M.; Suhonen, J. Microscopic study of muon-capture transitions in nuclei involved in double-beta-decay processes. Nucl. Phys. A 2003, 713, 501–521. [Google Scholar] [CrossRef]
- Kortelainen, M.; Suhonen, J. Nuclear muon capture as a powerful probe of double-beta decays in light nuclei. J. Phys. Nucl. Part. Phys. 2004, 30, 2003. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Suhonen, J.; Kotila, J. Comparative analysis of nuclear matrix elements of 0νβ+β+ decay and muon capture in 106Cd. Front. Phys. 2021, 9, 652536. [Google Scholar] [CrossRef]
- Šimkovic, F.; Pantis, G.; Vergados, J.D.; Faessler, A. Additional nucleon current contributions to neutrinoless double β decay. Phys. Rev. C 1999, 60, 055502. [Google Scholar] [CrossRef]
- Kolbe, E.; Langanke, K.; Vogel, P. Muon capture, continuum random phase approximation, and in-medium renormalization of the axial-vector coupling constant. Phys. Rev. C 1994, 50, 2576–2581. [Google Scholar] [CrossRef] [PubMed]
- Johnson, B.L.; Gorringe, T.P.; Armstrong, D.S.; Bauer, J.; Hasinoff, M.D.; Kovash, M.A.; Measday, D.F.; Moftah, B.A.; Porter, R.; Wright, D.H. Observables in muon capture on 23Na and the effective weak couplings g˜a and g˜p. Phys. Rev. C 1996, 54, 2714–2731. [Google Scholar] [CrossRef]
- Gorringe, T.P.; Armstrong, D.S.; Arole, S.; Boleman, M.; Gete, E.; Kuzmin, V.; Moftah, B.A.; Sedlar, R.; Stocki, T.J.; Tetereva, T. Measurement of partial muon capture rates in 1s − 0d shell nuclei. Phys. Rev. C 1999, 60, 055501. [Google Scholar] [CrossRef]
- Siiskonen, T.; Suhonen, J.; Hjorth-Jensen, M. Shell-model effective operators for muon capture in 20Ne. J. Phys. Nucl. Part. Phys. 1999, 25, L55. [Google Scholar] [CrossRef]
- Siiskonen, T.; Hjorth-Jensen, M.; Suhonen, J. Renormalization of the weak hadronic current in the nuclear medium. Phys. Rev. C 2001, 63, 055501. [Google Scholar] [CrossRef]
- Auerbach, N.; Brown, B.A. Weak interaction rates involving 12C, 14N, and 16O. Phys. Rev. C 2002, 65, 024322. [Google Scholar] [CrossRef]
- Gorringe, T.P.; Johnson, B.L.; Armstrong, D.S.; Bauer, J.; Kovash, M.A.; Hasinoff, M.D.; Measday, D.F.; Moftah, B.A.; Porter, R.; Wright, D.H. Hyperfine effect in μ− capture on 23Na and gp/ga. Phys. Rev. Lett. 1994, 72, 3472–3475. [Google Scholar] [CrossRef] [PubMed]
- Jonkmans, G.; Ahmad, S.; Armstrong, D.S.; Azuelos, G.; Bertl, W.; Blecher, M.; Chen, C.Q.; Depommier, P.; Doyle, B.C.; von Egidy, T.; et al. Radiative Muon Capture on Hydrogen and the Induced Pseudoscalar Coupling. Phys. Rev. Lett. 1996, 77, 4512–4515. [Google Scholar] [CrossRef]
- Gazit, D. Muon capture on 3He and the weak structure of the nucleon. Phys. Lett. B 2008, 666, 472–476. [Google Scholar] [CrossRef]
- Marcucci, L.E.; Kievsky, A.; Rosati, S.; Schiavilla, R.; Viviani, M. Chiral Effective Field Theory Predictions for Muon Capture on Deuteron and 3He. Phys. Rev. Lett. 2012, 108, 052502. [Google Scholar] [CrossRef]
- Brudanin, V.; Egorov, V.; Filipova, T.; Kachalkin, A.; Kovalenko, V.; Salamatin, A.; Shitov, Y.; Štekl, I.; Vassiliev, S.; Vorobel, V.; et al. Measurement of the induced pseudoscalar form factor in the capture of polarized muons by Si nuclei. Nucl. Phys. A 1995, 587, 577–595. [Google Scholar] [CrossRef]
- Siiskonen, T.; Suhonen, J.; Kuz’min, V.; Tetereva, T. Shell-model study of partial muon-capture rates in light nuclei. Nucl. Phys. A 1998, 635, 446–469. [Google Scholar] [CrossRef]
- Siiskonen, T.; Suhonen, J.; Kuz’min, V.; Tetereva, T. Shell-model study of partial muon-capture rates in light nuclei. Nucl. Phys. A 1999, 651, 437–438. [Google Scholar] [CrossRef]
- Siiskonen, T.; Suhonen, J.; Hjorth-Jensen, M. Towards the solution of the CP/CA anomaly in shell-model calculations of muon capture. Phys. Rev. C 1999, 59, R1839–R1843. [Google Scholar] [CrossRef]
- Gorringe, T.; Fearing, H.W. Induced pseudoscalar coupling of the proton weak interaction. Rev. Mod. Phys. 2003, 76, 31–91. [Google Scholar] [CrossRef]
- Šimkovic, F.; Dvornický, R.; Vogel, P. Muon capture rates: Evaluation within the quasiparticle random-phase approximation. Phys. Rev. C 2020, 102, 034301. [Google Scholar] [CrossRef]
- Araujo, G.R.; Bajpai, B.D.; Baudis, L.; Belov, V.; Bossio, E.; Cocolios, T.E.; Ejiri, H.; Fomina, F.; Gusev, K.; Hashim, I.H.; et al. The MONUMENT experiment: Ordinary muon capture studies for 0νββ decay. Eur. Phys. J. C 2024, 84, 1188. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Suhonen, J. Comparative analysis of muon-capture and 0νββ-decay matrix elements. Phys. Rev. C 2020, 102, 024303. [Google Scholar] [CrossRef]
- Gimeno, P.; Jokiniemi, L.; Kotila, J.; Ramalho, M.; Suhonen, J. Ordinary Muon Capture on 136Ba: Comparative Study Using the Shell Model and pnQRPA. Universe 2023, 9, 270. [Google Scholar] [CrossRef]
- Suhonen, J. From Nucleons to Nucleus: Concepts of Microscopic Nuclear Theory; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Brown, B.A.; Stone, N.J.; Stone, J.R.; Towner, I.S.; Hjorth-Jensen, M. Magnetic moments of the states around 132Sn. Phys. Rev. C 2005, 71, 044317. [Google Scholar] [CrossRef]
- Caurier, E.; Nowacki, F.; Poves, A.; Retamosa, J. Shell Model Studies of the Double Beta Decays of 76Ge, 82Se, and 136Xe. Phys. Rev. Lett. 1996, 77, 1954–1957. [Google Scholar] [CrossRef] [PubMed]
- Caurier, E.; Menéndez, J.; Nowacki, F.; Poves, A. Influence of Pairing on the Nuclear Matrix Elements of the Neutrinoless ββ Decays. Phys. Rev. Lett. 2008, 100, 052503. [Google Scholar] [CrossRef] [PubMed]
- Horoi, M.; Brown, B.A. Shell-Model Analysis of the 136Xe Double Beta Decay Nuclear Matrix Elements. Phys. Rev. Lett. 2013, 110, 222502. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Ejiri, H.; Frekers, D.; Suhonen, J. Neutrinoless ββ nuclear matrix elements using isovector spin-dipole Jπ=2− data. Phys. Rev. C 2018, 98, 024608. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R. Nuclear Structure; Benjamin: New York, NY, USA, 1969; Volume I. [Google Scholar]
- Holinde, K. Two-nucleon forces and nuclear matter. Phys. Rep. 1981, 68, 121–188. [Google Scholar] [CrossRef]
- Šimkovic, F.; Rodin, V.; Faessler, A.; Vogel, P. 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys. Rev. C 2013, 87, 045501. [Google Scholar] [CrossRef]
- Pirinen, P.; Suhonen, J. Systematic approach to β and 2νββ decays of mass A = 100 − 136 nuclei. Phys. Rev. C 2015, 91, 054309. [Google Scholar] [CrossRef]
- Yusef, M.; Rodin, V.; Faessler, A.; Šimkovic, F. Two-neutrino double β decay of deformed nuclei within the quasiparticle random-phase approximation with a realistic interaction. Phys. Rev. C 2009, 79, 014314. [Google Scholar] [CrossRef]
- Fang, D.; Faessler, A.; Rodin, V. Neutrinoless double-β decay of deformed nuclei within quasiparticle random-phase approximation with a realistic interaction. Phys. Rev. C 2011, 83, 034320. [Google Scholar] [CrossRef]
- Fang, D.; Faessler, A.; Šimkovic, F. 0νββ-decay nuclear matrix element for light and heavy neutrino mass mexhanisms from deformed quasiparticle random-phase approximation calculations for 76Ge, 82Se, 130Te, 136Xe, and 150Nb with isospin restoration. Phys. Rev. C 2018, 97, 045503. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Suhonen, J.; Ejiri, H.; Hashim, I. Pinning down the strength function for ordinary muon capture on 100Mo. Phys. Lett. B 2019, 794, 143–147. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Suhonen, J. Muon-capture strength functions in intermediate nuclei of 0νββ decays. Phys. Rev. C 2019, 100, 014619. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Miyagi, T.; Stroberg, S.R.; Holt, J.D.; Kotila, J.; Suhonen, J. Ab initio calculation of muon capture on 24Mg. Phys. Rev. C 2023, 107, 014327. [Google Scholar] [CrossRef]
- Hyvärinen, J.; Suhonen, J. Nuclear matrix elements for 0νββ decays with light or heavy Majorana-neutrino exchange. Phys. Rev. C 2015, 91, 024613. [Google Scholar] [CrossRef]
| [keV] | |||||
|---|---|---|---|---|---|
| 0 | 0 | −0.18 | 0.040 | −0.14 | |
| 102 | 0 | −0.28 | 0.037 | −0.24 | |
| 120 | 0.20 | −0.13 | −0.034 | −0.46 | |
| 154 | 0.07 | −0.02 | −0.006 | −0.13 | |
| 193 | 0 | −1.61 | 0.021 | −1.59 | |
| 203 | 4.96 | −0.32 | −0.13 | −7.65 | |
| 264 | 0 | −51.6 | 16.3 | −35.2 | |
| 281 | 0 | −10.1 | 0.88 | −9.20 | |
| 338 | 0 | −9.46 | −3.27 | −12.7 | |
| 367 | 0.01 | −0.16 | −0.0041 | −0.22 | |
| 458 | 0.02 | −0.16 | −0.0060 | −0.25 | |
| 494 | −0.007 | −0.24 | −0.089 | −0.32 | |
| 515 | 0.03 | −0.11 | −0.050 | −0.21 | |
| 558 | 0 | −0.42 | 0.068 | −0.35 | |
| 561 | 5.29 | −24.5 | −8.22 | −40.4 | |
| 637 | 0.07 | −0.01 | −0.004 | −0.12 | |
| 695 | 0 | −0.24 | 0.084 | −0.16 | |
| 704 | 0 | −0.49 | 0.097 | −0.40 | |
| 926 | 0.23 | −0.02 | −0.008 | −0.36 |
| [keV] | |||||
|---|---|---|---|---|---|
| 0 | 0 | −4.355 | 1.411 | −2.944 | |
| 23 | 0 | −5.695 | 1.445 | −4.250 | |
| 39 | 1.230 | −0.153 | −0.058 | −1.633 | |
| 83 | 6.993 | −5.160 | −1.433 | −14.677 | |
| 181 | 0 | −2.269 | −0.555 | −2.824 | |
| 224 | 0.894 | −4.481 | −1.748 | −7.262 | |
| 244 | 0 | −1.647 | −0.059 | −1.706 | |
| 323 | 1.989 | −2.575 | −1.019 | −5.895 | |
| 498 | 2.582 | −3.525 | −1.578 | −8.088 | |
| 517 | 0 | 6.540 | −0.289 | 6.251 | |
| 522 | 0.723 | −2.483 | −1.048 | −4.366 | |
| 545 | 0.379 | −4.893 | −1.701 | −7.033 | |
| 545 | 0 | 33.820 | −1.602 | 32.218 | |
| 547 | 0 | 5.565 | 0.589 | 6.154 | |
| 615 | −1.426 | 2.804 | 0.780 | 5.232 | |
| 670 | 1.313 | −0.511 | −0.210 | −2.239 | |
| 752 | 0 | 6.066 | −0.064 | 6.003 | |
| 760 | 0 | −1.281 | 0.309 | −0.972 | |
| 803 | 0.290 | −0.889 | −0.251 | −1.475 | |
| 885 | 0.082 | −0.108 | −0.044 | −0.248 | |
| 1016 | 0 | −44.144 | 0.371 | −43.772 |
| qrpa-phen | sm-phen | |||
|---|---|---|---|---|
| () | OMC() | () | OMC() | |
| −0.14 | 0.50 | −2.944 | 0.0 | |
| −8.10 | 20.4 | −15.864 | 9.8 | |
| −57.4 | 87.8 | −2.529 | 29.9 | |
| −41.0 | 201.1 | −18.182 | 34.9 | |
| −1.59 | 206.9 | 38.221 | 5.2 | |
| −0.33 | 0.80 | −6.605 | 0.6 | |
| −0.52 | 21.2 | 5.182 | 15.0 | |
| −0.61 | 38.7 | −7.033 | 9.7 | |
| −0.40 | 14.2 | −43.772 | 44.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agnihotri, A.; Kumar, V.; Suhonen, J. Correlating the 0νββ-Decay Amplitudes of 136Xe with the Ordinary Muon Capture (OMC) Rates of 136Ba. Universe 2025, 11, 138. https://doi.org/10.3390/universe11050138
Agnihotri A, Kumar V, Suhonen J. Correlating the 0νββ-Decay Amplitudes of 136Xe with the Ordinary Muon Capture (OMC) Rates of 136Ba. Universe. 2025; 11(5):138. https://doi.org/10.3390/universe11050138
Chicago/Turabian StyleAgnihotri, Aagrah, Vikas Kumar, and Jouni Suhonen. 2025. "Correlating the 0νββ-Decay Amplitudes of 136Xe with the Ordinary Muon Capture (OMC) Rates of 136Ba" Universe 11, no. 5: 138. https://doi.org/10.3390/universe11050138
APA StyleAgnihotri, A., Kumar, V., & Suhonen, J. (2025). Correlating the 0νββ-Decay Amplitudes of 136Xe with the Ordinary Muon Capture (OMC) Rates of 136Ba. Universe, 11(5), 138. https://doi.org/10.3390/universe11050138








