Evidence of Gapless Superfluidity in MXB 1659-29 With and Without Late Time Cooling
Abstract
:1. Introduction
- Fitting the quiescent X-ray spectra with an absorbed neutron star atmosphere model and allowing for a variation of the hydrogen column density along the line of sight , resulting in . The associated effective surface temperature eV (referred to as fit 1 in Table 1 and the following results) is consistent with the previous 2008 Chandra observation by Cackett et al. [66], and suggests that the thermal equilibrium between the crust and core was already restored in 2003–2004. Cackett et al. [67] invoked a thickening of the accretion disk or its precession as possible explanations of the significant increase in compared to the value deduced from the 2008 Chandra observation [66] ( ). However, the same authors emphasized that such a scenario is not expected from the standard accretion disk theory.
- Alternatively, the observed drop in X-ray luminosity might suggest a further decrease of the neutron star’s temperature. Keeping the hydrogen column density fixed to the value obtained from the 2008 Chandra observation [66] ( ) and using an absorbed neutron star atmosphere model yielded eV (referred to as fit 2). More refined spectral models including a neutron star atmosphere and a power-law component then lead to lower effective surface temperatures of eV (for a photon power-law index of , referred to as fit 3) and eV (for a photon power-law index of , labeled as fit 4).
2. Cooling Model
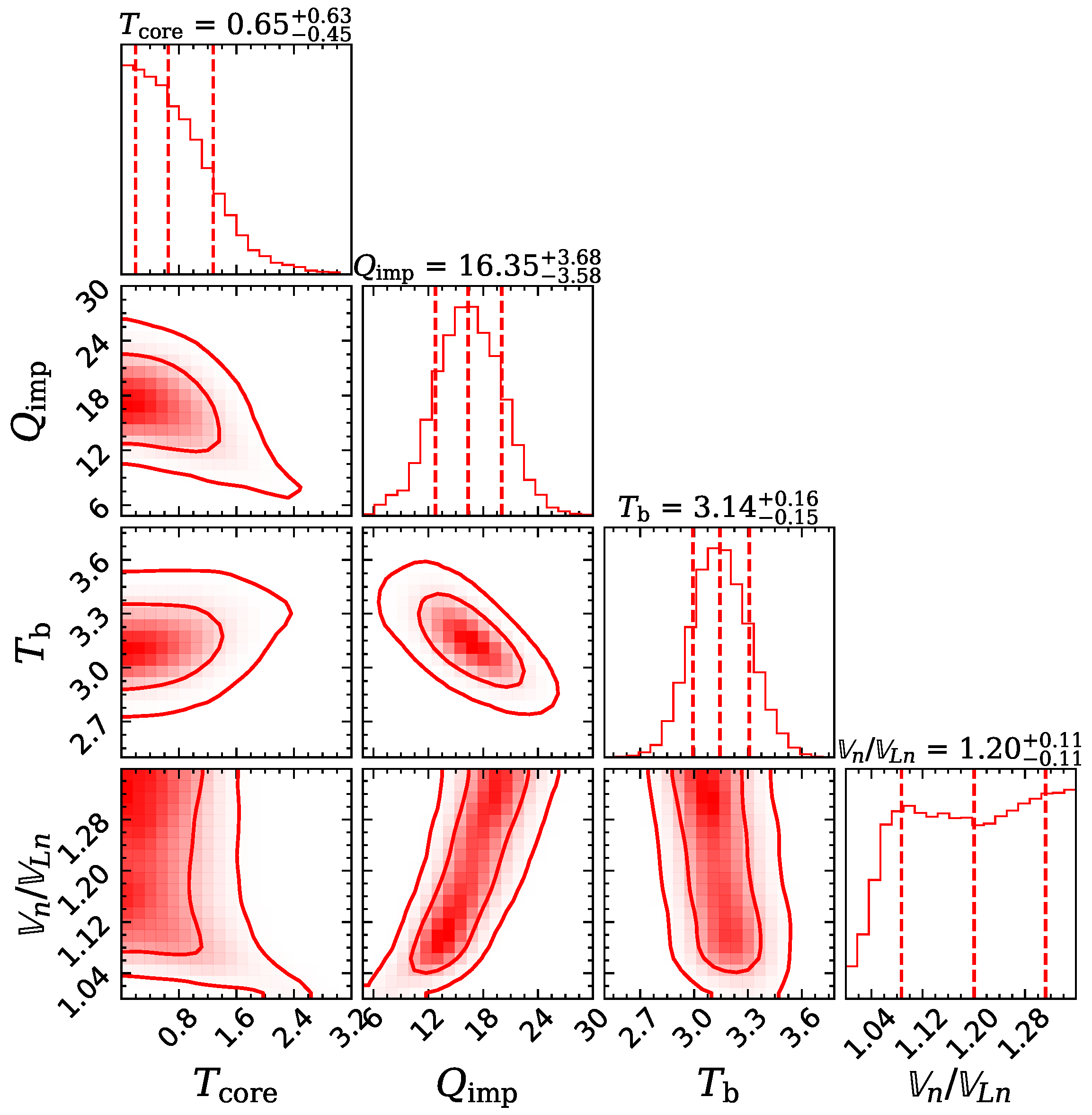
- The core temperature , which is constrained by the (late-time) observations.
- The normalized neutron effective superfluid velocity , which accounts for modification of the specific heat of superfluid neutrons in presence of superflow (see Equations (10) and (21) of [39]). We assume a uniform value of throughout the crust. We have also carried out simulations within the standard cooling theory (with a static neutron superfluid in the crust frame) by setting , which we refer to as the BCS superfluidity in what follows.
3. Results
3.1. With BCS Superfluidity
3.2. With Gapless Superfluidity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NS | Neutron Star |
| LMXB | Low-Mass X-ray binary |
| (q)SXT | quasipersistent Soft X-ray Transient |
| dch | Deep Crustal Heating |
| sh | Shallow Heating |
| nHD | Neutron diffusion |
| QMC | Quantum Monte Carlo |
| BHF | Brueckner Hartree-Fock |
| SCGF | Self-Consistent Green Function |
| MCMC | Markov Chain Monte Carlo |
| 1 | |
| 2 | https://github.com/andrewcumming/crustcool (accessed on 1 March 2024). |
| 3 | https://github.com/dfm/emcee (accessed on 1 March 2024). |
| 4 | https://github.com/dfm/corner.py (accessed on 1 March 2024). |
References
- Bahramian, A.; Degenaar, N. Low-Mass X-ray Binaries. In Handbook of X-Ray and Gamma-Ray Astrophysics; Bambi, C., Santangelo, A., Eds.; Springer Nature: Singapore, 2022; pp. 1–62. [Google Scholar] [CrossRef]
- Osaki, Y. Dwarf-Nova Outbursts. Publ. Astron. Soc. Pac. 1996, 108, 39. [Google Scholar] [CrossRef]
- Lasota, J.P. The disc instability model of dwarf novae and low-mass X-ray binary transients. New Astron. Rev. 2001, 45, 449–508. [Google Scholar] [CrossRef]
- Hameury, J. A review of the disc instability model for dwarf novae, soft X-ray transients and related objects. Adv. Space Res. 2020, 66, 1004–1024. [Google Scholar] [CrossRef]
- Bildsten, L.; Brown, E.F. Thermonuclear Burning on the Accreting X-Ray Pulsar GRO J1744–28. Astrophys. J. 1997, 477, 897. [Google Scholar] [CrossRef]
- Brown, E.F.; Bildsten, L.; Rutledge, R.E. Crustal Heating and Quiescent Emission from Transiently Accreting Neutron Stars. Astrophys. J. Lett. 1998, 504, L95–L98. [Google Scholar] [CrossRef]
- Wijnands, R.; Degenaar, N.; Page, D. Cooling of accretion-heated neutron stars. J. Astrophys. Astron. 2017, 38, 1–16. [Google Scholar] [CrossRef]
- Page, D.; Reddy, S. Thermal and transport properties of the neutron star inner crust. In Neutron Star Crust; Bertulani, C.A., Piekarewicz, J., Eds.; Nova Science Publishers: New York, NY, USA, 2012; pp. 281–308. [Google Scholar]
- Chaikin, E.A.; Kaminker, A.D.; Yakovlev, D.G. Afterburst thermal relaxation in neutron star crusts. Astrophys. Space Sci. 2018, 363, 209. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L. Non-equilibrium processes in the crust of an accreting neutron star. Astron. Astrophys. 1990, 227, 431–436. [Google Scholar]
- Haensel, P.; Zdunik, J.L. Nuclear composition and heating in accreting neutron-star crusts. Astron. Astrophys. 2003, 404, L33–L36. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L. Models of crustal heating in accreting neutron stars. Astron. Astrophys. 2008, 480, 459–464. [Google Scholar] [CrossRef]
- Fantina, A.F.; Zdunik, J.L.; Chamel, N.; Pearson, J.M.; Haensel, P.; Goriely, S. Crustal heating in accreting neutron stars from the nuclear energy-density functional theory. I. Proton shell effects and neutron-matter constraint. Astron. Astrophys. 2018, 620, A105. [Google Scholar] [CrossRef]
- Sedrakian, A.; Clark, J.W. Superfluidity in nuclear systems and neutron stars. Eur. Phys. J. A 2019, 55, 167. [Google Scholar] [CrossRef]
- Antonopoulou, D.; Haskell, B.; Espinoza, C.M. Pulsar glitches: Observations and physical interpretation. Rep. Prog. Phys. 2022, 85, 126901. [Google Scholar] [CrossRef]
- Anderson, P.W.; Itoh, N. Pulsar glitches and restlessness as a hard superfluidity phenomenon. Nature 1975, 256, 25–27. [Google Scholar] [CrossRef]
- Pines, D.; Alpar, M.A. Superfluidity in neutron stars. Nature 1985, 316, 27–32. [Google Scholar] [CrossRef]
- Page, D.; Prakash, M.; Lattimer, J.M.; Steiner, A.W. Rapid Cooling of the Neutron Star in Cassiopeia A Triggered by Neutron Superfluidity in Dense Matter. Phys. Rev. Lett. 2011, 106, 081101. [Google Scholar] [CrossRef]
- Shternin, P.S.; Yakovlev, D.G.; Heinke, C.O.; Ho, W.C.G.; Patnaude, D.J. Cooling neutron star in the Cassiopeia A supernova remnant: Evidence for superfluidity in the core. Mon. Not. R. Astron. Soc. 2011, 412, L108–L112. [Google Scholar] [CrossRef]
- Elshamouty, K.G.; Heinke, C.O.; Sivakoff, G.R.; Ho, W.C.G.; Shternin, P.S.; Yakovlev, D.G.; Patnaude, D.J.; David, L. Measuring the cooling of the neutron star in Cassiopeia A with all Chandra X-ray observatory detectors. Astrophys. J. 2013, 777, 22. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Elshamouty, K.G.; Heinke, C.O.; Potekhin, A.Y. Tests of the nuclear equation of state and superfluid and superconducting gaps using the Cassiopeia A neutron star. Phys. Rev. C 2015, 91, 015806. [Google Scholar] [CrossRef]
- Posselt, B.; Pavlov, G.G. Upper Limits on the Rapid Cooling of the Central Compact Object in Cas A. Astrophys. J. 2018, 864, 135. [Google Scholar] [CrossRef]
- Wijngaarden, M.J.P.; Ho, W.C.G.; Chang, P.; Heinke, C.O.; Page, D.; Beznogov, M.; Patnaude, D.J. Diffusive nuclear burning in cooling simulations and application to new temperature data of the Cassiopeia A neutron star. Mon. Not. R. Astron. Soc. 2019, 484, 974–988. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Zhao, Y.; Heinke, C.O.; Kaplan, D.L.; Shternin, P.S.; Wijngaarden, M.J.P. X-ray bounds on cooling, composition, and magnetic field of the Cassiopeia A neutron star and young central compact objects. Mon. Not. R. Astron. Soc. 2021, 506, 5015–5029. [Google Scholar] [CrossRef]
- Shternin, P.S.; Ofengeim, D.D.; Ho, W.C.G.; Heinke, C.O.; Wijngaarden, M.J.P.; Patnaude, D.J. Model-independent constraints on superfluidity from the cooling neutron star in Cassiopeia A. Mon. Not. R. Astron. Soc. 2021, 506, 709–726. [Google Scholar] [CrossRef]
- Posselt, B.; Pavlov, G.G. The Cooling of the Central Compact Object in Cas A from 2006 to 2020. Astrophys. J. 2022, 932, 83. [Google Scholar] [CrossRef]
- Shternin, P.S.; Ofengeim, D.D.; Heinke, C.O.; Ho, W.C.G. Constraints on neutron star superfluidity from the cooling neutron star in Cassiopeia A using all Chandra ACIS-S observations. Mon. Not. R. Astron. Soc. 2023, 518, 2775–2793. [Google Scholar] [CrossRef]
- Rutledge, R.E.; Bildsten, L.; Brown, E.F.; Pavlov, G.G.; Zavlin, V.E.; Ushomirsky, G. Crustal Emission and the Quiescent Spectrum of the Neutron Star in KS 1731-260. Astrophys. J. 2002, 580, 413–422. [Google Scholar] [CrossRef]
- Shternin, P.S.; Yakovlev, D.G.; Haensel, P.; Potekhin, A.Y. Neutron star cooling after deep crustal heating in the X-ray transient KS 1731-260. Mon. Not. R. Astron. Soc. 2007, 382, L43–L47. [Google Scholar] [CrossRef]
- Brown, E.F.; Cumming, A. Mapping crustal heating with the cooling light curves of quasi-persistent transients. Astrophys. J. 2009, 698, 1020–1032. [Google Scholar] [CrossRef]
- Turlione, A.; Aguilera, D.N.; Pons, J.A. Quiescent thermal emission from neutron stars in low-mass X-ray binaries. Astron. Astrophys. 2015, 577, A5. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Berry, D.K.; Briggs, C.M.; Caplan, M.E.; Cumming, A.; Schneider, A.S. Disordered Nuclear Pasta, Magnetic Field Decay, and Crust Cooling in Neutron Stars. Phys. Rev. Lett. 2015, 114, 031102. [Google Scholar] [CrossRef]
- Deibel, A.; Cumming, A.; Brown, E.F.; Reddy, S. Late-time cooling of neutron star transients and the physics of the inner crust. Astrophys. J. 2017, 839, 95. [Google Scholar] [CrossRef]
- Cumming, A.; Brown, E.F.; Fattoyev, F.J.; Horowitz, C.J.; Page, D.; Reddy, S. Lower limit on the heat capacity of the neutron star core. Phys. Rev. C 2017, 95, 025806. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Chabrier, G. Crust structure and thermal evolution of neutron stars in soft X-ray transients. Astron. Astrophys. 2021, 645, A102. [Google Scholar] [CrossRef]
- Lu, X.Y.; Lü, G.L.; Liu, H.L.; Zhu, C.H.; Wang, Z.J. Crust Cooling of Soft X-Ray Transients—The Uncertainties of Shallow Heating. Res. Astron. Astrophys. 2022, 22, 055018. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Gusakov, M.E.; Chugunov, A.I. Thermal evolution of neutron stars in soft X-ray transients with thermodynamically consistent models of the accreted crust. Mon. Not. R. Astron. Soc. 2023, 522, 4830–4840. [Google Scholar] [CrossRef]
- Allard, V.; Chamel, N. Gapless neutron superfluidity can explain the late time cooling of transiently accreting neutron stars. Phys. Rev. Lett. 2024, 132, 181001. [Google Scholar] [CrossRef] [PubMed]
- Allard, V.; Chamel, N. Gapless neutron superfluidity in the crust of the accreting neutron stars KS 1731-260 and MXB 1659-29. Eur. Phys. J. A 2024, 60, 116. [Google Scholar] [CrossRef]
- Potekhin, A.; Chugunov, A.; Shchechilin, N.; Gusakov, M. Cooling of neutron stars in soft X-ray transients with realistic crust composition. J. High Energy Astrophys. 2025, 45, 116–124. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F.; Zdunik, J.L.; Haensel, P. Experimental constraints on shallow heating in accreting neutron-star crusts. Phys. Rev. C 2020, 102, 015804. [Google Scholar] [CrossRef]
- Steiner, A.W. Deep crustal heating in a multicomponent accreted neutron star crust. Phys. Rev. C 2012, 85, 055804. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F.; Zdunik, J.L.; Haensel, P. Neutron drip transition in accreting and nonaccreting neutron star crusts. Phys. Rev. C 2015, 91, 055803. [Google Scholar] [CrossRef]
- Chugunov, A.I.; Shchechilin, N.N. Crucial role of neutron diffusion in the crust of accreting neutron stars. Mon. Not. R. Astron. Soc. 2020, 495, L32–L36. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Chugunov, A.I. Thermodynamically Consistent Equation of State for an Accreted Neutron Star Crust. Phys. Rev. Lett. 2020, 124, 191101. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Chugunov, A.I. Heat release in accreting neutron stars. Phys. Rev. D 2021, 103, L101301. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Kantor, E.M.; Chugunov, A.I. Nonequilibrium thermodynamics of accreted neutron-star crust. Phys. Rev. D 2021, 104, L081301. [Google Scholar] [CrossRef]
- Wlazłowski, G.; Sekizawa, K.; Magierski, P.; Bulgac, A.; Forbes, M.M. Vortex Pinning and Dynamics in the Neutron Star Crust. Phys. Rev. Lett. 2016, 117, 232701. [Google Scholar] [CrossRef]
- Klausner, P.; Barranco, F.; Pizzochero, P.M.; Roca-Maza, X.; Vigezzi, E. Microscopic calculation of the pinning energy of a vortex in the inner crust of a neutron star. Phys. Rev. C 2023, 108, 035808. [Google Scholar] [CrossRef]
- Haskell, B.; Melatos, A. Models of pulsar glitches. Int. J. Mod. Phys. D 2015, 24, 1530008. [Google Scholar] [CrossRef]
- Zhou, S.; Gügercinoğlu, E.; Yuan, J.; Ge, M.; Yu, C. Pulsar Glitches: A Review. Universe 2022, 8, 641. [Google Scholar] [CrossRef]
- Galloway, D.K.; Morgan, E.H.; Levine, A.M. A Frequency Glitch in an Accreting Pulsar. Astrophys. J. 2004, 613, 1164–1172. [Google Scholar] [CrossRef]
- Serim, M.M.; Şahiner, Ş.; Çerri-Serim, D.; Inam, S.Ç.; Baykal, A. Discovery of a glitch in the accretion-powered pulsar SXP 1062. Mon. Not. R. Astron. Soc. 2017, 471, 4982–4989. [Google Scholar] [CrossRef]
- Patruno, A.; Watts, A.L. Accreting Millisecond X-ray Pulsars. In Timing Neutron Stars: Pulsations, Oscillations and Explosions; Belloni, T.M., Méndez, M., Zhang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 143–208. [Google Scholar] [CrossRef]
- Salvo, T.D.; Sanna, A. Accretion Powered X-ray Millisecond Pulsars. In Millisecond Pulsars; Bhattacharyya, S., Papitto, A., Bhattacharya, D., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 87–124. [Google Scholar] [CrossRef]
- Papitto, A.; de Martino, D. Transitional Millisecond Pulsars. In Proceedings of the Astrophysics and Space Science Library; Bhattacharyya, S., Papitto, A., Bhattacharya, D., Eds.; Astrophysics and Space Science Library; Springer International Publishing: Cham, Switzerland, 2022; Volume 465, pp. 157–200. [Google Scholar] [CrossRef]
- Allard, V.; Chamel, N. Gapless superfluidity in neutron stars: Thermal properties. Phys. Rev. C 2023, 108, 015801. [Google Scholar] [CrossRef]
- Lewin, W.H.G.; Hoffman, J.A.; Doty, J.; Liller, W. X-Ray Bursts. IAU Cirulars 1976, 2994, 2. [Google Scholar] [CrossRef]
- in ’t Zand, J.; Heise, J.; Smith, M.J.S.; Cocchi, M.; Natalucci, L.; Celidonio, G.; Augusteijn, T.; Freyhammer, L. V2134 Ophiuchi = MXB 1659-29. IAU Cirulars 1999, 7138, 1. [Google Scholar]
- Wijnands, R.; Muno, M.P.; Miller, J.M.; Franco, L.M.; Strohmayer, T.; Galloway, D.; Chakrabarty, D. The Burst Behavior of the Eclipsing Low-Mass X-Ray Binary MXB 1659–298. Astrophys. J. 2002, 566, 1060. [Google Scholar] [CrossRef]
- Wijnands, R.; Strohmayer, T.; Franco, L.M. Discovery of Nearly Coherent Oscillations with a Frequency of ∼567 Hz during Type I X-Ray Bursts of the X-Ray Transient and Eclipsing Binary X1658-298. Astrophys. J. 2001, 549, L71–L75. [Google Scholar] [CrossRef]
- Wijnands, R.; Nowak, M.; Miller, J.M.; Homan, J.; Wachter, S.; Lewin, W.H.G. A Chandra Obs. Neutron Star X-Ray Transient Eclips. Bin. MXB 1659-29 Quiescence. Astrophys. J. 2003, 594, 952–960. [Google Scholar] [CrossRef]
- Galloway, D.K.; Muno, M.P.; Hartman, J.M.; Psaltis, D.; Chakrabarty, D. Thermonuclear (Type I) X-ray bursts observed by the Rossi X-Ray Timing Explorer. Astrophys. J. Suppl. Ser. 2008, 179, 360. [Google Scholar] [CrossRef]
- Wijnands, R.; Homan, J.; Miller, J.M.; Lewin, W.H.G. Monitoring Chandra Observations of the Quasi-persistent Neutron Star X-Ray Transient MXB 1659-29 in Quiescence: The Cooling Curve of the Heated Neutron Star Crust. Astrophys. J. Lett. 2004, 606, L61–L64. [Google Scholar] [CrossRef]
- Cackett, E.M.; Wijnands, R.; Linares, M.; Miller, J.M.; Homan, J.; Lewin, W.H.G. Cooling of the quasi-persistent neutron star X-ray transients KS 1731-260 and MXB 1659-29. Mon. Not. R. Astron. Soc. 2006, 372, 479–488. [Google Scholar] [CrossRef]
- Cackett, E.M.; Wijnands, R.; Miller, J.M.; Brown, E.F.; Degenaar, N. Cooling of the Crust in the Neutron Star Low-Mass X-Ray Binary MXB 1659-29. Astrophys. J. Lett. 2008, 687, L87. [Google Scholar] [CrossRef]
- Cackett, E.; Brown, E.; Cumming, A.; Degenaar, N.; Fridriksson, J.K.; Homan, J.; Miller, J.; Wijnands, R. A change in the quiescent X-Ray spectrum of the neutron star low-mass X-Ray binary MXB 1659-29. Astrophys. J. 2013, 774, 131. [Google Scholar] [CrossRef]
- Parikh, A.S.; Wijnands, R.; Ootes, L.S.; Page, D.; Degenaar, N.; Bahramian, A.; Brown, E.F.; Cackett, E.M.; Cumming, A.; Heinke, C.; et al. Consistent accretion-induced heating of the neutron-star crust in MXB 1659-29 during two different outbursts. Astron. Astrophys. 2019, 624, A84. [Google Scholar] [CrossRef]
- Sanchez-Fernandez, C.; Eckert, D.; Bozzo, E.; Kajava, J.; Kuulkers, E.; Chenevez, J. INTEGRAL confirms the detection of renewed activity from the NS transient H 1658-298. Astron. Telegr. 2015, 7946, 1. [Google Scholar]
- Iaria, R.; Gambino, A.F.; Di Salvo, T.; Burderi, L.; Matranga, M.; Riggio, A.; Sanna, A.; Scarano, F.; D’Aì, A. A possible solution of the puzzling variation of the orbital period of MXB 1659-298. Mon. Not. R. Astron. Soc. 2018, 473, 3490–3499. [Google Scholar] [CrossRef]
- Nandi, R.; Schramm, S. Transport Properties of the Nuclear Pasta Phase with Quantum Molecular Dynamics. Astrophys. J. 2018, 852, 135. [Google Scholar] [CrossRef]
- Gandolfi, S.; Illarionov, A.Y.; Fantoni, S.; Pederiva, F.; Schmidt, K.E. Equation of State of Superfluid Neutron Matter and the Calculation of the 1S0 Pairing Gap. Phys. Rev. Lett. 2008, 101, 132501. [Google Scholar] [CrossRef]
- Gandolfi, S.; Palkanoglou, G.; Carlson, J.; Gezerlis, A.; Schmidt, K.E. The 1S0 Pairing Gap in Neutron Matter. Condens. Matter 2022, 7, 19. [Google Scholar] [CrossRef]
- Cao, L.G.; Lombardo, U.; Shen, C.W.; Giai, N.V. From Brueckner approach to Skyrme-type energy density functional. Phys. Rev. C 2006, 73, 014313. [Google Scholar] [CrossRef]
- Krotscheck, E.; Papakonstantinou, P.; Wang, J. Triplet Pairing in Neutron Matter. Astrophys. J. 2023, 955, 76. [Google Scholar] [CrossRef]
- Brown, E.F.; Bildsten, L.; Chang, P. Variability in the thermal emission from accreting neutron star transients. Astrophys. J. 2002, 574, 920. [Google Scholar] [CrossRef]
- Beznogov, M.; Potekhin, A.; Yakovlev, D. Heat blanketing envelopes of neutron stars. Phys. Rep. 2021, 919, 1–68. [Google Scholar] [CrossRef]
- Brown, E.F.; Cumming, A.; Fattoyev, F.J.; Horowitz, C.J.; Page, D.; Reddy, S. Rapid Neutrino Cooling in the Neutron Star MXB 1659-29. Phys. Rev. Lett. 2018, 120, 182701. [Google Scholar] [CrossRef]
- Deibel, A.; Cumming, A.; Brown, E.F.; Page, D. A strong shallow heat source in the accreting neutron star MAXI J0556-332. Astrophys. J. 2015, 809, L31. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. PASP 2013, 125, 306–312. [Google Scholar] [CrossRef]
- Pizzochero, P.M. Angular momentum transfer in Vela-like pulsar glitches. Astrophys. J. Lett. 2011, 743, L20. [Google Scholar] [CrossRef]
- Seveso, S.; Pizzochero, P.M.; Grill, F.; Haskell, B. Mesoscopic pinning forces in neutron star crusts. Mon. Not. R. Astron. Soc. 2016, 455, 3952–3967. [Google Scholar] [CrossRef]
- Pȩcak, D.; Chamel, N.; Magierski, P.; Wlazłowski, G. Properties of a quantum vortex in neutron matter at finite temperatures. Phys. Rev. C 2021, 104, 055801. [Google Scholar] [CrossRef]
- Link, B.; Levin, Y. Vortex Pinning in Neutron Stars, Slipstick Dynamics, and the Origin of Spin Glitches. Astrophys. J. 2022, 941, 148. [Google Scholar] [CrossRef]
- Fujiwara, M.; Hamaguchi, K.; Nagata, N.; Ramirez-Quezada, M.E. Vortex creep heating in neutron stars. arXiv 2023, arXiv:2308.16066. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Pethick, C.J. Proton superconductivity in pasta phases in neutron star crusts. Phys. Rev. C 2021, 103, 055807. [Google Scholar] [CrossRef]
- Muslimov, A.G.; Tsygan, A.I. Vortex lines in neutron star superfluids and decay of pulsar magnetic fields. Astrophys. Space Sci. 1985, 115, 43–49. [Google Scholar] [CrossRef]
- Srinivasan, G.; Bhattacharya, D.; Muslimov, A.G.; Tsygan, A.J. A novel mechanism for the decay of neutron star magnetic fields. Curr. Sci. 1990, 59, 31–38. [Google Scholar]
- Sauls, J.A. Superfluidity in the Interiors of Neutron Stars. In Timing Neutron Stars; Ögelman, H., van den Heuvel, E.P.J., Eds.; NATO Advanced Science Institutes (ASI) Series C; Springer: Dordrecht, The Netherlands, 1989; pp. 457–490. [Google Scholar] [CrossRef]
- Ruderman, M.; Zhu, T.; Chen, K. Neutron Star Magnetic Field Evolution, Crust Movement, and Glitches. Astrophys. J. 1998, 492, 267–280. [Google Scholar] [CrossRef]
- Alpar, M.A. Flux-Vortex Pinning and Neutron Star Evolution. J. Astrophys. Astron. 2017, 38, 44. [Google Scholar] [CrossRef]
- Sourie, A.; Chamel, N. Vortex pinning in the superfluid core of neutron stars and the rise of pulsar glitches. Mon. Not. R. Astron. Soc. 2020, 493, L98–L102. [Google Scholar] [CrossRef]
- Antonelli, M.; Pizzochero, P.M. Axially symmetric equations for differential pulsar rotation with superfluid entrainment. Mon. Not. R. Astron. Soc. 2017, 464, 721–733. [Google Scholar] [CrossRef]
- Chamel, N. Neutron conduction in the inner crust of a neutron star in the framework of the band theory of solids. Phys. Rev. C 2012, 85, 035801. [Google Scholar] [CrossRef]
- Kantor, E.M.; Gusakov, M.E. Anti-glitches within the standard scenario of pulsar glitches. Astrophys. J. 2014, 797, L4. [Google Scholar] [CrossRef]
- Tuo, Y.; Serim, M.M.; Antonelli, M.; Ducci, L.; Vahdat, A.; Ge, M.; Santangelo, A.; Xie, F. Discovery of the First Antiglitch Event in the Rotation-powered Pulsar PSR B0540-69. Astrophys. J. Lett. 2024, 967, L13. [Google Scholar] [CrossRef]
- Allard, V.; Chamel, N. Gapless superfluidity in neutron stars: Normal-fluid fraction. Phys. Rev. C 2023, 108, 045801. [Google Scholar] [CrossRef]
- Degenaar, N.; Ootes, L.; Reynolds, M.; Wijnands, R.; Page, D. A cold neutron star in the transient low-mass X-ray binary HETE J1900.1–2455 after 10 yr of active accretion. Mon. Not. R. Astron. Soc. 2016, 465, L10–L14. [Google Scholar] [CrossRef]
- Degenaar, N.; Page, D.; van den Eijnden, J.; Beznogov, M.V.; Wijnands, R.; Reynolds, M. Constraining the properties of dense neutron star cores: The case of the low-mass X-ray binary HETE J1900.1-2455. Mon. Not. R. Astron. Soc. 2021, 508, 882–894. [Google Scholar] [CrossRef]
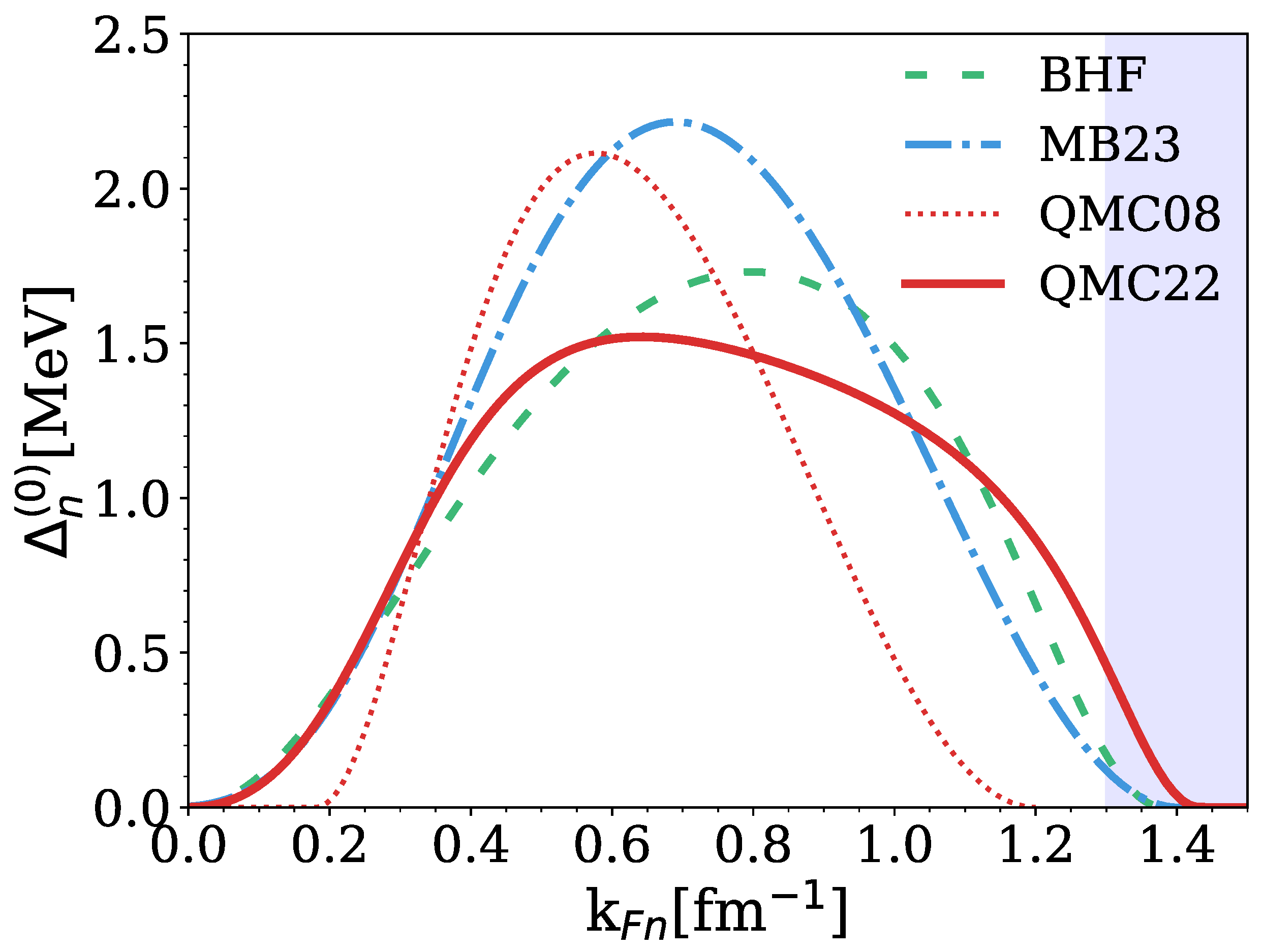

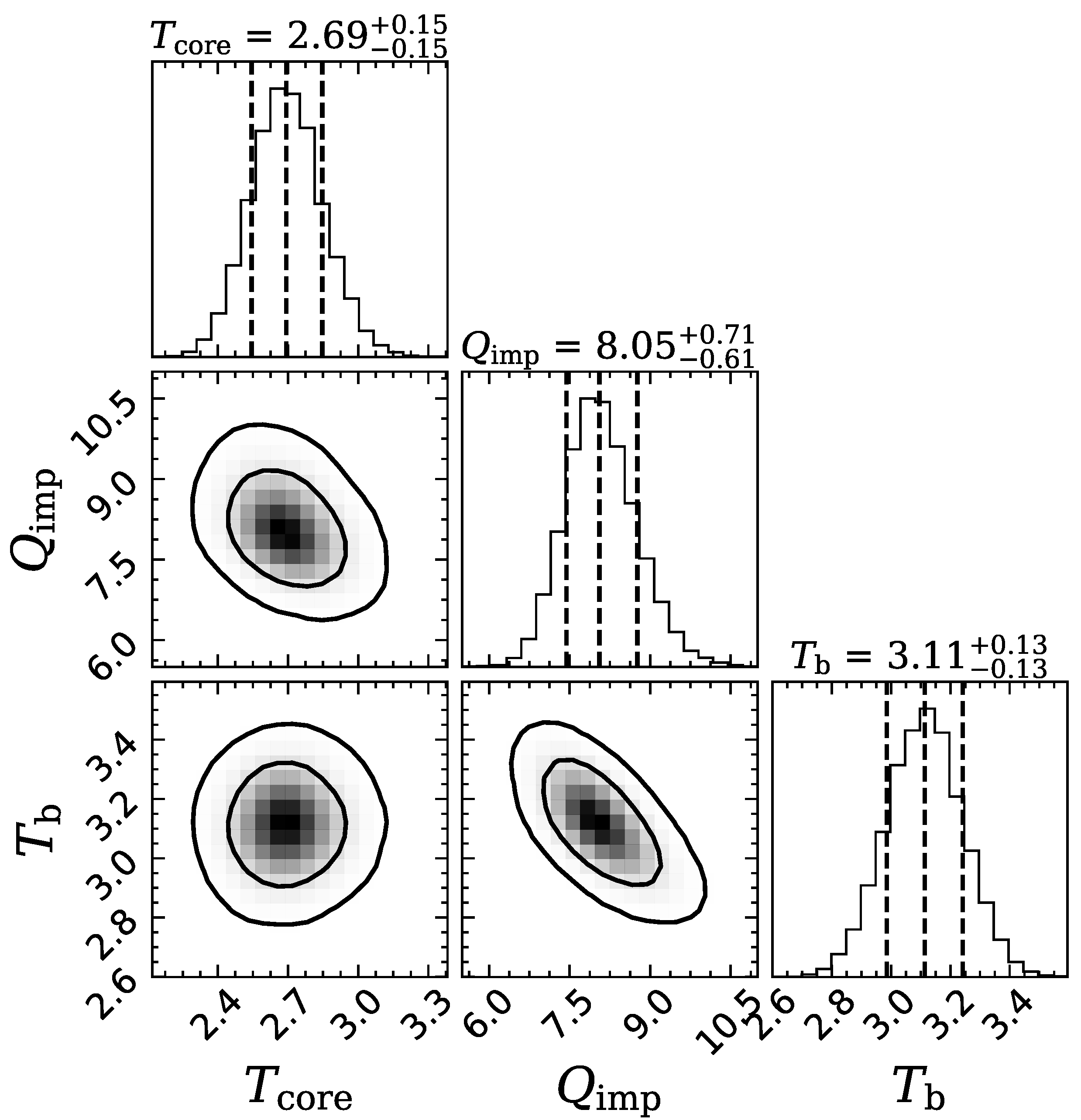

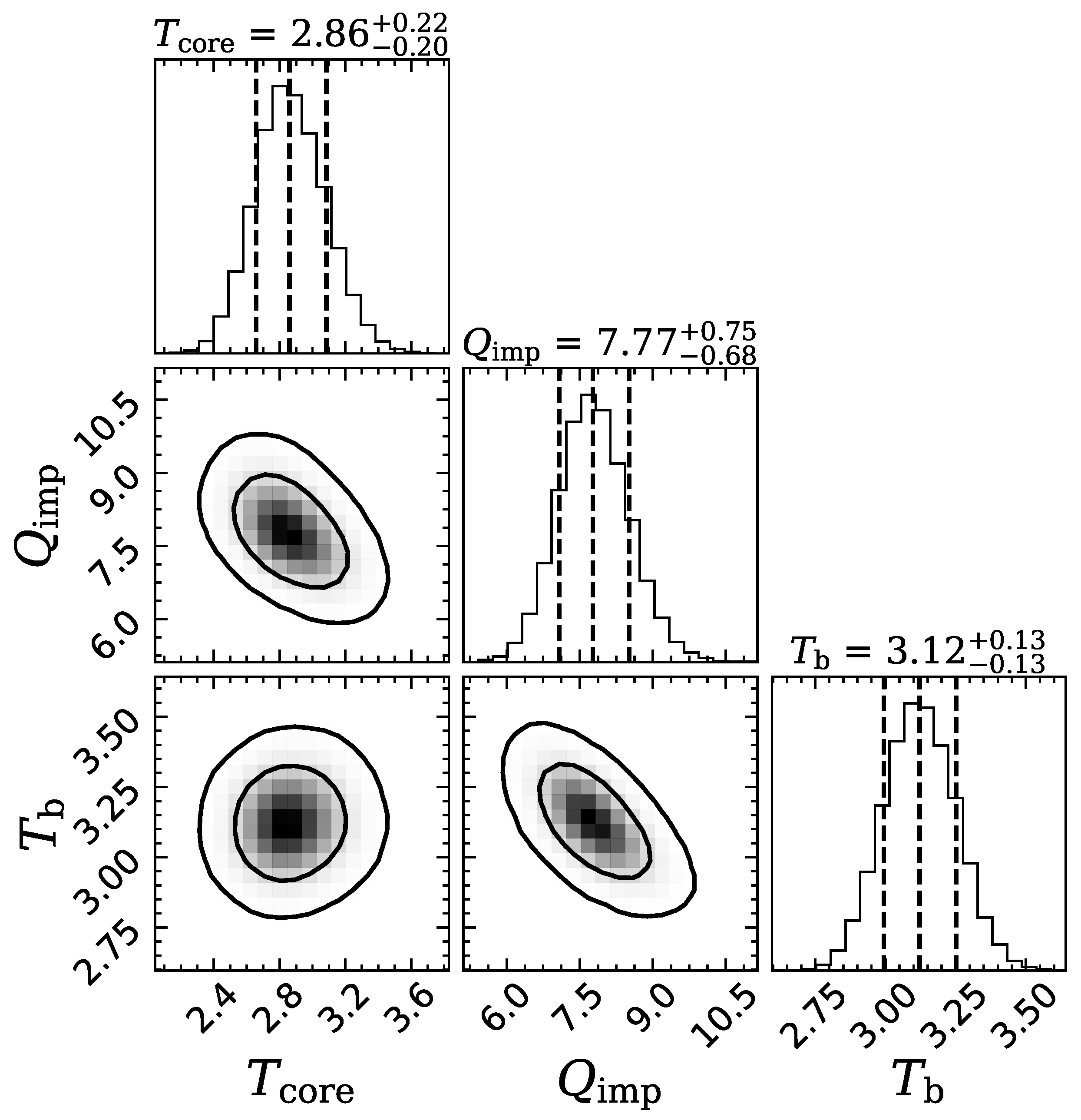
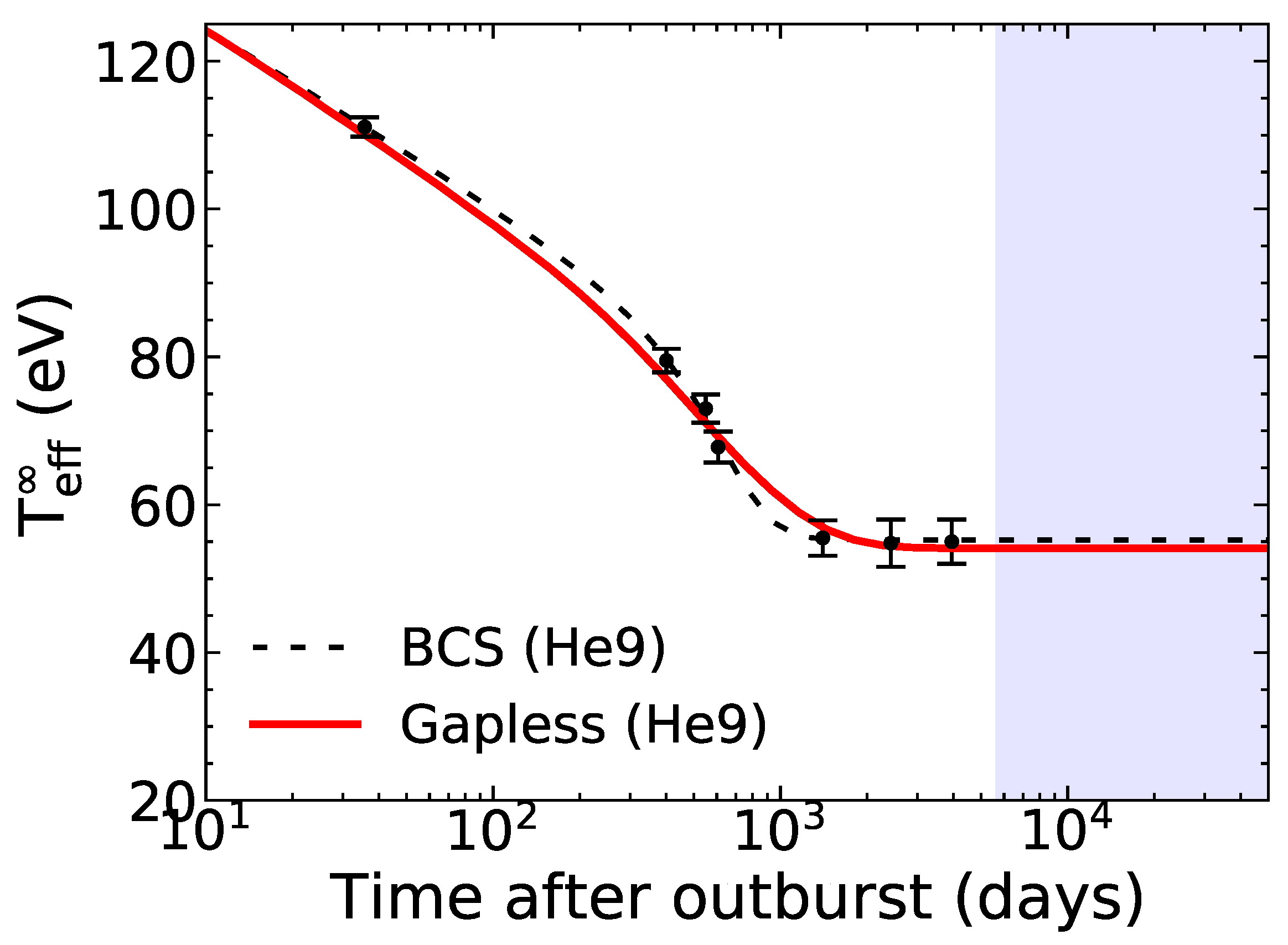
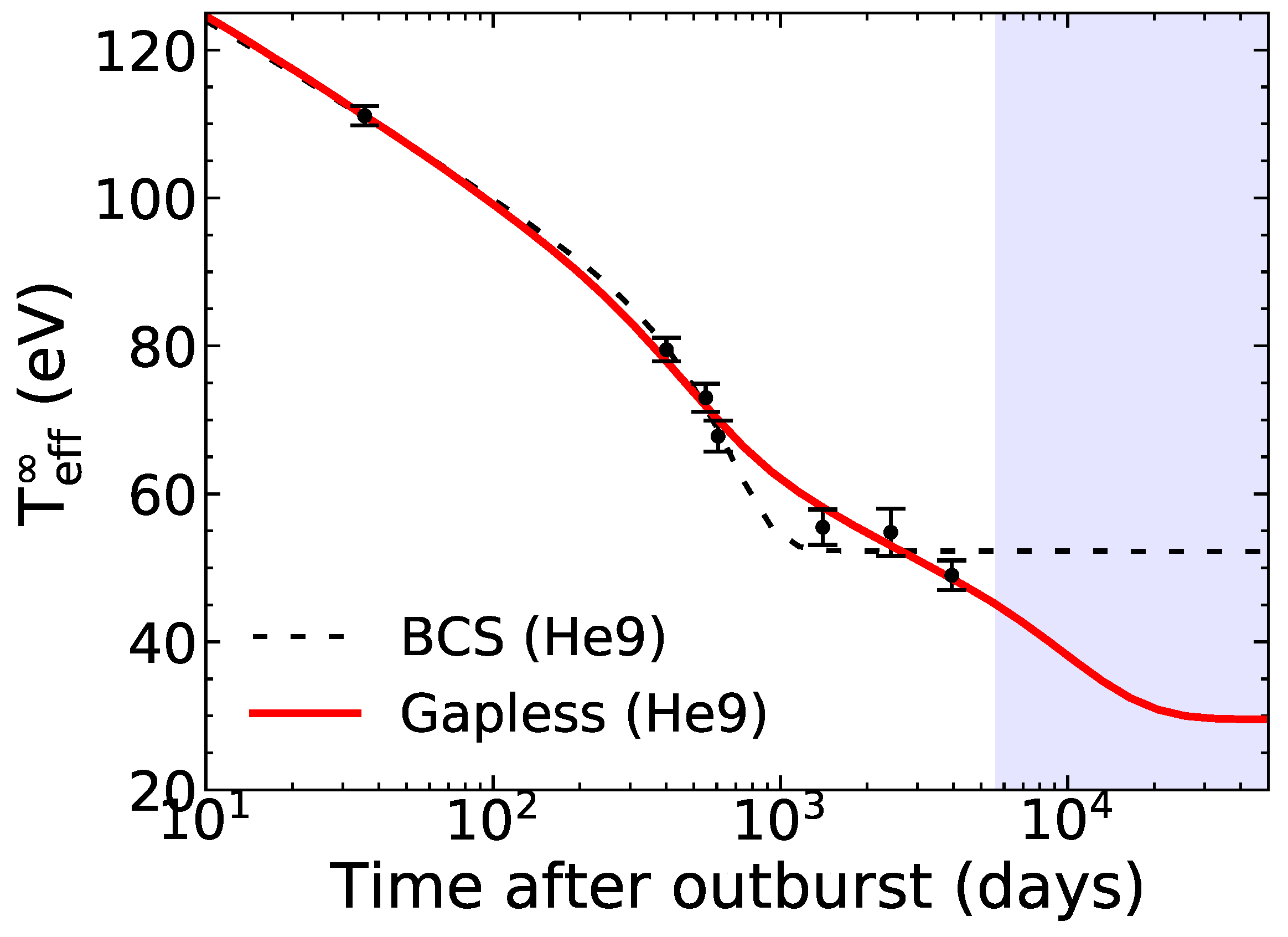
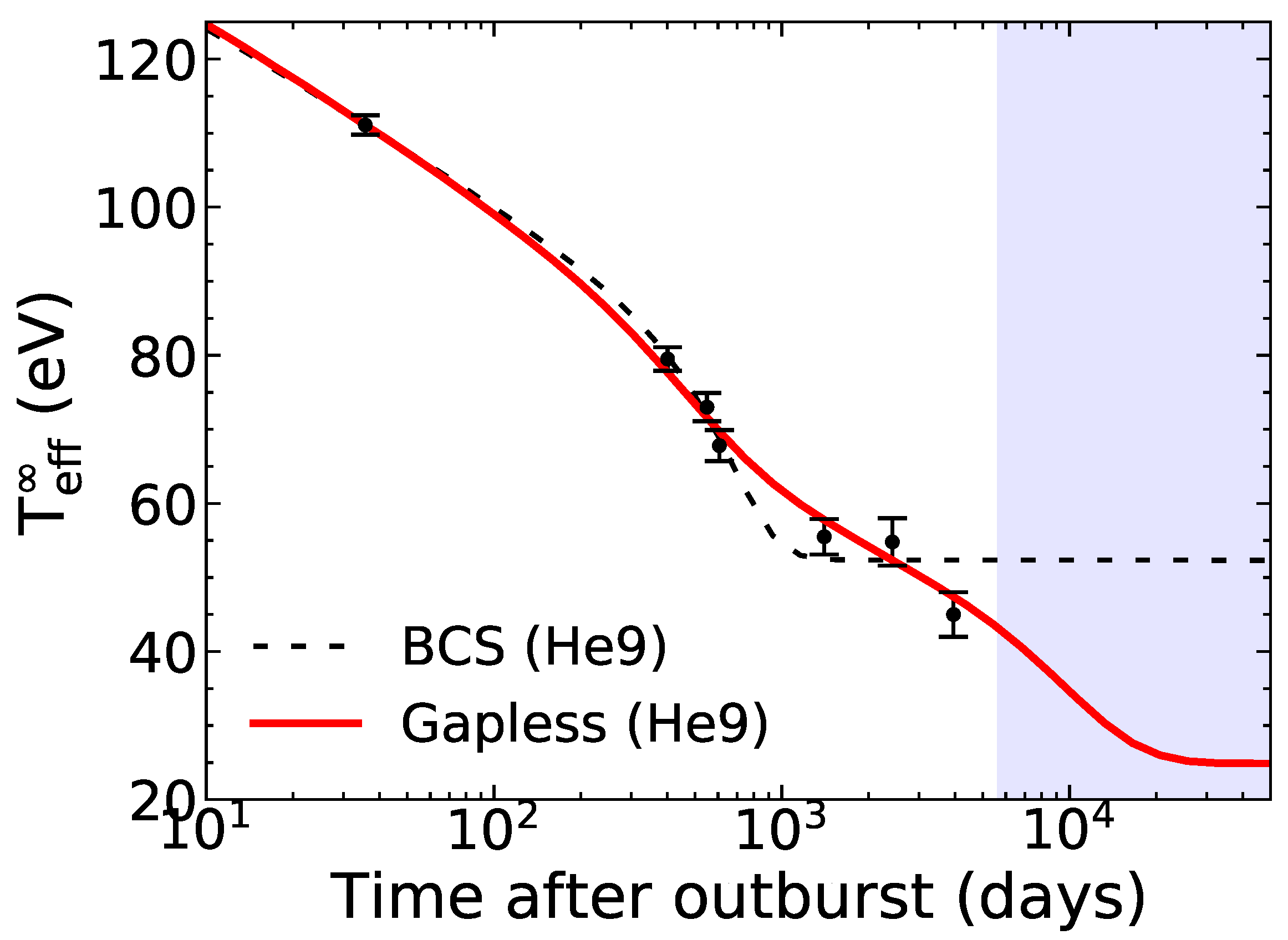
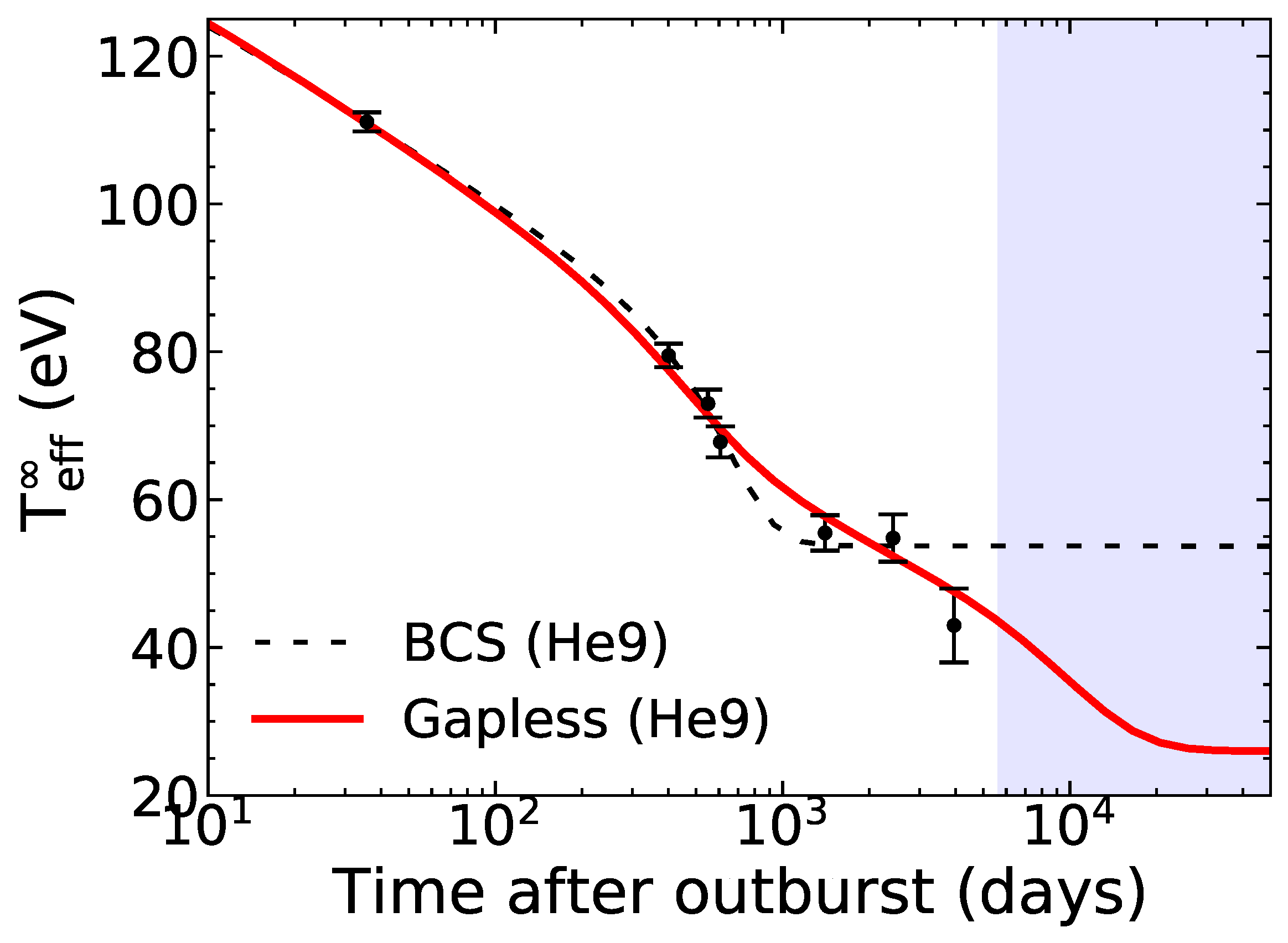

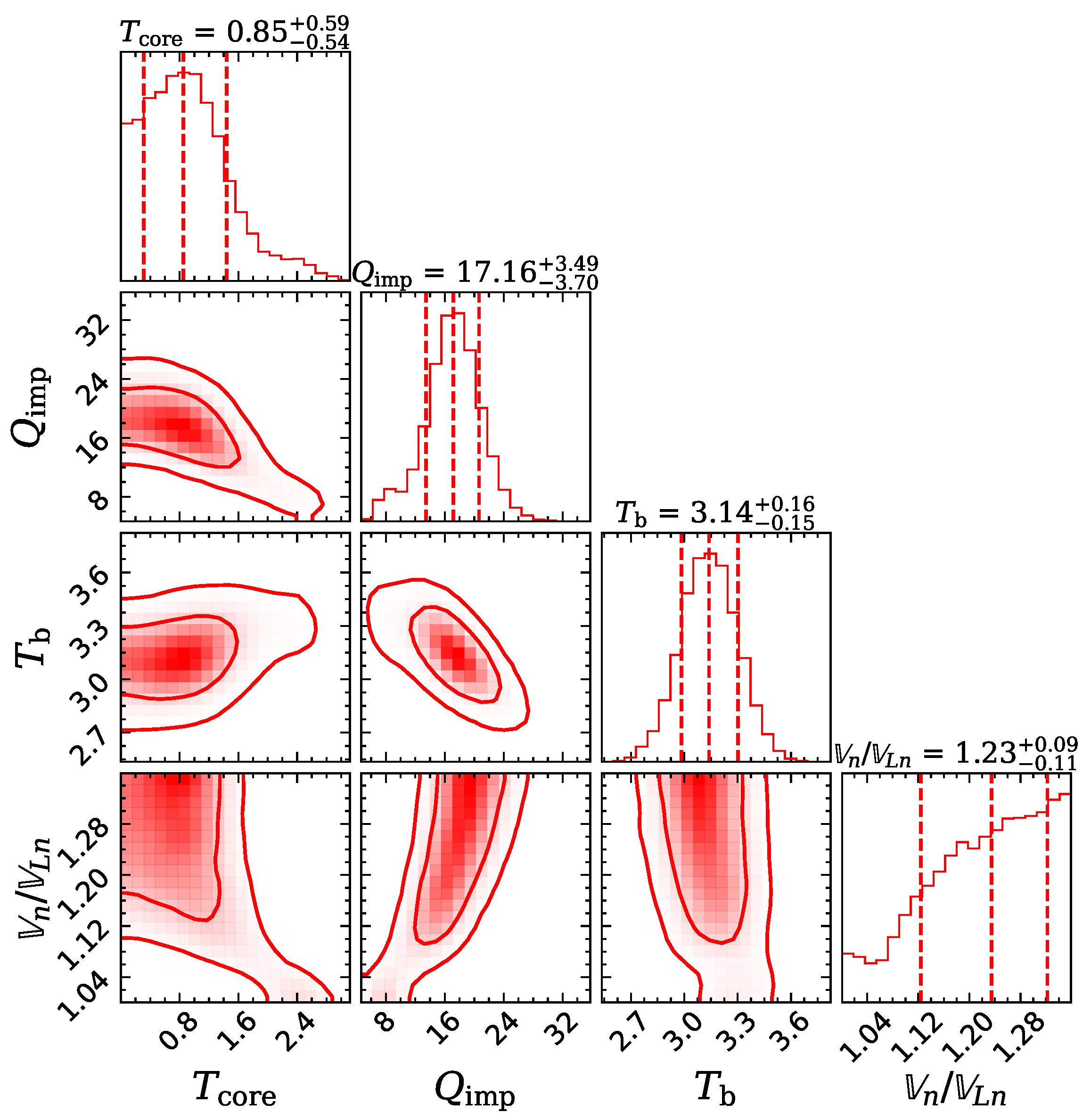

| Observatory | Obs ID | MJD | (eV) | |
|---|---|---|---|---|
| 1 | Chandra | 2688 | 52,197.7 | 111.1 ± 1.3 |
| 2 | Chandra | 3794 | 52,563.0 | 79.5 ± 1.6 |
| 3 | XMM-Newton | 0153190101 | 52,711.6 | 73.0 ± 1.9 |
| 4 | Chandra | 3795 | 52,768.7 | 67.8 ± 2.1 |
| 5 | Chandra | 5469/6337 | 53,566.4 | 55.5 ± 2.4 |
| 6 | Chandra | 8984 | 54,583.8 | 54.8 ± 3.2 |
| 7 (fit 1) | Chandra | 13711/14453 | 56,113 | 55.0 ± 3.0 |
| 7 (fit 2) | Chandra | 13711/14453 | 56,113 | 49.0 ± 2.0 |
| 7 (fit 3) | Chandra | 13711/14453 | 56,113 | 45.0 ± 3.0 |
| 7 (fit 4) | Chandra | 13711/14453 | 56,113 | 43.0 ± 5.0 |
| 2012 Chandra Observation | (107 K) | (108 K) | ||
|---|---|---|---|---|
| fit 1 | 3.14 ± 0.13 | 0 | ||
| fit 2 | 2.69 ± 0.15 | 3.11 ± 0.13 | 0 | |
| fit 3 | 3.12 ± 0.13 | 0 | ||
| fit 4 | 3.12 ± 0.13 | 0 | ||
| fit 1 | 2.89 | 6.28 | 3.22 | 1.01 |
| fit 2 | ||||
| fit 3 | ||||
| fit 4 | 1.20 ± 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allard, V.; Chamel, N. Evidence of Gapless Superfluidity in MXB 1659-29 With and Without Late Time Cooling. Universe 2025, 11, 140. https://doi.org/10.3390/universe11050140
Allard V, Chamel N. Evidence of Gapless Superfluidity in MXB 1659-29 With and Without Late Time Cooling. Universe. 2025; 11(5):140. https://doi.org/10.3390/universe11050140
Chicago/Turabian StyleAllard, Valentin, and Nicolas Chamel. 2025. "Evidence of Gapless Superfluidity in MXB 1659-29 With and Without Late Time Cooling" Universe 11, no. 5: 140. https://doi.org/10.3390/universe11050140
APA StyleAllard, V., & Chamel, N. (2025). Evidence of Gapless Superfluidity in MXB 1659-29 With and Without Late Time Cooling. Universe, 11(5), 140. https://doi.org/10.3390/universe11050140








