Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe
Abstract
:1. Introduction
2. Dynamical Equations
3. Coupled Phantom Field
3.1. Coupling
3.2. Coupling
3.3. Coupling
4. Coupled Tachyon Dynamics
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sahni, V.; Starobinsky, A.A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. A 2000, 9, 373. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 03501. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equation of state. Phys. Rev. Lett. 1998, 80, 1582. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef] [Green Version]
- Carroll, S.M.; Hoffman, M.; Trodden, M. Can the dark energy equation-of-state parameter w be less than −1? Phys. Rev. D 2003, 68, 023509. [Google Scholar] [CrossRef]
- Chimento, L.P. Extended tachyon field, Chaplygin gas, and solvable k-essence cosmologies. Phys. Rev. D 2004, 69, 123517. [Google Scholar] [CrossRef]
- Gorini, V.; Kamenshchik, A.; Moschella, U.; Pasquier, V. Tachyons, scalar fields, and cosmology. Phys. Rev. D 2004, 69, 123512. [Google Scholar] [CrossRef] [Green Version]
- Debnath, U.; Banerjee, A.; Chakraborty, S. Role of modified Chaplygin gas in accelerated universe. Class. Quantum Grav. 2004, 21, 5609. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 62, 043511. [Google Scholar] [CrossRef] [Green Version]
- Zimdahl, W.; Pavon, D.; Chimento, L.P. Interacting quintessence. Phys. Lett. B 2001, 521, 133. [Google Scholar] [CrossRef]
- Chimento, L.P. Linear and nonlinear interactions in the dark sector. Phys. Rev. D 2010, 81, 043525. [Google Scholar] [CrossRef]
- Verma, M.M.; Pathak, S.D. A Tachyonic scalar field with mutually interacting components. Int. J. Theor. Phys. 2012, 51, 2370. [Google Scholar] [CrossRef]
- Verma, M.M.; Pathak, S.D. Shifted cosmological parameter and shifted dust matter in a two-phase tachyonic field universe. Astrophys. Space Sci. 2013, 344, 505. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, S.N. Dynamics of quintom and hessence energies in loop quantum cosmology. Phys. Rev. D 2007, 76, 063005. [Google Scholar] [CrossRef] [Green Version]
- Setare, M.R.; Saridakis, E.N. Coupled oscillators as models of quintom dark energy. Phys. Lett. B 2008, 668, 177. [Google Scholar] [CrossRef]
- Setare, M.R.; Saridakis, E.N. Quintom cosmology with general potentials. Int. J. Mod. Phys. D 2009, 18, 549. [Google Scholar] [CrossRef]
- Chimento, L.P.; Jakubi, A.S.; Pavón, D.; Zimdahl, W. Interacting quintessence solution to the coincidence problem. Phys. Rev. D 2003, 67, 083513. [Google Scholar] [CrossRef] [Green Version]
- Chimento, L.P.; Pavón, D. Dual interacting cosmologies and late accelerated expansion. Phys. Rev. D 2006, 73, 063511. [Google Scholar] [CrossRef] [Green Version]
- Shahalam, M.; Pathak, S.D.; Verma, M.M.; Khlopov, M.Y.; Myrzakulov, R. Dynamics of interacting quintessence. Eur. Phys. J. C 2015, 75, 395. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Nunes, R.C.; Vagnozzie, S.; Motag, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. J. Cosmol. Astropart. Phys. 2018, 2018, 019. [Google Scholar] [CrossRef]
- Bogoyavlensky, O.I. Methods in the Qualitative Theory of Dynamical Systems in Astrophysics and Gas Dynamics; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Xiao, K.; Zhu, J. Stability analysis of an autonomous system in loop quantum cosmology. Phys. Rev. D 2011, 83, 083501. [Google Scholar] [CrossRef]
- Shahalam, M.; Pathak, S.D.; Li, S.; Myrzakulov, R.; Wang, A. Dynamics of coupled phantom and tachyon fields. Eur. Phys. J. C 2017, 77, 686. [Google Scholar] [CrossRef] [Green Version]
- Sharif, M.; Mughani, Q.A.T. Stability analysis of coupled phantom and tachyon field models in nonlinear electrodynamics. Int. J. Mod. Phys. D 2019, 28, 1950076. [Google Scholar] [CrossRef]
- Sharif, M.; Mumtaz, S. Stability of the universe model coupled with phantom and tachyon fields. Adv. High Energy Phys. 2019, 2019, 6582470. [Google Scholar]
- Waga, I.; Falcão, R.C.; Chanda, R. Bulk-viscosity-driven inflationary model. Phys. Rev. D 1986, 33, 1839. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Chitre, S.M. Viscous universes. Phys. Lett. A 1987, 120, 433. [Google Scholar] [CrossRef]
- Cheng, B. Bulk viscosity in the early universe. Phys. Lett. A 1991, 160, 329. [Google Scholar] [CrossRef]
- Zimdahl, W. Bulk viscous cosmology. Phys. Rev. D 1996, 53, 5483. [Google Scholar] [CrossRef]
- Acquaviva, G.; Beesham, A. Nonlinear bulk viscosity and the stability of accelerated expansion in FRW spacetime. Phys. Rev. D 2014, 90, 023503. [Google Scholar] [CrossRef] [Green Version]
- Sasidharan, A.; Mathew, T.K. Phase space analysis of bulk viscous matter dominated universe. J. High Energy Phys. 2016, 2016, 138. [Google Scholar] [CrossRef]
- Sharif, M.; Mumtaz, S. Stability analysis of bulk viscous anisotropic universe model. Astrophys. Space Sci. 2017, 362, 205. [Google Scholar] [CrossRef]
- Disconzi, M.M. On the well-posedness of relativistic viscous fluids. Nonlinearity 2014, 27, 1915. [Google Scholar] [CrossRef]
- Disconzi, M.M.; Kephart, T.W.; Scherrer, R.J. New approach to cosmological bulk viscosity. Phys. Rev. D 2015, 91, 043532. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, A.; Steinhardt, P.J.; Turner, M.S.; Wilczek, F. Reheating an inflationary universe. Phys. Rev. Lett. 1982, 48, 1437. [Google Scholar] [CrossRef]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Abdalla, E. Transition of the dark energy equation of state in an interacting holographic dark energy model. Phys. Lett. B 2005, 624, 141. [Google Scholar] [CrossRef]
- Gumjudpai, B.; Naskar, T.; Sami, M.; Tsujikawa, S. Coupled dark energy: Towards a general description of the dynamics. J. Cosmol. Astropart. Phys. 2005, 2005, 0506. [Google Scholar] [CrossRef]
- Campo, S.D.; Herrera, R.; Pavon, D. H(z) Diagnostics on the nature of dark eneryg. Int. J. Mod. Phys. D 2011, 20, 561. [Google Scholar] [CrossRef]
- Wei, H.; Cai, R.G. K-chameleon and the coincidence problem. Phys. Rev. D 2005, 71, 043504. [Google Scholar] [CrossRef] [Green Version]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23. [Google Scholar] [CrossRef]
- Sen, A. Rolling tachyon. J. High Energy Phys. 2002, 2002, 048. [Google Scholar] [CrossRef]
- Marra, V.; Amendola, L.; Sawicki, I.; Valkenburg, W. Cosmic variance and the measurement of the local Hubble parameter. Phys. Rev. Lett. 2013, 110, 241305. [Google Scholar] [CrossRef]
- Battye, R.A.; Charnock, T.; Moss, A. Tension between the power spectrum of density perturbations measured on large and small scales. Phys. Rev. D 2015, 91, 103508. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Copi, C.J.; Huterer, D.; Starkman, G.D. CMB Anomalies after Planck. Class. Quant. Grav. 2016, 33, 184001. [Google Scholar] [CrossRef]

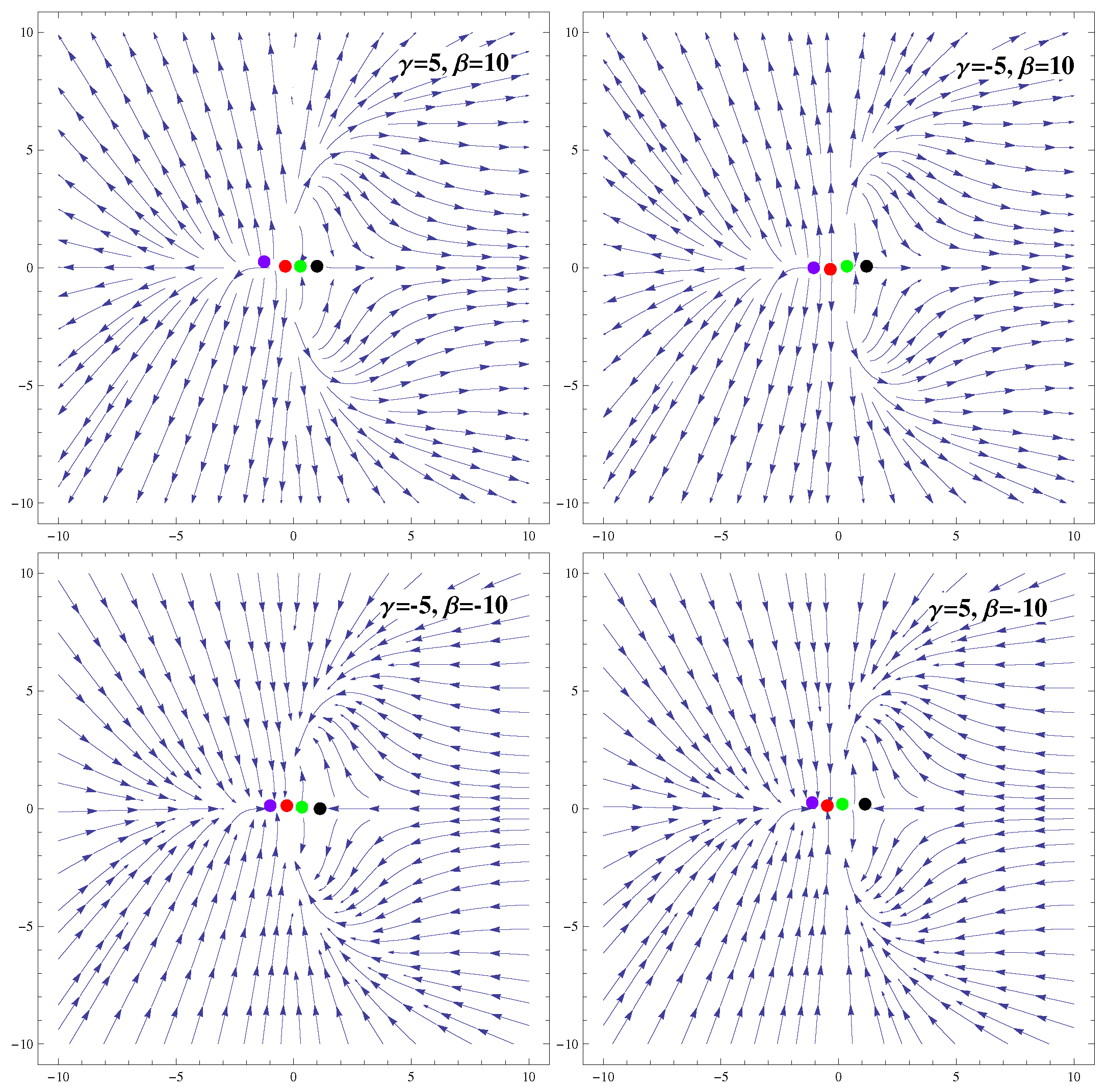

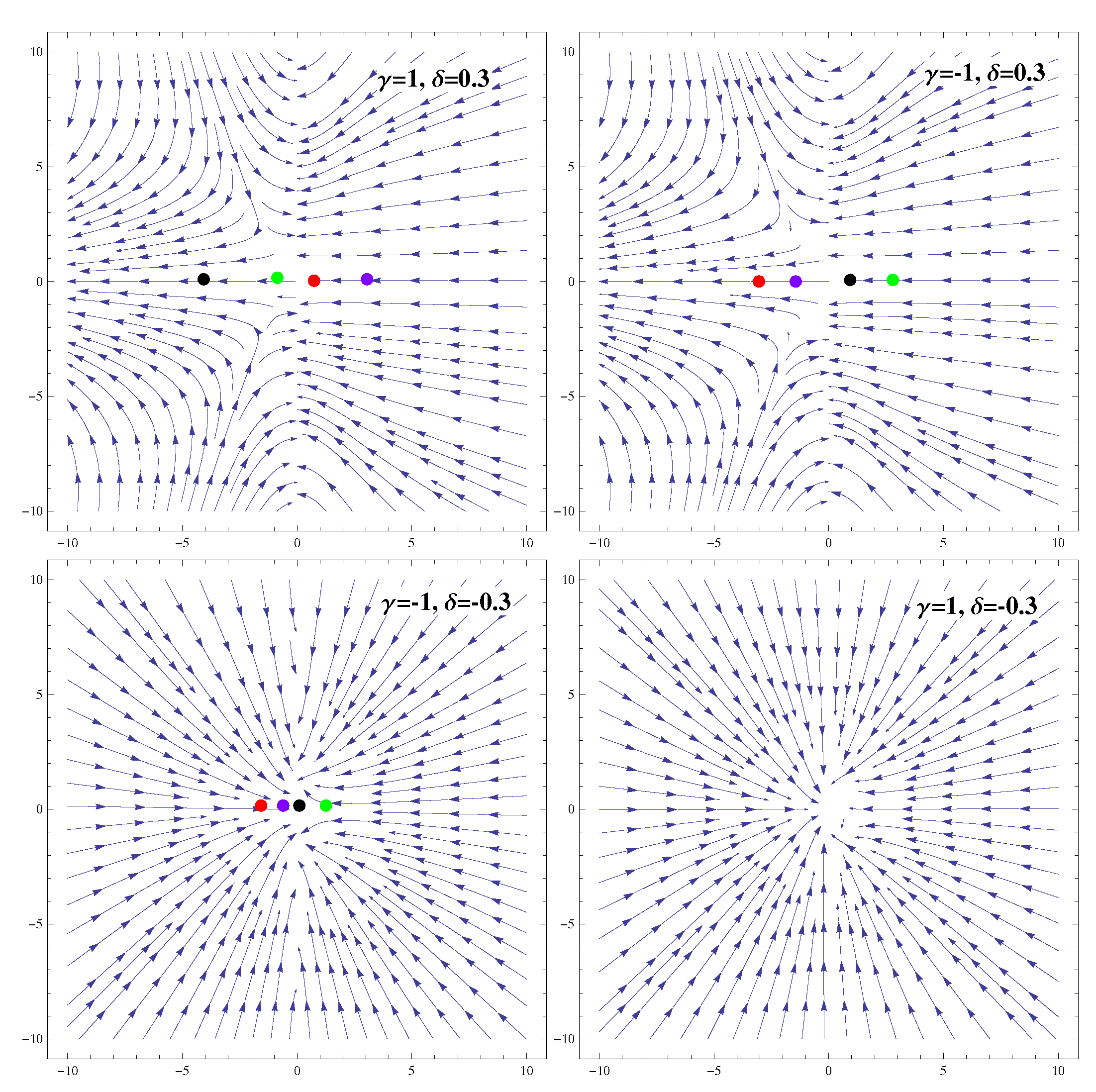
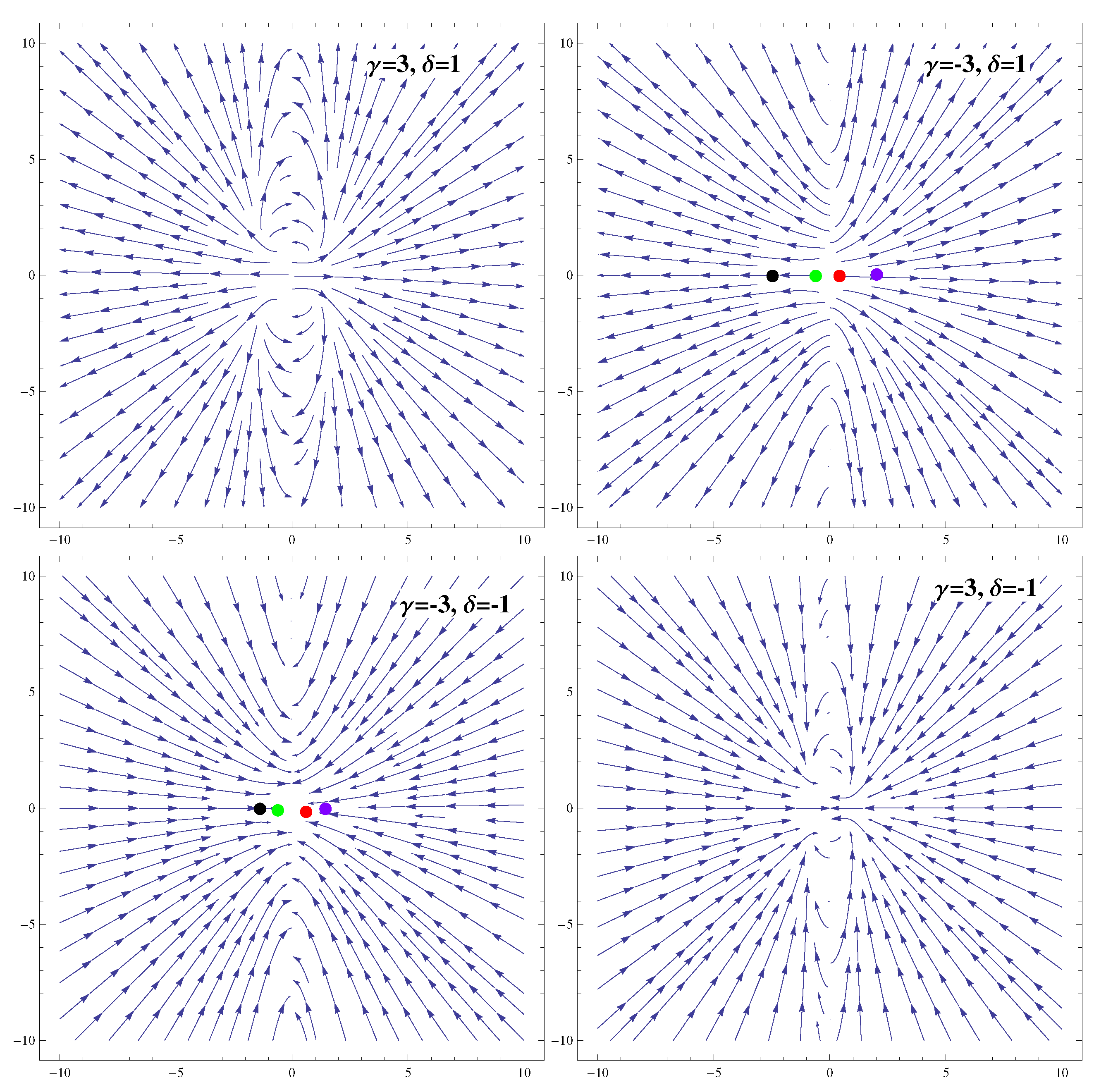
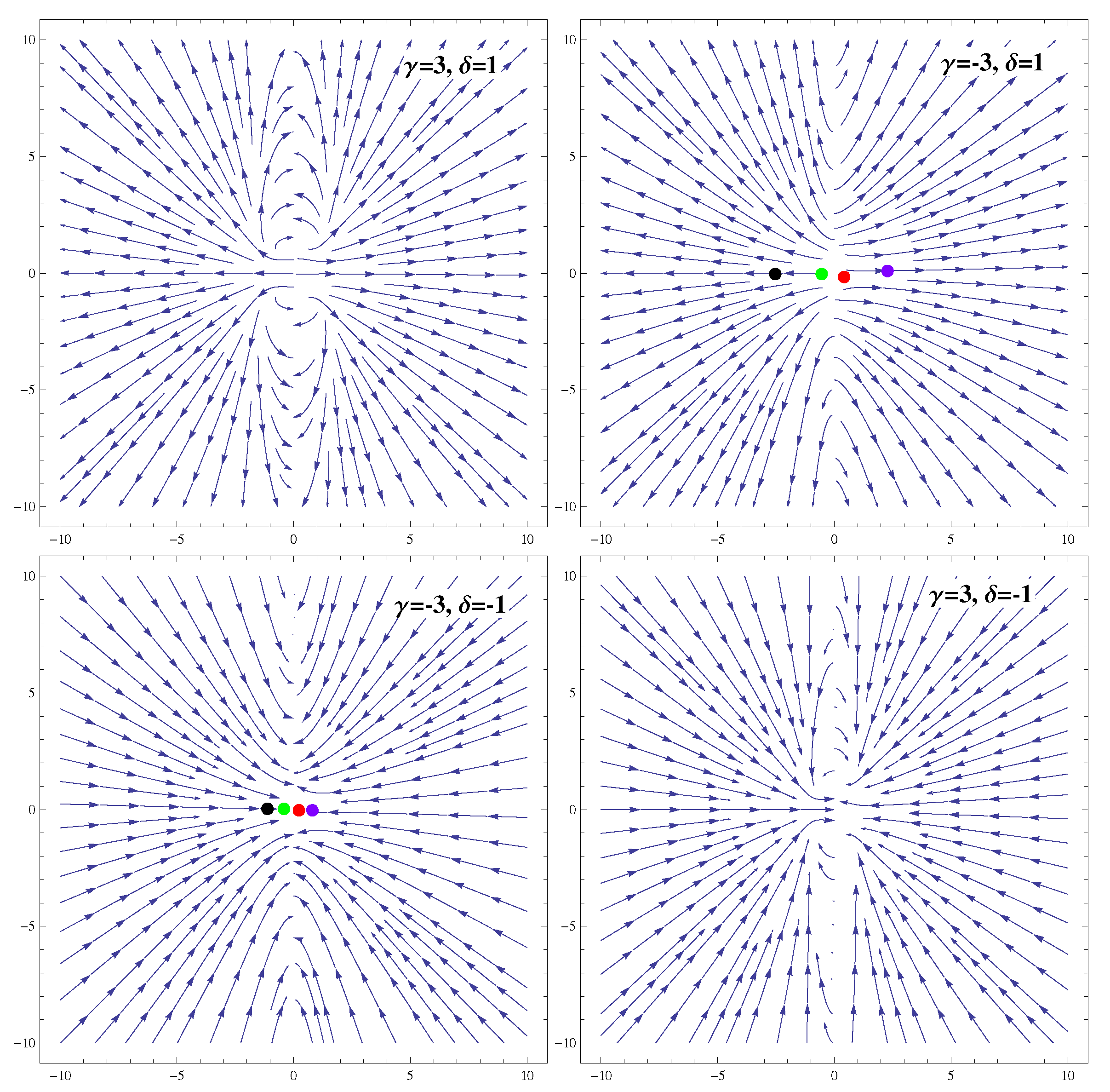


| Ranges of Model Parameters | Stability | Acceleration |
|---|---|---|
| For, | ||
| unstable | Yes | |
| stable | Yes | |
| stable | Yes | |
| unstable | Yes | |
| saddle | Yes | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | Yes | |
| unstable | Yes | |
| stable | No | |
| stable | No | |
| unstable | Yes | |
| stable | Yes | |
| unstable | No | |
| unstable | No | |
| stable | Yes | |
| For, | ||
| unstable | Yes | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | Yes | |
| unstable | Yes | |
| stable | Yes | |
| stable | Yes | |
| unstable | Yes | |
| stable | Yes | |
| unstable | No | |
| unstable | No | |
| stable | Yes | |
| unstable | Yes | |
| stable | No | |
| stable | No | |
| unstable | Yes |
| Ranges of Model Parameters | Stability | Acceleration |
|---|---|---|
| For, | ||
| stable | Yes | |
| stable if | No | |
| stable if | Yes | |
| stable for | - | |
| stable | Yes | |
| unstable for | No | |
| saddle for | ||
| saddle | Yes | |
| stable | - | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | No | |
| stable for , | - | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | No | |
| stable for , | - | |
| For, | ||
| stable | Yes | |
| unstable for | No | |
| saddle for | ||
| saddle | Yes | |
| stable for , | - | |
| saddle for | ||
| stable | Yes | |
| stable for , | No | |
| stable | Yes | |
| stable | - | |
| saddle | Yes | |
| stable for , | Yes | |
| unstable for | ||
| unstable | No | |
| stable for | - | |
| saddle | Yes | |
| saddle | Yes | |
| unstable | No | |
| stable for , | - |
| Ranges of Model Parameters | Stability | Acceleration |
|---|---|---|
| For, | ||
| stable | - | |
| stable for , | Yes | |
| saddle/unstable | No | |
| stable | - | |
| stable | - | |
| saddle/unstable | Yes | |
| saddle/unstable | No | |
| stable | - | |
| unstable | - | |
| saddle/unstable | No | |
| saddle | Yes | |
| stable for , | - | |
| saddle | - | |
| stable | No | |
| stable | Yes | |
| stable for | - | |
| For, | ||
| stable | - | |
| stable/saddle | Yes | |
| saddle | No | |
| stable | - | |
| stable | - | |
| stable | Yes | |
| saddle/unstable | No | |
| stable | - | |
| saddle | - | |
| stable for , | No | |
| stable | Yes | |
| stable for , | - | |
| unstable | - | |
| saddle/unstable | No | |
| saddle | Yes | |
| stable/saddle | - |
| Ranges of Model Parameters | Stability | Acceleration |
|---|---|---|
| saddle | Yes for | |
| saddle/unstable for | No | |
| unstable | No | |
| saddle for , | Yes for | |
| stable for |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharif, M.; Ama-Tul-Mughani, Q. Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe. Universe 2019, 5, 185. https://doi.org/10.3390/universe5080185
Sharif M, Ama-Tul-Mughani Q. Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe. Universe. 2019; 5(8):185. https://doi.org/10.3390/universe5080185
Chicago/Turabian StyleSharif, Muhammad, and Qanitah Ama-Tul-Mughani. 2019. "Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe" Universe 5, no. 8: 185. https://doi.org/10.3390/universe5080185
APA StyleSharif, M., & Ama-Tul-Mughani, Q. (2019). Dynamical Stability of Bulk Viscous Isotropic and Homogeneous Universe. Universe, 5(8), 185. https://doi.org/10.3390/universe5080185






