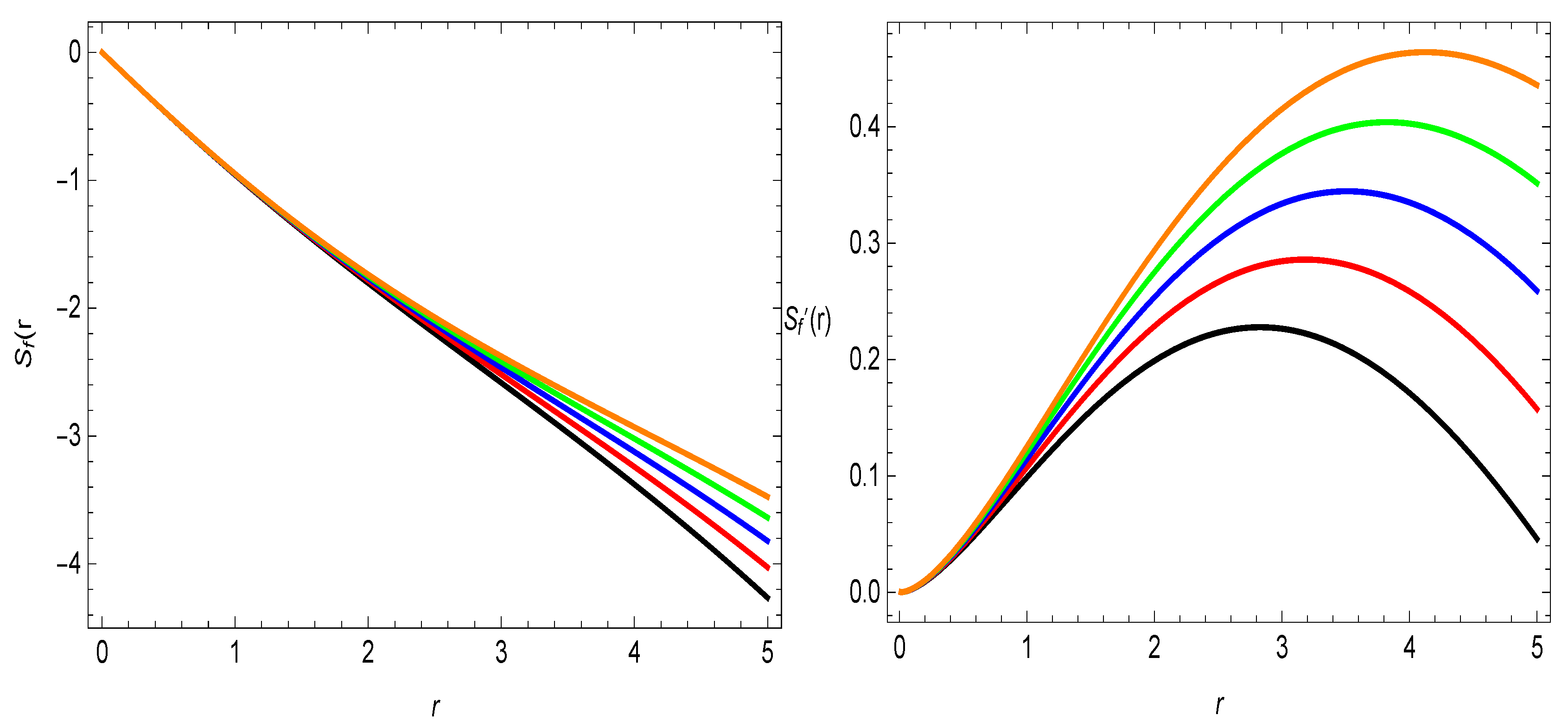Stable Wormholes in the Background of an Exponential f(R) Gravity

Abstract

The current paper is devoted to investigating wormhole solutions with an exponential gravity model in the background of $f\left(\mathcal{R}\right)$ theory. Spherically symmetric static spacetime geometry is chosen to explore wormhole solutions with anisotropic fluid source. The behavior of the traceless matter is studied by employing a particular equation of state to describe the important properties of the shape-function of the wormhole geometry. Furthermore, the energy conditions and stability analysis are done for two specific shape-functions. It is seen that the energy condition are to be violated for both of the shape-functions chosen here. It is concluded that our results are stable and realistic.

1. Introduction

The discussion on wormhole geometry is a very hot subject among the investigators of the different modified theories of gravity. The concept of wormhole was first expressed by Flamm [1] in 1916. After 20 years, Einstein and Rosen [2] calculated the wormhole geometry in a specific background. In fact, it was the second attempt to realize the basic structure of wormholes. Among many efforts, Morris et al. [3,4] also defined a wormhole geometry in the background of spherically symmetric static spacetime. The spherically symmetric static line element for a wormhole is given by

$$d{s}^2=-e^{2R_f\left(r\right)}d{t}^2+{\left(\frac{r+S_f\left(r\right)}{r}\right)}^{-1}d{r}^2+r^{2}d{\mathsf{\Omega }}^2,$$

(1)

where $R_f\left(r\right)$ denotes the red-shift function, $S_f\left(r\right)$ reveals the shape-function, and $d{\mathsf{\Omega }}^2=d{\theta }^2+si{n}^2\theta d{\varphi }^2$. Some important conditions for the existence of viable and traversable wormholes to be satisfied are the shape-function and red-shift function, which are summarized as follows [3]. The red-shift function $R_f\left(r\right)$ must be finite everywhere. $R_f\left(r\right)$ has no horizon restriction, for the two way journey, i.e the wormhole should be traversable. The proper radial distance in terms of the shape-function $S_f\left(r\right)$, $\mathcal{L}\left(r\right)=\pm {\int }_{r_0}^r{(1+\frac{S_f\left(r\right)}{r})}^{-1/2}dr$, with $r>r_0$, should be finite everywhere in the space. Here, the expression ± represents the two distinct parts, which are connected through the wormhole structure. The shape-function $S_f\left(r\right)$ must satisfy the conditions: (i) $(S_f\left(r\right)-S_f{\left(r\right)}^{{}^{\prime }}r)/S_f{\left(r\right)}^2>0$, (ii) $S_f\left(r\right)\left(r_0\right)=r_0$; and (iii) $S_f{\left(r\right)}^{{}^{\prime }}\left(r_0\right)<1$. The last one is known as flaring out condition. These conditions collectively define the criteria for the existence of a realistic wormhole model.

In the context of extended or modified theories of gravity, the $f\left(\mathcal{R}\right)$ theory has been considered a basic modification of Einstein’s general theory of relativity (GTR). This modified theory of gravity has attracted many researchers in the field in resent years. The $f\left(\mathcal{R}\right)$ theory of gravity has been considered most suitable due to cosmologically important $f\left(\mathcal{R}\right)$ models. Some viable $f\left(\mathcal{R}\right)$ gravity models have been proposed by different authors, which show the unification of early-time inflation and late-time acceleration of the Universe [5]. The accelerated expansion of the Universe or the cosmic acceleration can be justified by introducing the term $f\left(\mathcal{R}\right)=1/\mathcal{R}$, which is essential at small curvatures [6]. The dark matter problems can also be addressed by using viable $f\left(\mathcal{R}\right)$ gravity models [6]. The $f\left(\mathcal{R}\right)$ theory is based on a modification of the Einstein field equations that come after replacing the Ricci scalar, $\mathcal{R}$, with an arbitrary function of the Ricci scalar, i.e., $f\left(\mathcal{R}\right)$, in the Einstein–Hilbert Lagrangian. The increased interest in the extended theories of gravity can be depicted from the possibility of explaining accelerated expansion of the Universe. The main reason of the expansion of the Universe can be revealed from type Ia supernova [7,8], large scale structure [9], and cosmic microwave background radiation (CMBR) [10,11,12,13].

The study of wormholes in the background of the extended or modified theories of gravity, i.e., $f\left(T\right)$, Brans–Dicke theory of gravity, Gauss–Bonnet theory of gravity, scalar–tensor theory of gravity, $f\left(G\right)$ theory of gravity, $f(R,G)$ theory of gravity, and $f(R,T)$ theory of gravity is a very hot topic among researchers. In this context, Zubair et al. [14,15,16], Jawad et al. [17], Farooq at el. [18,19], and Sherif et al. [20,21,22] discussed wormhole solutions in different extended theories of gravity. Kimet Jusufi and Ali Övgün explored the deflection angle in the framework of a rotating Teo wormhole spacetime for the first time [23]. They constructed the Teo–Randers optical geometry and applied the Gauss–Bonnet term to the osculating geometry. Halilsoy et al. constructed thin-shell wormholes from the regular black holes (or non-black holes for certain range of parameters) discovered by Hayward [24]. Recently, Mustafa et al. [25] presented wormholes solutions in the $f(T,T_G)$ theory of gravity by adopting non-commutative geometry. Wormhole solutions in the background of $f\left(T\right)$ theory [26] and Rastall theory have also been explored in the literature [27]. In this study, we discuss the wormhole solutions for an anisotropic source of fluid, in the background of an exponential $f\left(\mathcal{R}\right)$ gravity model, which was first obtained by Samanta et al. [28], and was discussed in the context of inflation and the late-time accelerated expansion of the Universe (given in Section 2). Further, this study provides the necessary physical properties of shape-function and the energy conditions for traversable wormhole models.

The rest of this paper is organized as follows. In Section 2, we give some basics of the $f\left(\mathcal{R}\right)$ theory of gravity with an exponential model and anisotropic matter distribution. Section 3 is dedicated to the discussion of some physical properties of wormhole solutions obtained here. In the same section, we also present our result graphically. In Section 4, the stability of the obtained wormhole solution is given. In Section 5, the weak energy condition (WEC) and the null energy condition (NEC) for the two different shape-functions are investigated. A summary of the work done is presented in Section 6.

2. The $f\left(\mathcal{R}\right)$ Modified Theory of Gravity

The extended Einstein–Hilbert action for $f\left(\mathcal{R}\right)$ theory of gravity is [29]:

$$S=\frac{1}{2\kappa }\int d^{4}xf\left(\mathcal{R}\right)\sqrt{-g}+S_{\mathfrak{M}}(g^{\mu \nu },\xi ),$$

(2)

where $f\left(\mathcal{R}\right)$ is a function of the Ricci scalar. The expression $S_{\mathfrak{M}}(g^{\mu \nu },\xi )$ reveals the matter term of the action. In this paper, we assume $\kappa =1$ for simplicity. By variation of the above action, one can have the following field equations:

$${\mathcal{T}}_{\mu \nu }^{\mathfrak{M}}=f_{\mathcal{R}}\left(\mathcal{R}\right){\mathcal{R}}_{\mu \nu }-\frac{1}{2}f\left(\mathcal{R}\right)g_{\mu \nu }+(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu })f_{\mathcal{R}}\left(\mathcal{R}\right).$$

(3)

We can calculate the trace of the energy momentum tensor as,

$$\begin{array}{c}\hfill \mathcal{T}=f_{\mathcal{R}}\left(\mathcal{R}\right)\mathcal{R}+3\square f_{\mathcal{R}}\left(\mathcal{R}\right)-2f\left(\mathcal{R}\right),\end{array}$$

(4)

where □ is the d’Alembert operator, ∇ is the covariant derivative operator, and $f_{\mathcal{R}}\left(\mathcal{R}\right)$ is the derivatives with respect to $\mathcal{R}$. By plugging Equation (4) into Equation (3), the following relation is obtained

$${\mathcal{T}}_{\mu \nu }^{eff}={\mathcal{R}}_{\mu \nu }-\frac{1}{2}\mathcal{R}{g}_{\mu \nu }={\mathrm{G}}_{\mu \nu },$$

(5)

where ${\mathcal{T}}_{\mu \nu }^{eff}={\mathcal{T}}_{\mu \nu }^{\mathrm{c}}+{\tilde{\mathcal{T}}}_{\mu \nu }^m$ is effective stress–energy tensor and ${\tilde{\mathcal{T}}}_{\mu \nu }^m$ is defined by

$${\mathcal{T}}_{\mu \nu }^c=\frac{1}{f_{\mathcal{R}}\left(\mathcal{R}\right)}\left({\nabla }_{\mu }{\nabla }_{\nu }{f}_{\mathcal{R}}\left(\mathcal{R}\right)-\frac{1}{4}{g}_{\mu \nu }(\mathcal{R}{f}_{\mathcal{R}}\left(\mathcal{R}\right)+\square f_{\mathcal{R}}\left(\mathcal{R}\right)+\mathcal{T})\right),{\mathcal{T}}_{\mu \nu }^m={\tilde{\mathcal{T}}}_{\mu \nu }^m{f}_{\mathcal{R}}\left(\mathcal{R}\right).$$

(6)

The stress–energy tensor of the anisotropic fluid is given by

$${\mathcal{T}}_{\mu \nu }=(\rho +{\mathcal{P}}_t){\upsilon }_{\mu }{\upsilon }_{\nu }-{\mathcal{P}}_t{g}_{\mu \nu }+({\mathcal{P}}_r-{\mathcal{P}}_t){\epsilon }_{\mu }{\epsilon }_{\nu },$$

(7)

where ${\upsilon }_{\mu }$ denotes the 4-velocity vector with

$${\upsilon }^{\mu }=e^{-a}{\delta }_0^{\mu },{\epsilon }^{\mu }=e^{-b}{\delta }_1^{\mu },{\upsilon }^{\mu }{\upsilon }_{\mu }=-{\epsilon }^{\mu }{\epsilon }_{\mu }=1.$$

By using Equations (1) and (7) in Equation (5), the following expressions are perceived for the energy density, radial, and tangential components of pressure:

$$\frac{S_f^{{}^{\prime }}\left(r\right)}{r^2}=\frac{\rho }{f_{\mathcal{R}}\left(\mathcal{R}\right)}+\frac{\mathrm{Y}}{f_{\mathcal{R}}\left(\mathcal{R}\right)},$$

(8)

$$-\frac{S_f\left(r\right)}{r^3}=\frac{{\mathcal{P}}_r}{f_{\mathcal{R}}\left(\mathcal{R}\right)}+\frac{1}{f_{\mathcal{R}}\left(\mathcal{R}\right)}\left(1-\frac{S_f\left(r\right)}{r}\right)\left[(f_{\mathcal{R}}^{{}^{″}}\left(\mathcal{R}\right)-f_{\mathcal{R}}^{{}^{\prime }}\left(\mathcal{R}\right)\frac{(S_f^{{}^{\prime }}\left(r\right)r-S_f\left(r\right))}{2r^2(1-S_f\left(r\right)/r)})\right]-\frac{\mathrm{Y}}{f_{\mathcal{R}}\left(\mathcal{R}\right)},$$

(9)

$$-\frac{S_f{\left(r\right)}^{{}^{\prime }}r-S_f\left(r\right)}{2r^3}=\frac{{\mathcal{P}}_t}{f_{\mathcal{R}}\left(\mathcal{R}\right)}+\frac{1}{f_{\mathcal{R}}\left(\mathcal{R}\right)}\left(1-\frac{S_f\left(r\right)}{r}\right)\frac{f_{\mathcal{R}}^{{}^{\prime }}\left(\mathcal{R}\right)}{r}-\frac{\mathrm{Y}}{f_{\mathcal{R}}\left(\mathcal{R}\right)},$$

(10)

where

$$\mathrm{Y}=\mathrm{Y}\left(r\right)=\frac{1}{4}(f_{\mathcal{R}}\left(\mathcal{R}\right)\mathcal{R}+\square f_{\mathcal{R}}\left(\mathcal{R}\right)+T),$$

(11)

with curvature scalar

$$\mathcal{R}=\frac{2S_f^{{}^{\prime }}\left(r\right)}{r^2},$$

(12)

and

$$\square f_{\mathcal{R}}\left(\mathcal{R}\right)=\left(1-\frac{S_f\left(r\right)}{r}\right)\left[f_{\mathcal{R}}^{{}^{″}}\left(\mathcal{R}\right)-f_{\mathcal{R}}^{{}^{\prime }}\left(\mathcal{R}\right)\frac{(S_f{\left(r\right)}^{{}^{\prime }}r-S_f\left(r\right))}{2r^2(1-S_f\left(r\right)/r)}+\frac{2f_{\mathcal{R}}^{{}^{\prime }}\left(\mathcal{R}\right)}{r}\right].$$

(13)

We investigate wormhole solutions for an exponential $f\left(\mathcal{R}\right)$ model [28,30], which is represented by

$$f\left(\mathcal{R}\right)=\mathcal{R}-\alpha \gamma \left(1-\frac{1}{e^{\mathcal{R}/\gamma }}\right),\alpha \in (0,\infty ),\gamma =\sigma H_0^2,$$

(14)

where $\sigma$ is a dimensionless parameter and $H_0$ is the Hubble parameter, which we take equal to one for simplicity. For the model given by Equation (14), Cognola et al. [28] showed that the inflation and the current accelerated expansion of our Universe arise in a unified and natural way. They further showed that this model passes all the local test and is a viable $f\left(\mathcal{R}\right)$ gravity model.

By employing Equations (11)–(14) in Equations (8)–(10), we have the following modified field equations

$$\rho =\frac{S_f^{\prime }\left(r\right)}{r^2}\left(1-\alpha e^{-\frac{2S_f^{\prime }\left(r\right)}{\gamma r^2}}\right),$$

(15)

$$\begin{array}{ccc}\hfill {\mathcal{P}}_r& =& \frac{e^{-\frac{2S_f^{\prime }\left(r\right)}{\gamma r^2}}}{{\gamma }^2{r}^7}(S_f\left(r\right)\left(\alpha \left(-16S_f^{\prime }{\left(r\right)}^2+r^2\left(\gamma r^2\left(2S_f^{\left(3\right)}\left(r\right)+\gamma \right)-9\gamma r{S}_f^{″}\left(r\right)-4S_f^{″}{\left(r\right)}^2\right)\right.\right.\hfill \\ & +& \left.\left.2r{S}_f^{\prime }\left(r\right)\left(8S_f^{″}\left(r\right)+7\gamma r\right)\right)-{\gamma }^2{r}^4{e}^{\frac{2S_f^{\prime }\left(r\right)}{\gamma r^2}}\right)+\alpha r\left(-2\gamma r^4{S}_f^{\left(3\right)}\left(r\right)+4r^2{S}_f^{″}\left(r\right)\left(S_f^{″}\left(r\right)+2\gamma r\right)\right.\hfill \\ & -& \left.2\left(\gamma r^2-8\right)S_f^{\prime }{\left(r\right)}^2+r{S}_f^{\prime }\left(r\right)\left(\left(\gamma r^2-16\right)S_f^{″}\left(r\right)-12\gamma r\right)\right)),\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\mathcal{P}}_t& =& \frac{1}{2r^5}(r^2\left(S_f\left(r\right)-r{S}_f^{\prime }\left(r\right)\right)+\frac{1}{\gamma }\alpha e^{-\frac{2S_f^{\prime }\left(r\right)}{\gamma r^2}}\left(r\left(\left(\gamma r^2+8\right)S_f^{\prime }\left(r\right)-4r{S}_f^{″}\left(r\right)\right)\right.\hfill \\ & -& \left.S_f\left(r\right)\left(r\left(\gamma r-4S_f^{″}\left(r\right)\right)+8S_f^{\prime }\left(r\right)\right)\right)).\hfill \end{array}$$

(17)

In the next section, we analyze solutions of these equations.

3. Wormhole Solutions

To find the wormhole solutions in the background of the $f\left(\mathcal{R}\right)$ gravity with the specific exponential model given by Equation (14), we examine the energy conditions specially, $NEC$ and $WEC$. The violation of $NEC$ is the compulsory and fundamental requirement for the existence of wormhole solutions in GR, while in the $f\left(\mathcal{R}\right)$ theory of gravity it is not compulsory [5]. The violation of the energy condition gives the presence of exotic matter at the location of wormhole throat. Both $NEC$ and $WEC$ are formalized with the following relation

$$NEC:\rho \ge 0\Rightarrow \rho +{\mathcal{P}}_r\ge 0,WEC:\rho \ge 0\Rightarrow \rho +{\mathcal{P}}_t\ge 0.$$

The violation of $NEC$ and $WEC$ bounds leads to the violation of the other bounds, i.e., dominant energy condition $\left(DEC\right)$ and strong energy conditions $\left(SEC\right)$. Both $DEC$ and $SEC$ are defined as

$$DEC:\forall i,\rho \ge 0\Rightarrow \rho \pm {\mathcal{P}}_i\ge 0,SEC:\forall i,\rho +{\mathcal{P}}_i\ge 0\Rightarrow \rho +\sum {\mathcal{P}}_i\ge 0.$$

Traceless Fluid for $f\left(\mathcal{R}\right)=\mathcal{R}-\alpha \gamma \left(1-\frac{1}{e^{\mathcal{R}/\gamma }}\right)$ Model

Here, we discuss the traceless fluid [31,32,33,34,35,36,37,38,39,40,41,42] for the the specific exponential model. The $f\left(\mathcal{R}\right)=\mathcal{R}-\alpha \gamma \left(1-\frac{1}{e^{\mathcal{R}/\gamma }}\right)$ model can be depicted from specific form of the equation of state (EoS) to explore the wormhole solutions and energy conditions. The traceless part of the stress–energy tensor for the fluid is defined as:

$$\mathcal{T}=0,\Rightarrow \rho -{\mathcal{P}}_r-2{\mathcal{P}}_t=0.$$

(18)

The concept of traceless fluid is related with the concept of Casimir effect [43]. The traceless fluid is used to provide an exotic matter under this current scenario. Using Equations (15)–(17) in Equation (18) leads to the following nonlinear differential equation,

$$\begin{array}{c}\frac{e^{-\frac{2S_f^{\prime }\left(r\right)}{\gamma r^2}}}{{\gamma }^2{r}^7}(2\alpha \gamma r^4(r-S_f\left(r\right))S_f^{\left(3\right)}\left(r\right)+\alpha r^2{S}_f^{″}\left(r\right)\left(4(S_f\left(r\right)-r)S_f^{″}\left(r\right)+\gamma r(5S_f\left(r\right)-4r)\right)\hfill \\ +2\alpha \left(8S_f\left(r\right)+\gamma r^3-8r\right)\times S_f^{\prime }{\left(r\right)}^2+r{S}_f^{\prime }\left(r\right)\hfill \\ \left(-\alpha \left(16S_f\left(r\right)+\gamma r^3-16r\right)S_f^{″}\left(r\right)+2{\gamma }^2{r}^4{e}^{\frac{2S_f^{\prime }\left(r\right)}{\gamma r^2}}-2\alpha \gamma r\left(3S_f\left(r\right)+\gamma r^3-2r\right)\right))=0,\hfill \end{array}$$

(19)

Equation (20) is non-linear and we treat it numerically with the following initial conditions $S_f\left(0.01\right)=0.001,S_f^{\prime }\left(0.01\right)=0.0002$, and $S_f^{″}\left(0.01\right)=0.07$.

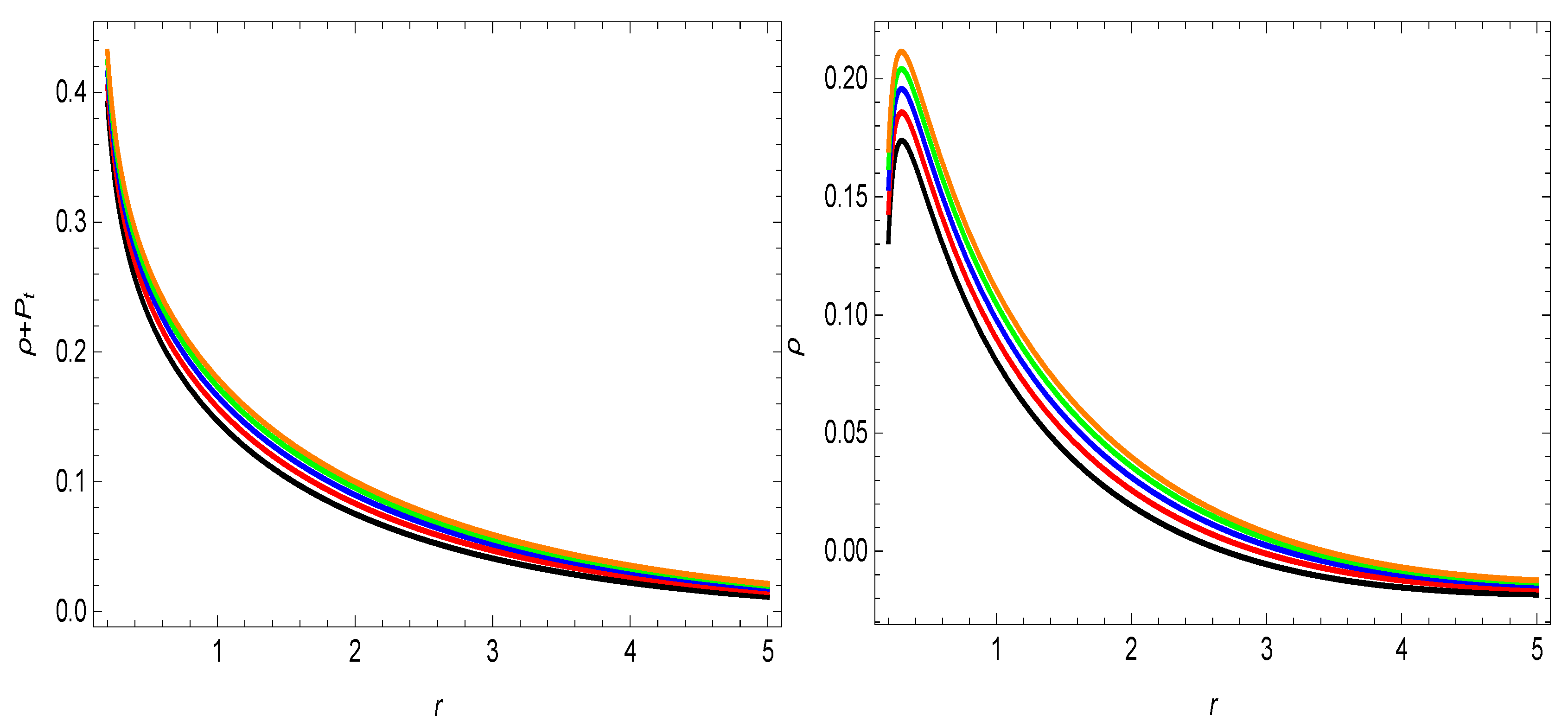
The parameter $\alpha$ is between zero and infinity and we have chosen some particular values within this range. For the other parameters of the model, we have assigned units of Km, as it is related to the Hubble parameter and is chosen equal to 1. With the variation of the parameter $\alpha$, the results change, as can be seen from the graphs for the different values of this parameter $\alpha$. For the variation of the other parameter $\gamma$, the results do not change and therefore we have chosen only one value for it. The first figure provides the shape-function properties, for the wormhole geometry. From the left panel of Figure 1, it is noticed that the shape-function, i.e., $S_f\left(r\right)$, is positive with regularly increasing development, which is a positive sign for the realistic wormhole geometry. From the right panel of Figure 1, the ratio of the shape-function and the radial coordinate, i.e.,$\frac{S_f\left(r\right)}{r}\to 0$ as $r\to \infty$ is not satisfied. It means that the wormhole geometry is not asymptotically flat and this behavior coincides with the behavior of the already existing wormhole models reported in the literature (see, for example, [18,20,36]). It is depicted from the left plot of Figure 2 that the difference of the shape-function with the radial coordinate, i.e., $S_f\left(r\right)-r$, provides the locations of the wormhole throat for the different values of the parameter $\alpha$, which are approximately observed at $r_0\equiv 0.016,r_0\equiv 0.017,r_0\equiv 0.018,r_0\equiv 0.019$, and $r_0\equiv 0.020$, for $\alpha =0.10$, $\alpha =0.20$, $\alpha =0.30$, $\alpha =0.40$, and $\alpha =0.50$, respectively. The flaring out condition of the shape-function can be seen from the right plot of Figure 2, which is satisfied. All the required properties of the shape-function for wormhole geometry are observed to be satisfied. In the context of energy conditions, it is confirmed in Figure 3 and Figure 4 that the energy density function $\rho$ is positive for this current study. $WEC$ and $NEC$, i.e., $\rho +{\mathcal{P}}_t$ and $\rho +{\mathcal{P}}_r$, can be seen in Figure 3. The behavior of the energy conditions is also revealed in Table 1, for the different values of the parameter $\alpha$. The violation of $NEC$ for the first two values of parameter $\alpha$ is evidence for the presence of the exotic matter, which may be required for the wormhole geometry. Our obtained results are similar to those wormhole solutions that are provided in [25,26,27].

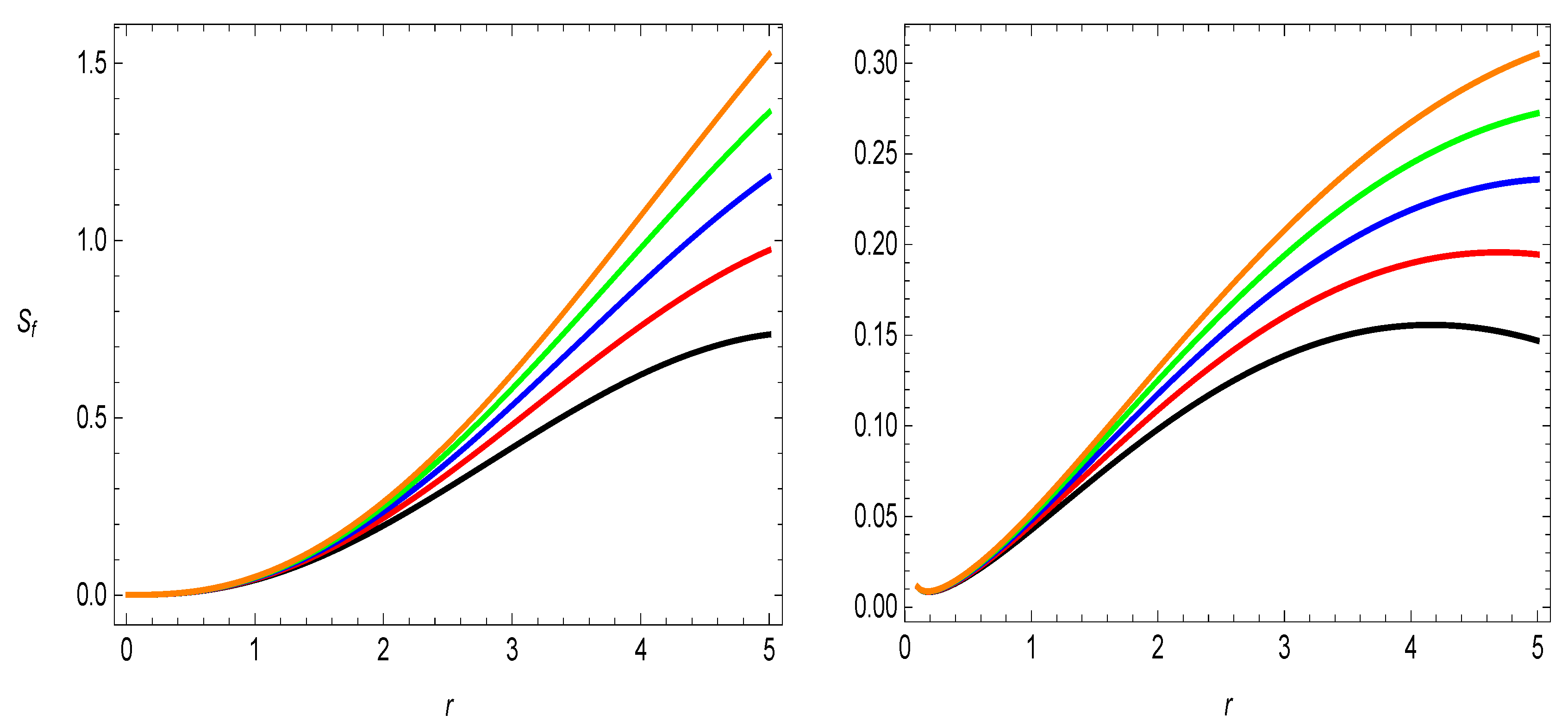
Figure 1. The behavior of $S_f\left(r\right)$ and $\frac{S_f\left(r\right)}{r}$. Here, $\alpha =0.40$ (★), $\alpha =0.50$ (★), $\alpha =0.60$ (★), $\alpha =0.70$ (★), $\alpha =0.80$ (★), and $\gamma =0.10$.

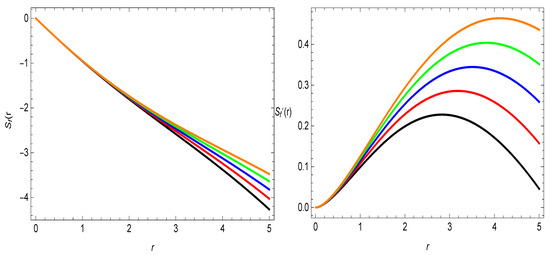
Figure 2. The development of $S_f\left(r\right)-r$ and $S_f^{{}^{\prime }}\left(r\right)$. Here, $\alpha =0.40$ (★), $\alpha =0.50$ (★), $\alpha =0.60$ (★), $\alpha =0.70$ (★), $\alpha =0.80$ (★), and $\gamma =0.10$.

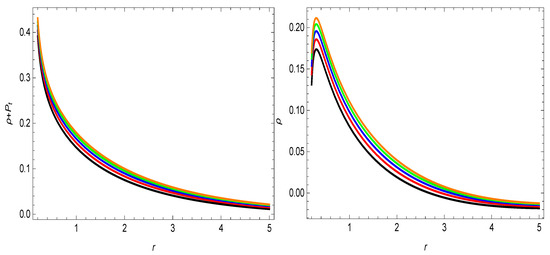
Figure 3. The variational behavior of $\rho +{\mathcal{P}}_t$, and $\rho +{\mathcal{P}}_r$. Here, $\alpha =0.40$ (★), $\alpha =0.50$ (★), $\alpha =0.60$ (★), $\alpha =0.70$ (★), $\alpha =0.80$ (★), and $\gamma =0.10$.

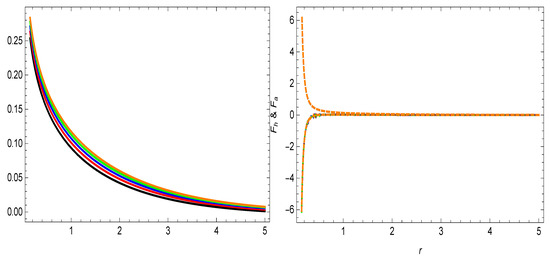
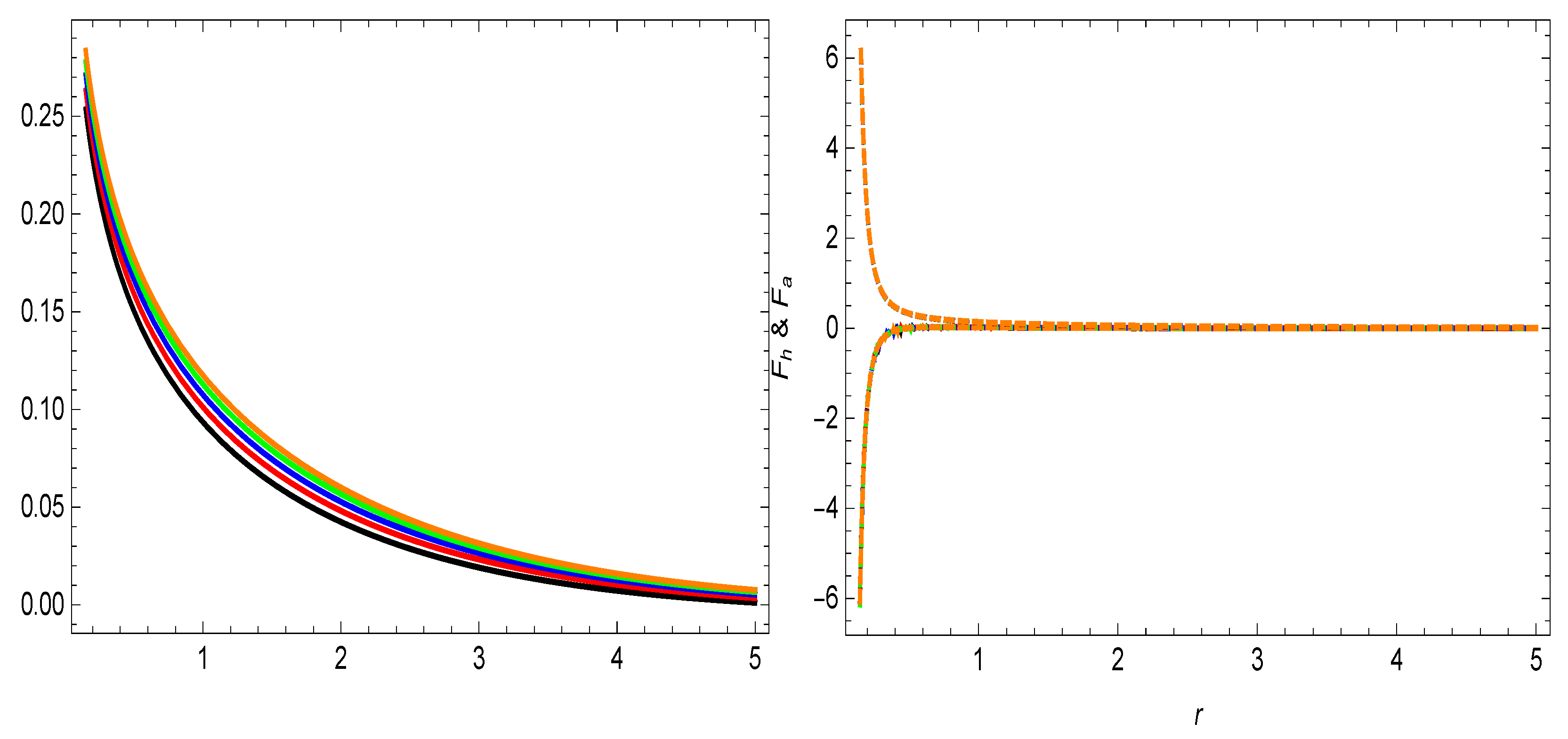
Figure 4. The variational development of $\rho$ and balancing behavior of ${\mathcal{F}}_{\mathrm{af}}$, and ${\mathcal{F}}_{\mathrm{hf}}$. Here, $\alpha =0.40$ (★), $\alpha =0.50$ (★), $\alpha =0.60$ (★), $\alpha =0.70$ (★), $\alpha =0.80$ (★), and $\gamma =0.10$.

Table 1. Summary of the results.

Properties of shape-function for $0<r\le 5$
expressions	$\alpha =0.40$ (★)	$\alpha =0.50$ (★)	$\alpha =0.60$ (★)	$\alpha =0.70$ (★)	$\alpha =0.80$ (★)
$S_f\left(r\right)$	$S_f\left(r\right)>0$	$S_f\left(r\right)>0$	$S_f\left(r\right)>0$	$S_f\left(r\right)>0$	$S_f\left(r\right)>0$
$\frac{S_f\left(r\right)}{r}$	$\underset{r\to 5}{\lim }\frac{S_f\left(r\right)}{r}=0.15$	$\underset{r\to 5}{\lim }\frac{S_f\left(r\right)}{r}=0.19$	$\underset{r\to 5}{\lim }\frac{S_f\left(r\right)}{r}=0.23$	$\underset{r\to 5}{\lim }\frac{S_f\left(r\right)}{r}=0.27$	$\underset{r\to 5}{\lim }\frac{S_f\left(r\right)}{r}=0.31$
$S_f\left(r\right)=r_0$	$r_0\equiv 0.016$	$r_0\equiv 0.017$	$r_0\equiv 0.018$	$r_0\equiv 0.019$	$r_0\equiv 0.020$
$S_f^{{}^{\prime }}\left(r\right)$	$S_f^{{}^{\prime }}\left(0.016\right)<1$	$S_f^{{}^{\prime }}\left(0.017\right)<1$	$S_f^{{}^{\prime }}\left(0.018\right)<1$	$S_f^{{}^{\prime }}\left(0.019\right)<1$	$S_f^{{}^{\prime }}\left(0.020\right)<1$
Energy conditions for $0<r\le 5$
$\rho +{\mathcal{P}}_t$	$\rho +{\mathcal{P}}_t>0$	$\rho +{\mathcal{P}}_t>0$	$\rho +{\mathcal{P}}_t>0$	$\rho +{\mathcal{P}}_t>0$	$\rho +{\mathcal{P}}_t>0$
$\rho +{\mathcal{P}}_r$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r>0$	$\rho +{\mathcal{P}}_r>0$	$\rho +{\mathcal{P}}_r>0$
$\rho$	$\rho >0$	$\rho >0$	$\rho >0$	$\rho >0$	$\rho >0$
Forces, i.e., ${\mathcal{F}}_{\mathrm{af}}$, and ${\mathcal{F}}_{\mathrm{hf}}$ for $0<r\le 5$
${\mathcal{F}}_{\mathrm{af}}$&${\mathcal{F}}_{\mathrm{hf}}$	Balanced	Balanced	Balanced	Balanced	Balanced

4. Equilibrium Conditions

Now, we describe the stability of the wormhole solutions calculated here, by considering the equilibrium equation. In this response, we discuss the following Tolman–Oppenheimer–Volkov (TOV) equation

$$\frac{d{\mathcal{P}}_r}{dr}+\frac{{\mathsf{\Pi }}^{\prime }}{2}(\rho +{\mathcal{P}}_r)+\frac{2}{r}({\mathcal{P}}_r-{\mathcal{P}}_t)=0,$$

(20)

where $\mathsf{\Pi }\left(r\right)=2R_f\left(r\right)$. The TOV equation reveals the equilibrium stage of configuration. The three terms of the above TOV equation define the three different kinds of forces, namely the gravitational, hydrostatic, and anisotropic forces, defined by

$${\mathcal{F}}_{\mathrm{gf}}=-\frac{{\mathsf{\Pi }}^{\prime }(\rho +{\mathcal{P}}_r)}{2},{\mathcal{F}}_{\mathrm{hf}}=-\frac{d{\mathcal{P}}_r}{dr},{\mathcal{F}}_{\mathrm{af}}=2\frac{({\mathcal{P}}_t-{\mathcal{P}}_r)}{r}.$$

Thus, Equation (20) takes the following form

$${\mathcal{F}}_{\mathrm{af}}+{\mathcal{F}}_{\mathrm{gf}}+{\mathcal{F}}_{\mathrm{hf}}=0.$$

In this study, we assume the shift-function as a constant, i.e., $R_f^{\prime }\left(r\right)=0$. It leads to ${\mathcal{F}}_{\mathrm{gf}}=0$ and, hence, the TOV equation reduces to the following form

$${\mathcal{F}}_{\mathrm{af}}+{\mathcal{F}}_{\mathrm{hf}}=0.$$

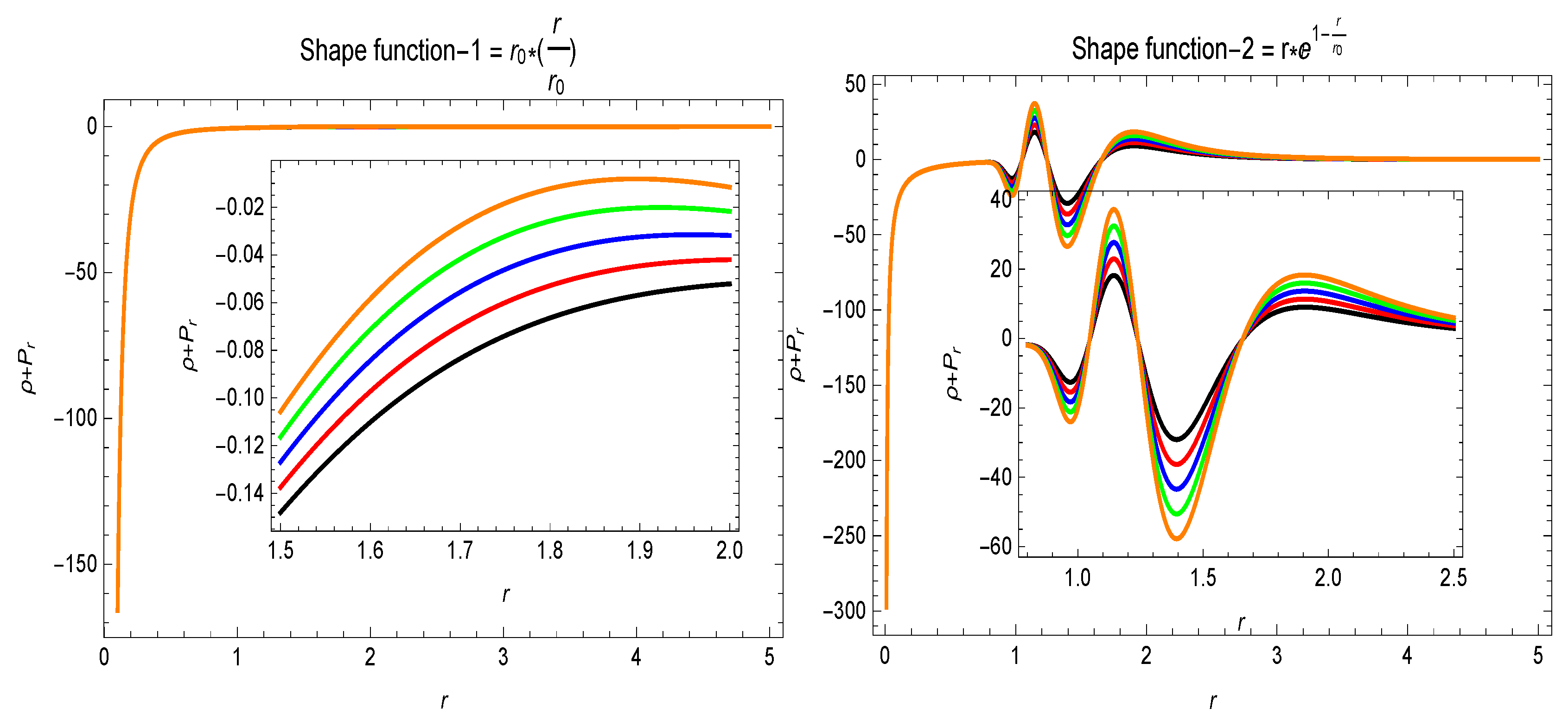
From the right plot in Figure 4, it can be perceived that both forces, i.e., ${\mathcal{F}}_{\mathrm{af}}$, and ${\mathcal{F}}_{\mathrm{hf}}$, are balanced by each other. This balancing development of these forces shows that our calculated wormholes are realistic and stable.

5. WEC and NEC for Two Specific Shape-Functions

Here, we explore the energy conditions, specially $WEC$ and $NEC$, for the two particular shape-functions i.e., $S_f\left(r\right)=r_0{\left(\frac{r}{r_0}\right)}^{\beta }$, $0<\beta <1$ and $S_f\left(r\right)=r{e}^{1-\frac{r}{r_0}}$ [44,45]. First, we calculate the field equations for both of these specific shape-functions by plugging them into Equations (15)–(17). We calculate the field equations for $S_f\left(r\right)=r_0{\left(\frac{r}{r_0}\right)}^{\beta }$ shape-function as

$$\rho =\frac{\beta r_0{\left(\frac{r}{r_0}\right)}^{\beta }\left(1-\alpha e^{-\frac{2\beta r_0{\left(\frac{r}{r_0}\right)}^{\beta }}{\gamma r^3}}\right)}{r^3},$$

(21)

$$\begin{array}{ccc}\hfill {\mathcal{P}}_r& =& \frac{r_0{\left(\frac{r}{r_0}\right)}^{\beta }{e}^{-\frac{2\beta r_0{\left(\frac{r}{r_0}\right)}^{\beta }}{\gamma r^3}}}{{\gamma }^2{r}^9}(\alpha {(\beta -3)}^2\beta r{r}_0\left(4\beta +3\gamma r^2\right){\left(\frac{r}{r_0}\right)}^{\beta }-4\alpha {(\beta -3)}^2{\beta }^2{r}_0^2{\left(\frac{r}{r_0}\right)}^{2\beta }\hfill \\ & +& \gamma r^4\left(\alpha \left(\gamma r^2-2(\beta -4)(\beta -3)\beta \right)-\gamma r^2{e}^{\frac{2\beta r_0{\left(\frac{r}{r_0}\right)}^{\beta }}{\gamma r^3}}\right)),\hfill \end{array}$$

(22)

$${\mathcal{P}}_t=\frac{r_0{\left(\frac{r}{r_0}\right)}^{\beta }{e}^{-\frac{2\beta r_0{\left(\frac{r}{r_0}\right)}^{\beta }}{\gamma r^3}}\left(-(\beta -1)\gamma r^3\left(e^{\frac{2\beta r_0{\left(\frac{r}{r_0}\right)}^{\beta }}{\gamma r^3}}-\alpha \right)-4\alpha (\beta -3)\beta r+4\alpha (\beta -3)\beta r_0{\left(\frac{r}{r_0}\right)}^{\beta }\right)}{2\gamma r^6}.$$

(23)

Now, we calculate the field equations for the shape-function $S_f\left(r\right)=r{e}^{1-\frac{r}{r_0}}$. It should be noted that we use the exponential shape-function here that is dimensionally correct, as it was dimensionally incorrect in [45]. The field equations are

$$\rho =\frac{e^{1-\frac{r}{r_0}}(r-r_0)\left(\alpha e^{\frac{2e^{1-\frac{r}{r_0}}(r-r_0)}{\gamma r^2{r}_0}}-1\right)}{r^2{r}_0},$$

(24)

$$\begin{array}{ccc}\hfill {\mathcal{P}}_r& =& \frac{e^{-\frac{2e^{1-\frac{r}{r_0}}}{\gamma r^2}-\frac{3r}{r_0}+1}}{{\gamma }^2{r}^6{r}_0^4}\times (-4\alpha {\left(r^2-2r_0^2\right)}^2{e}^{\frac{2e^{1-\frac{r}{r_0}}}{\gamma r{r}_0}+2}+{\gamma }^2{r}^4{r}_0^4\left(-e^{\frac{2e^{1-\frac{r}{r_0}}}{\gamma r^2}+\frac{2r}{r_0}}\right)+\alpha \gamma r^2{r}_0{e}^{\frac{2\left(r^2+\frac{e^{1-\frac{r}{r_0}}}{\gamma }\right)}{r{r}_0}}\hfill \\ & \times & \left(2r^3+r^2{r}_0\left(\gamma r_0^2+2\right)-4r{r}_0^2-12r_0^3\right)-\alpha e^{\frac{r^2+\frac{2e^{1-\frac{r}{r_0}}}{\gamma }}{r{r}_0}+1}\left(\gamma r^2{r}_0\left(3r^3+2r^2{r}_0-6r{r}_0^2-12r_0^3\right)\right.\hfill \\ & -& \left.4{\left(r^2-2r_0^2\right)}^2\right)),\hfill \end{array}$$

(25)

$${\mathcal{P}}_t=\frac{\gamma r^3{r}_0{e}^{1-\frac{r}{r_0}}-\alpha e^{\frac{\frac{2e^{1-\frac{r}{r_0}}(r-r_0)}{\gamma r^2}-2r+r_0}{r_0}}\left(e^{r/r_0}\left(r^2(\gamma r{r}_0+4)-8r_0^2\right)-4e\left(r^2-2r_0^2\right)\right)}{2\gamma r^4{r}_0^2}.$$

(26)

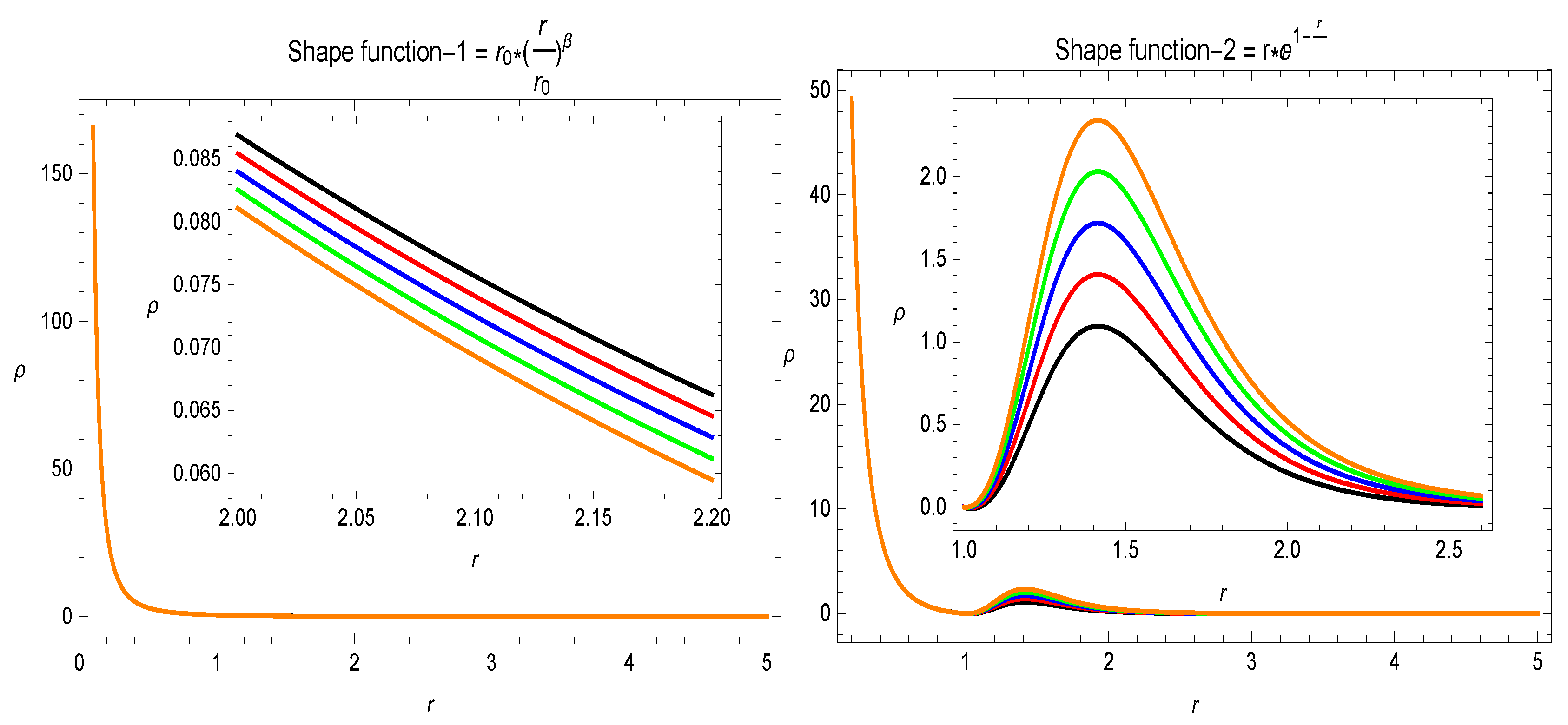
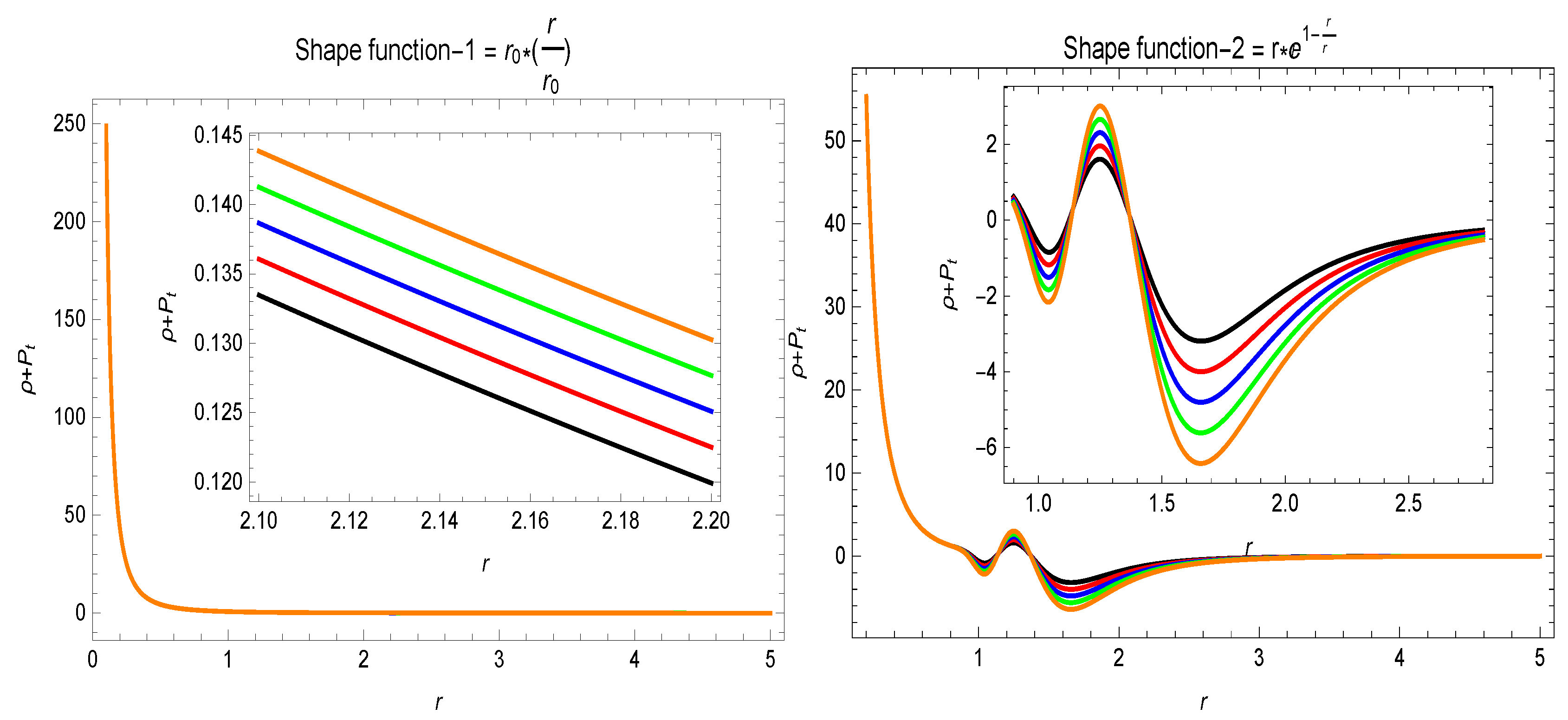
In the framework of GR, the violation $NEC$ is an important feature of static traversable wormholes [3], even though for the dynamic, i.e time-dependent wormhole solutions, $NEC$ and $WEC$ can be violated in certain regions and for some specific intervals of time at the throat of the wormhole. In extended theories of GR, one may argue that the stress–energy tensor for a wormhole model satisfies $NEC$. The violation of $NEC$ is correlated with the presence of an exotic matter. Justifying the existence of some exotic matter is a critical issue, which motivates one to investigate $NEC$ for different models. In the response of energy conditions, it is clear from the results in Figure 5 that the energy density function $\rho$ is positive for both specific shape-functions, i.e., $S_f\left(r\right)=r_0{\left(\frac{r}{r_0}\right)}^{\beta }$ and $S_f\left(r\right)=r{e}^{1-\frac{r}{r_0}}$. $WEC$ and $NEC$, i.e., $\rho +{\mathcal{P}}_t$ and $\rho +{\mathcal{P}}_r$, development can be seen in Figure 6 and Figure 7. The behavior of the energy conditions is also revealed in Table 2 for the different values of parameter $\alpha$. The violation of $NEC$ for the different values of parameter $\alpha$ is evidence for the presence of exotic matter, which may be a requirement for a traversable wormhole geometry.

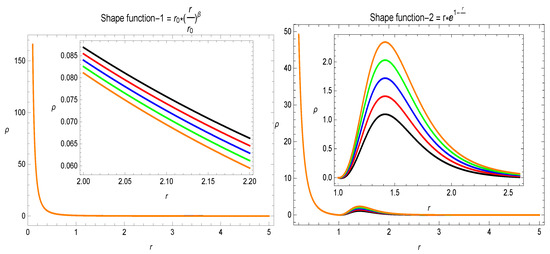
Figure 5. The variational behavior of $\rho$. Here, $\alpha =0.10$ (★), $\alpha =0.20$ (★), $\alpha =0.30$ (★), $\alpha =0.40$ (★), $\alpha =0.50$ (★), $\beta =0.25$, and $\gamma =0.10$.

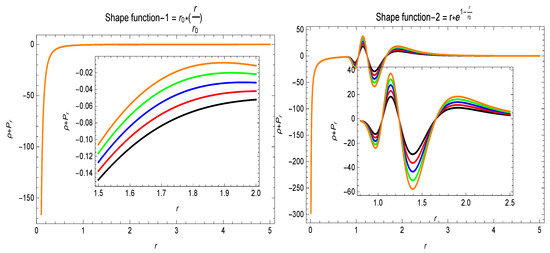
Figure 6. The variational behavior of $\rho +{\mathcal{P}}_r$. Here, $\alpha =0.10$ (★), $\alpha =0.20$ (★), $\alpha =0.30$ (★), $\alpha =0.40$ (★), $\alpha =0.50$ (★), $\beta =0.25$, and $\gamma =0.10$.

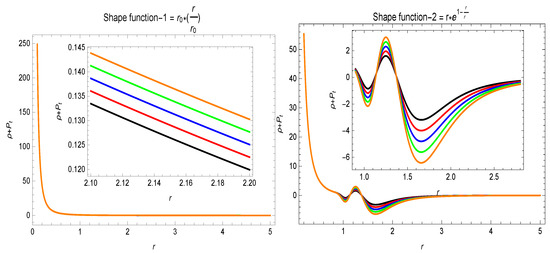
Figure 7. The variational behavior of $\rho +{\mathcal{P}}_t$. Here, $\alpha =0.10$ (★), $\alpha =0.20$ (★), $\alpha =0.30$ (★), $\alpha =0.40$ (★), $\alpha =0.50$ (★), $\beta =0.25$, and $\gamma =0.10$.

Table 2. Summary of the results.

Energy conditions for $S_f\left(r\right)=r_0{\left(\frac{r}{r_0}\right)}^{\beta }$ model with $0<r\le 5$ and $r_0=1.1$
expressions	$\alpha =0.40$ (★)	$\alpha =0.50$ (★)	$\alpha =0.60$ (★)	$\alpha =0.70$ (★)	$\alpha =0.80$ (★)
$\rho +{\mathcal{P}}_t$	$\rho +{\mathcal{P}}_t>0$	$\rho +{\mathcal{P}}_t>0$	$\rho +{\mathcal{P}}_t>0$	$\rho +{\mathcal{P}}_t>0$	$\rho +{\mathcal{P}}_t>0$
$\rho +{\mathcal{P}}_r$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$
$\rho$	$\rho >0$	$\rho >0$	$\rho >0$	$\rho >0$	$\rho >0$
Energy conditions for $S_f\left(r\right))=r{e}^{1-\frac{r}{r_0}}$ model with $0<r\le 5$ and $r_0=1.1$
$\rho +{\mathcal{P}}_t$	$\rho +{\mathcal{P}}_t<0$	$\rho +{\mathcal{P}}_t<0$	$\rho +{\mathcal{P}}_t<0$	$\rho +{\mathcal{P}}_t<0$	$\rho +{\mathcal{P}}_t<0$
$\rho +{\mathcal{P}}_r$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$	$\rho +{\mathcal{P}}_r<0$
$\rho$	$\rho >0$	$\rho >0$	$\rho >0$	$\rho >0$	$\rho >0$

6. Summary

In the present study, we have explored the exponential gravity model for the static spherically symmetric wormhole solutions in the $f\left(\mathcal{R}\right)$ theory gravity. In this response, the anisotropic matter has employed. We have calculated the modified field equations in the reference of exponential gravity model given by Equation (14), for energy density and pressure sources under anisotropic matter. We utilize a traceless fluid in the background of particular EoS to calculate the shape-function and its properties. The important results of the present study are given below.

• In Figure 1, the behavior of the shape-function, i.e., $S_f\left(r\right)$, is regularly increasing with positive nature for the five different values of the parameter $\alpha$.
• The ratio, i.e., $\frac{S_f\left(r\right)}{r}$, does not go to zero as the radial coordinate becomes larger and larger and thus the flatness condition is not satisfied here in this model of $f\left(\mathcal{R}\right)$ gravity and this behavior of $\frac{S_f\left(r\right)}{r}$ is depicted in Figure 1 and Table 1. This behavior of non-flatness is also reported in the literature for some other models in modified theories of gravity [18,20,36].
• It is evident from the left panel of the Figure 2 that the difference of the shape-function with radial coordinate, i.e., $S_f\left(r\right)-r$, provides the wormholes throat locations for the different values of the parameter $\alpha$, which are approximately observed at $r_0\equiv 0.016,r_0\equiv 0.017,r_0\equiv 0.018,r_0\equiv 0.019$, and $r_0\equiv 0.020$, for $\alpha =0.10$, $\alpha =0.20$, $\alpha =0.30$, $\alpha =0.40$, and $\alpha =0.50$, respectively.
• The flaring out condition, i.e., $S_f^{{}^{\prime }}<1$, of the shape-function can be seen in the right plot of Figure 2, which is satisfied, i.e., $S_f^{{}^{\prime }}\left(0.016\right)<1$, $S_f^{{}^{\prime }}\left(0.017\right)<1$, $S_f^{{}^{\prime }}\left(0.018\right)<1$, $S_f^{{}^{\prime }}\left(0.019\right)<1$, and $S_f^{{}^{\prime }}\left(0.020\right)<1$ for the five different values of the parameter $\alpha$.
• In the Figure 5, Figure 6 and Figure 7, the behavior for the two specific shape-functions given in Section 5 is given. $NEC$ is violated and the energy density $\rho$ is positive for different values of the parameter $\alpha$. This violation of $NEC$ indicates the presence of some exotic matter, which is a requirement for a traversable wormhole solution.

$NEC$ has been observed to be violated in this current study, which can be seen in Figure 3. All of our calculated results can be seen from the summery which is presented in Table 1 and Table 2. We comment here that our calculated results for $f\left(\mathcal{R}\right)$ theory under exponential gravity model with anisotropic fluid source are in agreement with the already explored results in the modified $f\left(\mathcal{R}\right)$ theory of gravity in different scenarios [15,16,17,18,19,20,21,22,25,26,27].