Observation of Atmospheric Neutrinos
Abstract
:1. Introduction
1.1. History
1.2. Atmospheric Neutrino Flux Prediction
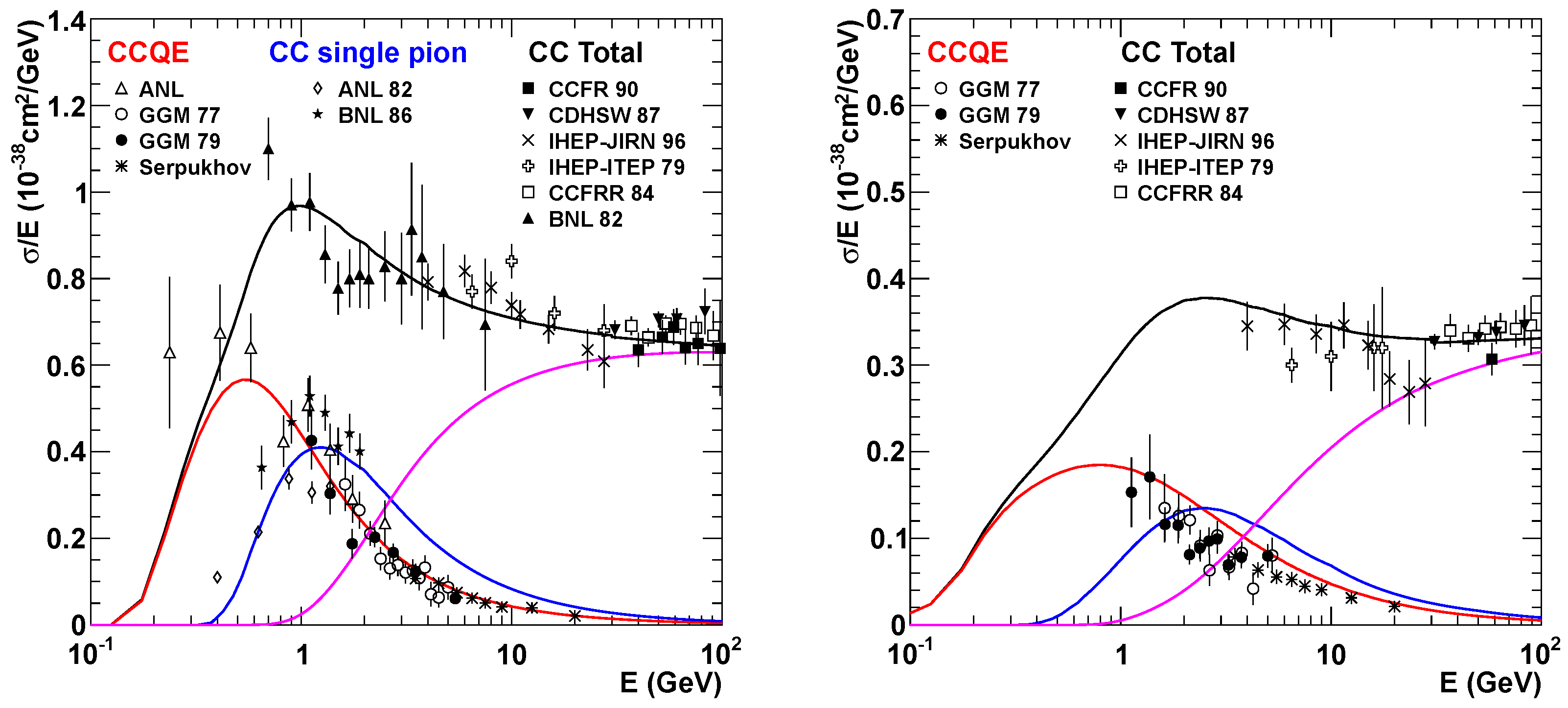
1.3. Neutrino Interaction
- Charged-Current quasi-elastic scattering: + N + N′
- Charged-Current pion production: + N + N′ +
- Deep Inelastic Scattering (DIS): + N + N′ + hadrons
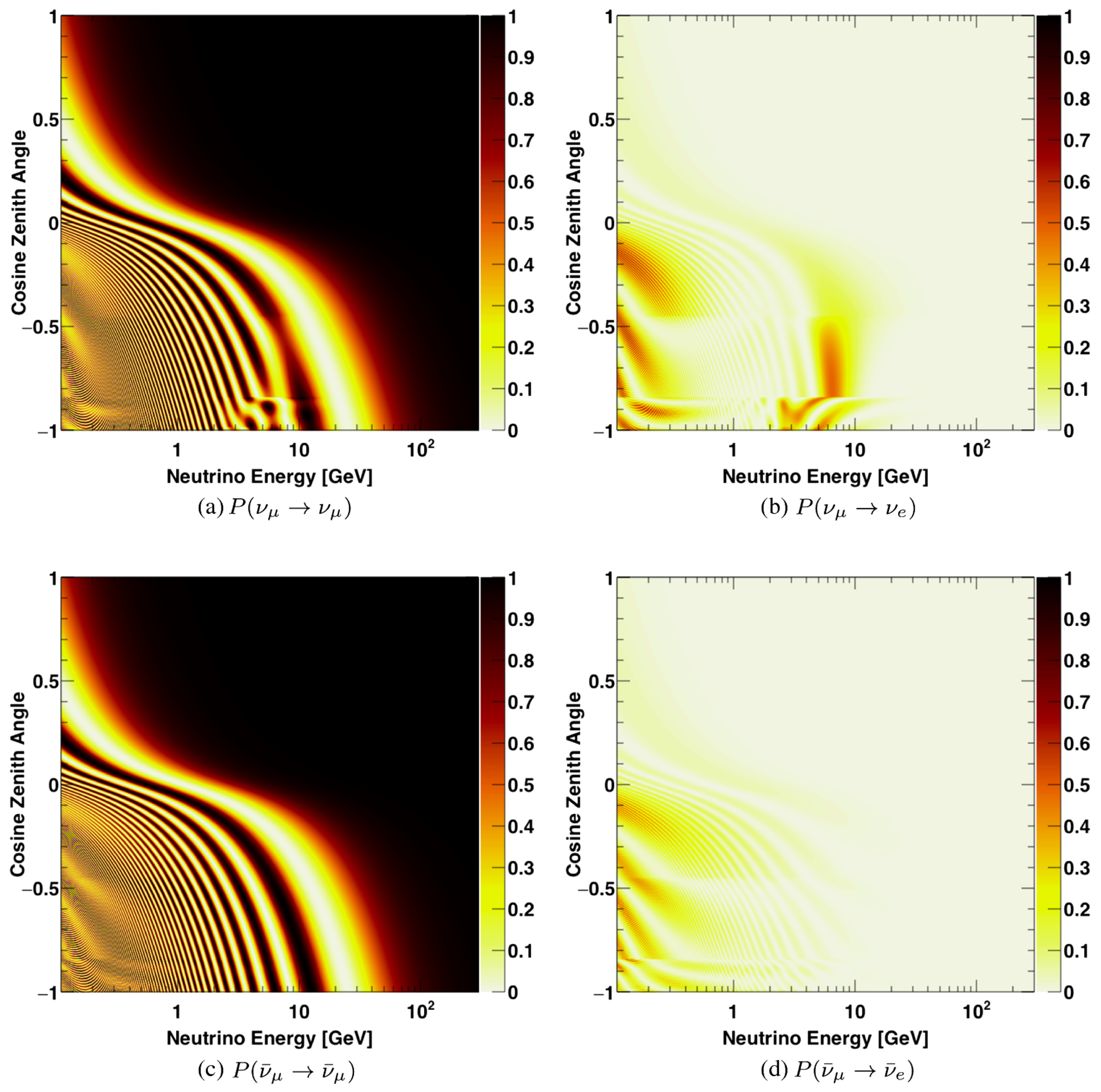
1.4. Neutrino Oscillation
2. Detectors
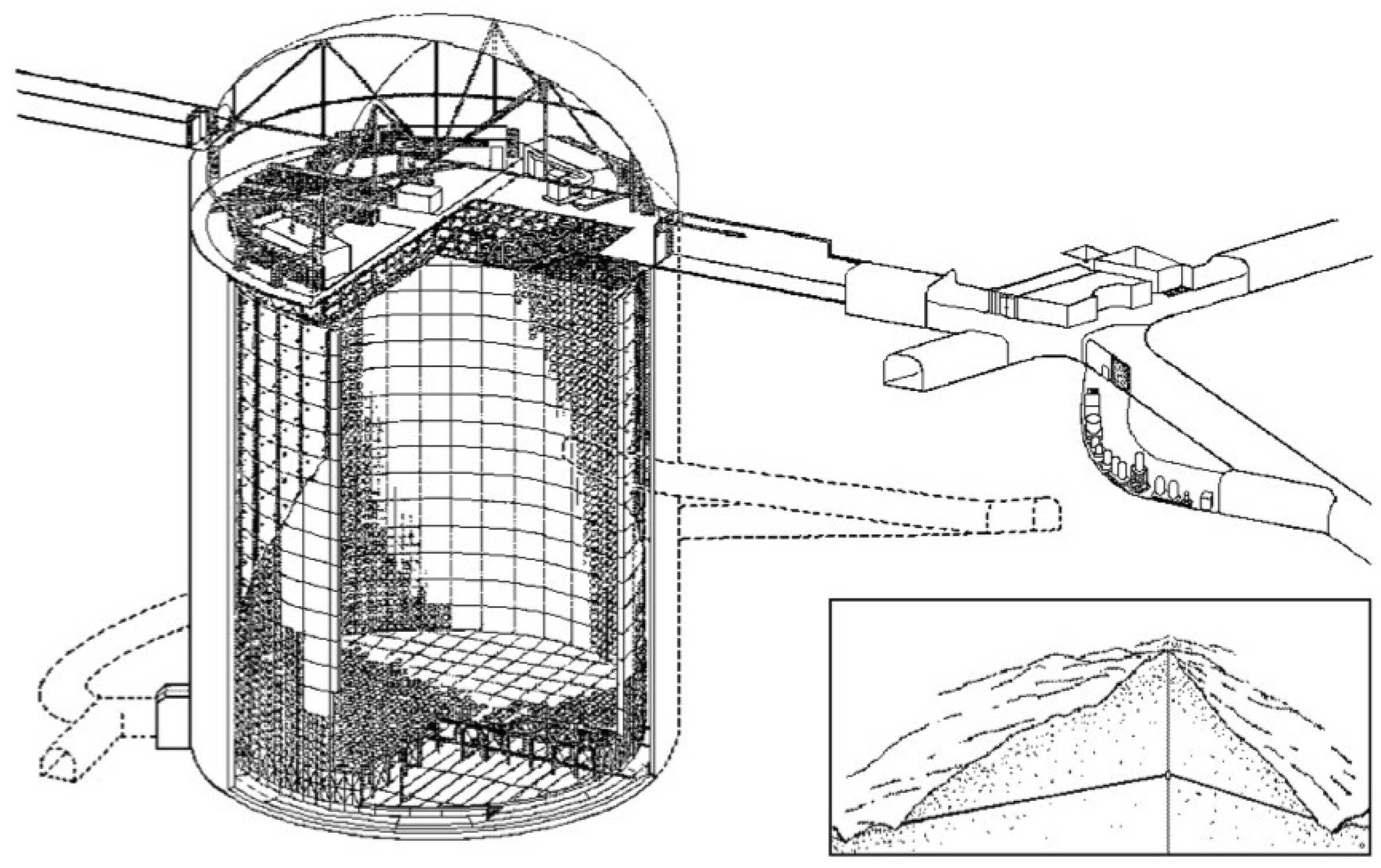
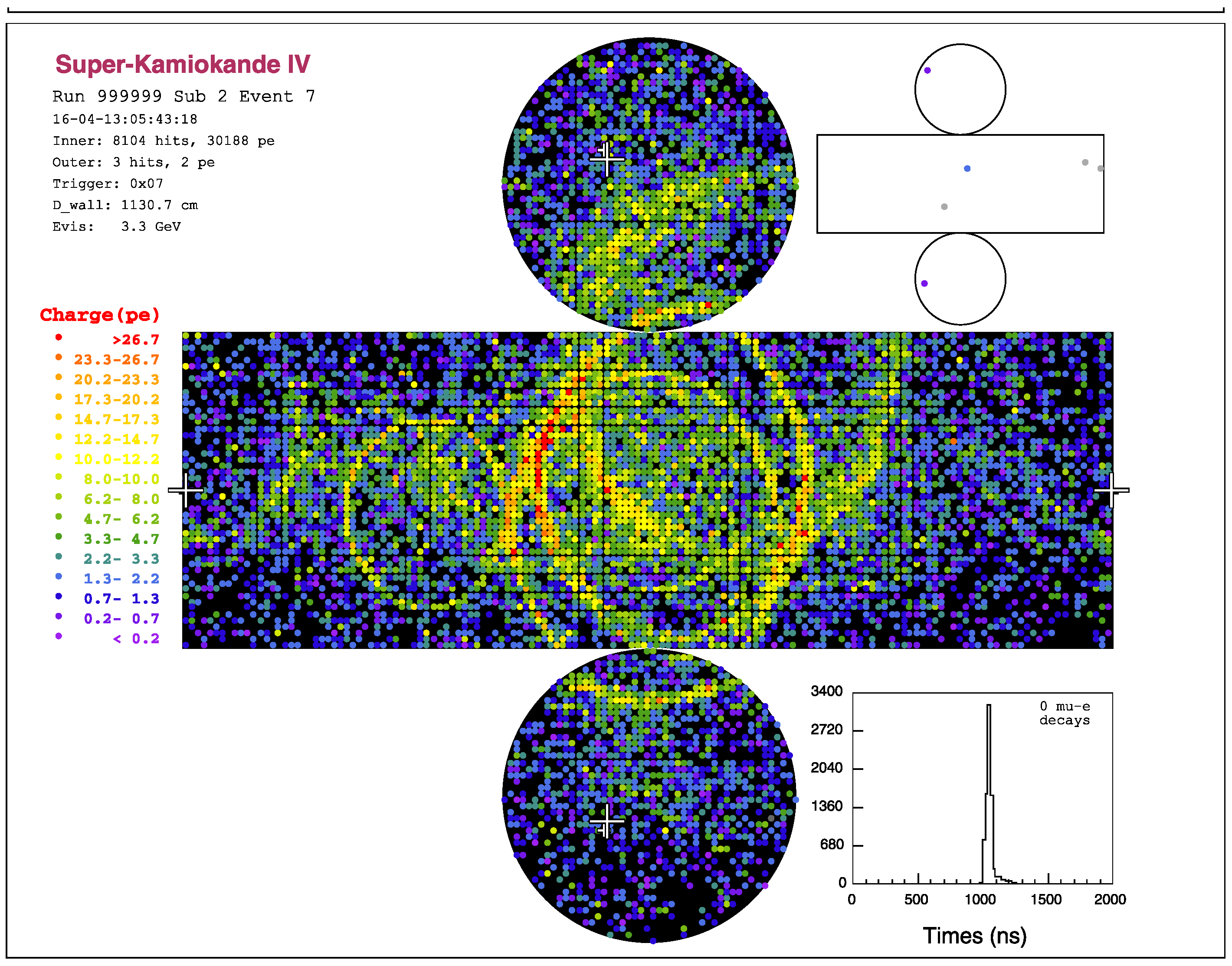
2.1. Super-Kamiokande
Discovery of the Neutrino Oscillation
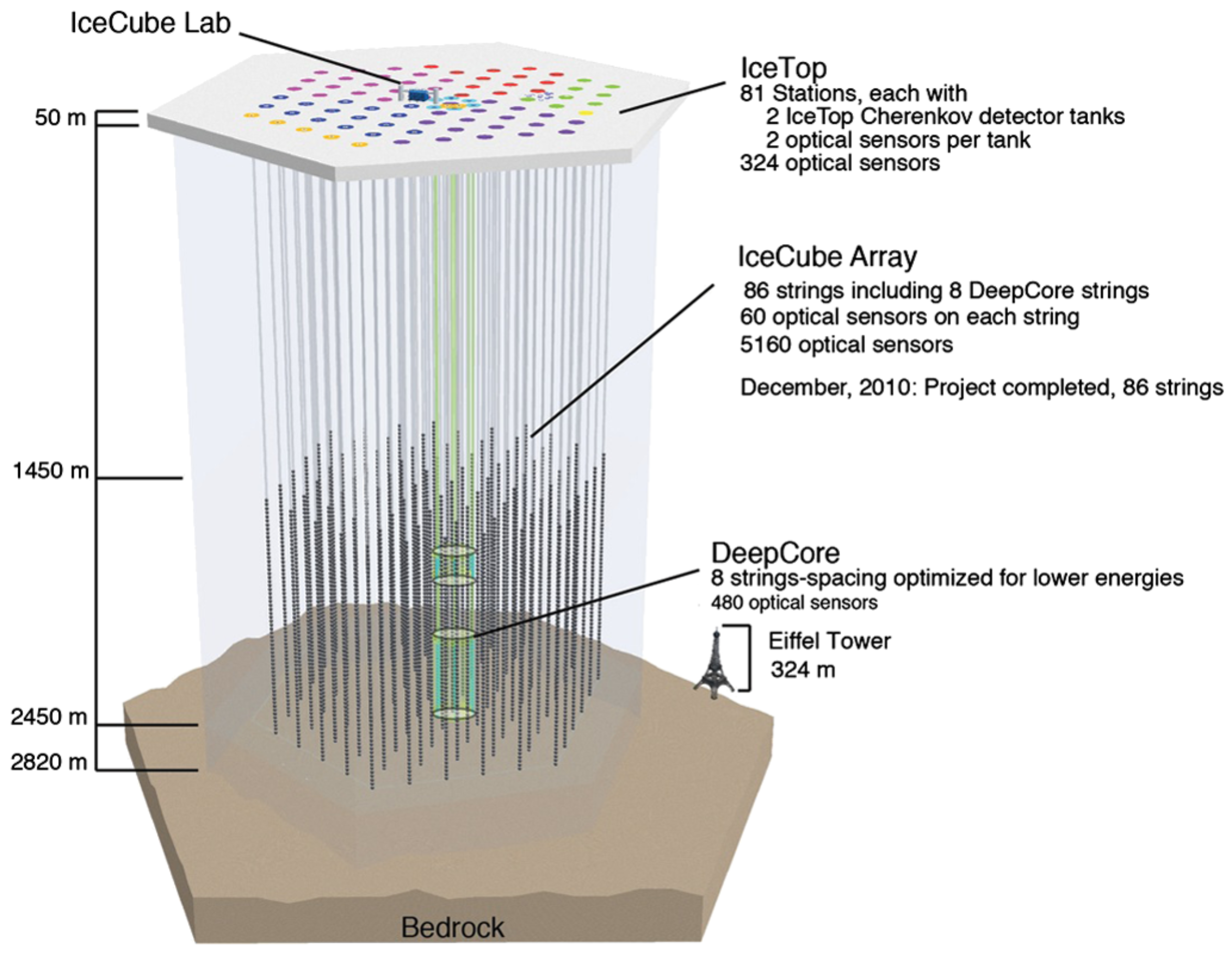
2.2. IceCube
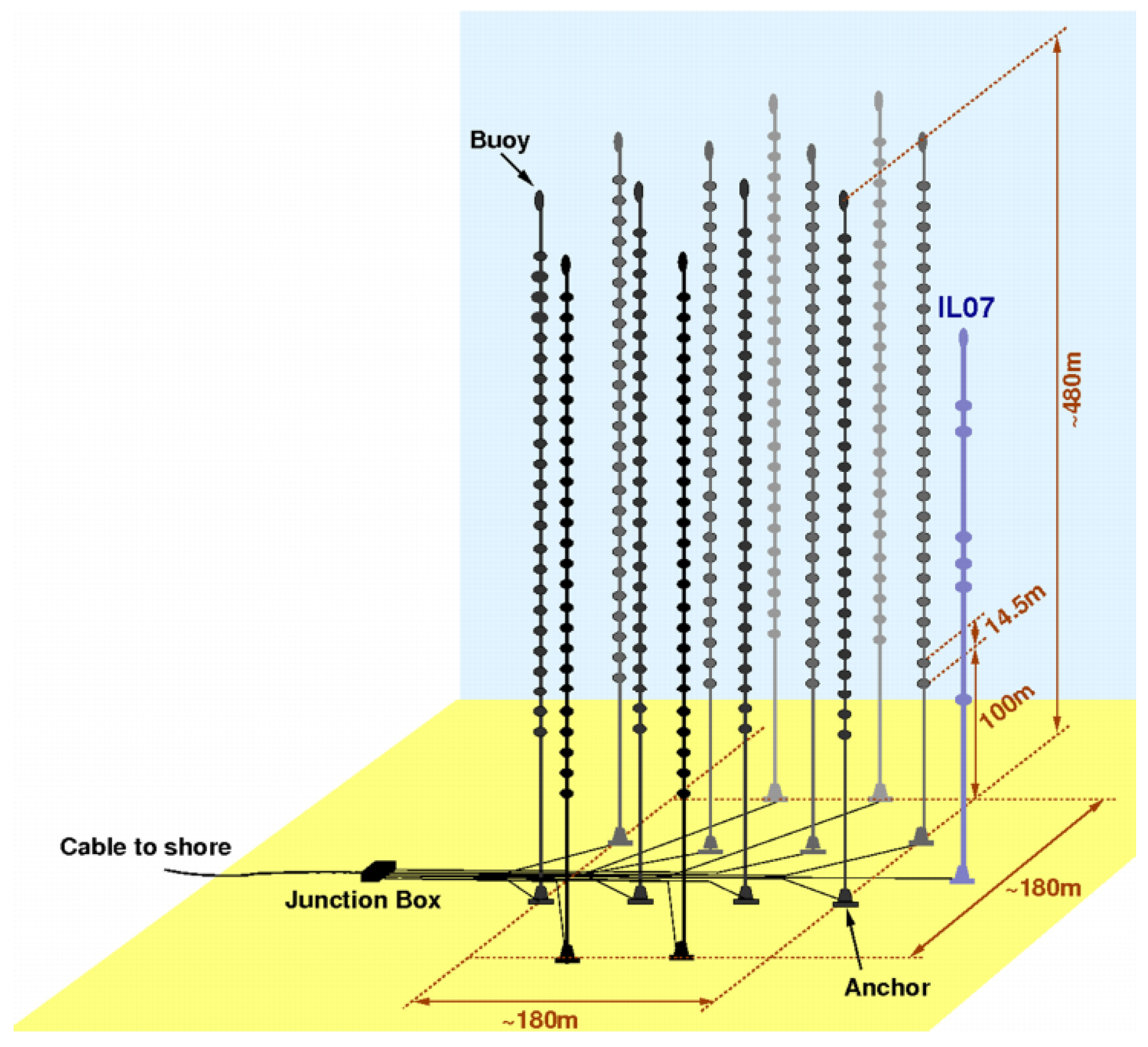
2.3. ANTARES
2.4. Detector Summary
3. Oscillation Analysis of Atmospheric Neutrinos
3.1. Oscillation Parameter Determination
3.1.1. Super-Kamiokande
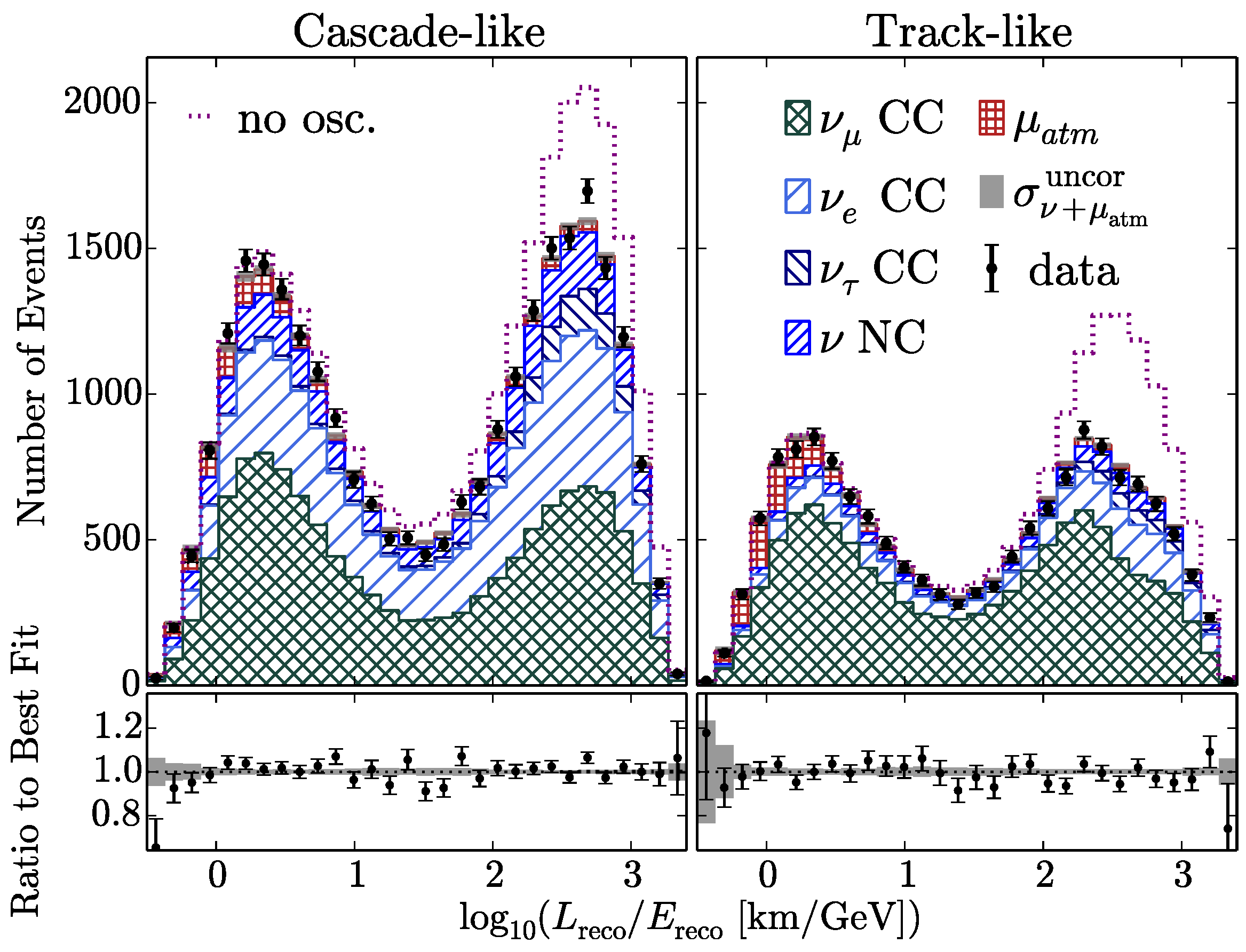
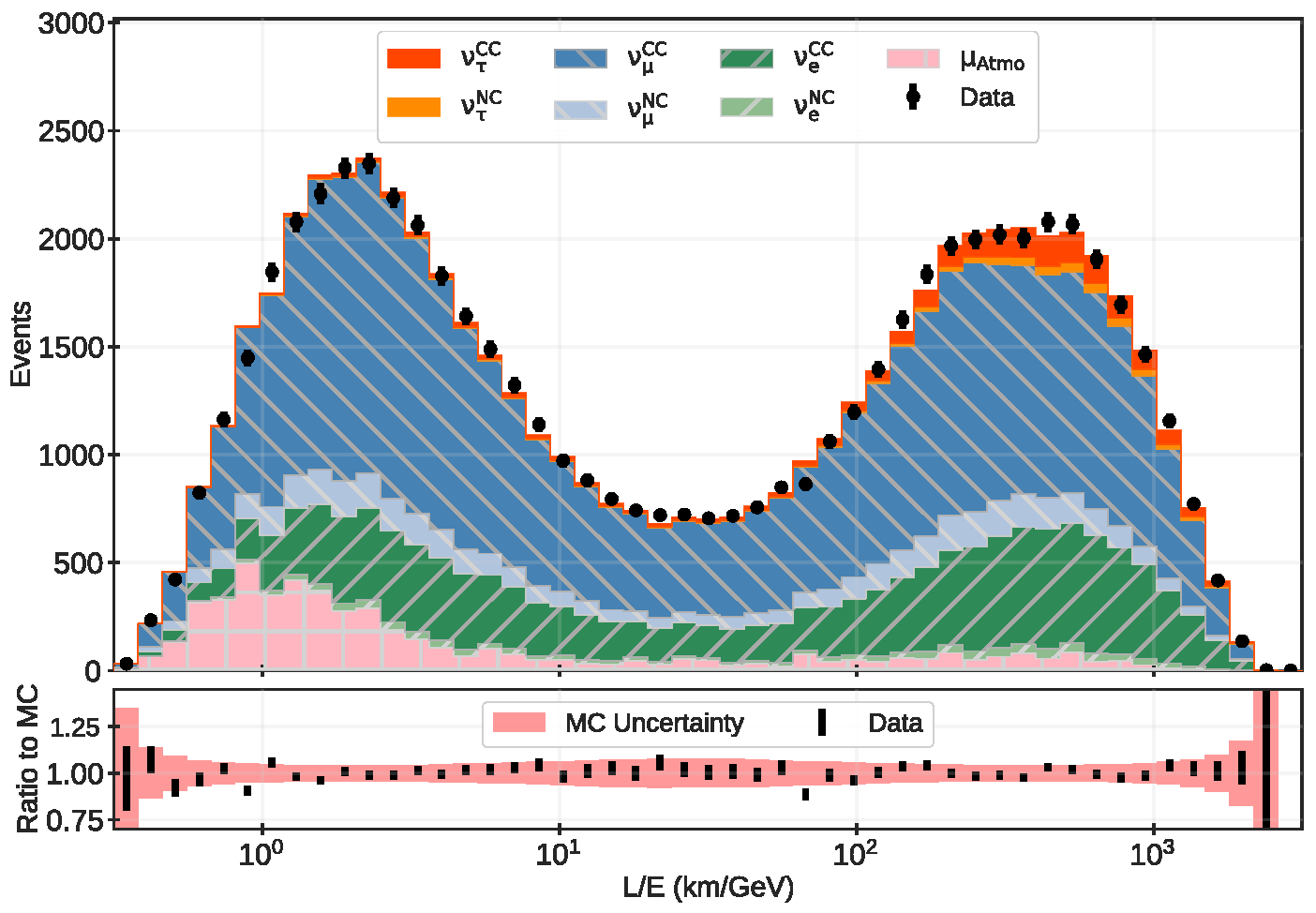
3.1.2. IceCube
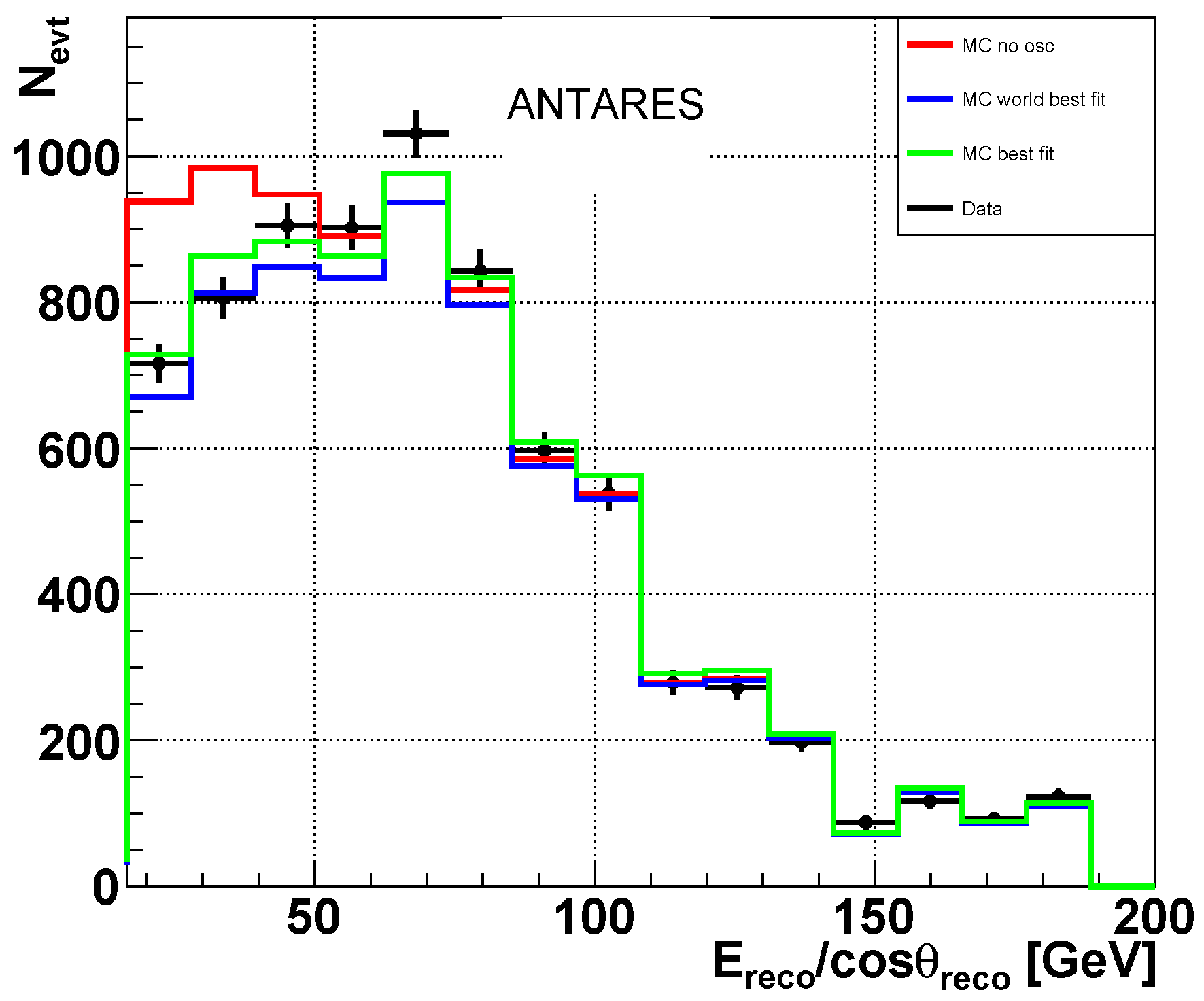
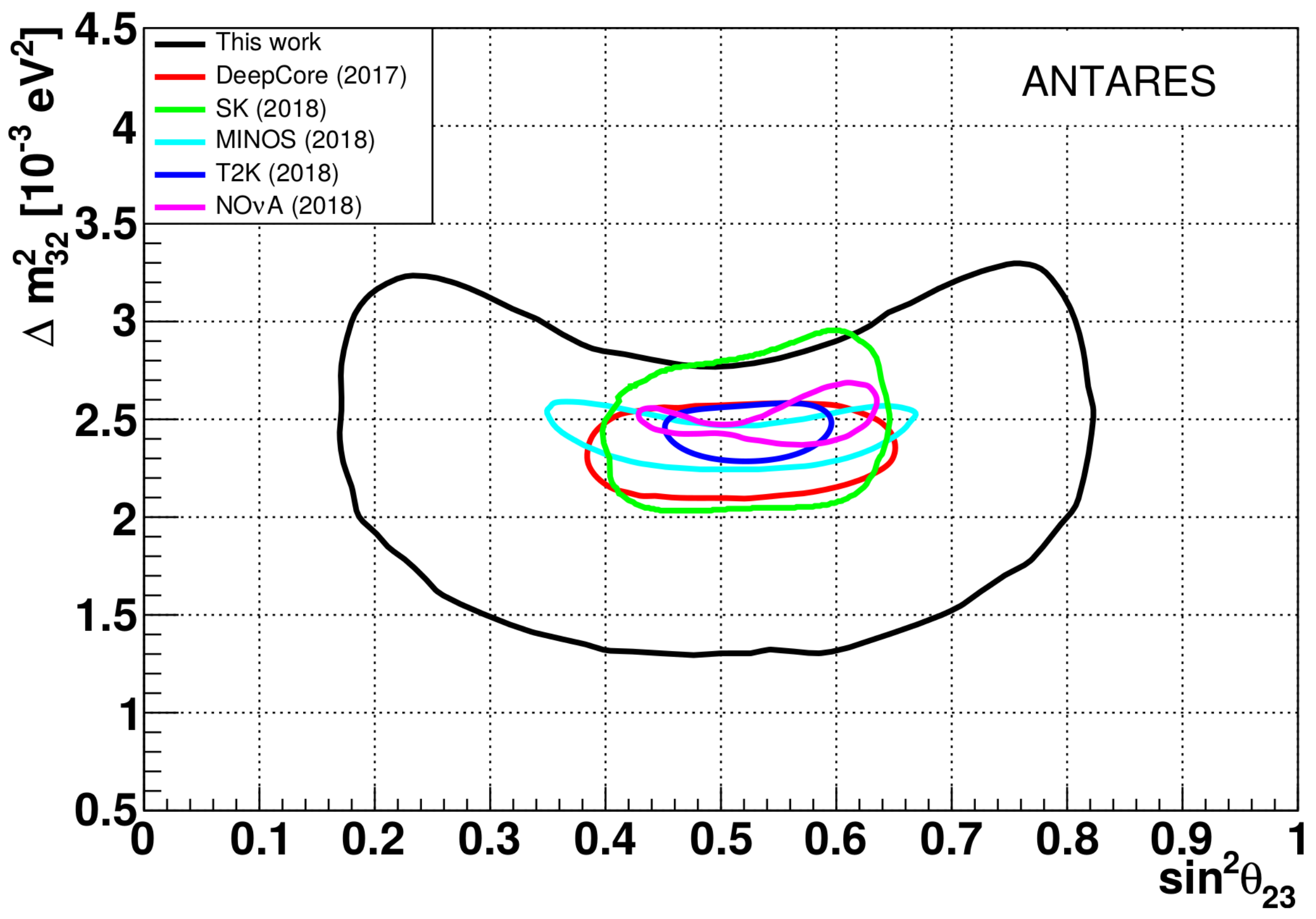
3.1.3. ANTARES
3.1.4. Constraints on and
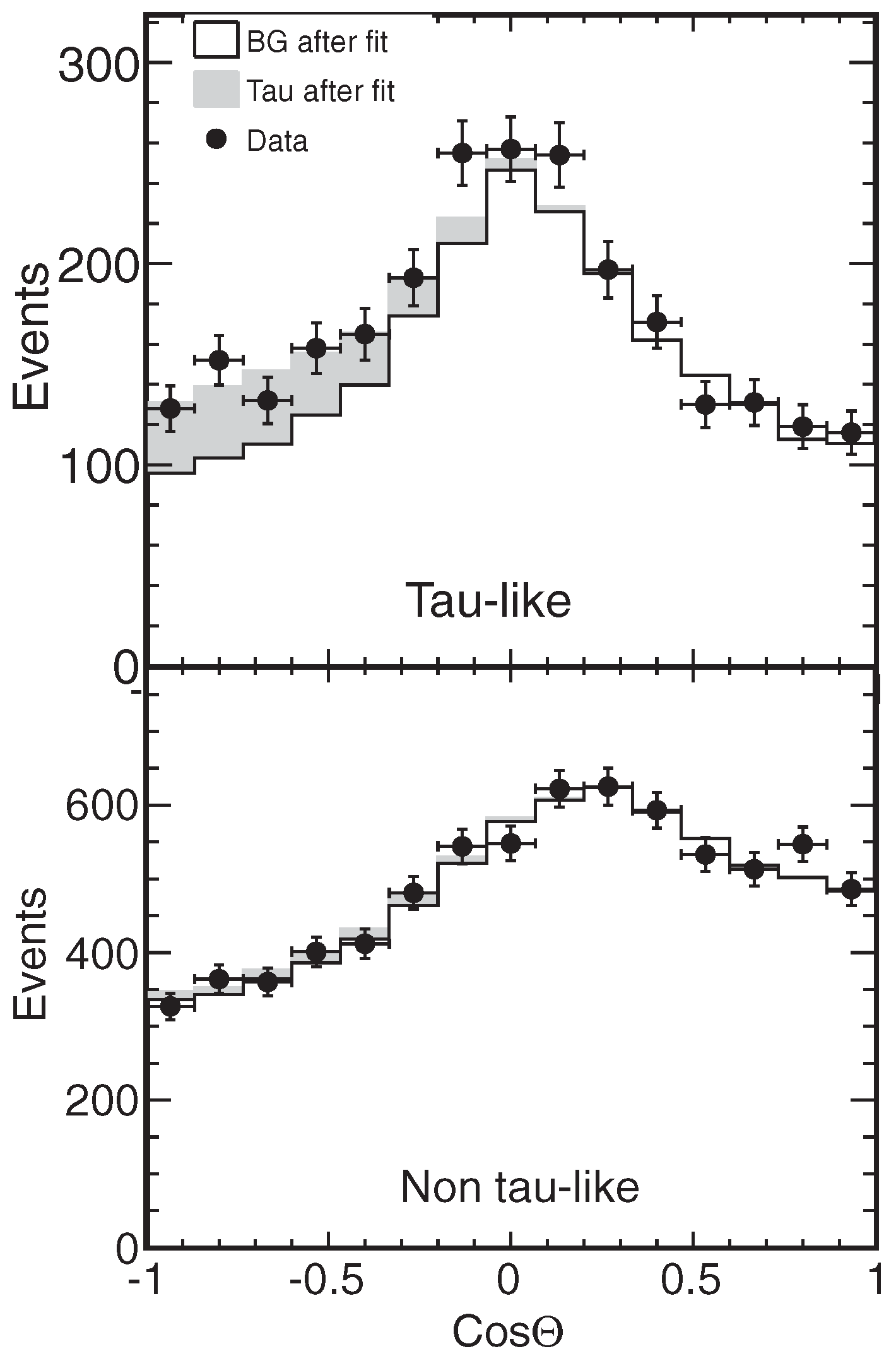
3.2. Tau-Neutrino Appearance
3.2.1. Super-Kamiokande
3.2.2. IceCube
3.3. Sterile Neutrino Analysis
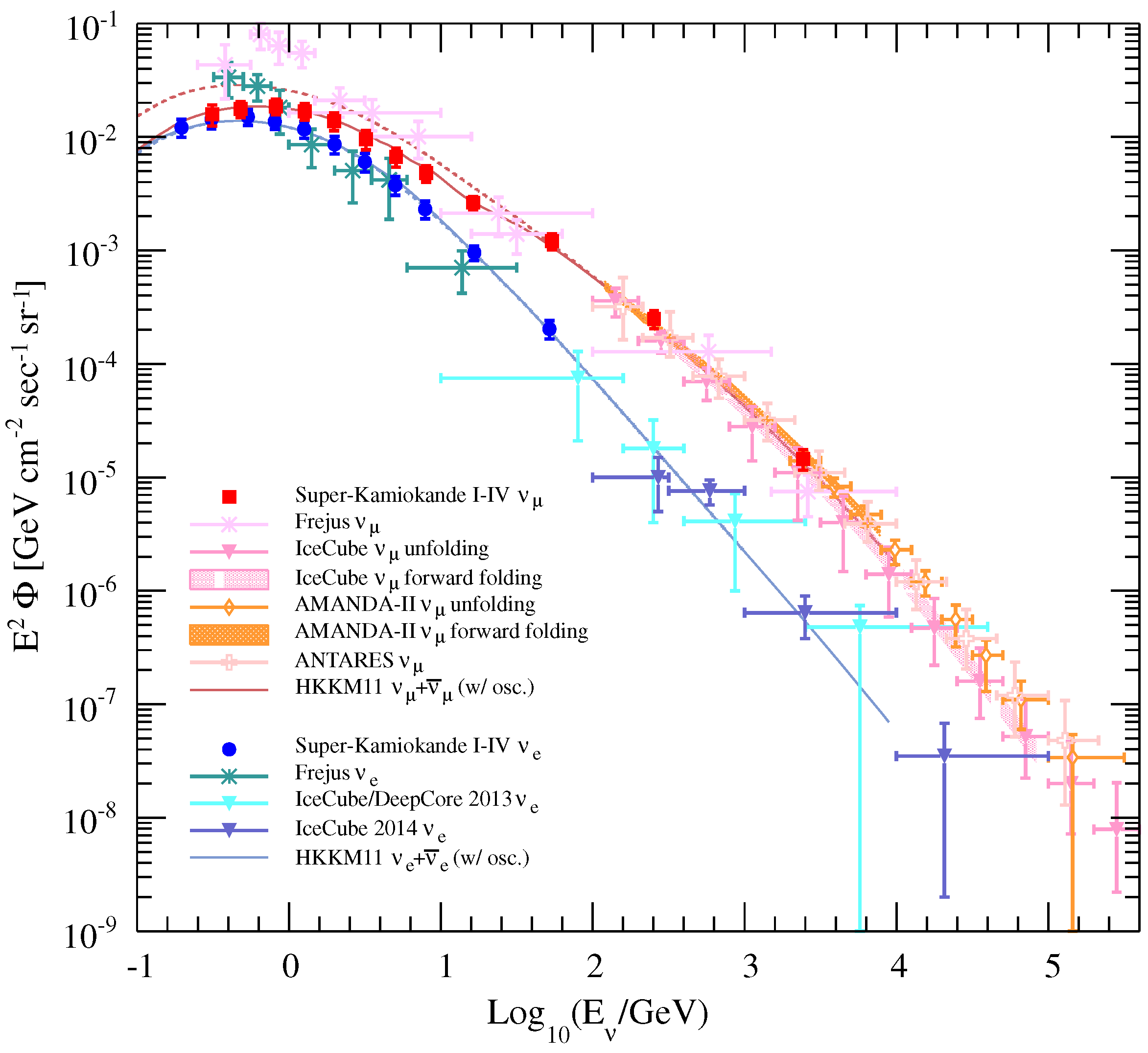
4. Atmospheric Neutrino Flux Measurements
5. Future Prospects
6. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Gaisser, T.K.; Honda, M. Flux of Atmospheric Neutrinos. Annu. Rev. Nucl. Part. Sci. 2002, 52, 153–199. [Google Scholar] [CrossRef] [Green Version]
- Markov, M.A.; Zheleznykh, I.M. On high energy neutrino physics in cosmic rays. Nucl. Phys. 1961, 27, 385–394. [Google Scholar] [CrossRef]
- Greisen, K. Cosmic ray showers. Annu. Rev. Nucl. Sci. 1960, 10, 63–108. [Google Scholar] [CrossRef]
- Achar, C.V.; Menon, M.G.K.; Narasimham, V.S.; Murthy, P.V.; Sreekantan, B.V.; Hinotani, K.; Miyake, S.; Creed, D.R.; Osbonee, J.L.; Pattison, J.B.M. Detection of muons produced by cosmic ray neutrinos deep underground. Phys. Lett. 1965, 18, 196–199. [Google Scholar] [CrossRef]
- Reines, F.; Crouch, M.F.; Jenkins, T.L.; Kropp, W.R.; Gurr, H.S.; Smith, G.R.; Sellschop, J.P.F.; Meyer, B. Evidence for High-Energy Cosmic-Ray Neutrino Interactions. Phys. Rev. Lett. 1965, 15, 429–433. [Google Scholar] [CrossRef]
- Hirata, K.S.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation of a neutrino burst from the supernova SN1987A. Phys. Rev. Lett. 1987, 58, 1490–1493. [Google Scholar] [CrossRef]
- Hirata, K.S.; Inoue, K.; Kajita, T.; Kifune, T.; Kihara, K.; Nakahata, M.; Nakamura, K.; Ohara, S.; Sato, N.; Suzuki, Y.; et al. Results from one thousand days of real-time, directional solar-neutrino data. Phys. Rev. Lett. 1990, 65, 1297–1300. [Google Scholar] [CrossRef]
- Davis, R., Jr.; Harmer, D.S.; Hoffman, K.C. Search for Neutirnos from the Sun. Phys. Rev. Lett. 1968, 20, 1205–1209. [Google Scholar] [CrossRef]
- Bahcall, J.N. Neutrino Astrophysics; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Hirata, K.S.; Kajita, T.; Koshiba, M.; Nakahata, M.; Ohara, S.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y. Experimental study of the atmospheric neutrino flux. Phys. Lett. B 1988, 205, 416–420. [Google Scholar] [CrossRef]
- Fukuda, Y.; Hayakawa, T.; Inoue, K.; Ishida, T.; Joukou, S.; Kajita, T.; Kasuga, S.; Koshio, Y.; Kumita, T.; Matsumoto, K.; et al. Atmospheric νμ/νe ratio in the multi-GeV energy range. Phys. Lett. B 1994, 335, 237–245. [Google Scholar] [CrossRef]
- Casper, D.; Becker-Szendy, R.; Bratton, C.B.; Cady, D.R.; Claus, R.; Dye, S.T.; Gajewski, W.; Goldhaber, M.; Haines, T.J.; Halverson, P.G.; et al. Measurement of atmospheric neutrino composition with the IMB-3 detector. Phys. Rev. Lett. 1991, 66, 2561–2564. [Google Scholar] [CrossRef] [PubMed]
- Becker-Szendy, R.; Bratton, C.B.; Casper, D.; Dye, S.T.; Gajewski, W.; Goldhaber, M.; Haines, T.J.; Halverson, P.G.; Kielczewska, D.; Kropp, W.R.; et al. Electron- and muon-neutrino content of the atmospheric flux. Phys. Rev. D 1992, 46, 3720–3724. [Google Scholar] [CrossRef] [PubMed]
- Berger, C.; Froehlich, M.; Moench, H.; Nisius, R.; Raupach, F.; Schleper, P.; Benadjal, Y.; Blum, D.; Bourdarios, C.; Dudelzak, B.; et al. Study of atmospheric neutrino interactions with the Frejus detector. Phys. Lett. B 1989, 227, 489–494. [Google Scholar] [CrossRef]
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; Kameda, J.; Kasuga, S.; et al. Evidence for Oscillation of Atmospheric Neutrinos. Phys. Rev. Lett. 1998, 81, 1562–1567. [Google Scholar] [CrossRef] [Green Version]
- Ambrosio, M.; Antolini, R.; Auriemma, G.; Bakari, D.; Baldini, A.; Barbarino, G.C.; Barish, B.C.; Battistoni, G.; Bellotti, R.; Bemporad, C.; et al. Low energy atmospheric muon neutrinos in MACRO. Phys. Lett. B 2000, 478, 5–13. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, M.; Allison, W.W.M.; Alner, G.J.; Ayres, D.S.; Barrett, W.L.; Border, P.M.; Cobb, J.H.; Cockerill, D.J.A.; Courant, H.; Demuth, D.M.; et al. Measurement of the L/E distributions of atmospheric ν in Soudan 2 and their interpretation as neutrino oscillations. Phys. Rev. D 2003, 68, 113004. [Google Scholar] [CrossRef] [Green Version]
- Enberg, R.; Reno, M.H.; Sarcevic, I. Prompt neutrino fluxes from atmospheric charm. Phys. Rev. D 2008, 78, 043005. [Google Scholar] [CrossRef] [Green Version]
- Sinegovskaya, T.S.; Morozova, A.D.; Sinegovsky, S.I. High-energy neutrino fluxes and flavor ratio in the Earth’s atmosphere. Phys. Rev. D 2015, 91, 063011. [Google Scholar] [CrossRef] [Green Version]
- Honda, M.; Kajita, T.; Kasahara, K.; Midorikawa, S. Improvement of low energy atmospheric neutrino flux calculation using the JAM nuclear interaction model. Phys. Rev. D 2011, 83, 123001. [Google Scholar] [CrossRef] [Green Version]
- Barr, G.; Gaisser, T.; Robbins, S.; Stanev, T. Three-dimensional calculation of atmospheric neutrinos. Phys. Rev. D 2004, 70, 023006. [Google Scholar] [CrossRef] [Green Version]
- Battistoni, G.; Ferrari, A.; Montaruli, T.; Sala, P. The FLUKA atmospheric neutrino flux calculation. Astropart. Phys. 2003, 19, 269–290. [Google Scholar] [CrossRef] [Green Version]
- Honda, M.; Kajita, T.; Kasahara, K.; Midorikawa, S.; Sanuki, T. Calculation of atmospheric neutrino flux using the interaction model calibrated with atmospheric muon data. Phys. Rev. D 2007, 75, 043006. [Google Scholar] [CrossRef] [Green Version]
- Hayato, Y. Neut. Nucl. Phys. B Proc. Suppl. 2002, 112, 171–176. [Google Scholar] [CrossRef]
- Llewellyn Smith, C.H. Neutrino reactions at accelerator energies. Phys. Rep. 1972, 3, 261–379. [Google Scholar] [CrossRef]
- Smith, R.A.; Moniz, E.J. Neutrino reactions on nuclear targets. Nucl. Phys. 1972, B43, 605–622. [Google Scholar] [CrossRef]
- Bradford, R.; Bodek, A.; Budd, H.S.; Arrington, J. A New Parameterization of the Nucleon Elastic Form Factors. Nucl. Phys. B Proc. Suppl. 2006, 159, 127–132. [Google Scholar] [CrossRef] [Green Version]
- Nieves, J.; Amaro, J.E.; Valverde, M. Inclusive quasielastic charged-current neutrino-nucleus reactions. Phys. Rev. C 2004, 70, 055503. [Google Scholar] [CrossRef] [Green Version]
- Rein, D.; Sehgal, L.M. Neutrino-excitation of baryon resonances and single pion production. Ann. Phys. 1981, 133, 79–153. [Google Scholar] [CrossRef]
- Graczyk, K.M.; Sobczyk, J.T. Form factors in the quark resonance model. Phys. Rev. D 2008, 77, 053001. [Google Scholar] [CrossRef] [Green Version]
- Barish, S.J.; Campbell, J.; Charlton, G.; Cho, Y.; Derrick, M.; Engelmann, R.; Hyman, L.G.; Jankowski, D.; Mann, A.; Musgrave, B.; et al. Study of neutrino interactions in hydrogen and deuterium: Description of the experiment and study of the reaction ν+d→μ−+p+Ps. Phys. Rev. D 1977, 16, 3103–3121. [Google Scholar] [CrossRef]
- Bonetti, S.; Carnesecchi, G.; Cavalli, D.; Negri, P.; Pullia, A.; Rollier, M.; Romano, F.; Schira, R. Study of Quasielastic Reactions of Neutrino and anti-neutrino in Gargamelle. Nuovo Cim. A 1977, 38, 260–270. [Google Scholar] [CrossRef]
- Ciampolillo, S.; Degrange, B.; Dewit, M.; François, T.; Haidt, D.; Jaffre, M.; Longuemare, C.; Matteuzzi, C.; Mattioli, F.; Pattison, J.B.M.; et al. Total cross section for neutrino charged current interactions at 3 GeV and 9 GeV. Phys. Lett. B 1979, 84, 281–284. [Google Scholar] [CrossRef] [Green Version]
- Armenise, N.; Erriquez, O.; Fogli Muciaccia, M.Y.; Nuzzo, S.; Ruggieri, F.; Halsteinslid, A.; Myklebost, K.; Rognebakke, A.; Skjeggestad, O.; Bonetti, S.; et al. Charged current elastic antineutrino interactions in propne. Nucl. Phys. B 1979, 152, 365–375. [Google Scholar] [CrossRef]
- Belikov, S.V.; Bygorsky, A.P.; Klimenko, L.A.; Kochetkov, V.I.; Kurbakov, V.I.; Mukhin, A.I.; Perelygin, V.F.; Shestermanov, K.E.; Sviridov, Y.M.; Volkov, A.A.; et al. Quasielastic neutrino and antineutrino scattering total cross-sections, axial-vector from-factor. Z. Phys. A 1985, 320, 625–633. [Google Scholar] [CrossRef] [Green Version]
- Radecky, G.M.; Barnes, V.E.; Carmony, D.D.; Garfinkel, A.F.; Derrick, M.; Fernandez, E.; Hyman, L.; Levman, G.; Koetke, D.; Musgrave, B.; et al. Study of single-pion production by weak charged currents in low-energy νd interactions. Phys. Rev. D 1982, 25, 1161–1173. [Google Scholar] [CrossRef]
- Kitagaki, T.; Yuta, H.; Tanaka, S.; Yamaguchi, A.; Abe, K.; Hasegawa, K.; Tamai, K.; Kunori, S.; Otani, Y.; Hayano, H.; et al. Charged-current exclusive pion production in neutrino-deuterium interactions. Phys. Rev. D 1986, 34, 2554–2565. [Google Scholar] [CrossRef]
- Auchincloss, P.S.; Blair, R.; Haber, C.; Oltman, E.; Leung, W.C.; Ruiz, M.; Mishra, S.R.; Quintas, P.Z.; Sciulli, F.J.; Shaevitz, M.H.; et al. Measurement of the inclusive charged-current cross section for neutrino and antineutrino scattering on isoscalar nucleons. Z. Phys. C 1990, 48, 411–431. [Google Scholar] [CrossRef]
- Berge, J.P.; Blondel, A.; Böckmann, P.; Burkhardt, H.; Dydak, F.; De Groot, J.G.H.; Grant, A.L.; Hagelberg, R.; Hughes, E.W.; Krasny, M.; et al. Total neutrino and antineutrino charged current cross section measurements in 100, 160, and 200 GeV narrow band beams. Z. Phys. C 1987, 35, 443–452. [Google Scholar] [CrossRef] [Green Version]
- Anikeev, V.B.; Belikov, S.V.; Borisov, A.A.; Bozhko, N.I.; Bugorsky, A.P.; Chernichenko, S.K.; Goryachev, V.N.; Gurgiev, S.N.; Kirsanov, M.M.; Kononov, A.I.; et al. Total cross section measurements for charged current interactions in 3 - 30 GeV energy range with IHEP-JINR neutrino detector. Z. Phys. C 1996, 70, 39–46. [Google Scholar] [CrossRef]
- Vovenko, A.S.; Volkov, A.A.; Zhigunov, V.P.; Mukhin, A.I.; Perelygin, V.F.; Shestermanov, K.E. Energy Dependence of Total Cross-sections for Neutrino and Anti-neutrino Interactions at Energies Below 35 GeV. Sov. J. Nucl. Phys. 1979, 30, 1014–1017. [Google Scholar]
- MacFarlane, D.; Purohit, M.V.; Messner, R.L.; Novikoff, D.B.; Blair, R.E.; Sciulli, F.J.; Shaevitz, M.H.; Fisk, H.E.; Fukushima, Y.; Jin, B.N.; et al. Nucleon structure functions from high energy neutrino interactions with iron and QCD results. Z. Phys. C 1984, 26, 1–12. [Google Scholar] [CrossRef]
- Baker, N.; Connolly, P.L.; Kahn, S.A.; Murtagh, M.J.; Palmer, R.B.; Samios, N.P.; Tanaka, M. Total cross sections for νμn and νμp charged-current interactions in the 7-foot bubble chamber. Phys. Rev. D 1982, 25, 617–623. [Google Scholar] [CrossRef]
- Pontecorvo, B. Neutrino Experiments and the Problem of Conservation of Leptonic Charge. J. Exp. Theor. Phys. 1968, 26, 984–988. [Google Scholar]
- Maki, Z.; Nakagawa, M.; Sakata, S. Remarks on the Unified Model of Elementary Particles. Prog. Theor. Phys. 1962, 28, 870–880. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, K.; Particle Data Group. Review of Particle Physics. J. Phys. G 2010, 37, 075021. [Google Scholar] [CrossRef] [Green Version]
- Barger, V.; Whisnant, K.; Pakvasa, S.; Phillips, R.J.N. Matter effects on three-neutrino oscillations. Phys. Rev. D 1980, 22, 2718–2726. [Google Scholar] [CrossRef]
- Abe, K.; Bronner, C.; Haga, Y.; Hayato, Y.; Ikeda, M.; Iyogi, K.; Kameda, J.; Kato, Y.; Kishimoto, Y.; Marti, L.; et al. Atmospheric neutrino oscillation analysis with external constraints in Super-Kamiokande I-IV. Phys. Rev. D 2018, 97, 072001. [Google Scholar] [CrossRef] [Green Version]
- Fukuda, S.; Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Ishitsuka, M.; Itow, Y.; Kajita, T.; Kameda, J.; Kaneyuki, K.; Kasuga, S.; et al. The Super-Kamiokande detector. Nucl. Instrum. Meth. 2003, A501, 418–462. [Google Scholar] [CrossRef]
- Nishino, H.; Awai, K.; Hayato, Y.; Nakayama, S.; Okumura, K.; Shiozawa, M.; Takeda, A.; Ishikawa, K.; Minegishi, A.; Arai, Y.; et al. High-speed charge-to-time converter ASIC for the Super-Kamiokande detector. Nucl. Instrum. Meth. A 2009, 610, 710–717. [Google Scholar] [CrossRef] [Green Version]
- Ashie, Y.; Hosaka, J.; Ishihara, K.; Itow, Y.; Kameda, J.; Koshio, Y.; Minamino, A.; Mitsuda, C.; Miura, M.; Moriyama, S.; et al. Measurement of atmospheric neutrino oscillation parameters by Super-Kamiokande I. Phys. Rev. D 2005, 71, 112005. [Google Scholar] [CrossRef] [Green Version]
- Aartsen, M.G.; Abbasi, R.; Abdou, Y.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Auffenberg, J.; Bai, X.; et al. First Observation of PeV-Energy Neutrinos with IceCube. Phys. Rev. Lett. 2013, 111, 021103. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Andeen, K.; Auffenberg, J.; Bai, X.; et al. Search for a diffuse flux of astrophysical muon neutrinos with the IceCube 40-string detector. Phys. Rev. D 2011, 84, 082001. [Google Scholar] [CrossRef] [Green Version]
- Ageron, M.; Aguilar, J.A.; Al Samarai, I.; Albert, A.; Ameli, F.; André, M.; Anghinolfi, M.; Anton, G.; Anvar, S.; Ardid, M.; et al. ANTARES: The first undersea neutrino telescope. Nucl. Instrum. Meth. A 2011, 656, 11–38. [Google Scholar] [CrossRef]
- Olive, K.A.; Particle Data Group. Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Abe, K.; Abgrall, H.; Aihara, Y.; Ajima, J.B.; Albert, D.; Allan, P.-A.; Amaudruz, C.; Andreopoulos, B.; Andrieu, M.D.; Anerella, C.; et al. The T2K experiment. Nucl. Instrum. Meth. A 2011, 659, 106–135. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Measurement of Atmospheric Neutrino Oscillations at 6-56 GeV with IceCube DeepCore. Phys. Rev. Lett. 2018, 120, 071801. [Google Scholar] [CrossRef] [Green Version]
- The ANTARES Collaboration. Measuring the atmospheric neutrino oscillation parameters and constraining the 3+1 neutrino model with ten years of ANTARES data. J. High Energy Phys. 2019, 6, 113. [Google Scholar]
- Wascko, M. T2K Status, Results, and Plans. Available online: https://doi.org/10.5281/zenodo.1286752 (accessed on 5 May 2020).
- Sanchez, M. NOvA Results and Prospects. Available online: https://doi.org/10.5281/zenodo.1286758 (accessed on 5 May 2020).
- Aurisano, A. Recent Results from MINOS and MINOS+. 2018. Available online: https://doi.org/10.5281/zenodo.1286760 (accessed on 5 May 2020).
- Agafanova, N.; Alexandrov, A.; Anokhina, A.; Aoki, S.; Ariga, A.; Ariga, T.; Bertolin, A.; Bozza, C.; Brugnera, R.; Buonaura, A.; et al. Final Results of the OPERA Experiment on ντ Appearance in the CNGS Neutrino Beam. Phys. Rev. Lett. 2018, 120, 211801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Abe, K.; Bronner, C.; Hayato, Y.; Ikeda, M.; Iyogi, K.; Kameda, J.; Kato, Y.; Kishimoto, Y.; Marti, L.; et al. Measurement of the tau neutrino cross section in atmospheric neutrino oscillations with Super-Kamiokande. Phys. Rev. D 2018, 98, 052006. [Google Scholar] [CrossRef] [Green Version]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Andeen, K.; Anderson, T.; Ansseau, I.; et al. Measurement of atmospheric tau neutrino appearance with IceCube DeepCore. Phys. Rev. D 2019, 99, 032007. [Google Scholar] [CrossRef] [Green Version]
- Aguilar, A.; Auerbach, L.B.; Burman, R.L.; Caldwell, D.O.; Church, E.D.; Cochran, A.K.; Donahue, J.B.; Fazely, A.; Garvey, G.T.; Gunasingha, R.M.; et al. Evidence for neutrino oscillations from the observation of appearance in a beam. Phys. Rev. D 2001, 64, 112007. [Google Scholar] [CrossRef] [Green Version]
- Aguilar-Arevalo, A.A. Improved Search for → Oscillations in the MiniBooNE Experiment. Phys. Rev. Lett. 2013, 110, 161801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mention, G.; Fechner, M.; Lasserre, T.; Mueller, T.; Lhuillier, D.; Cribier, M.; Letourneau, A. Reactor antineutrino anomaly. Phys. Rev. D 2011, 83, 073006. [Google Scholar] [CrossRef] [Green Version]
- Abdurashitov, J.N. Measurement of the response of a Ga solar neutrino experiment to neutrinos from a 37 Ar source. Phys. Rev. C 2006, 73, 045805. [Google Scholar] [CrossRef] [Green Version]
- Schael, S. (ALEPH Collaboration, DELPHI Collaboration, L3 Collaboration, OPAL Collaboration, SLD Collaboration, LEP Electroweak Working Group, SLD Electroweak Group, SLD Heavy Flavour Group), Precision electroweak measurements on the Z resonance. Phys. Rep. 2006, 427, 257. [Google Scholar]
- Abe, K. Limits on sterile neutrino mixing using atmospheric neutrinos in Super-Kamiokande. Phys. Rev. D 2015, 91, 052019. [Google Scholar] [CrossRef] [Green Version]
- Aartsen, M.G. Search for sterile neutrino mixing using three years of IceCube DeepCore data. Phys. Rev. D 2017, 95, 112002. [Google Scholar] [CrossRef] [Green Version]
- Richard, E. Measurements of the atmospheric neutrino flux by Super-Kamiokande: Energy spectra, geomagnetic ffects, and solar modulation. Phys. Rev. D 2016, 94, 052001. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, R. Measurement of the atmospheric neutrino energy spectrum from 100 GeV to 400 TeV with IceCube. Phys. Rev. D 2011, 83, 012001. [Google Scholar] [CrossRef] [Green Version]
- Aartsen, M.G. Measurement of the Atmospheric νe Spectrum with IceCube. Phys. Rev. D 2015, 91, 122004. [Google Scholar] [CrossRef] [Green Version]
- Aartsen, M.G.; Albert, A.; Al Samarai, I.; André, M.; Anghinolfi, M.; Anton, G.; Anvar, S.; Ardid, M.; Astraatmadja, T.; Aubert, J.-J.; et al. Measurement of the Atmospheric νe Flux in IceCube. Phys. Rev. Lett. 2013, 110, 151105. [Google Scholar] [CrossRef]
- Artsen, M.G.; Albert, A.; Al Samarai, I.; André, M.; Anghinolfi, M.; Anton, G.; Anvar, S.; Ardid, M.; Astraatmadja, T.; Aubert, J.-J.; et al. Measurement of the atmospheric νμ energy spectrum from 100 GeV to 200 TeV with the ANTARES telescope. Eur. Phys. J. C 2013, 73, 2606. [Google Scholar]
- Hyper-Kamiokande Proto-Collaboration. Hyper-Kamiokande: Design Report. arXiv 2018, arXiv:1805.04163.
- The Hyper-Kamiokande Proto-Collaboration. Physics potentials with the second Hyper-Kamiokande detector. Prog. Theor. Exp. Phys. 2018, 2018, 063C01. [Google Scholar]
- Aartsen, M.G.; Ackermann, N.; Adams, J.; Aguilar, A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Andeen, K.; Anderson, T.; Ansseau, I.; et al. Neutrino astronomy with the next generation IceCube Neutrino Observatory. arXiv 2019, arXiv:1911.02561. [Google Scholar]
- Ishihara, A. The IceCube Upgrade - Design and Science Goals. Proc. Sci. 2019, ICRC2019, 1031. [Google Scholar]
- Aartsen, M.G. PINGU: A vision for neutrino and particle physics at the South Pole. J. Phys. G 2017, 44, 054006. [Google Scholar] [CrossRef] [Green Version]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Andeen, K.; Anderson, T.; Ansseau, I.; et al. Combined sensitivity to the neutrino mass ordering with JUNO, the IceCube Upgrade, and PINGU. Phys. Rev. D 2020, 101, 032006. [Google Scholar] [CrossRef] [Green Version]
- Adrian-Martinez, S. Letter of intent for KM3NeT 2.0. J. Phys. G Nucl. Part. Phys. 2016, 43, 084001. [Google Scholar] [CrossRef]
- Taiuti, M. KM3NeT: Opening a New Window on Our Universe. 2019. Available online: https://doi.org/10.5281/zenodo.2711479 (accessed on 5 May 2020).
- DUNE Collaboration. Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE): Conceptual Design Report. arXiv 2015, arXiv:1512.06148.





| Detector | Type | Mass (MegaTon) | Future Possibility |
|---|---|---|---|
| Hyper-K | Water Cherenkov (Underground) | 0.187 (fiducial) | Second tank |
| IceCube Upgrade | Water Cherenkov (Ice) | 2 (instrumented) | PINGU |
| KM3NeT/ORCA | Water Cherenkov (Deep-Sea) | 8 (instrumented) | |
| DUNE | Liquid Argon TPC | 0.01 (fiducial for 1st module) | 40 kTon (in final) |
| SK | IceCUBE/DeepCore | ANTARES | |
|---|---|---|---|
| Target | Pure water | Ice | Deep-sea water |
| Volume | 22.5 kTon fiducial | 15 MTon instrumented | 10 MTon instrumented |
| PMT | 11,129 of 20" PMTs for inner | 647 of 10″ PMTs | 885 of 10″ PMTs |
| 1885 of 8″ PMTs for outer | 5160 of 10″ PMTs as veto | ||
| Attenuation length | ∼ 90 m | ∼ 45 m | ∼ 50 m |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koshio, Y. Observation of Atmospheric Neutrinos. Universe 2020, 6, 80. https://doi.org/10.3390/universe6060080
Koshio Y. Observation of Atmospheric Neutrinos. Universe. 2020; 6(6):80. https://doi.org/10.3390/universe6060080
Chicago/Turabian StyleKoshio, Yusuke. 2020. "Observation of Atmospheric Neutrinos" Universe 6, no. 6: 80. https://doi.org/10.3390/universe6060080
APA StyleKoshio, Y. (2020). Observation of Atmospheric Neutrinos. Universe, 6(6), 80. https://doi.org/10.3390/universe6060080





