Genuine Dilatons in Gauge Theories
Abstract
1. Introduction
- a scalar Nambu–Goldstone (NG) boson for exact conformal invariance of a Hamiltonian which has a scale-dependent ground state and hence scale-dependent amplitudes in the limit of scale invariance; or
- a scalar component of the gravitational field; or
- a scalar particle in a theory where conformal invariance is permitted only in the Wigner–Weyl (WW) mode (scale-invariant amplitudes). In terms of a Hamiltonian , scale-dependent effects such as fermion condensation exist only in the presence of a term which breaks scale invariance explicitly in . Both and its ground state are conformal invariant.
2. Hadronic Physics
3. Gauge Theories
- heavy enough to be decoupled, or
- light enough to be part of a chiral perturbation theory, or
- neither.
- (A)
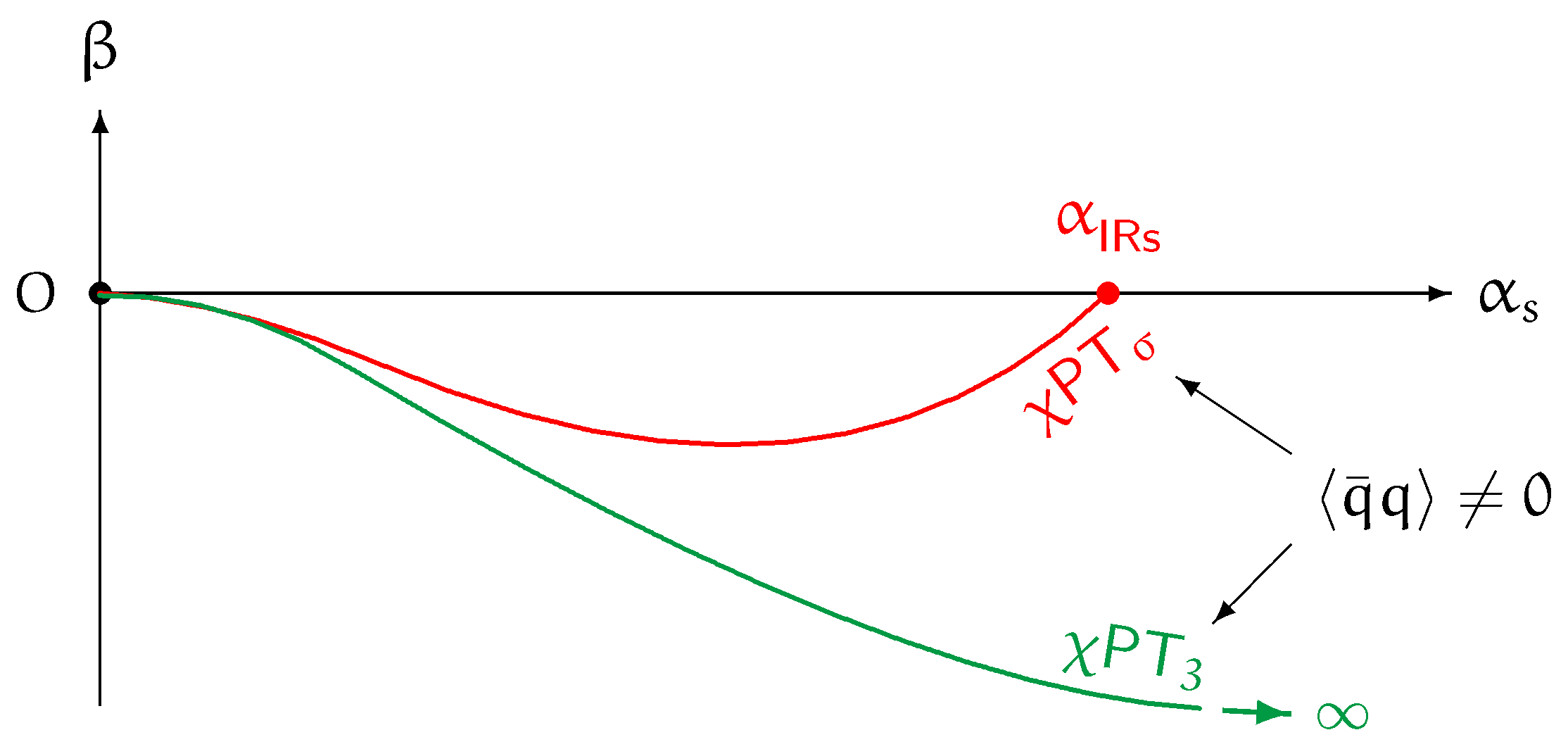
- This is the conventional alternative. The result is the green curve labelled PT in Figure 1, where remains negative and runs to . In that limit, the gluonic part of the trace is still present and breaks conformal invariance explicitly. Apart from the massless bosons , all hadrons, including , acquire their mass through this mechanism. Please note that the chiral condensate survives in this limit.
- (B)
- There is an IRFP at which vanishes and beyond which cannot go (the red curve in Figure 1 labelled PT):As a result, both the gluonic and quark-mass terms in Equation (20) vanish and the theory becomes conformal invariant:Since this is equivalent to the chiral limit (19), the NG bosons and hence the chiral condensate survive, and so acts as a scale condensate. That implies the presence of a massless dilaton at the IRFP, which permits all non-NG hadrons to be massive in the conformal limit (22). Chiral-scale perturbation theory PT is then a simultaneous expansion about and in the masses. Note the desirable scale separation between the NG-boson sector and heavy hadrons in Figure 2.
- (a)
- (b)
- (c)
- There is no light dilaton in hadronic physics because there is no scalar particle nearly degenerate with pions. This overlooks the role of , and comes from TC literature, where all chiral NG bosons are called ”technipions” and none “technikaons” or “technietas”.
- (d)
- (e)
- There may be an IRFP for which would, in analogy with the case , produce a spin- particle with mass , contrary to experiment. An IRFP at is not excluded but, as noted above, a connection with scale invariance can be obtained only by decoupling the s quark, and is a very bad approximation. The argument works only for .
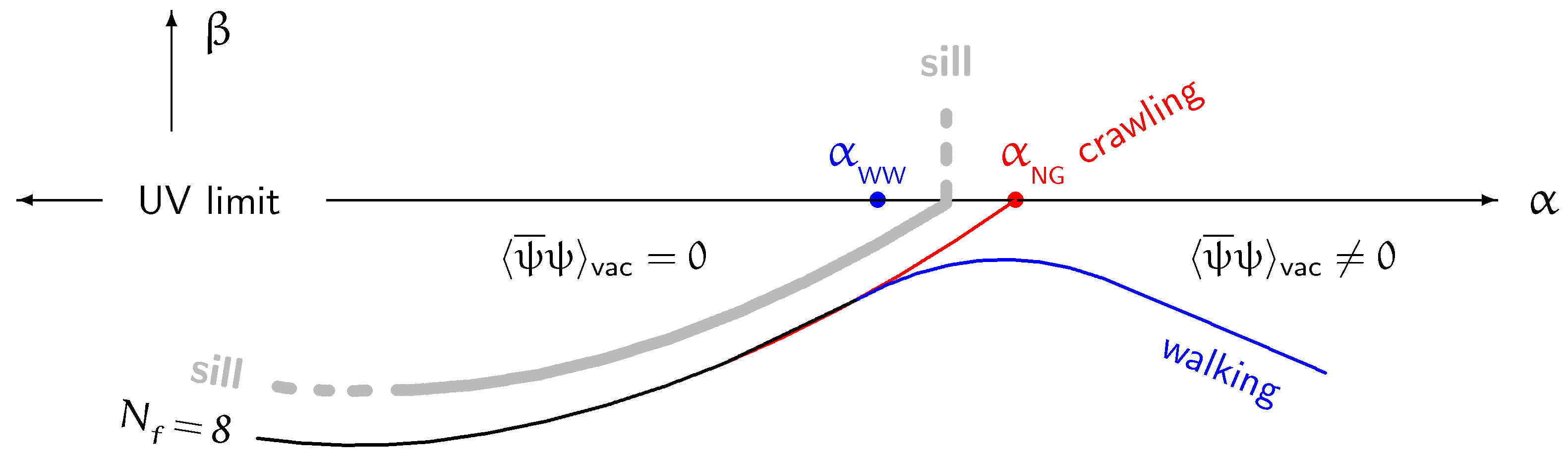
4. Comparison of Crawling and Walking TC
- Gildener and Weinberg (GW) [6] introduced the concept of a spin- “scalon” associated with a flat direction of the potential of a massless gauge theory in the tree approximation. Scale invariance is broken explicitly by one-loop corrections of the Coleman–Weinberg (CW) [64] type. The analysis is entirely consistent, except for a remark that the result is an example of a “spontaneous breaking” of scale invariance4. That is not so: the tree approximation is scale-free by construction, so the invariance is realized in the WW mode. In that limit, the “scalon” is massless but is not a genuine dilaton because it lacks a decay constant connecting to the vacuum. All breaking of conformal invariance is explicit: the one-loop corrections violate scale invariance of the Hamiltonian.
5. Scale Dependence in the Conformal Limit
- Fubini’s analysis is restricted to theories and therefore does not constitute a general proof that strict conformal invariance must be manifest, i.e., in WW mode. To obtain the NG mode for conformal invariance, simply omit the term and add other invariants to such as couplings to chiral NG bosons or (say) the 4-point self-interactionand [1] constrain , e.g., to a half line
- As noted in [1], Fubini’s conclusion was anticipated in 1970 by Zumino (page 472 of [40]), who observed that a dilaton Lagrangian is consistent only if the quartic term vanishes in the conformal limit:Here is a measure of the explicit breaking of conformal symmetry. Equation (35) reflects the fact that, like other genuine NG bosons, type-I dilatons for are massless and cannot self-interact at zero momentum: they correspond to a flat direction of the dilaton potential.
- All dilaton Lagrangians from 1968–1670 which obey Zumino’s rule (35) are counterexamples [32,33,34,37,38,40]: they exist in the limit of exact conformal symmetry and produce amplitudes which depend on a non-arbitrary scale, the dilaton decay constant of Equations (3) and (14). All except [32] allow chiral condensates to exist in the conformal limit .
- The “flat direction” is not associated with a continuum of scales. Instead, it corresponds to the continuum of degenerate vacuum states (13).
- 5.
- Again, the effective Lagrangians above are counterexamples. A tiny scale-violating perturbation can pick out one of the degenerate vacua (stabilization) and produce tiny corrections to the scale-dependent amplitudes and masses of the type-I theory at .
- 6.
- Implicit in this quote is the type-III assumption that there are no scales in the theory, so it is necessary to have a large discontinuity appear “spontaneously” at a small or infinitesimal value of to produce large scales. If the theory is in the WW scaling mode, it does not have scale-degenerate vacua, so there is nothing to stabilize.
- 7.
- The large discontinuity is a problem for type-III phenomenology, because is such a bad approximation.
6. Scale Dependence at an IRFP
- It is relatively easy to find scale-free IRFPs on the lattice: Green’s functions exhibit power-law behavior in the conformal window. That does not test the possibility of IRFP’s outside the conformal window (Section 7).
- There is a belief that dimensional transmutation, which produces nonperturbative scales like or , implies . If true, that would exclude scale dependence at IRFPs.
- (a)
- RG-invariant scales induced by the renormalization scale of ,where is a dimensionless constant that depends on but not on or . Examples of for massless QCD are non-NG hadron masses such as and dimensional constants like and , and for TC, their counterparts such as and .
- (b)
- The trace anomaly which, if present, is also induced by .
7. Nonperturbative Tests of Type-I Theories
- A true analogue of the Gell-Mann–Low function for quantum electrodynamics [72] is assumed to exist for non-Abelian gauge theories but is yet to be identified. Prescriptions for the running coupling exist beyond perturbation theory [73], but there is a danger that their properties are artefacts of their definition. We have no analytic proof that any of them runs monotonically and provides an unbiased test of whether the dynamics chooses to have an IRFP or not. The method of effective charges [74,75,76] is nonperturbative, but there are as many definitions as there are physical processes, and it is not obvious which of them has the desired properties all the way to the far infrared.
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IRFP | infrared fixed point |
| QCD | Quantum Chromodynamics |
| PT | chiral-scale perturbation theory |
| TC | Technicolor |
| NG | Nambu–Goldstone |
| WW | Wigner–Weyl |
| PT | chiral perturbation theory |
| PT | chiral perturbation theory |
| UPT | unitarized chiral perturbation theory |
| RG | renormalization group |
| LO | leading order |
| GW | Gildener–Weinberg |
| CW | Coleman–Weinberg |
| UV | ultraviolet |
References
- Catà, O.; Crewther, R.J.; Tunstall, L.C. Crawling technicolor. Phys. Rev. D 2019, 100, 095007. [Google Scholar] [CrossRef]
- Crewther, R.J.; Tunstall, L.C. Origin of ΔI = 1/2 rule for kaon decays: QCD infrared fixed point. arXiv 2012, arXiv:1203.1321. [Google Scholar]
- Crewther, R.J.; Tunstall, L.C. ΔI = 1/2 rule for kaon decays derived from QCD infrared fixed point. Phys. Rev. D 2015, 91, 034016. [Google Scholar] [CrossRef]
- Crewther, R.J.; Tunstall, L.C. Status of chiral-scale perturbation theory. Proc. Sci. 2015, CD15, 132. [Google Scholar] [CrossRef][Green Version]
- Del Debbio, L. IR fixed points in lattice field theories. Int. J. Mod. Phys. A 2014, 29, 1145006. [Google Scholar] [CrossRef]
- Gildener, E.; Weinberg, S. Symmetry breaking and scalar bosons. Phys. Rev. D 1976, 13, 3333–3341. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Leung, C.N.; Love, S.T. Dilaton and chiral-symmetry breaking. Phys. Rev. Lett. 1986, 56, 1230–1233. [Google Scholar] [CrossRef]
- Yamawaki, K.; Bando, M.; Matumoto, K.-I. Scale-invariant hypercolor model and a dilaton. Phys. Rev. Lett. 1986, 56, 1335–1338. [Google Scholar] [CrossRef]
- Holdom, B.; Terning, J. A light dilaton in gauge theories? Phys. Lett. 1987, 187, 357–361. [Google Scholar] [CrossRef]
- Holdom, B.; Terning, J. No light dilaton in gauge theories. Phys. Lett. 1988, 200, 338–342. [Google Scholar] [CrossRef]
- Appelquist, T.; Bai, Y. Light dilaton in walking gauge theories. Phys. Rev. D 2010, 82, 071701. [Google Scholar] [CrossRef]
- Hashimoto, M.; Yamawaki, K. Technidilaton at conformal edge. Phys. Rev. D 2011, 83, 015008. [Google Scholar] [CrossRef]
- Matsuzaki, S.; Yamawaki, K. Dilaton chiral perturbation theory: Determining the mass and decay constant of the technidilaton on the lattice. Phys. Rev. Lett. 2014, 113, 082002. [Google Scholar] [CrossRef] [PubMed]
- Golterman, M.; Shamir, Y. Low-energy effective action for pions and a dilatonic meson. Phys. Rev. D 2016, 94, 054502. [Google Scholar] [CrossRef]
- Golterman, M.; Shamir, Y. Large-mass regime of the dilaton-pion low-energy effective theory. Phys. Rev. D 2018, 98, 056025. [Google Scholar] [CrossRef]
- Meissner, K.A.; Nicolai, H. Conformal symmetry and the standard model. Phys. Lett. B 2007, 648, 312. [Google Scholar] [CrossRef]
- Chang, W.F.; Ng, J.N.; Wu, J.M.S. Shadow Higgs boson from a scale-invariant hidden U(1)s model. Phys. Rev. D 2007, 75, 115016. [Google Scholar] [CrossRef]
- Foot, R.; Kobakhidze, A.; Volkas, R.R. Electroweak Higgs as a pseudo-Goldstone boson of broken scale invariance. Phys. Lett. B 2007, 655, 156. [Google Scholar] [CrossRef]
- Goldberger, W.D.; Grinstein, B.; Skiba, W. Distinguishing the Higgs boson from the dilaton at the Large Hadron Collider. Phys. Rev. Lett. 2008, 100, 111802. [Google Scholar] [CrossRef]
- Vecchi, L. Phenomenology of a light scalar: The dilaton. Phys. Rev. D 2010, 82, 076009. [Google Scholar] [CrossRef]
- Bellazzini, B.; Csáki, C.; Hubisz, J.; Serra, J.; Terning, J. A Higgs-like dilaton. Eur. Phys. J. C 2013, 73, 2333. [Google Scholar] [CrossRef]
- Bellazzini, B.; Csáki, C.; Hubisz, J.; Serra, J.; Terning, J. A naturally light dilaton and a small cosmological constant. Eur. Phys. J. C 2014, 74, 2790. [Google Scholar] [CrossRef] [PubMed]
- Coradeschi, F.; Lodone, P.; Pappadopulo, D.; Rattazzi, R.; Vitale, L. A naturally light dilaton. J. High Energy Phys. 2013, 2013, 057. [Google Scholar] [CrossRef]
- Aoki, Y.; Aoyama, T.; Kurachi, M.; Maskawa, T.; Miura, K.; Nagai, K.I.; Ohki, H.; Rinaldi, E.; Shibata, A.; Yamawaki, K.; et al. [LatKMI Collaboration] Light composite scalar in eight-flavor QCD on the lattice. Phys. Rev. D 2014, 89, 111502(R). [Google Scholar] [CrossRef]
- Aoki, Y.; Aoyama, T.; Bennett, E.; Kurachi, M.; Maskawa, T.; Miura, K.; Nagai, K.I.; Ohki, H.; Rinaldi, E.; Shibata, A.; et al. [LatKMI Collaboration] Light flavor-singlet scalars and walking signals in Nf = 8 QCD on the lattice. Phys. Rev. D 2017, 976, 014508. [Google Scholar] [CrossRef]
- Appelquist, T.; Brower, R.C.; Fleming, G.T.; Hasenfratz, A.; Jin, X.Y.; Kiskis, J.; Neil, E.T.; Osborn, J.C.; Rebbi, C.; Rinaldi, E.; et al. [LSD Collaboration] Strongly interacting dynamics and search for new physics at the LHC. Phys. Rev. D 2016, 93, 114514. [Google Scholar] [CrossRef]
- Appelquist, T.; Brower, R.C.; Fleming, G.T.; Gasbarro, A.; Hasenfratz, A.; Jin, X.Y.; Neil, E.T.; Osborn, J.C.; Rebbi, C.; Rinaldi, E.; et al. [LSD Collaboration] Nonperturbative investigations of SU(3) gauge theory with eight dynamical flavors. Phys. Rev. D 2019, 99, 014509. [Google Scholar] [CrossRef]
- Fodor, Z.; Holland, K.; Kuti, J.; Nogradi, D.; Wong, C.H. Can a light Higgs impostor hide in composite gauge models? Proc. Sci. 2014, LATTICE2013, 062. [Google Scholar] [CrossRef][Green Version]
- Fodor, Z.; Holland, K.; Kuti, J.; Nogradi, D.; Wong, C.H. The twelve-flavor β-function and dilaton tests of the sextet scalar. Eur. Phys. J. Web Conf. 2018, 175, 08015. [Google Scholar] [CrossRef]
- Gell-Mann, M. Symmetries of baryons and mesons. Phys. Rev. 1962, 125, 1067–1084. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Coleman, S.; Jackiw, R. A new improved energy-momentum tensor. Ann. Phys. (N. Y.) 1970, 59, 42–73. [Google Scholar] [CrossRef]
- Freund, P.G.O.; Nambu, Y. Scalar fields coupled to the trace of the energy-momentum tensor. Phys. Rev. 1968, 174, 1741–1743. [Google Scholar] [CrossRef]
- Mack, G. Partially conserved dilatation current. Nucl. Phys. B 1968, 5, 499–507. [Google Scholar] [CrossRef]
- Mack, G.; Salam, A. Finite component field representations of the conformal group. Ann. Phys. (N. Y.) 1969, 53, 174–202. [Google Scholar] [CrossRef]
- Gell-Mann, M. Symmetry violation in hadron physics. In Hawaii 1969, Topical Conference on Particle Physics; Simmons, W.A., Tuan, S.-F., Eds.; Western Periodicals: Los Angeles, CA, USA, 1970; Volume 1, pp. 1–24, reprinted in Hawaii Topical Conferences in Particle Physics—Selected Lectures; Pakvasa S., Tuan, S.F., Eds.; World Scientific Publishing Co.: Singapore, 1983; Volume 1, pp. 161–188. [Google Scholar]
- Georgi, H. Unparticle physics. Phys. Rev. Lett. 2007, 98, 221601. [Google Scholar] [CrossRef] [PubMed]
- Isham, C.J.; Salam, A.; Strathdee, J.A. Broken chiral and conformal symmetry in an effective-Lagrangian formalism. Phys. Rev. D 1970, 2, 685–690. [Google Scholar] [CrossRef]
- Ellis, J.R. Aspects of conformal symmetry and chirality. Nucl. Phys. B 1970, 22, 478–492. [Google Scholar] [CrossRef]
- Crewther, R.J. Broken scale invariance and the width of a single dilaton. Phys. Lett. B 1970, 33, 305–308. [Google Scholar] [CrossRef]
- Zumino, B. Effective Lagrangians and broken symmetries. In Lectures on Elementary Particles and Quantum Field Theory, 1970 Brandeis University Summer Institute in Theoretical Physics; Deser, S., Grisaru, M., Pendleton, H., Eds.; M.I.T. Press: Cambridge, MA, USA, 1971; Volume 2, pp. 437–500. [Google Scholar]
- Carruthers, P. Broken scale invariance in particle physics. Phys. Rep. 1971, 1, 1–39. [Google Scholar] [CrossRef]
- Crewther, R.J. Spontaneous breakdown of conformal and chiral invariance. Phys. Rev. D 1971, 3, 3152–3165, Erratum: Phys. Rev. D 1971, 4, 3814. [Google Scholar] [CrossRef]
- Coleman, S. Dilatations. In Properties of the Fundamental Interactions, Proceedings of the 1971 International Summer School “Ettore Majorana”, Erice, Italy; Zichichi, A., Ed.; Editrice Compositori: Bologna, Italy, 1973; pp. 359–399, Reprinted in Aspects of Symmetry; Cambridge University Press: Cambridge, UK, 1985; Chapter 3, pp. 67–98; Available online: https://www.osti.gov/biblio/4288089 (accessed on 10 July 2020). [CrossRef]
- Crewther, R.J. Nonperturbative evaluation of the anomalies in low-energy theorems. Phys. Rev. Lett. 1972, 28, 1421–1424. [Google Scholar] [CrossRef]
- Chanowitz, M.S.; Ellis, J. Canonical anomalies and broken scale invariance. Phys. Lett. B 1972, 40, 397–400. [Google Scholar] [CrossRef]
- Chanowitz, M.S.; Ellis, J. Canonical trace anomalies. Phys. Rev. D 1973, 7, 2490–2506. [Google Scholar] [CrossRef]
- Caprini, I.; Colangelo, G.; Leutwyler, H. Mass and width of the lowest resonance in QCD. Phys. Rev. Lett. 2006, 96, 132001. [Google Scholar] [CrossRef] [PubMed]
- Törnqvist, N.A.; Roos, M. Confirmation of the sigma meson. Phys. Rev. Lett. 1996, 76, 1575–1578. [Google Scholar] [CrossRef] [PubMed]
- Peláez, J.R. From controversy to precision on the sigma meson: A review on the status of the non-ordinary f0(500) resonance. Phys. Rep. 2016, 658, 1–111. [Google Scholar] [CrossRef]
- Truong, T.N. Chiral perturbation theory and final-state theorem. Phys. Rev. Lett. 1988, 61, 2526–2529. [Google Scholar] [CrossRef]
- Minkowski, P. On The Anomalous Divergence of The Dilatation Current in Gauge Theories. ITP University of Berne preprint 1976, PRINT-76-0813. 1976. Available online: https://www.researchgate.net/profile/Peter_Minkowski/publication/275365591_traceanomaly1976pdf/links/553b40310cf29b5ee4b66a35.pdf (accessed on 10 July 2020).
- Adler, S.L.; Collins, J.C.; Duncan, A. Energy-momentum-tensor trace anomaly in spin 1/2 quantum electrodynamics. Phys. Rev. D 1977, 15, 1712–1721. [Google Scholar] [CrossRef]
- Nielsen, N.K. The energy-momentum tensor in a non-Abelian quark gluon theory. Nucl. Phys. B 1977, 120, 212–220. [Google Scholar] [CrossRef]
- Collins, J.C.; Duncan, A.; Joglekar, S.D. Trace and dilatation anomalies in gauge theories. Phys. Rev. D 1977, 16, 438–449. [Google Scholar] [CrossRef]
- Jaffe, R.L. Multiquark hadrons. I. Phenomenology of Q2Q¯2 mesons. Phys. Rev. D 1977, 15, 267–280. [Google Scholar] [CrossRef]
- Salam, A.; Strathdee, J. Nonlinear realizations. II. Conformal symmetry. Phys. Rev. 1969, 184, 1760–1768. [Google Scholar] [CrossRef]
- Weinberg, S. Implications of dynamical symmetry breaking. Phys. Rev. D 1976, 13, 974–996. [Google Scholar] [CrossRef]
- Weinberg, S. Implications of dynamical symmetry breaking: An addendum. Phys. Rev. D 1979, 19, 1277–1280. [Google Scholar] [CrossRef]
- Susskind, L. Dynamics of spontaneous symmetry breaking in the Weinberg-Salam theory. Phys. Rev. D 1979, 20, 2619–2625. [Google Scholar] [CrossRef]
- Fujii, Y. Dilaton and possible non-Newtonian gravity. Nat. Phys. Sci. 1971, 234, 5–7. [Google Scholar] [CrossRef]
- Gell-Mann, M. California Institute of Technology Ph 240 Seminar; 1971; unpublished; Available online: http://dx.doi.org/10.1063/1.3022730 (accessed on 10 July 2020).
- Crewther, R.J. Quarks and anomalies. In 50 Years of Quarks; Fritzsch, H., Gell-Mann, M., Eds.; World Scientific Publishing Co.: Singapore, 2015; pp. 435–452. [Google Scholar]
- Fubini, S. A new approach to conformal invariant field theories. Nuovo Cimento A 1976, 34, 521–554. [Google Scholar] [CrossRef]
- Coleman, S.; Weinberg, E. Radiative corrections as the origin of spontaneous symmetry breaking. Phys. Rev. D 1973, 7, 1888–1910. [Google Scholar] [CrossRef]
- Appelquist, T.; Terning, J.; Wijewardhana, L.C.R. Zero temperature chiral phase transition in SU(N) gauge theories. Phys. Rev. Lett. 1996, 77, 1214–1217. [Google Scholar] [CrossRef]
- Appelquist, T.; Terning, J.; Wijewardhana, L.C.R. Postmodern technicolor. Phys. Rev. Lett. 1997, 79, 2767–2770. [Google Scholar] [CrossRef]
- Appelquist, T.; Avakian, A.; Babich, R.; Brower, R.C.; Cheng, M.; Clark, M.A.; Cohen, S.D.; Fleming, G.T.; Kiskis, J.; Neil, E.T.; et al. [LSD Collaboration] Toward TeV conformality. Phys. Rev. Lett. 2010, 104, 071601. [Google Scholar] [CrossRef] [PubMed]
- Wess, J. The conformal invariance in quantum field theory. Nuovo Cimento 1960, 18, 1086–1107. [Google Scholar] [CrossRef]
- Caswell, W.E. Asymptotic behavior of non-Abelian gauge theories to two-loop order. Phys. Rev. Lett. 1974, 33, 244–246. [Google Scholar] [CrossRef]
- Banks, T.; Zaks, A. On the phase structure of vector-like gauge theories with massless fermions. Nucl. Phys. B 1982, 196, 189–204. [Google Scholar] [CrossRef]
- Appelquist, T.; Carazzone, J. Infrared singularities and massive fields. Phys. Rev. D 1975, 11, 2856–2861. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Low, F.E. Quantum electrodynamics at short distances. Phys. Rev. 1954, 95, 1300–1312. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.; de Téramond, G.F. The QCD running coupling. Prog. Part. Nucl. Phys. 2016, 90, 1–74. [Google Scholar] [CrossRef]
- Grunberg, G. Renormalization-scheme-invariant QCD and QED: The method of effective charges. Phys. Rev. D 1984, 29, 2315–2338. [Google Scholar] [CrossRef]
- Lüscher, M. Properties and uses of the Wilson flow in lattice QCD. J. High Energy Phys. 2010, 1008, 071, Erratum: J. High Energy Phys. 2014, 1403, 092. [Google Scholar] [CrossRef]
- Fodor, F.; Holland, K.; Kuti, J.; Nogradi, D.; Wong, C.H. The Yang-Mills gradient flow in finite volume. J. High Energy Phys. 2012, 1211, 007. [Google Scholar] [CrossRef]
- Aoki, S.; Aoki, Y.; Bečirević, D.; Blum, T.; Colangelo, G.; Collins, S.; Della Morte, M.; Dimopoulos, P.; Dürr, S.; Fukaya, H.; et al. FLAG Rev. 2019: Flavour Lattice Averaging Group. Eur. Phys. J. 2020, 80, 113. [Google Scholar] [CrossRef]
- Dalla Brida, M. on behalf of the ALPHA Collaboration. Precision determination of αs from lattice QCD. Universe 2018, 4, 148. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. Dilaton EFT framework for lattice data. J. High Energy Phys. 2017, 1707, 035. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. Analysis of a dilaton EFT for lattice data. J. High Energy Phys. 2018, 1803, 039. [Google Scholar] [CrossRef]
- Appelquist, T.; Ingoldby, J.; Piai, M. The dilaton potential and lattice data. Phys. Rev. D 2020, 101, 075025. [Google Scholar] [CrossRef]
- Fodor, Z.; Holland, K.; Kuti, J.; Wong, C.H. Tantalizing dilaton tests from a near-conformal EFT. Proc. Sci. 2019, LATTICE2018, 196. [Google Scholar] [CrossRef]
- Golterman, M.; Niel, E.T.; Shamir, Y. Application of dilaton chiral perturbation theory to Nf = 8, SU(3) spectral data. arXiv 2020, arXiv:2003.00114. [Google Scholar]
| 1. | This term was coined in 1969, and first appeared in print in [37]. |
| 2. | A successor (400–900) to the dormant resonance was first identified in 1996 [48] in the context of the linear sigma model. The key features of the 2006 analysis [47] were its model independence and precision, which led to the inclusion of in the 2008 Particle Data Tables. See [49] for an extensive review. Our symbol for the dilaton does not mean that we rely on the sigma model. |
| 3. | Including pion momenta, as in decay. Distinguish for momenta from the same process for momenta, where PT, a different theory, is applicable. See Footnote 7 and Figure 4 in [3]. |
| 4. | Coleman and E. Weinberg [64] stick to the textbook definition of the term “spontaneous”, i.e., for breaking which is not explicit, and apply it only to the breaking of chiral invariance. In footnote 8, they note that scale invariance is broken explicitly by the one-loop trace anomaly. |
| 5. | In walking TC, the decomposition is often not considered explicitly. Such theories involve extrapolations in , with an understanding that the extra flavor fields are almost decoupled. |
| 6. | The analysis does not appear to depend on their having an ultraviolet (UV) fixed point instead of an IRFP. |
| 7. | See Section 2 of [1], especially the text below Equation (27). |


© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crewther, R.J. Genuine Dilatons in Gauge Theories. Universe 2020, 6, 96. https://doi.org/10.3390/universe6070096
Crewther RJ. Genuine Dilatons in Gauge Theories. Universe. 2020; 6(7):96. https://doi.org/10.3390/universe6070096
Chicago/Turabian StyleCrewther, R. J. 2020. "Genuine Dilatons in Gauge Theories" Universe 6, no. 7: 96. https://doi.org/10.3390/universe6070096
APA StyleCrewther, R. J. (2020). Genuine Dilatons in Gauge Theories. Universe, 6(7), 96. https://doi.org/10.3390/universe6070096




