The Resonant Bremsstrahlung of Ultrarelativistic Electrons on a Nucleus with Radiation of Hard Gamma-Quanta in the Presence of a Pulsed Field of the X-ray Pulsar

Abstract

The investigation scrutinizes the circulation of the large-scaled fluxes of ultrarelativistic electrons near the neutron stars. This work focuses on the effects that occur during the adjustment of the strong electromagnetic field near the X-ray pulsars. Particularly, this study analyzes the resonant high-energy spontaneous bremsstrahlung of ultrarelativistic electrons in the pulsed fields of a nucleus and X-ray pulsar. Specific attention is given to the pulsed character of the field model. Under the resonant conditions the intermediate virtual electron within the electromagnetic field transforms into a real particle. As a result, the initial second-order process with accordance to the fine structure constant effectively splits into two first-order effects: the stimulated Compton process and the field-assisted scattering of an electron on a nucleus. In this research we obtain the resonant differential cross-sections with registration of frequency and radiation angle of a hard gamma-quantum. To summarize, the resonant differential cross-section of the effect within the external pulsed electromagnetic field of X-ray pulsar significantly exceeds the corresponding cross-section without an external field.

1. Introduction

Previous astronomical investigations explored the emissions of ultrarelativistic electrons in the cosmic rays [1,2] from neutron stars and magnetars. The actual paper scrutinizes the spectrum of the X-ray pulsars through the study of the processes that occur between the radiated particles (bremsstrahlung of ultrarelativistic electrons with considerable energies $E_i\sim {10}^2$ MeV $÷{10}^2$ GeV on a nucleus) during the adjustment of the external X-ray field with intensity $F_0\sim {10}^{13}÷{10}^{14}$ V/cm. Earlier researches derived [3,4,5,6,7] that the high-order quantum electrodynamics (QED) processes with respect to the fine structure constant in the external field may develop as the resonant or non-resonant processes. In addition, the low-order resonances that appear are the Oleinik resonances [8,9]. Under the conditions of Oleinik resonance an intermediate virtual electron in the wave field emerges to the mass shell. As a result, the initial second-order process with respect to the fine structure constant in the wave field effectively splits into two first-order processes: the external X-ray field-stimulated Compton effect and the X-ray field-assisted Mott process. For such arrangement, the resonant kinematics determine both the frequency of the spontaneous photon, which significantly depends on the reaction channel, and the corresponding angles of emission of the spontaneous photon in correlation to the momenta of the initial or final electrons. It is important to underline, that the probability of the resonant channel development exceeds the probability for the same phenomenon accounted in the absence of the external field [10,11] by several orders of magnitude.

It should be noted that in the considered problem of the electron on a nucleus bremsstrahlung in the field of a plane wave there are two characteristic parameters. The classical relativistic-invariant parameter [12,13,14,15,16]:

$${\eta }_0=\frac{e{F}_0ƛ}{m{c}^2}.$$

(1)

that is numerically equal to the ratio of the work of the field at a wavelength to the rest energy of the electron (e and m are the charge and mass of an electron, $F_0$ and $ƛ=c/\omega$ are the electric field strength and the wavelength, $\omega$ is the frequency of a wave, and c is the light velocity in vacuum). Within the diapason of the X-ray frequencies ($\omega \sim 1÷{10}^2$ keV) the classical parameter is ${\eta }_0\sim 1$ for the fields up till the magnitude of $F_0\lesssim {10}^{15}$ V/cm. The actual investigation considers the moderately weak X-ray fields in the studied bremsstrahlung effect:

$${\eta }_0\ll 1.$$

(2)

The second parameter is the quantum Bunkin–Fedorov parameter [13,14,15,16,17,18]:

$${\gamma }_0={\eta }_0\frac{m{v}_{i}c}{\hslash \omega }.$$

(3)

where $v_i$ is the velocity of the initial electrons.

Modern laser radiation sources may propose an approximation of the near X-ray pulsar conditions [19,20,21,22].

Described experimental and theoretical researches of the processes of QED within the strong external fields of magnetars and X-ray pulsars delineate an intensively developing area that can be applied in investigations of physics of neutron stars [8,9,10,11,13,14,15,16,17,18,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]). Thus, articles, essays [1,2,18,29,30,31] and reviews [12,13,14,15,26,27,28,59,60] accumulate main results.

Several works have investigated the strong field approximations. Thus, in [41] the authors scrutinize the spontaneous bremsstrahlung emission in a highly intense laser field. In this regime the interaction with the laser field has to be treated nonperturbatively by using the relativistic formalism including Dirac–Wolkow propagators, while the interaction with the Coulomb field and the bremsstrahlung radiation can be treated in first-order perturbation theory. Additionally, in the paper [42] the authors numerically evaluate the cross sections for spontaneous bremsstrahlung emission in a laser field for both circular and linear laser polarization, in a regime where the classical ponderomotive energies for the considered laser intensities are considerably larger than the rest mass of the electron.

The process of the spontaneous bremsstrahlung of ultrarelativistic electrons in the fields of a nucleus and plane monochromatic wave was previously studied in the articles [53,61]. In contrast to the earlier works, the authors scrutinize the process of the spontaneous bremsstrahlung of ultrarelativistic electrons with radiation of the high-energy gamma-quanta within the field of a nucleus and the pulsed electromagnetic field of the X-ray pulsar.

The calculations in articles comprehend the relativistic units system: $\hslash =c=1$.

2. The Process Amplitude

In order to simulate the conditions of the external field from the neutron star the study utilizes the following form of the 4-potential plane-wave electromagnetic momentum that propagates along the z axis:

$$\begin{array}{c}\hfill A\left(\varphi \right)=A_0·g\left(\frac{\phi }{\omega \tau }\right)·(e_{x}cos\phi +\delta e_{y}sin\phi ),\\ \hfill \phi =kx=\omega (t-z).\end{array}$$

(4)

where $A_0=F_0/\omega$, $k=(\omega ,\mathbf{k})$ is the wave 4-vector; $\delta$ is the polarization ellipticity parameter of a wave; $e_x=(0,{\mathbf{e}}_x),e_y=(0,{\mathbf{e}}_y)$ are the wave polarization 4-vectors, and $e_{x,y}^2=-1,\left(e_{x,y}k\right)=k^2=0$. The function $g(\phi /\omega \tau )$ is the envelope function of the potential and at the center of the momentum $g\left(0\right)=1$, when $g\left(0\right)\to 0$ the envelope function exponentially decreases with the condition: $\left|\phi \right|\gg \omega \tau$. Finally, $\tau$ is the duration of the X-ray field pulse.

The represented problem is usually studied in the field of intensities of moderately strong fields with the following conditions:

$$\omega \tau \gg 1.$$

(5)

The fields that correlate to the condition (5) are referred as quasimonochromatic. The actual study considers the ultrarelativistic electrons and weak quasimonochromatic fields (5)—the indicated conditions delineate that the electrons do not deviate from the initial direction of propagation as a result of the pomderomotive effect in the external field. For the represented arrangement the investigation neglects the spatial inhomogeneity of the beam in the transverse direction from the examination [11,21].

The paper analyzes the spontaneous bremsstrahlung of electrons on a nucleus in the pulsed electromagnetic field in the Born approximation of the electrons with nucleus field interaction ($Z{e}^2/v_i\ll 1$, Z is the charge of a nucleus). Consequently, two Feynman diagrams illustrate the delineated process near the neutron star (see Figure 1).

The following expression delineates the amplitude of the process:

$$\begin{array}{c}\hfill S_{fi}=-i{e}^2\int d^4{x}_1{d}^4{x}_2{\overline{\psi }}_f\left(x_2\right|A)·[{\tilde{\gamma }}_0{A}_0\left(\right|{\mathbf{x}}_{\mathbf{2}}\left|\right)G\left(x_2{x}_1\right|A)\widehat{A^{\prime }}(x_1,k^{\prime })+\\ \hfill +\widehat{A^{\prime }}(x_2,k^{\prime })G\left(x_2{x}_1\right|A){\tilde{\gamma }}_0{A}_0\left(\right|{\mathbf{x}}_{\mathbf{1}}\left|\right)]{\psi }_i\left(x_1\right|A).\end{array}$$

(6)

where ${\psi }_i\left(x_1\right|A)$ and ${\overline{\psi }}_f\left(x_2\right|A)$ are the wave functions of electron in the initial and final states in the field of a plane electromagnetic wave (Wolkow functions), and $G\left(x_2{x}_1\right|A)$ is the Green function of an intermediate electron within the field of a pulsed electromagnetic wave (4). The magnitudes with a hat imply the scalar product of the corresponding 4-vector on the Dirac gamma-matrix: ${\tilde{\gamma }}_{\mu }=({\tilde{\gamma }}_0,\tilde{\mathit{\gamma }})$, $\mu =0,1,2,3$. For example: $\widehat{A^{\prime }}=A_{\mu }^{\prime }{\tilde{\gamma }}^{\mu }=A_0^{\prime }{\tilde{\gamma }}^0-{\mathit{A}}^{\mathbf{\prime }}\tilde{\mathit{\gamma }}$. In the expression (6) $A_0\left(\right|{\mathbf{x}}_n\left|\right)$ is the Coulomb potential of a nucleus and $A_{\mu }^{\prime }(x_n,k^{\prime })$ is the 4-potential of a spontaneous photon, that have the structures:

$$A_0\left(\right|{\mathbf{x}}_n\left|\right)=\frac{Ze}{|{\mathbf{x}}_n|}.$$

(7)

$$A_{\mu }^{\prime }(x_n,k^{\prime })=\sqrt{\frac{2\pi }{{\omega }^{\prime }}}{\epsilon }_{\mu }^{*}{e}^{i{k}^{\prime }{x}_n},n=1,2.$$

(8)

where, ${\epsilon }_{\mu }^{*}$ and $k^{\prime }=({\omega }^{\prime },{\mathbf{k}}^{\prime })$ are the 4-vector of polarization and the 4-momentum of a spontaneous gamma-quantum, $\left(k^{\prime }{x}_n\right)=({\omega }^{\prime }{t}_n-{\mathbf{k}}^{\prime }{\mathbf{x}}_n)$. The constructed model utilizes circular polarization $({\delta }^2=1)$ and the main parameter value at the peak of the pulse is (2). For the energy of the gamma-quantum of 100 keV the actual magnitude of the characteristic parameter is:

$$\omega ={10}^{2}keV\Rightarrow F\left(\frac{V}{cm}\right)\approx 2.592\times {10}^{15}\times {\eta }_0\Rightarrow {\eta }_0\sim {10}^{-2}.$$

(9)

Furthermore, the study implements computational methods (see, for example [18]) and derives the amplitude of the resonant bremsstrahlung within the field of a weak plane quasimonochromatic (4) electromagnetic wave (10):

$$S_{fi}=\sum _{l=-\infty }^{\infty }{S}_{\left(l\right)}.$$

(10)

Here, $S_{\left(l\right)}$ is the partial amplitude with the radiation (absorption) of $\left|l\right|$ gamma-quanta.

$$S_{\left(l\right)}=-i\frac{2{\tau }^2\omega Z{e}^3\sqrt{\pi }}{\sqrt{2{\omega }^{\prime }{E}_f{E}_i}}\frac{\left({\overline{u}}_f{B}_{\left(l\right)}{u}_i\right)}{[{\mathbf{q}}^2+q_0(q_0-2q_z)]}.$$

(11)

where

$$B_{\left(l\right)}=B_{i\left(l\right)}+B_{f\left(l\right)}.$$

(12)

$$q=p_f-p_i+k^{\prime }+lk.$$

(13)

The $q=(q_0,\mathbf{q})$ is the transmitted 4-momentum, $B_{i\left(l\right)}$ and $B_{f\left(l\right)}$ are the amplitudes for the channels A and B.

$$\begin{array}{c}\hfill B_{i\left(l\right)}=\sum _{r=-\infty }^{\infty }{\int }_{-\infty }^{\infty }d{\varphi }_1{\int }_{-\infty }^{\infty }d{\varphi }_2{e}^{\left(i{q}_0\tau {\varphi }_2\right)}·M_{(l+r)}^0(p_f,q_i,{\varphi }_2)G(q_i,{\varphi }_1-{\varphi }_2)\left[{\epsilon }_{\mu }^{*}{F}_{(-r)}^{\mu }(q_i,p_i,{\varphi }_1)\right].\end{array}$$

(14)

$$\begin{array}{c}\hfill B_{f\left(l\right)}=\sum _{r=-\infty }^{\infty }{\int }_{-\infty }^{\infty }d{\varphi }_1{\int }_{-\infty }^{\infty }d{\varphi }_2{e}^{\left(i{q}_0\tau {\varphi }_1\right)}·\left[{\epsilon }_{\mu }^{*}{F}_{(-r)}^{\mu }(p_f,q_f,{\varphi }_2)\right]G(q_f,{\varphi }_2-{\varphi }_1)M_{(l+r)}^0(q_f,p_i,{\varphi }_1).\end{array}$$

(15)

$$\begin{array}{c}\hfill G(q_i,{\varphi }_1-{\varphi }_2)={\int }_{-\infty }^{\infty }d\xi \left[\frac{({\widehat{q}}_i+m)+\xi \widehat{k}}{(q_i^2-m^2)+2\xi \left(k{q}_i\right)}\right]·e^{i\left(\omega \tau \xi \right)({\varphi }_1-{\varphi }_2)}.\end{array}$$

(16)

$$q_i=p_i-k^{\prime }+rk,q_f=p_f+k^{\prime }-rk.$$

(17)

The term $G(q_f,{\varphi }_2-{\varphi }_1)$ in the expression (15) is derived from the ratio (16) with substitution: $q_i\to q_f$, ${\varphi }_1\leftrightarrow {\varphi }_2$. In addition, ${\varphi }_n={\phi }_n/\omega \tau (n=1,2)$, $q_i$, and $q_f$ are the 4-momenta of the intermediate electrons for channels A and B (see Figure 1). where:

$$M_{(l+r)}^0(p^{\prime },p,{\varphi }_n)={\tilde{\gamma }}^0{L}_{(l+r)}(p^{\prime },p,{\varphi }_n).$$

(18)

$$\begin{array}{c}\hfill F_{(-r)}^{\mu }(p^{\prime },p,{\varphi }_n)={\tilde{\gamma }}^{\mu }{L}_{(-r)}(p^{\prime },p,{\varphi }_n)+b_{p^{\prime }p(-)}^{\mu }\left({\varphi }_n\right)L_{(-r-1)}+b_{p^{\prime }p(+)}^{\mu }\left({\varphi }_n\right)L_{(-r+1)},n=1,2.\end{array}$$

(19)

Here, magnitudes $b_{p^{\prime }p(\pm )}^{\mu }$ from (18) and (19) and the special functions $L_{n^{\prime }}(p^{\prime },p,{\varphi }_n)$:

$$b_{p^{\prime }p(\pm )}^{\mu }\left({\varphi }_n\right)=\eta \left({\varphi }_n\right)[\frac{m}{4\left(k{p}^{\prime }\right)}{\widehat{e}}_{\pm }\widehat{k}{\tilde{\gamma }}^{\mu }+\frac{m}{4\left(kp\right)}{\tilde{\gamma }}^{\mu }\widehat{k}{\widehat{e}}_{\pm }].$$

(20)

$$L_{n^{\prime }}\equiv L_{n^{\prime }}(p^{\prime },p,{\varphi }_n)=e^{-is{\chi }_{p^{\prime }p}}{J}_{n^{\prime }}\left[{\gamma }_{p^{\prime }p}\left({\varphi }_n\right)\right].$$

(21)

where $J_{n^{\prime }}$ are the Bessel functions of an integer index, parameter ${\gamma }_{p^{\prime }p}$, and 4-vectors $e_{\pm }$ are equal to:

$${\gamma }_{p^{\prime }p}\left({\varphi }_n\right)=\eta \left({\varphi }_n\right)m\sqrt{-Q_{p^{\prime }p}^2},Q_{p^{\prime }p}=\frac{p^{\prime }}{\left(k{p}^{\prime }\right)}-\frac{p}{\left(kp\right)}.$$

(22)

$$e_{\pm }=e_x\pm i\delta e_y.$$

(23)

The derived amplitude (10), (12)–(14) is valid for the circular polarization of the weak quasimonochromatic laser wave (4) and (9).

The additional conditions for the constructed model delineate that the ultrarelativistic electron and spontaneous gamma-quantum propagate along the direction of the momentum of the initial electron [53].

$$E_{i,f}\gg m.$$

(24)

$${\theta }_{i,f}^{\prime }=\angle ({\mathbf{k}}^{\prime },{\mathbf{p}}_{i,f})\ll 1,{\overline{\theta }}_{if}=\angle ({\mathbf{p}}_i,{\mathbf{p}}_f)\ll 1.$$

(25)

$${\theta }^{\prime }=\angle ({\mathbf{k}}^{\prime },\mathbf{k})\sim 1,{\theta }_{i,f}=\angle (\mathbf{k},{\mathbf{p}}_{i,f})\sim 1({\theta }^{\prime }\approx {\theta }_{i,f}).$$

(26)

3. The Poles of the Resonant Bremsstrahlung Amplitude

As a result of the approximate fulfillment of the energy-momentum conservation law, the intermediate electron emerges close to the mass surface.

Therefore, the research uses the subsequent resonant conditions [18] for the channels A and B (see Figure 2):

$${\beta }_i=\frac{q_i^2-m^2}{4\left(k{q}_i\right)}\omega \tau ,{\beta }_f=\frac{q_f^2-m^2}{4\left(k{q}_f\right)}\omega \tau ,|{\beta }_j|\lesssim 1\Rightarrow |q_j^2-m^2|\lesssim \frac{4\left(k{q}_j\right)}{\omega \tau },j=i,f.$$

(27)

The resonant parameters ${\beta }_{i,f}$ (27) have the following form within the external field:

$${\beta }_i=\frac{r[{\epsilon }_r-(1+{\epsilon }_r+{\delta }_i^{\prime 2})x^{\prime }]}{2{\epsilon }_r(1-x^{\prime })}\left(\omega \tau \right).$$

(28)

$${\beta }_f=\frac{r\{x^{\prime }[1+{(1-x^{\prime })}^2{\delta }_f^{\prime 2}]-{\epsilon }_r(1-x^{\prime })\}}{2{\epsilon }_r(1-x^{\prime })}\left(\omega \tau \right).$$

(29)

where

$${\delta }_i^{\prime }=\frac{E_i{\theta }_i^{\prime }}{m},{\delta }_f^{\prime }=\frac{E_i{\theta }_f^{\prime }}{m},x^{\prime }=\frac{{\omega }^{\prime }}{E_i}.$$

(30)

$${\epsilon }_r=r{\epsilon }_1,{\epsilon }_1=\frac{E_i}{E_1},E_1=\frac{m^2}{4\omega {sin}^2({\theta }_i/2)}.$$

(31)

where $r=1,2,3,\dots$ is the number of resonance (the amount of X-ray photons of a wave that electron absorbs), ${\epsilon }_r$ is the characteristic parameter of a process that is equal to the ratio of the initial electron energy to the characteristic energy $E_r=E_1/r$. The characteristic energy is defined by: the rest energy of an electron, the angle between the momenta of the initial electron and propagating wave, and by the superposition of the energies of absorbed photons.

In this article the authors consider the cases when ${\epsilon }_1\sim 1$ and ${\epsilon }_1\gg 1$.

The resonant conditions (27) for the channels A and B change in correlation to the Equations (28) and (29):

$$\frac{r}{2{\epsilon }_r(1-x^{\prime })}|{\epsilon }_r-(1+{\epsilon }_r+{\delta }_i^{\prime 2})x^{\prime }|\lesssim \frac{1}{\left(\omega \tau \right)}\ll 1.$$

(32)

$$\frac{r}{2{\epsilon }_r(1-x^{\prime })}|x^{\prime }[1+{\epsilon }_r+{(1-x^{\prime })}^2{\delta }_f^{\prime 2}]-{\epsilon }_r|\lesssim \frac{1}{\left(\omega \tau \right)}\ll 1.$$

(33)

Subsequently, the research obtains the resonant frequencies for the channels A and B. Thus, for the channel A:

$$x_{i\left(r\right)}^{\prime }\left(\delta {{}^{\prime }}_i^2\right)\approx \frac{{\epsilon }_i}{1+{\epsilon }_r+{\delta }_i^{\prime 2}},x_{i\left(r\right)}^{\prime }=\frac{{\omega }_{i\left(r\right)}^{\prime }}{E_i}.$$

(34)

Parameter ${\epsilon }_r$ determines the resonant frequency with a single-value dependency on the angle of the emission of a hard gamma-quantum in accordance to the momentum of the initial electron. The resonant frequency has a maximum peak when gamma-quantum propagates along the momentum of the initial electron $({\delta }_i^{\prime 2}=0)$:

$$x_{i\left(r\right)}^{\prime }\left(0\right)=x_{\left(r\right)}^{\prime max}=\frac{{\epsilon }_r}{1+{\epsilon }_r}.$$

(35)

For the channel B, the research obtains a cubic equation:

$$\begin{array}{c}\hfill {\delta }_f^{\prime 2}{x}_{f\left(r\right)}^{\prime 3}-2{\delta }_f^{\prime 2}{x}_{f\left(r\right)}^{\prime 2}+(1+{\delta }_f^{\prime 2}+{\epsilon }_r)x_{f\left(r\right)}^{\prime }-{\epsilon }_r\approx 0,x_{f\left(r\right)}^{\prime }=\frac{{\omega }_{f\left(r\right)}^{\prime }}{E_i}.\end{array}$$

(36)

The channel B resonant frequency is defined by the angle of the hard gamma-quantum radiation in accordance to the momentum of the final electron.

The paper considers only the case when ${\delta }_f^{\prime 2}\ne 0$ as that condition may be a subject for a whole other research.

Therefore, for the channel B, the resonant frequency function depends on the parameter ${\epsilon }_r$ and has two distinctive areas of dependency: $0<{\epsilon }_r\le 8$ and ${\epsilon }_r>8$. Additionally, the parameter ${\delta }_f^{\prime 2}$ value designates 3 intervals of function: $0<{\delta }_f^{\prime 2}<{\delta }_{-\left(r\right)}^{\prime 2}$, ${\delta }_{-\left(r\right)}^{\prime 2}<{\delta }_f^{\prime 2}<{\delta }_{+\left(r\right)}^{\prime 2}$, and ${\delta }_f^{\prime 2}>{\delta }_{+\left(r\right)}^{\prime 2}$ in which the research obtains principally different results. All these areas of parameters ${\epsilon }_r$ and ${\delta }_f^{\prime 2}$ magnitudes may be represented in the following two solutions. For the first diapason:

$$0<{\delta }_f^{\prime 2}\le {\delta }_{fmax}^{\prime 2}=3(1+{\epsilon }_r),if0<{\epsilon }_r\le 8.$$

(37)

It is important to notice that lines $1^{\prime }$ and $2^{\prime }$ of the Figure 3 and line 1 on the Figure 5b and lines 1 and 2 on the Figure 6 are limited as they correspond to the parameter value within the interval (37). The resonant frequency of the spontaneous hard gamma-quantum within the first interval (37) is equal to:

$$x_{f\left(r\right)}^{\prime }=\frac{2}{3}+({\alpha }_{+\left(r\right)}+{\alpha }_{-\left(r\right)}).$$

(38)

where

$${\alpha }_{\pm \left(r\right)}={[-\frac{b_{\left(r\right)}}{2}\pm \sqrt{Q_{\left(r\right)}}]}^{1/3},Q_{\left(r\right)}={\left(\frac{a_{\left(r\right)}}{3}\right)}^3+{\left(\frac{b_{\left(r\right)}}{2}\right)}^2.$$

(39)

$$\begin{array}{c}\hfill a_{\left(r\right)}=\frac{1}{3{\delta }_f^{\prime 2}}[3(1+{\epsilon }_r)-{\delta }_f^{\prime 2}],b_{\left(r\right)}=\frac{1}{27{\delta }_f^{\prime 2}}[2(9+{\delta }_f^{\prime 2})-9{\epsilon }_r].\end{array}$$

(40)

within the second diapason:

$${\delta }_{-\left(r\right)}^{\prime 2}<{\delta }_f^{\prime 2}<{\delta }_{+\left(r\right)}^{\prime 2}.$$

(41)

where the limiting magnitudes for the interval are equal to:

$$\begin{array}{c}\hfill {\delta }_{\pm \left(r\right)}^{\prime 2}=3(1+{\epsilon }_r)+\frac{1}{8}({\epsilon }_r-8)[({\epsilon }_i+4)\pm \sqrt{{\epsilon }_r({\epsilon }_r-8)}],{\epsilon }_r>8.\end{array}$$

(42)

Thus, within diapason (41) the resonant frequency of a hard gamma-quantum obtains three various possible values as solutions of the cubic Equation (36):

$$\begin{array}{c}\hfill x_{f\left(r\right)1}^{\prime }=\frac{2}{3}+d_{\left(r\right)}^{\prime }cos\left(\frac{{\phi }_{\left(r\right)}^{\prime }}{3}\right),\\ \hfill x_{f\left(r\right)2}^{\prime }=\frac{2}{3}+d_{\left(r\right)}^{\prime }cos(\frac{{\phi }_{\left(r\right)}^{\prime }}{3}+\frac{2\pi }{3}),\\ \hfill x_{f\left(r\right)3}^{\prime }=\frac{2}{3}+d_{\left(r\right)}^{\prime }cos(\frac{{\phi }_{\left(r\right)}^{\prime }}{3}+\frac{4\pi }{3}).\end{array}$$

(43)

where

$$\begin{array}{c}\hfill d_{\left(r\right)}^{\prime }=\frac{2}{3{\delta }_f^{\prime }}\sqrt{{\delta }_f^{\prime 2}-3(1+{\epsilon }_r)},cos{\phi }_{\left(r\right)}^{\prime }=\frac{{\delta }_f^{\prime }[9{\epsilon }_r-2(9+{\delta }_f^{\prime 2})]}{2{[{\delta }_f^{\prime 2}-3(1+{\epsilon }_r)]}^{3/2}},0\le {\phi }_{\left(r\right)}^{\prime }\le \pi .\end{array}$$

(44)

The third interval ${\delta }_f^{\prime 2}>{\delta }_{+\left(r\right)}^{\prime 2}$ is similar to the first diapason and the resonance frequency has a single-value dependency with the emission angle of a spontaneous photon: decreasing from value $x_{f\left(r\right)+}^{\prime }$ to small values $x_{f\left(r\right)}^{\prime }\ll 1$. Here, the resonant frequency $x_{f\left(r\right)+}^{\prime }$ is obtained by substituting the value ${\delta }_f^{\prime 2}={\delta }_{+\left(r\right)}^{\prime 2}$ into solutions (38)–(40).

It is important to underline the difference between the resonant and non-resonant options of the reaction development. In the non-resonant conditions the resonant frequency of a hard gamma-quantum and the final electron energy are independent. Additionally, the energies of hard gamma-quanta do not depend on its radiation angles. In contrast, the resonant conditions implement absolutely different limitations. Under the resonant conditions the particle emission spectrum depends on the angles of hard gamma-quanta radiation with accordance to the initial or final electrons momenta.

Furthermore, the research states that the channels A and B do not interfere due to the fact that the resonant frequency is dependent on the correlation between angle of hard gamma-quantum emission to the initial electron momentum for the channel A and final electron momentum for the channel B.

For the illustrative representation of the results, see Figure 3 and the caption for it.

Additionally, the research scrutinizes the case when the initial electron energy is considerably bigger than the characteristic energy $E_1$ (31):

$${\epsilon }_1\gg 1\to E_i\gg E_1.$$

(45)

Thus, for such arrangement the frequencies of spontaneous gamma-quanta for the channels A and B are defined with the following equation:

$$x_{j\left(r\right)}^{\prime }\left({\delta }_j^{\prime 2}\right)\approx 1-\frac{1+{\delta }_j^{\prime 2}}{{\epsilon }_r},j=i,f({\delta }_j^{\prime 2}\ll {\epsilon }_r\gg 1).$$

(46)

In this equation, the term with ${\delta }_j^{\prime 2}$ and ${\epsilon }_r$ has a small magnitude. Therefore, when the energy of the initial electrons significantly exceeds the characteristic energy of the process, the energy of spontaneous gamma-quanta for channels A and B is close to the energy of electrons. The research accounts these corrections in the final derivations of the differential cross-sections.

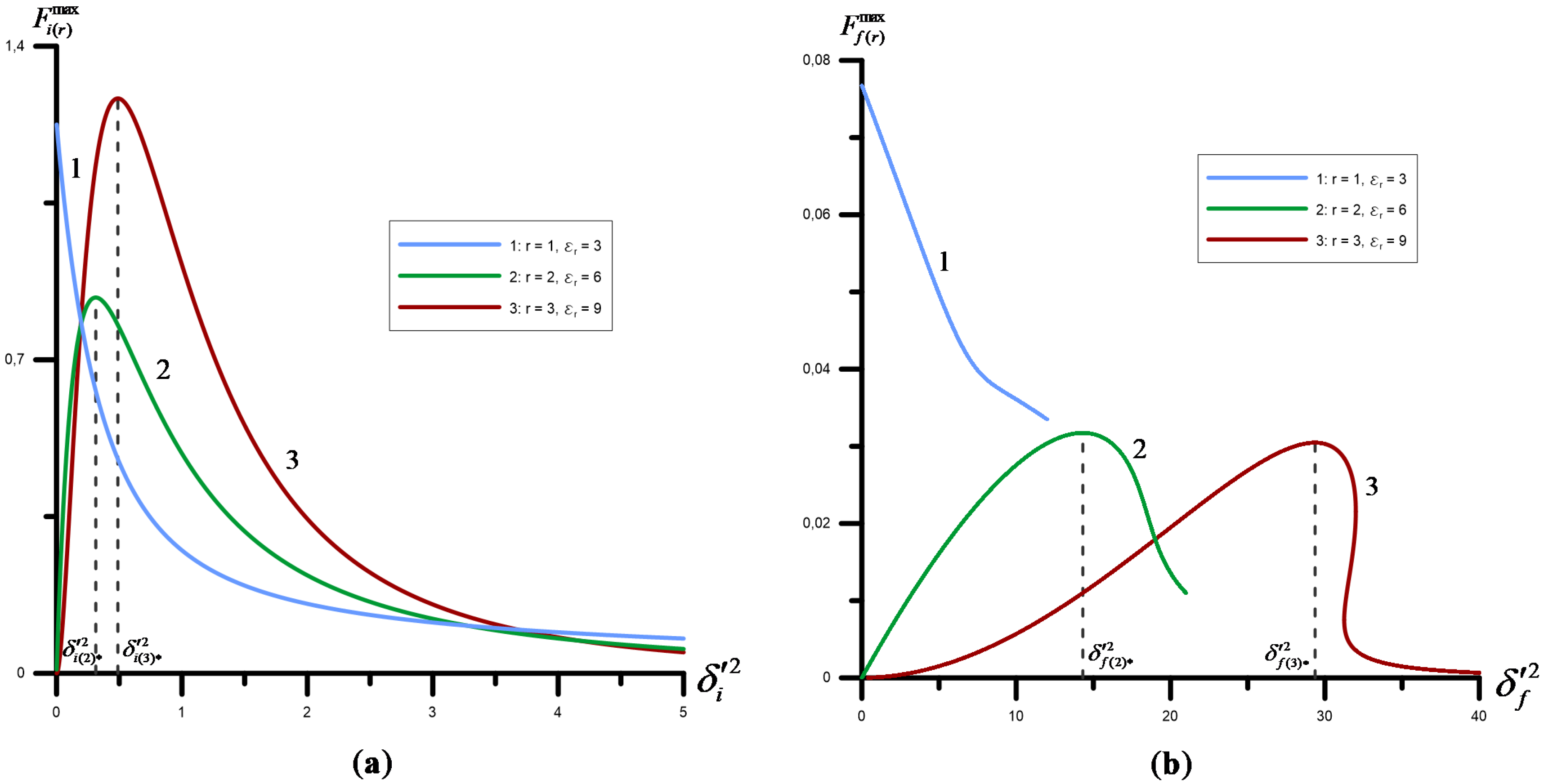
4. Results

4.1. The Cross-Section of the Resonant Bremsstrahlung Process

The next step in the investigation is to derive and analyze the cross-section of the considered effect. In order to do this, the authors simplify the amplitude (10)–(14) with attention of the resonant kinematics (24)–(26). Consequently, the amplitudes $M_{(l+r)}^0$ and $F_{(-r)}^{\mu }$ from (13) and (14):

$$M_{(l+r)}^0(p^{\prime },p,{\varphi }_j)\approx {\tilde{\gamma }}^0{L}_0(p^{\prime },p,{\varphi }_n)\approx {\tilde{\gamma }}^0(l=-r).$$

(47)

$$\begin{array}{c}\hfill F_{(-r)}^{\mu }(p^{\prime },p,{\varphi }_n)={\tilde{\gamma }}^{\mu }{L}_{(-r)}(p^{\prime },p,{\varphi }_n)+L_{(-r+1)}(p^{\prime },p,{\varphi }_n)\eta \left({\varphi }_1\right)[\frac{m}{4\left(k{p}^{\prime }\right)}{\widehat{e}}_{+}\widehat{k}{\tilde{\gamma }}^{\mu }+\frac{m}{4\left(kp\right)}{\tilde{\gamma }}^{\mu }\widehat{k}{\widehat{e}}_{+}].\end{array}$$

(48)

The computations are valid for a certain type of the potential envelope function:

$$g\left({\varphi }_n\right)=e^{-{\left(2{\varphi }_n\right)}^2},n=1,2.$$

(49)

Therefore, the authors expand Bessel functions (47) and (48) into series form and then make integration on the $d{\varphi }_1$ and $d{\varphi }_2$ for the channels A and B. The amplitude of the cross-section of the resonant bremsstrahlung effect:

$$S_{fi}=S_{(-r)}=\frac{{\pi }^2{\tau }^2\omega Z{e}^3}{\sqrt{2{\omega }^{\prime }{E}_f{E}_i}}\frac{\left({\overline{u}}_f{B}_{(-r)}^{\prime }{u}_i\right)}{[{\mathbf{q}}^2+q_0(q_0-2q_z)]}.$$

(50)

Here,

$$B_{(-r)}^{\prime }=B_{i\left(r\right)}^{\prime }+B_{f\left(r\right)}^{\prime }.$$

(51)

$B_{i\left(r\right)}^{\prime }$ and $B_{f\left(r\right)}^{\prime }$ are the channels A and B resonant amplitudes.

$$B_{i\left(r\right)}^{\prime }=U_{i\left(r\right)}·\left[{\tilde{\gamma }}^0({\widehat{q}}_i+m)\left({\epsilon }_{\mu }^{*}{z}_{i\left(r\right)}^{\mu }\right)\right].$$

(52)

$$B_{f\left(r\right)}^{\prime }=U_{f\left(r\right)}·\left[\left({\epsilon }_{\nu }^{*}{z}_{f\left(r\right)}^{\nu }\right)({\widehat{q}}_f+m){\tilde{\gamma }}^0\right].$$

(53)

$$U_{j\left(r\right)}=\frac{{\eta }_0^r}{\sqrt{r}\left(k{q}_j\right)}{e}^{-\frac{{\beta }_j^2}{4r}}{V}_r(q_0,{\beta }_j).$$

(54)

$$\begin{array}{c}\hfill V_r(q_0,{\beta }_j)={\int }_{-\infty }^{\infty }d\varphi e^{i(q_0\tau +2{\beta }_j)\varphi }erf(2\sqrt{r}\varphi +\frac{i{\beta }_j}{2\sqrt{r}}),j=i,f.\end{array}$$

(55)

where r is the number of the resonance. It is important to note that in the expressions (52) and (53) there is no summation on the argument r because there is no interference between the resonances.

The equations $z_{i\left(r\right)}^{\mu }$ and $z_{f\left(r\right)}^{\nu }$ are:

$$z_{i\left(r\right)}^{\mu }={\tilde{\gamma }}^{\mu }{c}_i^r+c_i^{r-1}[\frac{m}{4\left(k{q}_i\right)}{\widehat{e}}_{+}\widehat{k}{\tilde{\gamma }}^{\mu }+\frac{m}{4\left(k{p}_i\right)}{\tilde{\gamma }}^{\mu }\widehat{k}{\widehat{e}}_{+}].$$

(56)

$$z_{f\left(r\right)}^{\nu }={\tilde{\gamma }}^{\nu }{c}_f^r+c_f^{r-1}[\frac{m}{4\left(k{p}_f\right)}{\widehat{e}}_{+}\widehat{k}{\tilde{\gamma }}^{\nu }+\frac{m}{4\left(k{q}_f\right)}{\tilde{\gamma }}^{\nu }\widehat{k}{\widehat{e}}_{+}].$$

(57)

Here,

$$c_i^r=\frac{{(-1)}^r}{r!}{\gamma }_i^r{e}^{ir{\chi }_{q_i{p}_i}},c_f^r=\frac{{(-1)}^r}{r!}{\gamma }_f^r{e}^{ir{\chi }_{p_f{q}_f}}.$$

(58)

$${\gamma }_j=r\sqrt{\frac{u_j}{u_{jr}}·(1-\frac{u_j}{u_{jr}})},j=i,f.$$

(59)

The $u_i,u_{ir}$, $u_f,u_{fr}$ (59) are the relativistic-invariant parameters.

$$u_i=\frac{\left(k{k}^{\prime }\right)}{\left(k{q}_i\right)},u_{ir}=2r\frac{\left(k{p}_i\right)}{m^2},u_f=\frac{\left(k{k}^{\prime }\right)}{\left(k{p}_f\right)},u_{fr}=2r\frac{\left(k{q}_f\right)}{m^2}.$$

(60)

The next aim of the research is to derive the probability of the process:

$$\begin{array}{c}\hfill d{w}_{j\left(r\right)}=\frac{{\pi }^4{\tau }^4{\omega }^2{\left(Z{e}^3\right)}^2}{2{\omega }^{\prime }{E}_f{E}_i}\frac{|\left({\overline{u}}_f{B}_{j\left(r\right)}^{\prime }{u}_i\right){|}^2}{{[{\mathbf{q}}^2+q_0(q_0-2q_z)]}^2}·\frac{d^3{p}_f{d}^3{k}^{\prime }}{T{\left(2\pi \right)}^6},j=i,f.\end{array}$$

(61)

where T is a comparatively considerable time period of observation $(T\gtrsim \tau )$. Thus, the channel A cross-section:

$$\begin{array}{c}\hfill d{\sigma }_{i\left(r\right)}=\frac{\pi \tau {\left(\omega \tau \right)}^2}{16{\left(2\pi \right)}^3}\left(\frac{\tau }{T}\right)\frac{m^2\left|{\mathbf{q}}_i\right|}{r{\left(k{q}_i\right)}^2}{e}^{-\frac{{\beta }_i^2}{2r}}d{W}_{i\left(r\right)}^{\prime }(q_i,p_i)·\frac{2Z^2{r}_e^2{m}^2[m^2+E_f{q}_{i0}+{\mathbf{p}}_f{\mathbf{q}}_i]}{|{\mathbf{q}}_i|E_f{[{\mathbf{q}}^2+q_0(q_0-2q_z)]}^2}{\left|V_r(q_0,{\beta }_i)\right|}^2{d}^3{p}_f.\end{array}$$

(62)

$$\begin{array}{c}\hfill \mathbf{q}={\mathbf{p}}_f-{\mathbf{q}}_i.\end{array}$$

(63)

where $d{W}_{i\left(r\right)}^{\prime }(q_i,p_i)$ is the probability per time unit of hard gamma-quantum emission with $k^{\prime }$ 4-momentum by an electron with $p_i$ 4-momentum due to absorption of r X-ray photons [12].

$$\begin{array}{c}\hfill d{W}_{i\left(r\right)}^{\prime }(q_i,p_i)=\frac{\alpha }{{\omega }^{\prime }\left|{\mathbf{p}}_i\right|}{\eta }_0^{2r}{\left(\frac{r^r}{r!}\right)}^2{\left[\frac{u_i}{u_{ir}}(1-\frac{u_i}{u_{ir}})\right]}^{(r-1)}·\{2+\frac{u_i^2}{(1+u_i)}-\frac{4u_i}{u_{ir}}(1-\frac{u_i}{u_{ir}})\}{d}^3{k}^{\prime }.\end{array}$$

(64)

Subsequently, with integration of the Equation (62) on the final electron energy, the cross-sections of the resonant bremsstrahlung effect obtain the following form:

$$d{\sigma }_{i\left(r\right)}=d{\sigma }_{\left(0\right)}(p_f,q_i)·{\mathsf{\Psi }}_{i\left(r\right)}^{res}·d{W}_{i\left(r\right)}^{\prime }(q_i,p_i).$$

(65)

$$d{\sigma }_{f\left(r\right)}=d{W}_{f\left(r\right)}^{\prime }(p_f,q_f)·{\mathsf{\Psi }}_{f\left(r\right)}^{res}·d{\sigma }_{\left(0\right)}(q_f,p_i).$$

(66)

where ${\mathsf{\Psi }}_{i\left(r\right)}^{res}$ and ${\mathsf{\Psi }}_{f\left(r\right)}^{res}$ are the resonant functions:

$$\begin{array}{c}\hfill {\mathsf{\Psi }}_{i\left(r\right)}^{res}=\frac{m^2\left|{\mathbf{q}}_i\right|}{64{\pi }^2}\frac{{\left(\omega \tau \right)}^2{P}_{\left(r\right)}^{res}\left({\beta }_i\right)}{r{\left(k{q}_i\right)}^2},\\ \hfill {\mathsf{\Psi }}_{f\left(r\right)}^{res}=\frac{m^2\left|{\mathbf{p}}_f\right|}{64{\pi }^2}\frac{{\left(\omega \tau \right)}^2{P}_{\left(r\right)}^{res}\left({\beta }_f\right)}{r{\left(k{q}_f\right)}^2}.\end{array}$$

(67)

Parameter ${\beta }_j$ (27) determines the resonance profile function $P_{\left(r\right)}^{res}\left({\beta }_j\right)$:

$$\begin{array}{c}\hfill P_{\left(r\right)}^{res}\left({\beta }_j\right)=e^{(-\frac{{\beta }_j^2}{2r})}\frac{1}{2\rho }{\int }_{-\rho }^{\rho }{\left|erf(2\sqrt{r}\varphi +\frac{i{\beta }_j}{2\sqrt{r}})\right|}^{2}d\varphi ,j=i,f;\rho =T/\tau .\end{array}$$

(68)

if ${\beta }_j\ll 1$ function $P_{\left(r\right)}^{res}\left({\beta }_j\right)$ takes the form:

$$\begin{array}{c}\hfill P_{\left(r\right)}^{res}({\beta }_j\ll 1)\approx \frac{a_{\left(r\right)}{\mathsf{\Gamma }}_{j\left(r\right)}^2}{[{({\delta }_j^{\prime 2}-{\delta }_{j\left(r\right)}^{\prime 2})}^2+{\mathsf{\Gamma }}_{j\left(r\right)}^2]}\approx P_{max\left(r\right)}^{res}=a_{\left(r\right)},j=i,f.\end{array}$$

(69)

Here, the functions of the transit width are as follows:

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}_{i\left(r\right)}=\frac{2{\epsilon }_r{c}_{\left(r\right)}(1-x_{i\left(r\right)}^{\prime })}{\left(\omega \tau \right)x_{f\left(r\right)}^{\prime }},{\mathsf{\Gamma }}_{f\left(r\right)}=\frac{2{\epsilon }_r{c}_{\left(r\right)}}{\left(\omega \tau \right)x_{f\left(r\right)}^{\prime }(1-x_{f\left(r\right)}^{\prime })}.\end{array}$$

(70)

It is important to note that in the constructed model the transit width significantly exceeds the radiation width:

$${\mathsf{\Gamma }}_{j\left(r\right)}\gg {\mathsf{{\rm Y}}}_j$$

(71)

where ${\mathsf{{\rm Y}}}_j$ are the functions of the resonance radiation width [53]:

$${\mathsf{{\rm Y}}}_i=\frac{1}{4}\alpha {\eta }^2{K}_1\left(\frac{1-x_i^{\prime }}{x_i^{\prime }}\right),{\mathsf{{\rm Y}}}_f=\frac{1}{4}\alpha {\eta }^2\frac{K_1}{x_f^{\prime }(1-x_f^{\prime })}.$$

(72)

$$K_1=(1-\frac{4}{{\epsilon }_1}-\frac{8}{{\epsilon }_1^2})ln(1+{\epsilon }_1)+\frac{1}{2}+\frac{8}{{\epsilon }_1}-\frac{1}{2{(1+{\epsilon }_1)}^2}.$$

(73)

Thus, with reconsideration of the (70)–(72), it is possible to obtain the required upper limit of the laser pulse duration:

$$\omega \tau \ll {10}^3{\eta }_0^{-2}$$

(74)

The Figure 4 delineates the $P_{\left(r\right)}^{res}\left({\beta }_j\right)$ function (68) for the first, second, and third resonances. The resonances appear with the resonant parameter magnitudes of: $|{\beta }_{i,f}|\lesssim 1$ and with $|{\beta }_{i,f}|\gg 1$ the function of resonance profile $P_{\left(r\right)}^{res}\left({\beta }_j\right)$ decreases exponentially.

4.2. Additional Scrutiny of the Differential Cross-Section of the Resonant Bremsstrahlung Effect

For the following development of the investigation, the authors apply the resonant kinematic conditions (24)–(26) to the calculation of the differential cross-section (68) of the process:

$$\begin{array}{c}\hfill d{\sigma }_{j\left(r\right)}=\alpha r_e^2{Z}^2{\eta }_0^{2r}\frac{r{\left(\omega \tau \right)}^2(1-x_{j\left(r\right)}^{\prime })}{8\pi d_{j\left(r\right)}^2}·\frac{K_{j\left(r\right)}}{{\epsilon }_r^2}{P}_{\left(r\right)}^{res}\left({\beta }_j\right)·x_{j\left(r\right)}^{\prime }d{x}_{j\left(r\right)}^{\prime }d{\delta }_i^{\prime 2}d{\delta }_f^{\prime 2}d{\phi }_{-}^{\prime },j=i,f.\end{array}$$

(75)

where ${\phi }_{-}^{\prime }$ is the angle between planes $({\mathbf{k}}^{\prime },{\mathbf{p}}_i)$ and $({\mathbf{k}}^{\prime },{\mathbf{p}}_f)$. Additionally:

$$\begin{array}{c}\hfill K_{j\left(r\right)}={\left(\frac{r^r}{r!}\right)}^2{[\frac{x_{j\left(r\right)}^{\prime }}{{\epsilon }_r(1-x_{j\left(r\right)}^{\prime })}·(1-\frac{x_{j\left(r\right)}^{\prime }}{{\epsilon }_r(1-x_{j\left(r\right)}^{\prime })})]}^{(r-1)}\times \\ \hfill \times \{2+\frac{x_{j\left(r\right)}^{\prime 2}}{(1-x_{j\left(r\right)}^{\prime })}-\frac{4x_{j\left(r\right)}^{\prime }}{{\epsilon }_r(1-x_{j\left(r\right)}^{\prime })}(1-\frac{x_{j\left(r\right)}^{\prime }}{{\epsilon }_r(1-x_{j\left(r\right)}^{\prime })})\}.\end{array}$$

(76)

$$\begin{array}{c}\hfill d_{j\left(r\right)}=d_0\left(x_{j\left(r\right)}^{\prime }\right)+{\left(\frac{m}{2E_i}\right)}^2[g_0^2\left(x_{j\left(r\right)}^{\prime }\right)+\frac{{\epsilon }_r}{{sin}^2({\theta }_i/2)}({\epsilon }_r+g_0\left(x_{j\left(r\right)}^{\prime }\right))].\end{array}$$

(77)

Here:

$$\begin{array}{c}\hfill d_0\left(x_{j\left(r\right)}^{\prime }\right)={\tilde{\delta }}_f^{\prime 2}+{\delta }_i^2-2{\delta }_i{\tilde{\delta }}_f^{\prime }cos\left({\phi }_{-}\right),g_0\left(x_{j\left(r\right)}^{\prime }\right)=(1+{\delta }_i^2)-\frac{(1+{\tilde{\delta }}_f^{\prime 2})}{(1-x_{j\left(r\right)}^{\prime })}.\end{array}$$

(78)

$${\tilde{\delta }}_f^{\prime }=(1-x_{j\left(r\right)}^{\prime }){\delta }_f^{\prime }.$$

(79)

In order to compare the resonant bremsstrahlung in the field of an X-ray pulsar and the regular bremsstrahlung of particles in the absence of the external electromagnetic field, the research utilizes the cross-section without an external field $d{\sigma }_{*}$ in the following form [53,56]:

$$\begin{array}{c}\hfill d{\sigma }_{*}=\frac{2}{\pi }{Z}^2\alpha r_e^2{(1-x^{\prime })}^3\frac{[D_0\left(x^{\prime }\right)+{(m/E_i)}^2{D}_1\left(x^{\prime }\right)]}{{[d_0\left(x^{\prime }\right)+{(m/2E_i)}^2{g}_0^2\left(x^{\prime }\right)]}^2}·\frac{d{x}^{\prime }}{x^{\prime }}d{\delta }_i^{\prime 2}d{\delta }_f^{\prime 2}d{\phi }_{-}^{\prime }.\end{array}$$

(80)

where:

$$\begin{array}{c}\hfill D_0\left(x^{\prime }\right)=\frac{{\delta }_i^{\prime 2}}{{(1+{\delta }_i^{\prime 2})}^2}+\frac{{\tilde{\delta }}_f^{\prime 2}}{{(1+{\tilde{\delta }}_f^{\prime 2})}^2}+\frac{x{{}^{\prime }}^2}{2(1-x^{\prime })}·\\ \hfill ·\frac{({\delta }_i^{\prime 2}+{\tilde{\delta }}_f^{\prime 2})}{(1+{\delta }_i^{\prime 2})(1+{\tilde{\delta }}_f^{\prime 2})}-[(1-x^{\prime })+\frac{1}{(1-x^{\prime })}]·\frac{{\delta }_i^{\prime }{\tilde{\delta }}_f^{\prime }}{(1+{\delta }_i^{\prime 2})(1+{\tilde{\delta }}_f^{\prime 2})}cos{\phi }_{-}.\end{array}$$

(81)

$$D_1\left(x^{\prime }\right)=b_i\left(x^{\prime }\right)+\frac{b_f\left(x^{\prime }\right)}{{(1-x^{\prime })}^2}.$$

(82)

$$b_i\left(x^{\prime }\right)=\frac{{\delta }_i^{\prime 2}}{12{(1+{\delta }_i^{\prime 2})}^3}{\xi }_i.$$

(83)

$$\begin{array}{c}\hfill {\xi }_i=[(1-x^{\prime })+\frac{1}{(1-x^{\prime })}](9+4{\delta }_i^{\prime 2}+3{\delta }_i^{\prime 4})-2(1-{\delta }_i^{\prime 2})(3-{\delta }_i^{\prime 2})-\frac{x^{\prime 2}}{(1-x^{\prime })}(9+2{\delta }_i^{\prime 2}+{\delta }_i^{\prime 4}).\end{array}$$

(84)

It is possible to obtain $b_f\left(x^{\prime }\right)$ from (83) and (84) by substitution ${\delta }_i^{\prime 2}\to {\tilde{\delta }}_f^{\prime 2}$.

Furthermore, the authors make integration on the azimuthal angle ${\phi }_{-}$ of resonant cross-section (75) and cross-section without the electromagnetic X-ray pulsar field (80):

$$\begin{array}{c}\hfill d{\sigma }_{j\left(r\right)}=\alpha r_e^2{Z}^2{\eta }_0^{2r}\frac{r{\left(\omega \tau \right)}^2({\tilde{\delta }}_f^{\prime 2}+{\delta }_i^{\prime 2})(1-x_{j\left(r\right)}^{\prime })}{4G_{j\left(r\right)}^{3/2}·{\epsilon }_r^2}·K_{j\left(r\right)}{P}_{\left(r\right)}^{res}\left({\beta }_j\right)·d{x}_{j\left(r\right)}^{\prime }d{\delta }_i^{\prime 2}d{\delta }_f^{\prime 2}.\end{array}$$

(85)

Here,

$$\begin{array}{c}\hfill G_{j\left(r\right)}={({\tilde{\delta }}_f^{\prime 2}-{\delta }_i^{\prime 2})}^2+\frac{1}{2}{\left(\frac{m}{E_i}\right)}^2({\tilde{\delta }}_f^{\prime 2}+{\delta }_i^{\prime 2})[g_0^2\left(x_{j\left(r\right)}^{\prime }\right)+\frac{{\epsilon }_r}{{sin}^2({\theta }_i/2)}({\epsilon }_r+g_0\left(x_{j\left(r\right)}^{\prime }\right))].\end{array}$$

(86)

The cross-section in the absence of the external field:

$$d{\sigma }_{*}=4Z^2\alpha r_e^2\frac{{(1-x^{\prime })}^3}{G_0^{3/2}}({\delta }_i^{\prime 2}+{\tilde{\delta }}_f^{\prime 2})·D_2\left(x^{\prime }\right)·\frac{d{x}^{\prime }}{x^{\prime }}d{\delta }_i^{\prime 2}d{\delta }_f^{\prime 2}.$$

(87)

$G_{\left(0\right)}$ is obtained from $G_{j\left(r\right)}$ (86) when ${\epsilon }_r=0$. Additionally:

$$D_2\left(x^{\prime }\right)=D_0^{\prime }\left(x^{\prime }\right)+{(m/E_i)}^2{D}_1^{\prime }\left(x^{\prime }\right).$$

(88)

$$\begin{array}{c}\hfill D_0^{\prime }\left(x^{\prime }\right)=\frac{{\delta }_i^{\prime 2}}{{(1+{\delta }_i^{\prime 2})}^2}+\frac{{\tilde{\delta }}_f^{\prime 2}}{{(1+{\tilde{\delta }}_f^{\prime 2})}^2}+\frac{x{{}^{\prime }}^2}{2(1-x^{\prime })}·\\ \hfill ·\frac{({\delta }_i^{\prime 2}+{\tilde{\delta }}_f^{\prime 2})}{(1+{\delta }_i^{\prime 2})(1+{\tilde{\delta }}_f^{\prime 2})}-[(1-x^{\prime })+\frac{1}{(1-x^{\prime })}]·\frac{2{\delta }_i^{\prime 2}{\tilde{\delta }}_f^{\prime 2}}{(1+{\delta }_i^{\prime 2})(1+{\tilde{\delta }}_f^{\prime 2})({\delta }_i^{\prime 2}+{\tilde{\delta }}_f^{\prime 2})}.\end{array}$$

(89)

$$\begin{array}{c}\hfill D_1^{\prime }\left(x^{\prime }\right)=D_1\left(x^{\prime }\right)+[(1-x^{\prime })+\frac{1}{(1-x^{\prime })}]·\frac{g_0^2\left(x^{\prime }\right){\delta }_i^{\prime 2}{\tilde{\delta }}_f^{\prime 2}}{2(1+{\delta }_i^{\prime 2})(1+{\tilde{\delta }}_f^{\prime 2}){({\delta }_i^{\prime 2}+{\tilde{\delta }}_f^{\prime 2})}^2}.\end{array}$$

(90)

Finally, the investigation derives the ratio of the maximal resonant differential cross-section in the presence of the X-ray pulsar $d{\sigma }_{j\left(r\right)}^{max}\approx {\sigma }_{j\left(r\right)}\left(\right|{\beta }_j|\ll 1)$ (85) to the cross-section without the external field (87):

$$\begin{array}{c}\hfill R_{j\left(r\right)}^{max}=\frac{d{\sigma }_{j\left(r\right)}^{max}}{d{\sigma }_{*}}=r{a}_{\left(r\right)}{\left(\frac{{\eta }_0^r\omega \tau }{4{\epsilon }_r}\right)}^2{\left(\frac{x_{j\left(r\right)}^{\prime }}{1-x_{j\left(r\right)}^{\prime }}\right)}^2·\frac{K_{j\left(r\right)}}{D_2\left(x_{j\left(r\right)}^{\prime }\right)}{\left[\frac{G_0}{G_{j\left(r\right)}}\right]}^{3/2},j=i,f.\end{array}$$

(91)

The obtained Equation (91) defines the difference between the resonant differential cross-section and the non-resonant cross-section in the absence of the field from the neutron star for the channels A and B. The functions $R_{j\left(r\right)}^{max}$ depend on the emission angles of the final electron and hard gamma-quantum (parameters ${\delta }_i^{\prime 2}$ and ${\delta }_f^{\prime 2}$) and the frequency of the hard gamma-quantum within the diapason from ${\omega }_{i\left(r\right)}^{\prime }$ to $[{\omega }_{i\left(r\right)}^{\prime }+d{\omega }_{i\left(r\right)}^{\prime }]$ (for the channel A) and from ${\omega }_{f\left(r\right)}^{\prime }$ to $[{\omega }_{f\left(r\right)}^{\prime }+d{\omega }_{f\left(r\right)}^{\prime }]$ (for the channel B).

The dependency of the function $R_{j\left(r\right)}^{max}$ (91) on ${\delta }_j^{\prime 2}$ for channels A and B is illustrated on the Figure 5 for the fixed magnitude of hard gamma-quantum frequency. It is possible to observe that the magnitudes $D_0\left(x^{\prime }\right)\to 0$, $d_0\left(x^{\prime }\right)\to 0$ and the cross-sections obtain sharp maximums. Moreover, when the number of resonance (the amount of hard gamma-quanta that electron absorbs) increases the peak values decrease.

Therefore, to summarize the investigation the authors make integration of the resonant cross-section (85) on the parameters ${\delta }_f^{\prime 2}$ (channel A) and ${\delta }_i^{\prime 2}$ (channel B).

$$d{\sigma }_{i\left(r\right)}^{\prime }=\left(\alpha r_e^2{Z}^2\right)g_r{F}_{i\left(r\right)}d{x}_{i\left(r\right)}^{\prime }d{\delta }_i^{\prime 2}.$$

(92)

$$d{\sigma }_{f\left(r\right)}^{\prime }=\left(\alpha r_e^2{Z}^2\right)g_r{F}_{f\left(r\right)}d{x}_{f\left(r\right)}^{\prime }d{\delta }_f^{\prime 2}.$$

(93)

Here,

$$g_r={\left(\frac{E_1}{rm}\right)}^2{\left({\eta }_0^r\omega \tau \right)}^2.$$

(94)

$$F_{i\left(r\right)}=\frac{r}{{\epsilon }_r^2}\frac{x_{i\left(r\right)}^{\prime }}{(1-x_{i\left(r\right)}^{\prime })}{K}_{i\left(r\right)}{P}_{\left(r\right)}^{res}\left({\beta }_i\right).$$

(95)

$$F_{f\left(r\right)}=\frac{r}{{\epsilon }_r^2}{x}_{f\left(r\right)}^{\prime }(1-x_{f\left(r\right)}^{\prime })K_{f\left(r\right)}{P}_{\left(r\right)}^{res}\left({\beta }_f\right).$$

(96)

where functions $F_{i\left(r\right)}$ (95) and $F_{f\left(r\right)}$ (96) define the values of the cross-sections (92) and (93). Furthermore, for the resonant parameter magnitudes of $|{\beta }_i|\ll 1$ and $|{\beta }_f|\ll 1$ (28) and (29) the $F_{j\left(r\right)}$ functions reach maximums:

$$\begin{array}{c}\hfill d{\sigma }_{i\left(r\right)}^{\prime max}=\alpha r_e^2{Z}^2{\mathsf{\Phi }}_{i\left(r\right)}^{max}d{x}_{i\left(r\right)}^{\prime }d{\delta }_i^{\prime 2},\\ \hfill d{\sigma }_{f\left(r\right)}^{\prime max}=\alpha r_e^2{Z}^2{\mathsf{\Phi }}_{f\left(r\right)}^{max}d{x}_{f\left(r\right)}^{\prime }d{\delta }_f^{\prime 2}.\end{array}$$

(97)

$${\mathsf{\Phi }}_{i\left(r\right)}^{max}=g_r{F}_{i\left(r\right)}^{max},{\mathsf{\Phi }}_{f\left(r\right)}^{max}=g_r{F}_{f\left(r\right)}^{max}.$$

(98)

$$\begin{array}{c}\hfill F_{i\left(r\right)}^{max}=\frac{r{a}_{\left(r\right)}}{{\epsilon }_r^2}\frac{x_{i\left(r\right)}^{\prime }}{(1-x_{i\left(r\right)}^{\prime })}{K}_{i\left(r\right)},\\ \hfill F_{f\left(r\right)}^{max}=\frac{r{a}_{\left(r\right)}}{{\epsilon }_r^2}{x}_{f\left(r\right)}^{\prime }(1-x_{f\left(r\right)}^{\prime })K_{f\left(r\right)}.\end{array}$$

(99)

For the conditions of the considerable initial electron energies (45), the researchers make further calculations with the obtained functions (99):

$$\begin{array}{c}\hfill F_{i\left(r\right)}^{max}\approx r{a}_{\left(r\right)}{\left(\frac{r^r}{r!}\right)}^2\frac{{\delta }_i^{\prime 2(r-1)}}{{(1+{\delta }_i^{\prime 2})}^{2r}},F_{f\left(r\right)}^{max}\sim \frac{1}{{\epsilon }_r^2}\ll 1.\end{array}$$

(100)

This equation indicates that for the considerable initial electron energies, the channel B is suppressed in contrast to the channel A.

The functions $F_{j\left(r\right)}^{max},j=i,f$ (99) are delineated in Figure 6. The analysis of the Figure 6a,b illustrates that the channel A function $F_{i\left(r\right)}^{max}$ exceeds the channel B function $F_{f\left(r\right)}^{max}$ by several orders of magnitude. In other words, the level of the hard gamma-quanta emission in the channel A exceeds the radiation in the channel B. Thus, the resonant differential cross-section of the channel A may attain ${\mathsf{\Phi }}_{i\left(1\right)}^{max}\sim {10}^{10}$ with ${\eta }_0=0.01$ in the 1 resonance. The resonant cross-section decreases in accordance to the intensity as $\sim {\eta }_0^{2r}$. For the case ${\epsilon }_1\gg 1$ the function $F_{i\left(r\right)}^{max}$ (100) is delineated on the Figure 7 that is qualitatively similar to the Figure 6 with ${\epsilon }_1\sim 1$.

Additionally,

Table 1. The magnitudes of the differential cross-sections (${\mathsf{\Phi }}_{j\left(r\right)}^{max}$) (98) and resonant frequencies ${\delta }_j^{\prime 2},j=i,f$ (30) for channels A and B for the $r=$ 1, 2, and 3 resonances when $E_1=100$ MeV, $E_i=300$ MeV, $\left(\omega \tau \right)={10}^5$, ${\eta }_0={10}^{-2}$ ($F_0\sim {10}^{13}$ V/cm).

${\mathit{E}}_1=100$ MeV, ${\mathit{E}}_{\mathit{i}}=300$ MeV
r	Channel	${\mathit{\delta }}_{\mathit{j}}^{\mathbf{\prime }\mathbf{2}}$	${\mathit{\omega }}_{\mathit{j}\mathbf{\left(}\mathit{r}\mathbf{\right)}}^{\mathbf{\prime }}$, MeV	${\mathbf{\Phi }}_{\mathit{j}\mathbf{\left(}\mathit{r}\mathbf{\right)}}^{\mathit{max}}({\mathbf{\eta }}_{\mathbf{0}}=\mathbf{0.01})$
1	A	${\delta }_i^{\prime 2}\ge 0$	${\omega }_{i\left(1\right)}^{\prime }\le 225$	${\mathsf{\Phi }}_{i\left(1\right)}^{max}\approx 4.92·{10}^{10}$
	B	$0\le {\delta }_f^{\prime 2}\le 12$	$155\le {\omega }_{f\left(1\right)}^{\prime }\le 225$	${\mathsf{\Phi }}_{f\left(1\right)}^{max}\approx 3.08·{10}^9$
2	A	${\delta }_{i\left(2\right)*}^{\prime 2}\approx 0.314$	${\omega }_{i\left(2\right)}^{\prime }\approx 216.9$	${\mathsf{\Phi }}_{i\left(2\right)}^{max}\approx 8.39·{10}^5$
	B	${\delta }_{f\left(2\right)*}^{\prime 2}=14.317$	${\omega }_{f\left(2\right)}^{\prime }\approx 209.5$	${\mathsf{\Phi }}_{f\left(2\right)}^{max}\approx 3.2·{10}^4$
3	A	${\delta }_{i\left(3\right)*}^{\prime 2}\approx 0.49$	${\omega }_{i\left(3\right)}^{\prime }\approx 216.9$	${\mathsf{\Phi }}_{i\left(3\right)}^{max}\approx 56.32$
	B	${\delta }_{f\left(3\right)*}^{\prime 2}=29.362$	${\omega }_{f\left(3\right)}^{\prime }\approx 209.5$	${\mathsf{\Phi }}_{f\left(3\right)}^{max}\approx 1.34$

gives an overview of various magnitudes of differential cross-sections (${\mathsf{\Phi }}_{j\left(r\right)}^{max}$) and resonant frequencies for both channels A and B for intensities of a wave for the 1, 2, and 3 resonances when $E_1=100$ MeV, $E_i=300$ MeV, $\left(\omega \tau \right)={10}^5$, ${\eta }_0={10}^{-2}$ ($F_0\sim {10}^{13}$ V/cm). Table 1 outlines that the biggest frequency magnitudes for the high-numbered resonances position away from the first resonance radiation interval, on the other hand, the values of the high resonances cross-sections are still considerable and represent a certain scientific interest.

Table 2. The magnitudes of the differential cross-section (${\mathsf{\Phi }}_{j\left(r\right)}^{max},j=i$) (98) and resonant frequency ${\delta }_j^{\prime 2},j=i$ (30) for channel A for the $r=$ 1, 2, and 3 resonances when the energies of the initial electrons have magnitude of $E_i=100$ GeV (in such conditions channel B is essentially suppressed in comparison to the channel A). The data indicates that the anomalous emission of high-energy gamma-quanta is observable.

${\mathit{E}}_1=100$ MeV, ${\mathit{E}}_{\mathit{i}}=100$ GeV
r	Channel	${\mathit{\delta }}_{\mathit{j}}^{\mathbf{\prime }\mathbf{2}}$	${\mathit{\omega }}_{\mathit{j}\mathbf{\left(}\mathit{r}\mathbf{\right)}}^{\mathbf{\prime }}$, GeV	${\mathbf{\Phi }}_{\mathit{j}\mathbf{\left(}\mathit{r}\mathbf{\right)}}^{\mathit{max}}({\mathbf{\eta }}_{\mathbf{0}}=\mathbf{0.01})$
1	A	${\delta }_i^{\prime 2}\ge 0$	${\omega }_{i\left(1\right)}^{\prime }\le 99.90$	${\mathsf{\Phi }}_{i\left(1\right)}^{max}\approx 3.47·{10}^{10}$
2	A	${\delta }_{i\left(2\right)*}^{\prime 2}\approx 0.314$	${\omega }_{i\left(2\right)}^{\prime }\approx 99.93$	${\mathsf{\Phi }}_{i\left(2\right)}^{max}\approx 7.64·{10}^5$
3	A	${\delta }_{i\left(3\right)*}^{\prime 2}\approx 0.49$	${\omega }_{i\left(3\right)}^{\prime }\approx 99.95$	${\mathsf{\Phi }}_{i\left(3\right)}^{max}\approx 54.16$

represents the results for the frequencies and maximal probabilities of radiation of spontaneous gamma-quantum when the energies of the initial electrons have magnitude of $E_i=100$ GeV. In addition, it is important to underline that within such conditions the channel B is essentially suppressed in correlation to the channel A. Table 2 indicates that the anomalous emission of high-energy gamma-quanta is observable.

5. Conclusions

This paper scrutinized the effect of resonant bremsstrahlung of ultrarelativistic electrons on a nucleus with radiation of a hard gamma-quantum as a part of the processes that occur during the circulation of the large-scaled particle fluxes near the neutron stars. It is important to underline that the constructed theoretical model of the phenomenon simulates the pulsed character of the external field. The obtained results of the investigation may provide an opportunity for the deeper study of the spectrum of X-ray pulsars and magnetars. To summarize, the research systematizes the following statements:

• Under the resonant conditions, the resonant second-order bremsstrahlung process transforms into two first-order processes with respect to the fine structure constant: the external pulsed field-stimulated Compton-effect with simultaneous absorption of r gamma-quanta and neutron star field-assisted scattering of an ultrarelativistic electron on a nucleus.
• The paper analyzed the resonant bremsstrahlung of ultrarelativistic electrons and implemented various characteristic parameters in order to describe the process, for example, the article applied the effects characteristic energy (31) that has a magnitude of $E_1\sim 100$ MeV. The study focused on the ultrarelativistic electrons that propagate within a narrow angle cone along the waves propagation from the X-ray pulsar.
• The resonant frequency of a hard gamma-quantum significantly varies depending on the channel of interaction. Thus, for the channel B the radiation spectrum realizes a specific area of effect with three distinctive roots for resonant frequency magnitude. Additionally, it is important to note that the resonant frequency of a hard gamma-quantum obtains its maximum when the particle is being scattered at zero angle and propagates along the initial and final electrons.
• The higher resonances (with a bigger resonance number value $r=2,3,\dots$) designate distinctive maximum peaks and provide a significant impact on the cross-section distribution, however the first resonance (with characteristic resonant number $r=1$) still contributes a major impact.
• The computational calculations (Table 1 and Table 2) that were carried out on the basis of the constructed theoretical model propose that for the intensity of the neutron star wave of $F_0\sim {10}^{13}$ V/cm and the energies of the initial electrons of $E_i=300$ MeV and $E_i=100$ GeV, the hard gamma-quanta attain considerable values and the magnitude of the resonant cross-section of the bremsstrahlung effect obtains degree from $\sim {10}^{10}$ for the 1 resonance of channel A to $\sim 10$ (in the $\alpha Z^2{r}_e^2$ units) for the 3 resonance of channel B.

Finally, the obtained results provide the explanation of the anomalous radiation of the 100 GeV gamma-quanta near the neutron stars, magnetars and X-ray pulsars.