Statefinder and Om Diagnostics for New Generalized Chaplygin Gas Model
Abstract
:1. Introduction
2. New Generalized Chaplygin Gas Model
3. Geometrical Diagnostics
3.1. Statefinder Diagnostics
- For CDM →.
- For Quintessence →.
- For CG →.
- For SCDM →.
3.2. Diagnostics
4. Conclusions
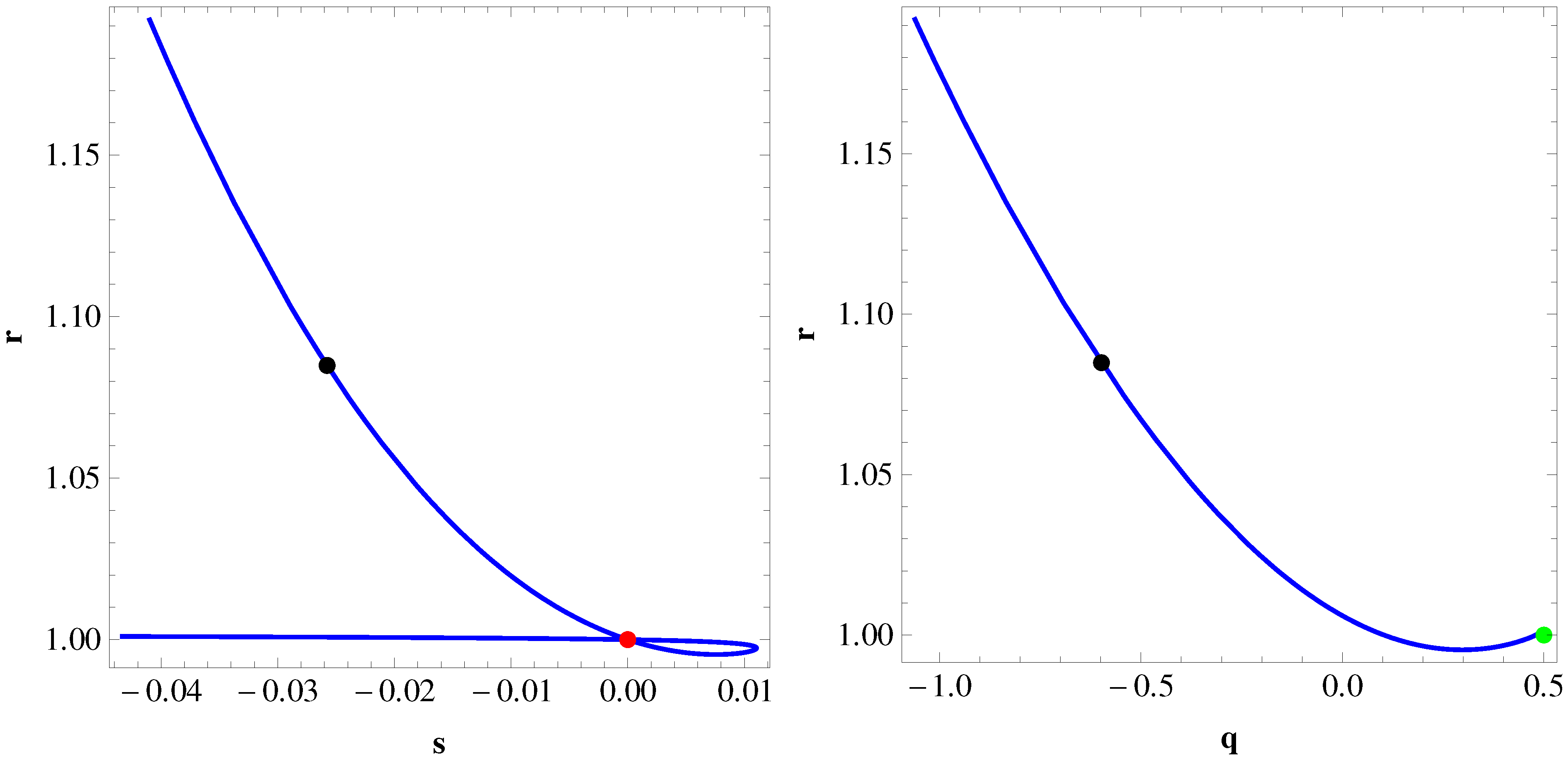
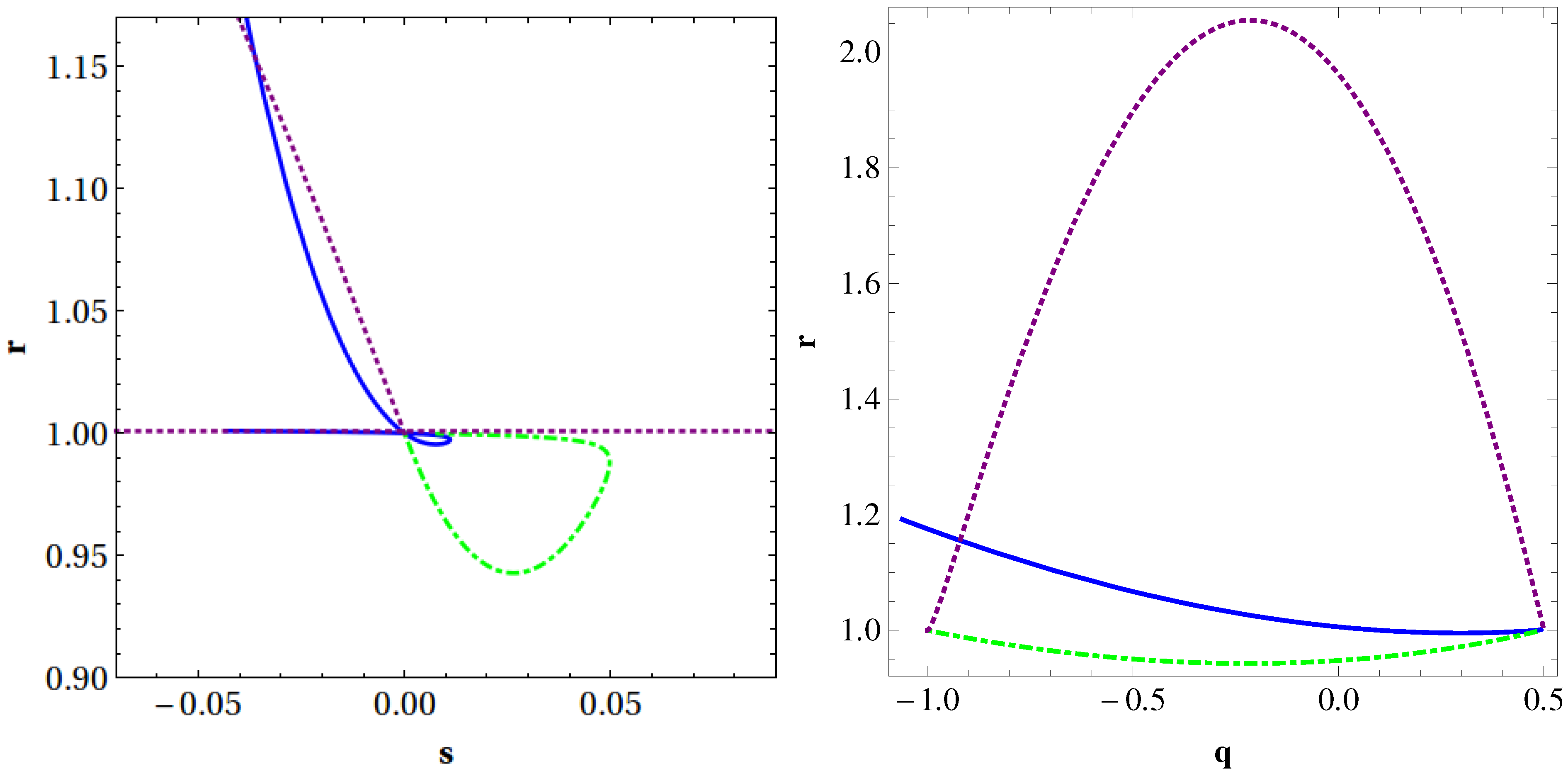
- The evolutionary curve in the plane of NGCG model shows Chaplygin gas behaviour at a late time, while starting its evolution along the line and passes through the CDM fixed point () by making a swirl initially.
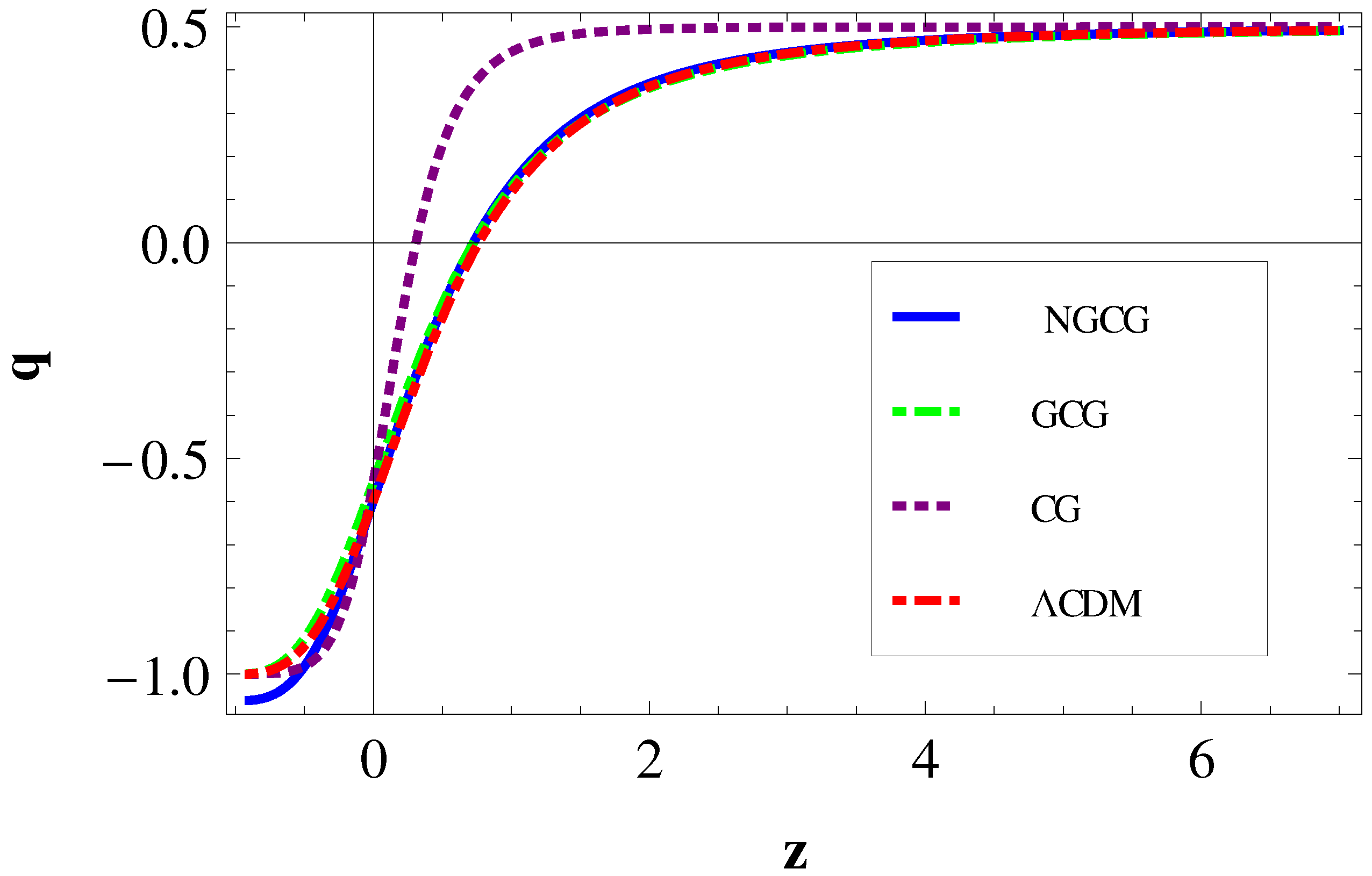
- The curve of the q-r plane of the NGCG model shows that it evolves from the matter-dominated Universe i.e., SCDM ( , ) initially and approaches above the de Sitter expansion () (, ) at a late time, and it always lies in the Chaplygin gas region throughout the evaluation.
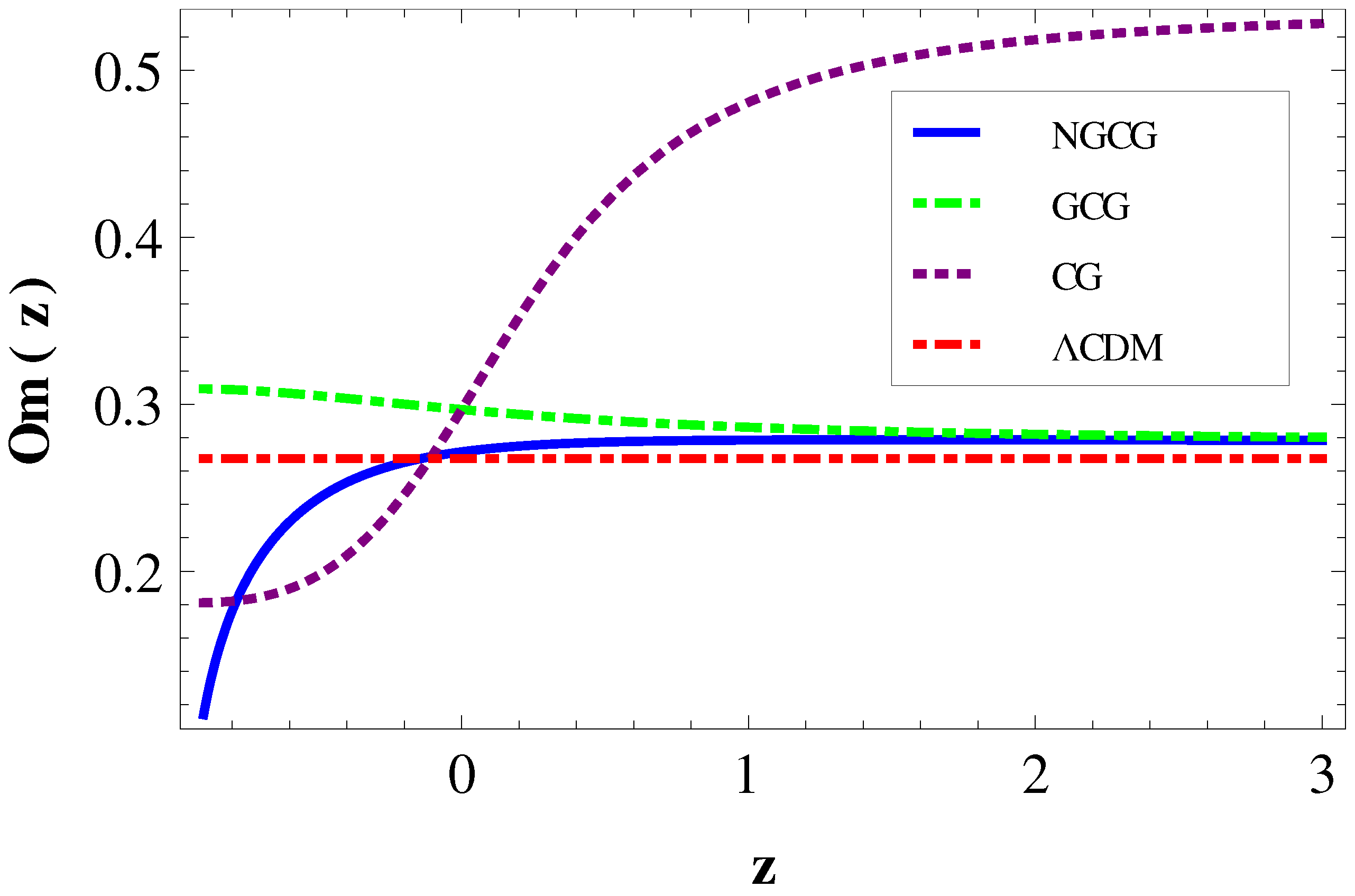
- The evolutionary trajectory of of NGCG model backs the growing DE model.
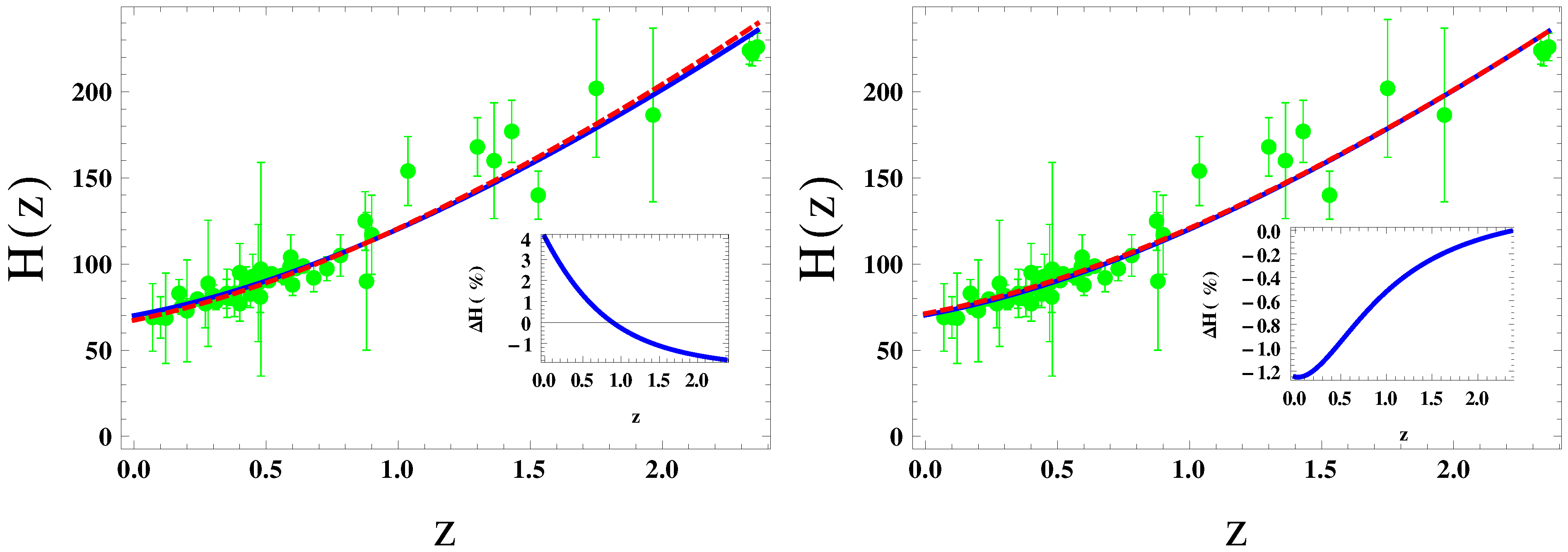
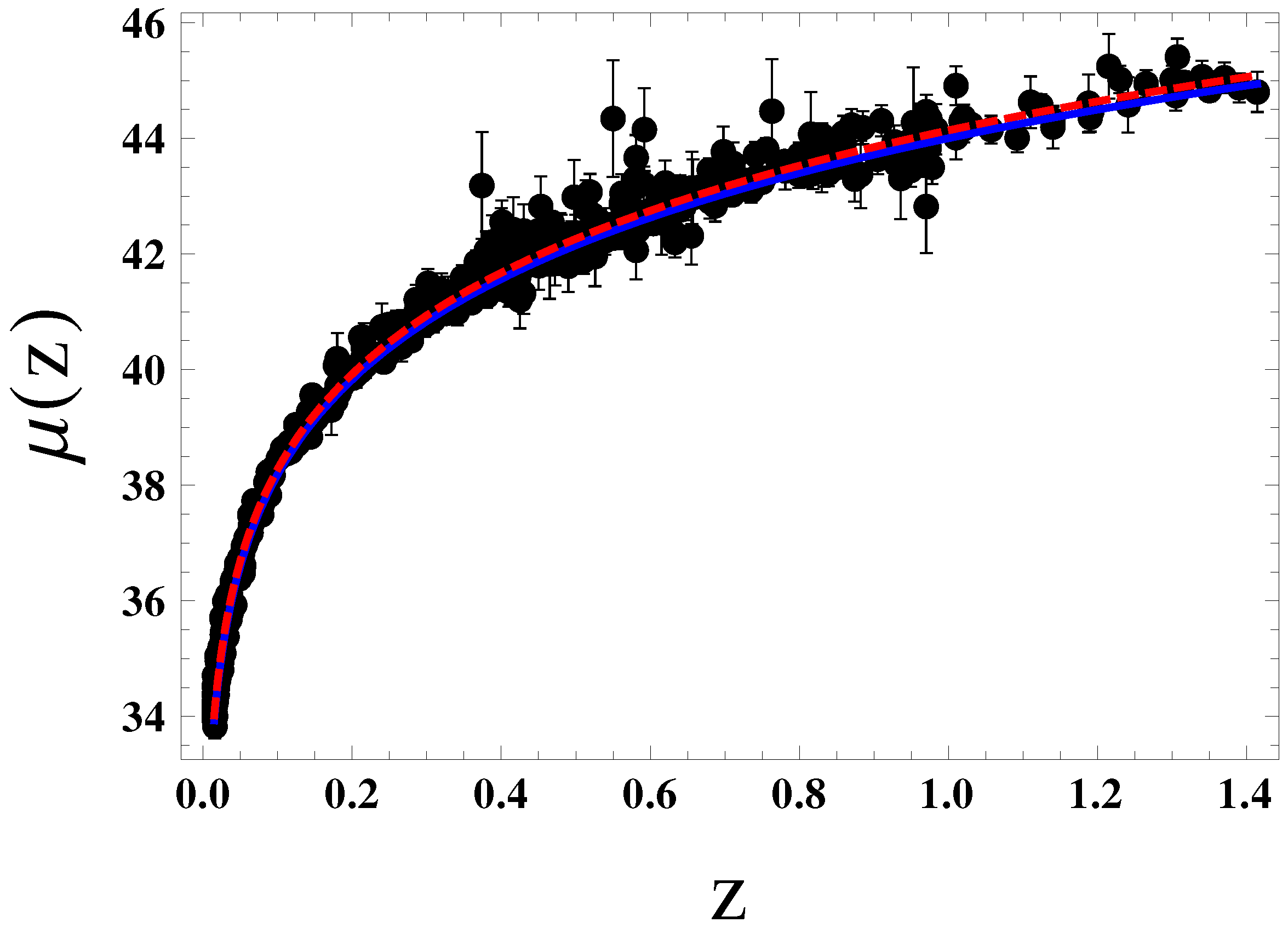
- Finally, we investigated the evolutions of the Hubble parameter and the distance modulus for the model under consideration and the standard CDM model and compare that with the observational datasets (see Figure 1 and Figure 2). For the best-fit case, it has been observed that the relative differences () between the two models (NGCG &CDM) are negligible around z∼ (see inset diagram of Figure 1 (left panel)). Furthermore, we have found from Figure 2 that the present model reproduces the observed values of the distance modulus quite effectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef] [Green Version]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% determination of the local value of the Hubble constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Font-Ribera, A.; Kirkby, D.; Busca, N.; Miralda-Escudé, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, É.; Bailey, S.; Bhardwaj, V.; et al. Quasar-Lyman α Forest Cross-Correlation from BOSS DR11: Baryon Acoustic Oscillations. JCAP 2014, 05, 027. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. arXiv 2021, arXiv:2105.05208. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Mena, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the Realm of the Hubble tension- a Review of Solutions. arXiv 2021, arXiv:2103.01183. [Google Scholar]
- Sahni, V.; Starobinsky, A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373–444. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom Energy: Dark Energy with w < −1 Causes a Cosmic Doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. A dynamical solution to the problem of a small cosmological constant and late time cosmic acceleration. Phys. Rev. Lett. 2000, 85, 4438–4441. [Google Scholar] [CrossRef] [Green Version]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef] [Green Version]
- Sami, M.; Chingangbam, P.; Qureshi, T. Aspects of tachyonic inflation with an exponential potential. Phys. Rev. D 2002, 66, 043530. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T.; Choudhury, T.R. Can the clustered dark matter and the smooth dark energy arise from the same scalar field? Phys. Rev. D 2002, 66, 081301. [Google Scholar] [CrossRef] [Green Version]
- Hooft, G.T. Dimensional reduction in quantum gravity. Conf. Proc. C 1993, 930308, 284–296. [Google Scholar]
- Susskind, L. The World as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef] [Green Version]
- Cohen, A.G.; Kaplan, D.B.; Nelson, A.E. Effective field theory, black holes, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 4971–4974. [Google Scholar] [CrossRef] [Green Version]
- Li, M. A Model of holographic dark energy. Phys. Lett. B 2004, 603, 1–5. [Google Scholar] [CrossRef]
- Setare, M.R.; Zhang, J.; Zhang, X. Statefinder diagnosis in a non-flat universe and the holographic model of dark energy. JCAP 2007, 0703, 007. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X. Statefinder diagnostic for holographic dark energy model. Int. J. Mod. Phys. D 2005, 14, 1597–1606. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Liu, H. Statefinder diagnosis for the interacting model of holographic dark energy. Phys. Lett. B 2008, 659, 26–33. [Google Scholar] [CrossRef] [Green Version]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265. [Google Scholar] [CrossRef] [Green Version]
- Gorini, V.; Kamenshchik, A.; Moschella, U. Can the Chaplygin gas be a plausible model for dark energy? Phys. Rev. D 2003, 67, 063509. [Google Scholar] [CrossRef] [Green Version]
- Bean, R.; Dore, O. Are Chaplygin gases serious contenders for the dark energy? Phys. Rev. D 2003, 68, 023515. [Google Scholar] [CrossRef] [Green Version]
- Sandvik, H.B.; Tegmark, M.; Zaldarriaga, M.; Waga, I. The end of unified dark matter? Phys. Rev. D 2004, 69, 123524. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion and dark energy matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef] [Green Version]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Revival of the unified dark energy-dark matter model? Phys. Rev. D. 2004, 70, 083519. [Google Scholar] [CrossRef] [Green Version]
- Fabris, J.C.; Goncalves SV, B.; de Sá Ribeiro, R. Generalized Chaplygin gas with alpha = 0 and the lambda-CDM cosmological model. Gen. Rel. Grav. 2004, 36, 211–216. [Google Scholar] [CrossRef] [Green Version]
- Barreiro, T.; Bertolami, O.; Torres, P. WMAP five-year data constraints on the unified model of dark energy and dark matter. Phys. Rev. D 2008, 78, 043530. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Wu, F.Q.; Zhang, J. New generalized Chaplygin gas as a scheme for unification of dark energy and dark matter. JCAP 2006, 0601, 003. [Google Scholar] [CrossRef]
- Liao, K.; Pan, Y.; Zhu, Z.H. Observational constraints on new generalized Chaplygin gas model. Res. Astron. Astrophys. 2013, 13, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wu, Y.B.; Wang, D.; Yang, W.Q. The Extended Analysis on New Generalized Chaplygin Gas. Chin. Phys. Lett. 2009, 26, 089801. [Google Scholar]
- Salahedin, F.; Pazhouhesh, R.; Malekjani, M. Cosmological constrains on new generalized Chaplygin gas model. Eur. Phys. J. Plus 2020, 135, 429. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Paliathanasis, A.; Ghosh, S.; Wu, Y. Observational constraints of a new unified dark fluid and the H0 tension. arXiv 2019, arXiv:1904.10436. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Vagnozzi, S.; Di Valentino, E.; Mota, D.F.; Capozziello, S. Dawn of the dark: Unified dark sectors and the EDGES Cosmic Dawn 21-cm signal. arXiv 2019, arXiv:1907.05344. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey: V. Improving the Dark Energy Constraints Above z > 1 and Building an Early-Type-Hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef] [Green Version]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Cooke, R.J.; Pettini, M.; Steidel, C.C. One Percent Determination of the Primordial Deuterium Abundance. Astrophys. J. 2018, 855, 102. [Google Scholar] [CrossRef] [Green Version]
- Magana, J.; Amante, M.H.; Garcia-Aspeitia, M.A.; Motta, V. The Cardassian expansion revisited: Constraints from updated Hubble parameter measurements and type Ia supernova data. Mon. Not. R. Astron. Soc. 2018, 476, 1036–1049. [Google Scholar] [CrossRef]
- Al Mamon, A.; Saha, S. Testing lambert W equation of state with observational hubble parameter data. New Astron. 2021, 86, 101567. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder—A new geometrical diagnostic of dark energy. J. Exp. Theor. Phys. Lett. 2003, 77, 201–206. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Saini, T.D.; Starobinsky, A.A. Exploring the Expanding Universe and Dark Energy using the Statefinder Diagnostic. Mon. Not. R. Astron. Soc. 2003, 344, 1057. [Google Scholar] [CrossRef]
- Feng, C.J. Statefinder Diagnosis for Ricci Dark Energy. Phys. Lett. B 2008, 670, 231–234. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.B.; Li, S.; Fu, M.H.; He, J. A modified Chaplygin gas model with interaction. Gen. Rel. Grav. 2007, 39, 653–662. [Google Scholar] [CrossRef]
- Zhang, X. Statefinder diagnostic for coupled quintessence. Phys. Lett. B 2005, 611, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Cui, J.; Zhang, J.; Zhang, X. Interacting model of new agegraphic dark energy: Cosmological evolution and statefinder diagnostic. Int. J. Mod. Phys. D 2010, 19, 21–35. [Google Scholar] [CrossRef] [Green Version]
- Malekjani, M.; Mohammadi, A.K. Statefinder diagnostic and w − w′ analysis for interacting polytropic gas dark energy model. Int. J. Theor. Phys. 2012, 51, 3141–3151. [Google Scholar] [CrossRef]
- Malekjani, M.; Mohammadi, A.K. Statefinder diagnosis and the interacting ghost model of dark energy. Astrophys. Space Sci. 2013, 343, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Malekjani, M.; Zarei, R.; Jafarpour, M.H. Holographic dark energy with time varying model parameter c2(z). Astrophys. Space Sci. 2013, 343, 799–806. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W. Statefinder diagnostic for Yang-Mills dark energy model. Int. J. Mod. Phys. D 2008, 17, 1245–1254. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, A.K.; Malekjani, M. Cosmic Behavior, Statefinder Diagnostic and w − w′ Analysis for Interacting NADE model in Non-flat Universe. Astrophys. Space Sci. 2011, 331, 265–273. [Google Scholar] [CrossRef] [Green Version]
- Shao, Y.; Gui, Y. Statefinder parameters for tachyon dark energy model. Mod. Phys. Lett. A 2008, 23, 65–71. [Google Scholar] [CrossRef] [Green Version]
- Malekjani, M.; Mohammadi, A.K.; Nazari-pooya, N. Cosmological evolution and statefinder diagnostic for new holographic dark energy model in non flat universe. Astrophys. Space Sci. 2011, 332, 515–524. [Google Scholar] [CrossRef] [Green Version]
- Tavayef, M.; Sheykhi, A.; Bamba, K.; Moradpour, H. Tsallis Holographic Dark Energy. Phys. Lett. B 2018, 781, 195–200. [Google Scholar] [CrossRef]
- Sharma, U.K.; Pradhan, A. Diagnosing Tsallis holographic dark energy models with statefinder and ω − ω′. pair. Mod. Phys. Lett. A 2019, 34, 1950101. [Google Scholar] [CrossRef]
- Sharma, U.K.; Dubey, V.C. Statefinder diagnostic for the Renyi holographic dark energy. New Astron. 2020, 80, 101419. [Google Scholar] [CrossRef]
- Upadhyay, S.; Dubey, V.C. Diagnosing the Sharma-Mittal Holographic Dark Energy Model through the Statefinder. Gravit. Cosmol. 2021, 27, 281–291. [Google Scholar] [CrossRef]
- Srivastava, S.; Dubey, V.C.; Sharma, U.K. Statefinder diagnosis for Tsallis agegraphic dark energy model with ωD − ωD′ pair. Int. J. Mod. Phys. A 2020, 35, 2050027. [Google Scholar] [CrossRef]
- Sami, M.; Shahalam, M.; Skugoreva, M.; Toporensky, A. Cosmological dynamics of a nonminimally coupled scalar field system and its late time cosmic relevance. Phys. Rev. D 2012, 86, 103532. [Google Scholar] [CrossRef] [Green Version]
- Myrzakulov, R.; Shahalam, M. Statefinder hierarchy of bimetric and galileon models for concordance cosmology. JCAP 2013, 10, 047. [Google Scholar] [CrossRef] [Green Version]
- Rani, S.; Altaibayeva, A.; Shahalam, M.; Singh, J.K.; Myrzakulov, R. Constraints on cosmological parameters in power-law cosmology. JCAP 2015, 03, 031. [Google Scholar] [CrossRef] [Green Version]
- Farooq, O.; Ratra, B. Hubble parameter measurement constraints on the cosmological deceleration-acceleration transition redshift. Astrophys. J. 2013, 766, L7. [Google Scholar] [CrossRef]
- Ishida, E.E.; Reis, R.R.; Toribio, A.V.; Waga, I. When did cosmic acceleration start? How fast was the transition? Astropart. Phys. 2008, 28, 547–552. [Google Scholar] [CrossRef] [Green Version]
- Magaña, J.; Cárdenas, V.H.; Motta, V. Cosmic slowing down of acceleration for several dark energy parametrizations. J. Cosmol. Astropart. Phys. 2014, 10, 017. [Google Scholar] [CrossRef] [Green Version]
- Al Mamon, A.; Bamba, K.; Das, S. Constraints on reconstructed dark energy model from SN Ia and BAO/CMB observations. Eur. Phys. J. C 2017, 77, 29. [Google Scholar] [CrossRef] [Green Version]
- Al Mamon, A. Constraints on a generalized deceleration parameter from cosmic chronometers. Mod. Phys. Lett. A 2018, 33, 1850056. [Google Scholar] [CrossRef] [Green Version]
- Al Mamon, A.; Das, S. A parametric reconstruction of the deceleration parameter. Eur. Phys. J. C 2017, 77, 495. [Google Scholar] [CrossRef]
- Al Mamon, A. Constraints on kinematic model from Pantheon SNIa, OHD and CMB shift parameter measurements. Mod. Phys. Lett. A 2021, 36, 2150049. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78, 103502. [Google Scholar] [CrossRef] [Green Version]
- Zunckel, C.; Clarkson, C. Consistency Tests for the Cosmological Constant. Phys. Rev. Lett. 2008, 101, 181301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| Parameters | + BAO + CMB + BBN + SNIa (Pantheon) | + BAO + CMB + BBN + SNIa (Union 2.1) |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Mamon, A.; Dubey, V.C.; Bamba, K. Statefinder and Om Diagnostics for New Generalized Chaplygin Gas Model. Universe 2021, 7, 362. https://doi.org/10.3390/universe7100362
Al Mamon A, Dubey VC, Bamba K. Statefinder and Om Diagnostics for New Generalized Chaplygin Gas Model. Universe. 2021; 7(10):362. https://doi.org/10.3390/universe7100362
Chicago/Turabian StyleAl Mamon, Abdulla, Vipin Chandra Dubey, and Kazuharu Bamba. 2021. "Statefinder and Om Diagnostics for New Generalized Chaplygin Gas Model" Universe 7, no. 10: 362. https://doi.org/10.3390/universe7100362
APA StyleAl Mamon, A., Dubey, V. C., & Bamba, K. (2021). Statefinder and Om Diagnostics for New Generalized Chaplygin Gas Model. Universe, 7(10), 362. https://doi.org/10.3390/universe7100362







