Optical Forces on an Oscillating Dipole Near VO2 Phase Transition
Abstract
1. Introduction
2. Methodology
2.1. Modelling the VO Metal-Insulator Transition
2.2. Optical Forces near a Planar Surface
3. Results and Discussions
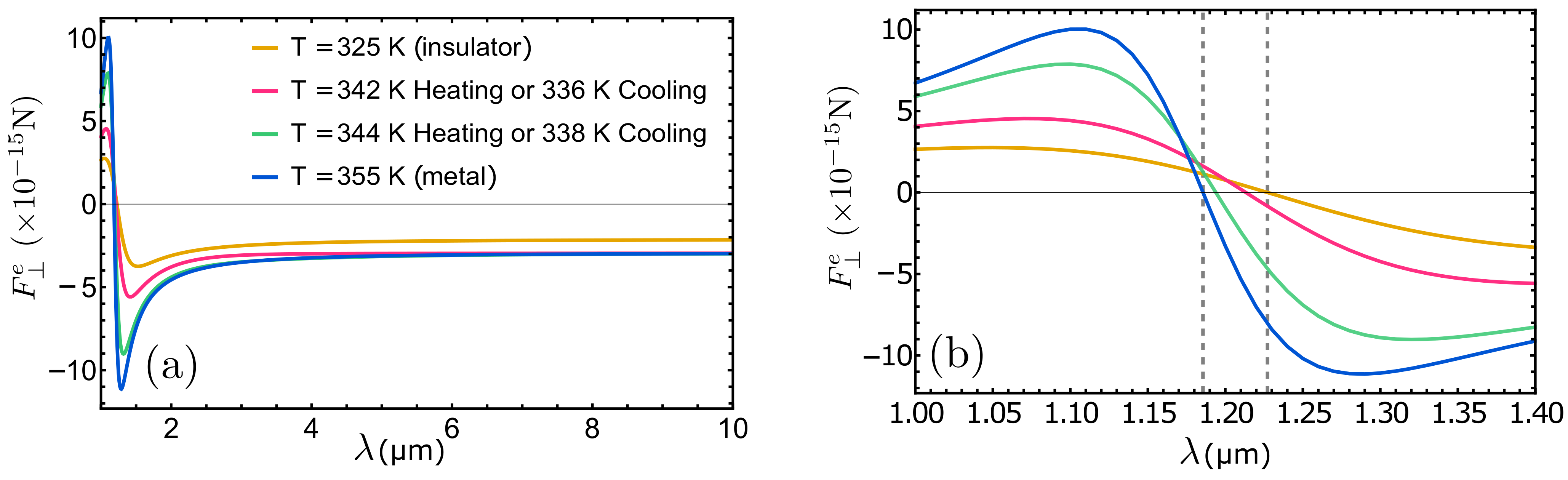
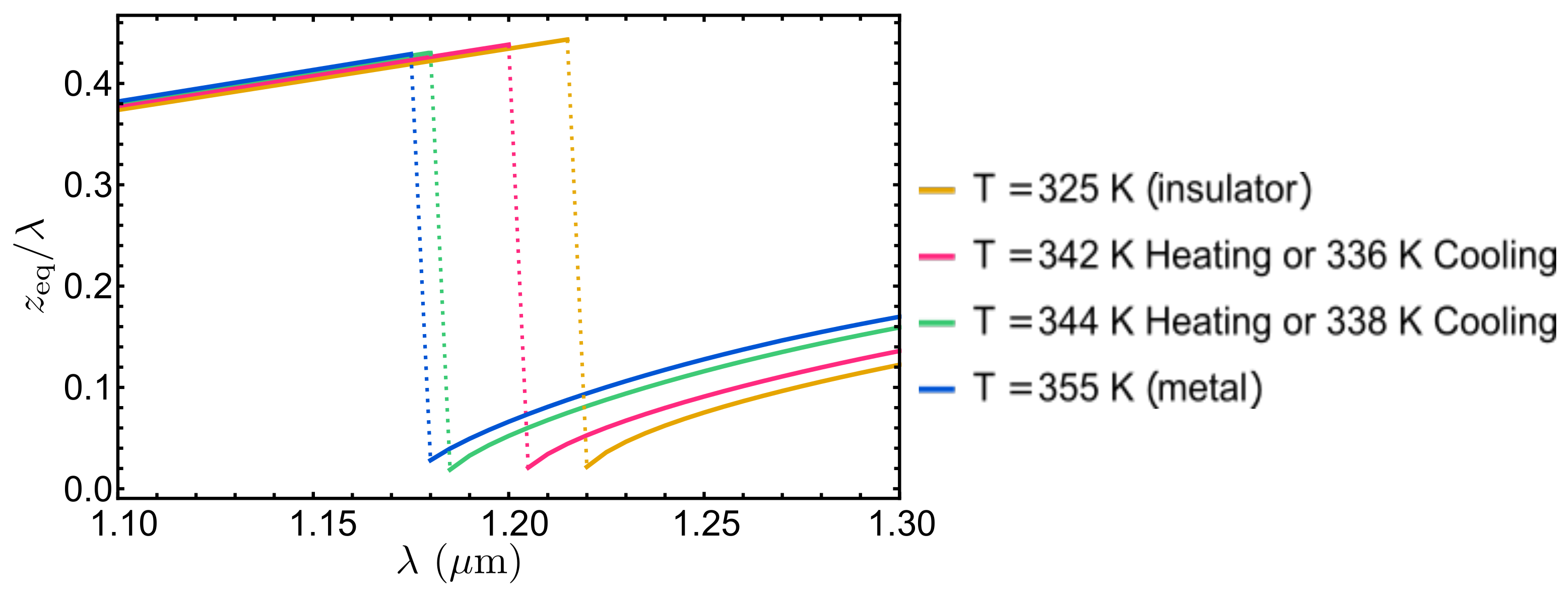
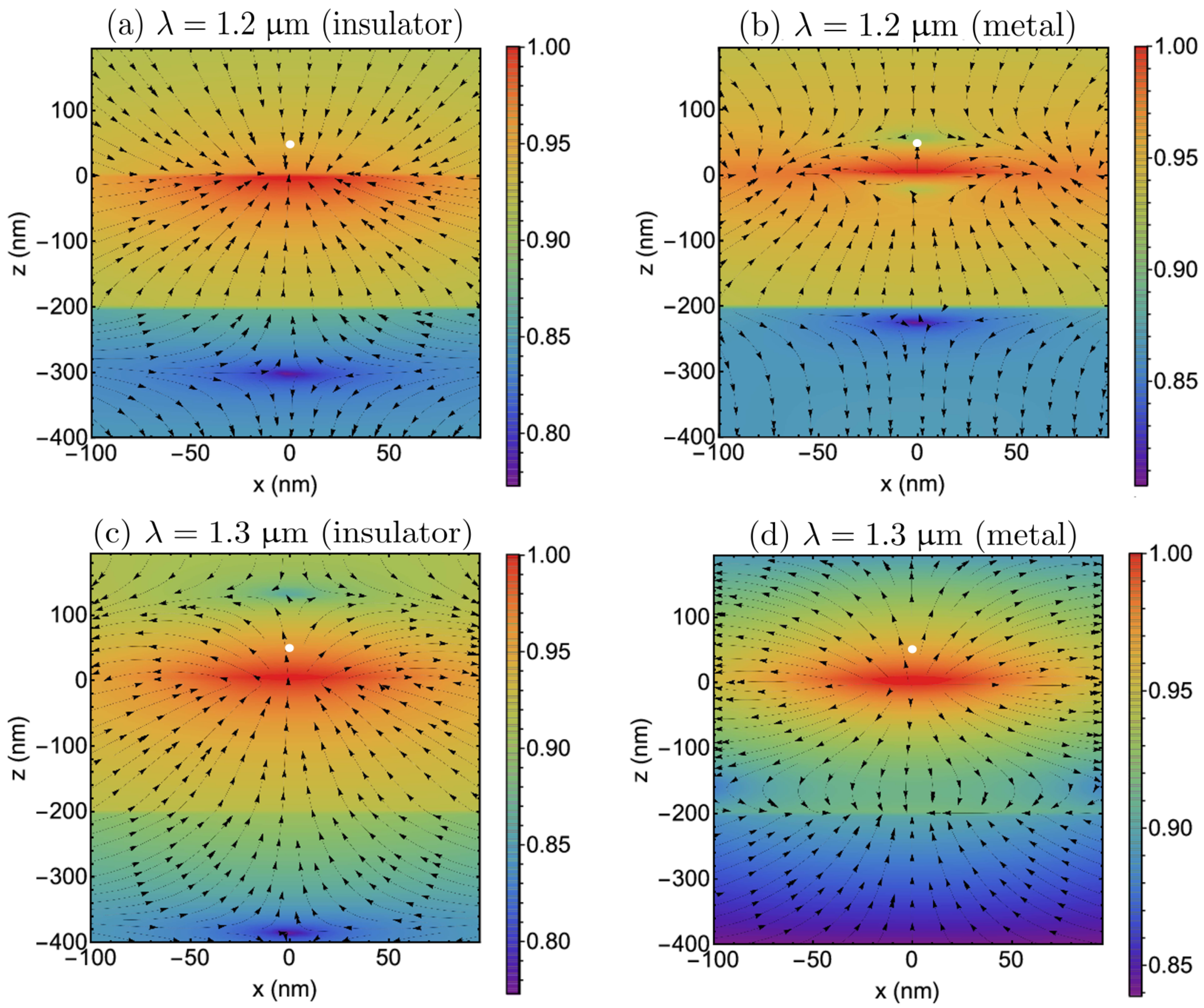
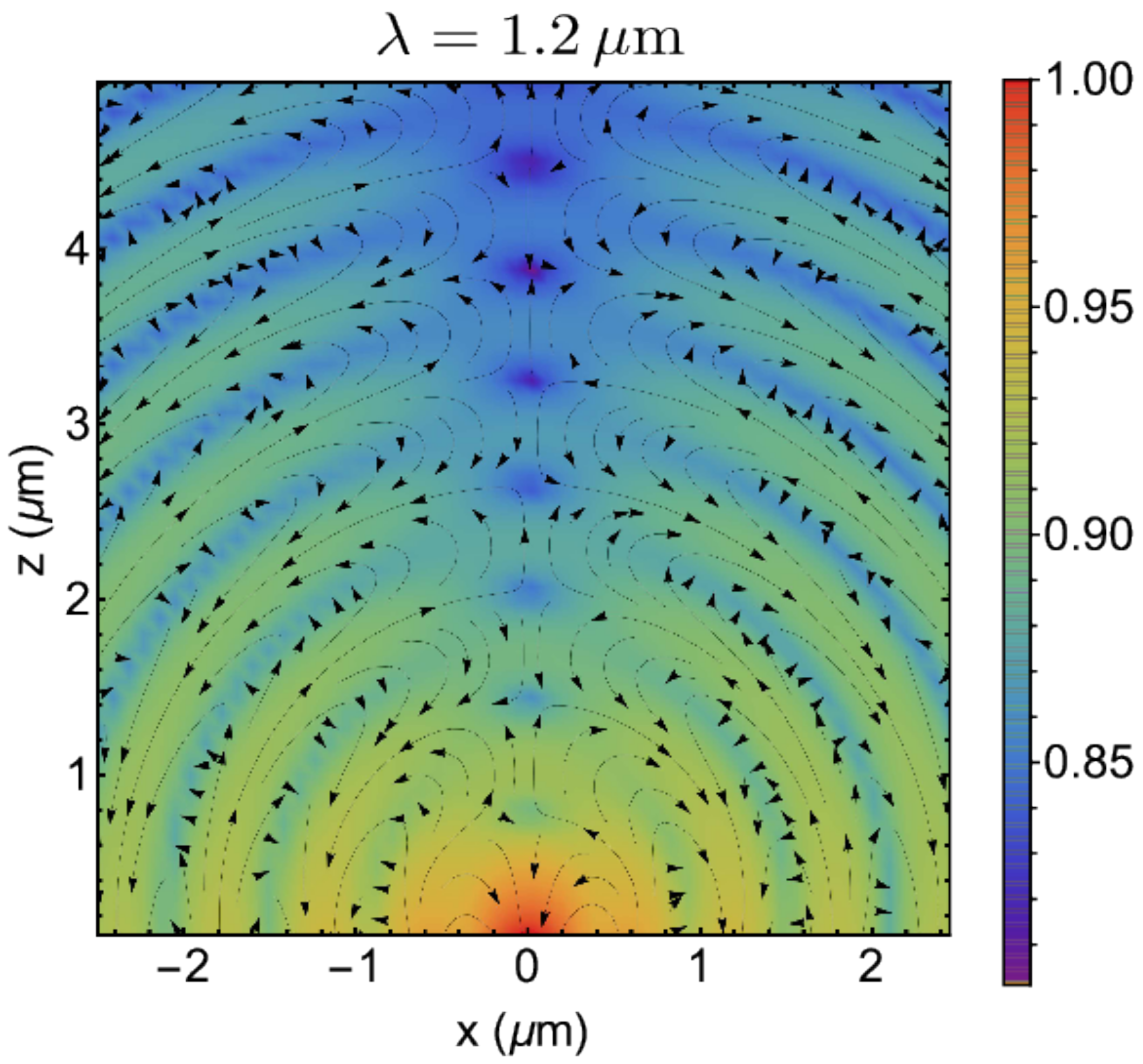
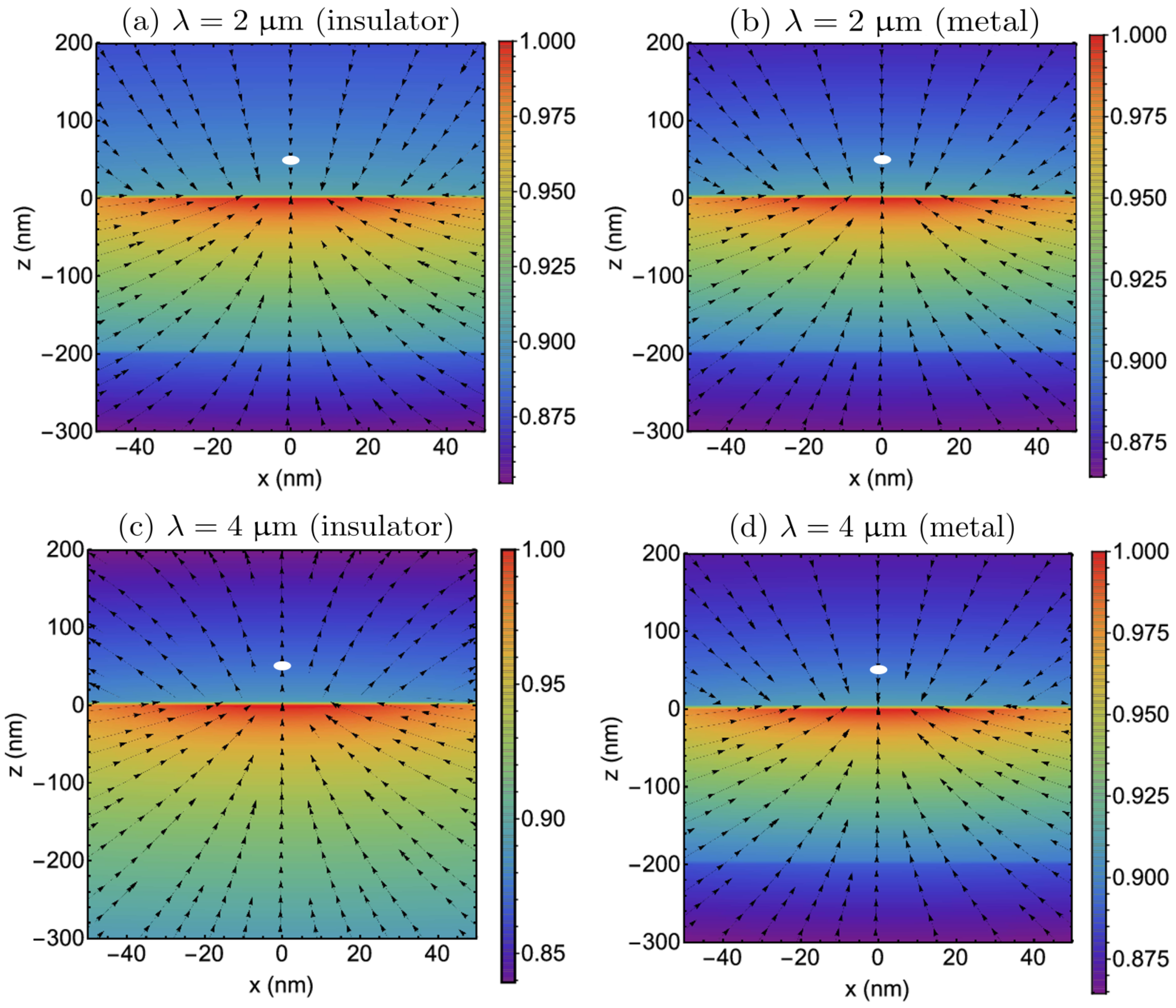
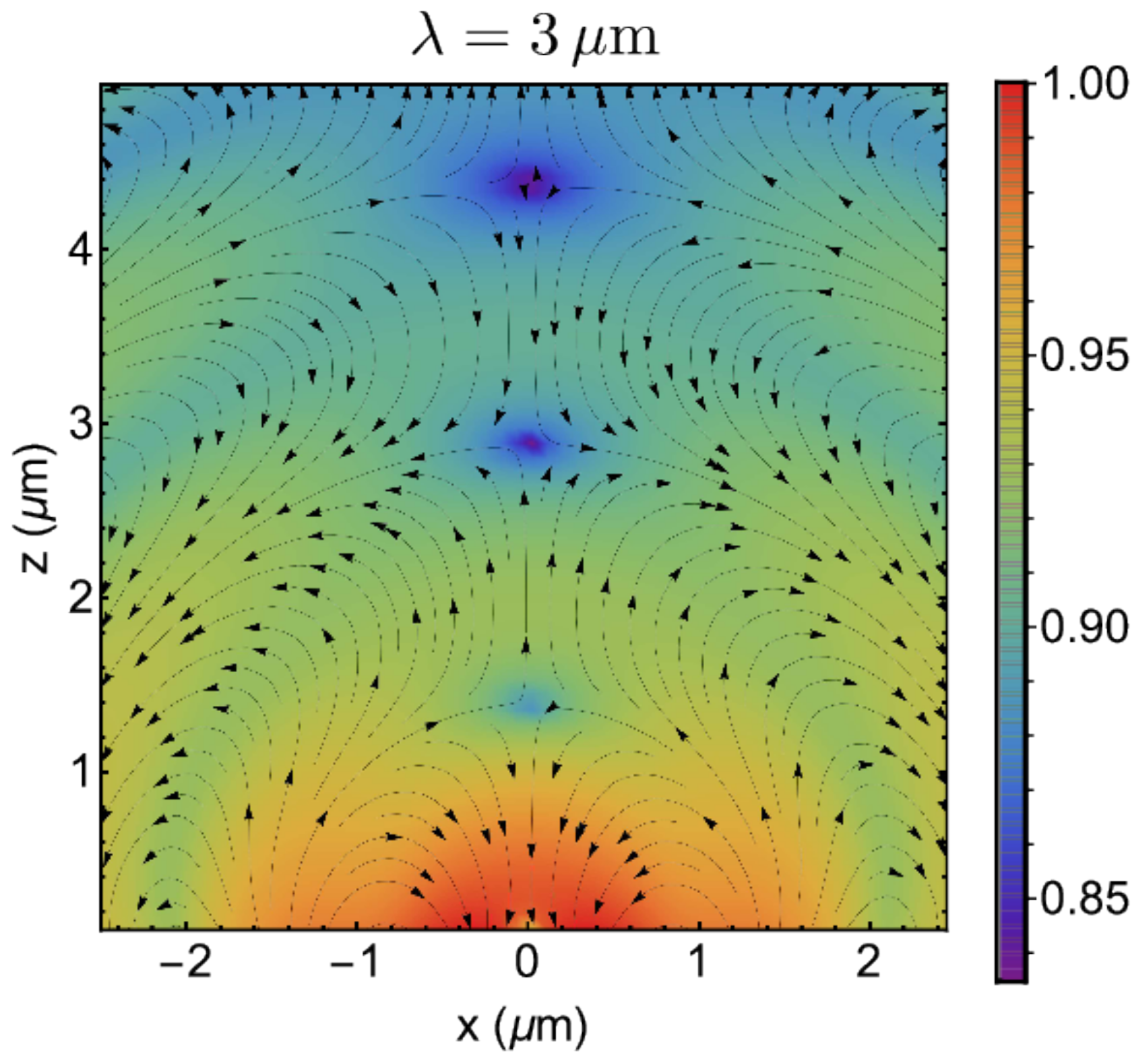
3.1. Electric Dipole
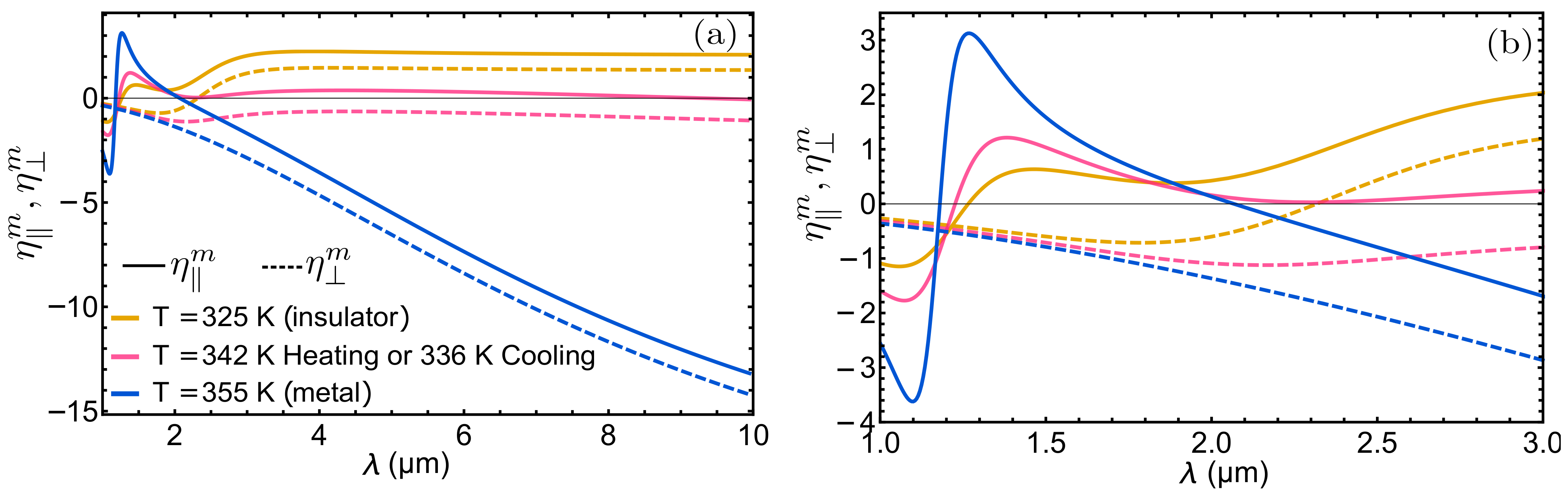
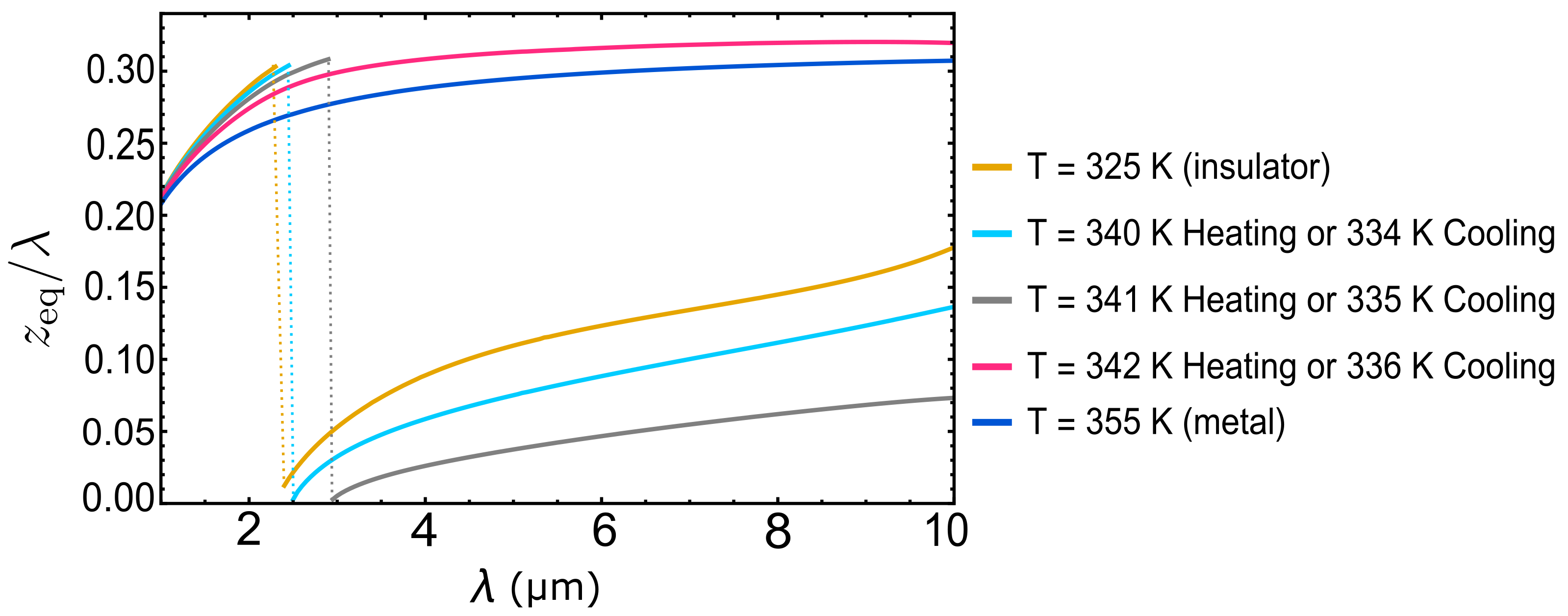
3.2. Magnetic Dipole
4. Final Remarks and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MIT | metal–insulator transition |
| PCM | phase-change material |
| BEMT | Bruggeman effective medium theory |
References
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical Levitation by Radiation Pressure. App. Phys. Lett. 1971, 19, 283–285. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Dholakia, K.; Čižmár, T. Shaping the future of manipulation. Nat. Photonics 2011, 5, 335–342. [Google Scholar] [CrossRef]
- Rodríguez-Fortuño, F.J.; Vakil, A.; Engheta, N. Electric Levitation Using ε-Near-Zero Metamaterials. Phys. Rev. Lett. 2014, 112, 033902. [Google Scholar] [CrossRef]
- De Abajo, F.J.G.; Brixner, T.; Pfeiffer, W. Nanoscale force manipulation in the vicinity of a metal nanostructure. J. Phys. B At. Mol. Opt. Phys. 2007, 40, S249. [Google Scholar] [CrossRef]
- Juan, M.L.; Righini, M.; Quidant, R. Plasmon nano-optical tweezers. Nat. Photonics 2011, 5, 349–356. [Google Scholar] [CrossRef]
- Yang, A.H.; Moore, S.D.; Schmidt, B.S.; Klug, M.; Lipson, M.; Erickson, D. Optical manipulation of nanoparticles and biomolecules in sub-wavelength slot waveguides. Nature 2009, 457, 71. [Google Scholar] [CrossRef]
- Shalin, A.S.; Ginzburg, P.; Belov, P.A.; Kivshar, Y.S.; Zayats, A.V. Nano-opto-mechanical effects in plasmonic waveguides. Laser Photonics Rev. 2014, 8, 131–136. [Google Scholar] [CrossRef]
- Xin, H.; Li, Y.; Liu, Y.C.; Zhang, Y.; Xiao, Y.F.; Li, B. Optical forces: From fundamental to biological applications. Adv. Mater. 2020, 32, 2001994. [Google Scholar] [CrossRef]
- Bagnato, V.S.; Lafyatis, G.P.; Martin, A.G.; Raab, E.L.; Ahmad-Bitar, R.N.; Pritchard, D.E. Continuous Stopping and Trapping of Neutral Atoms. Phys. Rev. Lett. 1987, 58, 2194–2197. [Google Scholar] [CrossRef]
- Phillips, W.D. Nobel Lecture: Laser cooling and trapping of neutral atoms. Rev. Mod. Phys. 1998, 70, 721–741. [Google Scholar] [CrossRef]
- Christodoulides, D.N. Optical trapping: Riding along an Airy beam. Nat. Photonics 2008, 2, 652–653. [Google Scholar] [CrossRef]
- Castillo-Garza, R.; Chang, C.C.; Jimenez, D.; Klimchitskaya, G.; Mostepanenko, V.; Mohideen, U. Experimental approaches to the difference in the Casimir force due to modifications in the optical properties of the boundary surface. Phys. Rev. A 2007, 75, 062114. [Google Scholar] [CrossRef]
- Torricelli, G.; van Zwol, P.; Shpak, O.; Binns, C.; Palasantzas, G.; Kooi, B.; Svetovoy, V.; Wuttig, M. Switching Casimir forces with phase-change materials. Phys. Rev. A 2010, 82, 010101. [Google Scholar] [CrossRef]
- Caride, A.; Klimchitskaya, G.; Mostepanenko, V.; Zanette, S. Dependences of the van der Waals atom-wall interaction on atomic and material properties. Phys. Rev. A 2005, 71, 042901. [Google Scholar] [CrossRef]
- Rodríguez-Fortuño, F.J.; Zayats, A.V. Repulsion of polarised particles from anisotropic materials with a near-zero permittivity component. Light Sci. Appl. 2016, 5, e16022-e16022. [Google Scholar] [CrossRef]
- Jeong, Y.G.; Bahk, Y.M.; Kim, D.S. Dynamic Terahertz Plasmonics Enabled by Phase-Change Materials. Adv. Opt. Mater. 2020, 8, 1900548. [Google Scholar] [CrossRef]
- Van de Groep, J.; Song, J.H.; Celano, U.; Li, Q.; Kik, P.G.; Brongersma, M.L. Exciton resonance tuning of an atomically thin lens. Nat. Photonics 2020, 1–5. [Google Scholar] [CrossRef]
- Howes, A.; Wang, W.; Kravchenko, I.; Valentine, J. Dynamic transmission control based on all-dielectric Huygens metasurfaces. Optica 2018, 5, 787–792. [Google Scholar] [CrossRef]
- Komar, A.; Paniagua-Dominguez, R.; Miroshnichenko, A.; Yu, Y.F.; Kivshar, Y.S.; Kuznetsov, A.I.; Neshev, D. Dynamic beam switching by liquid crystal tunable dielectric metasurfaces. ACS Photonics 2018, 5, 1742–1748. [Google Scholar] [CrossRef]
- Li, S.Q.; Xu, X.; Veetil, R.M.; Valuckas, V.; Paniagua-Domínguez, R.; Kuznetsov, A.I. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface. Science 2019, 364, 1087–1090. [Google Scholar] [CrossRef] [PubMed]
- Berto, P.; Philippet, L.; Osmond, J.; Liu, C.F.; Afridi, A.; Marques, M.M.; Agudo, B.M.; Tessier, G.; Quidant, R. Tunable and free-form planar optics. Nat. Photonics 2019, 13, 649–656. [Google Scholar] [CrossRef]
- Shcherbakov, M.R.; Vabishchevich, P.P.; Shorokhov, A.S.; Chong, K.E.; Choi, D.Y.; Staude, I.; Miroshnichenko, A.E.; Neshev, D.N.; Fedyanin, A.A.; Kivshar, Y.S. Ultrafast all-optical switching with magnetic resonances in nonlinear dielectric nanostructures. Nano Lett. 2015, 15, 6985–6990. [Google Scholar] [CrossRef]
- Pergament, A.; Stefanovich, G.; Velichko, A. Oxide electronics and vanadium dioxide perspective: A review. J. Select. Top. Nano Electron. Comput. 2013, 1, 24–43. [Google Scholar] [CrossRef]
- Cueff, S.; Li, D.; Zhou, Y.; Wong, F.J.; Kurvits, J.A.; Ramanathan, S.; Zia, R. Dynamic control of light emission faster than the lifetime limit using VO2 phase-change. Nat. Commun. 2015, 6, 8636. [Google Scholar] [CrossRef]
- Cavalleri, A.; Tóth, C.; Siders, C.W.; Squier, J.; Ráksi, F.; Forget, P.; Kieffer, J. Femtosecond structural dynamics in VO2 during an ultrafast solid-solid phase transition. Phys. Rev. Lett. 2001, 87, 237401. [Google Scholar] [CrossRef]
- Cavalleri, A.; Dekorsy, T.; Chong, H.H.W.; Kieffer, J.C.; Schoenlein, R.W. Evidence for a structurally-driven insulator-to-metal transition in VO2: A view from the ultrafast timescale. Phys. Rev. B 2004, 70, 161102. [Google Scholar] [CrossRef]
- Wan, C.; Zhang, Z.; Woolf, D.; Hessel, C.M.; Rensberg, J.; Hensley, J.M.; Xiao, Y.; Shahsafi, A.; Salman, J.; Richter, S.; et al. On the optical properties of thin-film vanadium dioxide from the visible to the far infrared. Ann. Der Phys. 2019, 531, 1900188. [Google Scholar] [CrossRef]
- Jostmeier, T.; Mangold, M.; Zimmer, J.; Karl, H.; Krenner, H.J.; Ruppert, C.; Betz, M. Thermochromic modulation of surface plasmon polaritons in vanadium dioxide nanocomposites. Opt. Express 2016, 24, 17321–17331. [Google Scholar] [CrossRef]
- Kumar, N.; Rúa, A.; Aldama, J.; Echeverría, K.; Fernández, F.E.; Lysenko, S. Photoinduced surface plasmon switching at VO2/Au interface. Opt. Express 2018, 26, 13773–13782. [Google Scholar] [CrossRef]
- Kruger, B.A.; Joushaghani, A.; Poon, J.K. Design of electrically driven hybrid vanadium dioxide (VO2) plasmonic switches. Opt. Express 2012, 20, 23598–23609. [Google Scholar] [CrossRef]
- Wang, L.; Radue, E.; Kittiwatanakul, S.; Clavero, C.; Lu, J.; Wolf, S.; Novikova, I.; Lukaszew, R. Surface plasmon polaritons in VO2 thin films for tunable low-loss plasmonic applications. Opt. Lett. 2012, 37, 4335–4337. [Google Scholar] [CrossRef]
- Jiang, N.; Zhuo, X.; Wang, J. Active plasmonics: Principles, structures, and applications. Chem. Rev. 2017, 118, 3054–3099. [Google Scholar] [CrossRef]
- Liu, H.; Lu, J.; Wang, X.R. Metamaterials based on the phase transition of VO2. Nanotechnology 2017, 29, 024002. [Google Scholar] [CrossRef]
- Ke, Y.; Yin, Y.; Zhang, Q.; Tan, Y.; Hu, P.; Wang, S.; Tang, Y.; Zhou, Y.; Wen, X.; Wu, S.; et al. Adaptive thermochromic windows from active plasmonic elastomers. Joule 2019, 3, 858–871. [Google Scholar] [CrossRef]
- Chang, T.C.; Cao, X.; Bao, S.H.; Ji, S.D.; Luo, H.J.; Jin, P. Review on thermochromic vanadium dioxide based smart coatings: From lab to commercial application. Adv. Manuf. 2018, 6, 1–19. [Google Scholar] [CrossRef]
- Howes, A.; Zhu, Z.; Curie, D.; Avila, J.R.; Wheeler, V.D.; Haglund, R.F.; Valentine, J.G. Optical Limiting Based on Huygens’ Metasurfaces. Nano Lett. 2020, 20, 4638–4644. [Google Scholar] [CrossRef]
- Kepic, P.; Ligmajer, F.; Hrton, M.; Ren, H.; Menezes, L.d.S.; Maier, S.A.; Sikola, T. Optically Tunable Mie Resonance VO2 Nanoantennas for Metasurfaces in the Visible. ACS Photonics 2021, 8, 1048–1057. [Google Scholar]
- Van Zwol, P.; Ranno, L.; Chevrier, J. Tuning near field radiative heat flux through surface excitations with a metal insulator transition. Phys. Rev. Lett. 2012, 108, 234301. [Google Scholar] [CrossRef] [PubMed]
- Szilard, D.; Kort-Kamp, W.; Rosa, F.; Pinheiro, F.; Farina, C. Hysteresis in the spontaneous emission induced by VO2 phase change. J. Opt. Soc. Am. B 2019, 36, C46–C51. [Google Scholar] [CrossRef]
- Ge, L.; Shi, X.; Xu, Z.; Gong, K. Tunable casimir equilibria with phase change materials: From quantum trapping to its release. Phys. Rev. B 2020, 101, 104107. [Google Scholar] [CrossRef]
- Galkina, E.; Ivanov, B.; Savel’ev, S.; Yampol’skii, V.; Nori, F. Drastic change of the Casimir force at the metal-insulator transition. Phys. Rev. B 2009, 80, 125119. [Google Scholar] [CrossRef]
- Pirozhenko, I.; Lambrecht, A. Influence of slab thickness on the Casimir force. Phys. Rev. A 2008, 77, 013811. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir-Polder Interaction of an Atom with a Cavity Wall Made of Phase-Change Material out of Thermal Equilibrium. Atoms 2021, 9, 4. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Rodríguez-Fortuño, F.J.; Engheta, N.; Martínez, A.; Zayats, A.V. Lateral forces on circularly polarizable particles near a surface. Nat. Commun. 2015, 6, 8799. [Google Scholar] [CrossRef]
- Wang, S.; Chan, C. Lateral optical force on chiral particles near a surface. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Nieto-Vesperinas, M.; Sáenz, J.; Gómez-Medina, R.; Chantada, L. Optical forces on small magnetodielectric particles. Opt. Express 2010, 18, 11428–11443. [Google Scholar] [CrossRef]
- Kort-Kamp, W.J.; Kramadhati, S.; Azad, A.K.; Reiten, M.T.; Dalvit, D.A. Passive radiative “thermostat” enabled by phase-change photonic nanostructures. ACS Photonics 2018, 5, 4554–4560. [Google Scholar] [CrossRef]
- Bruggeman, D. The calculation of various physical constants of heterogeneous substances. I. The dielectric constants and conductivities of mixtures composed of isotropic substances. Ann. Phys. 1935, 416, 636–791. [Google Scholar] [CrossRef]
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039. [Google Scholar] [CrossRef]
- Qazilbash, M.M.; Brehm, M.; Chae, B.G.; Ho, P.C.; Andreev, G.O.; Kim, B.J.; Yun, S.J.; Balatsky, A.; Maple, M.; Keilmann, F.; et al. Mott transition in VO2 revealed by infrared spectroscopy and nano-imaging. Science 2007, 318, 1750–1753. [Google Scholar] [CrossRef]
- Qazilbash, M.; Brehm, M.; Andreev, G.; Frenzel, A.; Ho, P.C.; Chae, B.G.; Kim, B.J.; Yun, S.J.; Kim, H.T.; Balatsky, A.; et al. Infrared spectroscopy and nano-imaging of the insulator-to-metal transition in vanadium dioxide. Phys. Rev. B 2009, 79, 075107. [Google Scholar] [CrossRef]
- Choy, T. Effective Medium Theory: Principles and Applications; International Series of Monographs on Physics; OUP Oxford: Oxford, UK, 2015. [Google Scholar]
- Peterseim, T.; Dressel, M.; Dietrich, M.; Polity, A. Optical properties of VO2 films at the phase transition: Influence of substrate and electronic correlations. J. Appl. Phys. 2016, 120, 075102. [Google Scholar] [CrossRef]
- Gordon, J.P. Radiation forces and momenta in dielectric media. Phys. Rev. A 1973, 8, 14. [Google Scholar] [CrossRef]
- Chaumet, P.C.; Nieto-Vesperinas, M. Time-averaged total force on a dipolar sphere in an electromagnetic field. Opt. Lett. 2000, 25, 1065–1067. [Google Scholar] [CrossRef]
- Buhmann, S. Dispersion Forces II: Many-Body Effects, Excited Atoms, Finite Temperature and Quantum Friction; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kort-Kamp, W.; Farina, C. On the exact electric and magnetic fields of an electric dipole. Am. J. Phys. 2011, 79, 111–114. [Google Scholar] [CrossRef]
- Farina, C.; Santos, F.C.; Tort, A.C. A simple model for the nonretarded dispersive force between an electrically polarizable atom and a magnetically polarizable one. Am. J. Phys. 2002, 70, 421–423. [Google Scholar] [CrossRef]
- Feinberg, G.; Sucher, J. General theory of the van der Waals interaction: A model-independent approach. Phys. Rev. A 1970, 2, 2395. [Google Scholar] [CrossRef]
- Farina, C.; Santos, F.; Tort, A. On the force between an electrically polarizable atom and a magnetically polarizable one. J. Phys. A Math. Gen. 2002, 35, 2477. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szilard, D.; Abrantes, P.P.; Pinheiro, F.A.; Rosa, F.S.S.; Farina, C.; Kort-Kamp, W.J.M. Optical Forces on an Oscillating Dipole Near VO2 Phase Transition. Universe 2021, 7, 159. https://doi.org/10.3390/universe7060159
Szilard D, Abrantes PP, Pinheiro FA, Rosa FSS, Farina C, Kort-Kamp WJM. Optical Forces on an Oscillating Dipole Near VO2 Phase Transition. Universe. 2021; 7(6):159. https://doi.org/10.3390/universe7060159
Chicago/Turabian StyleSzilard, Daniela, Patrícia P. Abrantes, Felipe A. Pinheiro, Felipe S. S. Rosa, Carlos Farina, and Wilton J. M. Kort-Kamp. 2021. "Optical Forces on an Oscillating Dipole Near VO2 Phase Transition" Universe 7, no. 6: 159. https://doi.org/10.3390/universe7060159
APA StyleSzilard, D., Abrantes, P. P., Pinheiro, F. A., Rosa, F. S. S., Farina, C., & Kort-Kamp, W. J. M. (2021). Optical Forces on an Oscillating Dipole Near VO2 Phase Transition. Universe, 7(6), 159. https://doi.org/10.3390/universe7060159





