Consistency of Cubic Galileon Cosmology: Model-Independent Bounds from Background Expansion and Perturbative Analyses
Abstract
1. Introduction
2. Swampland Conjectures and Late-Time Cosmology
- For the late-time model we are interested in, the field space excursion is automatically small , thereby satisfying the distance conjecture.
- For explicit potentials involving scalar fields, Equation (2) must always be satisfied with some number c consistent with the TCC.
- Since the lifetime of any consistent dS space is strictly constrained by the TCC Equation (5), it means that our alternate scenario should never asymptote towards a dS attractor.
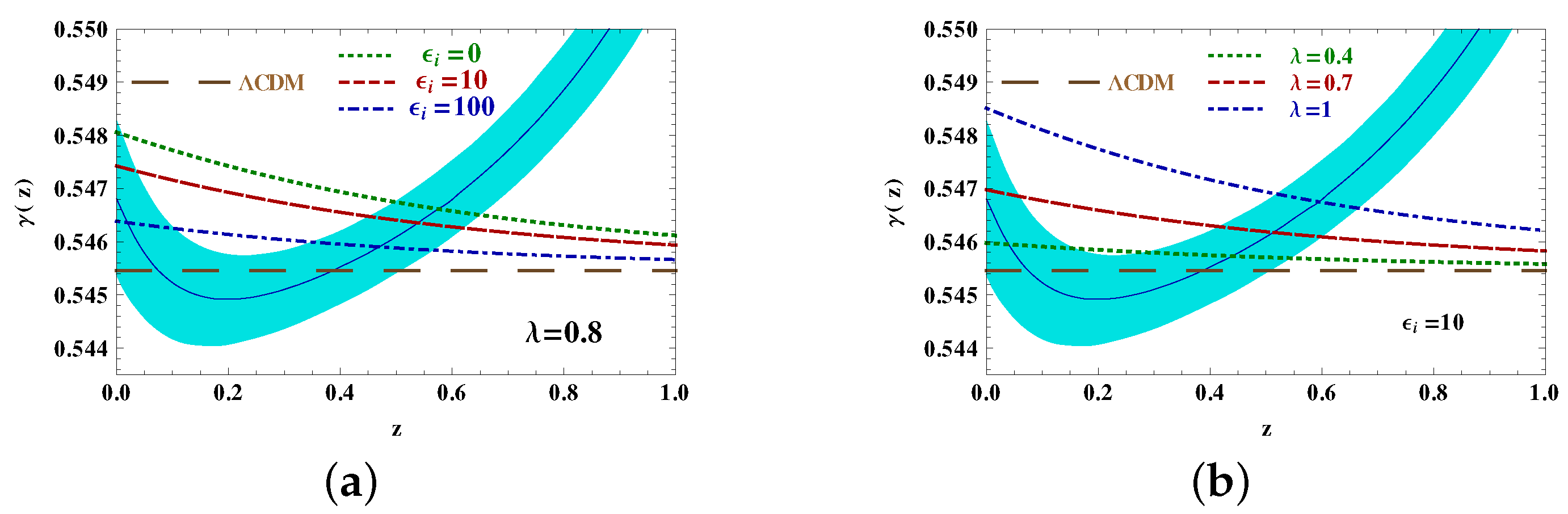
3. The Cubic Galileon Model
4. Comparison with Model-Independent Analyses of Snia Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Sahni, V.; Starobinsky, A.A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373–444. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW XIII. A 2.4% measurement of H0 from lensed quasars: 5.3σ tension between early and late-Universe probes. arXiv 2019, arXiv:1907.04869. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2, 013028. [Google Scholar] [CrossRef]
- Riess, A.G. The Expansion of the Universe is Faster than Expected. Nature Rev. Phys. 2019, 2, 10–12. [Google Scholar] [CrossRef]
- Macaulay, E.; Wehus, I.K.; Eriksen, H.K. Lower Growth Rate from Recent Redshift Space Distortion Measurements than Expected from Planck. Phys. Rev. Lett. 2013, 111, 161301. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.; Blake, C.; Dossett, J.; Koda, J.; Parkinson, D.; Joudaki, S. Searching for Modified Gravity: Scale and Redshift Dependent Constraints from Galaxy Peculiar Velocities. Mon. Not. R. Astron. Soc. 2016, 458, 2725–2744. [Google Scholar] [CrossRef]
- Tsujikawa, S. Possibility of realizing weak gravity in redshift space distortion measurements. Phys. Rev. D 2015, 92, 044029. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Evolution of the fσ8 tension with the Planck15/ΛCDM determination and implications for modified gravity theories. Phys. Rev. D 2018, 97, 103503. [Google Scholar] [CrossRef]
- Martin, J. Everything You Always Wanted To Know About The Cosmological Constant Problem (But Were Afraid To Ask). C. R. Phys. 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Vafa, C. The String Landscape and the Swampland. 2005. Available online: http://xxx.lanl.gov/abs/hep-th/0509212 (accessed on 20 May 2021).
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:1806.08362. [Google Scholar]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter Conjectures on the Swampland. Phys. Lett. B 2019, 788, 180–184. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Van Riet, T. What if string theory has no de Sitter vacua? Int. J. Mod. Phys. D 2018, 27, 1830007. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C. On Exclusion of Positive Cosmological Constant. Fortsch. Phys. 2019, 67, 1800092. [Google Scholar] [CrossRef]
- Martin, J.; Brandenberger, R.H. The TransPlanckian problem of inflationary cosmology. Phys. Rev. 2001, D63, 123501. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Martin, J. The Robustness of inflation to changes in superPlanck scale physics. Mod. Phys. Lett. 2001, A16, 999–1006. [Google Scholar] [CrossRef]
- Bedroya, A.; Vafa, C. Trans-Planckian Censorship and the Swampland. arXiv 2019, arXiv:1909.11063. [Google Scholar] [CrossRef]
- Bedroya, A.; Brandenberger, R.; Loverde, M.; Vafa, C. Trans-Planckian Censorship and Inflationary Cosmology. arXiv 2019, arXiv:1909.11106. [Google Scholar]
- Brahma, S. Trans-Planckian censorship conjecture from the swampland distance conjecture. Phys. Rev. 2020, D101, 046013. [Google Scholar] [CrossRef]
- Cai, R.G.; Wang, S.J. A refined trans-Planckian censorship conjecture. arXiv 2019, arXiv:hep-th/1912.00607. [Google Scholar]
- Wetterich, C. Cosmologies With Variable Newton’s ‘Constant’. Nucl. Phys. B 1988, 302, 645–667. [Google Scholar] [CrossRef]
- Wetterich, C. Cosmology and the Fate of Dilatation Symmetry. Nucl. Phys. B 1988, 302, 668–696. [Google Scholar] [CrossRef]
- Peebles, P.; Ratra, B. Cosmology with a Time Variable Cosmological Constant. Astrophys. J. Lett. 1988, 325, L17. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P. Cosmological Consequences of a Rolling Homogeneous Scalar Field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Fierz, M.; Pauli, W. On relativistic wave equations for particles of arbitrary spin in an electromagnetic field. Proc. R. Soc. Lond. A 1939, A173, 211–232. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Adv. Ser. Astrophys. Cosmol. 1987, 3, 130–133. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of Phase Transition in the New Inflationary Universe Scenario and Generation of Perturbations. Phys. Lett. B 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Dvali, G.; Gabadadze, G.; Porrati, M. 4-D gravity on a brane in 5-D Minkowski space. Phys. Lett. B 2000, 485, 208–214. [Google Scholar] [CrossRef]
- Cartier, C.; Hwang, J.C.; Copeland, E.J. Evolution of cosmological perturbations in nonsingular string cosmologies. Phys. Rev. D 2001, 64, 103504. [Google Scholar] [CrossRef]
- Hwang, J.C.; Noh, H. Classical evolution and quantum generation in generalized gravity theories including string corrections and tachyon: Unified analyses. Phys. Rev. D 2005, 71, 063536. [Google Scholar] [CrossRef]
- Nicolis, A.; Rattazzi, R.; Trincherini, E. The Galileon as a local modification of gravity. Phys. Rev. D 2009, 79, 064036. [Google Scholar] [CrossRef]
- de Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef] [PubMed]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rept. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- de Rham, C. Massive Gravity. Living Rev. Rel. 2014, 17, 7. [Google Scholar] [CrossRef] [PubMed]
- de Rham, C. Galileons in the Sky. C. R. Phys. 2012, 13, 666–681. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.; Odintsov, S.D. f (R, T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.; Sebastiani, L.; Zerbini, S. A Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Odintsov, S.; Oikonomou, V. Swampland Implications of GW170817-compatible Einstein-Gauss-Bonnet Gravity. Phys. Lett. B 2020, 805, 135437. [Google Scholar] [CrossRef]
- Deffayet, C.; Esposito-Farese, G.; Vikman, A. Covariant Galileon. Phys. Rev. D 2009, 79, 084003. [Google Scholar] [CrossRef]
- Gannouji, R.; Sami, M. Galileon gravity and its relevance to late time cosmic acceleration. Phys. Rev. D 2010, 82, 024011. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. Cosmology of a covariant Galileon field. Phys. Rev. Lett. 2010, 105, 111301. [Google Scholar] [CrossRef] [PubMed]
- De Felice, A.; Tsujikawa, S. Generalized Galileon cosmology. Phys. Rev. D 2011, 84, 124029. [Google Scholar] [CrossRef]
- Ali, A.; Gannouji, R.; Sami, M. Modified gravity a la Galileon: Late time cosmic acceleration and observational constraints. Phys. Rev. D 2010, 82, 103015. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy After GW170817: Dead Ends and the Road Ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef] [PubMed]
- Zumalacarregui, M. Gravity in the Era of Equality: Towards solutions to the Hubble problem without fine-tuned initial conditions. arXiv 2020, arXiv:astro-ph.CO/2003.06396. [Google Scholar] [CrossRef]
- Kase, R.; Tsujikawa, S. Dark energy in Horndeski theories after GW170817: A review. Int. J. Mod. Phys. D 2019, 28, 1942005. [Google Scholar] [CrossRef]
- Creminelli, P.; Tambalo, G.; Vernizzi, F.; Yingcharoenrat, V. Dark-Energy Instabilities induced by Gravitational Waves. JCAP 2020, 5, 2. [Google Scholar] [CrossRef]
- Chow, N.; Khoury, J. Galileon Cosmology. Phys. Rev. D 2009, 80, 024037. [Google Scholar] [CrossRef]
- Silva, F.P.; Koyama, K. Self-Accelerating Universe in Galileon Cosmology. Phys. Rev. D 2009, 80, 121301. [Google Scholar] [CrossRef]
- Barreira, A.; Li, B.; Hellwing, W.A.; Baugh, C.M.; Pascoli, S. Nonlinear structure formation in the Cubic Galileon gravity model. JCAP 2013, 10, 027. [Google Scholar] [CrossRef]
- Bartolo, N.; Bellini, E.; Bertacca, D.; Matarrese, S. Matter bispectrum in cubic Galileon cosmologies. JCAP 2013, 3, 034. [Google Scholar] [CrossRef]
- Dinda, B.R.; Wali Hossain, M.; Sen, A.A. Observed galaxy power spectrum in cubic Galileon model. JCAP 2018, 1, 045. [Google Scholar] [CrossRef]
- Dinda, B.R. Weak lensing probe of cubic Galileon model. JCAP 2018, 6, 017. [Google Scholar] [CrossRef]
- Zhang, J.; Dinda, B.R.; Hossain, M.W.; Sen, A.A.; Luo, W. A study on Cubic Galileon Gravity Using N-body Simulations. arXiv 2020, arXiv:astro-ph.CO/2004.12659. [Google Scholar] [CrossRef]
- Ali, A.; Gannouji, R.; Hossain, M.; Sami, M. Light mass galileons: Cosmological dynamics, mass screening and observational constraints. Phys. Lett. B 2012, 718, 5–14. [Google Scholar] [CrossRef]
- Hossain, M.; Sen, A.A. Do Observations Favour Galileon Over Quintessence? Phys. Lett. B 2012, 713, 140–144. [Google Scholar] [CrossRef]
- Hossain, M.W. First and second order cosmological perturbations in light mass Galileon models. Phys. Rev. D 2017, 96, 023506. [Google Scholar] [CrossRef]
- Brahma, S.; Hossain, M.W. Dark energy beyond quintessence: Constraints from the swampland. JHEP 2019, 6, 070. [Google Scholar] [CrossRef]
- Deffayet, C.; Pujolas, O.; Sawicki, I.; Vikman, A. Imperfect Dark Energy from Kinetic Gravity Braiding. JCAP 2010, 10, 026. [Google Scholar] [CrossRef]
- Pujolas, O.; Sawicki, I.; Vikman, A. The Imperfect Fluid behind Kinetic Gravity Braiding. JHEP 2011, 11, 156. [Google Scholar] [CrossRef]
- Brando, G.; Falciano, F.T.; Linder, E.V.; Velten, H.E.S. Modified gravity away from a ΛCDM background. JCAP 2019, 11, 018. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Haude, S.; Salehi, S.; Vidal, S.; Maturi, M.; Bartelmann, M. Model-Independent Determination of the Cosmic Growth Factor. arXiv 2019, arXiv:astro-ph.CO/1912.04560. [Google Scholar]
- Heisenberg, L. Generalization of the Proca Action. JCAP 2014, 5, 015. [Google Scholar] [CrossRef]
- Palti, E. The Swampland: Introduction and Review. Fortsch. Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef]
- Brennan, T.D.; Carta, F.; Vafa, C. The String Landscape, the Swampland, and the Missing Corner. PoS 2017, TASI2017, 015. [Google Scholar] [CrossRef]
- Kim, H.C.; Tarazi, H.C.; Vafa, C. Four Dimensional = 4 SYM and the Swampland. arXiv 2019, arXiv:hep-th/1912.06144. [Google Scholar]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. JHEP 2019, 11, 075. [Google Scholar] [CrossRef]
- Andriot, D.; Roupec, C. Further refining the de Sitter swampland conjecture. Fortsch. Phys. 2019, 67, 1800105. [Google Scholar] [CrossRef]
- Ooguri, H.; Vafa, C. On the Geometry of the String Landscape and the Swampland. Nucl. Phys. 2007, B766, 21–33. [Google Scholar] [CrossRef]
- Baume, F.; Palti, E. Backreacted Axion Field Ranges in String Theory. JHEP 2016, 8, 043. [Google Scholar] [CrossRef]
- Klaewer, D.; Palti, E. Super-Planckian Spatial Field Variations and Quantum Gravity. JHEP 2017, 1, 088. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Kläwer, D.; Schlechter, L.; Wolf, F. The Refined Swampland Distance Conjecture in Calabi-Yau Moduli Spaces. JHEP 2018, 6, 052. [Google Scholar] [CrossRef]
- Grimm, T.W.; Li, C.; Palti, E. Infinite Distance Networks in Field Space and Charge Orbits. JHEP 2019, 3, 016. [Google Scholar] [CrossRef]
- Grimm, T.W.; Palti, E.; Valenzuela, I. Infinite Distances in Field Space and Massless Towers of States. JHEP 2018, 8, 143. [Google Scholar] [CrossRef]
- Landete, A.; Shiu, G. Mass Hierarchies and Dynamical Field Range. Phys. Rev. 2018, D98, 066012. [Google Scholar] [CrossRef]
- Bousso, R. A Covariant entropy conjecture. JHEP 1999, 7, 004. [Google Scholar] [CrossRef]
- Dvali, G. Black Holes and Large N Species Solution to the Hierarchy Problem. Fortsch. Phys. 2010, 58, 528–536. [Google Scholar] [CrossRef]
- Dvali, G.; Redi, M. Black Hole Bound on the Number of Species and Quantum Gravity at LHC. Phys. Rev. 2008, D77, 045027. [Google Scholar] [CrossRef]
- Veneziano, G. Large N bounds on, and compositeness limit of, gauge and gravitational interactions. JHEP 2002, 6, 051. [Google Scholar] [CrossRef]
- Hebecker, A.; Wrase, T. The Asymptotic dS Swampland Conjecture—A Simplified Derivation and a Potential Loophole. Fortsch. Phys. 2019, 67, 1800097. [Google Scholar] [CrossRef]
- Weiss, N. Constraints on Hamiltonian Lattice Formulations of Field Theories in an Expanding Universe. Phys. Rev. 1985, D32, 3228. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, T. Trans Planckian redshifts and the substance of the space-time river. Prog. Theor. Phys. Suppl. 1999, 136, 1–17. [Google Scholar] [CrossRef]
- Berera, A.; Brahma, S.; Calderón, J.R. Role of trans-Planckian modes in cosmology. arXiv 2020, arXiv:hep-th/2003.07184. [Google Scholar]
- Westphal, A. Lifetime of Stringy de Sitter Vacua. JHEP 2008, 1, 012. [Google Scholar] [CrossRef]
- Dasgupta, K.; Emelin, M.; Faruk, M.M.; Tatar, R. de Sitter Vacua in the String Landscape. arXiv 2019, arXiv:hep-th/1908.05288. [Google Scholar]
- Dasgupta, K.; Emelin, M.; Faruk, M.M.; Tatar, R. How a four-dimensional de Sitter solution remains outside the swampland. arXiv 2019, arXiv:hep-th/1911.02604. [Google Scholar]
- Dvali, G.; Gomez, C.; Zell, S. Quantum Breaking Bound on de Sitter and Swampland. Fortsch. Phys. 2019, 67, 1800094. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dubovsky, S.; Nicolis, A.; Trincherini, E.; Villadoro, G. A Measure of de Sitter entropy and eternal inflation. JHEP 2007, 5, 055. [Google Scholar] [CrossRef]
- Luty, M.A.; Porrati, M.; Rattazzi, R. Strong interactions and stability in the DGP model. JHEP 2003, 9, 029. [Google Scholar] [CrossRef]
- Nicolis, A.; Rattazzi, R. Classical and quantum consistency of the DGP model. JHEP 2004, 6, 059. [Google Scholar] [CrossRef]
- Vainshtein, A. To the problem of nonvanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Renk, J.; Zumalacárregui, M.; Montanari, F.; Barreira, A. Galileon gravity in light of ISW, CMB, BAO and H0 data. JCAP 2017, 10, 020. [Google Scholar] [CrossRef]
- Kimura, R.; Kobayashi, T.; Yamamoto, K. Observational Constraints on Kinetic Gravity Braiding from the Integrated Sachs-Wolfe Effect. Phys. Rev. D 2012, 85, 123503. [Google Scholar] [CrossRef]
- Heisenberg, L.; Bartelmann, M.; Brandenberger, R.; Refregier, A. Dark Energy in the Swampland. Phys. Rev. D 2018, 98, 123502. [Google Scholar] [CrossRef]
- Heisenberg, L.; Bartelmann, M.; Brandenberger, R.; Refregier, A. Model Independent Analysis of Supernova Data, Dark Energy, Trans-Planckian Censorship and the Swampland. arXiv 2020, arXiv:hep-th/2003.13283. [Google Scholar]
- Akrami, Y.; Kallosh, R.; Linde, A.; Vardanyan, V. The Landscape, the Swampland and the Era of Precision Cosmology. Fortsch. Phys. 2019, 67, 1800075. [Google Scholar] [CrossRef]
- Pirtskhalava, D.; Santoni, L.; Trincherini, E.; Vernizzi, F. Weakly Broken Galileon Symmetry. JCAP 2015, 9, 007. [Google Scholar] [CrossRef]
- Agrawal, P.; Obied, G.; Steinhardt, P.J.; Vafa, C. On the Cosmological Implications of the String Swampland. Phys. Lett. B 2018, 784, 271–276. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Wands, D. Exponential potentials and cosmological scaling solutions. Phys. Rev. D 1998, 57, 4686–4690. [Google Scholar] [CrossRef]
- Peebles, P. Tests of Cosmological Models Constrained by Inflation. Astrophys. J. 1984, 284, 439–444. [Google Scholar] [CrossRef]
- Lahav, O.; Lilje, P.B.; Primack, J.R.; Rees, M.J. Dynamical effects of the cosmological constant. Mon. Not. R. Astron. Soc. 1991, 251, 128–136. [Google Scholar] [CrossRef]
- Belloso, A.B.; García-Bellido, J.; Sapone, D. A parametrization of the growth index of matter perturbations in various Dark Energy models and observational prospects using a Euclid-like survey. J. Cosmol. Astropart. Phys. 2011, 2011, 010. [Google Scholar] [CrossRef]
- Wang, L.M.; Steinhardt, P.J. Cluster abundance constraints on quintessence models. Astrophys. J. 1998, 508, 483–490. [Google Scholar] [CrossRef]
- De Felice, A.; Heisenberg, L.; Kase, R.; Mukohyama, S.; Tsujikawa, S.; Zhang, Y.l. Cosmology in generalized Proca theories. JCAP 2016, 6, 048. [Google Scholar] [CrossRef]
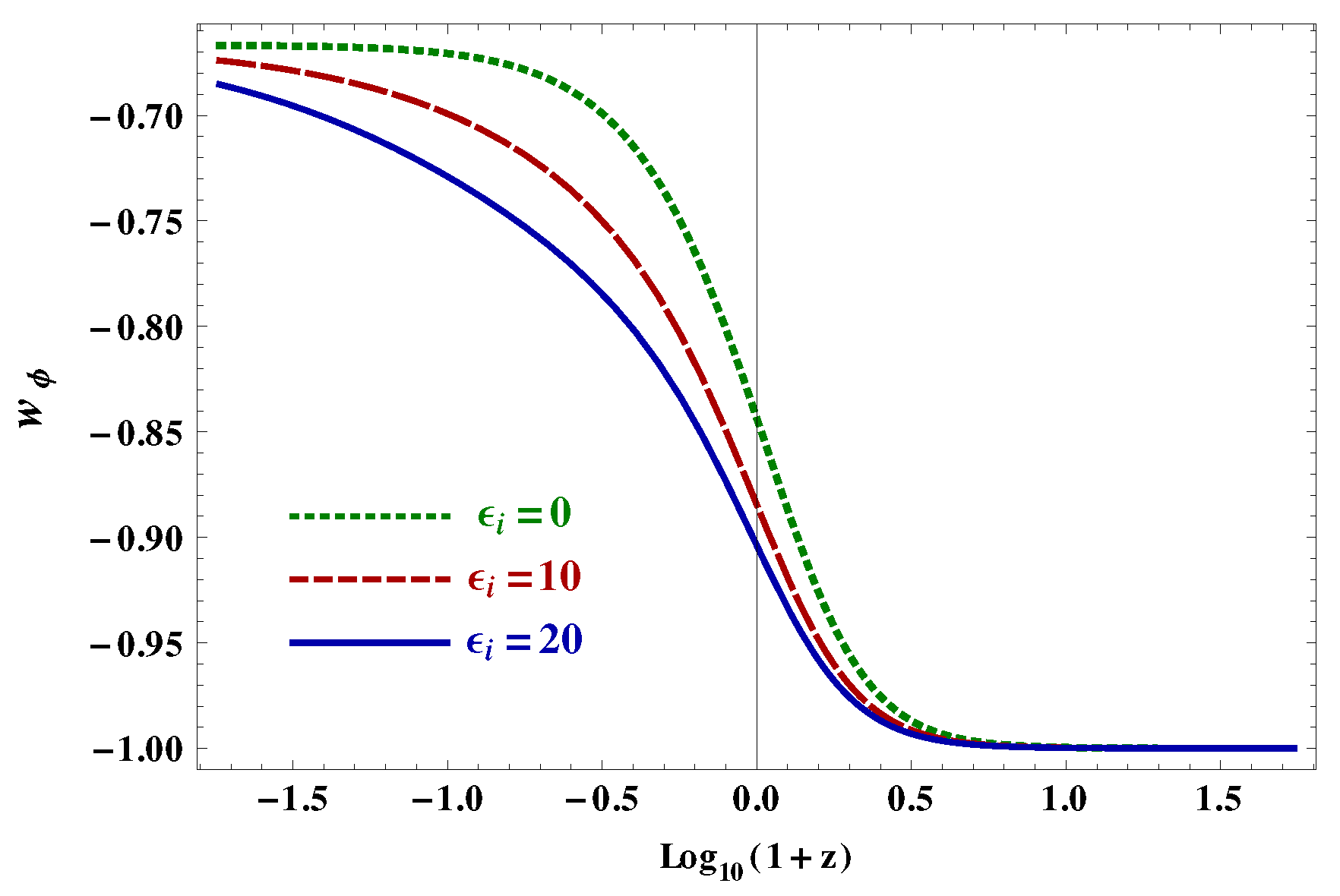
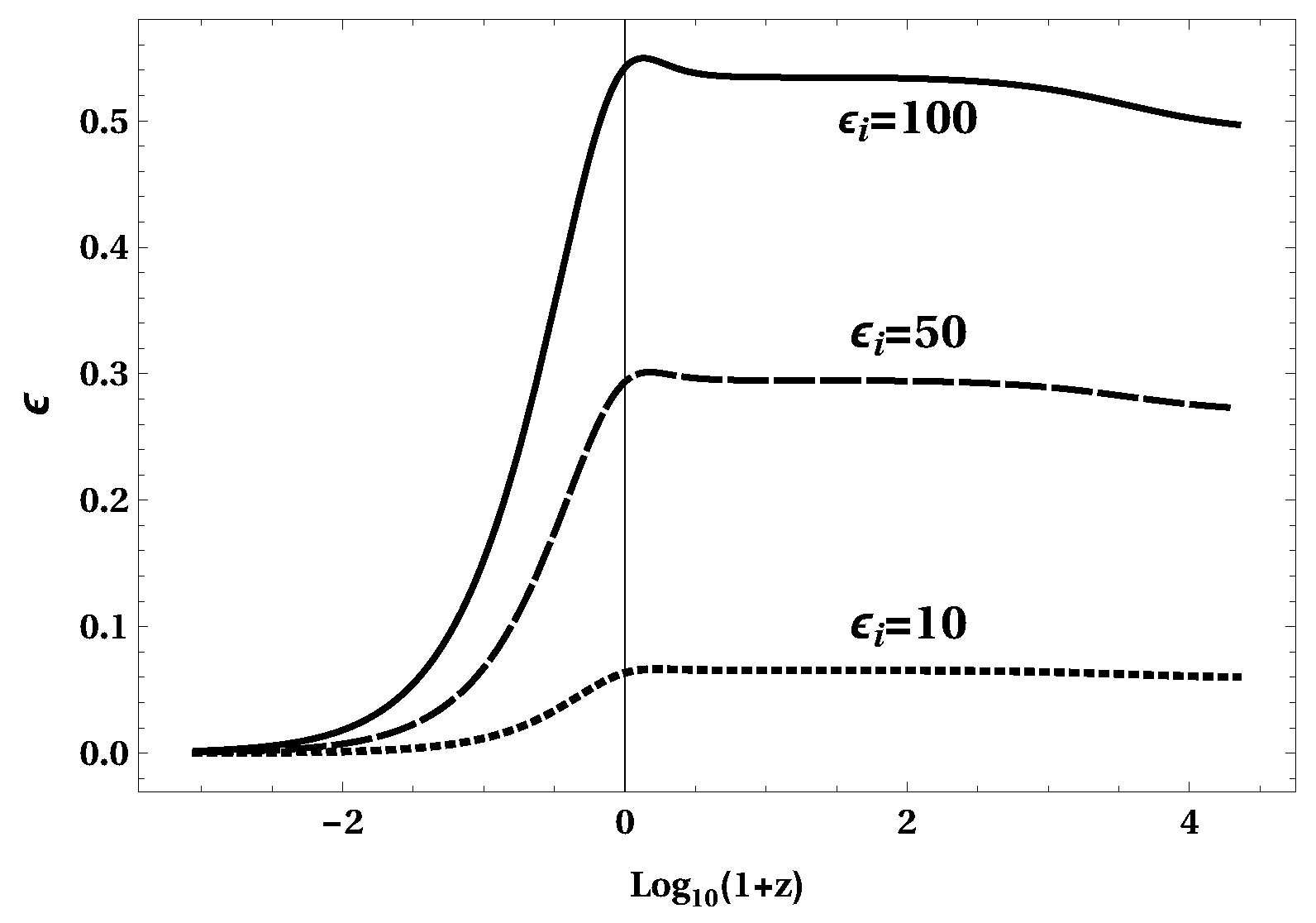
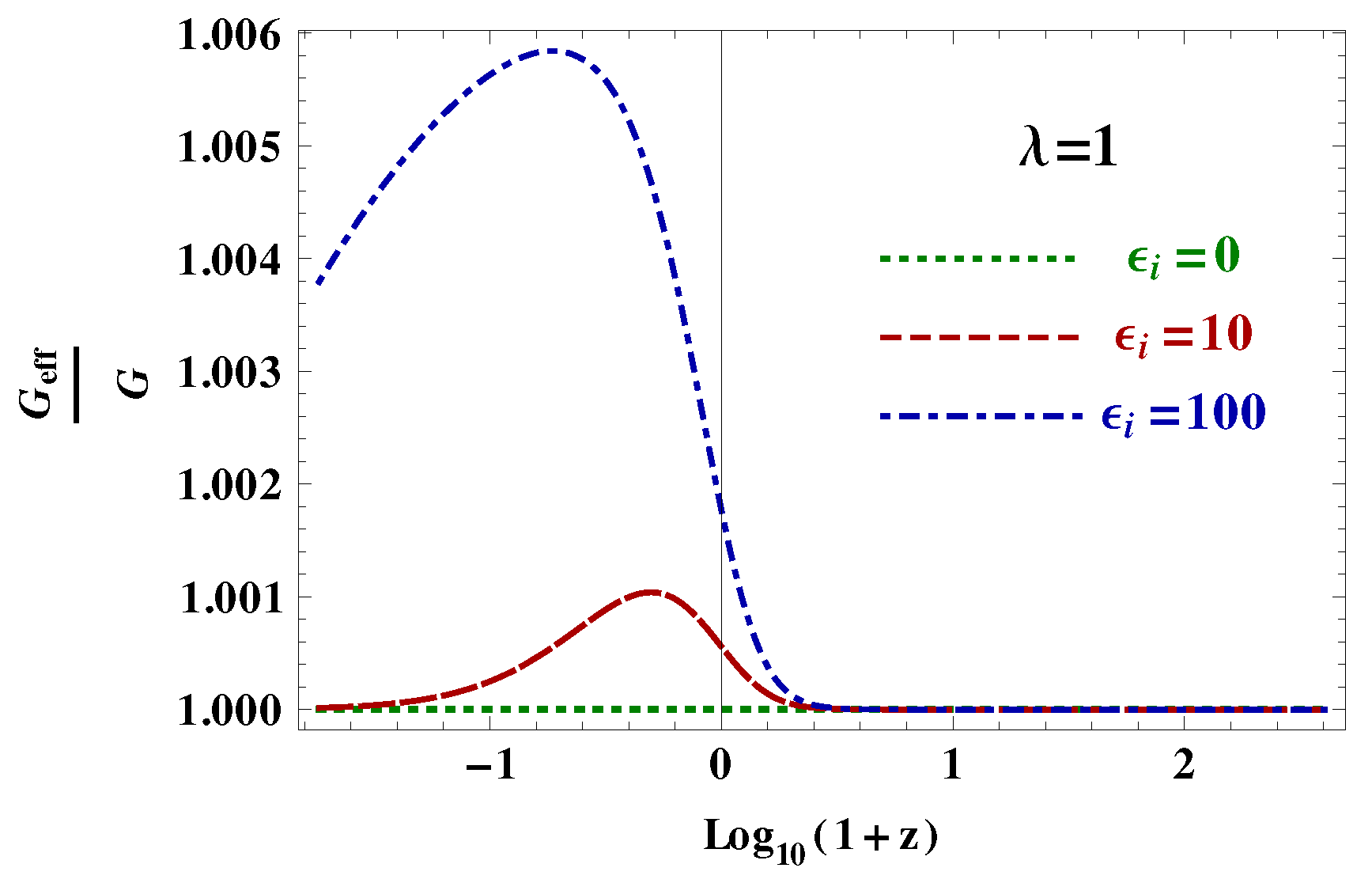
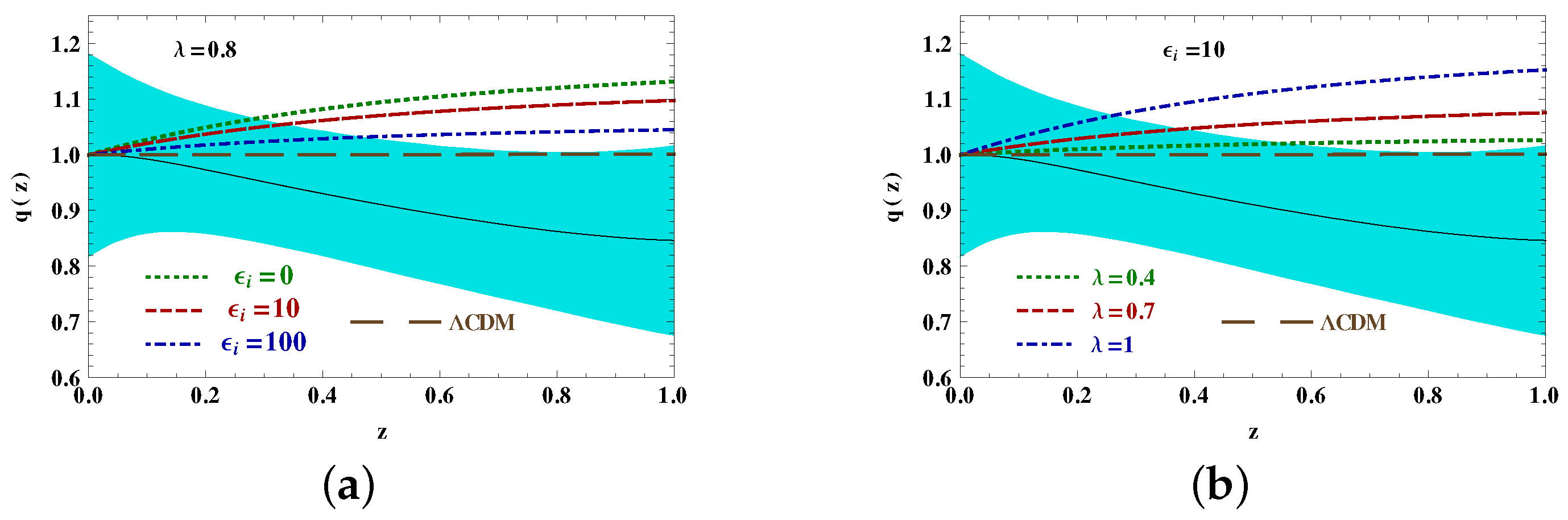
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brahma, S.; Hossain, M.W. Consistency of Cubic Galileon Cosmology: Model-Independent Bounds from Background Expansion and Perturbative Analyses. Universe 2021, 7, 167. https://doi.org/10.3390/universe7060167
Brahma S, Hossain MW. Consistency of Cubic Galileon Cosmology: Model-Independent Bounds from Background Expansion and Perturbative Analyses. Universe. 2021; 7(6):167. https://doi.org/10.3390/universe7060167
Chicago/Turabian StyleBrahma, Suddhasattwa, and Md. Wali Hossain. 2021. "Consistency of Cubic Galileon Cosmology: Model-Independent Bounds from Background Expansion and Perturbative Analyses" Universe 7, no. 6: 167. https://doi.org/10.3390/universe7060167
APA StyleBrahma, S., & Hossain, M. W. (2021). Consistency of Cubic Galileon Cosmology: Model-Independent Bounds from Background Expansion and Perturbative Analyses. Universe, 7(6), 167. https://doi.org/10.3390/universe7060167





