Geometric Approach to Analytic Marginalisation of the Likelihood Ratio for Continuous Gravitational Wave Searches
Abstract
:1. Introduction
2. Geometric View of the Likelihood Ratio
3. Analytic Marginalisation of the Likelihood Ratio
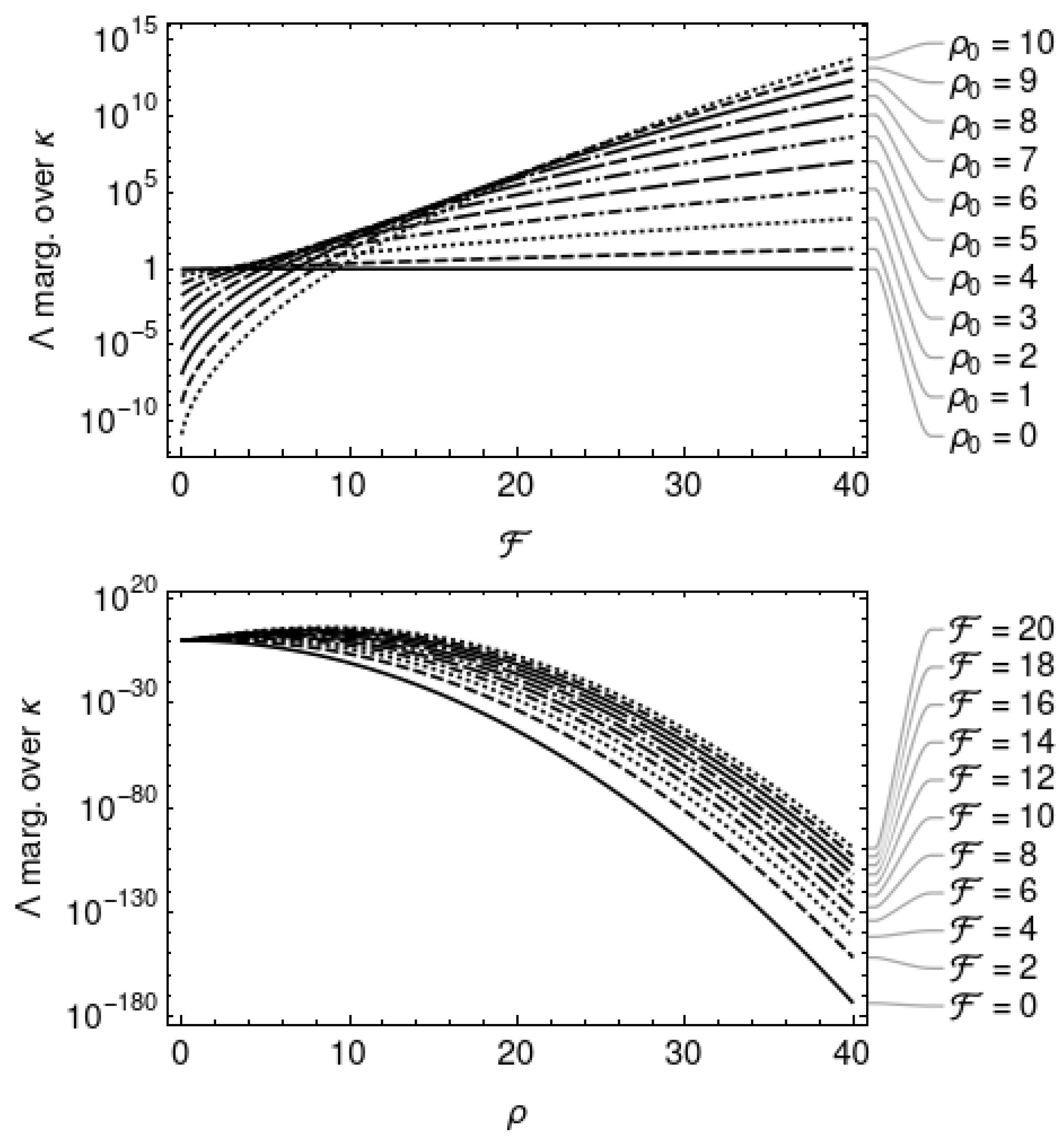
3.1. Marginalisation over
3.2. Marginalisation over
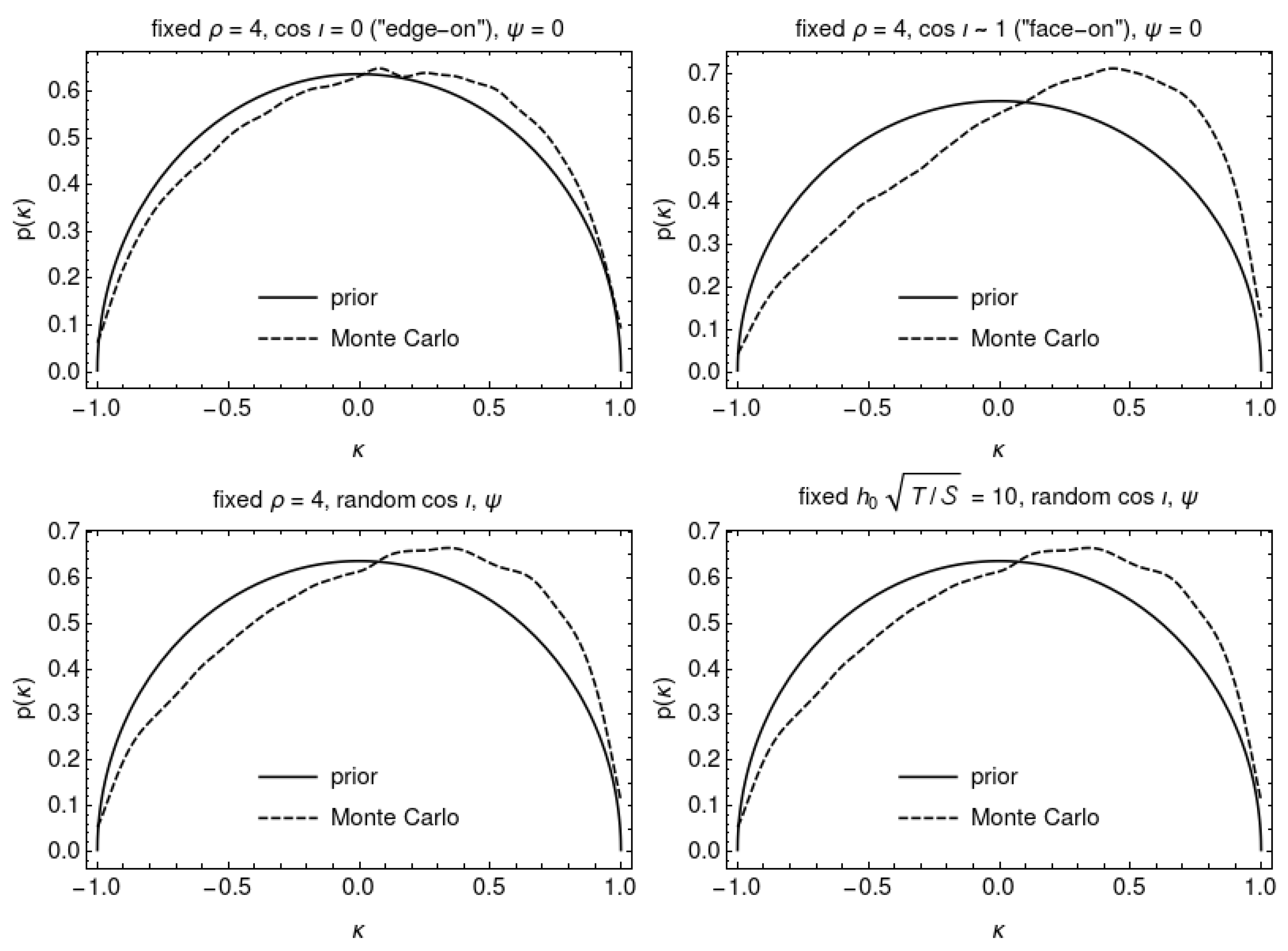
4. Receiver–Operator Curves
- (i)
- fixed , (i.e., the neutron star is viewed “edge-on”), ;
- (ii)
- fixed , 3 (i.e., the neutron star is viewed “face-on”), ;
- (iii)
- fixed , randomly drawn , ; and
- (iv)
- fixed , randomly drawn , ;
5. Discussion
Funding
Acknowledgments
Conflicts of Interest
| 1. | The dot product henceforth denotes the contraction of the last index of the tensor with the first index of the tensor . |
| 2. | It is common in the literature to quote values of twice the -statistic, i.e., . This convention is not followed in this paper, however. |
| 3. | This choice of follows that of [36]. |
References
- LIGO Scientific Collaboration; Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Advanced LIGO. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
- Acernese, F.; Adams, T.; Agatsuma, K.; Aiello, L.; Allocca, A.; Amato, A.; Antier, S.; Arnaud, N.; Ascenzi, S.; Astone, P.; et al. Status of Advanced Virgo. Eur. Phys. J. Web Conf. 2018, 182, 02003. [Google Scholar] [CrossRef]
- KAGRA Collaboration, LIGO Scientific Collaboration, and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2020, 23, 3. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; et al. All-sky search for continuous gravitational waves from isolated neutron stars using Advanced LIGO O2 data. Phys. Rev. D 2019, 100, 024004. [Google Scholar] [CrossRef] [Green Version]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.; et al. Narrow-band search for gravitational waves from known pulsars using the second LIGO observing run. Phys. Rev. D 2019, 99, 122002. [Google Scholar] [CrossRef] [Green Version]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.; et al. Search for gravitational waves from Scorpius X-1 in the second Advanced LIGO observing run with an improved hidden Markov model. Phys. Rev. D 2019, 100, 122002. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.; et al. Searches for Gravitational Waves from Known Pulsars at Two Harmonics in 2015–2017 LIGO Data. Astrophys. J. 2019, 879, 10. [Google Scholar] [CrossRef] [Green Version]
- Palomba, C.; D’Antonio, S.; Astone, P.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Miller, A.L.; Muciaccia, F.; et al. Direct Constraints on the Ultralight Boson Mass from Searches of Continuous Gravitational Waves. Phys. Rev. Lett. 2019, 123, 171101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Covas, P.B.; Sintes, A.M. First All-Sky Search for Continuous Gravitational-Wave Signals from Unknown Neutron Stars in Binary Systems Using Advanced LIGO Data. Phys. Rev. Lett. 2020, 124, 191102. [Google Scholar] [CrossRef] [PubMed]
- Dergachev, V.; Papa, M.A. Results from the First All-Sky Search for Continuous Gravitational Waves from Small-Ellipticity Sources. Phys. Rev. Lett. 2020, 125, 171101. [Google Scholar] [CrossRef]
- Fesik, L.; Papa, M.A. First Search for r-mode Gravitational Waves from PSR J0537-6910. Astrophys. J. 2020, 895, 11. [Google Scholar] [CrossRef]
- Lindblom, L.; Owen, B.J. Directed searches for continuous gravitational waves from twelve supernova remnants in data from Advanced LIGO’s second observing run. Phys. Rev. D 2020, 101, 083023. [Google Scholar] [CrossRef] [Green Version]
- Middleton, H.; Clearwater, P.; Melatos, A.; Dunn, L. Search for gravitational waves from five low mass X-ray binaries in the second Advanced LIGO observing run with an improved hidden Markov model. Phys. Rev. D 2020, 102, 023006. [Google Scholar] [CrossRef]
- Millhouse, M.; Strang, L.; Melatos, A. Search for gravitational waves from 12 young supernova remnants with a hidden Markov model in Advanced LIGO’s second observing run. Phys. Rev. D 2020, 102, 083025. [Google Scholar] [CrossRef]
- Piccinni, O.J.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Miller, A.; Palomba, C. Directed search for continuous gravitational-wave signals from the Galactic Center in the Advanced LIGO second observing run. Phys. Rev. D 2020, 101, 082004. [Google Scholar] [CrossRef]
- Sun, L.; Brito, R.; Isi, M. Search for ultralight bosons in Cygnus X-1 with Advanced LIGO. Phys. Rev. D 2020, 101, 063020. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Papa, M.A.; Krishnan, B.; Watts, A.L. Search for Continuous Gravitational Waves from Scorpius X-1 in LIGO O2 Data. Astrophys. J. Lett. 2021, 906, L14. [Google Scholar] [CrossRef]
- Jones, D.; Sun, L. Search for continuous gravitational waves from Fomalhaut b in the second Advanced LIGO observing run with a hidden Markov model. Phys. Rev. D 2021, 103, 023020. [Google Scholar] [CrossRef]
- Beniwal, D.; Clearwater, P.; Dunn, L.; Melatos, A.; Ottaway, D. Search for continuous gravitational waves from ten H.E.S.S. sources using a hidden Markov model. Phys. Rev. D 2021, 103, 083009. [Google Scholar] [CrossRef]
- Wette, K.; Dunn, L.; Clearwater, P.; Melatos, A. Deep exploration for continuous gravitational waves at 171–172 Hz in LIGO second observing run data. Phys. Rev. D 2021, 103, 083020. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational-wave Constraints on the Equatorial Ellipticity of Millisecond Pulsars. Astrophys. J. 2020, 902, L21. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; et al. All-sky search in early O3 LIGO data for continuous gravitational-wave signals from unknown neutron stars in binary systems. Phys. Rev. D 2021, 103, 064017. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E. Gravitational waves from pulsars: Emission by the magnetic field induced distortion. Astron. Astrophys. 1996, 312, 675. [Google Scholar]
- Ushomirsky, G.; Cutler, C.; Bildsten, L. Deformations of accreting neutron star crusts and gravitational wave emission. Mon. Not. R. Astron. Soc. 2000, 319, 902. [Google Scholar] [CrossRef] [Green Version]
- Owen, B.J. Maximum Elastic Deformations of Compact Stars with Exotic Equations of State. Phys. Rev. Lett. 2005, 95, 211101. [Google Scholar] [CrossRef] [Green Version]
- Haskell, B.; Samuelsson, L.; Glampedakis, K.; Andersson, N. Modelling magnetically deformed neutron stars. Mon. Not. R. Astron. Soc. 2008, 385, 531. [Google Scholar] [CrossRef] [Green Version]
- Glampedakis, K.; Jones, D.I.; Samuelsson, L. Gravitational Waves from Color-Magnetic “Mountains” in Neutron Stars. Phys. Rev. Lett. 2012, 109, 081103. [Google Scholar] [CrossRef] [Green Version]
- Johnson-McDaniel, N.K.; Owen, B.J. Maximum elastic deformations of relativistic stars. Phys. Rev. D 2013, 88, 044004. [Google Scholar] [CrossRef] [Green Version]
- Woan, G.; Pitkin, M.D.; Haskell, B.; Jones, D.I.; Lasky, P.D. Evidence for a Minimum Ellipticity in Millisecond Pulsars. Astrophys. J. 2018, 863, L40. [Google Scholar] [CrossRef]
- Osborne, E.L.; Jones, D.I. Gravitational waves from magnetically induced thermal neutron star mountains. Mon. Not. R. Astron. Soc. 2020, 494, 2839–2850. [Google Scholar] [CrossRef]
- Neyman, J.; Pearson, E.S. On the Problem of the Most Efficient Tests of Statistical Hypotheses. Philos. Trans. R. Soc. A 1933, 231, 289. [Google Scholar] [CrossRef] [Green Version]
- Jaranowski, P.; Królak, A.; Schutz, B.F. Data analysis of gravitational-wave signals from spinning neutron stars: The signal and its detection. Phys. Rev. D 1998, 58, 063001. [Google Scholar] [CrossRef] [Green Version]
- Thrane, E.; Talbot, C. An introduction to Bayesian inference in gravitational-wave astronomy: Parameter estimation, model selection, and hierarchical models. Publ. Astron. Soc. Aust. 2019, 36, e010. [Google Scholar] [CrossRef] [Green Version]
- Searle, A.C.; Sutton, P.J.; Tinto, M.; Woan, G. Robust Bayesian detection of unmodelled bursts. Class. Quantum Gravity 2008, 25, 114038. [Google Scholar] [CrossRef] [Green Version]
- Searle, A.C. Monte-Carlo and Bayesian techniques in gravitational wave burst data analysis. arXiv 2008, arXiv:0804.1161. [Google Scholar]
- Prix, R.; Krishnan, B. Targeted search for continuous gravitational waves: Bayesian versus maximum-likelihood statistics. Class. Quantum Gravity 2009, 26, 204013. [Google Scholar] [CrossRef] [Green Version]
- Prix, R. The F-Statistic and Its Implementation in ComputeFStatistic_v2; Technical Report T0900149-v5; LIGO: Hanford, WA, USA, 21 June 2011. [Google Scholar]
- Patel, P.; Siemens, X.; Dupuis, R.; Betzwieser, J. Implementation of barycentric resampling for continuous wave searches in gravitational wave data. Phys. Rev. D 2010, 81, 084032. [Google Scholar] [CrossRef] [Green Version]
- Poghosyan, G.; Matta, S.; Streit, A.; Bejger, M.; Królak, A. Architecture, implementation and parallelization of the software to search for periodic gravitational wave signals. Comput. Phys. Commun. 2015, 188, 167–176. [Google Scholar] [CrossRef] [Green Version]
- Dergachev, V. Loosely coherent searches for sets of well-modeled signals. Phys. Rev. D 2012, 85, 062003. [Google Scholar] [CrossRef] [Green Version]
- Whelan, J.T.; Prix, R.; Cutler, C.J.; Willis, J.L. New coordinates for the amplitude parameter space of continuous gravitational waves. Class. Quantum Gravity 2014, 31, 065002. [Google Scholar] [CrossRef] [Green Version]
- Dhurandhar, S.; Krishnan, B.; Willis, J.L. Marginalizing the likelihood function for modeled gravitational wave searches. arXiv 2017, arXiv:1707.08163. [Google Scholar]
- Bero, J.J.; Whelan, J.T. An analytic approximation to the Bayesian detection statistic for continuous gravitational waves. Class. Quantum Gravity 2019, 36, 015013. [Google Scholar] [CrossRef] [Green Version]
- Prix, R. Search for continuous gravitational waves: Metric of the multidetector F-statistic. Phys. Rev. D 2007, 75, 023004. [Google Scholar] [CrossRef] [Green Version]
- Brady, P.R.; Creighton, T.; Cutler, C.; Schutz, B.F. Searching for periodic sources with LIGO. Phys. Rev. D 1998, 57, 2101. [Google Scholar] [CrossRef] [Green Version]
- Balasubramanian, R.; Sathyaprakash, B.S.; Dhurandhar, S.V. Gravitational waves from coalescing binaries: Detection strategies and Monte Carlo estimation of parameters. Phys. Rev. D 1996, 53, 3033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Owen, B.J. Search templates for gravitational waves from inspiraling binaries: Choice of template spacing. Phys. Rev. D 1996, 53, 6749. [Google Scholar] [CrossRef] [Green Version]
- Wette, K.; Prix, R. Flat parameter-space metric for all-sky searches for gravitational-wave pulsars. Phys. Rev. D 2013, 88, 123005. [Google Scholar] [CrossRef] [Green Version]
- Królak, A.; Tinto, M.; Vallisneri, M. Optimal filtering of the LISA data. Phys. Rev. D 2004, 70, 022003. [Google Scholar] [CrossRef] [Green Version]
- Whelan, J.T.; Prix, R.; Khurana, D. Improved search for galactic white-dwarf binaries in Mock LISA Data Challenge 1B using an F-statistic template bank. Class. Quantum Gravity 2008, 25, 184029. [Google Scholar] [CrossRef]
- Marsaglia, G. Choosing a Point from the Surface of a Sphere. Ann. Math. Stat. 1972, 43, 645. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration. LIGO Algorithm Library—LALSuite; LIGO Scientific Collaboration: Hanford, WA, USA, 2018. [Google Scholar] [CrossRef]
- Sun, L.; Goetz, E.; Kissel, J.S.; Betzwieser, J.; Karki, S.; Viets, A.; Wade, M.; Bhattacharjee, D.; Bossilkov, V.; Covas, P.B.; et al. Characterization of systematic error in Advanced LIGO calibration. Class. Quantum Gravity 2020, 37, 225008. [Google Scholar] [CrossRef]
- Zimmermann, M.; Szedenits, E., Jr. Gravitational waves from rotating and precessing rigid bodies—Simple models and applications to pulsars. Phys. Rev. D 1979, 20, 351. [Google Scholar] [CrossRef]
- Owen, B.J.; Lindblom, L.; Cutler, C.; Schutz, B.F.; Vecchio, A.; Andersson, N. Gravitational waves from hot young rapidly rotating neutron stars. Phys. Rev. D 1998, 58, 084020. [Google Scholar] [CrossRef] [Green Version]
- Van Den Broeck, C. The gravitational wave spectrum of non-axisymmetric, freely precessing neutron stars. Class. Quantum Gravity 2005, 22, 1825. [Google Scholar] [CrossRef] [Green Version]
- Pitkin, M.; Isi, M.; Veitch, J.; Woan, G. A nested sampling code for targeted searches for continuous gravitational waves from pulsars. arXiv 2017, arXiv:1705.08978. [Google Scholar]
- Cutler, C.; Schutz, B.F. Generalized F-statistic: Multiple detectors and multiple gravitational wave pulsars. Phys. Rev. D 2005, 72, 063006. [Google Scholar] [CrossRef] [Green Version]
- Pitkin, M.; Messenger, C.; Fan, X. Hierarchical Bayesian method for detecting continuous gravitational waves from an ensemble of pulsars. Phys. Rev. D 2018, 98, 063001. [Google Scholar] [CrossRef] [Green Version]
- Mathematica, Version 12.0; Wolfram Research, Inc.: Champaign, IL, USA, 2019.
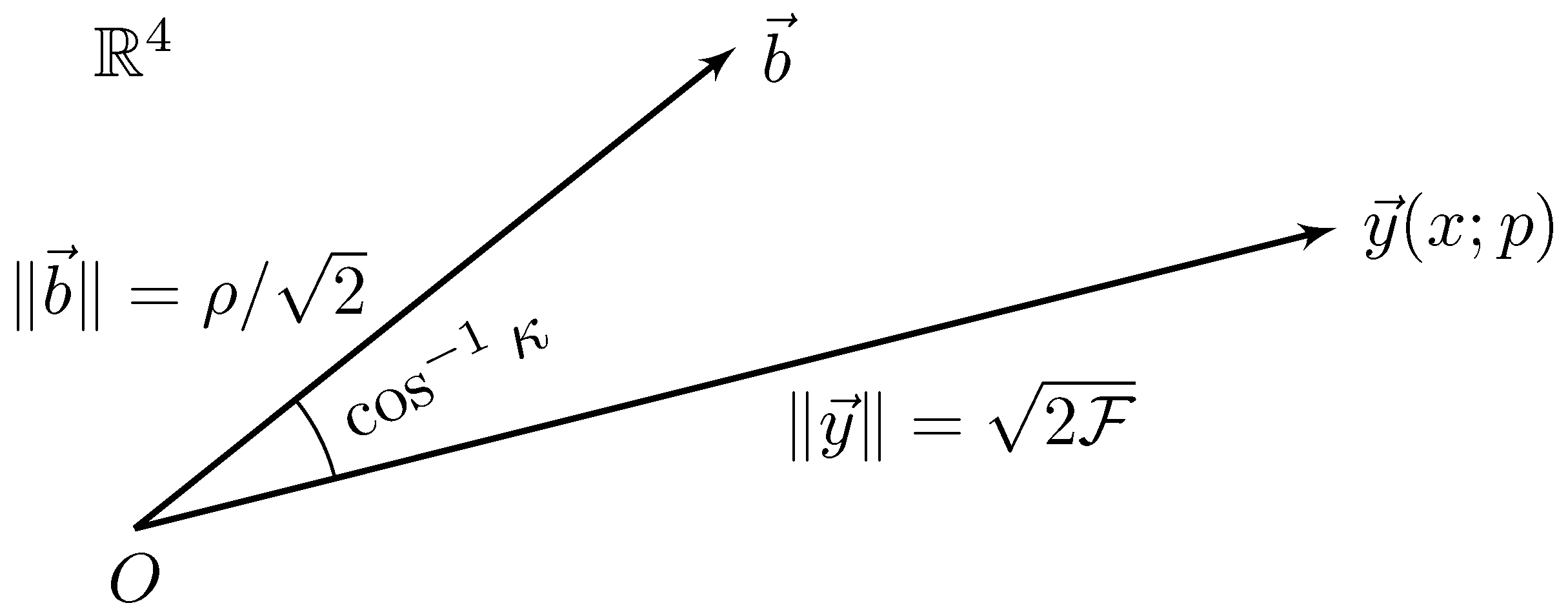




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wette, K. Geometric Approach to Analytic Marginalisation of the Likelihood Ratio for Continuous Gravitational Wave Searches. Universe 2021, 7, 174. https://doi.org/10.3390/universe7060174
Wette K. Geometric Approach to Analytic Marginalisation of the Likelihood Ratio for Continuous Gravitational Wave Searches. Universe. 2021; 7(6):174. https://doi.org/10.3390/universe7060174
Chicago/Turabian StyleWette, Karl. 2021. "Geometric Approach to Analytic Marginalisation of the Likelihood Ratio for Continuous Gravitational Wave Searches" Universe 7, no. 6: 174. https://doi.org/10.3390/universe7060174
APA StyleWette, K. (2021). Geometric Approach to Analytic Marginalisation of the Likelihood Ratio for Continuous Gravitational Wave Searches. Universe, 7(6), 174. https://doi.org/10.3390/universe7060174





