Neutrinoless Double Beta Decay with Germanium Detectors: 1026 yr and Beyond
Abstract
:1. Introduction
2. Neutrinoless Double Beta Decay
3. The Choice of the Ge Isotope
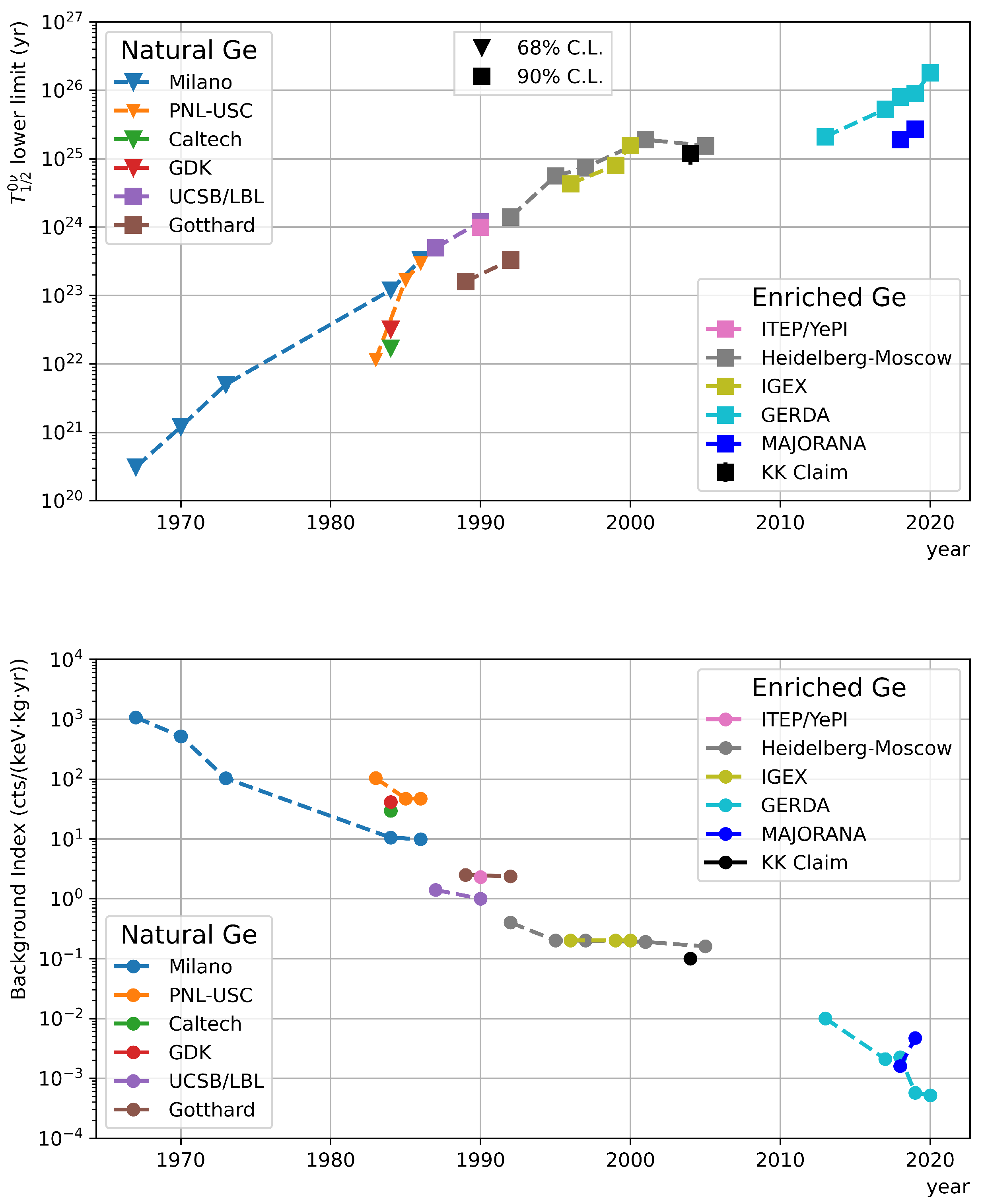
4. Neutrinoless Double Beta Decay Search with Ge Detectors
5. The GERDA Experiment
5.1. Experimental Setup
5.2. Data Analysis Flow and Active Background Suppression
5.3. Statistical Analysis and Results
6. The Majorana Experiment
6.1. Data-Taking and Event Selection
6.2. Energy Estimation
6.3. Background Suppression
6.4. Search Results
7. The LEGEND Project
7.1. LEGEND-200 Germanium Detectors and Experimental Setup
7.2. Readout Electronics
7.3. Background Mitigation Techniques
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; Kameda, J.; Kasuga, S.; et al. Evidence for Oscillation of Atmospheric Neutrinos. Phys. Rev. Lett. 1998, 81, 1562–1567. [Google Scholar] [CrossRef] [Green Version]
- Eguchi, K.; Enomoto, S.; Furuno, K.; Goldman, J.; Hanada, H.; Ikeda, H.; Ikeda, K.; Inoue, K.; Ishihara, K.; Itoh, W.; et al. First Results from KamLAND: Evidence for Reactor Antineutrino Disappearance. Phys. Rev. Lett. 2003, 90, 021802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McDonald, A.B. Nobel Lecture: The Sudbury Neutrino Observatory: Observation of flavor change for solar neutrinos. Rev. Mod. Phys. 2016, 88, 030502. [Google Scholar] [CrossRef]
- Kajita, T. Nobel Lecture: Discovery of atmospheric neutrino oscillations. Rev. Mod. Phys. 2016, 88, 030501. [Google Scholar] [CrossRef] [Green Version]
- Cowan, C.L.; Reines, F.; Harrison, F.B.; Kruse, H.W.; McGuire, A.D. Detection of the Free Neutrino: A Confirmation. Science 1956, 124, 103–104. [Google Scholar] [CrossRef] [Green Version]
- Agostini, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; Bezrukov, L.; et al. Probing Majorana neutrinos with double-β decay. Science 2019, 365, 1445–1448. [Google Scholar] [CrossRef] [Green Version]
- Alvis, S.I.; Arnquist, I.J.; Avignone, F.T.; Barabash, A.S.; Barton, C.J.; Basu, V.; Bertrand, F.E.; Bos, B.; Busch, M.; Buuck, M.; et al. Search for neutrinoless double-β decay in 76Ge with 26 kg yr of exposure from the Majorana Demonstrator. Phys. Rev. C 2019, 100, 025501. [Google Scholar] [CrossRef] [Green Version]
- Azzolini, O.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Capelli, S.; Cardani, L.; Carniti, P.; et al. Final result of CUPID-0 phase-I in the search for the 82Se Neutrinoless Double-β Decay. Phys. Rev. Lett. 2019, 123, 032501. [Google Scholar] [CrossRef] [Green Version]
- Alenkov, V.; Bae, H.W.; Beyer, J.; Boiko, R.S.; Boonin, K.; Buzanov, O.; Chanthima, N.; Cheoun, M.K.; Chernyak, D.M.; Choe, J.S.; et al. First Results from the AMoRE-Pilot neutrinoless double beta decay experiment. Eur. Phys. J. C 2019, 79, 791. [Google Scholar] [CrossRef] [Green Version]
- Arnold, R.; Augier, C.; Baker, J.D.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Brudanin, V.; Busto, J.; et al. Results of the search for neutrinoless double-β decay in 100Mo with the NEMO-3 experiment. Phys. Rev. D 2015, 92, 072011. [Google Scholar] [CrossRef] [Green Version]
- Armengaud, E.; Augier, C.; Barabash, A.S.; Bellini, F.; Benato, G.; Benoît, A.; Beretta, M.; Bergé, L.; Billard, J.; Borovlev, Y.A.; et al. The CUPID-Mo experiment for neutrinoless double-beta decay: Performance and prospects. Eur. Phys. J. C 2020, 80, 44. [Google Scholar] [CrossRef]
- Adams, D.Q.; Alduino, C.; Alfonso, K.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Biassoni, M.; Branca, A.; et al. Improved Limit on Neutrinoless Double-Beta Decay in 130Te with CUORE. Phys. Rev. Lett. 2020, 124, 122501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andringa, S.; Arushanova, E.; Asahi, S.; Askins, M.; Auty, D.J.; Back, A.R.; Barnard, Z.; Barros, N.; Beier, E.W.; Bialek, A.; et al. Current Status and Future Prospects of the SNO+ Experiment. Adv. High Energy Phys. 2016, 2016, 6194250. [Google Scholar] [CrossRef] [Green Version]
- Anton, G.; Badhrees, I.; Barbeau, P.S.; Beck, D.; Belov, V.; Bhatta, T.; Breidenbach, M.; Brunner, T.; Cao, G.F.; Cen, W.R.; et al. Search for Neutrinoless Double-β Decay with the Complete EXO-200 Dataset. Phys. Rev. Lett. 2019, 123, 161802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gando, A.; Gando, Y.; Hachiya, T.; Hayashi, A.; Hayashida, S.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; Karino, Y.; Koga, M.; et al. Search for Majorana Neutrinos near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys. Rev. Lett. 2016, 117, 082503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martín-Albo, J.; Muñoz Vidal, J.; Ferrario, P.; Nebot-Guinot, M.; Gómez-Cadenas, J.J.; Álvarez, V.; Azevedo, C.D.R.; Borges, F.I.G.; Cárcel, S.; Cebrián, S.; et al. Sensitivity of NEXT-100 to Neutrinoless Double Beta Decay. JHEP 2016, 5, 159. [Google Scholar] [CrossRef] [Green Version]
- Fiorini, E.; Pullia, A.; Bertolini, G.; Cappellani, F.; Restelli, G. A search for lepton non-conservation in double beta decay with a germanium detector. Phys. Lett. B 1967, 25, 602–603. [Google Scholar] [CrossRef]
- Goeppert-Mayer, M. Double beta-disintegration. Phys. Rev. 1935, 48, 512–516. [Google Scholar] [CrossRef]
- Furry, W.H. On transition probabilities in double beta-disintegration. Phys. Rev. 1939, 56, 1184–1193. [Google Scholar] [CrossRef]
- Barabash, A. Precise Half-Life Values for Two-Neutrino Double-β Decay: 2020 review. Universe 2020, 6, 159. [Google Scholar] [CrossRef]
- Doi, M.; Kotani, T.; Nishiura, H.; Okuda, K.; Takasugi, E. Neutrino Mass, the Right-Handed Interaction and the Double Beta Decay. II: General Properties and Data Analysis. Prog. Theor. Phys. 1981, 66, 1765–1788. [Google Scholar] [CrossRef] [Green Version]
- Menéndez, J.; Poves, A.; Caurier, E.; Nowacki, F. Disassembling the nuclear matrix elements of the neutrinoless ββ decay. Nucl. Phys. A 2009, 818, 139–151. [Google Scholar] [CrossRef] [Green Version]
- Šimkovic, F.; Rodin, V.; Faessler, A.; Vogel, P. 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys. Rev. C 2013, 87, 045501. [Google Scholar] [CrossRef] [Green Version]
- Barea, J.; Kotila, J.; Iachello, F. 0νββ and 2νββ nuclear matrix elements in the interacting boson model with isospin restoration. Phys. Rev. C 2015, 91, 034304. [Google Scholar] [CrossRef] [Green Version]
- Dolinski, M.J.; Poon, A.W.P.; Rodejohann, W. Neutrinoless Double-Beta Decay: Status and Prospects. Ann. Rev. Nucl. Part Sci. 2019, 69, 219–251. [Google Scholar] [CrossRef] [Green Version]
- Šimkovic, F.; Pantis, G.; Vergados, J.D.; Faessler, A. Additional nucleon current contributions to neutrinoless double β decay. Phys. Rev. C 1999, 60, 055502. [Google Scholar] [CrossRef] [Green Version]
- Deppisch, F.F.; Hati, C.; Patra, S.; Pritimita, P.; Sarkar, U. Neutrinoless double beta decay in left-right symmetric models with a universal seesaw mechanism. Phys. Rev. D 2018, 97, 035005. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, W.R.; Chang, C.; Hafidi, K.; Lisovenko, M.; Novosad, V.; Pearson, J.; Polakovic, T.; Wang, G.; Yefremenko, V.; Zhang, J.; et al. CUPID Pre-CDR. Working Paper. 2019. Available online: https://hal.archives-ouvertes.fr/hal-02283520 (accessed on 1 August 2021).
- Albert, J.B.; Anton, G.; Badhrees, I.; Barbeau, P.S.; Bayerlein, R.; Beck, D.; Belov, V.; Breidenbach, M.; Brunner, T.; Cao, G.F.; et al. Search for Neutrinoless Double-Beta Decay with the Upgraded EXO-200 Detector. Phys. Rev. Lett. 2018, 120, 072701. [Google Scholar] [CrossRef] [Green Version]
- Monrabal, F.; Gómez-Cadenas, J.J.; Toledo, J.F.; Álvarez, V.; Benlloch-Rodríguez, J.M.; Cárcel, S.; Carrión, J.V.; Esteve, R.; Felkai, R.; Herreroet, V.; et al. The NEXT White (NEW) detector. JINST 2018, 13, P12010. [Google Scholar] [CrossRef] [Green Version]
- Gando, Y. First results of KamLAND-Zen 800. J. Phys. Conf. Ser. 2020, 1468, 012142. [Google Scholar] [CrossRef]
- Kotila, J.; Iachello, F. Phase space factors for double-β decay. Phys. Rev. C 2012, 85, 034316. [Google Scholar] [CrossRef] [Green Version]
- Stoica, S.; Mirea, M. New calculations for phase space factors involved in double-β decay. Phys. Rev. C 2013, 88, 037303. [Google Scholar] [CrossRef] [Green Version]
- Primakoff, H.; Rosen, S. Alpha, Beta, and Gamma-Ray Spectroscopy. Phys. Today 1965, 18, 76. [Google Scholar] [CrossRef]
- Fiorini, E.; Pullia, A.; Bertolini, G.; Cappellani, F.; Restelli, G. An underground experiment on neutrinoless double beta-decay. Lett. Nuovo Cimento (1969–1970) 1970, 3, 149–152. [Google Scholar] [CrossRef]
- Fiorini, E.; Pullia, A.; Bertolini, G.; Cappellani, F.; Restelli, G. Neutrinoless double-beta decay of 76Ge. Il Nuovo Cimento A (1965–1970) 1973, 13, 747–763. [Google Scholar] [CrossRef]
- Avignone, F.T.; Elliott, S.R. The Search for Double Beta Decay With Germanium Detectors: Past, Present, and Future. Front. Phys. 2019, 7, 6. [Google Scholar] [CrossRef]
- Bellotti, E.; Cremonesi, O.; Fiorini, E.; Liguori, C.; Pullia, A.; Sverzellati, P.P.; Zanotti, L. New limits on double beta decay of 76Ge. Phys. Lett. B 1984, 146, 450–456. [Google Scholar] [CrossRef]
- Bellotti, E.; Cremonesi, O.; Fiorini, E.; Liguori, C.; Pullia, A.; Sverzellati, P.P.; Zanotti, L. The milano experiment on lepton number nonconservation in double beta-decay of 76Ge. Il Nuovo Cimento A (1965–1970) 1986, 95, 1–46. [Google Scholar] [CrossRef]
- Forster, A.; Kwon, H.; Markey, J.K.; Boehm, F.; Henrikson, H.E. Low background study of the neutrinoless double beta decay of 76-GE and upper limit for neutrino mass. Phys. Lett. B 1984, 138, 301–303. [Google Scholar] [CrossRef]
- Simpson, J.J.; Jagam, P.; Campbell, J.L.; Malm, H.L.; Robertson, B.C. New Limit for Neutrinoless Double β Decay of 76Ge. Phys. Rev. Lett. 1984, 53, 141–143. [Google Scholar] [CrossRef]
- Fisher, P.; Boehm, F.; Bovet, E.; Egger, J.P.; Henrikson, H.; Gabathuler, K.; Mitchell, L.W.; Reusser, D.; Treichel, M.; Vuilleumier, J.L. A search for double beta decay in 76Ge. Phys. Lett. B 1989, 218, 257–262. [Google Scholar] [CrossRef]
- Reusser, D.; Treichel, M.; Boehm, F.; Fisher, P.; Gabathuler, K.; Henrikson, H.E.; Jörgens, V.; Mitchell, L.W.; Nussbaum, C.; Vuilleumier, J.L. Final report on the search for neutrinoless double-β decay of 76Ge from the Gotthard underground experiment. Phys. Rev. D 1992, 45, 2548–2551. [Google Scholar] [CrossRef]
- Avignone, F.T.; Brodzinski, R.L.; Brown, D.P.; Evans, J.C.; Hensley, W.K.; Reeves, J.H.; Wogman, N.A. New Limits on the Neutrino Mass, Lepton Conservation, and No-Neutrino Double Beta Decay of 76Ge. Phys. Rev. Lett. 1983, 50, 721–724. [Google Scholar] [CrossRef]
- Avignone, F.T.; Brodzinski, R.L.; Brown, D.P.; Evans, J.C.; Hensley, W.K.; Miley, H.S.; Reeves, J.H.; Wogman, N.A. Ultralow-Background Study of Neutrinoless Double β Decay of 76Ge: New Limit on the Majorana Mass of νe. Phys. Rev. Lett. 1985, 54, 2309–2312. [Google Scholar] [CrossRef]
- Avignone, F.T.; Brodzinski, R.L.; Evans, J.C.; Hensley, W.K.; Miley, H.S.; Reeves, J.H. Search for the double-β decay of 76Ge. Phys. Rev. C 1986, 34, 666–677. [Google Scholar] [CrossRef]
- Caldwell, D.O.; Eisberg, R.M.; Grumm, D.M.; Witherell, M.S.; Goulding, F.S.; Smith, A.R. Limits on neutrinoless ββ decay, including that with majoron emission. Phys. Rev. Lett. 1987, 59, 419–422. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, D.O. Double beta decay-present and future. J. Phys. G Nucl. Part Phys. 1991, 17, S137–S144. [Google Scholar] [CrossRef]
- Vasenko, A.; Kirpichnikov, I.V.; Kuznetsov, V.A.; Starostin, A.S.; Dzhanian, A.G.; Markosian, G.E.; Oganesian, V.M.; Pogosov, V.S.; Tamanian, A.G.; Shakhazizian, S.R. New results in the ITEP/YePI double beta-decay experiment with enriched germanium detectors. Mod. Phys. Lett. A 1990, 5, 1299–1306. [Google Scholar] [CrossRef]
- Balysh, A.; Beck, M.; Belyaev, S.T.; Bockholt, J.; Demehin, A.; Echternach, J.; Gurov, A.; Heusser, G.; Hirsch, M.; Klapdor-Kleingrothaus, H.V.; et al. The Heidelberg-Moscow double beta decay experiment with enriched 76Ge. First results. Phys. Lett. B 1992, 283, 32–36. [Google Scholar] [CrossRef]
- Balysh, A.; Beck, M.; Belyaev, S.T.; Bockholt, J.; Demehin, A.; Gurov, A.; Hellmig, J.; Heusser, G.; Hirsch, M.; Hoffmann, C.; et al. Sub-eV limit for the neutrino mass from 76Ge double beta decay by the HEIDELBERG-MOSCOW experiment. Phys. Lett. B 1995, 356, 450–455. [Google Scholar] [CrossRef]
- Günther, M.; Hellmig, J.; Heusser, G.; Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Maier, B.; Päs, H.; Petry, F.; Ramachers, Y.; Strecker, H.; et al. Heidelberg-Moscow ββ experiment with76Ge: Full setup with five detectors. Phys. Rev. D 1997, 55, 54–67. [Google Scholar] [CrossRef]
- Klapdor-Kleingrothaus, H.V.; Dietz, A.; Baudis, L.; Heusser, G.; Krivosheina, I.V.; Kolb, S.; Majorovits, B.; Paes, H.; Strecker, H.; Alexeev, V.; et al. Latest results from the Heidelberg-Moscow double beta decay experiment. Eur. Phys. J. 2001, A12, 147–154. [Google Scholar] [CrossRef] [Green Version]
- Bakalyarov, A.M.; Balysh, A.Y.; Belyaev, S.T.; Lebedev, V.I.; Zhukov, S.V. Results of the experiment on investigation of Germanium-76 double beta decay: Experimental data of Heidelberg-Moscow collaboration November 1995–August 2001. Phys. Part Nucl. Lett. 2005, 2, 77–81. [Google Scholar]
- Aalseth, C.E.; Avignone, F.T.; Brodzinski, R.L.; Collar, J.I.; Garcia, E.; Gonzalez, D.; Hasenbalg, F.; Hensley, W.K.; Kirpichnikov, I.V.; Klimenko, A.A.; et al. Neutrinoless double-β decay of76Ge: First results from the International Germanium Experiment (IGEX) with six isotopically enriched detectors. Phys. Rev. C 1999, 59, 2108–2113. [Google Scholar] [CrossRef]
- Aalseth, C.E.; Avignone, F.T.; Brodzinski, R.L.; Cebrian, S.; Garcia, E.; Gonzalez, D.; Hensley, W.K.; Irastorza, I.G.; Kirpichnikov, I.V.; Klimenko, A.A.; et al. The IGEX Ge-76 neutrinoless double beta decay experiment: Prospects for next generation experiments. Phys. Rev. D 2002, 65, 092007. [Google Scholar] [CrossRef] [Green Version]
- Klapdor-Kleingrothaus, H.V.; Dietz, A.; Harney, H.L.; Krivosheina, I.V. Evidence for neutrinoless double beta decay. Mod. Phys. Lett. A 2001, 16, 2409–2420. [Google Scholar] [CrossRef]
- Klapdor-Kleingrothaus, H.V.; Krivosheina, I.V.; Dietz, A.; Chkvorets, O. Search for neutrinoless double beta decay with enriched Ge-76 in Gran Sasso 1990–2003. Phys. Lett. 2004, B586, 198–212. [Google Scholar] [CrossRef] [Green Version]
- Klapdor-Kleingrothaus, H.V.; Krivosheina, I.V. The evidence for the observation of 0nu beta beta decay: The identification of 0nu beta beta events from the full spectra. Mod. Phys. Lett. A 2006, 21, 1547–1566. [Google Scholar] [CrossRef]
- Schwingenheuer, B. Status and prospects of searches for neutrinoless double beta decay. Ann. Phys. 2013, 525, 269–280. [Google Scholar] [CrossRef] [Green Version]
- Agostini, M.; Allardt, M.; Andreotti, E.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barnabé Heider, M.; Barros, N.; Baudis, L.; Bauer, C.; et al. Results on Neutrinoless Double-β Decay of 76Ge from Phase I of the GERDA Experiment. Phys. Rev. Lett. 2013, 111, 122503. [Google Scholar] [CrossRef] [Green Version]
- Agostini, M.; Allardt, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Belyaev, S.T.; et al. Background free search for neutrinoless double beta decay with GERDA Phase II. Nature 2017, 544, 47. [Google Scholar] [CrossRef]
- Agostini, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; Bezrukov, L.; et al. Improved Limit on Neutrinoless Double-β Decay of 76Ge from GERDA Phase II. Phys. Rev. Lett. 2018, 120, 132503. [Google Scholar] [CrossRef] [Green Version]
- Agostini, M.; Araujo, G.R.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; et al. Final Results of GERDA on the Search for Neutrinoless Double-β Decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar] [CrossRef]
- Aalseth, C.E.; Abgrall, N.; Aguayo, E.; Alvis, S.I.; Amman, M.; Arnquist, I.J.; Avignone, F.T.; Back, H.O.; Barabash, A.S.; Barbeau, P.S.; et al. Search for Neutrinoless Double-β Decay in 76Ge with the Majorana Demonstrator. Phys. Rev. Lett. 2018, 120, 132502. [Google Scholar] [CrossRef] [Green Version]
- Abgrall, N.; Abramov, A.; Abrosimov, N.; Abt, I.; Agostini, M.; Agartioglu, M.; Ajjaq, A.; Alvis, S.I.; Avignone, F.T.; Bai, X.; et al. The Large Enriched Germanium Experiment for Neutrinoless Double Beta Decay (LEGEND). AIP Conf. Proc. 2017, 1894, 020027. [Google Scholar] [CrossRef] [Green Version]
- Ackermann, K.H.; Agostini, M.; Allardt, M.; Altmann, M.; Andreotti, E.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barnabé Heider, M.; Barros, N.; et al. The GERDA experiment for the search of 0νββ decay in 76Ge. Eur. Phys. J. C 2013, 73, 2330. [Google Scholar] [CrossRef] [Green Version]
- Agostini, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Belyaev, S.T.; Benato, G.; et al. Upgrade for Phase II of the Gerda experiment. Eur. Phys. J. C 2018, 78, 388. [Google Scholar] [CrossRef] [Green Version]
- Heusser, G. Low-radioactivity background techniques. Ann. Rev. Nucl. Part Sci. 1995, 45, 543–590. [Google Scholar] [CrossRef]
- Agostini, M.; Bakalyarov, A.M.; Andreotti, E.; Balata, M.; Barabanov, I.; Baudis, L.; Barros, N.; Bauer, C.; Bellotti, E.; Belogurov, S.; et al. Characterization of 30 76Ge enriched Broad Energy Ge detectors for GERDA Phase II. Eur. Phys. J. C 2019, 79, 978. [Google Scholar] [CrossRef]
- Cooper, R.; Radford, D.; Hausladen, P.; Lagergren, K. A novel HPGe detector for gamma-ray tracking and imaging. Nucl. Instrum. Methods A 2011, 665, 25–32. [Google Scholar] [CrossRef]
- Agostini, M.; Araujo, G.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; et al. Characterization of inverted coaxial 76Ge detectors in GERDA for future double-β decay experiments. Eur. Phys. J. C 2021, 81, 505. [Google Scholar] [CrossRef]
- Freund, K.; Falkenstein, R.; Grabmayr, P.; Hegai, A.; Jochum, J.; Knapp, M.; Lubsandorzhiev, B.; Ritter, F.; Schmitt, C.; Schütz, A.-K.; et al. The Performance of the Muon Veto of the GERDA Experiment. Eur. Phys. J. C 2016, 76, 298. [Google Scholar] [CrossRef] [Green Version]
- Barabanov, I.; Bezrukov, L.; Demidova, E.; Gurentsov, V.; Kianovsky, S.; Knopfle, K.T.; Kornouhkov, V.; Schwingenheuer, B.; Vasenko, A. Shielding of the GERDA experiment against external gamma background. Nucl. Instrum. Methods A 2009, 606, 790–794. [Google Scholar] [CrossRef]
- Agostini, M.; Allardt, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barros, N.; Baudis, L.; Bauer, C.; Becerici-Schmidt, N.; Bellotti, E.; et al. Improvement of the energy resolution via an optimized digital signal processing in GERDA Phase I. Eur. Phys. J. C 2015, 75, 255. [Google Scholar] [CrossRef]
- Agostini, M.; Allardt, M.; Andreotti, E.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barnabé Heider, M.; Barros, N.; Baudis, L.; Bauer, C.; et al. Pulse shape discrimination for GERDA Phase I data. Eur. Phys. J. C 2013, 73, 2583. [Google Scholar] [CrossRef] [Green Version]
- Budjáš, D.; Barnabé Heider, M.; Chkvorets, O.; Khanbekov, N.; Schönert, S. Pulse shape discrimination studies with a Broad-Energy Germanium detector for signal identification and background suppression in the GERDA double beta decay experiment. JINST 2009, 4, P10007. [Google Scholar] [CrossRef] [Green Version]
- Agostini, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; Bezrukov, L.; et al. First Search for Bosonic Superweakly Interacting Massive Particles with Masses up to 1 MeV/c2 with GERDA. Phys. Rev. Lett. 2020, 125, 011801. [Google Scholar] [CrossRef] [PubMed]
- Agostini, M.; Allardt, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barros, N.; Baudis, L.; Bauer, C.; Becerici-Schmidt, N.; Bellotti, E.; et al. Results on ββ decay with emission of two neutrinos or Majorons in76 Ge from GERDA Phase I. Eur. Phys. J. C 2015, 75, 416. [Google Scholar] [CrossRef] [Green Version]
- Agostini, M.; Allardt, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barros, N.; Baudis, L.; Bauer, C.; Becerici-Schmidt, N.; Bellotti, E.; et al. 2νββ decay of 76Ge into excited states with GERDA Phase I. J. Phys. G 2015, 42, 115201. [Google Scholar] [CrossRef] [Green Version]
- Abgrall, N.; Aguayo, E.; Avignone, F.T.; Barabash, A.S.; Bertrand, F.E.; Boswell, M.; Brudanin, V.; Busch, M.; Caldwell, A.S.; Chan, Y.-D.; et al. The Majorana Demonstrator Neutrinoless Double-Beta Decay Experiment. Adv. High Energy Phys. 2014, 2014, 365432. [Google Scholar] [CrossRef] [Green Version]
- Luke, P.; Goulding, F.; Madden, N.; Pehl, R. Low capacitance large volume shaped-field germanium detector. IEEE Trans. Nucl. Sci. 1989, 36, 926–930. [Google Scholar] [CrossRef] [Green Version]
- Barbeau, P.S.; Collar, J.I.; Tench, O. Large-mass ultralow noise germanium detectors: Performance and applications in neutrino and astroparticle physics. J. Cosmol. Astropart. Phys. 2007, 2007, 9. [Google Scholar] [CrossRef]
- Abgrall, N.; Arnquist, I.J.; Avignone, F.T.; Barabash, A.S.; Bertrand, F.E.; Boswell, M.; Bradley, A.W.; Brudanin, V.; Busch, M.; Buuck, M.; et al. The Majorana Demonstrator calibration system. Nucl. Instrum. Methods A 2017, 872, 16–22. [Google Scholar] [CrossRef]
- Guinn, I.; Arnquist, I.J.; Avignone, F.T.; Barabash, A.S.; Barton, C.J.; Bertrand, F.E.; Bos, B.; Busch, M.; Buuck, M.; Caldwell, T.S.; et al. Results of the Majorana Demonstrator’s Search for Double-Beta Decay of 76Ge to Excited States of 76Se. J. Phys. Conf. Ser. 2020, 1468, 012115. [Google Scholar] [CrossRef]
- Guinn, I.; Abgrall, N.; Avignone, F.T.; Barabash, A.S.; Bertrand, F.E.; Brudanin, V.; Busch, M.; Buuck, M.; Byram, D.; Caldwell, A.S.; et al. Low Background Signal Readout Electronics for the Majorana Demonstrator. J. Phys. Conf. Ser. 2015, 606, 012009. [Google Scholar] [CrossRef]
- Abgrall, N.; Allmond, J.M.; Arnquist, I.J.; Avignone, F.T.; Barabash, A.S.; Barton, C.J.; Bertrand, F.E.; Bos, B.; Busch, M.; Buuck, M.; et al. ADC Nonlinearity Correction for the Majorana Demonstrator. IEEE Trans. Nucl. Sci. 2021, 68, 359–367. [Google Scholar] [CrossRef]
- Vetter, K.; Kuhn, A.; Lee, I.Y.; Clark, R.; Cromaz, M.; Deleplanque, M.; Diamond, R.; Fallon, P.; Lane, G.; Macchiavelli, A.; et al. Performance of the GRETA prototype detectors. Nucl. Instrum. Methods Phys. Res. Sect. A 2000, 452, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Fano, U. Ionization Yield of Radiations. II. The Fluctuations of the Number of Ions. Phys. Rev. 1947, 72, 26–29. [Google Scholar] [CrossRef]
- Alvis, S.I.; Arnquist, I.J.; Avignone, F.T.; Barabash, A.S.; Barton, C.J.; Basu, V.; Bertrand, F.E.; Bos, B.; Buuck, M.; Caldwell, T.S.; et al. Multisite event discrimination for the Majorana Demonstrator. Phys. Rev. C 2019, 99, 065501. [Google Scholar] [CrossRef] [Green Version]
- Boswell, M.; Chan, Y.-D.; Detwiler, J.; Finnerty, P.; Henning, R.; Gehman, V.; Johnson, R.A.; Jordan, D.V.; Kazkaz, K.; Knapp, M.; et al. MaGe-a Geant4-Based Monte Carlo Application Framework for Low-Background Germanium Experiments. IEEE Trans. Nucl. Sci. 2011, 58, 1212–1220. [Google Scholar] [CrossRef] [Green Version]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods A 2003, 506, 250–303. [Google Scholar] [CrossRef] [Green Version]
- Feldman, G.J.; Cousins, R.D. Unified approach to the classical statistical analysis of small signals. Phys. Rev. D 1998, 57, 3873–3889. [Google Scholar] [CrossRef] [Green Version]
- Verkerke, W.; Kirkby, D.P. The RooFit toolkit for data modeling. arXiv 2003, arXiv:physics/0306116. [Google Scholar]
- Schott, G. RooStats for Searches. In PHYSTAT 2011; CERN: Geneva, Switzerland, 2011. [Google Scholar] [CrossRef]
- Horoi, M.; Neacsu, A. Shell model predictions for 124Sn double-β decay. Phys. Rev. C 2016, 93, 024308. [Google Scholar] [CrossRef] [Green Version]
- Hyvärinen, J.; Suhonen, J. Nuclear matrix elements for 0νββ decays with light or heavy Majorana-neutrino exchange. Phys. Rev. C 2015, 91, 024613. [Google Scholar] [CrossRef]
- López Vaquero, N.; Rodríguez, T.R.; Egido, J.L. Shape and pairing fluctuations effects on neutrinoless double beta decay nuclear matrix elements. Phys. Rev. Lett. 2013, 111, 142501. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.M.; Song, L.S.; Hagino, K.; Ring, P.; Meng, J. Systematic study of nuclear matrix elements in neutrinoless double-β decay with a beyond-mean-field covariant density functional theory. Phys. Rev. C 2015, 91, 024316. [Google Scholar] [CrossRef] [Green Version]
- Mirea, M.; Pahomi, T.; Stoica, S. Values of the phase space factors involved in double beta decay. Rom. Rep. Phys. 2015, 67, 872. [Google Scholar]
- LEGEND Collaboration. The Large Enriched Germanium Experiment for Neutrinoless ββ decay, LEGEND-1000 Pre-Conceptual Design Report. Unpublished work. 2021. [Google Scholar]
- Domula, A.; Hult, M.; Kermaïdic, Y.; Marissens, G.; Schwingenheuer, B.; Wester, T.; Zuber, K. Pulse shape discrimination performance of inverted coaxial Ge detectors. Nucl. Instrum. Methods A 2018, 891, 106–110. [Google Scholar] [CrossRef] [Green Version]
- Abgrall, N.; Aguayo, E.; Avignone, F.T.; Barabash, A.S.; Bertrand, F.E.; Boswell, M.; Brudanin, V.; Busch, M.; Byram, D.; Caldwell, A.S.; et al. The Majorana Low-noise Low-background Front-end Electronics. Phys. Procedia 2015, 61, 654–657. [Google Scholar] [CrossRef] [Green Version]
- Riboldi, S.; Pullia, A.; Cattadori, C. Improvement of the “CC2” charge sensitive preamplifier for the GERDA phase II experiment. In Proceedings of the 2012 IEEE Nuclear Science Symposium and Medical Imaging Conference and 19th Workshop on Room-Temperature Semiconductor X-ray and Gamma-ray Detectors, Anaheim, CA, USA, 27 October–3 November 2012. [Google Scholar] [CrossRef]
- Willers, M. Signal Readout Electronics for LEGEND-200. J. Phys. Conf. Ser. 2020, 1468, 012113. [Google Scholar] [CrossRef]
- Abgrall, N.; Arnquist, I.J.; Avignone, F.T.; Back, H.O.; Barabash, A.S.; Bertrand, F.; Boswell, M.; Bradley, A.W.; Brudanin, V.; Busch, M.; et al. The Majorana Demonstrator radioassay program. Nucl. Instrum. Methods A 2016, 828, 22–36. [Google Scholar] [CrossRef] [Green Version]
- Myslik, J. LEGEND: The Large Enriched Germanium Experiment for Neutrinoless Double-Beta Decay. In Proceedings of the 13th Conference on the Intersections of Particle and Nuclear Physics, Palm Springs, CA, USA, 29 May–3 June 2018. [Google Scholar]
- Efremenko, Y.; Fajt, L.; Hodák, R.; Štekl, I.; Febbraro, M.; Radford, D.; Fischer, F.; Hayward, C.; Kraetzschmar, T.; Majorovits, B.; et al. Use of poly(ethylene naphthalate) as a self-vetoing structural material. JINST 2019, 14, P07006. [Google Scholar] [CrossRef]
- Manzanillas, L.; Abt, I.; Efremenko, Y.; Febbraro, M.; Fischer, F.; Guitart, M.; Gusev, K.; Hackett, B.; Hayward, C.; Hodák, R.; et al. Usage of PEN as self-vetoing structural material in low background experiments. arXiv 2020, arXiv:2011.08983. [Google Scholar] [CrossRef]
- Zsigmond, A.J. et al. [LEGEND Collaboration]. LEGEND: The future of neutrinoless double-beta decay search with germanium detectors. J. Phys. Conf. Ser. 2020, 1468, 012111. [Google Scholar] [CrossRef]
- Edzards, F. et al. [LEGEND Collaboration]. The Future of Neutrinoless Double Beta Decay Searches with Germanium Detectors. J. Phys. Conf. Ser. 2020, 1690, 012180. [Google Scholar] [CrossRef]














| Isotope | Natural | Q | T |
|---|---|---|---|
| Abundance (%) | (MeV) | (yr) | |
| Ca | 0.187 | 4.263 | |
| Ge | 7.8 | 2.039 | |
| Se | 9.2 | 2.998 | |
| Zr | 2.8 | 3.348 | |
| Mo | 9.6. | 3.035 | |
| Cd | 7.6 | 2.813 | |
| Te | 34.08 | 2.527 | |
| Xe | 8.9 | 2.459 | |
| Nd | 5.6 | 3.371 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Andrea, V.; Di Marco, N.; Junker, M.B.; Laubenstein, M.; Macolino, C.; Morella, M.; Salamida, F.; Vignoli, C. Neutrinoless Double Beta Decay with Germanium Detectors: 1026 yr and Beyond. Universe 2021, 7, 341. https://doi.org/10.3390/universe7090341
D’Andrea V, Di Marco N, Junker MB, Laubenstein M, Macolino C, Morella M, Salamida F, Vignoli C. Neutrinoless Double Beta Decay with Germanium Detectors: 1026 yr and Beyond. Universe. 2021; 7(9):341. https://doi.org/10.3390/universe7090341
Chicago/Turabian StyleD’Andrea, Valerio, Natalia Di Marco, Matthias Bernhard Junker, Matthias Laubenstein, Carla Macolino, Michele Morella, Francesco Salamida, and Chiara Vignoli. 2021. "Neutrinoless Double Beta Decay with Germanium Detectors: 1026 yr and Beyond" Universe 7, no. 9: 341. https://doi.org/10.3390/universe7090341
APA StyleD’Andrea, V., Di Marco, N., Junker, M. B., Laubenstein, M., Macolino, C., Morella, M., Salamida, F., & Vignoli, C. (2021). Neutrinoless Double Beta Decay with Germanium Detectors: 1026 yr and Beyond. Universe, 7(9), 341. https://doi.org/10.3390/universe7090341







