Architecture of Hierarchical Stellar Systems and Their Formation
Abstract
:1. Introduction
2. Properties of Hierarchical Systems
2.1. The Multiple-Star Catalog
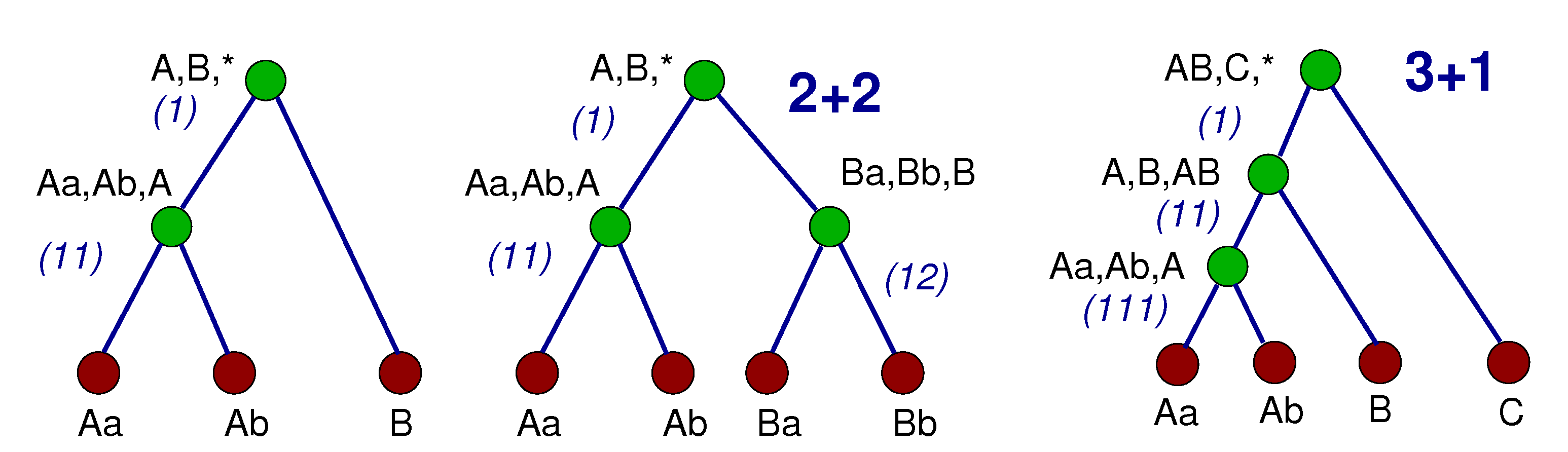
2.2. Types of Hierarchy
2.3. Main Parameters of Hierarchies
2.4. Statistical Trends
3. Formation of Multiple Stars
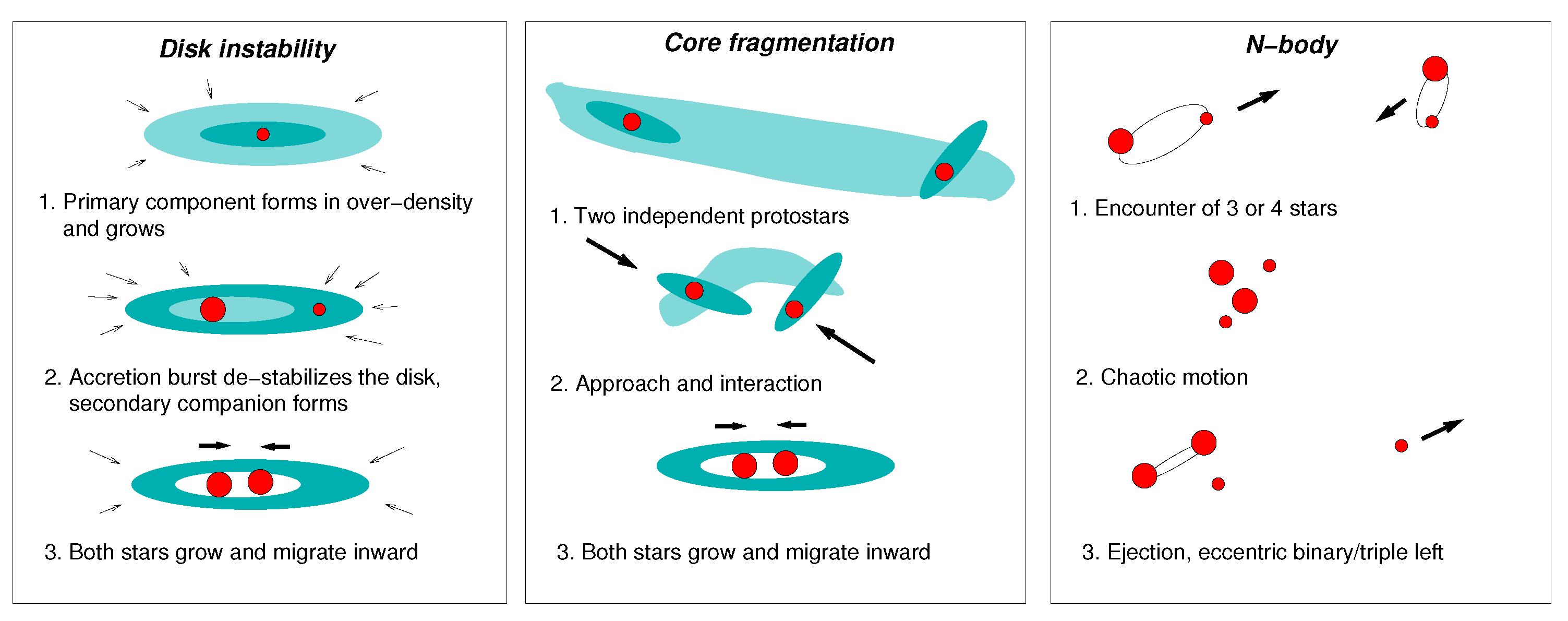
3.1. Physics of Star Formation
3.2. Binary-Star Formation
3.3. Formation Scenarios of Hierarchical Systems
3.4. Sequential Disk Instability (DI+DI)
3.5. Core Fragmentation and Capture (CF+CF, DI+CF)
3.6. Collisions
3.7. Dynamical Interactions
4. Families of Hierarchical Systems
4.1. Planar Systems
4.2. Compact Hierarchies
4.3. Castor-Type Quadruples
4.4. Quadruples of 2+2 Hierarchy
4.5. Misaligned Hierarchies
4.6. High-Multiplicity Systems
4.7. Young Hierarchies
5. Summary and Discussion
5.1. Evolution of Concepts
5.2. Observational Perspective
5.3. Theoretical Perspective
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | http://www.ctio.noirlab.edu/~atokovin/stars, accessed on 20 September 2021. |
| 2 | vizier.u-strasbg.fr/viz-bin/VizierR-4?-source=J/ApJS/235/6, accessed on 8 September 2021. |
References
- Duquennoy, A.; Mayor, M. Multiplicity among solar-type stars in the solar neighbourhood. II—Distribution of the orbital elements in an unbiased sample. Astron. Astrophys. 1991, 500, 337–376. [Google Scholar]
- Raghavan, D.; McAlister, H.A.; Henry, T.J.; Latham, D.W.; Marcy, G.W.; Mason, B.D.; Gies, D.R.; White, R.J.; ten Brummelaar, T.A. A Survey of Stellar Families: Multiplicity of Solar-type Stars. Astrophys. J. Suppl. 2010, 190, 1–42. [Google Scholar] [CrossRef]
- Duchêne, G.; Kraus, A. Stellar Multiplicity. Annu. Rev. Astron. Astrophys. 2013, 51, 269–310. [Google Scholar] [CrossRef] [Green Version]
- Moe, M.; Di Stefano, R. Mind Your Ps and Qs: The Interrelation between Period (P) and Mass-ratio (Q) Distributions of Binary Stars. Astrophys. J. Suppl. 2017, 230, 15. [Google Scholar] [CrossRef] [Green Version]
- Bate, M.R. The statistical properties of stars and their dependence on metallicity. Mon. Not. R. Astron. Soc. 2019, 484, 2341–2361. [Google Scholar] [CrossRef]
- Lee, A.T.; Offner, S.S.R.; Kratter, K.M.; Smullen, R.A.; Li, P.S. The Formation and Evolution of Wide-orbit Stellar Multiples In Magnetized Clouds. Astrophys. J. 2019, 887, 232. [Google Scholar] [CrossRef] [Green Version]
- Kuffmeier, M.; Calcutt, H.; Kristensen, L.E. The bridge: A transient phenomenon of forming stellar multiples. Sequential formation of stellar companions in filaments around young protostars. Astron. Astrophys. 2019, 628, A112. [Google Scholar] [CrossRef] [Green Version]
- Batten, A.H. Binary and Multiple Systems of Stars; Pergamon Press: Oxford, UK, 1973. [Google Scholar]
- Fekel, F.C.J. The properties of close multiple stars. Astrophys. J. 1981, 246, 879–898. [Google Scholar] [CrossRef]
- Chambliss, C.R. Eclipsing Binaries in Multiple Star Systems. Publ. Astron. Soc. Pac. 1992, 104, 663. [Google Scholar] [CrossRef]
- Tokovinin, A.A. MSC—A catalogue of physical multiple stars. Astron. Astrophys. Suppl. 1997, 124, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A.A.; Smekhov, M.G. Statistics of spectroscopic sub-systems in visual multiple stars. Astron. Astrophys. 2002, 382, 118–123. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A. From Binaries to Multiples. II. Hierarchical Multiplicity of F and G Dwarfs. Astron. J. 2014, 147, 87. [Google Scholar] [CrossRef] [Green Version]
- Hirsch, L.A.; Rosenthal, L.; Fulton, B.J.; Howard, A.W.; Ciardi, D.R.; Marcy, G.W.; Nielsen, E.; Petigura, E.A.; de Rosa, R.J.; Isaacson, H.; et al. Understanding the Impacts of Stellar Companions on Planet Formation and Evolution: A Survey of Stellar and Planetary Companions within 25 pc. Astron. J. 2021, 161, 134. [Google Scholar] [CrossRef]
- Sana, H. The multiplicity of massive stars: A 2016 view. In The Lives and Death-Throes of Massive Stars; Eldridge, J.J., Bray, J.C., McClelland, L.A.S., Xiao, L., Eds.; Proc. IAU Symposium 329; Cambridge University Press: Cambridge, UK, 2017; Volume 329, pp. 110–117. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A. The Updated Multiple Star Catalog. Astrophys. J. Suppl. 2018, 235, 6. [Google Scholar] [CrossRef] [Green Version]
- He, M.Y.; Ford, E.B.; Ragozzine, D.; Carrera, D. Architectures of Exoplanetary Systems. III. Eccentricity and Mutual Inclination Distributions of AMD-stable Planetary Systems. Astron. J. 2020, 160, 276. [Google Scholar] [CrossRef]
- Mason, B.D.; Wycoff, G.L.; Hartkopf, W.I.; Douglass, G.G.; Worley, C.E. The 2001 US Naval Observatory Double Star CD-ROM. I. The Washington Double Star Catalog. Astron. J. 2001, 122, 3466–3471. [Google Scholar] [CrossRef]
- Eggleton, P.P.; Tokovinin, A.A. A catalogue of multiplicity among bright stellar systems. Mon. Not. R. Astron. Soc. 2008, 389, 869–879. [Google Scholar] [CrossRef] [Green Version]
- Deacon, N.R.; Kraus, A.L. Wide binaries are rare in open clusters. Mon. Not. R. Astron. Soc. 2020, 496, 5176–5200. [Google Scholar] [CrossRef]
- Kamann, S.; Giesers, B.; Bastian, N.; Brinchmann, J.; Dreizler, S.; Göttgens, F.; Husser, T.O.; Latour, M.; Weilbacher, P.M.; Wisotzki, L. The binary content of multiple populations in NGC 3201. Astron. Astrophys. 2020, 635, A65. [Google Scholar] [CrossRef] [Green Version]
- Worley, C.E. Multiple star systems as related to double stars: Multiple stars among the visual binaries. In On the Evolution of Double Stars; Dommanget, J., Ed.; Communications of the Royal Observatory: Brussels, Belgium, 1967; Volume 17, p. 221. [Google Scholar]
- Sterzik, M.F.; Tokovinin, A.A. Relative orientation of orbits in triple stars. Astron. Astrophys. 2002, 384, 1030–1037. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A. Orbit Alignment in Triple Stars. Astrophys. J. 2017, 844, 103. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A.; Thomas, S.; Sterzik, M.; Udry, S. Tertiary companions to close spectroscopic binaries. Astron. Astrophys. 2006, 450, 681–693. [Google Scholar] [CrossRef] [Green Version]
- Hwang, H.C.; Hamer, J.H.; Zakamska, N.L.; Schlaufman, K.C. Very wide companion fraction from Gaia DR2: A weak or no enhancement for hot Jupiter hosts, and a strong enhancement for contact binaries. Mon. Not. R. Astron. Soc. 2020, 497, 2250–2259. [Google Scholar] [CrossRef]
- Joncour, I.; Duchêne, G.; Moraux, E. Multiplicity and clustering in Taurus star-forming region. I. Unexpected ultra-wide pairs of high-order multiplicity in Taurus. Astron. Astrophys. 2017, 599, A14. [Google Scholar] [CrossRef] [Green Version]
- Meibom, S.; Mathieu, R.D.; Stassun, K.G. An Observational Study of Tidal Synchronization in Solar-Type Binary Stars in the Open Clusters M35 and M34. Astrophys. J. 2006, 653, 621–635. [Google Scholar] [CrossRef]
- Moe, M.; Kratter, K.M. Dynamical Formation of Close Binaries during the Pre-main-sequence Phase. Astrophys. J. 2018, 854, 44. [Google Scholar] [CrossRef] [Green Version]
- Naoz, S. The Eccentric Kozai-Lidov Effect and Its Applications. Annu. Rev. Astron. Astrophys. 2016, 54, 441–489. [Google Scholar] [CrossRef] [Green Version]
- Fabrycky, D.; Tremaine, S. Shrinking Binary and Planetary Orbits by Kozai Cycles with Tidal Friction. Astrophys. J. 2007, 669, 1298–1315. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A. Comparative statistics and origin of triple and quadruple stars. Mon. Not. R. Astron. Soc. 2008, 389, 925–938. [Google Scholar] [CrossRef] [Green Version]
- Vázquez-Semadeni, E.; Palau, A.; Ballesteros-Paredes, J.; Gómez, G.C.; Zamora-Avilés, M. Global hierarchical collapse in molecular clouds. Towards a comprehensive scenario. Mon. Not. R. Astron. Soc. 2019, 490, 3061–3097. [Google Scholar] [CrossRef] [Green Version]
- Larson, R.B. The Collapse of a Rotating Cloud. Mon. Not. R. Astron. Soc. 1972, 156, 437. [Google Scholar] [CrossRef] [Green Version]
- Moe, M.; Kratter, K.M.; Badenes, C. The Close Binary Fraction of Solar-type Stars Is Strongly Anticorrelated with Metallicity. Astrophys. J. 2019, 875, 61. [Google Scholar] [CrossRef]
- Hwang, H.C.; Ting, Y.S.; Schlaufman, K.C.; Zakamska, N.L.; Wyse, R.F.G. The non-monotonic, strong metallicity dependence of the wide-binary fraction. Mon. Not. R. Astron. Soc. 2021, 501, 4329–4343. [Google Scholar] [CrossRef]
- Larson, R.B. KEY ISSUES REVIEW: Insights from simulations of star formation. Rep. Prog. Phys. 2007, 70, 337–356. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A.; Moe, M. Formation of close binaries by disc fragmentation and migration, and its statistical modelling. Mon. Not. R. Astron. Soc. 2020, 491, 5158–5171. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.N.; Offner, S.S.R.; Hennebelle, P.; André, P.; Zinnecker, H.; Ballesteros-Paredes, J.; Inutsuka, S.I.; Kruijssen, J.M.D. The Origin of the Stellar Mass Distribution and Multiplicity. Space Sci. Rev. 2020, 216, 70. [Google Scholar] [CrossRef]
- Clark, P.C.; Whitworth, A.P. On the emergent system mass function: The contest between accretion and fragmentation. Mon. Not. R. Astron. Soc. 2021, 500, 1697–1707. [Google Scholar] [CrossRef]
- Kratter, K.M.; Matzner, C.D.; Krumholz, M.R.; Klein, R.I. On the Role of Disks in the Formation of Stellar Systems: A Numerical Parameter Study of Rapid Accretion. Astrophys. J. 2010, 708, 1585–1597. [Google Scholar] [CrossRef] [Green Version]
- Heath, R.M.; Nixon, C.J. On the orbital evolution of binaries with circumbinary discs. Astron. Astrophys. 2020, 641, A64. [Google Scholar] [CrossRef]
- Offner, S.S.R.; Kratter, K.M.; Matzner, C.D.; Krumholz, M.R.; Klein, R.I. The Formation of Low-mass Binary Star Systems via Turbulent Fragmentation. Astrophys. J. 2010, 725, 1485–1494. [Google Scholar] [CrossRef] [Green Version]
- Sterzik, M.F.; Durisen, R.H.; Zinnecker, H. How do binary separations depend on cloud initial conditions? Astron. Astrophys. 2003, 411, 91–97. [Google Scholar] [CrossRef]
- Dupuy, T.J.; Liu, M.C. On the Distribution of Orbital Eccentricities for Very Low-mass Binaries. Astrophys. J. 2011, 733, 122. [Google Scholar] [CrossRef] [Green Version]
- Rohde, P.F.; Walch, S.; Clarke, S.D.; Seifried, D.; Whitworth, A.P.; Klepitko, A. The impact of episodic outflow feedback on stellar multiplicity and the star formation efficiency. Mon. Not. R. Astron. Soc. 2021, 500, 3594–3612. [Google Scholar] [CrossRef]
- Tokovinin, A. Dancing Twins: Stellar Hierarchies That Formed Sequentially? Astron. J. 2018, 155, 160. [Google Scholar] [CrossRef] [Green Version]
- Tobin, J.J.; Kratter, K.M.; Persson, M.V.; Looney, L.W.; Dunham, M.M.; Segura-Cox, D.; Li, Z.Y.; Chandler, C.J.; Sadavoy, S.I.; Harris, R.J.; et al. A triple protostar system formed via fragmentation of a gravitationally unstable disk. Nature 2016, 538, 483–486. [Google Scholar] [CrossRef]
- Tremaine, S. Resonant capture in quadruple stellar systems. Mon. Not. R. Astron. Soc. 2020, 493, 5583–5595. [Google Scholar] [CrossRef]
- Ryu, T.; Leigh, N.W.C.; Perna, R. Numerical study of N = 4 binary-binary scatterings in a background potential. Mon. Not. R. Astron. Soc. 2017, 467, 4447–4461. [Google Scholar] [CrossRef] [Green Version]
- Yuan, L.; Li, G.X.; Zhu, M.; Liu, T.; Wang, K.; Liu, X.; Kim, K.T.; Tatematsu, K.; Yuan, J.; Wu, Y. Edge collapse and subsequent longitudinal accretion in filament S242. Astron. Astrophys. 2020, 637, A67. [Google Scholar] [CrossRef]
- Bonnell, I.; Bastien, P. Fragmentation of Elongated Cylindrical Clouds. VI. Comparison with Observations. Astrophys. J. 1993, 406, 614. [Google Scholar] [CrossRef]
- Sadavoy, S.I.; Stahler, S.W. Embedded binaries and their dense cores. Mon. Not. R. Astron. Soc. 2017, 469, 3881–3900. [Google Scholar] [CrossRef] [Green Version]
- Bodenheimer, P. Evolution of rotating interstellar clouds. III. On the formation of multiple star systems. Astrophys. J. 1978, 224, 488–496. [Google Scholar] [CrossRef]
- Delgado-Donate, E.J.; Clarke, C.J.; Bate, M.R. Accretion and dynamical interactions in small-N star-forming clusters: N = 5. Mon. Not. R. Astron. Soc. 2003, 342, 926–938. [Google Scholar] [CrossRef] [Green Version]
- Whitworth, A.P. Impulsively Triggered Binary Star Formation. In Symposium—International Astronomical Union, Volume 200: The Formation of Binary Stars; Zinnecker, H., Mathieu, R., Eds.; Cambridge University Press: Cambridge, UK, 2001; p. 33. [Google Scholar]
- Docobo, J.A.; Piccotti, L.; Abad, A.; Campo, P.P. A Study about the Secular Evolution of the Hierarchical Three-body Problem Using the Numerical Integrator TIDES. Astron. J. 2021, 161, 43. [Google Scholar] [CrossRef]
- Valtonen, M.; Karttunen, H. The Three-Body Problem; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Anosova, J.P. Dynamical Evolution of Triple Systems. Astrophys. Space Sci. 1986, 124, 217–241. [Google Scholar] [CrossRef]
- Manwadkar, V.; Trani, A.A.; Leigh, N.W.C. Chaos and Lévy flights in the three-body problem. Mon. Not. R. Astron. Soc. 2020, 497, 3694–3712. [Google Scholar] [CrossRef]
- Stone, N.C.; Leigh, N.W.C. A statistical solution to the chaotic, non-hierarchical three-body problem. Nature 2019, 576, 406–410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mardling, R.A.; Aarseth, S.J. Tidal interactions in star cluster simulations. Mon. Not. R. Astron. Soc. 2001, 321, 398–420. [Google Scholar] [CrossRef]
- Antognini, J.M.O.; Thompson, T.A. Dynamical formation and scattering of hierarchical triples: Cross-sections, Kozai-Lidov oscillations, and collisions. Mon. Not. R. Astron. Soc. 2016, 456, 4219–4246. [Google Scholar] [CrossRef]
- Reipurth, B.; Mikkola, S. Formation of the widest binary stars from dynamical unfolding of triple systems. Nature 2012, 492, 221–224. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A. Formation of wide binary stars from adjacent cores. Mon. Not. R. Astron. Soc. 2017, 468, 3461–3467. [Google Scholar] [CrossRef] [Green Version]
- Eggleton, P.P.; Kisseleva-Eggleton, L. A Mechanism for Producing Short-Period Binaries. Astrophys. Space Sci. 2006, 304, 75–79. [Google Scholar] [CrossRef]
- Eggleton, P. Evolutionary Processes in Binary and Multiple Stars; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Hamers, A.S. A census of main-sequence interactions in the Multiple Star Catalogue. Mon. Not. R. Astron. Soc. 2020, 494, 5298–5313. [Google Scholar] [CrossRef]
- Toonen, S.; Portegies Zwart, S.; Hamers, A.S.; Bandopadhyay, D. The evolution of stellar triples. The most common evolutionary pathways. Astron. Astrophys. 2020, 640, A16. [Google Scholar] [CrossRef]
- Xia, F.; Fu, Y.; Wang, X. The Nearby Very Low Mass Triple Star LHS 1070. Astrophys. J. 2019, 882, 147. [Google Scholar] [CrossRef]
- Tokovinin, A.; Latham, D.W.; Mason, B.D. The Unusual Quadruple System HD 91962 with a “Planetary” Architecture. Astron. J. 2015, 149, 195. [Google Scholar] [CrossRef] [Green Version]
- Borkovits, T.; Sperauskas, J.; Tokovinin, A.; Latham, D.W.; Csányi, I.; Hajdu, T.; Molnár, L. The compact multiple system HIP 41431. Mon. Not. R. Astron. Soc. 2019, 487, 4631–4647. [Google Scholar] [CrossRef]
- Quirrenbach, A.; Trifonov, T.; Lee, M.H.; Reffert, S. Precise radial velocities of giant stars. XI. Two brown dwarfs in 6:1 mean motion resonance around the K giant star ν Ophiuchi. Astron. Astrophys. 2019, 624, A18. [Google Scholar] [CrossRef] [Green Version]
- Brandt, T.D. The Hipparcos-Gaia Catalog of Accelerations. Astrophys. J. Suppl. 2018, 239, 31. [Google Scholar] [CrossRef] [Green Version]
- Kervella, P.; Arenou, F.; Mignard, F.; Thévenin, F. Stellar and substellar companions of nearby stars from Gaia DR2. Binarity from proper motion anomaly. Astron. Astrophys. 2019, 623, A72. [Google Scholar] [CrossRef] [Green Version]
- Borkovits, T.; Hajdu, T.; Sztakovics, J.; Rappaport, S.; Levine, A.; Bíró, I.B.; Klagyivik, P. A comprehensive study of the Kepler triples via eclipse timing. Mon. Not. R. Astron. Soc. 2016, 455, 4136–4165. [Google Scholar] [CrossRef] [Green Version]
- Borkovits, T.; Rappaport, S.A.; Tan, T.G.; Gagliano, R.; Jacobs, T.; Huang, X.; Mitnyan, T.; Hambsch, F.J.; Kaye, T.; Maxted, P.F.L.; et al. The compact triply eclipsing triple star TIC 209409435 discovered with TESS. Mon. Not. R. Astron. Soc. 2020, 496, 4624–4636. [Google Scholar] [CrossRef]
- Alonso, R.; Deeg, H.J.; Hoyer, S.; Lodieu, N.; Palle, E.; Sanchis-Ojeda, R. HD 144548: A young triply eclipsing system in the Upper Scorpius OB association. Astron. Astrophys. 2015, 584, L8. [Google Scholar] [CrossRef] [Green Version]
- Pribulla, T.; Puha, E.; Borkovits, T.; Budaj, J.; Garai, Z.; Guenther, E.; Hambálek, L.; Komžík, R.; Kundra, E.; Szabó, G.M.; et al. Secular changes in the orbits of the quadruple system VW LMi. Mon. Not. R. Astron. Soc. 2020, 494, 178–189. [Google Scholar] [CrossRef]
- Kostov, V.B.; Powell, B.P.; Torres, G.; Borkovits, T.; Rappaport, S.A.; Tokovinin, A.; Zasche, P.; Anderson, D.; Barclay, T.; Berlind, P.; et al. TIC 454140642: A Compact, Coplanar, Quadruple-lined Quadruple Star System Consisting of Two Eclipsing Binaries. arXiv 2021, arXiv:2105.12586. [Google Scholar]
- Zasche, P.; Vokrouhlický, D.; Wolf, M.; Kučáková, H.; Kára, J.; Uhlař, R.; Mašek, M.; Henzl, Z.; Cagaš, P. Doubly eclipsing systems. Astron. Astrophys. 2019, 630, A128. [Google Scholar] [CrossRef]
- Lane, B.F.; Muterspaugh, M.W.; Fekel, F.C.; Williamson, M.; Browne, S.; Konacki, M.; Burke, B.F.; Colavita, M.M.; Kulkarni, S.R.; Shao, M. The Orbits of the Quadruple Star System 88 Tauri A from PHASES Differential Astrometry and Radial Velocity. Astrophys. J. 2007, 669, 1209–1219. [Google Scholar] [CrossRef] [Green Version]
- Powell, B.P.; Kostov, V.B.; Rappaport, S.A.; Borkovits, T.; Zasche, P.; Tokovinin, A.; Kruse, E.; Latham, D.W.; Montet, B.T.; Jensen, E.L.N.; et al. TIC 168789840: A Sextuply-Eclipsing Sextuple Star System. arXiv 2021, arXiv:2101.03433. [Google Scholar]
- Tokovinin, A. Orbits and Structure of the Quadruple Systems GJ 225.1 and FIN 332. Astron. Lett. 2020, 46, 612–620. [Google Scholar] [CrossRef]
- Tokovinin, A. The Triple System Zeta Aquarii. Astrophys. J. 2016, 831, 151. [Google Scholar] [CrossRef] [Green Version]
- Schaefer, G.H.; Hummel, C.A.; Gies, D.R.; Zavala, R.T.; Monnier, J.D.; Walter, F.M.; Turner, N.H.; Baron, F.; ten Brummelaar, T.; Che, X.; et al. Orbits, Distance, and Stellar Masses of the Massive Triple Star σ Orionis. Astron. J. 2016, 152, 213. [Google Scholar] [CrossRef] [Green Version]
- Wolf, M.; Kučáková, H.; Zasche, P.; Vraštil, J.; Hoňková, K.; Hornoch, K.; Lehký, M.; Mašek, M.; Šmelcer, L.; Tylšar, M.; et al. Possible substellar companions in low-mass eclipsing binaries: GU Bootis and YY Geminorum. Astron. Astrophys. 2018, 620, A72. [Google Scholar] [CrossRef] [Green Version]
- Tokovinin, A. Nearby Quintuple Systems κ Tucanae and ξ Scorpii. Astron. J. 2020, 159, 265. [Google Scholar] [CrossRef]
- Kasper, M.; Santhakumari, K.K.R.; Herbst, T.M.; van Boekel, R.; Menard, F.; Gratton, R.; van Holstein, R.G.; Langlois, M.; Ginski, C.; Boccaletti, A.; et al. A triple star in disarray. Multi-epoch observations of T Tauri with VLT-SPHERE and LBT-LUCI. Astron. Astrophys. 2020, 644, A114. [Google Scholar] [CrossRef]
- Kraus, S.; Kreplin, A.; Young, A.K.; Bate, M.R.; Monnier, J.D.; Harries, T.J.; Avenhaus, H.; Kluska, J.; Laws, A.S.E.; Rich, E.A.; et al. A triple-star system with a misaligned and warped circumstellar disk shaped by disk tearing. Science 2020, 369, 1233–1238. [Google Scholar] [CrossRef] [PubMed]
- Ménard, F.; Cuello, N.; Ginski, C.; van der Plas, G.; Villenave, M.; Gonzalez, J.F.; Pinte, C.; Benisty, M.; Boccaletti, A.; Price, D.J.; et al. Ongoing flyby in the young multiple system UX Tauri. Astron. Astrophys. 2020, 639, L1. [Google Scholar] [CrossRef]
- Reipurth, B.; Friberg, P. HH 175: A giant Herbig-Haro flow emanating from a multiple protostar. Mon. Not. R. Astron. Soc. 2021, 501, 5938–5947. [Google Scholar] [CrossRef]
- Reipurth, B. Disintegrating Multiple Systems in Early Stellar Evolution. Astron. J. 2000, 120, 3177–3191. [Google Scholar] [CrossRef] [Green Version]
- Keppler, M.; Penzlin, A.; Benisty, M.; van Boekel, R.; Henning, T.; van Holstein, R.G.; Kley, W.; Garufi, A.; Ginski, C.; Brandner, W.; et al. Gap, shadows, spirals, and streamers: SPHERE observations of binary-disk interactions in GG Tauri A. Astron. Astrophys. 2020, 639, A62. [Google Scholar] [CrossRef]
- Boden, A.F.; Sargent, A.I.; Akeson, R.L.; Carpenter, J.M.; Torres, G.; Latham, D.W.; Soderblom, D.R.; Nelan, E.; Franz, O.G.; Wasserman, L.H. Dynamical Masses for Low-Mass Pre-Main-Sequence Stars: A Preliminary Physical Orbit for HD 98800 B. Astrophys. J. 2005, 635, 442–451. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, G.M.; Matrà, L.; Facchini, S.; Milli, J.; Panić, O.; Price, D.; Wilner, D.J.; Wyatt, M.C.; Yelverton, B.M. A circumbinary protoplanetary disk in a polar configuration. Nat. Astron. 2019, 3, 230–235. [Google Scholar] [CrossRef]
- Zúñiga-Fernández, S.; Olofsson, J.; Bayo, A.; Haubois, X.; Corral-Santana, J.M.; Lopera-Mejía, A.; Ronco, M.P.; Tokovinin, A.; Gallenne, A.; Kennedy, G.M.; et al. The HD 98800 quadruple pre-main sequence system. Towards full orbital characterisation using long-baseline infrared interferometry. arXiv 2021, arXiv:2109.02841. [Google Scholar]
- Krumholz, M.R.; McKee, C.F. How do bound star clusters form? Mon. Not. R. Astron. Soc. 2020, 494, 624–641. [Google Scholar] [CrossRef] [Green Version]
- Bowler, B.P.; Hillenbrand, L.A. Near-infrared Spectroscopy of 2M0441+2301 AabBab: A Quadruple System Spanning the Stellar to Planetary Mass Regimes. Astrophys. J. Lett. 2015, 811, L30. [Google Scholar] [CrossRef] [Green Version]
- Gaia, C.; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Mignard, F. Gaia Data Release 1. Summary of the astrometric, photometric, and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar] [CrossRef] [Green Version]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). In Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference, Series; Oschmann, J.M., Clampin, M., Fazio, G.G., MacEwen, H.A., Eds.; SPIE: Bellingham, WA, USA, 2014; Volume 9143, p. 914320. [Google Scholar] [CrossRef] [Green Version]
- Shatsky, N. The long-period companions of multiple stars tend to have moderate eccentricities. Astron. Astrophys. 2001, 380, 238–244. [Google Scholar] [CrossRef] [Green Version]








| Scenario | Predictions | Products |
|---|---|---|
| Sequential disk instability | Aligned orbits with moderate | 1. Compact planar triples |
| (DI+DI) | eccentricity, , | 2. Double-twin triples |
| moderate period ratios, | 3. Quadruples of 3+1 type | |
| no 2+2 quadruples. | ||
| Sequential core fragmentation | Non-coplanar, eccentric orbits. | 1. Typical triples |
| (CF+CF, DI+CF) | Wide range of mass ratios. | 2. Quadruples 2+2 |
| Late disk instability | Small , misaligned | Castor-type quadruples |
| (CF+DI2) | inner subsystems. | |
| Cloud collisions | Wide 2+2 quadruples, | Lyr-type quadruples |
| comparable masses | ||
| Dynamical interactions | Eccentric and | Misaligned triples |
| misaligned orbits, small | ||
| period ratio |
| Group | WDS | Names | N | H | Periods |
|---|---|---|---|---|---|
| Planar | 00247−2653 | LHS 1070, GJ 2005 | 3 | 3 | 99 yr (18.2 yr) |
| Large-N | 01158−6853 | Tuc, GJ 55.3 | 5 | 3+2 | 270 kyr (1.2 kyr (22 yr); 85 yr) |
| Compact | 01379−8259 | HIP 7601 | 3 | 3 | 1.75 yr (19.4 d) |
| Misaligned | 02460−0457 | HD 17251, ADS 2111 | 3 | 3 | 1 kyr (38.5 yr) |
| Compact | 03009−3427 | TIC 209409435 | 3 | 3 | 121.9 d (5.7 d) |
| Misaligned | 04007+1229 | Tau, HR 1239 | 3 | 3 | 33 d (4 d) |
| Castor | 04141−3155 | TIC 168789839 | 6 | (2+2)+2 | 1.6 kyr (3.9 yr (1.6 d; 1.3 d); 8.2 d) |
| Compact | 04191+0054 | TIC 454140642 | 4 | 2+2 | 432 d (13.6 d; 10.4 d) |
| Castor? | 04357+1010 | HR 1458, 88 Tau | 6 | (2+2)+2 | 80 kyr (18 yr (3.6 d; 7.9 d); 3.7 yr) |
| Misaligned | 05387−0236 | Ori, ADS 4241 | 3+ | 3 | 157 yr (143 d) |
| Castor | 07346+3153 | Castor, Gem | 7 | (2+2)+3 | 15 kyr (460 yr (9.2 d; 2.9 d); 55 yr (0.8 d)) |
| Planar | 08270+2157 | HIP 41431, GJ 307 | 4 | 3+1 | 3.9 yr (59 d (2.9 d)) |
| Large-N | 08316+1924 | HIP 41824, GJ 2069, CU Cnc | 5 | 3+2 | 2 kyr (66 yr (2.8 d); 23 yr) |
| Lyr | 08571−2951 | HIP 43947 | 4 | 2+2 | 14 kyr (106 yr; 100 yr) |
| Planar | 10370−0850 | HD 91962 | 4 | 3+1 | 205 yr (8.8 yr (170 d)) |
| Compact | 11029+3025 | VW LMi, HD 95660 | 4 | 2+2 | 355 d (7.9 d; 0.5 d) |
| Large-N | 11551+4629 | 65 UMa, ADS 8347 | 7 | … | 500 kyr (8 kyr (118 yr (641 d (1.7 d))); 80 yr) |
| Large-N | 16044−1122 | Sco, ADS 9909 | 5 | 3+2 | 285 kyr (1.5 kyr (46 yr); 4.4 kyr) |
| Large-N | 16555−0820 | HIP 81817, GJ 644, Wolf 630 | 5 | 3+1+1 | 50 kyr (9 kyr (1.7 yr (3 d))) |
| Planar | 16057−3252 | HIP 78842 | 4 | 3+1 | 4.4 kyr (133 yr (10.5 yr)) |
| Compact | 16073−2204 | HD 144548 | 3+ | 3 | 33.9 d (1.63 d) |
| Compact | 17521−2920 | OGLE BLG-ECL-145467 | 4 | 2+2 | 4.2 yr(4.9 d; 3.3 d) |
| Compact | 18278+2442 | V994 Her, ADS 11373 | 6 | (2+2)+2 | 1.4 kyr (2.9 yr (2.1 d; 1.4 d); 2 d) |
| Lyr | 18443+3940 | Lyr | 4 | 2+2 | 450 kyr (1804 yr; 724 yr) |
| Lyr | 18455+0530 | FIN 332, ADS 11640 | 4 | 2+2 | 3 kyr (40 yr; 28 yr) |
| Compact | 19499+4107 | KIC 5897826, KOI-126 | 3 | 3 | 33.9 d (1.8 d) |
| Misaligned | 20396+0458 | HIP 101955, GJ 795 | 3 | 3 | 38.7 yr (2.5 yr) |
| Misaligned | 22288−0001 | Aqr, ADS 15971 | 3 | 3 | 540 yr (26 yr) |
| Compact | 22366−0034 | HIP 111598 | 3 | 3 | 271 d (5.9 d) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tokovinin, A. Architecture of Hierarchical Stellar Systems and Their Formation. Universe 2021, 7, 352. https://doi.org/10.3390/universe7090352
Tokovinin A. Architecture of Hierarchical Stellar Systems and Their Formation. Universe. 2021; 7(9):352. https://doi.org/10.3390/universe7090352
Chicago/Turabian StyleTokovinin, Andrei. 2021. "Architecture of Hierarchical Stellar Systems and Their Formation" Universe 7, no. 9: 352. https://doi.org/10.3390/universe7090352
APA StyleTokovinin, A. (2021). Architecture of Hierarchical Stellar Systems and Their Formation. Universe, 7(9), 352. https://doi.org/10.3390/universe7090352






