Mixing and Magnetic Fields in Asymptotic Giant Branch Stars in the Framework of FRUITY Models
Abstract
:1. Introduction
2. Mixing Processes in AGB Stars
3. Updating FRUITY Stellar Models
3.1. Input Physics
| Reaction | Reference | Reaction | Reference | Reaction | Reference |
|---|---|---|---|---|---|
| Li(p, )He | [67] | Na(p, )Mg | [68] | O(, )Ne | [69] |
| N(p, )O | [70] | Na(p, )Ne | [71] | O(, )Ne | [71] |
| O(p, )F | [72] | Mg(p, )Al | [71] | Ne(, n)Mg | [73] |
| O(p, )N | [74] | Mg(p, )Al | [75] | Ne(, )Mg | [73] |
| C(p, )N | [71] | Mg(p, )Al | [75] | N(, p)O | [76] |
| O(p, )F | [77] | Mg(p, )Al | [71] | N(, )F | [71] |
| O(p, )N | [78] | Al(p, )Si | [71] | O(, )Ne | [79] |
| F(p, )O | [80] | Al(p, )Si | [71] | O(, n)Ne | [79] |
| Be(p, )Li | [81] | Al(p, )Mg | [71] | O(, n)Ne | [82] |
| B(p, )Be | [81] | He(2, )C | [83] | F(, p)Ne | [84] |
| Ne(p, )Na | [71] | C(, )O | [85] | Ne(, )Mg | [71] |
| Ne(p, )Na | [71] | C(, n)O | [86] | Mg(, )Si | [71] |
| Ne(p, )Na | [87] | C(, )O | [88] | ||
| Na(p, )Mg | [89] | N(, )F | [71] |
| Reaction | Reference | Reaction | Reference | Reaction | Reference |
|---|---|---|---|---|---|
| C(n, )C | [90] | As(n, )As | [91] | Lu(n, )Lu | [92] |
| N(n, p)C | [90] | Br(n, )Br | [93] | Hf(n, )Hf | [94] |
| O(n, )C | [95] | Br(n, )Br | [93] | Hf(n, )Hf | [96] |
| F(n, )F | [97] | Kr(n, )Kr | [98] | Hf(n, )Hf | [96] |
| Ne(n, )Ne | [99] | Kr(n, )Kr | [98] | Hf(n, )Hf | [96] |
| Ne(n, )Ne | [99] | Kr(n, )Kr | [98] | Hf(n, )Hf | [96] |
| Ne(n, )Ne | [99] | Km(n, )Kr | [98] | Hf(n, )Hf | [96] |
| Na(n, )Na | [100] | Kr(n, )Kr | [98] | Hf(n, )Hf | [94] |
| Mg(n, )Mg | [101] | Rb(n, )Rb | [93] | W(n, )W | [102] |
| Mg(n, )Mg | [103] | Rb(n, )Rb | [93] | W(n, )W | [104] |
| Mg(n, )Mg | [101] | Sr(n, )Sr | [105] | W(n, )W | [104] |
| Cl(n, )Cl | [106] | Zr(n, )Zr | [107] | Os(n, )Os | [102] |
| Ar(n, )Ar | [108] | Zr(n, )Zr | [109] | Os(n, )Os | [110] |
| K(n, )K | [111] | Zr(n, )Zr | [112] | Os(n, )Os | [110] |
| Ca(n, )Ca | [113] | Zr(n, )Zr | [114] | Os(n, )Os | [110] |
| Sc(n, )Sc | [111] | Zr(n, )Zr | [115] | Os(n, )Os | [116] |
| Fe(n, )Fe | [117] | Zr(n, )Zr | [118] | Os(n, )Os | [116] |
| Fe(n, )Fe | [119] | Ru(n, )Ru | [120] | Pt(n, )Pt | [102] |
| Co(n, )Co | [119] | Ru(n, )Ru | [120] | Pt(n, )Pt | [121] |
| Ni(n, )Ni | [122] | Ru(n, )Ru | [120] | Pt(n, )Pt | [121] |
| Ni(n, )Ni | [123] | Pd(n, )Pd | [124] | Pt(n, )Pt | [121] |
| Ni(n, )Ni | [125] | Te(n, )Te | [124] | Pt(n, )Pt | [121] |
| Ni(n, )Ni | [126] | Ba(n, )Ba | [124] | Pt(n, )Pt | [116] |
| Ni(n, )Ni | [119] | Ba(n, )Ba | [124] | Au(n, )Au | [127] |
| Cu(n, )Cu | [128] | La(n, )La | [129] | Hg(n, )Hg | [102] |
| Cu(n, )Cu | [130] | Sm(n, )Sm | [131] | Hg(n, )Hg | [116] |
| Zn(n, )Zn | [132] | Gd(n, )Gd | [133] | Hg(n, )Hg | [116] |
| Zn(n, )Zn | [132] | Dy(n, )Dy | [124] | Pb(n, )Pb | [134] |
| Ge(n, )Ge | [135] | Yb(n, )Yb | [102] | Pb(n, )Pb | [136] |
| Ge(n, )Ge | [91] | Yb(n, )Yb | [116] | Pb(n, )Pb | [137] |
| Ge(n, )Ge | [91] | Yb(n, )Yb | [116] | Bi(n, )Bi | [138] |
3.2. Magnetic-Buoyancy-Induced Mixing and the Pocket Formation
4. Nucleosynthesis and Chemical Enrichment in Magnetic FRUITY Models
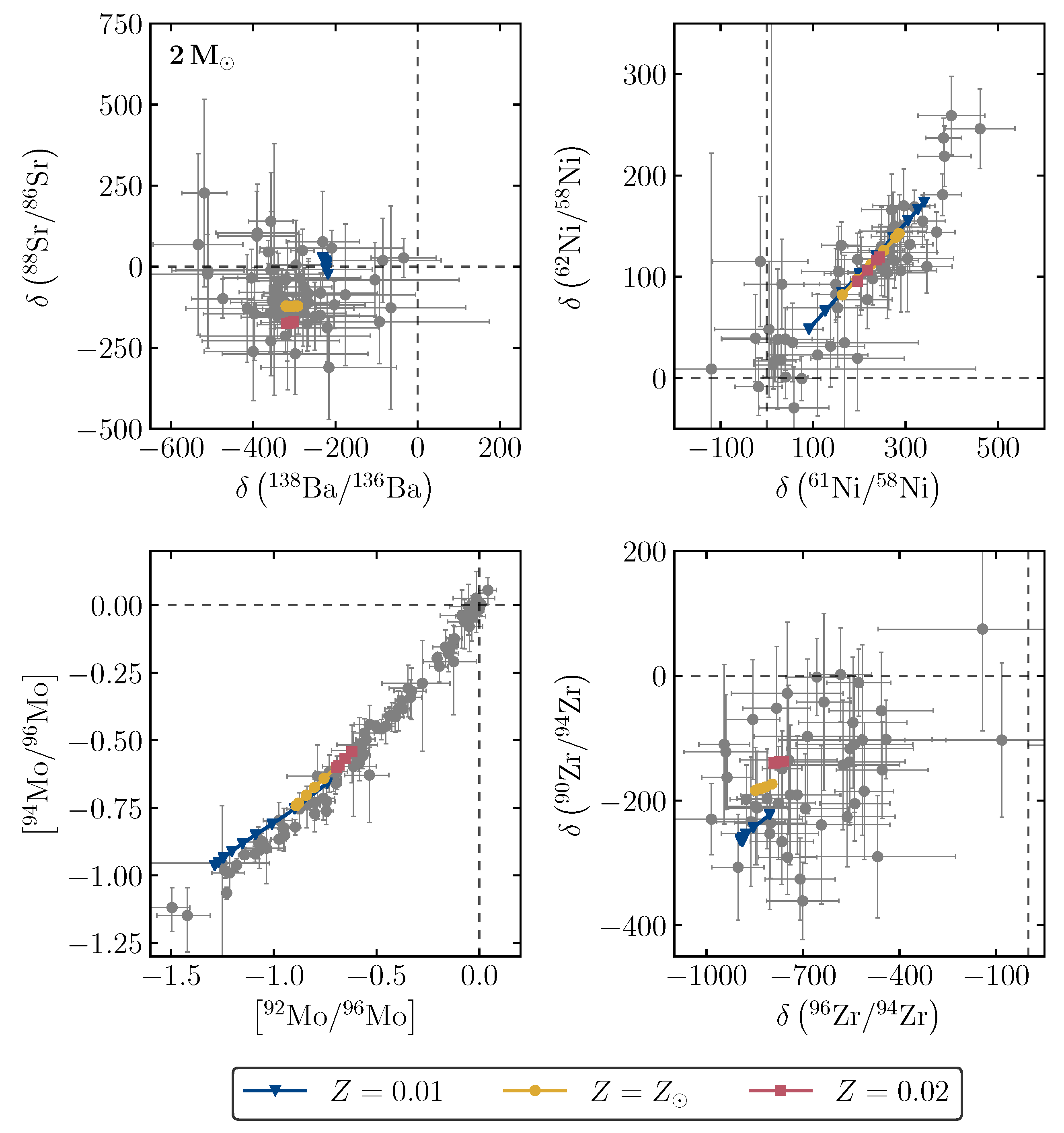
4.1. SiC Grains
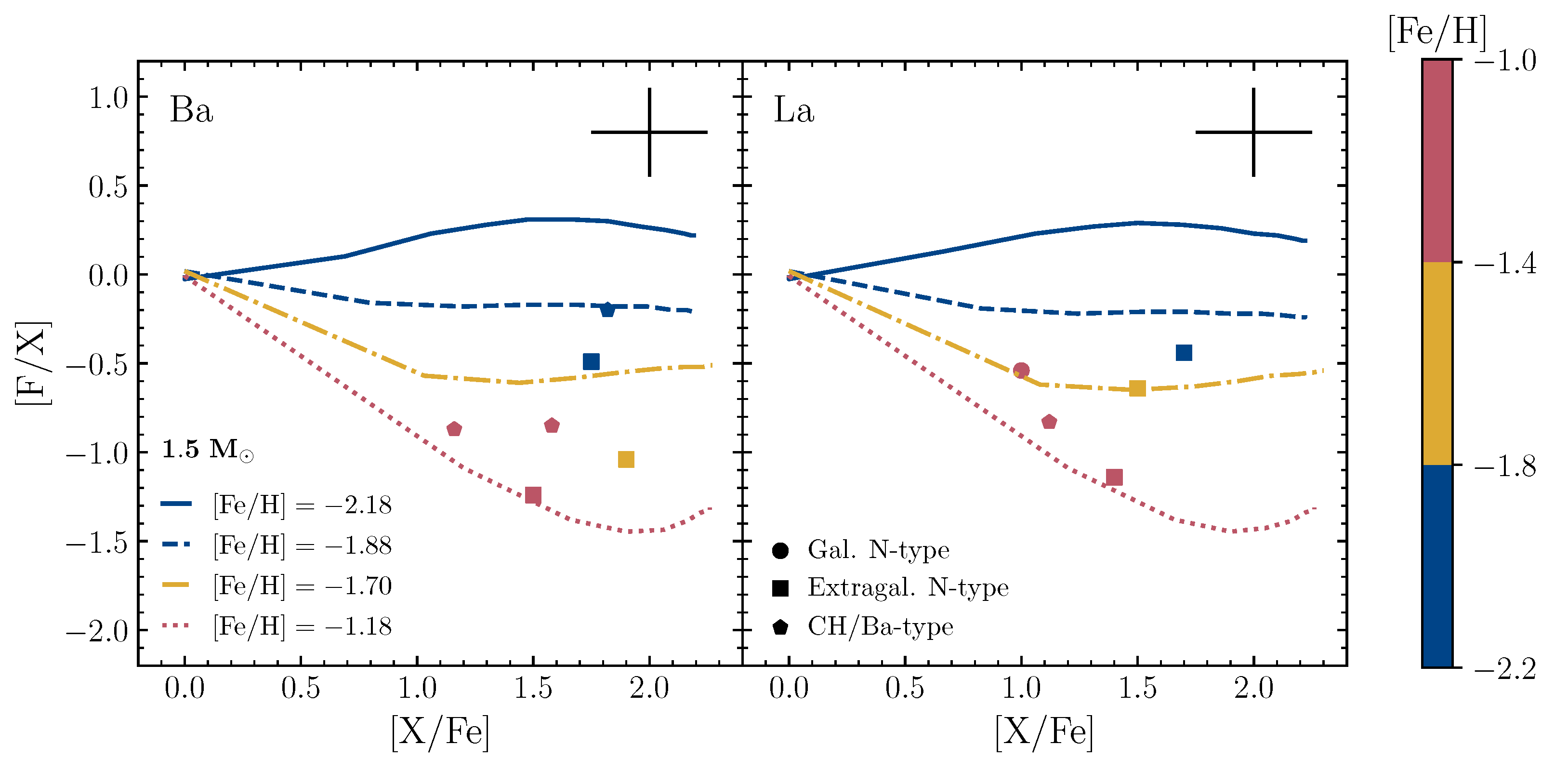
4.2. Fluorine Nucleosynthesis
4.3. Stellar Yields and the Galactic Evolution of Yttrium Abundance
5. Summary and Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Käppeler, F.; Gallino, R.; Bisterzo, S.; Aoki, W. The s process: Nuclear physics, stellar models, and observations. Rev. Mod. Phys. 2011, 83, 157–194. [Google Scholar] [CrossRef] [Green Version]
- Cowan, J.J.; Sneden, C.; Lawler, J.E.; Aprahamian, A.; Wiescher, M.; Langanke, K.; Martínez-Pinedo, G.; Thielemann, F.K. Origin of the heaviest elements: The rapid neutron-capture process. Rev. Mod. Phys. 2021, 93, 015002. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef] [Green Version]
- Busso, M.; Gallino, R.; Wasserburg, G.J. Nucleosynthesis in Asymptotic Giant Branch Stars: Relevance for Galactic Enrichment and Solar System Formation. Annu. Rev. Astron. Astrophys. 1999, 37, 239–309. [Google Scholar] [CrossRef] [Green Version]
- Raiteri, C.M.; Gallino, R.; Busso, M.; Neuberger, D.; Käppeler, F. The Weak s-Component and Nucleosynthesis in Massive Stars. Astrophys. J. 1993, 419, 207. [Google Scholar] [CrossRef]
- Karakas, A.I.; Lattanzio, J.C. The Dawes Review 2: Nucleosynthesis and Stellar Yields of Low- and Intermediate-Mass Single Stars. Publ. Astron. Soc. Aust. 2014, 31, e030. [Google Scholar] [CrossRef] [Green Version]
- Cristallo, S.; Straniero, O.; Piersanti, L.; Gobrecht, D. Evolution, Nucleosynthesis, and Yields of AGB Stars at Different Metallicities. III. Intermediate-mass Models, Revised Low-mass Models, and the ph-FRUITY Interface. Astrophys. J. Suppl. 2015, 219, 40. [Google Scholar] [CrossRef]
- Straniero, O.; Gallino, R.; Busso, M.; Chiefei, A.; Raiteri, C.M.; Limongi, M.; Salaris, M. Radiative 13C Burning in Asymptotic Giant Branch Stars and s-Processing. Astrophys. J. Lett. 1995, 440, L85. [Google Scholar] [CrossRef]
- Gallino, R.; Arlandini, C.; Busso, M.; Lugaro, M.; Travaglio, C.; Straniero, O.; Chieffi, A.; Limongi, M. Evolution and Nucleosynthesis in Low-Mass Asymptotic Giant Branch Stars. II. Neutron Capture and the S-Process. Astrophys. J. 1998, 497, 388–403. [Google Scholar] [CrossRef]
- Busso, M.; Gallino, R.; Lambert, D.L.; Travaglio, C.; Smith, V.V. Nucleosynthesis and Mixing on the Asymptotic Giant Branch. III. Predicted and Observed s-Process Abundances. Astrophys. J. 2001, 557, 802–821. [Google Scholar] [CrossRef] [Green Version]
- Cox, J.P.; Giuli, R.T. Principles of Stellar Structure; Gordon and Breach: New York, NY, USA, 1968. [Google Scholar]
- Cristallo, S.; Straniero, O.; Gallino, R.; Piersanti, L.; Domínguez, I.; Lederer, M.T. Evolution, Nucleosynthesis, and Yields of Low-Mass Asymptotic Giant Branch Stars at Different Metallicities. Astrophys. J. 2009, 696, 797–820. [Google Scholar] [CrossRef] [Green Version]
- Trippella, O.; Busso, M.; Palmerini, S.; Maiorca, E.; Nucci, M.C. s-Processing in AGB Stars Revisited. II. Enhanced 13C Production through MHD-induced Mixing. Astrophys. J. 2016, 818, 125. [Google Scholar] [CrossRef] [Green Version]
- Herwig, F.; Bloecker, T.; Schoenberner, D.; El Eid, M. Stellar evolution of low and intermediate-mass stars. IV. Hydrodynamically-based overshoot and nucleosynthesis in AGB stars. Astron. Astrophys. 1997, 324, L81–L84. [Google Scholar]
- Frost, C.A.; Lattanzio, J.C. On the Numerical Treatment and Dependence of the Third Dredge-up Phenomenon. Astrophys. J. 1996, 473, 383. [Google Scholar] [CrossRef] [Green Version]
- Herwig, F. The evolution of AGB stars with convective overshoot. Astron. Astrophys. 2000, 360, 952–968. [Google Scholar]
- Straniero, O.; Gallino, R.; Cristallo, S. s process in low-mass asymptotic giant branch stars. Nucl. Phys. A 2006, 777, 311–339. [Google Scholar] [CrossRef] [Green Version]
- Goriely, S.; Siess, L. Sensitivity of the s-process nucleosynthesis in AGB stars to the overshoot model. Astron. Astrophys. 2018, 609, A29. [Google Scholar] [CrossRef] [Green Version]
- Freytag, B.; Ludwig, H.G.; Steffen, M. Hydrodynamical models of stellar convection. The role of overshoot in DA white dwarfs, A-type stars, and the Sun. Astron. Astrophys. 1996, 313, 497–516. [Google Scholar]
- Herwig, F.; Freytag, B.; Fuchs, T.; Hansen, J.P.; Hueckstaedt, R.M.; Porter, D.H.; Timmes, F.X.; Woodward, P.R. Convective and Non-Convective Mixing in AGB Stars. arXiv 2007, arXiv:0709.0197. [Google Scholar]
- Battino, U.; Pignatari, M.; Ritter, C.; Herwig, F.; Denisenkov, P.; Den Hartogh, J.W.; Trappitsch, R.; Hirschi, R.; Freytag, B.; Thielemann, F.; et al. Application of a Theory and Simulation-based Convective Boundary Mixing Model for AGB Star Evolution and Nucleosynthesis. Astrophys. J. 2016, 827, 30. [Google Scholar] [CrossRef]
- Battino, U.; Tattersall, A.; Lederer-Woods, C.; Herwig, F.; Denissenkov, P.; Hirschi, R.; Trappitsch, R.; den Hartogh, J.W.; Pignatari, M.; NuGrid Collaboration. NuGrid stellar data set-III. Updated low-mass AGB models and s-process nucleosynthesis with metallicities Z= 0.01, Z = 0.02, and Z = 0.03. Month. Not. R. Astron. Soc. 2019, 489, 1082–1098. [Google Scholar] [CrossRef]
- Denissenkov, P.A.; Tout, C.A. Partial mixing and formation of the 13C pocket by internal gravity waves in asymptotic giant branch stars. Month. Not. R. Astron. Soc. 2003, 340, 722–732. [Google Scholar] [CrossRef] [Green Version]
- Maeder, A. Physics, Formation and Evolution of Rotating Stars; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Aerts, C. Probing the interior physics of stars through asteroseismology. arXiv 2019, arXiv:1912.12300. [Google Scholar] [CrossRef]
- Langer, N.; Heger, A.; Wellstein, S.; Herwig, F. Mixing and nucleosynthesis in rotating TP-AGB stars. Astron. Astrophys. 1999, 346, L37–L40. [Google Scholar]
- Herwig, F.; Langer, N.; Lugaro, M. The s-Process in Rotating Asymptotic Giant Branch Stars. Astrophys. J. 2003, 593, 1056–1073. [Google Scholar] [CrossRef] [Green Version]
- Siess, L.; Goriely, S.; Langer, N. Nucleosynthesis of s-elements in rotating AGB stars. Astron. Astrophys. 2004, 415, 1089–1097. [Google Scholar] [CrossRef]
- Piersanti, L.; Cristallo, S.; Straniero, O. The Effects of Rotation on s-process Nucleosynthesis in Asymptotic Giant Branch Stars. Astrophys. J. 2013, 774, 98. [Google Scholar] [CrossRef] [Green Version]
- den Hartogh, J.W.; Hirschi, R.; Lugaro, M.; Doherty, C.L.; Battino, U.; Herwig, F.; Pignatari, M.; Eggenberger, P. The s process in rotating low-mass AGB stars. Nucleosynthesis calculations in models matching asteroseismic constraints. Astron. Astrophys. 2019, 629, A123. [Google Scholar] [CrossRef]
- Braithwaite, J.; Spruit, H.C. Magnetic fields in non-convective regions of stars. R. Soc. Open Sci. 2017, 4, 160271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Busso, M.; Wasserburg, G.J.; Nollett, K.M.; Calandra, A. Can Extra Mixing in RGB and AGB Stars Be Attributed to Magnetic Mechanisms? Astrophys. J. 2007, 671, 802–810. [Google Scholar] [CrossRef] [Green Version]
- Aerts, C.; Mathis, S.; Rogers, T.M. Angular Momentum Transport in Stellar Interiors. Annu. Rev. Astron. Astrophys. 2019, 57, 35–78. [Google Scholar] [CrossRef] [Green Version]
- Nucci, M.C.; Busso, M. Magnetohydrodynamics and Deep Mixing in Evolved Stars. I. Two- and Three-dimensional Analytical Models for the Asymptotic Giant Branch. Astrophys. J. 2014, 787, 141. [Google Scholar] [CrossRef] [Green Version]
- Parker, E.N. The Hydrodynamic Theory of Solar Corpuscular Radiation and Stellar Winds. Astrophys. J. 1960, 132, 821. [Google Scholar] [CrossRef]
- Spruit, H.C. Differential rotation and magnetic fields in stellar interiors. Astron. Astrophys. 1999, 349, 189–202. [Google Scholar]
- Schuessler, M. On buoyant magnetic flux tube in the solar convection zone. Astron. Astrophys. 1977, 56, 439–442. [Google Scholar]
- Trippella, O.; Busso, M.; Maiorca, E.; Käppeler, F.; Palmerini, S. s-Processing in AGB Stars Revisited. I. Does the Main Component Constrain the Neutron Source in the 13C Pocket? Astrophys. J. 2014, 787, 41. [Google Scholar] [CrossRef] [Green Version]
- Vescovi, D.; Busso, M.; Palmerini, S.; Trippella, O.; Cristallo, S.; Piersanti, L.; Chieffi, A.; Limongi, M.; Hoppe, P.; Kratz, K.-L. On the Origin of Early Solar System Radioactivities: Problems with the Asymptotic Giant Branch and Massive Star Scenarios. Astrophys. J. 2018, 863, 115. [Google Scholar] [CrossRef]
- Ventura, P.; D’Antona, F.; Mazzitelli, I.; Gratton, R. Predictions for Self-Pollution in Globular Cluster Stars. Astrophys. J. Lett. 2001, 550, L65–L69. [Google Scholar] [CrossRef] [Green Version]
- Herwig, F. Evolution and Yields of Extremely Metal-poor Intermediate-Mass Stars. Astrophys. J. Suppl. 2004, 155, 651–666. [Google Scholar] [CrossRef] [Green Version]
- Karakas, A.; Lattanzio, J.C. Stellar Models and Yields of Asymptotic Giant Branch Stars. Publ. Astron. Soc. Aust. 2007, 24, 103–117. [Google Scholar] [CrossRef] [Green Version]
- Cristallo, S.; Piersanti, L.; Straniero, O.; Gallino, R.; Domínguez, I.; Abia, C.; Di Rico, G.; Quintini, M.; Bisterzo, S. Evolution, Nucleosynthesis, and Yields of Low-mass Asymptotic Giant Branch Stars at Different Metallicities. II. The FRUITY Database. Astrophys. J. Suppl. 2011, 197, 17. [Google Scholar] [CrossRef] [Green Version]
- Ritter, C.; Herwig, F.; Jones, S.; Pignatari, M.; Fryer, C.; Hirschi, R. NuGrid stellar data set-II. Stellar yields from H to Bi for stellar models with MZAMS = 1–25 M⊙ and Z = 0.0001–0.02. Month. Not. R. Astron. Soc. 2018, 480, 538–571. [Google Scholar] [CrossRef] [Green Version]
- Rogers, F.J.; Swenson, F.J.; Iglesias, C.A. OPAL Equation-of-State Tables for Astrophysical Applications. Astrophys. J. 1996, 456, 902. [Google Scholar] [CrossRef]
- Straniero, O. A tabulation of thermodynamical properties of fully ionized matter in stellar interiors. Astron. Astrophys. Suppl. 1988, 76, 157–184. [Google Scholar]
- Prada Moroni, P.G.; Straniero, O. Calibration of White Dwarf Cooling Sequences: Theoretical Uncertainty. Astrophys. J. 2002, 581, 585–597. [Google Scholar] [CrossRef]
- Lodders, K. Relative Atomic Solar System Abundances, Mass Fractions, and Atomic Masses of the Elements and Their Isotopes, Composition of the Solar Photosphere, and Compositions of the Major Chondritic Meteorite Groups. Space Sci. Rev. 2021, 217, 44. [Google Scholar] [CrossRef]
- Vescovi, D.; Cristallo, S.; Palmerini, S.; Abia, C.; Busso, M. Magnetic-buoyancy-induced mixing in AGB Stars: Fluorine nucleosynthesis at different metallicities. arXiv 2021, arXiv:2106.08241. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Rogers, F.J. Updated Opal Opacities. Astrophys. J. 1996, 464, 943. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Baiko, D.A.; Haensel, P.; Yakovlev, D.G. Transport properties of degenerate electrons in neutron star envelopes and white dwarf cores. Astron. Astrophys. 1999, 346, 345–353. [Google Scholar]
- Shternin, P.S.; Yakovlev, D.G. Electron thermal conductivity owing to collisions between degenerate electrons. Phys. Rev. D 2006, 74, 043004. [Google Scholar] [CrossRef] [Green Version]
- Marigo, P.; Aringer, B. Low-temperature gas opacity. ÆSOPUS: A versatile and quick computational tool. Astron. Astrophys. 2009, 508, 1539–1569. [Google Scholar] [CrossRef]
- Höfner, S.; Olofsson, H. Mass loss of stars on the asymptotic giant branch. Mechanisms, models and measurements. Astron. Astrophys. Rev. 2018, 26, 1. [Google Scholar] [CrossRef] [Green Version]
- Ventura, P.; Karakas, A.I.; Dell’Agli, F.; Boyer, M.L.; García-Hernández, D.A.; Di Criscienzo, M.; Schneider, R. The Large Magellanic Cloud as a laboratory for hot bottom burning in massive asymptotic giant branch stars. Month. Not. R. Astron. Soc. 2015, 450, 3181–3190. [Google Scholar] [CrossRef] [Green Version]
- Vassiliadis, E.; Wood, P.R. Evolution of Low- and Intermediate-Mass Stars to the End of the Asymptotic Giant Branch with Mass Loss. Astrophys. J. 1993, 413, 641. [Google Scholar] [CrossRef]
- Whitelock, P.A.; Feast, M.W.; van Loon, J.T.; Zijlstra, A.A. Obscured asymptotic giant branch variables in the Large Magellanic Cloud and the period-luminosity relation. Month. Not. R. Astron. Soc. 2003, 342, 86–104. [Google Scholar] [CrossRef] [Green Version]
- Abia, C.; de Laverny, P.; Cristallo, S.; Kordopatis, G.; Straniero, O. Properties of carbon stars in the solar neighbourhood based on Gaia DR2 astrometry. Astron. Astrophys. 2020, 633, A135. [Google Scholar] [CrossRef] [Green Version]
- Buzzoni, A.; Patelli, L.; Bellazzini, M.; Pecci, F.F.; Oliva, E. Bolometric correction and spectral energy distribution of cool stars in Galactic clusters. Month. Not. R. Astron. Soc. 2010, 403, 1592–1610. [Google Scholar] [CrossRef] [Green Version]
- Dillmann, I.; Plag, R.; Käppeler, F.; Rauscher, T. EFNUDAT Fast Neutrons-Scientific Workshop on Neutron Measurements, Theory & Applications. JRC-IRMM. 2009. Available online: http://www.kadonis.org (accessed on 28 August 2009).
- Rugel, G.; Faestermann, T.; Knie, K.; Korschinek, G.; Poutivtsev, M.; Schumann, D.; Kivel, N.; Günther-Leopold, I.; Weinreich, R.; Wohlmuther, M. New Measurement of the Fe60 Half-Life. Phys. Rev. L 2009, 103, 072502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uberseder, E.; Reifarth, R.; Schumann, D.; Dillmann, I.; Pardo, C.D.; Görres, J.; Heil, M.; Käppeler, F.; Marganiec, J.; Neuhausen, J.; et al. Measurement of the 60Fe(n,γ)61Fe cross-section at Stellar Temperatures. Phys. Rev. Lett. 2009, 102, 151101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simonucci, S.; Taioli, S.; Palmerini, S.; Busso, M. Theoretical Estimates of Stellar e—Captures. I. The Half-life of 7Be in Evolved Stars. Astrophys. J. 2013, 764, 118. [Google Scholar] [CrossRef] [Green Version]
- Vescovi, D.; Piersanti, L.; Cristallo, S.; Busso, M.; Vissani, F.; Palmerini, S.; Simonucci, S.; Taioli, S. Effects of a revised 7Be e−-capture rate on solar neutrino fluxes. Astron. Astrophys. 2019, 623, A126. [Google Scholar] [CrossRef] [Green Version]
- Reifarth, R.; Erbacher, P.; Fiebiger, S.; Göbel, K.; Heftrich, T.; Heil, M.; Käppeler, F.; Klapper, N.; Kurtulgil, D.; Langer, C.; et al. Neutron-induced cross-sections. From raw data to astrophysical rates. Eur. Phys. J. Plus 2018, 133, 424. [Google Scholar] [CrossRef]
- Vescovi, D.; Reifarth, R. s-Processing in Asymptotic Giant Branch Stars in the Light of Revised Neutron-Capture cross-sections. Universe 2021, 7, 239. [Google Scholar] [CrossRef]
- Lamia, L.; Spitaleri, C.; La Cognata, M.; Palmerini, S.; Pizzone, R.G. Recent evaluation of the 7Li(p, α)4He reaction rate at astrophysical energies via the Trojan Horse method. Astron. Astrophys. 2012, 541, A158. [Google Scholar] [CrossRef] [Green Version]
- Cesaratto, J.M.; Champagne, A.E.; Buckner, M.Q.; Clegg, T.B.; Daigle, S.; Howard, C.; Iliadis, C.; Longland, R.; Newton, J.R.; Oginni, B.M. Measurement of the Erc.m. = 138 keV resonance in the 23Na(p,γ)24Mg reaction and the abundance of sodium in AGB stars. Phys. Rev. C 2013, 88, 065806. [Google Scholar] [CrossRef]
- Costantini, H.; deBoer, R.J.; Azuma, R.E.; Couder, M.; Görres, J.; Hammer, J.W.; LeBlanc, P.J.; Lee, H.Y.; O’Brien, S.; Palumbo, A.; et al. 16O(α,γ)20Ne S factor: Measurements and R-matrix analysis. Phys. Rev. C 2010, 82, 035802. [Google Scholar] [CrossRef] [Green Version]
- LeBlanc, P.J.; Imbriani, G.; Görres, J.; Junker, M.; Azuma, R.; Beard, M.; Bemmerer, D.; Best, A.; Broggini, C.; Caciolli, A.; et al. Constraining the S factor of 15N(p,γ)16O at astrophysical energies. Phys. Rev. C 2010, 82, 055804. [Google Scholar] [CrossRef] [Green Version]
- Iliadis, C.; Longland, R.; Champagne, A.E.; Coc, A.; Fitzgerald, R. Charged-particle thermonuclear reaction rates: II. Tables and graphs of reaction rates and probability density functions. Nucl. Phys. A 2010, 841, 31–250. [Google Scholar] [CrossRef] [Green Version]
- Di Leva, A.; Scott, D.A.; Caciolli, A.; Formicola, A.; Strieder, F.; Aliotta, M.; Anders, M.; Bemmerer, D.; Broggini, C.; Corvisiero, P.; et al. Underground study of the 17O(p,γ)18F reaction relevant for explosive hydrogen burning. Phys. Rev. C 2014, 89, 015803. [Google Scholar] [CrossRef]
- Adsley, P.; Battino, U.; Best, A.; Caciolli, A.; Guglielmetti, A.; Imbriani, G.; Jayatissa, H.; La Cognata, M.; Lamia, L.; Masha, E.; et al. Reevaluation of the 22Ne(α, γ) 26Mg and 22Ne(α, n)25Mg reaction rates. Phys. Rev. C 2021, 103, 015805. [Google Scholar] [CrossRef]
- Bruno, C.G.; Scott, D.A.; Aliotta, M.; Formicola, A.; Best, A.; Boeltzig, A.; Bemmerer, D.; Broggini, C.; Caciolli, A.; Cavanna, F.; et al. Improved Direct Measurement of the 64.5 keV Resonance Strength in the 17O(p,α)14N Reaction at LUNA. Phys. Rev. Lett. 2016, 117, 142502. [Google Scholar] [CrossRef] [Green Version]
- Straniero, O.; Imbriani, G.; Strieder, F.; Bemmerer, D.; Broggini, C.; Caciolli, A.; Corvisiero, P.; Costantini, H.; Cristallo, S.; DiLeva, A.; et al. Impact of a Revised 25Mg(p, γ)26Al Reaction Rate on the Operation of the Mg-Al Cycle. Astrophys. J. 2013, 763, 100. [Google Scholar] [CrossRef] [Green Version]
- Buckner, M.Q.; Iliadis, C.; Kelly, K.J.; Downen, L.N.; Champagne, A.E.; Cesaratto, J.M.; Howard, C.; Longland, R. High-intensity-beam study of 17O(p,γ)18F and thermonuclear reaction rates for 17O+p. Phys. Rev. C 2015, 91, 015812. [Google Scholar] [CrossRef] [Green Version]
- Best, A.; Pantaleo, F.R.; Boeltzig, A.; Imbriani, G.; Aliotta, M.; Balibrea-Correa, J.; Bemmerer, D.; Broggini, C.; Bruno, C.G.; Buompane, R.; et al. cross-section of the reaction 18O(p,γ)19F at astrophysical energies: The 90 keV resonance and the direct capture component. Phys. Lett. B 2019, 797, 134900. [Google Scholar] [CrossRef]
- Bruno, C.G.; Aliotta, M.; Descouvemont, P.; Best, A.; Davinson, T.; Bemmerer, D.; Boeltzig, A.; Broggini, C.; Caciolli, A.; Cavanna, F.; et al. Improved astrophysical rate for the 18O(p,α)15N reaction by underground measurements. Phys. Lett. B 2019, 790, 237–242. [Google Scholar] [CrossRef]
- Best, A.; Beard, M.; Görres, J.; Couder, M.; deBoer, R.; Falahat, S.; Güray, R.T.; Kontos, A.; Kratz, K.-L.; LeBlanc, P.J.; et al. Measurement of the reaction 17O(α,n)20Ne and its impact on the s process in massive stars. Phys. Rev. C 2013, 87, 045805. [Google Scholar] [CrossRef] [Green Version]
- Indelicato, I.; La Cognata, M.; Spitaleri, C.; Burjan, V.; Cherubini, S.; Gulino, M.; Hayakawa, S.; Hons, Z.; Kroha, V.; Lamia, L.; et al. New Improved Indirect Measurement of the 19F(p, α)16O Reaction at Energies of Astrophysical Relevance. Astrophys. J. 2017, 845, 19. [Google Scholar] [CrossRef]
- Lamia, L.; Spitaleri, C.; Tognelli, E.; Degl’Innocenti, S.; Pizzone, R.G.; Prada Moroni, P.G. Astrophysical Impact of the Updated 9Be(p,α)6Li and 10B(p,α)7Be Reaction Rates As Deduced By THM. Astrophys. J. 2015, 811, 99. [Google Scholar] [CrossRef] [Green Version]
- Best, A.; Falahat, S.; Görres, J.; Couder, M.; deBoer, R.; Güray, R.T.; Kontos, A.; Kratz, K.L.; LeBlanc, P.J.; Li, Q.; et al. Measurement of the reaction 18O(α,n)21Ne. Phys. Rev. C 2013, 87, 045806. [Google Scholar] [CrossRef] [Green Version]
- Angulo, C.; Arnould, M.; Rayet, M.; Descouvemont, P.; Baye, D.; Leclercq-Willain, C.; Coc, A.; Barhoumi, S.; Aguer, P.; Rolfs, C.; et al. A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 1999, 656, 3–183. [Google Scholar] [CrossRef]
- D’Agata, G.; Pizzone, R.G.; La Cognata, M.; Indelicato, I.; Spitaleri, C.; Palmerini, S.; Trippella, O.; Vescovi, D.; Blagus, S.; Cherubini, S.; et al. The 19F(α, p)22Ne Reaction at Energies of Astrophysical Relevance by Means of the Trojan Horse Method and Its Implications in AGB Stars. Astrophys. J. 2018, 860, 61. [Google Scholar] [CrossRef]
- Kunz, R.; Fey, M.; Jaeger, M.; Mayer, A.; Hammer, J.W.; Staudt, G.; Harissopulos, S.; Paradellis, T. Astrophysical Reaction Rate of 12C(α, γ)16O. Astrophys. J. 2002, 567, 643–650. [Google Scholar] [CrossRef]
- Ciani, G.F.; Csedreki, L.; Rapagnani, D.; Aliotta, M.; Balibrea-Correa, J.; Barile, F.; Bemmerer, D.; Best, A.; Boeltzig, A.; Broggini, C.; et al. Direct Measurement of the 13C(α,n)16O cross-section into the s-Process Gamow Peak. Phys. Rev. Lett. 2021, 127, 152701. [Google Scholar] [CrossRef] [PubMed]
- Depalo, R.; Cavanna, F.; Aliotta, M.; Anders, M.; Bemmerer, D.; Best, A.; Boeltzig, A.; Broggini, C.; Bruno, C.G.; Caciolli, A.; et al. Direct measurement of low-energy 22Ne(p, γ) 23Na resonances. Phys. Rev. C 2016, 94, 055804. [Google Scholar] [CrossRef] [Green Version]
- Johnson, E.D.; Rogachev, G.V.; Mitchell, J.; Miller, L.; Kemper, K.W. C14(α,γ) reaction rate. Phys. Rev. C 2009, 80, 045805. [Google Scholar] [CrossRef]
- Sallaska, A.L.; Iliadis, C.; Champange, A.E.; Goriely, S.; Starrfield, S.; Timmes, F.X. STARLIB: A Next-generation Reaction-rate Library for Nuclear Astrophysics. Astrophys. J. Suppl. 2013, 207, 18. [Google Scholar] [CrossRef]
- Wallner, A.; Bichler, M.; Buczak, K.; Dillmann, I.; Käppeler, F.; Karakas, A.; Lederer, C.; Lugaro, M.; Mair, K.; Mengoni, A.; et al. Accelerator mass spectrometry measurements of the 13C (n, γ)14C and 14N(n, p)14C cross-sections. Phys. Rev. C 2016, 93, 045803. [Google Scholar] [CrossRef] [Green Version]
- Marganiec, J.; Dillmann, I.; Pardo, C.D.; Käppeler, F.; Reifarth, R.; Gallino, R.; Pignatari, M.; Grabmayr, P. Neutron capture cross-sections of Ge74, Ge76, and As75 at 25 keV. Phys. Rev. C 2009, 79, 065802. [Google Scholar] [CrossRef]
- Roig, O.; Jandel, M.; Méot, V.; Bond, E.M.; Bredeweg, T.A.; Couture, A.J.; Haight, R.C.; Keksis, A.L.; Rundberg, R.S.; Ullmann, J.L.; et al. Radiative neutron capture cross-sections on 176Lu at DANCE. Phys. Rev. C 2016, 93, 034602. [Google Scholar] [CrossRef] [Green Version]
- Heil, M.; Käppeler, F.; Uberseder, E.; Gallino, R.; Bisterzo, S.; Pignatari, M. Stellar (n,γ) cross-sections for Br and Rb: Matching the weak and main s-process components. Phys. Rev. C 2008, 78, 025802. [Google Scholar] [CrossRef]
- Vockenhuber, C.; Dillmann, I.; Heil, M.; Käppeler, F.; Winckler, N.; Kutschera, W.; Wallner, A.; Bichler, M.; Dababneh, S.; Bisterzo, S.; et al. Stellar (n,γ) cross-sections of Hf174 and radioactive Hf182. Phys. Rev. C 2007, 75, 015804. [Google Scholar] [CrossRef]
- Guardo, G.L.; Spitaleri, C.; Lamia, L.; Gulino, M.; La Cognata, M.; Tang, X.; deBoer, R.; Fang, X.; Goldberg, V.; Mrazek, J.; et al. Assessing the near threshold cross-section of the 17O(n, α)14C reaction by means of the Trojan horse method. Phys. Rev. C 2017, 95, 025807. [Google Scholar] [CrossRef] [Green Version]
- Wisshak, K.; Voss, F.; Käppeler, F.; Kazakov, L.; Bečvář, F.; Krtička, M.; Gallino, R.; Pignatari, M. Fast neutron capture on the Hf isotopes: Cross-sections, isomer production, and stellar aspects. Phys. Rev. C 2006, 73, 045807. [Google Scholar] [CrossRef]
- Uberseder, E.; Heil, M.; Käppeler, F.; Görres, J.; Wiescher, M. New measurements of the F19(n,γ)F20 cross section and their implications for the stellar reaction rate. Phys. Rev. C 2007, 75, 035801. [Google Scholar] [CrossRef]
- Tessler, M.; Zappala, J.; Cristallo, S.; Roberti, L.; Paul, M.; Halfon, S.; Heftrich, T.; Jiang, W.; Kijel, D.; Kreisel, A.; et al. Stellar s-process neutron capture cross-sections on 78,80,84,86Kr determined via activation, atom trap trace analysis, and decay counting. Phys. Rev. C 2021, 104, 015806. [Google Scholar] [CrossRef]
- Heil, M.; Plag, R.; Uberseder, E.; Gallino, R.; Bisterzo, S.; Juseviciute, A.; Käppeler, F.; Lederer, C.; Mengoni, A.; Pignatari, M. Stellar neutron capture cross-sections of 20,21,22Ne. Phys. Rev. C 2014, 90, 045804. [Google Scholar] [CrossRef] [Green Version]
- Uberseder, E.; Heil, M.; Käppeler, F.; Lederer, C.; Mengoni, A.; Bisterzo, S.; Pignatari, M.; Wiescher, M. Stellar (n, γ) cross-sections of 23Na. Phys. Rev. C 2017, 95, 025803. [Google Scholar] [CrossRef] [Green Version]
- Massimi, C.; Koehler, P.; Bisterzo, S.; Colonna, N.; Gallino, R.; Gunsing, F.; Käppeler, F.; Lorusso, G.; Mengoni, A.; Pignatari, M.; et al. Resonance neutron-capture cross-sections of stable magnesium isotopes and their astrophysical implications. Phys. Rev. C 2012, 85, 044615. [Google Scholar] [CrossRef] [Green Version]
- Marganiec, J.; Dillmann, I.; Pardo, C.D.; Käppeler, F.; Walter, S. Stellar (n,γ) cross-sections of p-process isotopes. II. Yb168, W180, Os184, Pt190, and Hg196. Phys. Rev. C 2010, 82, 035806. [Google Scholar] [CrossRef]
- Massimi, C.; Altstadt, S.; Andrzejewski, J.; Audouin, L.; Barbagallo, M.; Bécares, V.; Bečvář, F.; Belloni, F.; Berthoumieux, E.; Billowes, J.; et al. Neutron spectroscopy of 26Mg states: Constraining the stellar neutron source 22Ne(α,n)25Mg. Phys. Lett. B 2017, 768, 1–6. [Google Scholar] [CrossRef]
- Marganiec, J.; Dillmann, I.; Pardo, C.D.; Käppeler, F. Neutron capture cross-sections of W184 and W186. Phys. Rev. C 2009, 80, 025804. [Google Scholar] [CrossRef]
- Koehler, P.E.; Winters, R.R.; Guber, K.H.; Rauscher, T.; Harvey, J.A.; Raman, S.; Spencer, R.R.; Blackmon, J.C.; Larson, D.C.; Bardayan, D.W.; et al. High-resolution neutron capture and transmission measurements, and the stellar neutron-capture cross-section of 88Sr. Phys. Rev. C 2000, 62, 055803. [Google Scholar] [CrossRef]
- Pavetich, S.; Wallner, A.; Martschini, M.; Akhmadaliev, S.; Dillmann, I.; Fifield, K.; Halfon, S.; Heftrich, T.; Käppeler, F.; Lederer-Woods, C.; et al. Accelerator mass spectrometry measurement of the reaction 35Cl(n, γ)36Cl at keV energies. Phys. Rev. C 2019, 99, 015801. [Google Scholar] [CrossRef] [Green Version]
- Tagliente, G.; Fujii, K.; Milazzo, P.M.; Moreau, C.; Aerts, G.; Abbondanno, U.; Alvarez, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; et al. Neutron capture cross-section of Zr90: Bottleneck in the s-process reaction flow. Phys. Rev. C 2008, 77, 035802. [Google Scholar] [CrossRef]
- Beer, H.; Sedyshev, P.V.; Rochow, W.; Rauscher, T.; Mohr, P. Neutron capture of 30Si. Nucl. Phys. A 2002, 709, 453–466. [Google Scholar] [CrossRef]
- Tagliente, G.; Milazzo, P.M.; Fujii, K.; Aerts, G.; Abbondanno, U.; Álvarez, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Assimakopoulos, P.; et al. Experimental study of the Zr91(n,γ) reaction up to 26 keV. Phys. Rev. C 2008, 78, 045804. [Google Scholar] [CrossRef] [Green Version]
- Mosconi, M.; Fujii, K.; Mengoni, A.; Domingo-Pardo, C.; Käppeler, F.; Abbondanno, U.; Aerts, G.; Alvarez-Pol, H.; Alvarez-Velarde, F.; Andriamonje, S.; et al. Neutron physics of the Re/Os clock. I. Measurement of the (n,γ) cross-sections of Os186,187,188 at the CERN n_TOF facility. Phys. Rev. C 2010, 82, 015802. [Google Scholar] [CrossRef] [Green Version]
- Heil, M.; Plag, R.; Uberseder, E.; Bisterzo, S.; Käppeler, F.; Mengoni, A.; Pignatari, M. Stellar neutron capture cross-sections of 41K and 45Sc. Phys. Rev. C 2016, 93, 055807. [Google Scholar] [CrossRef] [Green Version]
- Tagliente, G.; Milazzo, P.M.; Fujii, K.; Abbondanno, U.; Aerts, G.; Alvarez, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Audouin, L.; et al. The Zr92(n,γ) reaction and its implications for stellar nucleosynthesis. Phys. Rev. C 2010, 81, 055801. [Google Scholar] [CrossRef] [Green Version]
- Dillmann, I.; Domingo-Pardo, C.; Heil, M.; Käppeler, F.; Wallner, A.; Forstner, O.; Golser, R.; Kutschera, W.; Priller, A.; Steier, P.; et al. Determination of the stellar (n,γ) cross-section of Ca40 with accelerator mass spectrometry. Phys. Rev. C 2009, 79, 065805. [Google Scholar] [CrossRef]
- Tagliente, G.; Milazzo, P.M.; Fujii, K.; Abbondanno, U.; Aerts, G.; Álvarez, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Audouin, L.; et al. The 93Zr(n,γ) reaction up to 8 keV neutron energy. Phys. Rev. C 2013, 87, 014622. [Google Scholar] [CrossRef]
- Tagliente, G.; Milazzo, P.M.; Fujii, K.; Abbondanno, U.; Aerts, G.; Alvarez, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Audouin, L.; et al. Neutron capture on Zr94: Resonance parameters and Maxwellian-averaged cross-sections. Phys. Rev. C 2011, 84, 015801. [Google Scholar] [CrossRef] [Green Version]
- Marganiec, J.; Dillmann, I.; Domingo-Pardo, C.; Käppeler, F. Stellar (n, γ) cross-sections of neutron-rich nuclei: Completing the isotope chains of Yb, Os, Pt, and Hg. Phys. Rev. C 2014, 90, 065801. [Google Scholar] [CrossRef]
- Wallner, A.; Buczak, K.; Belgya, T.; Bichler, M.; Coquard, L.; Dillmann, I.; Golser, R.; Käppeler, F.; Karakas, A.; Kutschera, W.; et al. Precise measurement of the thermal and stellar 54Fe(n, γ)55Fe cross-sections via accelerator mass spectrometry. Phys. Rev. C 2017, 96, 025808. [Google Scholar] [CrossRef] [Green Version]
- Tagliente, G.; Milazzo, P.M.; Fujii, K.; Abbondanno, U.; Aerts, G.; Álvarez, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Audouin, L.; et al. 96Zr(n,γ) measurement at the n_TOF facility at CERN. Phys. Rev. C 2011, 84, 055802. [Google Scholar] [CrossRef] [Green Version]
- Heil, M.; Käppeler, F.; Uberseder, E.; Gallino, R.; Pignatari, M. Neutron capture cross-sections for the weak s process in massive stars. Phys. Rev. C 2008, 77, 015808. [Google Scholar] [CrossRef]
- Rapp, W.; Heil, M.; Hentschel, D.; Käppeler, F.; Reifarth, R.; Brede, H.J.; Klein, H.; Rauscher, T. α- and neutron-induced reactions on ruthenium isotopes. Phys. Rev. C 2002, 66, 015803. [Google Scholar] [CrossRef]
- Koehler, P.E.; Guber, K.H. Improved 192,194,195,196Pt(n,γ) and 192Ir(n,γ) astrophysical reaction rates. Phys. Rev. C 2013, 88, 035802. [Google Scholar] [CrossRef] [Green Version]
- Žugec, P.; Barbagallo, M.; Colonna, N.; Bosnar, D.; Altstadt, S.; Andrzejewski, J.; Audouin, L.; Becares, V.; Bečvář, F.; Belloni, F.; et al. Experimental neutron capture data of 58Ni from the CERN n_TOF facility. Phys. Rev. C 2014, 89, 014605. [Google Scholar] [CrossRef] [Green Version]
- Guber, K.H.; Derrien, H.; Leal, L.C.; Arbanas, G.; Wiarda, D.; Koehler, P.E.; Harvey, J.A. Astrophysical reaction rates for Ni58,60(n,γ) from new neutron capture cross-section measurements. Phys. Rev. C 2010, 82, 057601. [Google Scholar] [CrossRef]
- Dillmann, I.; Domingo-Pardo, C.; Heil, M.; Käppeler, F.; Walter, S.; Dababneh, S.; Rauscher, T.; Thielemann, F.K. Stellar (n,γ) cross-sections of p-process isotopes Part I: Pd102, Te120, Ba130,132, and Dy156. Phys. Rev. C 2010, 81, 015801. [Google Scholar] [CrossRef]
- Lederer, C.; Massimi, C.; Berthoumieux, E.; Colonna, N.; Dressler, R.; Guerrero, C.; Gunsing, F.; Käppeler, F.; Kivel, N.; Pignatari, M.; et al. Erratum: 62Ni(n,γ) and 63Ni(n,γ) cross-sections measured at the n_TOF facility at CERN [Phys. Rev. C 89, 025810 (2014)]. Phys. Rev. C 2015, 92, 019903. [Google Scholar] [CrossRef] [Green Version]
- Lederer, C.; Massimi, C.; Altstadt, S.; Andrzejewski, J.; Audouin, L.; Barbagallo, M.; Bécares, V.; Bečvář, F.; Belloni, F.; Berthoumieux, E.; et al. Neutron Capture cross-section of Unstable Ni63: Implications for Stellar Nucleosynthesis. Phys. Rev. L 2013, 110, 022501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Massimi, C.; Becker, B.; Dupont, E.; Kopecky, S.; Lampoudis, C.; Massarczyk, R.; Moxon, M.; Pronyaev, V.; Schillebeeckx, P.; Sirakov, I.; et al. Neutron capture cross-section measurements for 197Au from 3.5 to 84 keV at GELINA. Eur. Phys. J. A 2014, 50, 124. [Google Scholar] [CrossRef] [Green Version]
- Weigand, M.; Beinrucker, C.; Couture, A.; Fiebiger, S.; Fonseca, M.; Göbel, K.; Heftrich, M.; Heftrich, T.; Jandel, M.; Käppeler, F.; et al. 63Cu(n,γ) cross-section measured via 25 keV activation and time of flight. Phys. Rev. C 2017, 95, 015808. [Google Scholar] [CrossRef] [Green Version]
- Calviño, F.; Cortes, G.; Poch, A.; Pretel, M. The La139(n,γ) cross-section: Key for the onset of the s-process. Phys. Rev. C 2007, 75, 035807. [Google Scholar] [CrossRef] [Green Version]
- Prokop, C.J.; Couture, A.; Jones, S.; Mosby, S.; Rusev, G.; Ullmann, J.; Krtička, M. Measurement of the 65Cu(n, γ) cross section using the Detector for Advanced Neutron Capture Experiments at LANL. Phys. Rev. C 2019, 99, 055809. [Google Scholar] [CrossRef]
- Capote, R.; Lozano Leyva, M.L.; Molina-Coballes, A.; Quesada Molina, J.M.; Marrone, S.; Abbondanno, U.; Aerts, G.; Álvarez Velarde, F. Measurement of the Sm151(n,γ) cross-section from 0.6 eV to 1 MeV via the neutron time-of-flight technique at the CERN n_TOF facility. Phys. Rev. C 2006, 73, 034604. [Google Scholar] [CrossRef] [Green Version]
- Reifarth, R.; Dababneh, S.; Heil, M.; Käppeler, F.; Plag, R.; Sonnabend, K.; Uberseder, E. Neutron activation of natural zinc samples at kT = 25 keV. Phys. Rev. C 2012, 85, 035802. [Google Scholar] [CrossRef] [Green Version]
- Mazzone, A.; Cristallo, S.; Aberle, O.; Alaerts, G.; Alcayne, V.; Amaducci, S.; Andrzejewski, J.; Audouin, L.; Babiano-Suarez, V.; Bacak, M.; et al. Measurement of the 154Gd(n,γ) cross-section and its astrophysical implications. Phys. Lett. B 2020, 804, 135405. [Google Scholar] [CrossRef]
- Domingo-Pardo, C.; Abbondanno, U.; Aerts, G.; Álvarez-Pol, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Assimakopoulos, P.; Audouin, L.; Badurek, G.; et al. Measurement of the neutron capture cross-section of the s-only isotope Pb204 from 1 eV to 440 keV. Phys. Rev. C 2007, 75, 015806. [Google Scholar] [CrossRef] [Green Version]
- Lederer-Woods, C.; Battino, U.; Ferreira, P.; Gawlik, A.; Guerrero, C.; Gunsing, F.; Heinitz, S.; Lerendegui-Marco, J.; Mengoni, A.; Reifarth, R.; et al. Measurement of 73Ge(n,γ) cross-sections and implications for stellar nucleosynthesis. Phys. Lett. B 2019, 790, 458–465. [Google Scholar] [CrossRef]
- Domingo-Pardo, C.; Abbondanno, U.; Aerts, G.; Álvarez, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Assimakopoulos, P.; Audouin, L.; Badurek, G.; et al. Measurement of the radiative neutron capture cross-section of Pb206 and its astrophysical implications. Phys. Rev. C 2007, 76, 045805. [Google Scholar] [CrossRef] [Green Version]
- Domingo-Pardo, C.; Abbondanno, U.; Aerts, G.; Álvarez-Pol, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Assimakopoulos, P.; Audouin, L.; Badurek, G.; et al. Resonance capture cross-section of Pb207. Phys. Rev. C 2006, 74, 055802. [Google Scholar] [CrossRef]
- Domingo-Pardo, C.; Abbondanno, U.; Aerts, G.; Álvarez-Pol, H.; Alvarez-Velarde, F.; Andriamonje, S.; Andrzejewski, J.; Assimakopoulos, P.; Audouin, L.; Badurek, G.; et al. New measurement of neutron capture resonances in Bi209. Phys. Rev. C 2006, 74, 025807. [Google Scholar] [CrossRef] [Green Version]
- Vescovi, D.; Mascaretti, C.; Vissani, F.; Piersanti, L.; Straniero, O. The luminosity constraint in the era of precision solar physics. J. Phys. Nucl. Phys. 2021, 48, 015201. [Google Scholar] [CrossRef]
- Chieffi, A.; Domínguez, I.; Limongi, M.; Straniero, O. Evolution and Nucleosynthesis of Zero-Metal Intermediate-Mass Stars. Astrophys. J. 2001, 554, 1159–1174. [Google Scholar] [CrossRef] [Green Version]
- Guandalini, R.; Cristallo, S. Luminosities of carbon-rich asymptotic giant branch stars in the Milky Way. Astron. Astrophys. 2013, 555, A120. [Google Scholar] [CrossRef] [Green Version]
- Cristallo, S.; Abia, C.; Straniero, O.; Piersanti, L. On the Need for the Light Elements Primary Process (LEPP). Astrophys. J. 2015, 801, 53. [Google Scholar] [CrossRef] [Green Version]
- Prantzos, N.; Abia, C.; Cristallo, S.; Limongi, M.; Chieffi, A. Chemical evolution with rotating massive star yields II. A new assessment of the solar s- and r-process components. Month. Not. R. Astron. Soc. 2020, 491, 1832–1850. [Google Scholar] [CrossRef]
- Vescovi, D.; Cristallo, S.; Busso, M.; Liu, N. Magnetic-buoyancy-induced Mixing in AGB Stars: Presolar SiC Grains. Astrophys. J. Lett. 2020, 897, L25. [Google Scholar] [CrossRef]
- Nordhaus, J.; Busso, M.; Wasserburg, G.J.; Blackman, E.G.; Palmerini, S. Magnetic Mixing in Red Giant and Asymptotic Giant Branch Stars. Astrophys. J. Lett. 2008, 684, L29. [Google Scholar] [CrossRef] [Green Version]
- Denissenkov, P.A.; Pinsonneault, M.; MacGregor, K.B. Magneto-Thermohaline Mixing in Red Giants. Astrophys. J. 2009, 696, 1823–1833. [Google Scholar] [CrossRef] [Green Version]
- Busso, M.; Vescovi, D.; Palmerini, S.; Cristallo, S.; Antonuccio-Delogu, V. s-processing in AGB Stars Revisited. III. Neutron Captures from MHD Mixing at Different Metallicities and Observational Constraints. Astrophys. J. 2021, 908, 55. [Google Scholar] [CrossRef]
- Acheson, D.J.; Gibbons, M.P. On the Instability of Toroidal Magnetic Fields and Differential Rotation in Stars. Philos. Trans. R. Soc. Lond. Ser. A 1978, 289, 459–500. [Google Scholar] [CrossRef]
- Magrini, L.; Vescovi, D.; Casali, G.; Cristallo, S.; Viscasillas Vázquez, C.; Cescutti, G.; Spina, L.; Van Der Swaelmen, M.; Randich, S. Magnetic-buoyancy-induced mixing in AGB stars: A theoretical explanation of the non-universal relation of [Y/Mg] to age. Astron. Astrophys. 2021, 646, L2. [Google Scholar] [CrossRef]
- Zinner, E. 1.4—Presolar Grains. In Treatise on Geochemistry, 2nd ed.; Holland, H.D., Turekian, K.K., Eds.; Elsevier: Oxford, UK, 2014; pp. 181–213. [Google Scholar] [CrossRef]
- Liu, N.; Savina, M.R.; Gallino, R.; Davis, A.M.; Bisterzo, S.; Gyngard, F.; Käppeler, F.; Cristallo, S.; Dauphas, N.; Pellin, M.J.; et al. Correlated Strontium and Barium Isotopic Compositions of Acid-cleaned Single Mainstream Silicon Carbides from Murchison. Astrophys. J. 2015, 803, 12. [Google Scholar] [CrossRef] [Green Version]
- Hoppe, P.; Annen, P.; Strebel, R.; Eberhardt, P.; Gallino, R.; Lugaro, M.; Amari, S.; Lewis, R.S. Meteoritic Silicon Carbide Grains with Unusual Si Isotopic Compositions: Evidence for an Origin in Low-Mass, Low-Metallicity Asymptotic Giant Branch Stars. Astrophys. J. Lett. 1997, 487, L101–L104. [Google Scholar] [CrossRef] [Green Version]
- Lewis, K.M.; Lugaro, M.; Gibson, B.K.; Pilkington, K. Decoding the Message from Meteoritic Stardust Silicon Carbide Grains. Astrophys. J. Lett. 2013, 768, L19. [Google Scholar] [CrossRef] [Green Version]
- Gail, H.P.; Zhukovska, S.V.; Hoppe, P.; Trieloff, M. Stardust from Asymptotic Giant Branch Stars. Astrophys. J. 2009, 698, 1136–1154. [Google Scholar] [CrossRef] [Green Version]
- Cristallo, S.; Nanni, A.; Cescutti, G.; Minchev, I.; Liu, N.; Vescovi, D.; Gobrecht, D.; Piersanti, L. Mass and metallicity distribution of parent AGB stars of presolar SiC. Astron. Astrophys. 2020, 644, A8. [Google Scholar] [CrossRef]
- Lugaro, M.; Cseh, B.; Világos, B.; Karakas, A.I.; Ventura, P.; Dell’Agli, F.; Trappitsch, R.; Hampel, M.; D’Orazi, V.; Pereira, C.B.; et al. Origin of Large Meteoritic SiC Stardust Grains in Metal-rich AGB Stars. Astrophys. J. 2020, 898, 96. [Google Scholar] [CrossRef]
- Nicolussi, G.K.; Davis, A.M.; Pellin, M.J.; Lewis, R.S.; Clayton, R.N.; Amari, S. s-Process Zirconium in Presolar Silicon Carbide Grains. Science 1997, 277, 1281–1284. [Google Scholar] [CrossRef] [Green Version]
- Barzyk, J.G.; Savina, M.R.; Davis, A.M.; Gallino, R.; Gyngard, F.; Amari, S.; Zinner, E.; Pellin, M.J.; Lewis, R.S.; Clayton, R.N. Constraining the 13C neutron source in AGB stars through isotopic analysis of trace elements in presolar SiC. Meteorit. Planet. Sci. 2007, 42, 1103–1119. [Google Scholar] [CrossRef]
- Liu, N.; Savina, M.R.; Davis, A.M.; Gallino, R.; Straniero, O.; Gyngard, F.; Pellin, M.J.; Willingham, D.G.; Dauphas, N.; Pignatari, M.; et al. Barium Isotopic Composition of Mainstream Silicon Carbides from Murchison: Constraints for s-process Nucleosynthesis in Asymptotic Giant Branch Stars. Astrophys. J. 2014, 786, 66. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Stephan, T.; Boehnke, P.; Nittler, L.R.; O’D. Alexander, C.M.; Wang, J.; Davis, A.M.; Trappitsch, R.; Pellin, M.J. J-type Carbon Stars: A Dominant Source of 14N-rich Presolar SiC Grains of Type AB. Astrophys. J. Lett. 2017, 844, L12. [Google Scholar] [CrossRef] [Green Version]
- Trappitsch, R.; Stephan, T.; Savina, M.R.; Davis, A.M.; Pellin, M.J.; Rost, D.; Gyngard, F.; Gallino, R.; Bisterzo, S.; Cristallo, S.; et al. Simultaneous iron and nickel isotopic analyses of presolar silicon carbide grains. Geochim. Cosmochim. Acta 2018, 221, 87–108. [Google Scholar] [CrossRef]
- Stephan, T.; Trappitsch, R.; Davis, A.M.; Pellin, M.J.; Rost, D.; Savina, M.R.; Jadhav, M.; Kelly, C.H.; Gyngard, F.; Hoppe, P.; et al. Strontium and barium isotopes in presolar silicon carbide grains measured with CHILI—Two types of X grains. Geochim. Cosmochim. Acta 2018, 221, 109–126. [Google Scholar] [CrossRef]
- Stephan, T.; Trappitsch, R.; Hoppe, P.; Davis, A.M.; Pellin, M.J.; Pardo, O.S. Molybdenum Isotopes in Presolar Silicon Carbide Grains: Details of s-process Nucleosynthesis in Parent Stars and Implications for r- and p-processes. Astrophys. J. 2019, 877, 101. [Google Scholar] [CrossRef]
- Palmerini, S.; Trippella, O.; Busso, M.; Vescovi, D.; Petrelli, M.; Zucchini, A.; Frondini, F. s-Processing from MHD-induced mixing and isotopic abundances in presolar SiC grains. Geochim. Cosmochim. Acta 2018, 221, 21–36. [Google Scholar] [CrossRef] [Green Version]
- Palmerini, S.; Busso, M.; Vescovi, D.; Naselli, E.; Pidatella, A.; Mucciola, R.; Cristallo, S.; Mascali, D.; Mengoni, A.; Simonucci, S.; et al. Presolar Grain Isotopic Ratios as Constraints to Nuclear and Stellar Parameters of Asymptotic Giant Branch Star Nucleosynthesis. Astrophys. J. 2021, 921, 7. [Google Scholar] [CrossRef]
- Grisoni, V.; Romano, D.; Spitoni, E.; Matteucci, F.; Ryde, N.; Jönsson, H. Fluorine in the solar neighbourhood: Modelling the Galactic thick and thin discs. Month. Not. R. Astron. Soc. 2020, 498, 1252–1258. [Google Scholar] [CrossRef]
- Jorissen, A.; Smith, V.V.; Lambert, D.L. Fluorine in red giant stars: Evidence for nucleosynthesis. Astron. Astrophys. 1992, 261, 164–187. [Google Scholar]
- Abia, C.; Recio-Blanco, A.; de Laverny, P.; Cristallo, S.; Domínguez, I.; Straniero, O. Fluorine in Asymptotic Giant Branch Carbon Stars Revisited. Astrophys. J. 2009, 694, 971–977. [Google Scholar] [CrossRef]
- Abia, C.; Cunha, K.; Cristallo, S.; de Laverny, P.; Domínguez, I.; Eriksson, K.; Gialanella, L.; Hinkle, K.; Imbriani, G.; Recio-Blanco, A.; et al. Fluorine Abundances in Galactic Asymptotic Giant Branch Stars. Astrophys. J. Lett. 2010, 715, L94–L98. [Google Scholar] [CrossRef]
- Abia, C.; Cunha, K.; Cristallo, S.; de Laverny, P.; Domínguez, I.; Recio-Blanco, A.; Smith, V.V.; Straniero, O. The First Fluorine Abundance Determinations in Extragalactic Asymptotic Giant Branch Carbon Stars. Astrophys. J. Lett. 2011, 737, L8. [Google Scholar] [CrossRef] [Green Version]
- Abia, C.; Cristallo, S.; Cunha, K.; de Laverny, P.; Smith, V.V. Additional fluorine abundance determinations in evolved stars. Astron. Astrophys. 2019, 625, A40. [Google Scholar] [CrossRef] [Green Version]
- Lucatello, S.; Masseron, T.; Johnson, J.A.; Pignatari, M.; Herwig, F. Fluorine and Sodium in C-rich Low-metallicity Stars. Astrophys. J. 2011, 729, 40. [Google Scholar] [CrossRef]
- Goriely, S.; Mowlavi, N. Neutron-capture nucleosynthesis in AGB stars. Astron. Astrophys. 2000, 362, 599–614. [Google Scholar]
- Lugaro, M.; Ugalde, C.; Karakas, A.I.; Görres, J.; Wiescher, M.; Lattanzio, J.C.; Cannon, R.C. Reaction Rate Uncertainties and the Production of 19F in Asymptotic Giant Branch Stars. Astrophys. J. 2004, 615, 934–946. [Google Scholar] [CrossRef] [Green Version]
- Cristallo, S.; Di Leva, A.; Imbriani, G.; Piersanti, L.; Abia, C.; Gialanella, L.; Straniero, O. Effects of nuclear cross-sections on 19F nucleosynthesis at low metallicities. Astron. Astrophys. 2014, 570, A46. [Google Scholar] [CrossRef]
- Abia, C.; Cunha, K.; Cristallo, S.; de Laverny, P. The origin of fluorine: Abundances in AGB carbon stars revisited. Astron. Astrophys. 2015, 581, A88. [Google Scholar] [CrossRef] [Green Version]
- Limongi, M.; Chieffi, A. Presupernova Evolution and Explosive Nucleosynthesis of Rotating Massive Stars in the Metallicity Range −3 ≤ [Fe/H] ≤ 0. Astrophys. J. Suppl. 2018, 237, 13. [Google Scholar] [CrossRef]
- Casali, G.; Spina, L.; Magrini, L.; Karakas, A.I.; Kobayashi, C.; Casey, A.R.; Feltzing, S.; Van der Swaelmen, M.; Tsantaki, M.; Jofré, P.; et al. The Gaia-ESO survey: The non-universality of the age-chemical-clocks-metallicity relations in the Galactic disc. Astron. Astrophys. 2020, 639, A127. [Google Scholar] [CrossRef]
- Liu, N.; Gallino, R.; Cristallo, S.; Bisterzo, S.; Davis, A.M.; Trappitsch, R.; Nittler, L.R. New Constraints on the Major Neutron Source in Low-mass AGB Stars. Astrophys. J. 2018, 865, 112. [Google Scholar] [CrossRef] [Green Version]
- Cristallo, S.; La Cognata, M.; Massimi, C.; Best, A.; Palmerini, S.; Straniero, O.; Trippella, O.; Busso, M.; Ciani, G.F.; Mingrone, F.; et al. The Importance of the 13C(α,n)16O Reaction in Asymptotic Giant Branch Stars. Astrophys. J. 2018, 859, 105. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vescovi, D. Mixing and Magnetic Fields in Asymptotic Giant Branch Stars in the Framework of FRUITY Models. Universe 2022, 8, 16. https://doi.org/10.3390/universe8010016
Vescovi D. Mixing and Magnetic Fields in Asymptotic Giant Branch Stars in the Framework of FRUITY Models. Universe. 2022; 8(1):16. https://doi.org/10.3390/universe8010016
Chicago/Turabian StyleVescovi, Diego. 2022. "Mixing and Magnetic Fields in Asymptotic Giant Branch Stars in the Framework of FRUITY Models" Universe 8, no. 1: 16. https://doi.org/10.3390/universe8010016
APA StyleVescovi, D. (2022). Mixing and Magnetic Fields in Asymptotic Giant Branch Stars in the Framework of FRUITY Models. Universe, 8(1), 16. https://doi.org/10.3390/universe8010016






