Exploring Anisotropic Lorentz Invariance Violation from the Spectral-Lag Transitions of Gamma-Ray Bursts
Abstract
:1. Introduction
2. Theoretical Framework
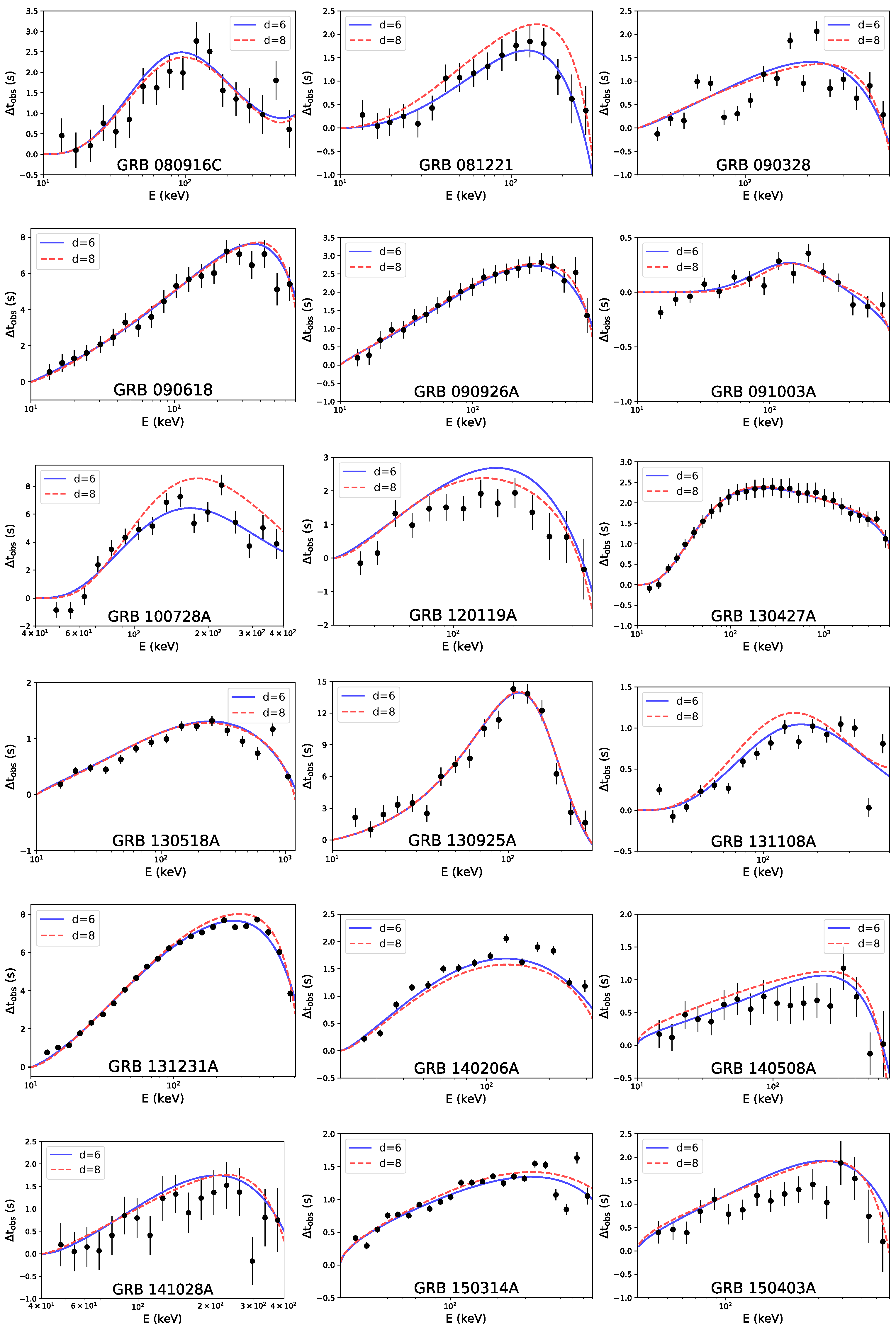
3. Constraints on Anisotropic LIV
4. Discussion
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kostelecký, V.A.; Russell, N. Data tables for Lorentz and CPT violation. Rev. Mod. Phys. 2011, 83, 11–32. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Samuel, S. Spontaneous breaking of Lorentz symmetry in string theory. Phys. Rev. D 1989, 39, 683–685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kostelecký, V.A.; Potting, R. CPT and strings. Nucl. Phys. B 1991, 359, 545. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Potting, R. CPT, strings, and meson factories. Phys. Rev. D 1995, 51, 3923–3935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mattingly, D. Modern Tests of Lorentz Invariance. Living Rev. Relativ. 2005, 8, 5. [Google Scholar] [CrossRef] [Green Version]
- Amelino-Camelia, G. Quantum-Spacetime Phenomenology. Living Rev. Relativ. 2013, 16, 5. [Google Scholar] [CrossRef] [Green Version]
- Tasson, J.D. What do we know about Lorentz invariance? Rep. Prog. Phys. 2014, 77, 62901. [Google Scholar] [CrossRef]
- Wei, J.J.; Wu, X.F. Testing fundamental physics with astrophysical transients. Front. Phys. 2021, 16, 44300. [Google Scholar] [CrossRef]
- He, P.; Ma, B.Q. Lorentz Symmetry Violation of Cosmic Photons. Universe 2022, 8, 323. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Ellis, J.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of quantum gravity from observations of γ-ray bursts. Nature 1998, 393, 763–765. [Google Scholar] [CrossRef]
- Ellis, J.; Farakos, K.; Mavromatos, N.E.; Mitsou, V.A.; Nanopoulos, D.V. A Search in Gamma-Ray Burst Data for Nonconstancy of the Velocity of Light. Astrophys. J. 2000, 535, 139–151. [Google Scholar] [CrossRef] [Green Version]
- Pavlopoulos, T.G. Are we observing Lorentz violation in gamma ray bursts? [rapid communication]. Phys. Lett. B 2005, 625, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Ellis, J.; Mavromatos, N.E.; Nanopoulos, D.V.; Sakharov, A.S.; Sarkisyan, E.K.G. Robust limits on Lorentz violation from gamma-ray bursts. Astropart. Phys. 2006, 25, 402–411. [Google Scholar] [CrossRef] [Green Version]
- Jacob, U.; Piran, T. Lorentz-violation-induced arrival delays of cosmological particles. J. Cosmol. Astropart. Phys. 2008, 2008, 31. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Astrophysical Tests of Lorentz and CPT Violation with Photons. Astrophys. J. Lett. 2008, 689, L1. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Electrodynamics with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2009, 80, 015020. [Google Scholar] [CrossRef] [Green Version]
- Abdo, A.A.; Ackermann, M.; Arimoto, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. Fermi Observations of High-Energy Gamma-Ray Emission from GRB 080916C. Science 2009, 323, 1688. [Google Scholar] [CrossRef]
- Ellis, J.; Mavromatos, N.E. Probes of Lorentz violation. Astropart. Phys. 2013, 43, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Vasileiou, V.; Jacholkowska, A.; Piron, F.; Bolmont, J.; Couturier, C.; Granot, J.; Stecker, F.W.; Cohen-Tanugi, J.; Longo, F. Constraints on Lorentz invariance violation from Fermi-Large Area Telescope observations of gamma-ray bursts. Phys. Rev. D 2013, 87, 122001. [Google Scholar] [CrossRef] [Green Version]
- Kislat, F.; Krawczynski, H. Search for anisotropic Lorentz invariance violation with γ -rays. Phys. Rev. D 2015, 92, 045016. [Google Scholar] [CrossRef]
- Wei, J.J.; Zhang, B.B.; Shao, L.; Wu, X.F.; Mészáros, P. A New Test of Lorentz Invariance Violation: The Spectral Lag Transition of GRB 160625B. Astrophys. J. Lett. 2017, 834, L13. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.J.; Wu, X.F.; Zhang, B.B.; Shao, L.; Mészáros, P.; Kostelecký, V.A. Constraining Anisotropic Lorentz Violation via the Spectral-lag Transition of GRB 160625B. Astrophys. J. 2017, 842, 115. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.J.; Wu, X.F. A Further Test of Lorentz Violation from the Rest-frame Spectral Lags of Gamma-Ray Bursts. Astrophys. J. 2017, 851, 127. [Google Scholar] [CrossRef] [Green Version]
- Du, S.S.; Lan, L.; Wei, J.J.; Zhou, Z.M.; Gao, H.; Jiang, L.Y.; Zhang, B.B.; Liu, Z.K.; Wu, X.F.; Liang, E.W.; et al. Lorentz Invariance Violation Limits from the Spectral-lag Transition of GRB 190114C. Astrophys. J. 2021, 906, 8. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhang, B.B.; Meng, Y.Z. Spectral Lag Transition of 32 Fermi Gamma-Ray Bursts and Their Application on Constraining Lorentz Invariance Violation. Astrophys. J. 2022, 935, 79. [Google Scholar] [CrossRef]
- Xiao, S.; Xiong, S.L.; Wang, Y.; Zhang, S.N.; Gao, H.; Zhang, Z.; Cai, C.; Yi, Q.B.; Zhao, Y.; Tuo, Y.L.; et al. A Robust Estimation of Lorentz Invariance Violation and Intrinsic Spectral Lag of Short Gamma-Ray Bursts. Astrophys. J. Lett. 2022, 924, L29. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Cosmological Constraints on Lorentz Violation in Electrodynamics. Phys. Rev. Lett. 2001, 87, 251304. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Sensitive Polarimetric Search for Relativity Violations in Gamma-Ray Bursts. Phys. Rev. Lett. 2006, 97, 140401. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Lorentz-Violating Electrodynamics and the Cosmic Microwave Background. Phys. Rev. Lett. 2007, 99, 011601. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Constraints on Relativity Violations from Gamma-Ray Bursts. Phys. Rev. Lett. 2013, 110, 201601. [Google Scholar] [CrossRef]
- Gubitosi, G.; Pagano, L.; Amelino-Camelia, G.; Melchiorri, A.; Cooray, A. A constraint on Planck-scale modifications to electrodynamics with CMB polarization data. J. Cosmol. Astropart. Phys. 2009, 2009, 021. [Google Scholar] [CrossRef] [Green Version]
- Laurent, P.; Götz, D.; Binétruy, P.; Covino, S.; Fernandez-Soto, A. Constraints on Lorentz Invariance Violation using integral/IBIS observations of GRB041219A. Phys. Rev. D 2011, 83, 121301. [Google Scholar] [CrossRef] [Green Version]
- Stecker, F.W. A new limit on Planck scale Lorentz violation from γ-ray burst polarization. Astropart. Phys. 2011, 35, 95–97. [Google Scholar] [CrossRef] [Green Version]
- Toma, K.; Mukohyama, S.; Yonetoku, D.; Murakami, T.; Gunji, S.; Mihara, T.; Morihara, Y.; Sakashita, T.; Takahashi, T.; Wakashima, Y.; et al. Strict Limit on CPT Violation from Polarization of γ-Ray Bursts. Phys. Rev. Lett. 2012, 109, 241104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kislat, F.; Krawczynski, H. Planck-scale constraints on anisotropic Lorentz and C P T invariance violations from optical polarization measurements. Phys. Rev. D 2017, 95, 083013. [Google Scholar] [CrossRef] [Green Version]
- Friedman, A.S.; Leon, D.; Crowley, K.D.; Johnson, D.; Teply, G.; Tytler, D.; Keating, B.G.; Cole, G.M. Constraints on Lorentz invariance and C P T violation using optical photometry and polarimetry of active galaxies BL Lacertae and S5 B 0716 +714. Phys. Rev. D 2019, 99, 035045. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.J. New constraints on Lorentz invariance violation with polarized gamma-ray bursts. Mon. Not. R. Astron. Soc. 2019, 485, 2401–2406. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.Q.; Yi, S.X.; Wei, J.J.; Wu, X.F. Constraints on Lorentz Invariance Violation with Multiwavelength Polarized Astrophysical Sources. Galaxies 2021, 9, 44. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecký, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760–6774. [Google Scholar] [CrossRef] [Green Version]
- Colladay, D.; Kostelecký, V.A. Lorentz-violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Kostelecký, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef] [Green Version]
- Boggs, S.E.; Wunderer, C.B.; Hurley, K.; Coburn, W. Testing Lorentz Invariance with GRB 021206. Astrophys. J. Lett. 2004, 611, L77–L80. [Google Scholar] [CrossRef]
- Band, D.L. Gamma-Ray Burst Spectral Evolution through Cross-Correlations of Discriminator Light Curves. Astrophys. J. 1997, 486, 928–937. [Google Scholar] [CrossRef]
- Norris, J.P.; Nemiroff, R.J.; Bonnell, J.T.; Scargle, J.D.; Kouveliotou, C.; Paciesas, W.S.; Meegan, C.A.; Fishman, G.J. Attributes of Pulses in Long Bright Gamma-Ray Bursts. Astrophys. J. 1996, 459, 393. [Google Scholar] [CrossRef]
- Cheng, L.X.; Ma, Y.Q.; Cheng, K.S.; Lu, T.; Zhou, Y.Y. The time delay of gamma-ray bursts in the soft energy band. Astron. Astrophys. 1995, 300, 746. [Google Scholar]
- Kostelecký, V.A.; Mewes, M. Signals for Lorentz violation in electrodynamics. Phys. Rev. D 2002, 66, 056005. [Google Scholar] [CrossRef] [Green Version]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef] [Green Version]
- von Kienlin, A.; Meegan, C.A.; Paciesas, W.S.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Burns, E.; Cleveland, W.H.; Gibby, M.H.; Giles, M.M.; et al. The Fourth Fermi-GBM Gamma-Ray Burst Catalog: A Decade of Data. Astrophys. J. 2020, 893, 46. [Google Scholar] [CrossRef] [Green Version]
- Ajello, M.; Arimoto, M.; Axelsson, M.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bhat, P.N.; Bissaldi, E.; Blandford, R.D.; et al. A decade of gamma-ray bursts observed by Fermi-LAT: The second GRB catalog. Astrophys. J. 2019, 878, 52. [Google Scholar] [CrossRef] [Green Version]
- Selsing, J.; Fynbo, J.P.U.; Heintz, K.E.; Watson, D. GRB 190114C: NOT optical counterpart and redshift. GRB Coord. Netw. 2019, 23695, 1. [Google Scholar]
- Belkin, S.; Pozanenko, A.; Rumyantsev, V.; Volnova, A.; Mazaeva, E.; larger GRB follow-up Collaboration. GRB 200613A: CrAO optical observations. GRB Coord. Netw. 2020, 28000, 1. [Google Scholar]
- Oates, S.R.; Kuin, N.P.M.; De Pasquale, M.; Campana, S.; Tohuvavohu, A.; Siegel, M.H.; Neil Gehrels Swift Observatory Team. GRB 200829A: Swift/UVOT-XRT photometric redshift. GRB Coord. Netw. 2020, 28338, 1. [Google Scholar]
- Vielfaure, J.B.; Izzo, L.; Xu, D.; Vergani, S.D.; Malesani, D.B.; de Ugarte Postigo, A.; D’Elia, V.; Fynbo, J.P.U.; Kann, D.A.; Levan, A.J.; et al. GRB 201216C: VLT X-shooter spectroscopy and potential high redshift of a VHE-emitting GRB. GRB Coord. Netw. 2020, 29077, 1. [Google Scholar]
- Xu, D.; Izzo, L.; Fynbo, J.P.U.; Kann, D.A.; Vergani, S.D.; Malesani, D.B.; Arabsalmani, M.; Rossi, A.; Pugliese, G.; Vielfaure, J.B.; et al. GRB 210204A: Redshift revision of ZTF21aagwbjr/AT2021buv (correction to GCN 29411). GRB Coord. Netw. 2021, 29432, 1. [Google Scholar]
- de Ugarte Postigo, A.; Thoene, C.; Agui Fernandez, J.F.; Blazek, M.; Kann, D.A.; Fynbo, J.P.U.; Izzo, L.; Garcia Alvarez, D. GRB 210610B: Redshift confirmation from GTC. GRB Coord. Netw. 2021, 30194, 1. [Google Scholar]
- de Ugarte Postigo, A.; Kann, D.A.; Thoene, C.; Blazek, M.; Agui Fernandez, J.F.; Izzo, L.; Tanvir, N.R.; Fynbo, J.P.U.; Garcia Rodriguez, A.M.; Gomez, G. GRB 210619B: Redshift from OSIRIS/GTC. GRB Coord. Netw. 2021, 30272, 1. [Google Scholar]
- Biesiada, M.; Piórkowska, A. Lorentz invariance violation-induced time delays in GRBs in different cosmological models. Class. Quantum Gravity 2009, 26, 125007. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Liddle, A.R. Information criteria for astrophysical model selection. Mon. Not. R. Astron. Soc. 2007, 377, L74–L78. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]


| R.A. | Dec. | Redshift | ||
|---|---|---|---|---|
| Name | J2000 [] | J2000 [] | z1 | Ref. 2 |
| GRB 080916C | 119.8 | −56.6 | 4.35 | [48] |
| GRB 081221 | 15.8 | −24.5 | 2.26 | [48] |
| GRB 090328 | 155.7 | +33.4 | 0.736 | [48] |
| GRB 090618 | 294.0 | +78.4 | 0.54 | [48] |
| GRB 090926A | 353.4 | −66.3 | 2.1062 | [48] |
| GRB 091003A | 251.5 | −36.6 | 0.8969 | [48] |
| GRB 100728A | 88.8 | −15.3 | 1.567 | [48] |
| GRB 120119A | 120.0 | −9.8 | 1.728 | [48] |
| GRB 130427A | 173.1 | +27.7 | 0.3399 | [48] |
| GRB 130518A | 355.7 | +47.5 | 2.488 | [48] |
| GRB 130925A | 41.2 | −26.1 | 0.347 | [48] |
| GRB 131108A | 156.5 | +9.7 | 2.40 | [48] |
| GRB 131231A | 10.6 | −1.6 | 0.642 | [48] |
| GRB 140206A | 145.3 | +66.8 | 2.73 | [48] |
| GRB 140508A | 255.5 | +46.8 | 1.027 | [48] |
| GRB 141028A | 322.6 | −0.2 | 2.33 | [48] |
| GRB 150314A | 126.7 | +63.8 | 1.758 | [48] |
| GRB 150403A | 311.5 | −62.7 | 2.06 | [48] |
| GRB 150514A | 74.8 | −60.9 | 0.807 | [48] |
| GRB 150821A | 341.9 | −57.9 | 0.755 | [48] |
| GRB 160509A | 310.1 | +76.0 | 1.17 | [48] |
| GRB 160625B | 308.6 | +6.9 | 1.41 | [48] |
| GRB 171010A | 66.6 | −10.5 | 0.3285 | [48] |
| GRB 180703A | 6.5 | −67.1 | 0.6678 | [48] |
| GRB 180720B | 0.59 | −3.0 | 0.654 | [49] |
| GRB 190114C | 54.5 | −26.9 | 0.425 | [50] |
| GRB 200613A | 153.0 | +45.8 | 1.22 | [51] |
| GRB 200829A | 251.1 | +72.4 | 1.25 | [52] |
| GRB 201216C | 16.4 | +16.5 | 1.10 | [53] |
| GRB 210204A | 109.1 | +9.7 | 0.876 | [54] |
| GRB 210610B | 243.9 | +14.4 | 1.13 | [55] |
| GRB 210619B | 319.7 | +33.9 | 1.937 | [56] |
| Name | d | (keV) | ||||||
|---|---|---|---|---|---|---|---|---|
| Units for | Units for | |||||||
| Units for | Untis for | |||||||
| GRB 080916C | 6 | |||||||
| 8 | ||||||||
| GRB 081221 | 6 | |||||||
| 8 | ||||||||
| GRB 090328 | 6 | |||||||
| 8 | ||||||||
| GRB 090618 | 6 | |||||||
| 8 | ||||||||
| GRB 090926A | 6 | |||||||
| 8 | ||||||||
| GRB 091003A | 6 | |||||||
| 8 | ||||||||
| GRB 100728A | 6 | |||||||
| 8 | ||||||||
| GRB 120119A | 6 | |||||||
| 8 | ||||||||
| GRB 130427A | 6 | |||||||
| 8 | ||||||||
| GRB 130518A | 6 | |||||||
| 8 | ||||||||
| GRB 130925A | 6 | |||||||
| 8 | ||||||||
| GRB 131108A | 6 | |||||||
| 8 | ||||||||
| GRB 131231A | 6 | |||||||
| 8 | ||||||||
| GRB 140206A | 6 | |||||||
| 8 | ||||||||
| GRB 140508A | 6 | |||||||
| 8 | ||||||||
| GRB 141028A | 6 | |||||||
| 8 | ||||||||
| GRB 150314A | 6 | |||||||
| 8 | ||||||||
| GRB 150403A | 6 | |||||||
| 8 | ||||||||
| GRB 150514A | 6 | |||||||
| 8 | ||||||||
| GRB 150821A | 6 | |||||||
| 8 | ||||||||
| GRB 160509A | 6 | |||||||
| 8 | ||||||||
| GRB 160625B | 6 | |||||||
| 8 | ||||||||
| GRB 171010A | 6 | |||||||
| 8 | ||||||||
| GRB 180703A | 6 | |||||||
| 8 | ||||||||
| GRB 180720B | 6 | |||||||
| 8 | ||||||||
| GRB 190114C | 6 | |||||||
| 8 | ||||||||
| GRB 200613A | 6 | |||||||
| 8 | ||||||||
| GRB 200829A | 6 | |||||||
| 8 | ||||||||
| GRB 201216C | 6 | |||||||
| 8 | ||||||||
| GRB 210204A | 6 | |||||||
| 8 | ||||||||
| GRB 210610B | 6 | |||||||
| 8 | ||||||||
| GRB 210619B | 6 | |||||||
| 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.-N.; Liu, Z.-K.; Wei, J.-J.; Zhang, B.-B.; Wu, X.-F. Exploring Anisotropic Lorentz Invariance Violation from the Spectral-Lag Transitions of Gamma-Ray Bursts. Universe 2022, 8, 519. https://doi.org/10.3390/universe8100519
Wei J-N, Liu Z-K, Wei J-J, Zhang B-B, Wu X-F. Exploring Anisotropic Lorentz Invariance Violation from the Spectral-Lag Transitions of Gamma-Ray Bursts. Universe. 2022; 8(10):519. https://doi.org/10.3390/universe8100519
Chicago/Turabian StyleWei, Jin-Nan, Zi-Ke Liu, Jun-Jie Wei, Bin-Bin Zhang, and Xue-Feng Wu. 2022. "Exploring Anisotropic Lorentz Invariance Violation from the Spectral-Lag Transitions of Gamma-Ray Bursts" Universe 8, no. 10: 519. https://doi.org/10.3390/universe8100519
APA StyleWei, J.-N., Liu, Z.-K., Wei, J.-J., Zhang, B.-B., & Wu, X.-F. (2022). Exploring Anisotropic Lorentz Invariance Violation from the Spectral-Lag Transitions of Gamma-Ray Bursts. Universe, 8(10), 519. https://doi.org/10.3390/universe8100519








