Performance of NeQuick-2 and IRI-Plas 2017 Models during Solar Maximum Years in 2013–2014 over Equatorial and Low Latitude Regions
Abstract
:1. Introduction
2. Data and Methods
3. Result
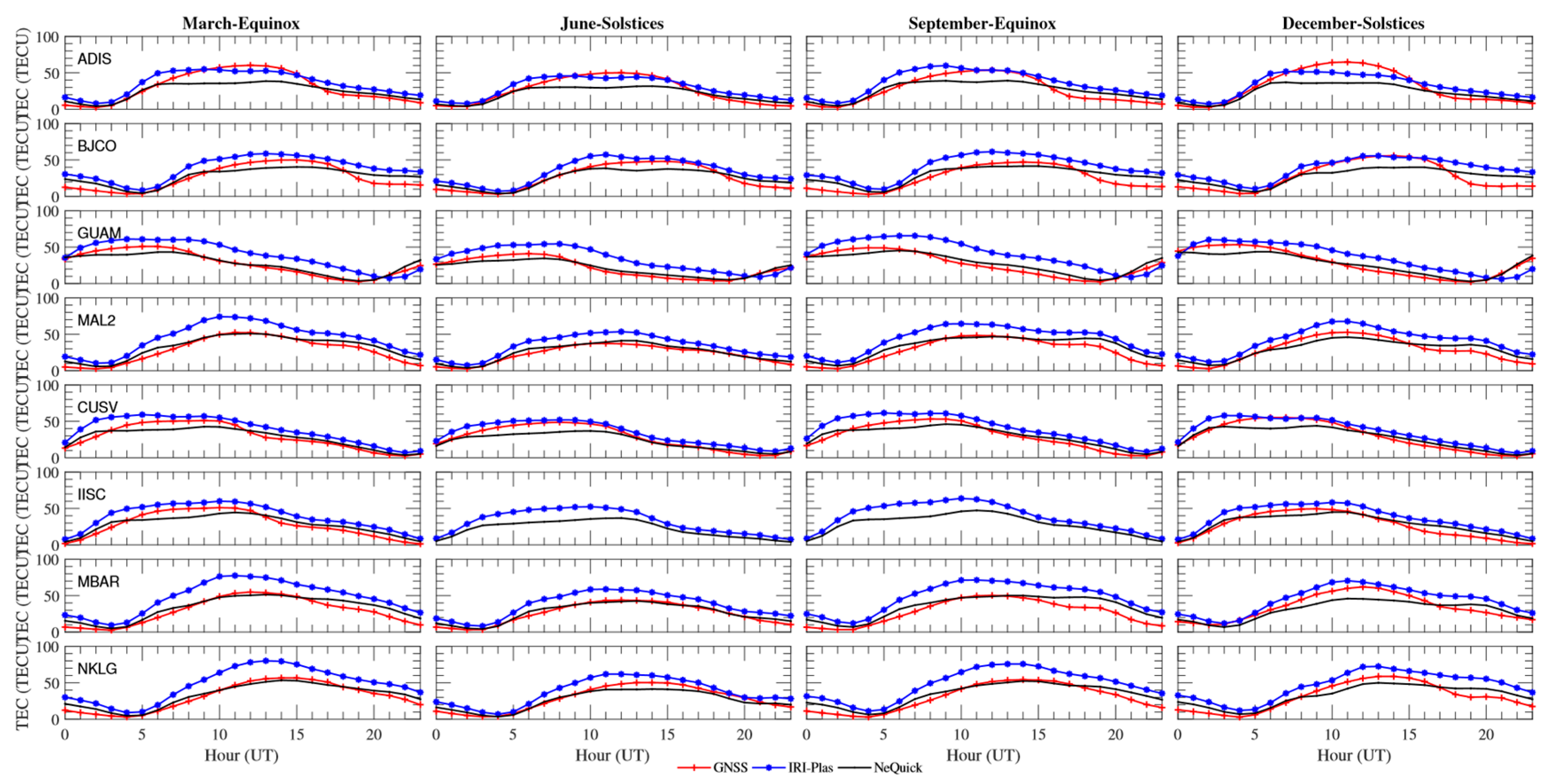
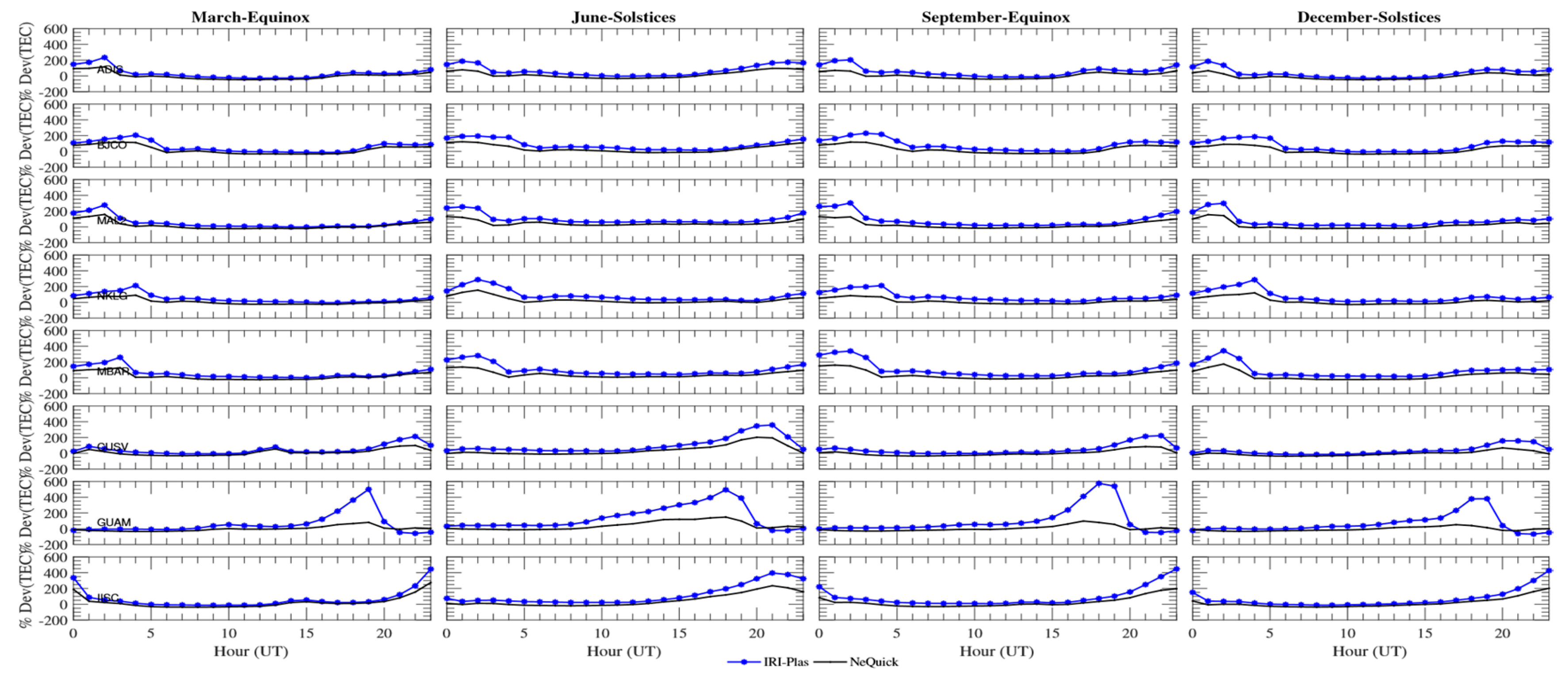
3.1. Seasonal Comparison of GPS-TEC with NeQuick and IRI-Plas Model at Mbarar in Uganda
3.2. Seasonal Comparison of GPS-TEC with NeQuick and IRI-Plas Model at Malinda in Kenya
3.3. Seasonal Comparison of GPS-TEC with NeQuick and IRI-Plas Model at Librevile in Gabon
3.4. Seasonal Comparison of GPS-TEC with NeQuick and IRI-Plas Model at Cotonou in Benin
3.5. Seasonal Comparison of GPS-TEC with NeQuick and IRI-Plas Model at Addis Ababa in Ethiopia
3.6. Seasonal Comparison of GPS-TEC with NeQuick and IRI-Plas Model at Bangalore in India
3.7. Seasonal Comparison of GPS-TEC with NeQuick and IRI-Plas Model at Dodedo in Guam
3.8. Seasonal Comparison of GPS-TEC with NeQuick and IRI-Plas Model at Patumwen in Thailand
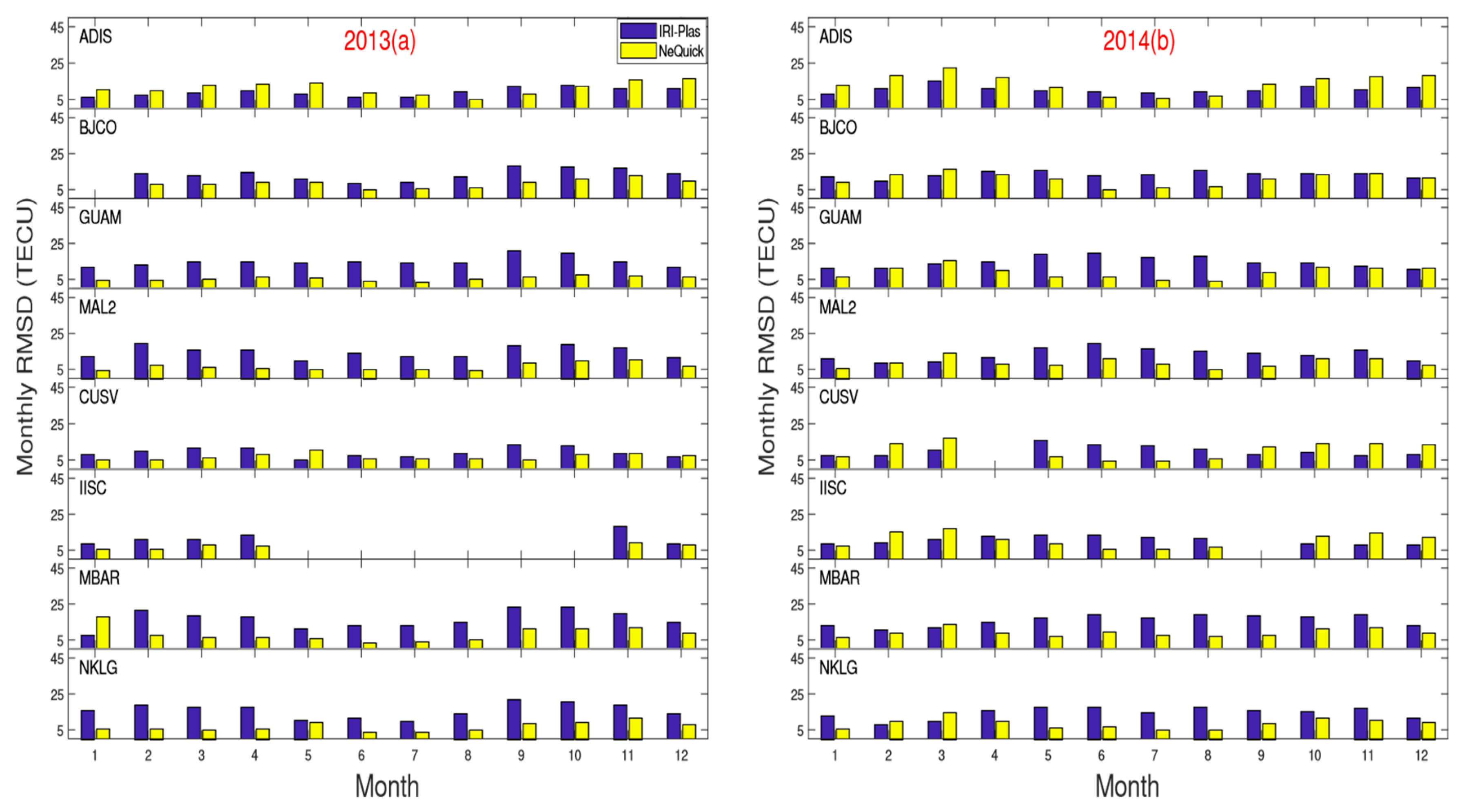
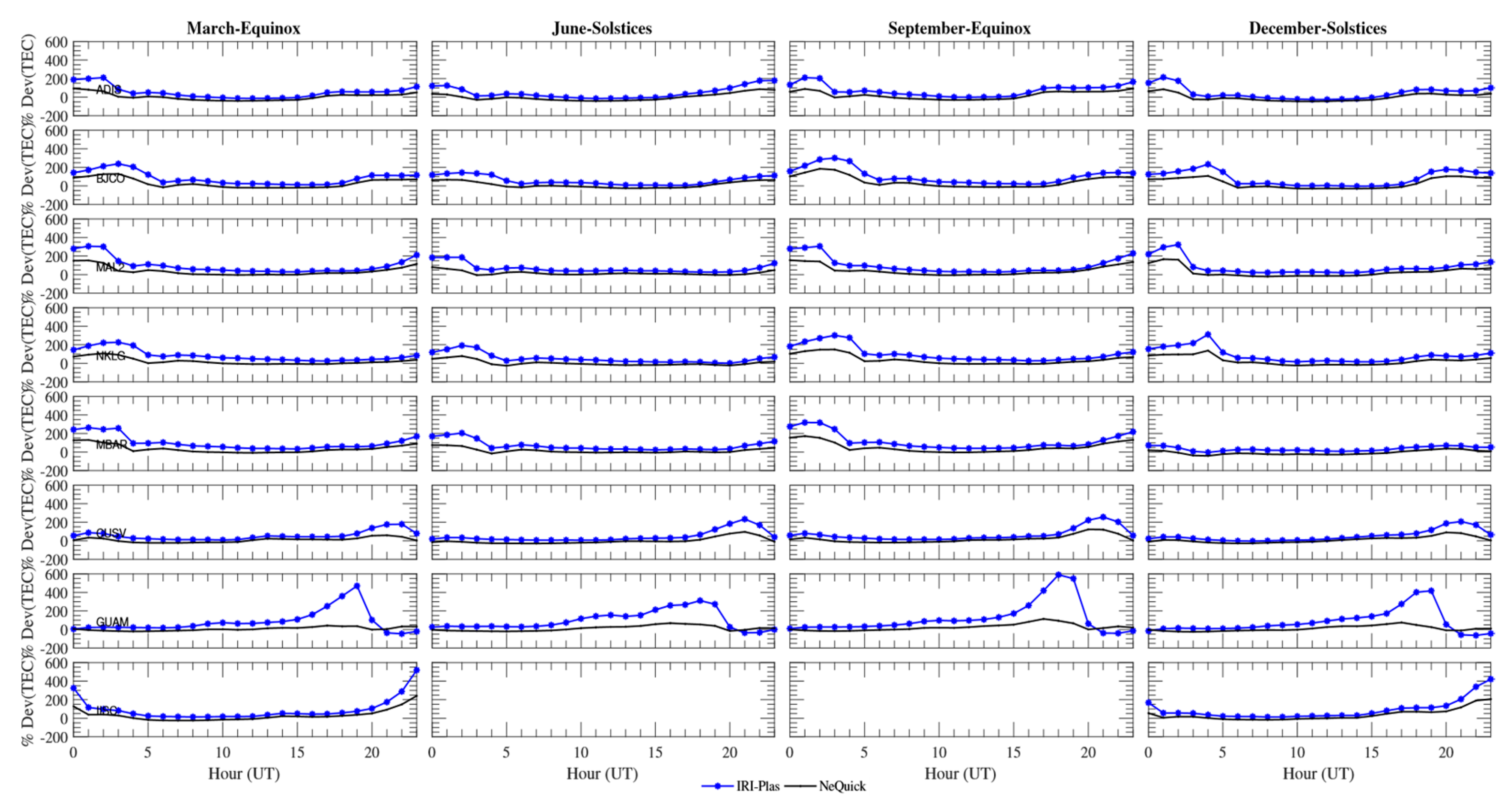
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Budden, K.G. The Theory of Radio Waves of Low Power in the Ionosphere and Magnetosphere; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Bhuyan, P.; Borah, R.R. TEC derived from GPS network in India and comparison with the IRI. Adv. Space Res. 2007, 39, 830–840. [Google Scholar] [CrossRef]
- Bilitza, D.; Reinisch, B. International Reference Ionosphere 2007: Improvements and new parameters. Adv. Space Res. 2008, 42, 599–609. [Google Scholar] [CrossRef]
- Maltseva, O.A.; Zhbankov, G.A.; Mozhaeva, N.S. Advantages of the new model of IRI (IRI-Plas) to simulate the ionospheric electron density: Case of the European area. Adv. Radio Sci. 2013, 11, 307–311. [Google Scholar] [CrossRef] [Green Version]
- Ezquer, R.; Scidá, L.; Orué, Y.M.; Nava, B.; Cabrera, M.; Brunini, C. NeQuick 2 and IRI Plas VTEC predictions for low latitude and South American sector. Adv. Space Res. 2018, 61, 1803–1818. [Google Scholar] [CrossRef]
- Radicella, S.; Leitinger, R. The evolution of the DGR approach to model electron density profiles. Adv. Space Res. 2001, 27, 35–40. [Google Scholar] [CrossRef]
- Nava, B.; Coïsson, P.; Radicella, S. A new version of the NeQuick ionosphere electron density model. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Hochegger, G.; Nava, B.; Radicella, S.; Leitinger, R. A family of ionospheric models for different uses. Phys. Chem. Earth Part C Sol. Terr. Planet. Sci. 2000, 25, 307–310. [Google Scholar] [CrossRef]
- Jodogne, J.-C.; Nebdi, H.; Warnant, R. GPS TEC and ITEC from digisonde data compared with NEQUICK model. Adv. Radio Sci. 2005, 2, 269–273. [Google Scholar] [CrossRef]
- Bidaine, B.; Warnant, R. Assessment of the NeQuick model at mid-latitudes using GNSS TEC and ionosonde data. Adv. Space Res. 2010, 45, 1122–1128. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Yuan, Y.; Li, Z.; Li, Y.; Huo, X.; Li, M. An examination of the Galileo NeQuick model: Comparison with GPS and JASON TEC. GPS Solut. 2017, 21, 605–615. [Google Scholar] [CrossRef]
- Di Giovanni, G.; Radicella, S. An analytical model of the electron density profile in the ionosphere. Adv. Space Res. 1990, 10, 27–30. [Google Scholar] [CrossRef]
- Radicella, S.M.; Zhang, M.L. The improved DGR analytical model of electron density height profile and total electron content in the ionosphere. Ann. Geophys. 1995, 38, 35–41. [Google Scholar] [CrossRef]
- Leitinger, R.; Zhang, M.L.; Radicella, S.M. An improved bottomside for the ionospheric electron density model NeQuick. Ann. Geophys. 2009, 48, 525–534. [Google Scholar] [CrossRef]
- Coïsson, P.; Radicella, S.; Leitinger, R.; Nava, B. Topside electron density in IRI and NeQuick: Features and limitations. Adv. Space Res. 2006, 37, 937–942. [Google Scholar] [CrossRef]
- Nava, B.; Radicella, S.M. The NeQuick model: Characteristics and uses. In Proceedings of the IGS Workshop, Pasadena, CA, USA, 23–27 June 2014; pp. 23–27. [Google Scholar]
- Chauhan, V.; Singh, O. A morphological study of GPS-TEC data at Agra and their comparison with the IRI model. Adv. Space Res. 2010, 46, 280–290. [Google Scholar] [CrossRef]
- Kenpankho, P.; Supnithi, P.; Nagatsuma, T. Comparison of observed TEC values with IRI-2007 TEC and IRI-2007 TEC with optional foF2 measurements predictions at an equatorial region, Chumphon, Thailand. Adv. Space Res. 2013, 52, 1820–1826. [Google Scholar] [CrossRef]
- Adebiyi, S.; Adimula, I.; Oladipo, O. Characterisation of GPS-TEC in the African equatorial and low latitude region and the regional evaluation of the IRI model. J. Atmos. Sol.-Terr. Phys. 2016, 143–144, 53–70. [Google Scholar] [CrossRef]
- Adebiyi, S.J.; Adimula, I.A.; Oladipo, O.A.; Joshua, B.W. Assessment of IRI and IRI-Plas models over the African equatorial and low-latitude region. J. Geophys. Res. Space Phys. 2016, 121, 7287–7300. [Google Scholar] [CrossRef] [Green Version]
- Okoh, D.; Sylvester, O.; Gopi, S.; Shuanggen, J.; Babtunde, R.; Bruno, N.; Jean, U. Assessment of the NeQuick-2 and IRI-Plas (2017) models using global and long-term GNSS measurements. J. Atmos. Sol.-Terr. Phys. 2018, 170, 1–10. [Google Scholar] [CrossRef]
- Zakharenkova, I.; Cherniak, I.; Krankowski, A.; Shagimuratov, I. Vertical TEC representation by IRI 2012 and IRI Plas models for European midlatitudes. Adv. Space Res. 2015, 55, 2070–2076. [Google Scholar] [CrossRef]
- Kumar, S.; Tan, E.L.; Razul, S.G.; See, C.M.S.; Siingh, D. Validation of the IRI-2012 model with GPS-based ground observation over a low-latitude Singapore station. Earth Planets Space 2014, 66, 17. [Google Scholar] [CrossRef] [Green Version]
- Tariku, Y.A. TEC prediction performance of IRI-2012 model during a very low and a high solar activity phase over equatorial regions, Uganda. J. Geophys. Res. Space Phys. 2015, 120, 5973–5982. [Google Scholar] [CrossRef]
- Venkatesh, K.; Fagundes, P.R.; Seemala, G.K.; de Jesus, R.; de Abreu, A.J.; Pillat, V.G. On the performance of the IRI-2012 and NeQuick2 models during the increasing phase of the unusual 24th solar cycle in the Brazilian equatorial and low-latitude sectors. J. Geophys. Res. Space Phys. 2014, 119, 5087–5105. [Google Scholar] [CrossRef]
- Bolaji, O.; Oyeyemi, E.; Adewale, A.; Wu, Q.; Okoh, D.; Doherty, P.; Kaka, R.; Abbas, M.; Owolabi, C.; Jidele, P. Assessment of IRI-2012, NeQuick-2 and IRI-Plas 2015 models with observed equatorial ionization anomaly in Africa during 2009 sudden stratospheric warming event. J. Atmos. Sol.-Terr. Phys. 2017, 164, 203–214. [Google Scholar] [CrossRef]
- Lyon, A.J.; Thomas, L. The F2-region equatorial anomaly in the African, American and East Asia sectors during sunspot maximum. J. Atmos. Terr. Phys. 1963, 25, 373–386. [Google Scholar] [CrossRef]
- Gulyaeva, T.I.; Bilitza, D. Towards standard earth ionosphere and plasmasphere model. In Larsen; Nova Science Publishers: Hauppauge, NY, USA, 2012; pp. 1–39. [Google Scholar]
- Gulyaeva, T. Storm time behavior of topside scale height inferred from the ionosphere–plasmasphere model driven by the F2 layer peak and GPS-TEC observations. Adv. Space Res. 2011, 47, 913–920. [Google Scholar] [CrossRef]
- Gopi, S. Rinex GPS-TEC program, version 1.45. Satellite navig. Sci and tech for Africa. Presented at the Workshop, ICTP, Trieste, Italy, 23 March–9 April 2009. [Google Scholar]
- Seemala, G.; Valladares, C.E. Statistics of total electron content depletions observed over the South American continent for the year 2008. Radio Sci. 2011, 46, RS5019. [Google Scholar] [CrossRef]
- Oron, S.; D’ujanga, F.M.; Senyonga, T.J. Ionospheric TEC variations during the ascending solar activity phase at an equatorial station, Uganda. Indian J. Radio Space Phys. 2013, 42, 7–17. [Google Scholar]
- Rama Rao, P.V.S.R.; Krishna, S.G.; Niranjan, K.; Prasad, D.S.V.V.D. Temporal and spatial variations in TEC using simultaneous measurements from the Indian GPS network of receivers during the low solar activity period of 2004–2005. Ann. Geophys. 2006, 24, 3279–3292. [Google Scholar] [CrossRef]
- Akala, A.O.; Adeloye, A.B.; Somoye, E.O. Ionospheric foF2 variability over the Southeast Asian sector. J. Geophys. Res. Earth Surf. 2010, 115, 09329. [Google Scholar] [CrossRef] [Green Version]
- Okoh, D.; Eze, A.; Adedoja, O.; Okere, B.; Okeke, P.N. A comparison of IRI-TEC predictions with GPS-TEC measurements over Nsukka, Nigeria. Space Weather 2012, 10, S10002. [Google Scholar] [CrossRef]
- Lunt, N.; Kersley, L.; Bishop, G.J.; Mazzella, A.J. The contribution of the protonosphere to GPS total electron content: Experimental measurements. Radio Sci. 1999, 34, 1273–1280. [Google Scholar] [CrossRef] [Green Version]
- Balan, N.; Otsuka, Y.; Tsugawa, T.; Miyazaki, S.; Ogawa, T.; Shiokawa, K. Plasmaspheric electron content in the GPS ray paths over Japan under magnetically quiet conditions at high solar activity. Earth Planets Space 2002, 54, 71–79. [Google Scholar] [CrossRef] [Green Version]
- Klimenko, M.; Zakharenkova, I.; Cherniak, I. The global morphology of the plasmaspheric electron content during Northern winter 2009 based on GPS/COSMIC observation and GSM TIP model results. Adv. Space Res. 2015, 55, 2077–2085. [Google Scholar] [CrossRef]
- Srinivas, V.S.; Sarma, A.; Swamy, K.; Satyanarayana, K. Performance evaluation of IRI-2007 at equatorial latitudes and its Matlab version for GNSS applications. Adv. Space Res. 2013, 52, 1845–1858. [Google Scholar] [CrossRef]
- Yizengaw, E.; Moldwin, M.; Galvan, D.; Iijima, B.; Komjathy, A.; Mannucci, A. Global plasmaspheric TEC and its relative contribution to GPS TEC. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1541–1548. [Google Scholar] [CrossRef]
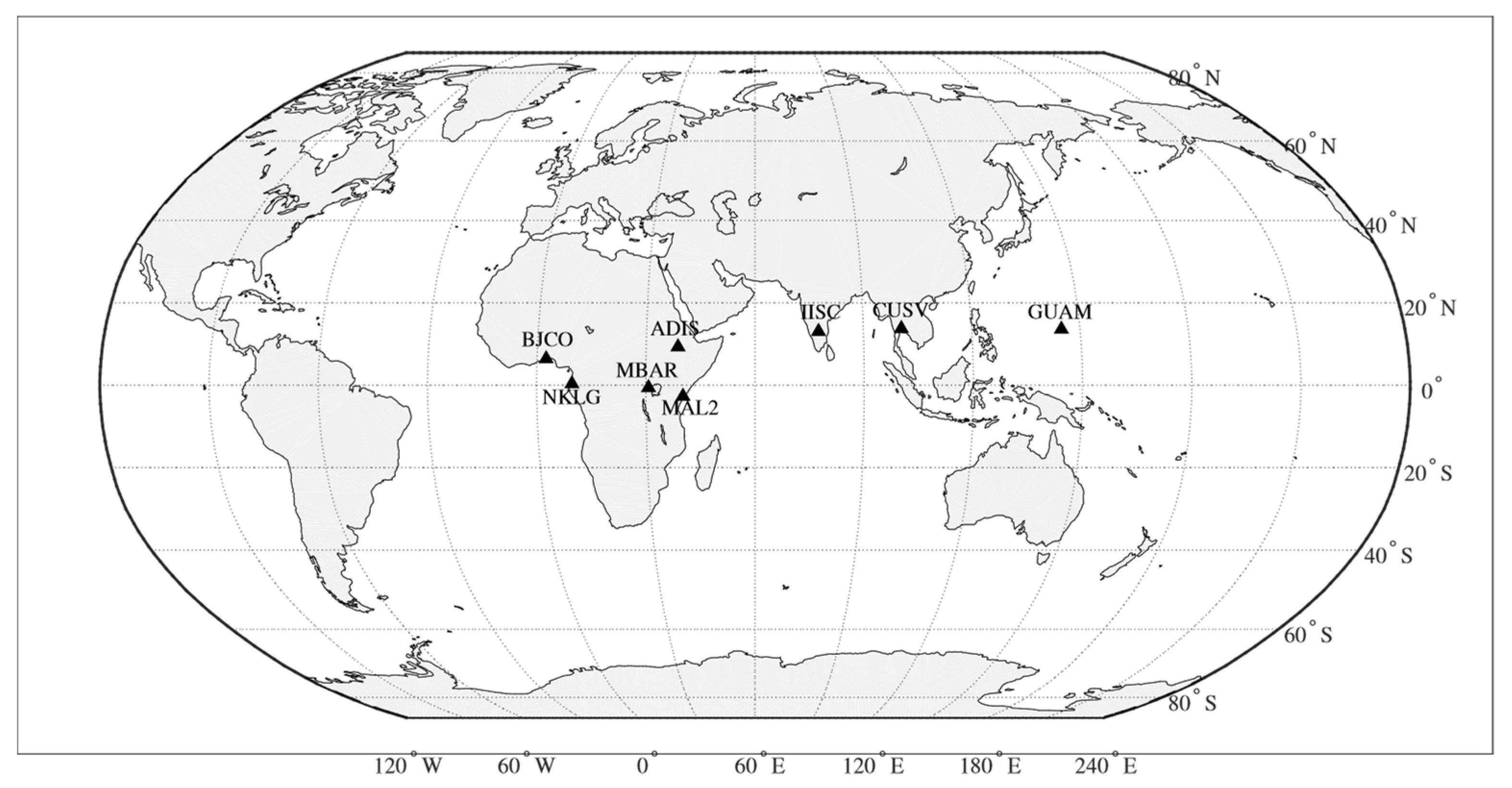

| Geographic Coordinates | Geomagnetic Coordinates | ||||
|---|---|---|---|---|---|
| Stations/Country | Station Code | ||||
| Malinda, Kenya | MAL2 | −2.7 | 40.19 | 6.41 | 111.92 |
| Mbarara, Uganda | MBAR | −0.6 | 30.74 | −10.22 | 102.36 |
| Librevile, Gabon | NKLG | 0.35 | 9.7 | −8.01 | 81.08 |
| Cotonou, Benin | BJCO | 6.4 | 2.5 | −3.07 | 74.59 |
| Addis Ababa, Ethiopia | ADIS | 9.3 | 38.76 | 0.16 | 110.46 |
| Bangalore, India | IISC | 13.02 | 77.57 | 4.49 | 150.93 |
| Dodedo, Guam | GUAM | 13.58 | 144.86 | 5.75 | −143.51 |
| Patumwen, Thailand | CUSV | 13.73 | 100.53 | 4.02 | 173.33 |
| Year | Station | Seasons | IRI-Plas | NeQuick-2 | Year | Station | Seasons | IRI-Plas | NeQuick-2 |
|---|---|---|---|---|---|---|---|---|---|
| 2013 | MAL2 | MAREQUI | 17.07 a | 19.12 | 2014 | MAL2 | MAREQUI | 9.56 | 9.97 |
| JUNSOLS | 11.91 | 4.79 | JUNSOLS | 17.4 | 8.7 | ||||
| SEPEQUI | 16.43 | 7.51 | SEPEQUI | 13.9 | 7.51 | ||||
| DECSOLS | 13.48 | 7.04 | DECSOLS | 12.07 | 7.71 | ||||
| MBAR | MAREQUI | 19.12 | 6.29 | MBAR | MAREQUI | 12.2 | 10.37 | ||
| JUNSOLS | 12.29 | 4.21 | JUNSOLS | 17.99 | 7.85 | ||||
| SEPEQUI | 29.59 | 9.24 | SEPEQUI | 18.49 | 8.59 | ||||
| DECSOLS | 17.14 | 10.26 | DECSOLS | 15.02 | 9.07 | ||||
| NKLG | MAREQUI | 17.92 | 5.46 | NKLG | MAREQUI | 11.06 | 11.33 | ||
| JUNSOLS | 10.44 | 5.23 | JUNSOLS | 16.59 | 5.86 | ||||
| SEPEQUI | 18.97 | 7.47 | SEPEQUI | 16.21 | 8.37 | ||||
| DECSOLS | 16.24 | 8.23 | DECSOLS | 13.84 | 8.34 | ||||
| BJCO | MAREQUI | 13.36 | 8.27 | BJCO | MAREQUI | 12.67 | 14.22 | ||
| JUNSOLS | 9.33 | 6.55 | JUNSOLS | 13.94 | 7.11 | ||||
| SEPEQUI | 16.05 | 8.45 | SEPEQUI | 14.4 | 10.38 | ||||
| DECSOLS | 15.32 | 10.98 | DECSOLS | 12.68 | 11.4 | ||||
| ADIS | MAREQUI | 8.68 | 11.83 | ADIS | MAREQUI | 12.44 | 19.18 | ||
| JUNSOLS | 6.94 | 10.06 | JUNSOLS | 9.16 | 7.93 | ||||
| SEPEQUI | 11.42 | 8.55 | SEPEQUI | 10.4 | 12.19 | ||||
| DECSOLS | 9.4 | 14.22 | DECSOLS | 10.21 | 16.04 | ||||
| IISC | MAREQUI | nan | nan | IISC | MAREQUI | nan | 10.85 | ||
| JUNSOLS | nan | nan | JUNSOLS | nan | 12.67 | ||||
| SEPEQUI | nan | nan | SEPEQUI | nan | nan | ||||
| DECSOLS | 8.58 | 5.57 | DECSOLS | 8.11 | 13.2 | ||||
| GUAM | MAREQUI | 14.15 | 5.08 | GUAM | MAREQUI | 13.26 | 11.97 | ||
| JUNSOLS | 14.46 | 4.3 | JUNSOLS | 18.69 | 5.77 | ||||
| SEPEQUI | 18.21 | 6.4 | SEPEQUI | 15.39 | 8.22 | ||||
| DECSOLS | 12.76 | 2.98 | DECSOLS | 11.29 | 9.49 | ||||
| CUSV | MAREQUI | 10.98 | 6.41 | CUSV | MAREQUI | 8.89 | 15.65 | ||
| JUNSOLS | 6.48 | 7.37 | JUNSOLS | 13.99 | 5.36 | ||||
| SEPEQUI | 11.72 | 6.15 | SEPEQUI | 9.45 | 10.66 | ||||
| DECSOLS | 7.94 | 7.03 | DECSOLS | 7.59 | 11.5 |
| Year | Station | Seasons | IRI-Plas | NeQuick-2 | Year | Station | Seasons | IRI-Plas | NeQuick-2 |
|---|---|---|---|---|---|---|---|---|---|
| 2013 | MAL2 | MAREQUI | 35.23 | 17.74 | 2014 | MAL2 | MAREQUI | 17.69 | 23.69 |
| JUNSOLS | 33.18 | 17.51 | JUNSOLS | 42.57 | 27.34 | ||||
| SEPEQUI | 34.75 | 20.37 | SEPEQUI | 29.48 | 20.55 | ||||
| DECSOLS | 30.09 | 21.39 | DECSOLS | 26.64 | 23.68 | ||||
| MBAR | MAREQUI | 37.06 | 19.22 | MBAR | MAREQUI | 21.36 | 24.03 | ||
| JUNSOLS | 30.93 | 14.19 | JUNSOLS | 40.13 | 23.18 | ||||
| SEPEQUI | 39.69 | 23.79 | SEPEQUI | 35.44 | 22.47 | ||||
| DECSOLS | 28.57 | 41.37 | DECSOLS | 31.17 | 27.07 | ||||
| NKLG | MAREQUI | 34.29 | 15.16 | NKLG | MAREQUI | 18.94 | 26.4 | ||
| JUNSOLS | 25.45 | 17.52 | JUNSOLS | 35.29 | 17.03 | ||||
| SEPEQUI | 36.23 | 19.81 | SEPEQUI | 30.49 | 22.11 | ||||
| DECSOLS | 33.06 | 22.84 | DECSOLS | 27.43 | 23.42 | ||||
| BJCO | MAREQUI | 36.95 | 27.89 | BJCO | MAREQUI | 27.39 | 40.67 | ||
| JUNSOLS | 24.67 | 23.44 | JUNSOLS | 32.68 | 21.71 | ||||
| SEPEQUI | 37.11 | 26.72 | SEPEQUI | 32.74 | 32.88 | ||||
| DECSOLS | 35.78 | 34.41 | DECSOLS | 31.03 | 38.23 | ||||
| ADIS | MAREQUI | 22.13 | 42.63 | ADIS | MAREQUI | 29.07 | 59.04 | ||
| JUNSOLS | 21.23 | 42.94 | JUNSOLS | 25.46 | 29.62 | ||||
| SEPEQUI | 28.46 | 29.07 | SEPEQUI | 25.32 | 41.56 | ||||
| DECSOLS | 26.11 | 54.3 | DECSOLS | 23.32 | 60.87 | ||||
| IISC | MAREQUI | 27.37 | 22.38 | IISC | MAREQUI | 22.99 | 39.81 | ||
| JUNSOLS | nan | nan | JUNSOLS | 31.62 | 22.94 | ||||
| SEPEQUI | nan | nan | SEPEQUI | 22.63 | 29.41 | ||||
| DECSOLS | 27.76 | 23.72 | DECSOLS | 20.17 | 35.46 | ||||
| GUAM | MAREQUI | 32.64 | 17.74 | GUAM | MAREQUI | 27.44 | 33.11 | ||
| JUNSOLS | 39.31 | 18.67 | JUNSOLS | 44.89 | 21.35 | ||||
| SEPEQUI | 39.57 | 20.26 | SEPEQUI | 33.09 | 25.25 | ||||
| DECSOLS | 31.29 | 19.6 | DECSOLS | 27.27 | 30.62 | ||||
| CUSV | MAREQUI | 25.85 | 20.7 | CUSV | MAREQUI | 19.99 | 44.58 | ||
| JUNSOLS | 17.98 | 28.44 | JUNSOLS | 33.89 | 18.07 | ||||
| SEPEQUI | 26.22 | 18.85 | SEPEQUI | 20.93 | 32.07 | ||||
| DECSOLS | 19.89 | 22.3 | DECSOLS | 18.57 | 36.22 |
| Year | Station | IRI-Plas | NeQuick-2 | Year | Station | IRI-Plas | NeQuick-2 |
|---|---|---|---|---|---|---|---|
| 2013 | MAL2 | 33.31 | 19.25 | 2014 | MAL2 | 29.09 | 37.43 |
| MBAR | 34.06 | 24.64 | MBAR | 32.03 | 24.19 | ||
| NKLG | 32.26 | 18.83 | NKLG | 28.04 | 22.24 | ||
| BJCO | 33.63 | 28.12 | BJCO | 30.96 | 33.37 | ||
| ADIS | 24.5 | 42.24 | ADIS | 25.8 | 47.77 | ||
| IISC | 27.56 | 23.05 | IISC | 24.35 | 31.91 | ||
| GUAM | 35.7 | 19.07 | GUAM | 33.17 | 27.58 | ||
| CUSV | 22.49 | 22.57 | CUSV | 23.35 | 32.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iluore, K.; Lu, J.; Okeke, F.; Ozegin, K.O. Performance of NeQuick-2 and IRI-Plas 2017 Models during Solar Maximum Years in 2013–2014 over Equatorial and Low Latitude Regions. Universe 2022, 8, 125. https://doi.org/10.3390/universe8020125
Iluore K, Lu J, Okeke F, Ozegin KO. Performance of NeQuick-2 and IRI-Plas 2017 Models during Solar Maximum Years in 2013–2014 over Equatorial and Low Latitude Regions. Universe. 2022; 8(2):125. https://doi.org/10.3390/universe8020125
Chicago/Turabian StyleIluore, Kenneth, Jianyong Lu, Francisca Okeke, and Kesyton Oyamenda Ozegin. 2022. "Performance of NeQuick-2 and IRI-Plas 2017 Models during Solar Maximum Years in 2013–2014 over Equatorial and Low Latitude Regions" Universe 8, no. 2: 125. https://doi.org/10.3390/universe8020125
APA StyleIluore, K., Lu, J., Okeke, F., & Ozegin, K. O. (2022). Performance of NeQuick-2 and IRI-Plas 2017 Models during Solar Maximum Years in 2013–2014 over Equatorial and Low Latitude Regions. Universe, 8(2), 125. https://doi.org/10.3390/universe8020125







