Classification of Circular Equatorial Orbits around Regular Rotating Black Holes and Solitons with the de Sitter/ Phantom Interiors
Abstract
:1. Introduction
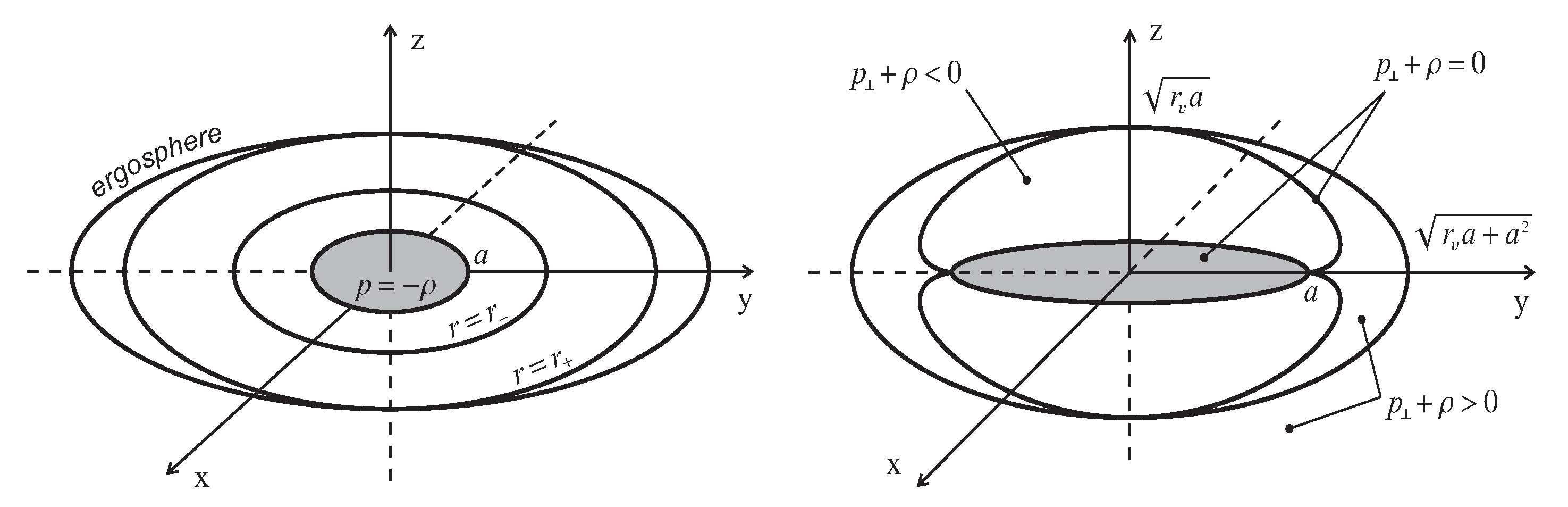
2. Structure of the de Sitter–Kerr Compact Objects
3. Basic Equations
4. Generic Properties of Orbits
4.1. Photon Orbits
4.2. Particle Orbits
5. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | Non-singular compact Kerr–Newman–de Sitter instantons are presented and comprehensively studied in [64]. |
References
- Iso, S.; Umetsu, H.; Wilczek, F. Anomalies, Hawking radiations, and regularity in rotating black holes. Phys. Rev. D 2006, 74, 044017. [Google Scholar] [CrossRef] [Green Version]
- Caravelli, F.; Modesto, L. Spinning loop black holes. Class. Quant. Grav. 2010, 27, 245022. [Google Scholar] [CrossRef]
- Bambi, C.; Modesto, L. Rotating regular black holes. Phys. Lett. B 2013, 721, 329–334. [Google Scholar] [CrossRef] [Green Version]
- Balart, L.; Vagenas, E.C. Regular black hole metrics and the weak energy condition. Phys. Lett. B 2014, 730, 14–17. [Google Scholar] [CrossRef] [Green Version]
- Toshmatov, B.; Ahmedov, B.; Abdujabbarov, A.; Stuchlik, Z. Rotating regular black hole solution. Phys. Rev. D 2014, 89, 104017. [Google Scholar] [CrossRef] [Green Version]
- Neves, J.C.S.; Saa, A. Regular rotating black holes and the weak energy condition. Phys. Lett. B 2014, 734, 44–48. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.G. A nonsingular rotating black hole. Eur. Phys. J. C 2015, 75, 532. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, S. Hawking fluxes and Anomalies in Rotating Regular Black Holes with a Time-Delay. Class. Quant. Grav. 2016, 33, 225016. [Google Scholar] [CrossRef] [Green Version]
- de Lorenzo, T.; Giusti, A.; Speziale, S. Non-singular rotating black hole with a time delay in the center. Gen. Rel. Grav. 2016, 48, 31. [Google Scholar] [CrossRef] [Green Version]
- Torres, R.; Fayos, F. On regular rotating black holes. Gen. Rel. Grav. 2017, 49, 2. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Basic Generic Properties of Regular Rotating Black Holes and Solitons. Adv. Math. Phys. 2017, 2017, 1035381. [Google Scholar] [CrossRef] [Green Version]
- Newman, E.T.; Janis, A.J. Note on the Kerr Spinning Particle Metric. J. Math. Phys. 1965, 6, 915–917. [Google Scholar] [CrossRef]
- Gürses, M.; Gürsey, F. Lorentz covariant treatment of the Kerr-Schild geometry. J. Math. Phys. 1975, 16, 2385–2390. [Google Scholar] [CrossRef] [Green Version]
- Kerr, R.P.; Schild, A. Some algebraically degenerate solutions of Einstein’s gravitational field equations. Proc. Symp. Appl. Math. 1965, 17, 199. [Google Scholar]
- Burinskii, A. The Kerr theorem, Kerr-Schild formalism and multi-particle Kerr-Schild solutions. Grav. Cosmol. 2006, 12, 119–125. [Google Scholar]
- Nicolini, P.; Smailagic, A.; Spalucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. B 2006, 632, 547–551. [Google Scholar] [CrossRef] [Green Version]
- Ansoldi, S.; Nicolini, P.; Smailagic, A. Noncommutative geometry inspired charged black holes. Phys. Lett. B 2007, 645, 261–266. [Google Scholar] [CrossRef] [Green Version]
- Modesto, L.; Nicolini, P. Charged rotating noncommutative black holes. Phys. Rev. D 2010, 82, 104035. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Galaktionov, E. Vacuum dark fluid. Phys. Lett. B 2007, 645, 358–364. [Google Scholar] [CrossRef] [Green Version]
- Burinskii, A.; Elizalde, E.; Hildebrandt, S.R.; Magli, G. Regular sources of the Kerr-Schild class for rotating and nonrotating black hole solutions. Phys. Rev. D 2002, 65, 064039. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. Spinning self-gravitating electrovacuum soliton. Phys. Lett. B 2006, 639, 368–372. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I.; Galaktionov, E. Regular rotating de Sitter-Kerr black holes and solitons. Class. Quant. Grav. 2016, 33, 145010. [Google Scholar] [CrossRef]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Rel. Grav. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Dymnikova, I. The algebraic structure of a cosmological term in spherically symmetric solutions. Phys. Lett. B 2000, 472, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. The cosmological term as a source of mass. Class. Quant. Grav. 2002, 19, 725–740. [Google Scholar] [CrossRef] [Green Version]
- Dymnikova, I. Spherically symmetric space-time with the regular de Sitter center. Int. J. Mod. Phys. D 2003, 12, 1015–1034. [Google Scholar] [CrossRef] [Green Version]
- Coleman, S. Classical lumps and their quantum descendants. In New Phenomena in Subnuclear Physics; Zichichi, A., Ed.; Plenum: New York, NY, USA, 1977; p. 297. [Google Scholar]
- Cardoso, V.; Crispino, L.C.B.; Macedo, C.F.B.; Okawa, H.; Pani, P. Light rings as observational evidence for event horizons: Long-lived modes, ergoregions and nonlinear instabilities of ultracompact objects. Phys. Rev. D 2014, 90, 044069. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R. Stationary Black Holes and Light Rings. Phys. Rev. Lett. 2020, 124, 181101. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Rubin, S.G. Black Holes, Cosmology and Extra Dimensions; World Scientific: Singapore, 2013. [Google Scholar]
- Gibbons, G.W. Phantom Matter and the Cosmological Constant; DAMTP-2003-19; Cambridge University: Cambridge, UK, 2003. [Google Scholar]
- Dymnikova, I. Mass, Spacetime Symmetry, de Sitter Vacuum, and the Higgs Mechanism. Symmetry 2020, 12, 634. [Google Scholar] [CrossRef] [Green Version]
- Grib, A.A.; Pavlov, Y.V.; Piattella, O.F. On collisions with unlimited energies in the vicinity of Kerr and Schwarzschild black hole horizons. Grav. Cosmol. 2012, 18, 70–75. [Google Scholar] [CrossRef] [Green Version]
- Grib, A.A.; Pavlov, Y.V.; Vertogradov, V.D. Geodesics with negative energy in the ergosphere of rotating black holes. Mod. Phys. Lett. A 2014, 29, 1450110. [Google Scholar] [CrossRef]
- Banados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef] [Green Version]
- Jacobson, T.; Sotiriou, T.P. Spinning Black Holes as Particle Accelerators. Phys. Rev. Lett. 2010, 104, 021101. [Google Scholar] [CrossRef] [Green Version]
- Zaslawski, O.B. Energy extraction from extremal charged black holes due to the Banados-Silk-West effect. Phys. Rev. D 2012, 86, 124039. [Google Scholar] [CrossRef] [Green Version]
- Harada, T.; Kimura, M. Black holes as particle accelerators: A brief review. Class. Quant. Grav. 2014, 31, 243001. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Sheoran, P.; Amir, M. Rotating Ayón-Beato-García black hole as a particle accelerator. Phys. Rev. D 2014, 90, 103006. [Google Scholar] [CrossRef] [Green Version]
- Patil, M.; Joshi, P.S. Naked singularities as particle accelerators. Phys. Rev. D 2010, 82, 104049. [Google Scholar] [CrossRef] [Green Version]
- Patil, M.; Joshi, P.S. Kerr Naked Singularities as Particle Accelerators. Class. Quant. Grav. 2011, 28, 235012. [Google Scholar] [CrossRef]
- Patil, M.; Joshi, P.S.; Malafaria, D. Naked singularities as particle accelerators. II. Phys. Rev. D 2011, 83, 064007. [Google Scholar] [CrossRef] [Green Version]
- Patil, M.; Joshi, P.S.; Kimura, M.; Nakao, K.I. Acceleration of particles and shells by Reissner-Nordström naked singularities. Phys. Rev. D 2012, 86, 084023. [Google Scholar] [CrossRef] [Green Version]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular motion in Kerr spacetime. Phys. Rev. D 2011, 84, 044030. [Google Scholar] [CrossRef] [Green Version]
- Newman, E.T.; Cough, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 1965, 6, 918. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular orbits of neutral test particles in the Kerr-Newman spacetime. Phys. Rev. D 2013, 88, 024042. [Google Scholar] [CrossRef] [Green Version]
- Ulbricht, S.; Meinel, R. A note on circular geodesics in the equatorial plane of an extreme Kerr-Newman black hole. Class. Quant. Grav. 2015, 32, 147001. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.U.; Ren, J. Circular geodesics in Kerr-Newman-Kasuya black hole. AIP Conf. Proc. 2021, 2319, 040005. [Google Scholar]
- Toshmatov, B.; Abdujabbarov, A.; Ahmedov, B.; Stuchlik, Z. Particle motion and Penrose processes around rotating regular black hole. Astroph. Space Sci. 2015, 357, 41. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. Regular Black Hole in General Relativity Coupled to Nonlinear Electrodynamics. Phys. Rev. Lett. 1998, 80, 5056. [Google Scholar] [CrossRef] [Green Version]
- Toshmatov, B.; Stuchlik, Z.; Ahmedov, B. Generic rotating regular black holes in general relativity coupled to nonlinear electrodynamics. Phys. Rev. D 2017, 95, 084037. [Google Scholar] [CrossRef] [Green Version]
- Chiba, T.; Kimura, M. A note on geodesics in the Hayward metric. Prog. Theor. Exp. Phys. 2017, 2017, 043E01. [Google Scholar] [CrossRef] [Green Version]
- Bautista-Olvera, B.; Degollado, J.C.; German, G. Geodesic structure of a rotating regular black hole. arXiv 2019, arXiv:1908.01886. [Google Scholar]
- Johannsen, T. Photon rings around Kerr and Kerr-like black holes. Astrophys. J. 2013, 777, 170. [Google Scholar] [CrossRef] [Green Version]
- Mokdad, M. Reissner-Nordstrøm-de Sitter Manifold: Photon Sphere and Maximal Analytic Extension. arXiv 2017, arXiv:1701.06982. [Google Scholar] [CrossRef] [Green Version]
- Dolan, S.R.; Shipley, J.O. Stable photon orbits in stationary axisymmetric electrovacuum spacetimes. Phys. Rev. D 2016, 94, 044038. [Google Scholar] [CrossRef] [Green Version]
- Hod, S. On the number of light rings in curved spacetimes of ultra-compact objects. Phys. Lett. B 2018, 776, 1–4. [Google Scholar] [CrossRef]
- Hod, S. Analytic study of self-gravitating polytropic spheres with light rings. Eur. Phys. J. C 2018, 78, 417. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Berti, E.; Herdeiro, C.A.R. Light-Ring Stability for Ultracompact Objects. Phys. Rev. Lett. 2017, 119, 251102. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Gao, S. Universal properties of light rings for stationary axisymmetric spacetimes. Phys. Rev. D 2021, 103, 104031. [Google Scholar] [CrossRef]
- Ghosh, R.; Sarkar, S. Light rings of stationary spacetimes. Phys. Rev. D 2021, 104, 044019. [Google Scholar] [CrossRef]
- Dymnikova, I.; Kraav, K. Identification of a regular black hole by its shadow. Universe 2019, 5, 163. [Google Scholar] [CrossRef] [Green Version]
- Chrusciel, P.T.; Hörzinger, M. Compact singularity-free Kerr–Newman–de Sitter instantons. Phys. Rev. D 2017, 95, 086012. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon Press: Oxford, UK, 1983. [Google Scholar]
- Dymnikova, I.; Galaktionov, E. Regular rotating electrically charged black holes and solitons in nonlinear electrodynamics minimally coupled to gravity. Class. Quant. Grav. 2015, 32, 165015. [Google Scholar] [CrossRef]
- Dymnikova, I. The Fundamental Roles of the de Sitter Vacuum. Universe 2020, 6, 101. [Google Scholar] [CrossRef]
- Dymnikova, I. Regular electrically charged vacuum structures with de Sitter center in nonlinear electrodynamics coupled to general relativity. Class. Quant. Grav. 2004, 21, 4417. [Google Scholar] [CrossRef]
- Poisson, E.; Israel, W. Structure of the black hole nucleus. Class. Quant. Grav. 1988, 5, L201–L205. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Black holes as possible sources of closed and semiclosed worlds. Phys. Rev. D 1990, 41, 383–394. [Google Scholar] [CrossRef]
- Dymnikova, I. De Sitter-Schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529–540. [Google Scholar] [CrossRef]
- Dymnikova, I. Internal structure of nonsingular spherical black holes. In Internal Sructure of Black Holes and Spacetime Singularities; Burko, M., Ori, A., Eds.; Bristol In-t of Physics Pulishing: Bristol, TN, USA; Philadelphia, PA, USA; Annals of the Israel Physical Society 13: Jerusalem, Israel, 1997; pp. 422–440. [Google Scholar]
- Bonanno, A.; Reuter, M. Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. D 2006, 73, 083005. [Google Scholar] [CrossRef] [Green Version]
- Modesto, L.; Moffat, J.W.; Nicolini, P. Black holes in an ultraviolet complete quantum gravity. Phys. Lett. B 2011, 695, 397–400. [Google Scholar] [CrossRef] [Green Version]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the Galactic Center. Astrophys. J. Lett. bf 2000, 528, L13–L16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alberdi, A.; Gómez Fernández, J.L.; The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near the Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Övgün, A.; Sakallı, İ.; Saavedra, J. Shadow cast and deflection angle of Kerr-Newman-Kasuya spacetime. J. Cosmol. Astropart. Phys. 2018, 10, 041. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dymnikova, I.; Dobosz, A.; Sołtysek, B. Classification of Circular Equatorial Orbits around Regular Rotating Black Holes and Solitons with the de Sitter/ Phantom Interiors. Universe 2022, 8, 65. https://doi.org/10.3390/universe8020065
Dymnikova I, Dobosz A, Sołtysek B. Classification of Circular Equatorial Orbits around Regular Rotating Black Holes and Solitons with the de Sitter/ Phantom Interiors. Universe. 2022; 8(2):65. https://doi.org/10.3390/universe8020065
Chicago/Turabian StyleDymnikova, Irina, Anna Dobosz, and Bożena Sołtysek. 2022. "Classification of Circular Equatorial Orbits around Regular Rotating Black Holes and Solitons with the de Sitter/ Phantom Interiors" Universe 8, no. 2: 65. https://doi.org/10.3390/universe8020065
APA StyleDymnikova, I., Dobosz, A., & Sołtysek, B. (2022). Classification of Circular Equatorial Orbits around Regular Rotating Black Holes and Solitons with the de Sitter/ Phantom Interiors. Universe, 8(2), 65. https://doi.org/10.3390/universe8020065





