Onset of Electron Captures and Shallow Heating in Magnetars
Abstract
:1. Introduction
2. Equation of State of Magnetar Crusts
2.1. Main Equations
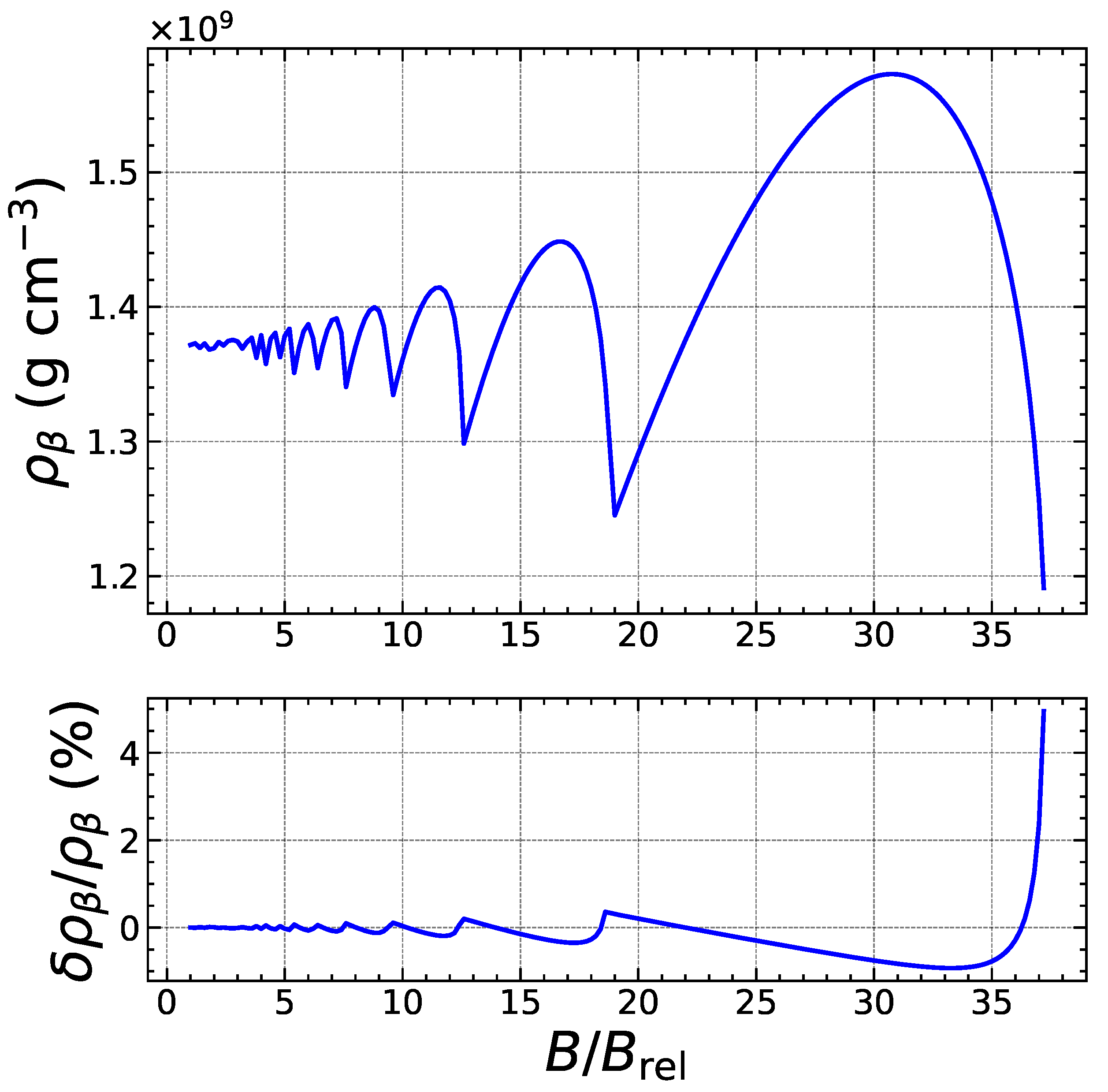
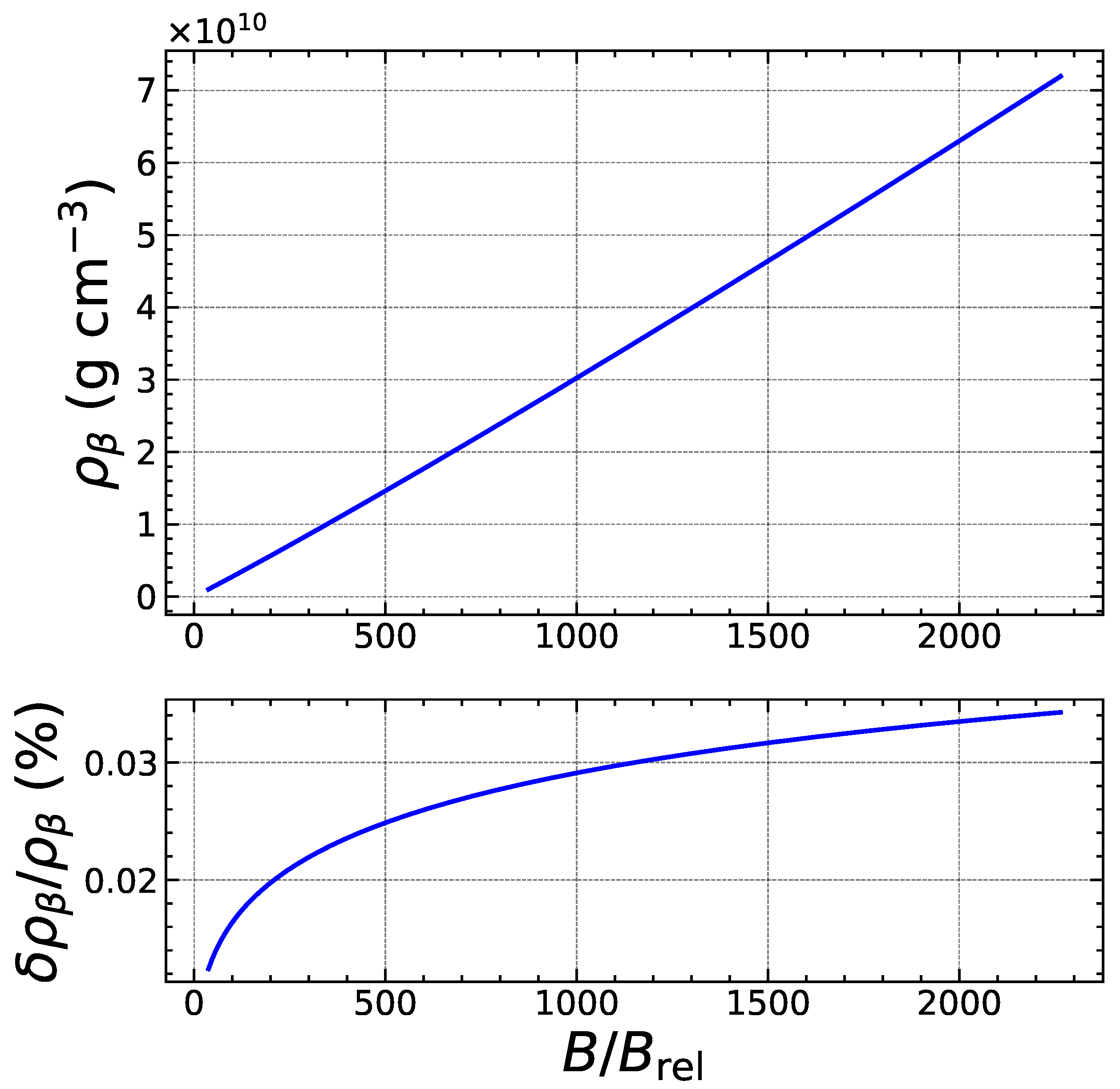
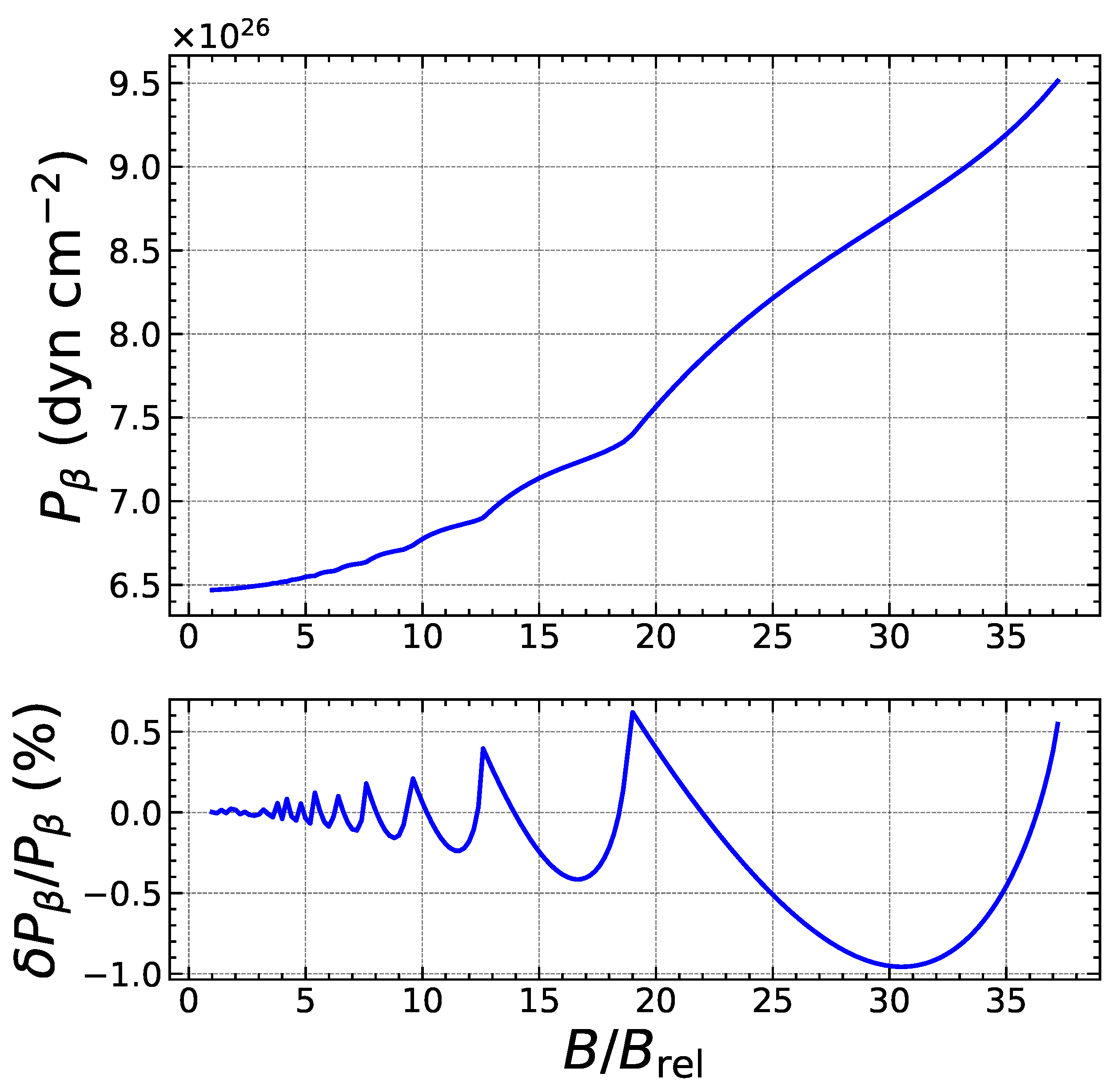
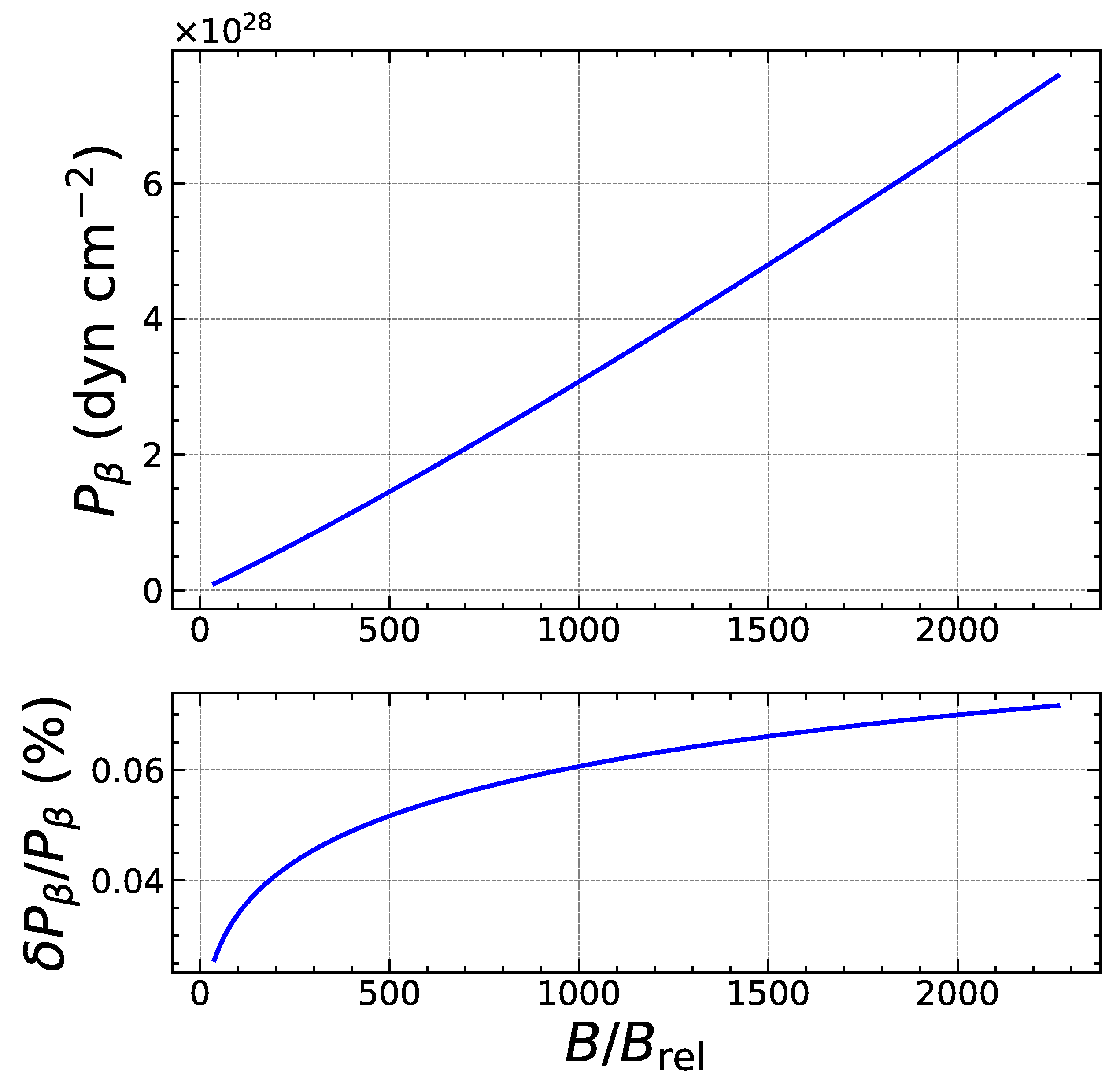
2.2. Weakly Quantizing Magnetic Field
2.3. Strongly Quantizing Magnetic Field
3. Initial Composition of Magnetar Crusts
3.1. Interface between Adjacent Crustal Layers
3.2. No Magnetic Field
3.3. Strongly Quantizing Magnetic Field
- and
- and
- and
3.4. Intermediate Magnetic Fields
4. Magnetic Field Decay and Electron Captures
4.1. Onset of Electron Captures
4.2. No Magnetic Field
4.3. Intermediate Magnetic Field
4.4. Strongly Quantizing Magnetic Field
4.5. Heat Released
4.6. Neutron Delayed Emission
5. Results and Discussions
5.1. Initial Composition of the Outer Crust
5.2. Heating
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notes
| 1 | http://www.astro.ulb.ac.be/bruslib/, accessed on 9 June 2022. |
| 2 | https://compose.obspm.fr, accessed on 9 June 2022. |
| 3 | https://www-nds.iaea.org/relnsd/NdsEnsdf/QueryForm.html, accessed on 9 June 2022. |
References
- Esposito, P.; Rea, N.; Israel, G.L. Magnetars: A Short Review and Some Sparse Considerations. In Astrophysics and Space Science Library; Belloni, T.M., Méndez, M., Zhang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 461, pp. 97–142. [Google Scholar] [CrossRef]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-Ray Bursts. Astrophys. J. Lett. 1992, 392, L9. [Google Scholar] [CrossRef]
- Olausen, S.A.; Kaspi, V.M. The McGill Magnetar Catalog. Astrophys. J. Suppl. 2014, 212, 6. [Google Scholar] [CrossRef]
- Viganò, D.; Rea, N.; Pons, J.A.; Perna, R.; Aguilera, D.N.; Miralles, J.A. Unifying the observational diversity of isolated neutron stars via magneto-thermal evolution models. Mon. Not. R. Astron. Soc. 2013, 434, 123–141. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Li, X. Magnetar Heating. Astrophys. J. 2016, 833, 261. [Google Scholar] [CrossRef]
- De Grandis, D.; Turolla, R.; Wood, T.S.; Zane, S.; Taverna, R.; Gourgouliatos, K.N. Three-dimensional Modeling of the Magnetothermal Evolution of Neutron Stars: Method and Test Cases. Astrophys. J. 2020, 903, 40. [Google Scholar] [CrossRef]
- Fantina, A.F.; De Ridder, S.; Chamel, N.; Gulminelli, F. Crystallization of the outer crust of a non-accreting neutron star. Astron. Astrophys. 2020, 633, A149. [Google Scholar] [CrossRef]
- Carreau, T.; Gulminelli, F.; Chamel, N.; Fantina, A.F.; Pearson, J.M. Crystallization of the inner crust of a neutron star and the influence of shell effects. Astron. Astrophys. 2020, 635, A84. [Google Scholar] [CrossRef]
- Kaminker, A.D.; Yakovlev, D.G.; Potekhin, A.Y.; Shibazaki, N.; Shternin, P.S.; Gnedin, O.Y. Magnetars as cooling neutron stars with internal heating. Mon. Not. R. Astron. Soc. 2006, 371, 477–483. [Google Scholar] [CrossRef]
- Kaminker, A.D.; Potekhin, A.Y.; Yakovlev, D.G.; Chabrier, G. Heating and cooling of magnetars with accreted envelopes. Mon. Not. R. Astron. Soc. 2009, 395, 2257–2267. [Google Scholar] [CrossRef]
- Cooper, R.L.; Kaplan, D.L. Magnetic Field-Decay-Induced Electron Captures: A Strong Heat Source in Magnetar Crusts. Astrophys. J. Lett. 2010, 708, L80–L83. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L. Non-equilibrium processes in the crust of an accreting neutron star. Astron. Astrophys. 1990, 227, 431–436. [Google Scholar]
- Chamel, N.; Fantina, A.F.; Suleiman, L.; Zdunik, J.L.; Haensel, P. Heating in Magnetar Crusts from Electron Captures. Universe 2021, 7, 193. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XIII. The 2012 atomic mass evaluation and the symmetry coefficient. Phys. Rev. C 2013, 88, 024308. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals—I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. II. Pasta phases in semiclassical approximation. Phys. Rev. C 2020, 101, 015802. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. III. Inclusion of microscopic corrections to pasta phases. Phys. Rev. C 2022, 105, 015803. [Google Scholar] [CrossRef]
- Mutafchieva, Y.D.; Chamel, N.; Stoyanov, Z.K.; Pearson, J.M.; Mihailov, L.M. Role of Landau-Rabi quantization of electron motion on the crust of magnetars within the nuclear energy density functional theory. Phys. Rev. C 2019, 99, 055805. [Google Scholar] [CrossRef]
- Rabi, I.I. Das freie Elektron im homogenen Magnetfeld nach der Diracschen Theorie. Z. Fur. Phys. 1928, 49, 507–511. [Google Scholar] [CrossRef]
- Landau, L. Diamagnetismus der Metalle. Z. Fur Phys. 1930, 64, 629–637. [Google Scholar] [CrossRef]
- Tiengo, A.; Esposito, P.; Mereghetti, S.; Turolla, R.; Nobili, L.; Gastaldello, F.; Götz, D.; Israel, G.L.; Rea, N.; Stella, L.; et al. A variable absorption feature in the X-ray spectrum of a magnetar. Nature 2013, 500, 312–314. [Google Scholar] [CrossRef]
- An, H.; Kaspi, V.M.; Beloborodov, A.M.; Kouveliotou, C.; Archibald, R.F.; Boggs, S.E.; Christensen, F.E.; Craig, W.W.; Gotthelf, E.V.; Grefenstette, B.W.; et al. NuSTAR Observations of X-Ray Bursts from the Magnetar 1E 1048.1-5937. Astrophys. J. 2014, 790, 60. [Google Scholar] [CrossRef]
- Uryū, K.; Yoshida, S.; Gourgoulhon, E.; Markakis, C.; Fujisawa, K.; Tsokaros, A.; Taniguchi, K.; Eriguchi, Y. New code for equilibriums and quasiequilibrium initial data of compact objects. IV. Rotating relativistic stars with mixed poloidal and toroidal magnetic fields. Phys. Rev. D 2019, 100, 123019. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F.; Zdunik, J.L.; Haensel, P. Neutron drip transition in accreting and nonaccreting neutron star crusts. Phys. Rev. C 2015, 91, 055803. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars. 1. Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Van Vleck, J.H. The Theory of Electric and Magnetic Susceptibilities; Oxford University Press: London, UK, 1932. [Google Scholar]
- Baiko, D.A. Coulomb crystals in the magnetic field. Phys. Rev. E 2009, 80, 046405. [Google Scholar] [CrossRef]
- Baiko, D.A.; Potekhin, A.Y.; Yakovlev, D.G. Thermodynamic functions of harmonic Coulomb crystals. Phys. Rev. E 2001, 64, 057402. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Chabrier, G. Equation of state for magnetized Coulomb plasmas. Astron. Astrophys. 2013, 550, A43. [Google Scholar] [CrossRef]
- Salpeter, E.E. Electrons Screening and Thermonuclear Reactions. Aust. J. Phys. 1954, 7, 373. [Google Scholar] [CrossRef]
- Dib, C.O.; Espinosa, O. The magnetized electron gas in terms of Hurwitz zeta functions. Nucl. Phys. B 2001, 612, 492–518. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F. Electron capture instability in magnetic and nonmagnetic white dwarfs. Phys. Rev. D 2015, 92, 023008. [Google Scholar] [CrossRef]
- Chamel, N. Analytical determination of the structure of the outer crust of a cold nonaccreted neutron star. Phys. Rev. C 2020, 101, 032801. [Google Scholar] [CrossRef]
- Chamel, N.; Stoyanov, Z.K. Analytical determination of the structure of the outer crust of a cold nonaccreted neutron star: Extension to strongly quantizing magnetic fields. Phys. Rev. C 2020, 101, 065802. [Google Scholar] [CrossRef]
- Chamel, N. Equilibrium Structure of the Outer Crust of a Cold Nonaccreted Neutron Star; Zenodo: Geneva, Switzerland, 2020. [Google Scholar] [CrossRef]
- Chamel, N.; Stoyanov, Z. Equilibrium Structure of the Outer Crust of a Magnetar; Zenodo: Geneva, Switzerland, 2020. [Google Scholar] [CrossRef]
- Pons, J.A.; Viganò, D. Magnetic, thermal and rotational evolution of isolated neutron stars. Living Rev. Comput. Astrophys. 2019, 5, 3. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F. Binary and ternary ionic compounds in the outer crust of a cold nonaccreting neutron star. Phys. Rev. C 2016, 94, 065802. [Google Scholar] [CrossRef]
- Peña Arteaga, D.; Grasso, M.; Khan, E.; Ring, P. Nuclear structure in strong magnetic fields: Nuclei in the crust of a magnetar. Phys. Rev. C 2011, 84, 045806. [Google Scholar] [CrossRef]
- Fantina, A.F.; Chamel, N.; Mutafchieva, Y.D.; Stoyanov, Z.K.; Mihailov, L.M.; Pavlov, R.L. Role of the symmetry energy on the neutron-drip transition in accreting and nonaccreting neutron stars. Phys. Rev. C 2016, 93, 015801. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.J.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Xu, Y.; Goriely, S.; Jorissen, A.; Chen, G.L.; Arnould, M. Databases and tools for nuclear astrophysics applications. BRUSsels Nuclear LIBrary (BRUSLIB), Nuclear Astrophysics Compilation of REactions II (NACRE II) and Nuclear NETwork GENerator (NETGEN). Astron. Astrophys. 2013, 549, A106. [Google Scholar] [CrossRef]
- Allard, V.; Chamel, N. 1S0 Pairing Gaps, Chemical Potentials and Entrainment Matrix in Superfluid Neutron-Star Cores for the Brussels-Montreal Functionals. Universe 2021, 7, 470. [Google Scholar] [CrossRef]
- Perot, L.; Chamel, N.; Sourie, A. Role of the symmetry energy and the neutron-matter stiffness on the tidal deformability of a neutron star with unified equations of state. Phys. Rev. C 2019, 100, 035801. [Google Scholar] [CrossRef]
- Chamel, N.; Fantina, A.F. Onset of Electron Captures and Shallow Heating in Magnetars [Data Set]; Zenodo: Geneva, Switzerland, 2022. [Google Scholar] [CrossRef]


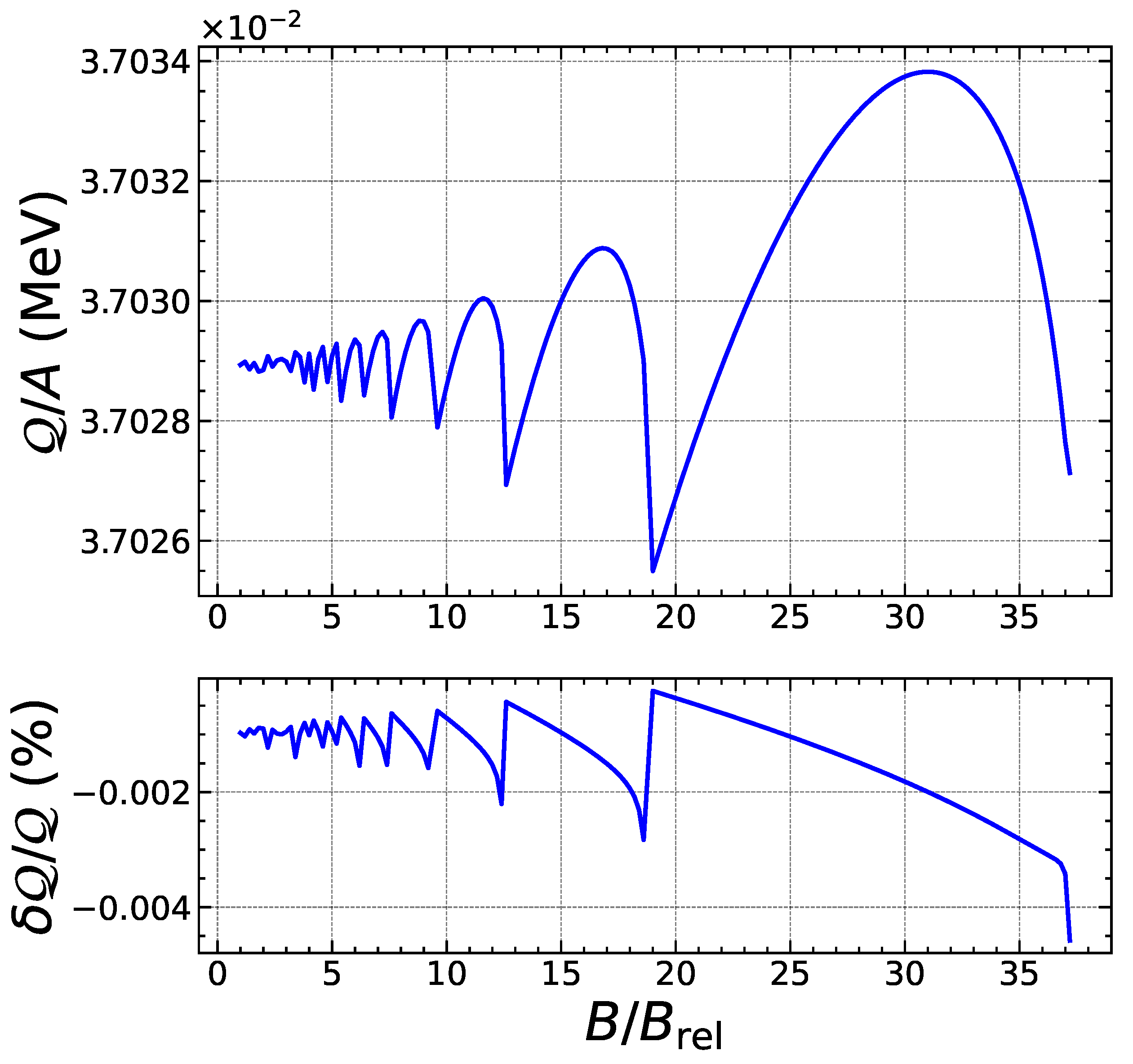
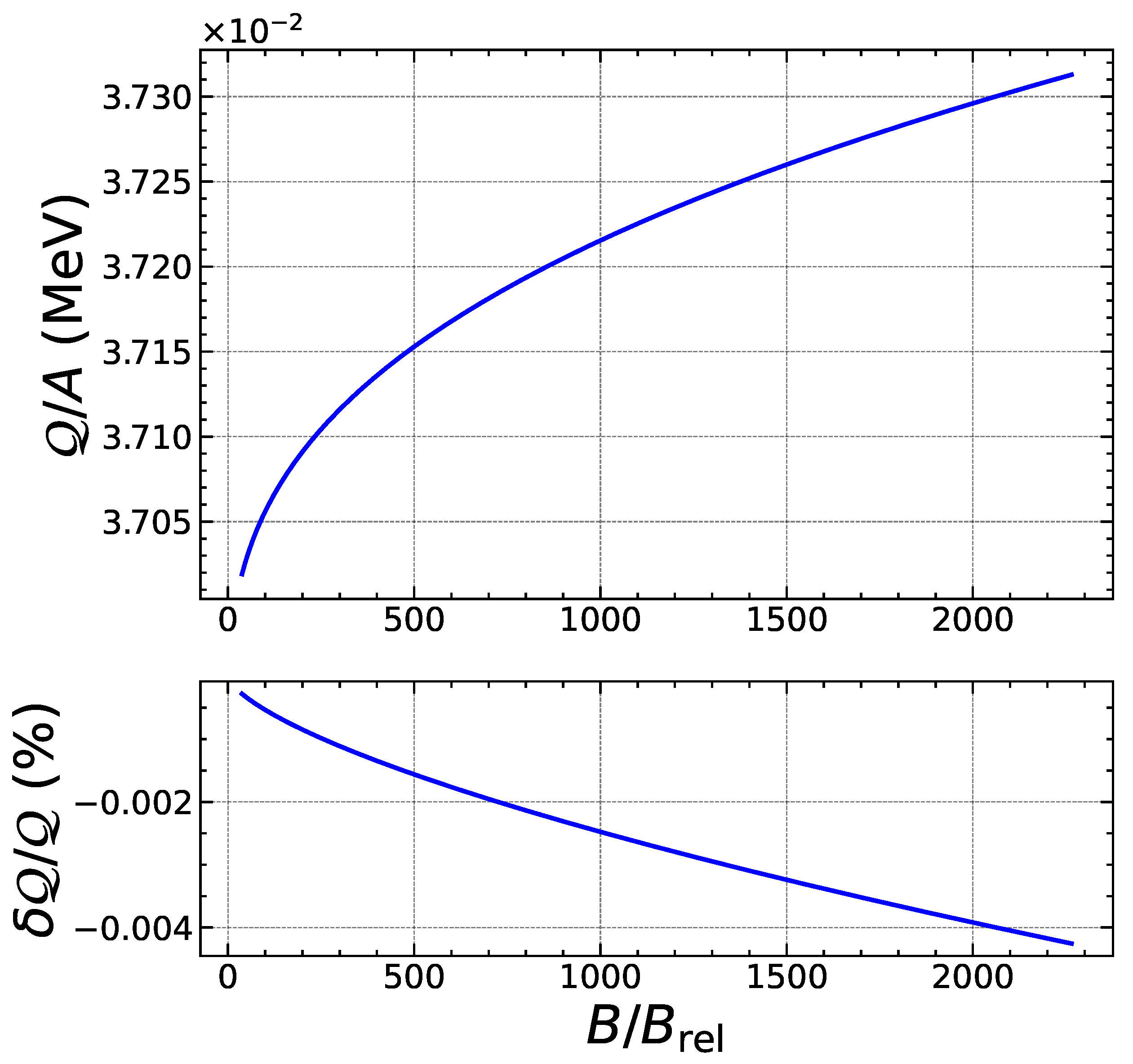

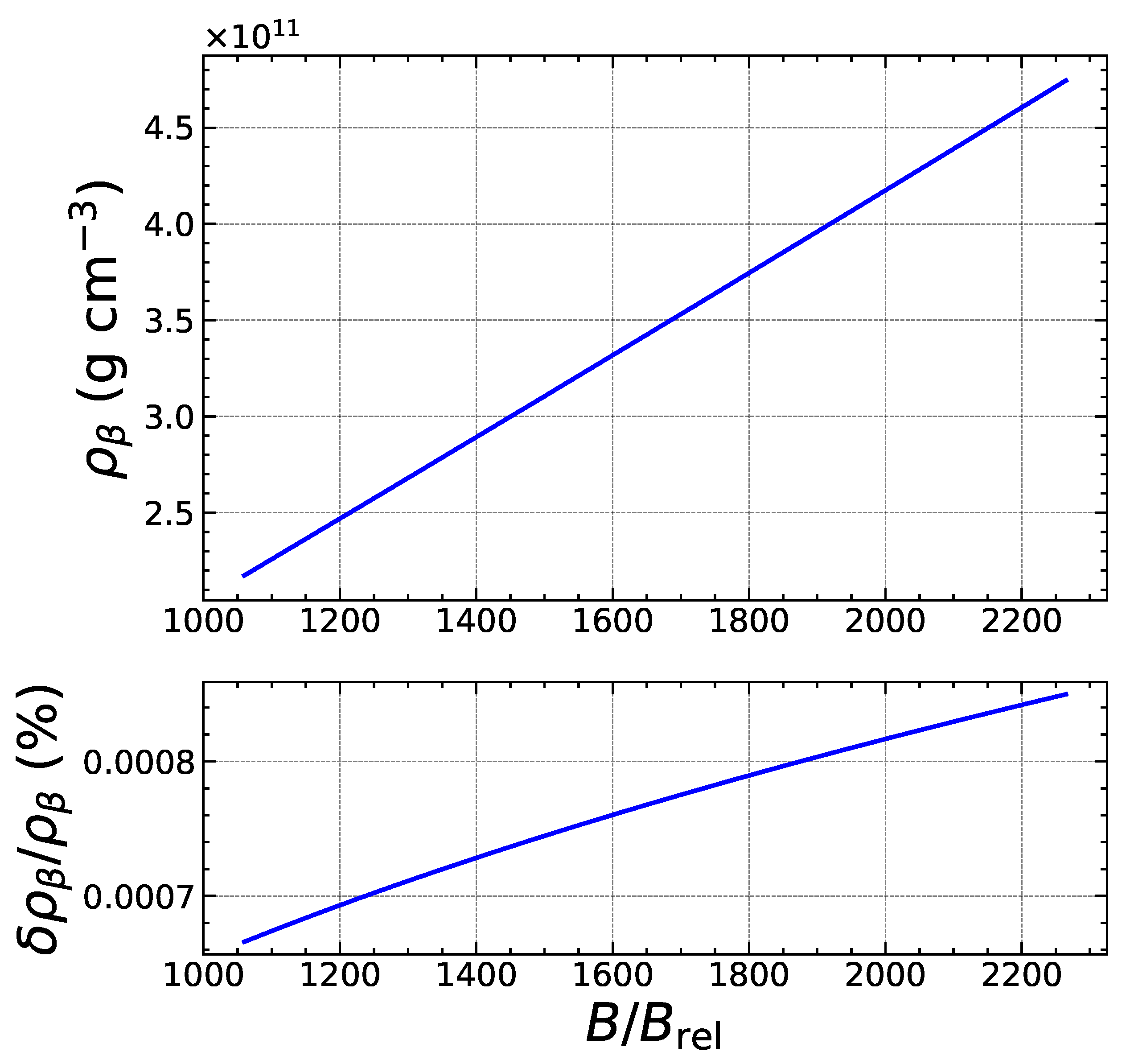

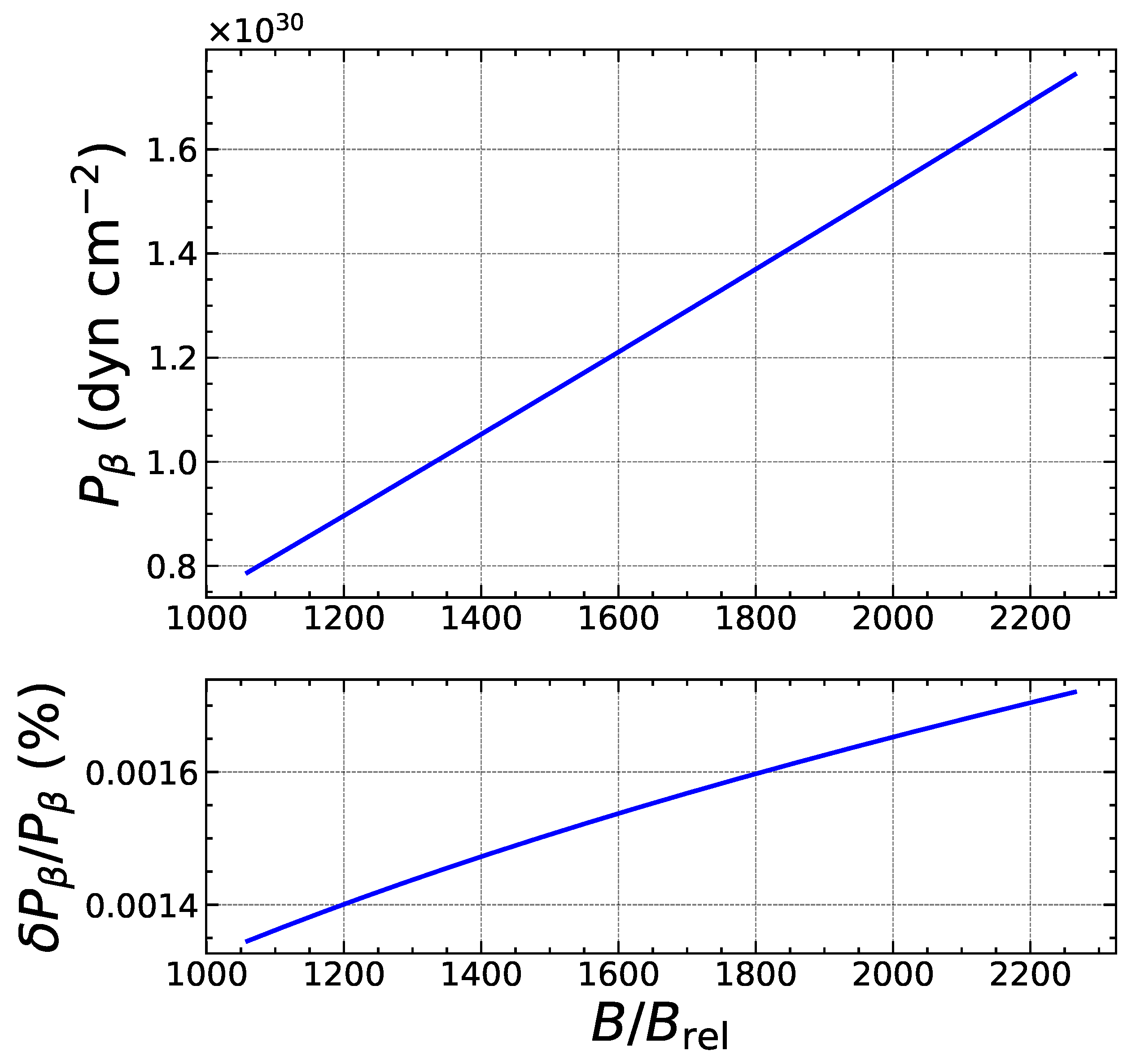
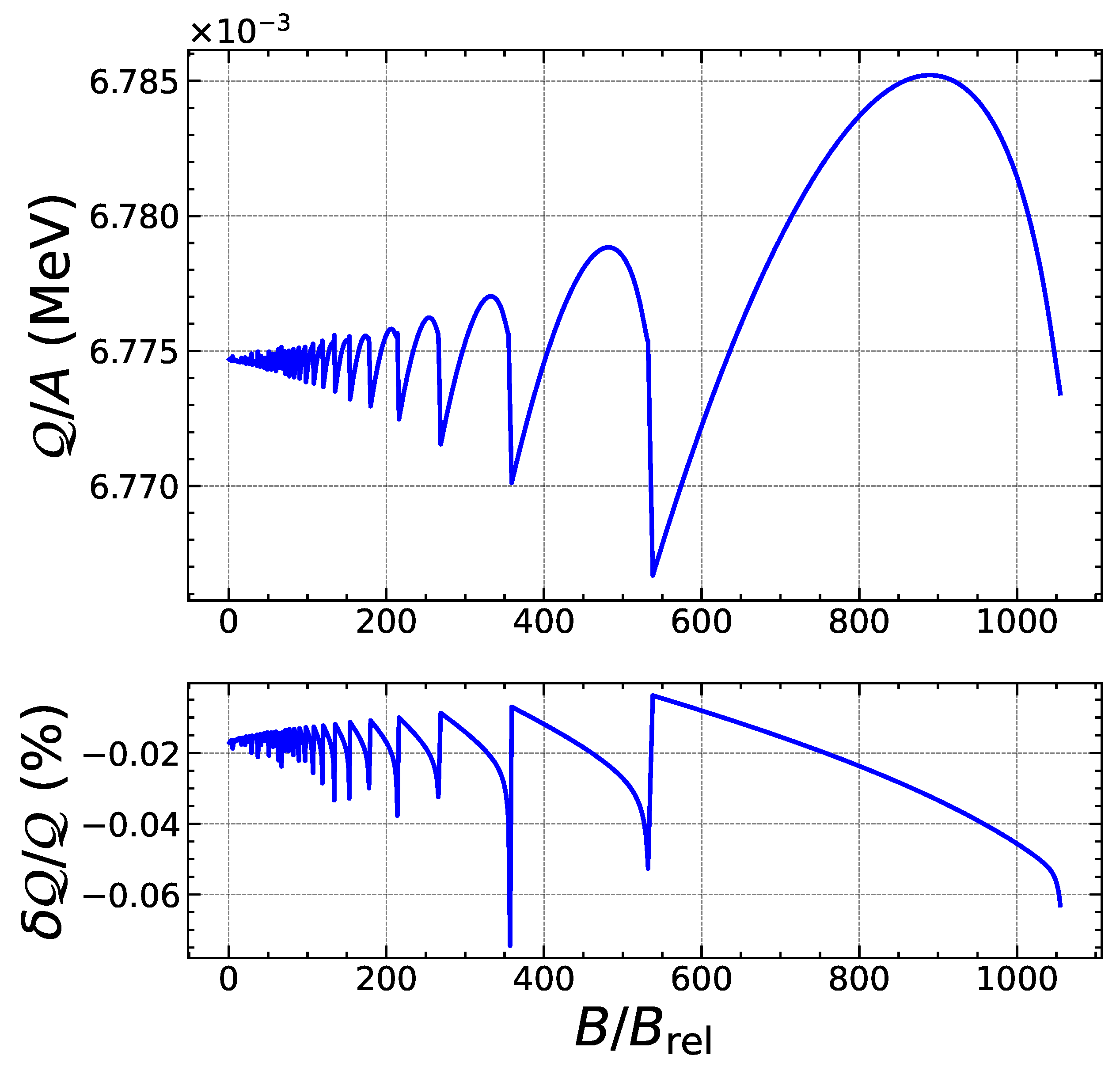
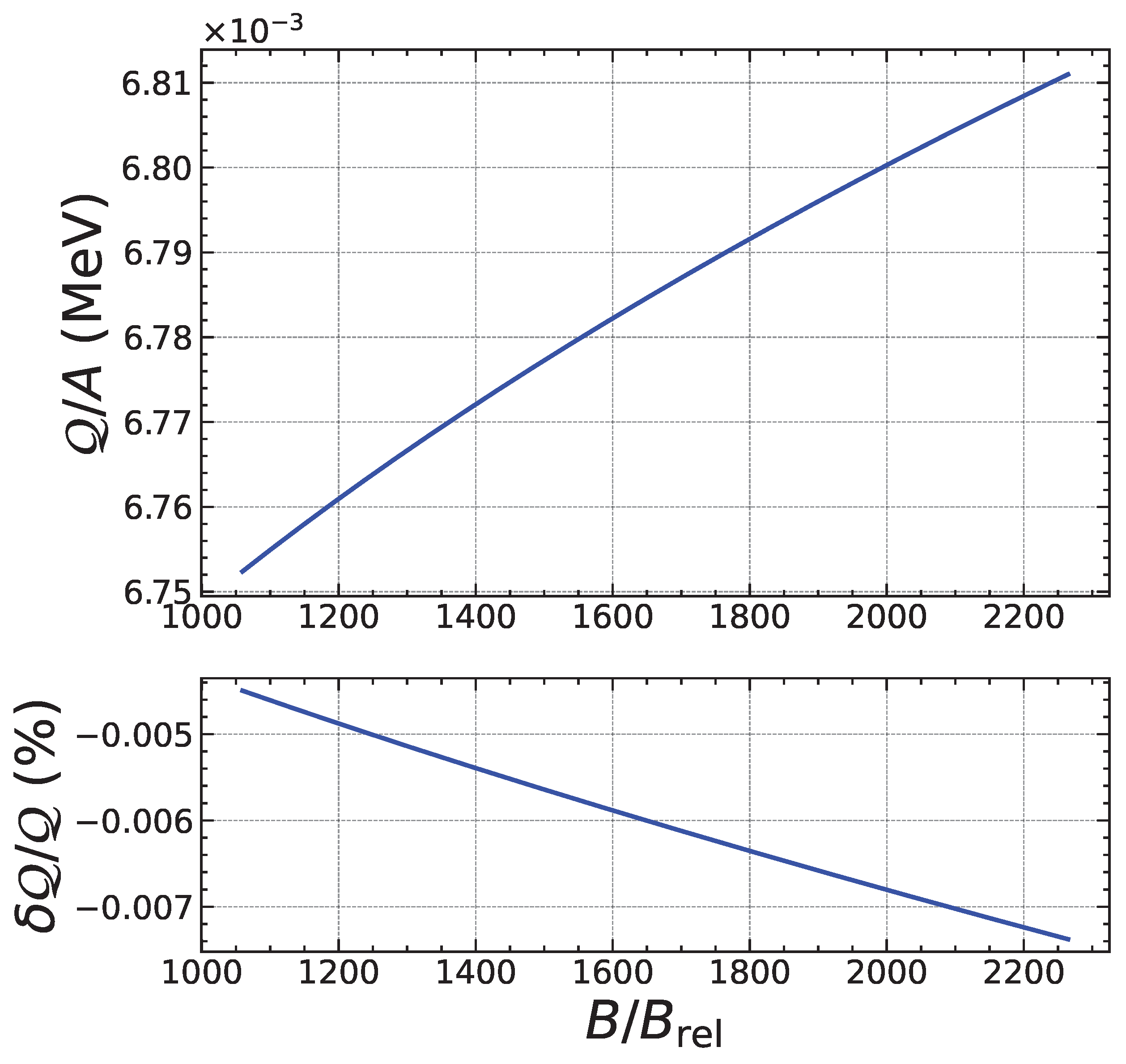
| Nuclide | |
|---|---|
| Ni(−) | 67 |
| Sr(+) | 858 |
| Ru(+) | 1023 |
| Ni(−) | 1072 |
| Pd(+) | 1249 |
| Ni(−) | 1416 |
| Ni(−) | 1669 |
| Zr(+) | 1872 |
| Y(−) | 1907 |
| Sn(+) | 1986 |
| Ni(−) | 2087 |
| 67 | 858 | 1023 | 1072 | 1249 | 1416 | 1669 | 1872 | 1907 | 1986 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Fe | Fe | Fe | Fe | Fe | Fe | Fe | Fe | Fe | Fe | Fe |
| Ni | Ni | Ni | Ni | Ni | Ni | Ni | Ni | Ni | Ni | Ni |
| Ni | Ni | Ni | Ni | Ni | Ni | Ni | – | – | – | – |
| Ni | – | – | – | – | – | – | – | – | – | – |
| – | – | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr |
| Kr | Kr | Kr | Kr | Kr | Kr | Kr | Kr | Kr | Kr | Kr |
| Se | Se | Se | Se | Se | Se | Se | Se | Se | Se | Se |
| Ge | Ge | Ge | Ge | Ge | Ge | Ge | Ge | Ge | Ge | Ge |
| – | – | – | – | – | – | – | – | – | – | Sn |
| Zn | Zn | Zn | Zn | Zn | Zn | Zn | Zn | Zn | Zn | Zn |
| Ni | Ni | Ni | Ni | Ni | Ni | – | – | – | – | – |
| Ni | Ni | Ni | Ni | – | – | – | – | – | – | – |
| – | – | – | – | – | Pd | Pd | Pd | Pd | Pd | Pd |
| – | – | – | Ru | Ru | Ru | Ru | Ru | Ru | Ru | Ru |
| Mo | Mo | Mo | Mo | Mo | Mo | Mo | Mo | Mo | Mo | Mo |
| Zr | Zr | Zr | Zr | Zr | Zr | Zr | Zr | Zr | Zr | Zr |
| – | – | – | – | – | – | – | – | Zr | Zr | Zr |
| Y | Y | Y | Y | Y | Y | Y | Y | Y | – | – |
| Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr |
| Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr |
| Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr | Sr |
| Interface | |
|---|---|
| 1.8908 | – |
| 4.8972 | – |
| 8.6863 | – |
| 8.1312 | – |
| 9.3317 | – |
| 18.098 | – |
| 12.155 | – |
| 10.044 | – |
| 5.5622 | – |
| 15.330 | – |
| 20.519 | – |
| 38.310 | – |
| 25.926 | – |
| 37.083 | – |
| – | |
| 32.978 | – |
| – | |
| 48.055 | – |
| 45.122 | – |
| 218.54 | – |
| 30.039 | – |
| 32.010 | – |
| 37.441 | – |
| 40.352 | – |
| 42.293 | – |
| 1.8541 | – |
| 39.031 | – |
| 40.786 | – |
| 44.857 | – |
| 47.747 | – |
| Reaction | (MeV) | |
|---|---|---|
| 8.232 | 2.069 | |
| 18.867 | 2.295 | |
| 29.313 | 3.514 | |
| 43.710 | 2.045 | |
| 11.415 | 2.776 | |
| 21.262 | 2.725 | |
| 31.174 | 2.442 | |
| 41.470 | 2.490 | |
| 15.299 | 2.484 | |
| 24.445 | 2.471 | |
| 34.581 | 1.865 | |
| 19.782 | 3.257 | |
| 27.062 | 1.287 | |
| 38.397 | 3.540 | |
| 15.938 | 2.504 | |
| 23.585 | 1.979 | |
| 30.980 | 2.310 | |
| 38.926 | 2.320 | |
| 20.754 | 2.389 | |
| 28.517 | 1.903 | |
| 36.362 | 2.390 | |
| 25.431 | 1.868 | |
| 34.256 | 2.154 | |
| 44.640 | 2.080 | |
| 31.233 | 1.879 | |
| 39.435 | 2.070 | |
| 41.842 | 2.920 | |
| 42.722 | 0.790 | |
| 11.397 | 2.395 | |
| 18.564 | 2.144 | |
| 26.761 | 2.582 | |
| 34.601 | 2.740 | |
| 36.695 | 1.860 | |
| 34.444 | 2.290 | |
| 28.662 | 1.987 | |
| 33.237 | 2.863 | |
| 38.084 | 2.940 |
| Reaction | (MeV) | |
|---|---|---|
| 8.448 | 2.290 | |
| 12.405 | 3.788 | |
| 20.726 | 7.397 | |
| 31.260 | 7.825 | |
| 15.764 | 6.858 | |
| 22.290 | 5.951 | |
| 31.010 | 4.387 |
| Reaction | (MeV) | |
|---|---|---|
| 21.393 | 2.411 | |
| 27.163 | 1.661 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamel, N.; Fantina, A.F. Onset of Electron Captures and Shallow Heating in Magnetars. Universe 2022, 8, 328. https://doi.org/10.3390/universe8060328
Chamel N, Fantina AF. Onset of Electron Captures and Shallow Heating in Magnetars. Universe. 2022; 8(6):328. https://doi.org/10.3390/universe8060328
Chicago/Turabian StyleChamel, Nicolas, and Anthea Francesca Fantina. 2022. "Onset of Electron Captures and Shallow Heating in Magnetars" Universe 8, no. 6: 328. https://doi.org/10.3390/universe8060328
APA StyleChamel, N., & Fantina, A. F. (2022). Onset of Electron Captures and Shallow Heating in Magnetars. Universe, 8(6), 328. https://doi.org/10.3390/universe8060328







