Topological Gauge Actions on the Lattice as Overlap Fermion Determinants
Abstract
:1. Introduction
2. Overlap Formalism in Three Dimensions
3. Introducing Chern–Simons and Half-Chern–Simons Terms on the Lattice
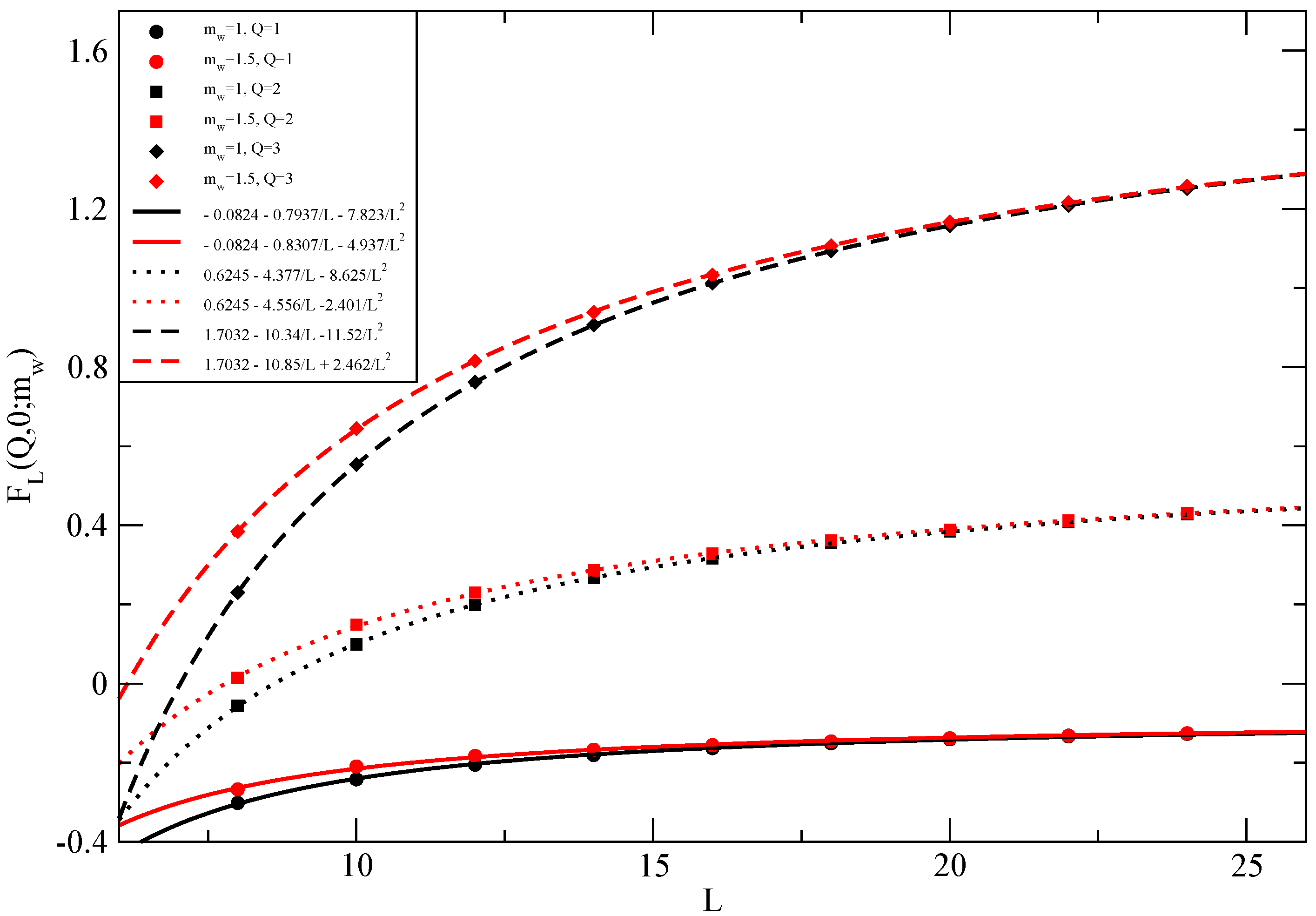
4. Fermion Determinant in an Abelian Background with Uniform Magnetic Flux and Non-Trivial Temporal Wilson Loop
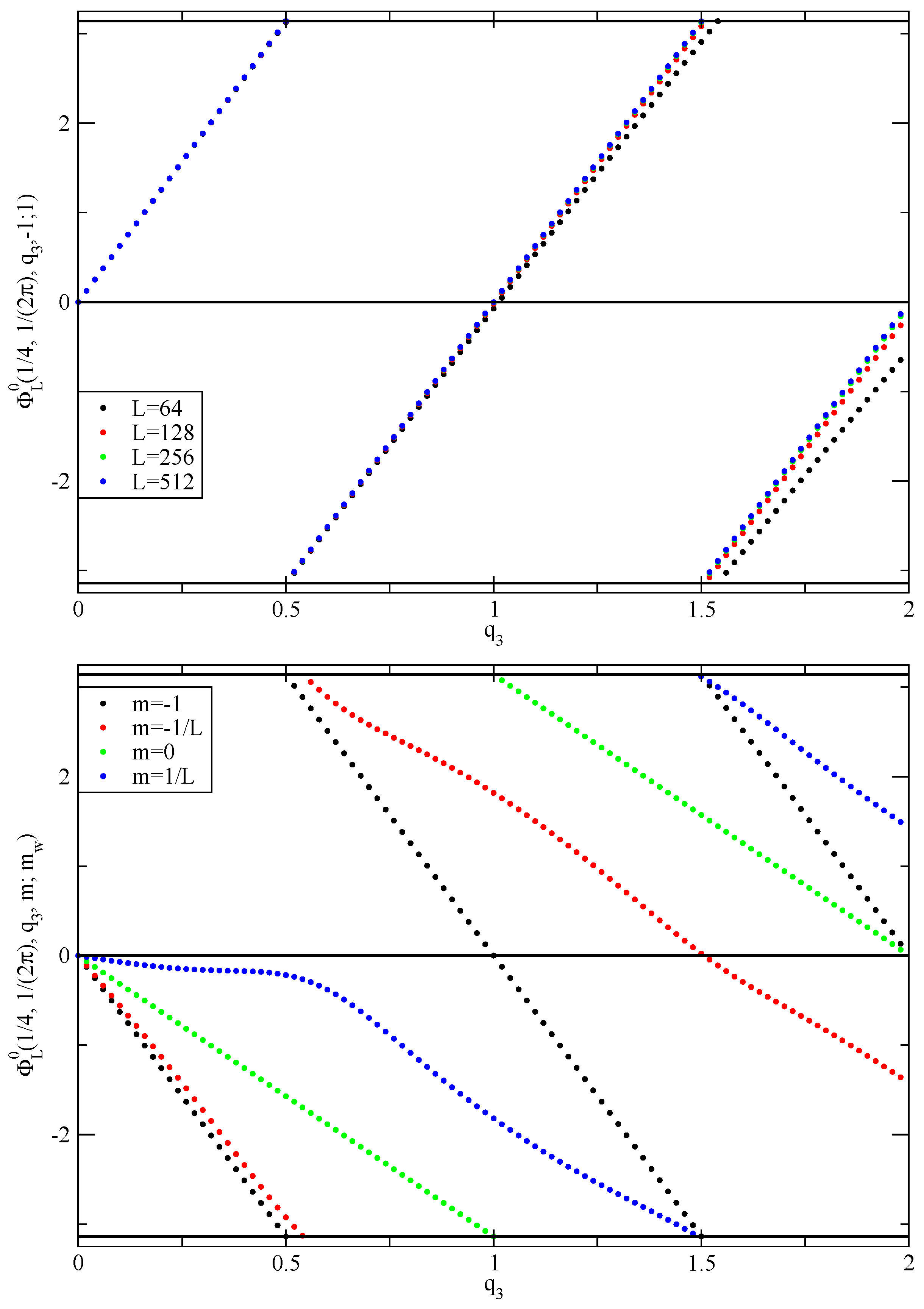
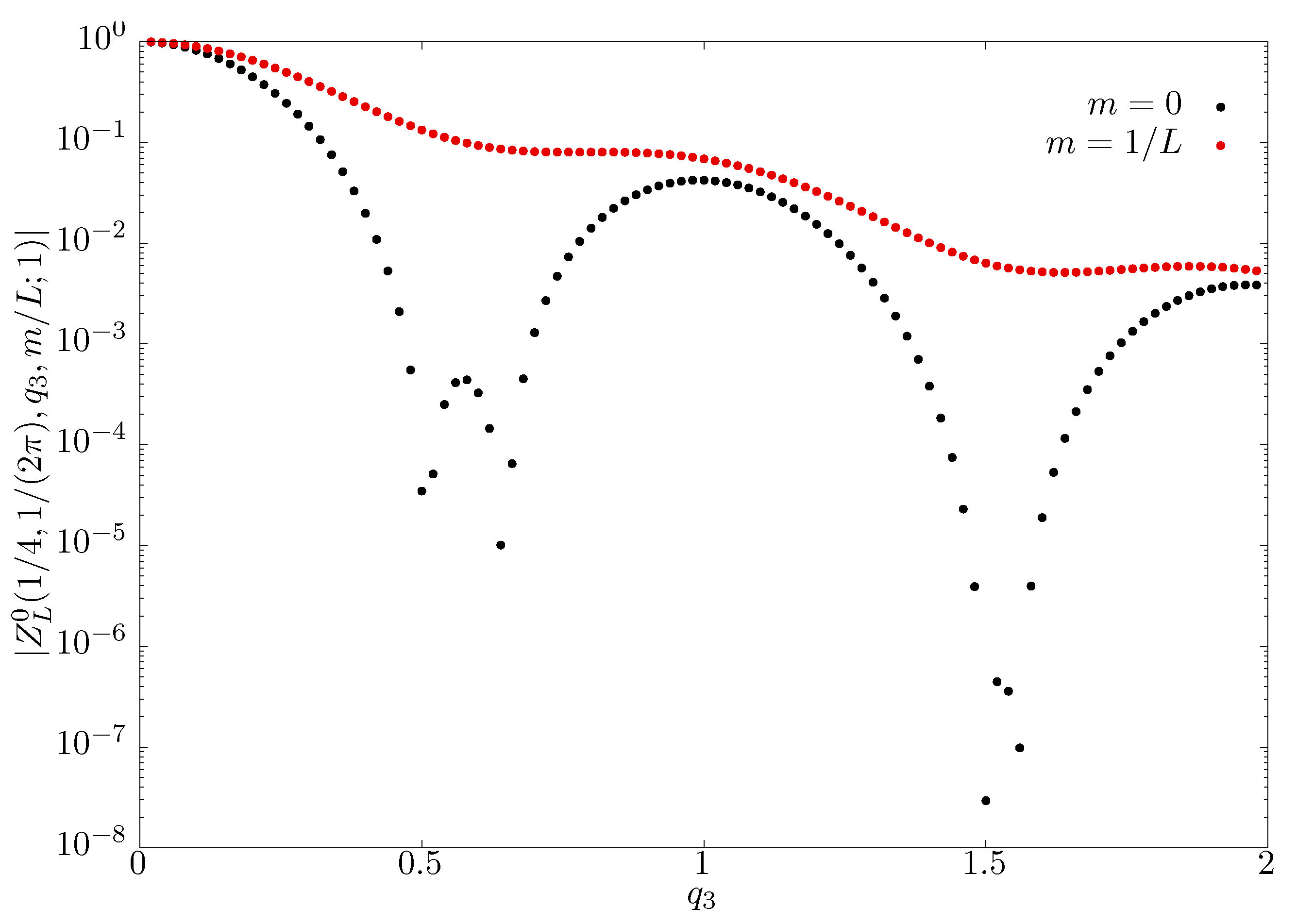
5. Fermion Determinant in a Non-Abelian Background with Non-Zero
6. Mixed Chern–Simons (BF) Action and Dualities
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dunne, G.V. Aspects of Chern–Simons theory. In Aspects Topologiques de la Physique en Basse Dimension. Topological Aspects of Low Dimensional Systems; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Seiberg, N.; Senthil, T.; Wang, C.; Witten, E. A Duality Web in 2+1 Dimensions and Condensed Matter Physics. Ann. Phys. 2016, 374, 395–433. [Google Scholar] [CrossRef] [Green Version]
- Karch, A.; Tong, D. Particle-Vortex Duality from 3d Bosonization. Phys. Rev. 2016, X6, 031043. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Nahum, A.; Metlitski, M.A.; Xu, C.; Senthil, T. Deconfined quantum critical points: Symmetries and dualities. Phys. Rev. 2017, X7, 031051. [Google Scholar] [CrossRef] [Green Version]
- Bilal, A. Lectures on Anomalies. arXiv 2008, arXiv:0802.0634. [Google Scholar]
- Atiyah, M.F.; Singer, I.M. The index of elliptic operators on compact manifolds. Bull. Am. Math. Soc. 1969, 69, 422–433. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, R.; Neuberger, H. A Construction of lattice chiral gauge theories. Nucl. Phys. 1995, B443, 305–385. [Google Scholar] [CrossRef] [Green Version]
- Neuberger, H. Geometrical aspects of chiral anomalies in the overlap. Phys. Rev. 1999, D59, 085006. [Google Scholar] [CrossRef] [Green Version]
- Coste, A.; Luscher, M. Parity Anomaly and Fermion Boson Transmutation in Three-dimensional Lattice QED. Nucl. Phys. 1989, B323, 631. [Google Scholar] [CrossRef]
- Kikukawa, Y.; Neuberger, H. Overlap in odd dimensions. Nucl. Phys. 1998, B513, 735–757. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, R.; Nishimura, J. Parity invariant lattice regularization of three-dimensional gauge fermion system. Nucl. Phys. 1997, B508, 371–387. [Google Scholar] [CrossRef]
- Bietenholz, W.; Nishimura, J. Ginsparg-Wilson fermions in odd dimensions. JHEP 2001, 7, 015. [Google Scholar] [CrossRef] [Green Version]
- Bietenholz, W.; Nishimura, J.; Sodano, P. Chern–Simons theory on the lattice. Nucl. Phys. B Proc. Suppl. 2003, 119, 935–937. [Google Scholar] [CrossRef] [Green Version]
- Karthik, N.; Narayanan, R. Phase of the fermion determinant in QED3 using a gauge invariant lattice regularization. Phys. Rev. 2015, D92, 025003. [Google Scholar]
- Alvarez-Gaume, L.; Della Pietra, S.; Moore, G.W. Anomalies and Odd Dimensions. Ann. Phys. 1985, 163, 288. [Google Scholar] [CrossRef]
- Witten, E. Three lectures on topological phases of matter. Riv. Nuovo Cim. 2016, 39, 313–370. [Google Scholar]
- Karthik, N.; Narayanan, R. Scale-invariance of parity-invariant three-dimensional QED. Phys. Rev. 2016, D94, 065026. [Google Scholar] [CrossRef] [Green Version]
- Karthik, N.; Narayanan, R. Parity Anomaly Cancellation in Three-Dimensional QED with a Single Massless Dirac Fermion. Phys. Rev. Lett. 2018, 121, 041602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cordova, C.; Hsin, P.S.; Seiberg, N. Time-Reversal Symmetry, Anomalies, and Dualities in (2 + 1)d. SciPost Phys. 2018, 5, 6. [Google Scholar] [CrossRef]
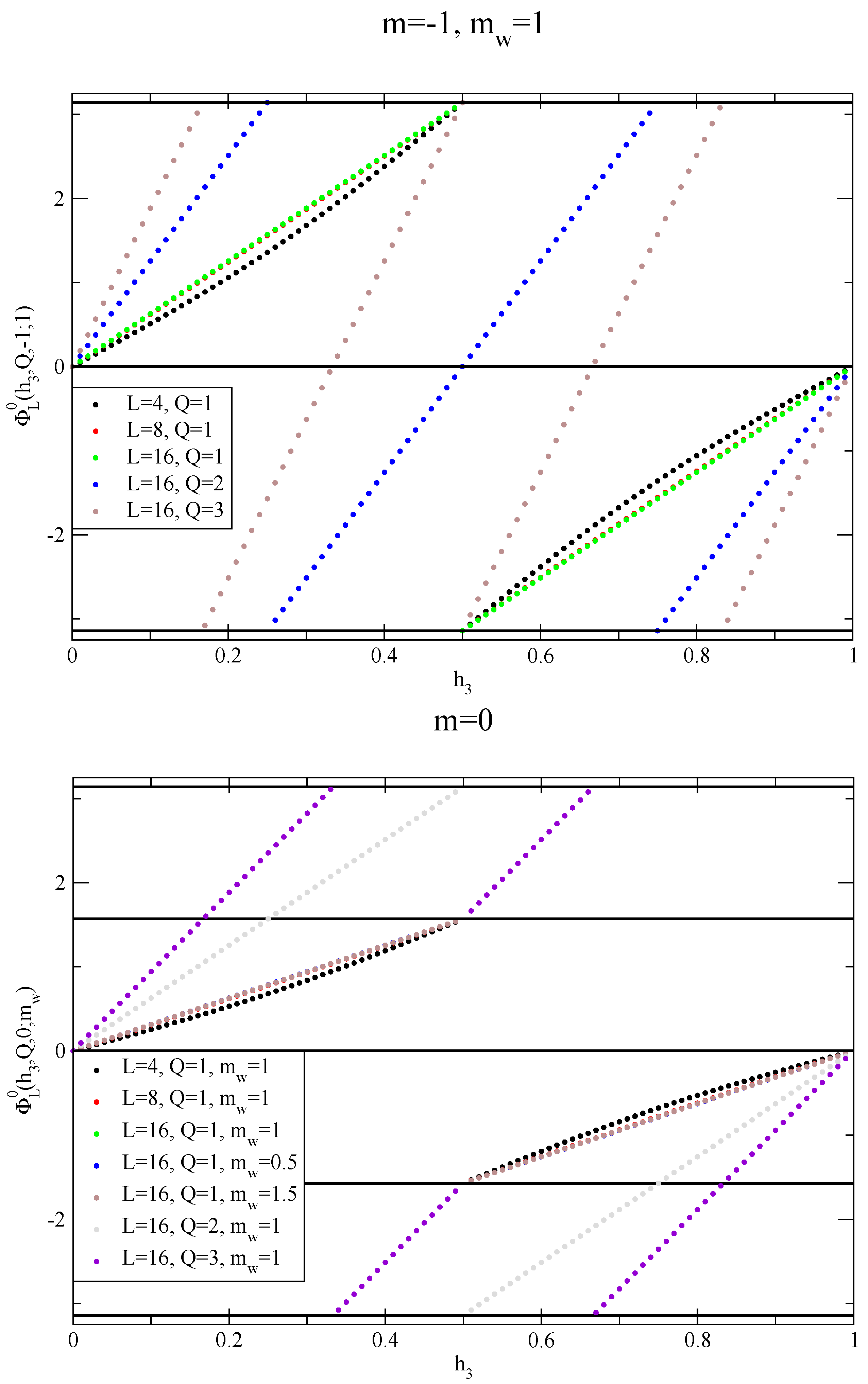
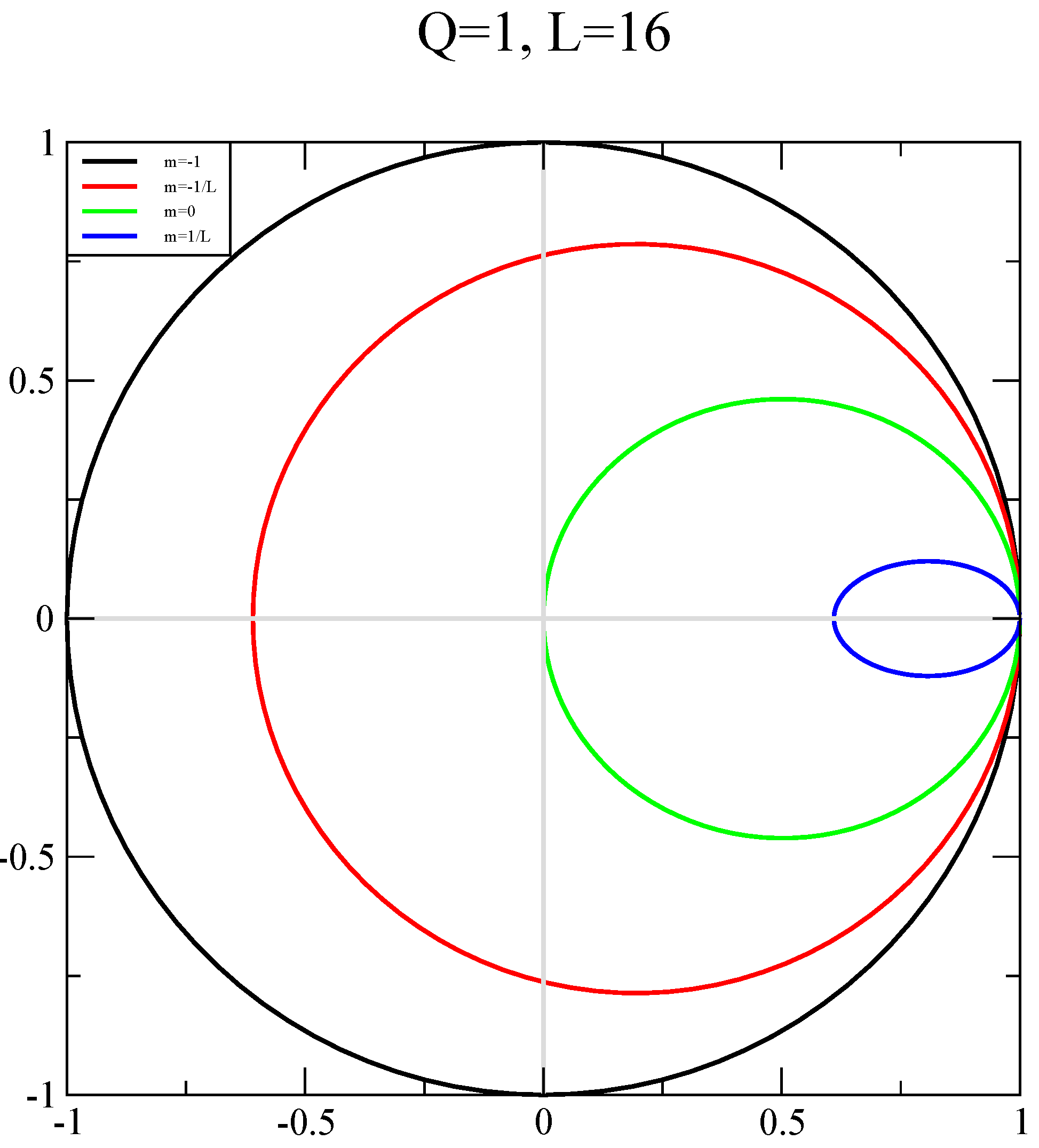
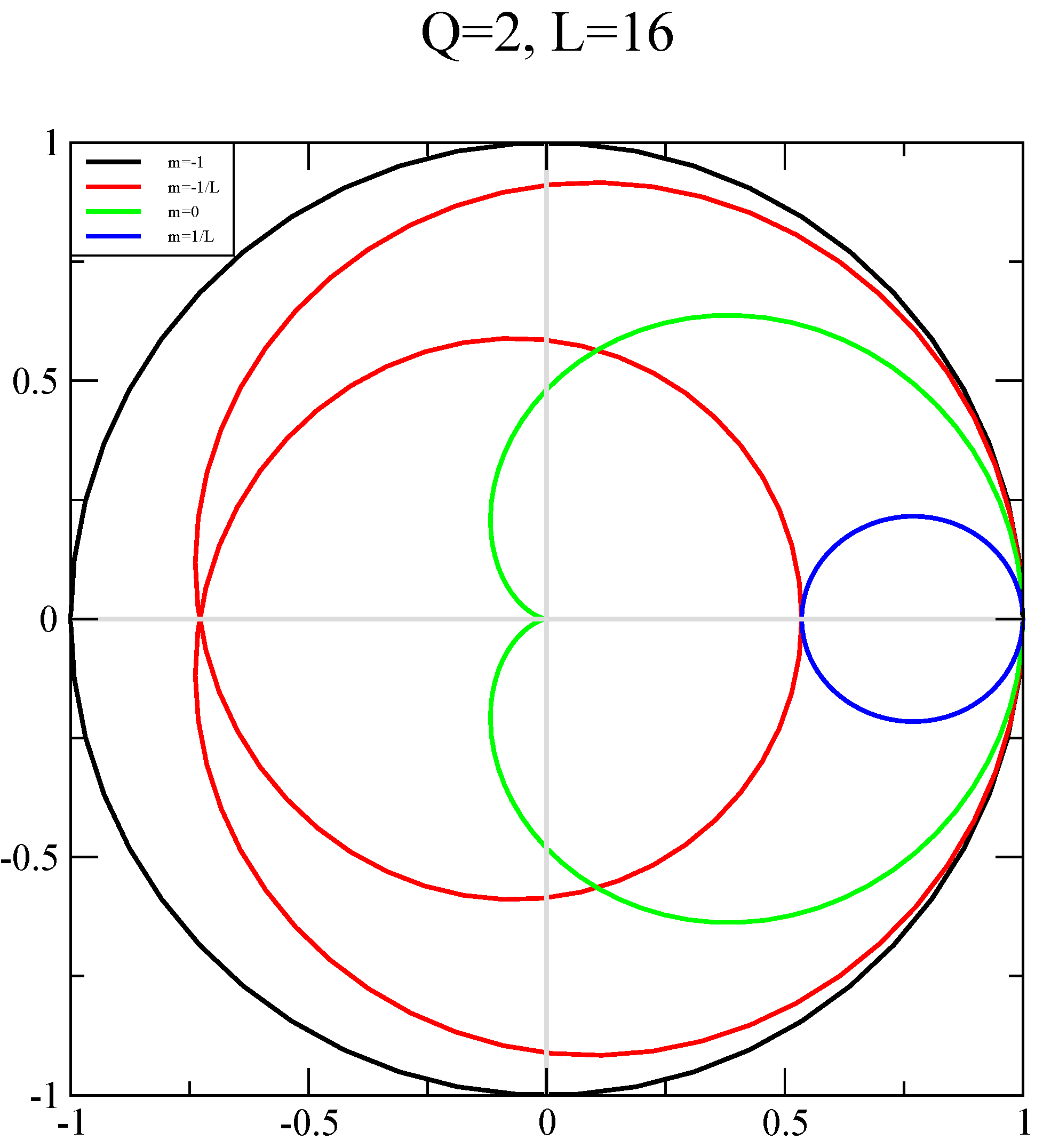
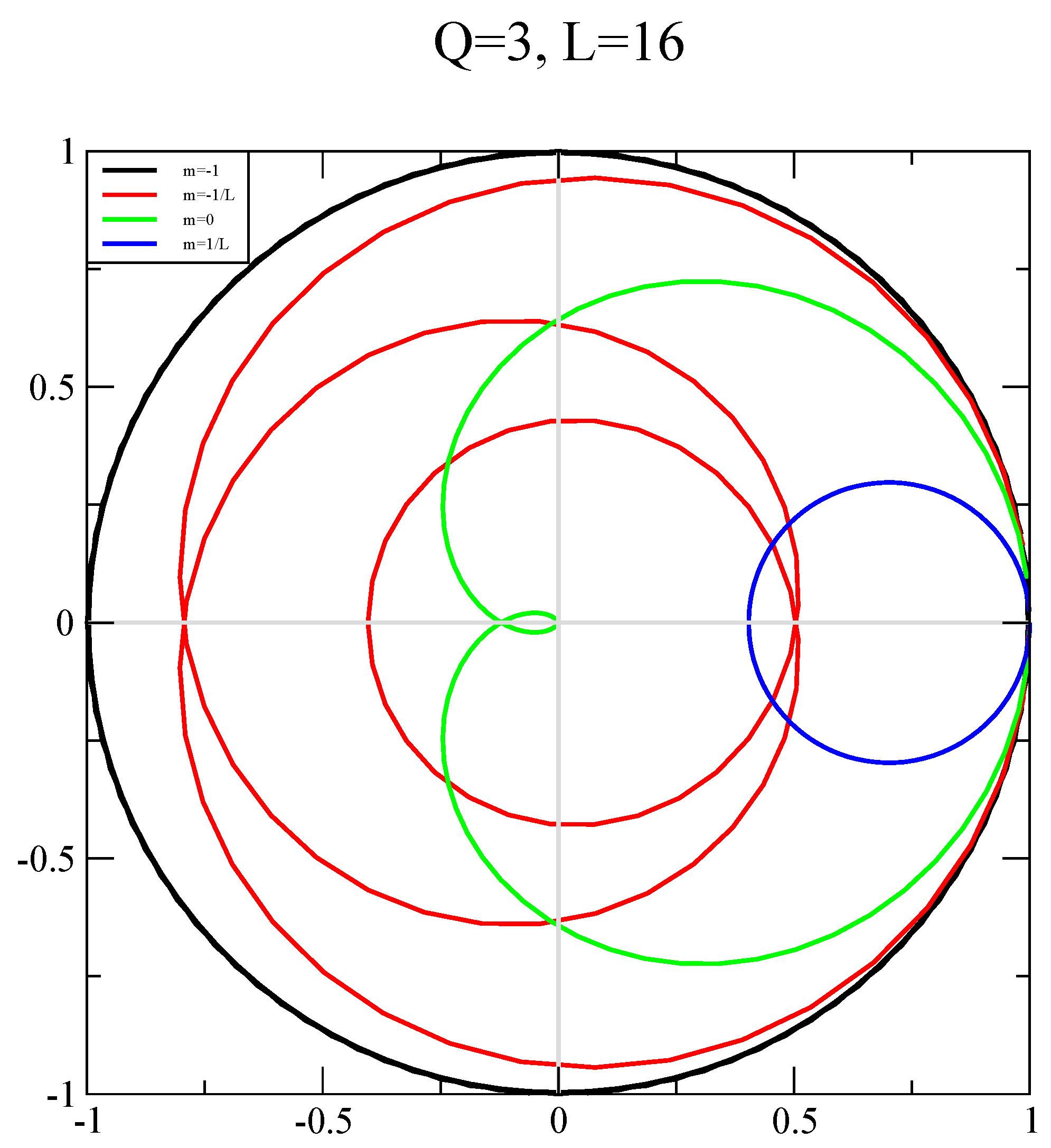
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karthik, N.; Narayanan, R. Topological Gauge Actions on the Lattice as Overlap Fermion Determinants. Universe 2022, 8, 332. https://doi.org/10.3390/universe8060332
Karthik N, Narayanan R. Topological Gauge Actions on the Lattice as Overlap Fermion Determinants. Universe. 2022; 8(6):332. https://doi.org/10.3390/universe8060332
Chicago/Turabian StyleKarthik, Nikhil, and Rajamani Narayanan. 2022. "Topological Gauge Actions on the Lattice as Overlap Fermion Determinants" Universe 8, no. 6: 332. https://doi.org/10.3390/universe8060332
APA StyleKarthik, N., & Narayanan, R. (2022). Topological Gauge Actions on the Lattice as Overlap Fermion Determinants. Universe, 8(6), 332. https://doi.org/10.3390/universe8060332




