Contrasting Scaling Properties of Near-Sun Sub-Alfvénic and Super-Alfvénic Regions
Abstract
:1. Introduction
2. Data
3. Methods
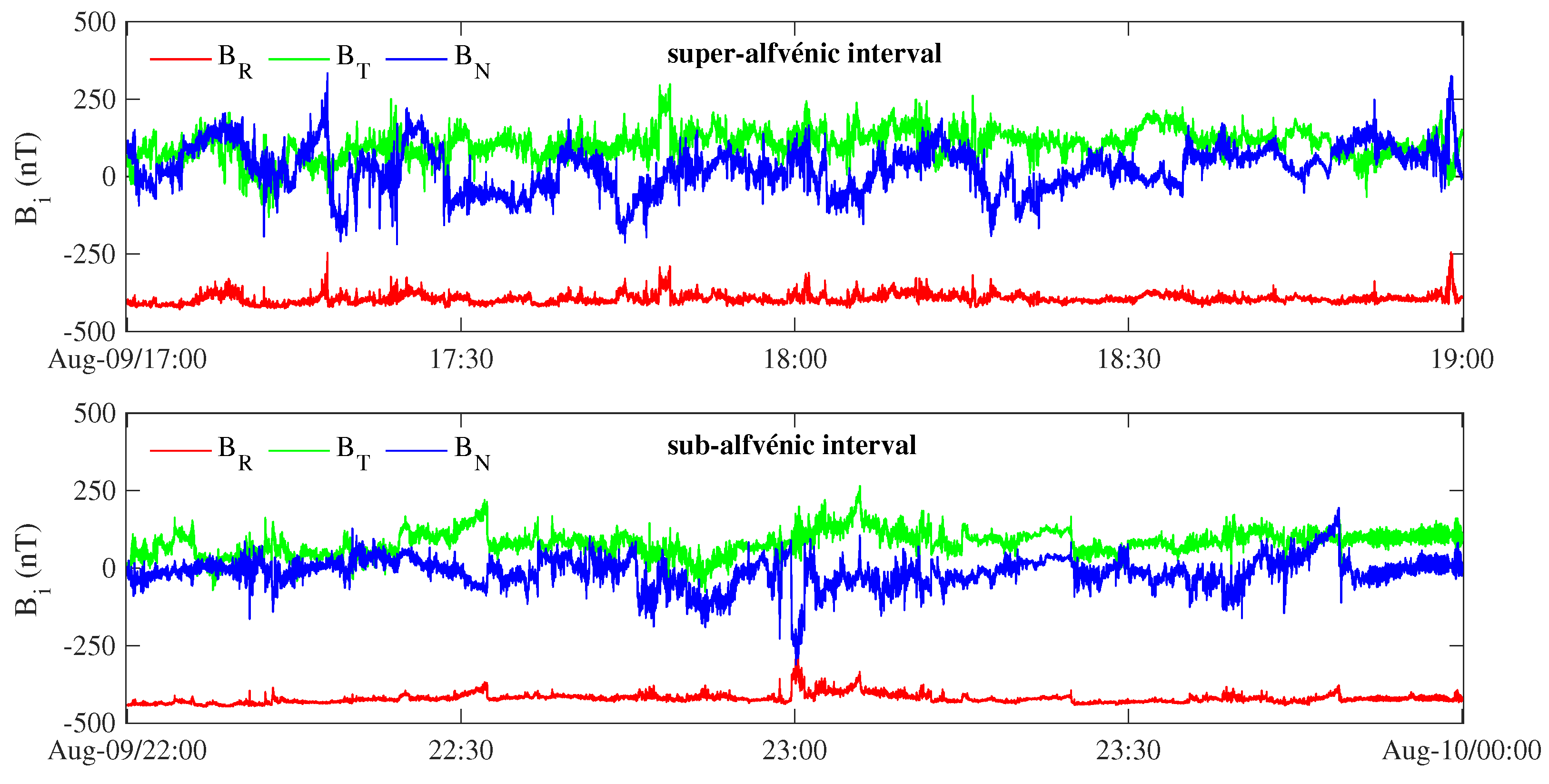
4. Results
- 1.
- It provides an accurate determination of scaling exponents;
- 2.
- It holds down to the dissipative regime;
- 3.
- It holds for both high and mid-to-low Reynolds numbers.
- If , then the two intervals are characterized by the same fractal topology, i.e., they share the same geometrical structures and the same symmetries;
- If , then the two intervals are characterized by a fractal topology belonging to the same class, i.e., they share the same geometrical structures but with different symmetries;
- If , then the two intervals are characterized by a different fractal topology, i.e., they do not share neither the same geometrical structures nor the same symmetries.
5. Discussions and Conclusions
- 1.
- An extended self-similarity is observed for both the MHD/inertial and the sub-ion/kinetic regimes during both intervals;
- 2.
- A multifractal nature of field fluctuations is reported across inertial scales for both solar wind intervals;
- 3.
- A mono-fractal character is observed for field fluctuations at small scales during both solar wind intervals.
5.1. Extended Self-Similarity
5.2. Multifractality of Inertial Range
5.3. Mono-Fractality at Sub-Ion/Kinetic Scales
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AU | Astronomical Unit |
| ESS | Extended Self-Similarity |
| FGM | Flux-Gate Magnetometer |
| MHD | Magnetohydrodynamic |
| PSD | Power Spectral Density |
| PSP | Parker Solar Probe |
| RTN | Radial–Tangential–Normal |
| SCM | Search Coil Magnetometer |
| SL | She–Leveque |
| UT | Universal Time |
| 1 | The RTN is a spacecraft-centered reference system in which the radial (R) direction is identified as the spacecraft-Sun line, the tangential (T) direction is identified as the tangent to the orbit of the spacecraft, and the N direction is obtained as the curl product of R and T, completing a right-handed triad. |
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. Turbulence in the Solar Wind; Springer: Berlin/Heidelberg, Germany, 2016; Volume 928. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. The Weather and Climate: Emergent Laws and Multifractal Cascades; Cambridge Press Univeristy: Cambridge, UK, 2013; p. 512. [Google Scholar]
- Dubrulle, B. Beyond Kolmogorov cascades. J. Fluid Mech. 2019, 867, P1. [Google Scholar] [CrossRef] [Green Version]
- Benzi, R.; Paladin, G.; Vulpiani, A.; Parisi, G. On the multifractal nature of fully developed turbulence and chaotic systems. J. Phys. Math. Gen. 1984, 17, 3521–3531. [Google Scholar] [CrossRef]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frisch, U. Turbulence. The Legacy of A.N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Hofman, M.A. The Fractal Geometry of the Human Brain: An Evolutionary Perspective. In The Fractal Geometry of the Brain; Di Ieva, A., Ed.; Springer: New York, NY, USA, 2016; pp. 169–186. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals and Scaling in Finance: Discontinuity, Concentration, Risk, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Narita, Y. Space-time structure and wavevector anisotropy in space plasma turbulence. Living Rev. Sol. Phys. 2018, 15, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kiyani, K.H.; Osman, K.T.; Chapman, S.C. Dissipation and heating in solar wind turbulence: From the macro to the micro and back again. Philos. Trans. R. Soc. Lond. Ser. A 2015, 373, 20140155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carbone, V.; Bruno, R.; Veltri, P. Scaling Laws in the Solar Wind Turbulence. In Small-Scale Structures in Three-Dimensional Hydrodynamic and Magnetohydrodynamic Turbulence; Meneguzzi, M., Pouquet, A., Sulem, P.L., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; Volume 462, p. 153. [Google Scholar] [CrossRef] [Green Version]
- Chapman, S.C.; Nicol, R.M.; Leonardis, E.; Kiyani, K.; Carbone, V. Observation of Universality in the Generalized Similarity of Evolving Solar Wind Turbulence as Seen by Ulysses. Astrophys. J. Lett. 2009, 695, L185–L188. [Google Scholar] [CrossRef]
- Consolini, G.; Alberti, T.; Yordanova, E.; Marcucci, M.F.; Echim, M. A Hilbert-Huang transform approach to space plasma turbulence at kinetic scales. Proc. J. Phys. Conf. Ser. 2017, 900, 012003. [Google Scholar] [CrossRef] [Green Version]
- Alberti, T.; Consolini, G.; Carbone, V.; Yordanova, E.; Marcucci, M.; De Michelis, P. Multifractal and Chaotic Properties of Solar Wind at MHD and Kinetic Domains: An Empirical Mode Decomposition Approach. Entropy 2019, 21, 320. [Google Scholar] [CrossRef] [Green Version]
- Chhiber, R.; Matthaeus, W.H.; Bowen, T.A.; Bale, S.D. Subproton-scale Intermittency in Near-Sun Solar Wind Turbulence Observed by the Parker Solar Probe. Astrophys. J. Lett. 2021, 911, L7. [Google Scholar] [CrossRef]
- Vasko, I.Y.; Alimov, K.; Phan, T.; Bale, S.D.; Mozer, F.S.; Artemyev, A.V. Kinetic-scale Current Sheets in the Solar Wind at 1 au: Scale-dependent Properties and Critical Current Density. Astrophys. J. Lett. 2022, 926, L19. [Google Scholar] [CrossRef]
- Lotekar, A.B.; Vasko, I.Y.; Phan, T.; Bale, S.D.; Bowen, T.A.; Halekas, J.; Artemyev, A.V.; Khotyaintsev, Y.V.; Mozer, F.S. Kinetic-scale Current Sheets in Near-Sun Solar Wind: Properties, Scale-dependent Features and Reconnection Onset. Astrophys. J. 2022, 929, 58. [Google Scholar] [CrossRef]
- Macek, W.M.; Wawrzaszek, A.; Carbone, V. Observation of the multifractal spectrum at the termination shock by Voyager 1. Geophys. Res. Lett. 2011, 38, L19103. [Google Scholar] [CrossRef] [Green Version]
- Macek, W.M.; Wawrzaszek, A.; Carbone, V. Observation of the multifractal spectrum in the heliosphere and the heliosheath by Voyager 1 and 2. J. Geophys. Res. (Space Phys.) 2012, 117, A12101. [Google Scholar] [CrossRef] [Green Version]
- Wawrzaszek, A.; Echim, M. On the variation of intermittency of fast and slow solar wind with radial Distance, heliospheric Latitude, and Solar Cycle. Front. Astron. Space Sci. 2021, 7, 99. [Google Scholar] [CrossRef]
- Fox, N.J.; McComas, D.J. Editorial: Topical Volume on Developing the Solar Probe Plus Mission. Space Sci. Rev. 2016, 204, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kasper, J.C.; Klein, K.G.; Lichko, E.; Huang, J.; Chen, C.H.K.; Badman, S.T.; Bonnell, J.; Whittlesey, P.L.; Livi, R.; Larson, D.; et al. Parker Solar Probe Enters the Magnetically Dominated Solar Corona. Phys. Rev. Lett. 2021, 127, 255101. [Google Scholar] [CrossRef]
- Chhiber, R.; Usmanov, A.V.; Matthaeus, W.H.; Goldstein, M.L. Contextual Predictions for the Parker Solar Probe. I. Critical Surfaces and Regions. Astrophys. J. Suppl. Ser. 2019, 241, 11. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, R.; Matthaeus, W.H.; McComas, D.J.; Chhiber, R.; Usmanov, A.V.; Huang, J.; Livi, R.; Larson, D.E.; Kasper, J.C.; Case, A.W.; et al. Sub-Alfvénic Solar Wind Observed by the Parker Solar Probe: Characterization of Turbulence, Anisotropy, Intermittency, and Switchback. Astrophys. J. Lett. 2022, 926, L1. [Google Scholar] [CrossRef]
- Zank, G.P.; Zhao, L.L.; Adhikari, L.; Telloni, D.; Kasper, J.C.; Stevens, M.; Rahmati, A.; Bale, S.D. Turbulence in the Sub-Alfvénic Solar Wind. Astrophys. J. Lett. 2022, 926, L16. [Google Scholar] [CrossRef]
- Benella, S.; Stumpo, M.; Consolini, G.; Alberti, T.; Carbone, V.; Laurenza, M. Markovian Features of the Solar Wind at Subproton Scales. Astrophys. J. Lett. 2022, 928, L21. [Google Scholar] [CrossRef]
- Kiyani, K.H.; Chapman, S.C.; Khotyaintsev, Y.V.; Dunlop, M.W.; Sahraoui, F. Global Scale-Invariant Dissipation in Collisionless Plasma Turbulence. Phys. Rev. Lett. 2009, 103, 075006. [Google Scholar] [CrossRef] [PubMed]
- Bale, S.D.; Goetz, K.; Harvey, P.R.; Turin, P.; Bonnell, J.W.; Dudok de Wit, T.; Ergun, R.E.; MacDowall, R.J.; Pulupa, M.; Andre, M.; et al. The FIELDS Instrument Suite for Solar Probe Plus. Measuring the Coronal Plasma and Magnetic Field, Plasma Waves and Turbulence, and Radio Signatures of Solar Transients. Space Sci. Rev. 2016, 204, 49–82. [Google Scholar] [CrossRef]
- Bowen, T.A.; Bale, S.D.; Bonnell, J.W.; Dudok de Wit, T.; Goetz, K.; Goodrich, K.; Gruesbeck, J.; Harvey, P.R.; Jannet, G.; Koval, A.; et al. A Merged Search-Coil and Fluxgate Magnetometer Data Product for Parker Solar Probe FIELDS. J. Geophys. Res. (Space Phys.) 2020, 125, e27813. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. Haar wavelets, fluctuations and structure functions: Convenient choices for geophysics. Nonlinear Process. Geophys. 2012, 19, 513–527. [Google Scholar] [CrossRef] [Green Version]
- Elsasser, W.M. The Hydromagnetic Equations. Phys. Rev. 1950, 79, 183. [Google Scholar] [CrossRef]
- Biskamp, D. Magnetohydrodynamic Turbulence; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Carbone, V. Cascade model for intermittency in fully developed magnetohydrodynamic turbulence. Phys. Rev. Lett. 1993, 71, 1546–1548. [Google Scholar] [CrossRef]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akad. Nauk SSSR Dokl. 1941, 30, 301–305. [Google Scholar]
- Iroshnikov, P.S. Turbulence of a Conducting Fluid in a Strong Magnetic Field. Sov. Ast. 1964, 7, 566. [Google Scholar]
- Kraichnan, R.H. Inertial-Range Spectrum of Hydromagnetic Turbulence. Phys. Fluids 1965, 8, 1385–1387. [Google Scholar] [CrossRef] [Green Version]
- Frisch, U. From global scaling, a la Kolmogorov, to local multifractal scaling in fully developed turbulence. Proc. R. Soc. Lond. Ser. A 1991, 434, 89–99. [Google Scholar] [CrossRef]
- Dudok de Wit, T. Can high-order moments be meaningfully estimated from experimental turbulence measurements? Phys. Rev. E 2004, 70, 055302. [Google Scholar] [CrossRef] [PubMed]
- Alexandrova, O.; Saur, J.; Lacombe, C.; Mangeney, A.; Mitchell, J.; Schwartz, S.J.; Robert, P. Universality of Solar-Wind Turbulent Spectrum from MHD to Electron Scales. Phys. Rev. Lett. 2009, 103, 165003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benzi, R.; Ciliberto, S.; Tripiccione, R.; Baudet, C.; Massaioli, F.; Succi, S. Extended self-similarity in turbulent flows. Phys. Rev. E 1993, 48, R29–R32. [Google Scholar] [CrossRef]
- Carbone, V.; Bruno, R.; Veltri, P. Evidences for extended self-similarity in hydromagnetic turbulence. Geophys. Res. Lett. 1996, 23, 121–124. [Google Scholar] [CrossRef]
- Benzi, R.; Marrocu, M.; Mazzino, A.; Trovatore, E. Characterization of the Long-Time and Short-Time Predictability of Low-Order Models of the Atmosphere. J. Atmos. Sci. 1999, 56, 3495–3507. [Google Scholar] [CrossRef]
- Benzi, R.; Biferale, L.; Ciliberto, S.; Struglia, M.V.; Tripiccione, R. Generalized scaling in fully developed turbulence. Phys. D Nonlinear Phenom. 1996, 96, 162–181. [Google Scholar] [CrossRef] [Green Version]
- Benzi, R.; Ciliberto, S.; Baudet, C.; Chavarria, G.R. On the scaling of three-dimensional homogeneous and isotropic turbulence. Phys. D Nonlinear Phenom. 1995, 80, 385–398. [Google Scholar] [CrossRef]
- Einaudi, G.; Velli, M.; Politano, H.; Pouquet, A. Energy Release in a Turbulent Corona. Astrophys. J. Lett. 1996, 457, L113. [Google Scholar] [CrossRef]
- Leamon, R.J.; Smith, C.W.; Ness, N.F.; Matthaeus, W.H.; Wong, H.K. Observational constraints on the dynamics of the interplanetary magnetic field dissipation range. J. Geophys. Res. 1998, 103, 4775–4788. [Google Scholar] [CrossRef]
- Gary, S.P.; Borovsky, J.E. Alfvén-cyclotron fluctuations: Linear Vlasov theory. J. Geophys. Res. (Space Phys.) 2004, 109, A06105. [Google Scholar] [CrossRef]
- Narita, Y.; Roberts, O.W.; Vörös, Z.; Hoshino, M. Transport ratios of the kinetic Alfvén mode in space plasmas. Front. Phys. 2020, 8, 166. [Google Scholar] [CrossRef]
- Cranmer, S.R. Some Turbulent Predictions for Parker Solar Probe. Res. Notes AAS 2018, 2, 158. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 1987, 59, 1424–1427. [Google Scholar] [CrossRef]
- She, Z.S.; Leveque, E. Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 1994, 72, 336–339. [Google Scholar] [CrossRef]
- Grauer, R.; Krug, J.; Marliani, C. Scaling of high-order structure functions in magnetohydrodynamic turbulence. Phys. Lett. A 1994, 195, 335–338. [Google Scholar] [CrossRef]
- Politano, H.; Pouquet, A. Model of intermittency in magnetohydrodynamic turbulence. Phys. Rev. E 1995, 52, 636–641. [Google Scholar] [CrossRef]
- Retinò, A.; Sundkvist, D.; Vaivads, A.; Mozer, F.; André, M.; Owen, C.J. In situ evidence of magnetic reconnection in turbulent plasma. Nat. Phys. 2007, 3, 236–238. [Google Scholar] [CrossRef] [Green Version]
- Alexandrova, O.; Lacombe, C.; Mangeney, A.; Grappin, R.; Maksimovic, M. Solar Wind Turbulent Spectrum at Plasma Kinetic Scales. Astrophys. J. 2012, 760, 121. [Google Scholar] [CrossRef] [Green Version]




| Sub-Alfvénic | Super-Alfvénic | |||||
|---|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alberti, T.; Benella, S.; Carbone, V.; Consolini, G.; Quattrociocchi, V.; Stumpo, M. Contrasting Scaling Properties of Near-Sun Sub-Alfvénic and Super-Alfvénic Regions. Universe 2022, 8, 338. https://doi.org/10.3390/universe8070338
Alberti T, Benella S, Carbone V, Consolini G, Quattrociocchi V, Stumpo M. Contrasting Scaling Properties of Near-Sun Sub-Alfvénic and Super-Alfvénic Regions. Universe. 2022; 8(7):338. https://doi.org/10.3390/universe8070338
Chicago/Turabian StyleAlberti, Tommaso, Simone Benella, Vincenzo Carbone, Giuseppe Consolini, Virgilio Quattrociocchi, and Mirko Stumpo. 2022. "Contrasting Scaling Properties of Near-Sun Sub-Alfvénic and Super-Alfvénic Regions" Universe 8, no. 7: 338. https://doi.org/10.3390/universe8070338







