Constraining the Viscous Dark Energy Equation of State in f (R, Lm) Gravity
Abstract
:1. Introduction
2. Gravity Theory
3. Motion Equations in Gravity
4. Cosmological Model
5. Data, Methodology, and Physical Interpretation
5.1. H(z) Dataset
5.2. Pantheon Dataset
6. Statefinder Diagnostic
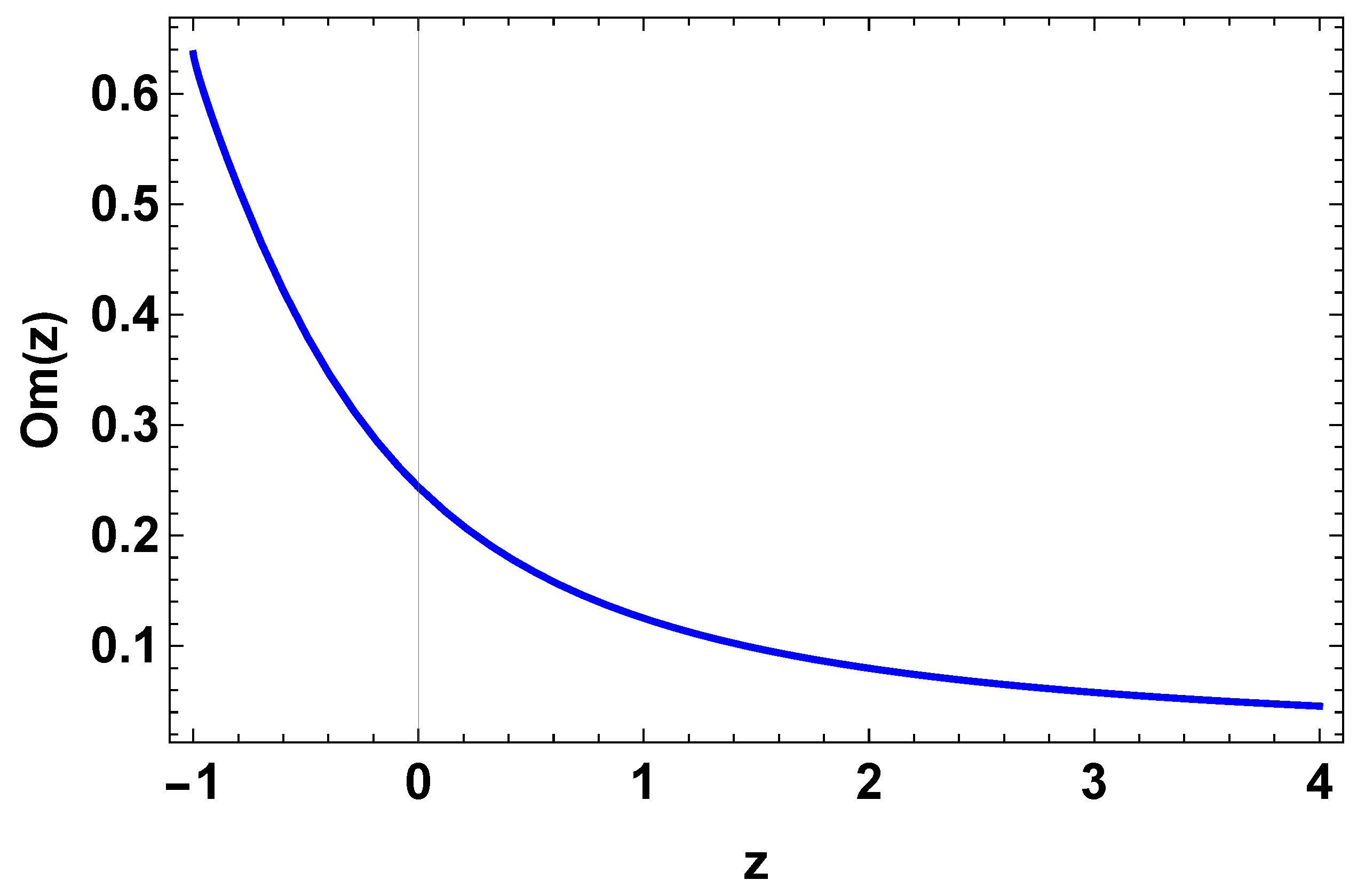
7. Om Diagnostics
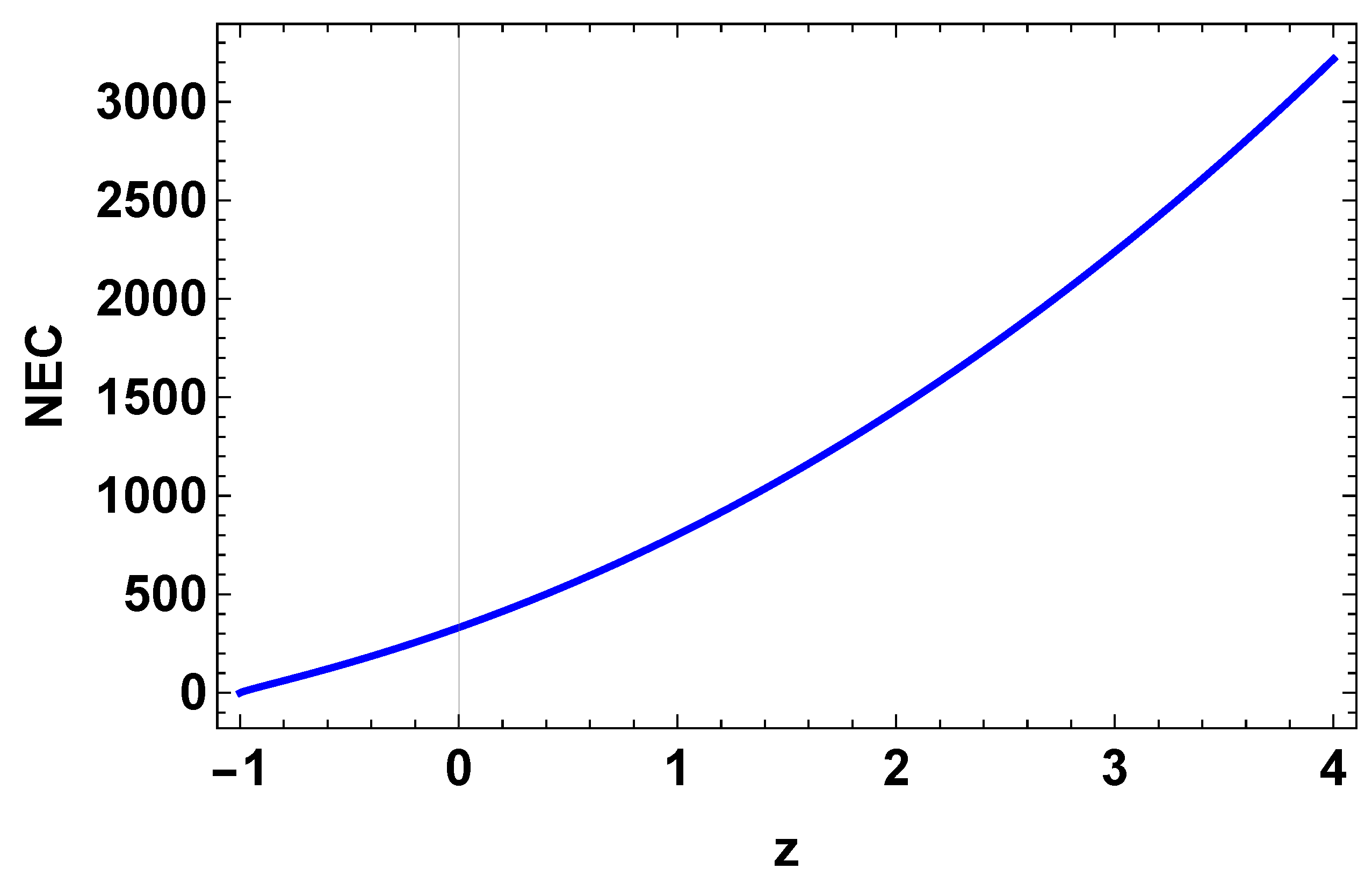
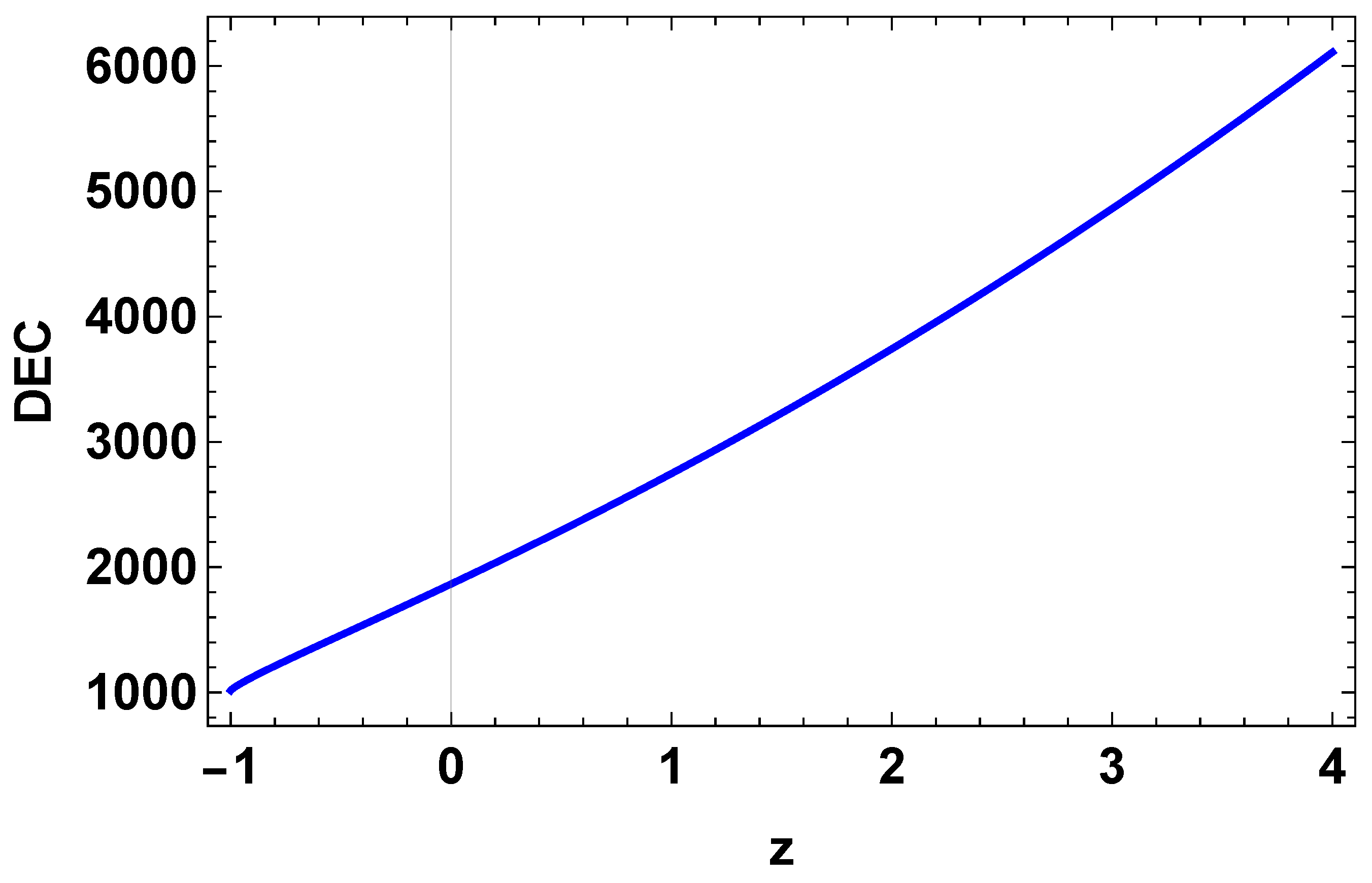
8. Energy Conditions
- Null energy condition (NEC): ;
- Weak energy condition (WEC): and ;
- Dominant energy condition (DEC): ;
- Strong energy condition (SEC): ,
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Scoville, N.; Aussel, H.; Brusa, M.; Capak, P.; Carollo, C.M.; Elvis, M.; Giavalisco, M.; Guzzo, L.; Hasinger, G.; Impey, C. The Cosmic Evolution Survey (COSMOS): Overview. Astrophys. J. Suppl. Ser. 2007, 172, 1. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 2003, 148, 175. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; Page, L.; Spergel, D.N.; Tucker, G.S. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results Astrophys. J. Suppl. 2003, 148, 119–134. [Google Scholar] [CrossRef] [Green Version]
- Caldwell, R.R.; Doran, M. Cosmic microwave background and supernova constraints on quintessence: Concordance regions and target models. Phys. Rev. D 2004, 69, 103517. [Google Scholar] [CrossRef] [Green Version]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560. [Google Scholar] [CrossRef]
- Percival, W.J.; Reid, B.A.; Eisenstein, D.J.; Bahcall, N.A.; Budavari, T.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Ivezic, Z.; Knapp, G.R.; et al. Baryon acoustic oscillations in the Sloan Digital Sky Survey Data Release 7 galaxy sample. Mon. Not. R. Astron. Soc. 2010, 401, 2148. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck Collaboration. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Buchdahl, H.A. Non-Linear Lagrangians and Cosmological Theory. Mon. Not. R. Astron. Soc. 1970, 150, 1. [Google Scholar] [CrossRef] [Green Version]
- Kerner, R. Cosmology without singularity and nonlinear gravitational Lagrangians. Gen. Relativ. Gravit. 1982, 14, 453. [Google Scholar] [CrossRef]
- Kleinert, H.; Schmidt, H.J. Cosmology with Curvature-Saturated Gravitational Lagrangian R. Gen. Relativ. Gravit. 2002, 34, 1295. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D.; Troisi, A. Cosmological viability of f (R)-gravity as an ideal fluid and its compatibility with a matter dominated phase. Phys. Lett. B 2006, 639, 135. [Google Scholar] [CrossRef] [Green Version]
- Tsujikawa, S. Observational signatures of f (R) dark energy models that satisfy cosmological and local gravity constraints. Phys. Rev. D 2008, 77, 023507. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; Tsujikawa, S. Solar system and equivalence principle constraints on gravity by the chameleon approach. Phys. Rev. D 2008, 77, 107501. [Google Scholar] [CrossRef] [Green Version]
- Starobinsky, A.A. Disappearing cosmological constant in f (R) gravity. JETP Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef] [Green Version]
- Faraoni, V. Solar system experiments do not yet veto modified gravity models. Phys. Rev. D 2006, 74, 023529. [Google Scholar] [CrossRef] [Green Version]
- Amendola, L.; Tsujikawa, S. Phantom crossing, equation-of-state singularities, and local gravity constraints in f (R) models. Phys. Lett. B 2008, 660, 125. [Google Scholar] [CrossRef] [Green Version]
- Odintsov, S.D.; Gomez, D.S.C.; Sharov, G.S. Analyzing the H0 tension in f (R) gravity models. Nucl. Phys. B 2021, 966, 115377. [Google Scholar] [CrossRef]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D. The role of energy conditions in f (R) cosmology. Phys. Lett. B 2018, 781, 99–106. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S. Unified cosmic history in modified gravity: From f (R) theory to Lorentz non-invariant models. Phys. Lett. B 2007, 657, 238. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Modified f (R) gravity unifying Rm inflation with the ΛCDM epoch. Phys. Rev. D 2008, 77, 026007. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.; Alcaniz, J.S.; Reboucas, M.J.; Carvalho, F.C. Energy conditions in f (R) gravity. Phys. Rev. D 2007, 76, 083513. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.; Oikonomou, V.K. Unifying inflation with early and late-time dark energy in f (R) gravity. Phys. Dark Univ. 2020, 29, 100602. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inflationary attractors in f (R) gravity. Phys. Lett. B 2020, 807, 135576. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Dark energy oscillations in mimetic f (R) gravity. Phys. Rev. D 2016, 94, 044012. [Google Scholar] [CrossRef] [Green Version]
- Paliathanasis, A. Similarity solutions for the Wheeler–DeWitt equation in f (R)-cosmology. Eur. Phys. J. C 2019, 79, 1031. [Google Scholar] [CrossRef] [Green Version]
- Bertolami, O.; Boehmer, C.G.; Harko, T.; Lobo, F.S.N. Extra force in f (R) modified theories of gravity. Phys. Rev. D 2007, 75, 104016. [Google Scholar] [CrossRef] [Green Version]
- Harko, T. Modified gravity with arbitrary coupling between matter and geometry. Phys. Lett. B 2008, 669, 376. [Google Scholar] [CrossRef] [Green Version]
- Lobo, F.S.N.; Harko, T. Palatini formulation of the conformally invariant f (R, Lm) gravity theory. Int. J. Mod. Phys. D 2022, 31, 2240010. [Google Scholar] [CrossRef]
- Harko, T. Galactic rotation curves in modified gravity with nonminimal coupling between matter and geometry. Phys. Rev. D 2010, 81, 084050. [Google Scholar] [CrossRef] [Green Version]
- Harko, T. The matter Lagrangian and the energy-momentum tensor in modified gravity with nonminimal coupling between matter and geometry. Phys. Rev. D 2010, 81, 044021. [Google Scholar] [CrossRef] [Green Version]
- Harko, T. Thermodynamic interpretation of the generalized gravity models with geometry-matter coupling. Phys. Rev. D 2014, 90, 044067. [Google Scholar] [CrossRef] [Green Version]
- Harko, T.; Shahidi, S. Coupling matter and curvature in Weyl geometry: Conformally invariant f (R, Lm) gravity. Eur. Phys. J. C 2022, 82, 219. [Google Scholar] [CrossRef]
- Bertolami, O.; Harko, T.; Lobo, F.S.N.; Paramos, J. Non-minimal curvature-matter couplings in modified gravity. arXiv 2008, arXiv:0811.2876v1. [Google Scholar]
- Faraoni, V. Viability criterion for modified gravity with an extra force. Phys. Rev. D 2007, 76, 127501. [Google Scholar] [CrossRef] [Green Version]
- Harko, T.; Lobo, F.S.N. f (R, Lm) gravity. Eur. Phys. J. C 2010, 70, 373–379. [Google Scholar]
- Faraoni, V. Cosmology in Scalar-Tensor Gravity; Kluwer Academic: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Bertolami, O.; Páramos, J.; Turyshev, S. General Theory of Relativity: Will it survive the next decade? arXiv 2006, arXiv:grqc/0602016. [Google Scholar]
- Goncalves, B.S.; Moraes, P.H.R.S. Cosmology from non-minimal geometry-matter coupling. arXiv 2021, arXiv:2101.05918. [Google Scholar]
- Labato, R.V.; Carvalho, G.A.; Kelkar, N.G.; Nowakowski, M. Massive white dwarfs in f (R, Lm) gravity. Eur. Phys. J. C 2022, 82, 540. [Google Scholar] [CrossRef]
- Labato, R.V.; Carvalho, G.A.; Bertulani, C.A. Neutron stars in f (R, Lm) gravity with realistic equations of state: Joint-constrains with GW170817, massive pulsars, and the PSR J0030+0451 mass-radius from NICER data. Eur. Phys. J. C 2021, 81, 1013. [Google Scholar] [CrossRef]
- Jaybhaye, L.V.; Mandal, S.; Sahoo, P.K. Constraints on Energy Conditions in f (R, Lm) Gravity. Int. J. Geom. Methods Mod. 2022, 19, 2250050. [Google Scholar] [CrossRef]
- Brevik, I. Viscosity in Modified Gravity. Entropy 2012, 2012, 2302–2310. [Google Scholar] [CrossRef] [Green Version]
- Brevik, I.; Gron, O. Universe Models with Negative Bulk Viscosity. Astrophys. Space Sci. 2013, 347, 399. [Google Scholar] [CrossRef] [Green Version]
- Brevik, I.; Gron, O.; Haro, J.; Odintsov, S.D.; Saridakis, E.N. Viscous cosmology for early- and late-time universe. Int. J. Mod. Phys. D 2017, 26, 1730024. [Google Scholar] [CrossRef] [Green Version]
- Brevik, I.; Makarenko, A.N.; Timoshkin, A.V. Viscous accelerating universe with nonlinear and logarithmic equation of state fluid. Int. J. Geom. Methods Mod. 2019, 16, 1950150. [Google Scholar] [CrossRef]
- Brevik, I.; Normann, B.D. Remarks on cosmological bulk viscosity in different epochs. Symmetry 2020, 2020, 1085. [Google Scholar] [CrossRef]
- Mohan, N.D.J.; Sasidharan, A.; Mathew, T.K. Bulk viscous matter and recent acceleration of the universe based on causal viscous theory. Eur. Phys. J. C 2017, 77, 849. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Odintsov, S.D.; Tepliakov, A.S. The unified history of the viscous accelerating universe and phase transitions. Nucl. Phys. B 2022, 974, 115646. [Google Scholar] [CrossRef]
- Sasidharan, A.; Mathew, T.K. Bulk viscous matter and recent acceleration of the universe. Eur. Phys. J. C 2015, 75, 348. [Google Scholar] [CrossRef] [Green Version]
- Ryden, B. Introduction to Cosmology; Addison Wesley: San Francisco, CA, USA, 2003. [Google Scholar]
- Ren, J.; Meng, X.H. Cosmological model with viscosity media (dark fluid) described by an effective equation of state. Phys. Lett. B 2006, 633, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Brevik, I.; Gorbunova, O. Dark Energy and Viscous Cosmology. Gen. Rel. Grav. 2005, 37, 2039. [Google Scholar] [CrossRef]
- Gron, O. Viscous inflationary universe models. Astrophys. Sci. 1990, 173, 191–225. [Google Scholar] [CrossRef]
- Eckart, C. The Thermodynamics of Irreversible Processes. III. Relativistic Theory of the Simple Fluid. Phys. Rev. 1940, 58, 919. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Gomez, D.S.C.; Sharov, G.S. Testing the equation of state for viscous dark energy. Phys. Rev. D 2020, 101, 044010. [Google Scholar] [CrossRef] [Green Version]
- Fabris, J.C.; Goncalves, S.V.B.; Ribeiro, R.S. Bulk viscosity driving the acceleration of the Universe. Gen. Rel. Grav. 2006, 3, 495. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.H.; Dou, X. Singularity and entropy of the viscosity dark energy model. Comm. Theor. Phys. 2009, 52, 377. [Google Scholar]
- Jaybhaye, L.V.; Solanki, R.; Mandal, S.; Sahoo, P.K. Cosmology in f (R, Lm) gravity. Phys. Lett. B 2022, 831, 137148. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N. Generalized Curvature-Matter Couplings in Modified Gravity. Galaxies 2014, 2014, 410–465. [Google Scholar] [CrossRef] [Green Version]
- Harko, T.; Lobo, F.S.N.; Mimoso, J.P.; Pavon, D. Gravitational induced particle production through a nonminimal curvature–matter coupling. Eur. Phys. J. C 2015, 75, 386. [Google Scholar] [CrossRef] [Green Version]
- Mackey, D.F.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef] [Green Version]
- Sharov, G.S.; Vasiliev, V.O. How predictions of cosmological models depend on Hubble parameter data sets. Math. Model. Geom. 2018, 6, 1. [Google Scholar] [CrossRef]
- Solanki, R.; Pacif, S.K.J.; Parida, A.; Sahoo, P.K. Cosmic acceleration with bulk viscosity in modified f (Q) gravity. Phys. Dark Univ. 2021, 32, 100820. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from PanSTARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder—A new geometrical diagnostic of dark energy. JETP Lett. 2003, 77, 201. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78, 103502. [Google Scholar] [CrossRef] [Green Version]
- Raychaudhuri, A. Relativistic Cosmology I. Phys. Rev. 1955, 98, 1123. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaybhaye, L.V.; Solanki, R.; Mandal, S.; Sahoo, P.K. Constraining the Viscous Dark Energy Equation of State in f (R, Lm) Gravity. Universe 2023, 9, 163. https://doi.org/10.3390/universe9040163
Jaybhaye LV, Solanki R, Mandal S, Sahoo PK. Constraining the Viscous Dark Energy Equation of State in f (R, Lm) Gravity. Universe. 2023; 9(4):163. https://doi.org/10.3390/universe9040163
Chicago/Turabian StyleJaybhaye, Lakhan V., Raja Solanki, Sanjay Mandal, and Pradyumn Kumar Sahoo. 2023. "Constraining the Viscous Dark Energy Equation of State in f (R, Lm) Gravity" Universe 9, no. 4: 163. https://doi.org/10.3390/universe9040163
APA StyleJaybhaye, L. V., Solanki, R., Mandal, S., & Sahoo, P. K. (2023). Constraining the Viscous Dark Energy Equation of State in f (R, Lm) Gravity. Universe, 9(4), 163. https://doi.org/10.3390/universe9040163






