Running Vacuum in the Universe: Phenomenological Status in Light of the Latest Observations, and Its Impact on the σ8 and H0 Tensions
Abstract
:1. Introduction
2. Running Vacuum in the Universe
3. Type I: Running Vacuum Interacting with Dark Matter
3.1. Background Equations
3.2. Perturbation Equations
3.3. Type I with Threshold
4. Type II: Running Vacuum with Running
4.1. Background Equations
| Survey | z | Observable | Measurement | References |
|---|---|---|---|---|
| 6dFGS+SDSS MGS | [Mpc] | [Mpc] | [125] | |
| DR12 BOSS | 0.32 | [127] | ||
| 0.57 | ||||
| WiggleZ | 0.44 | [Mpc] | [Mpc] | [126] |
| 0.60 | [Mpc] | [Mpc] | ||
| 0.73 | [Mpc] | [Mpc] | ||
| DESY3 | [128] | |||
| eBOSS Quasar | 1.48 | [129] | ||
| Ly-Forests | [130] | |||
| z | [km/s/Mpc] | References |
|---|---|---|
| [132] | ||
| [133] | ||
| [132] | ||
| [134] | ||
| 0.1791 * | [135] | |
| 0.1993 * | [135] | |
| [132] | ||
| [134] | ||
| [132] | ||
| 0.3519 * | [135] | |
| 0.3802 * | [136] | |
| [134] | ||
| 0.4004 * | [136] | |
| 0.4247 * | [136] | |
| 0.4497 * | [136] | |
| [137] | ||
| 0.4783 * | [136] | |
| [138] | ||
| 0.5929 * | [135] | |
| 0.6797 * | [135] | |
| [139] | ||
| 0.7812 * | [135] | |
| 0.8754 * | [135] | |
| [138] | ||
| [134] | ||
| 1.037 * | [135] | |
| [134] | ||
| 1.363 * | [140] | |
| [134] | ||
| [134] | ||
| [134] | ||
| 1.965 * | [140] |
4.2. Perturbation Equations
5. Data and Methodology
- Baseline: In our Baseline dataset, we consider the string SNIa+BAO++LSS+CMB. Note that here we do not include the SH0ES data.
- Baseline+SH0ES: The Baseline dataset is in this case complemented with the apparent magnitudes of the SNIa in the host galaxies and their distance moduli employed by SH0ES.
- Baseline (No pol.): The same as in the Baseline case, but now removing the high-ℓ polarization data from the CMB likelihood. That is to say, we have replaced the “CMB” dataset with “CMB (No pol.)”.
- Baseline (No pol.)+SH0ES: The same as in “Baseline (No pol.)”, but including also the data from SH0ES.
| Baseline | |||||
|---|---|---|---|---|---|
| Parameter | CDM | Type-I RRVM | Type-I RRVMthr. | Type-II RRVM | XCDM |
| (km/s/Mpc) | |||||
| - | - | ||||
| - | - | - | - | ||
| - | - | - | - | ||
| M | |||||
| (Mpc) | |||||
| - | −2.04 | +15.34 | −4.18 | ||
| Baseline +SH0ES | |||||
|---|---|---|---|---|---|
| Parameter | CDM | Type-I RRVM | Type-I RRVMthr. | Type-II RRVM | XCDM |
| (km/s/Mpc) | |||||
| - | - | ||||
| - | - | - | - | ||
| - | - | - | - | ||
| M | |||||
| (Mpc) | |||||
| - | |||||
| Baseline (No pol.) | |||||
|---|---|---|---|---|---|
| Parameter | CDM | Type-I RRVM | Type-I RRVMthr. | Type-II RRVM | XCDM |
| (km/s/Mpc) | |||||
| - | - | ||||
| - | - | - | - | ||
| - | - | - | - | ||
| M | |||||
| (Mpc) | |||||
| - | |||||
| Baseline (No pol.) +SH0ES | |||||
|---|---|---|---|---|---|
| Parameter | CDM | Type-I RRVM | Type-I RRVMthr. | Type-II RRVM | XCDM |
| (km/s/Mpc) | |||||
| - | - | ||||
| - | - | - | - | ||
| - | - | - | - | ||
| M | |||||
| (Mpc) | |||||
| - | |||||
6. Discussion of the Results
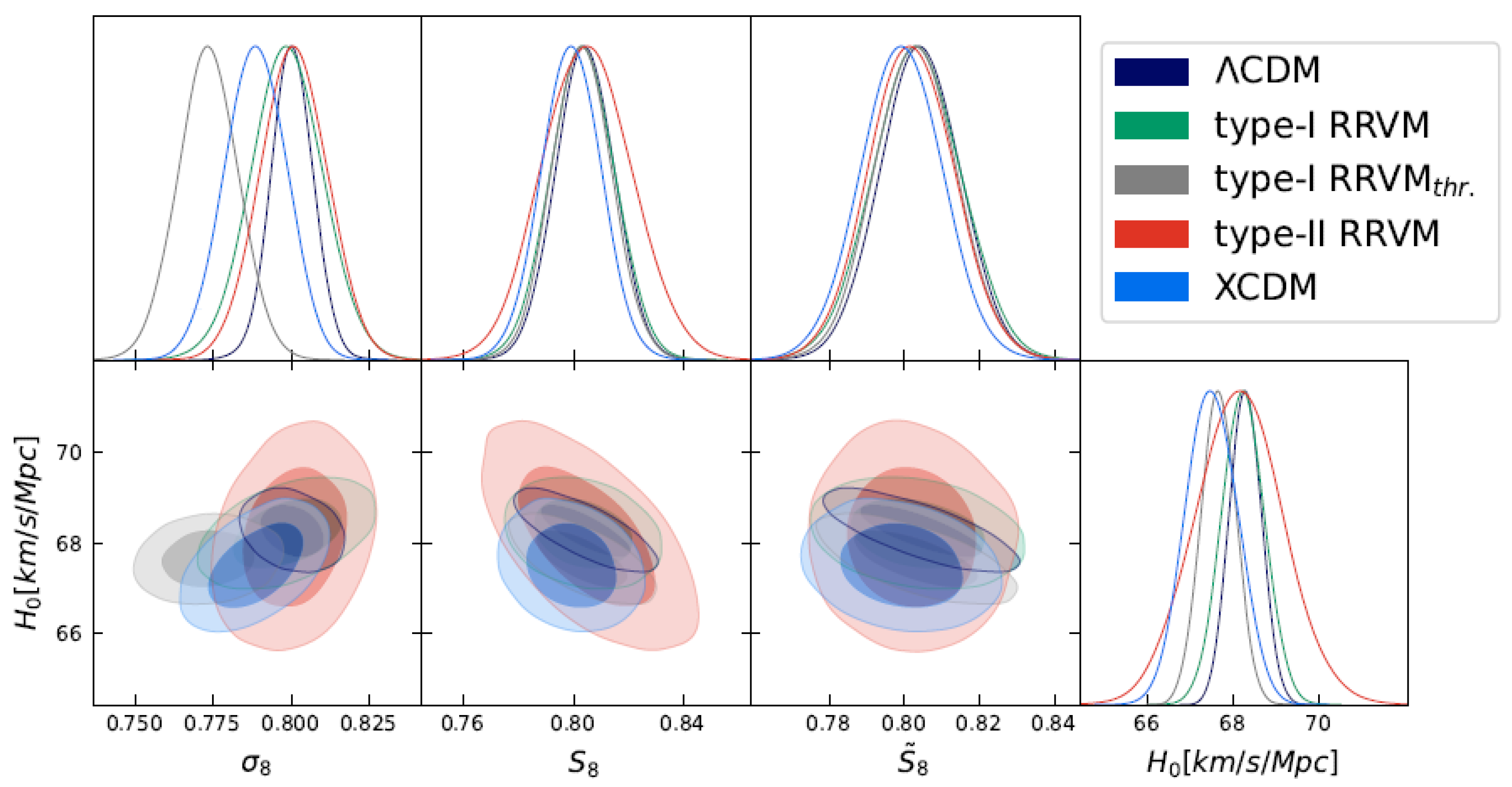
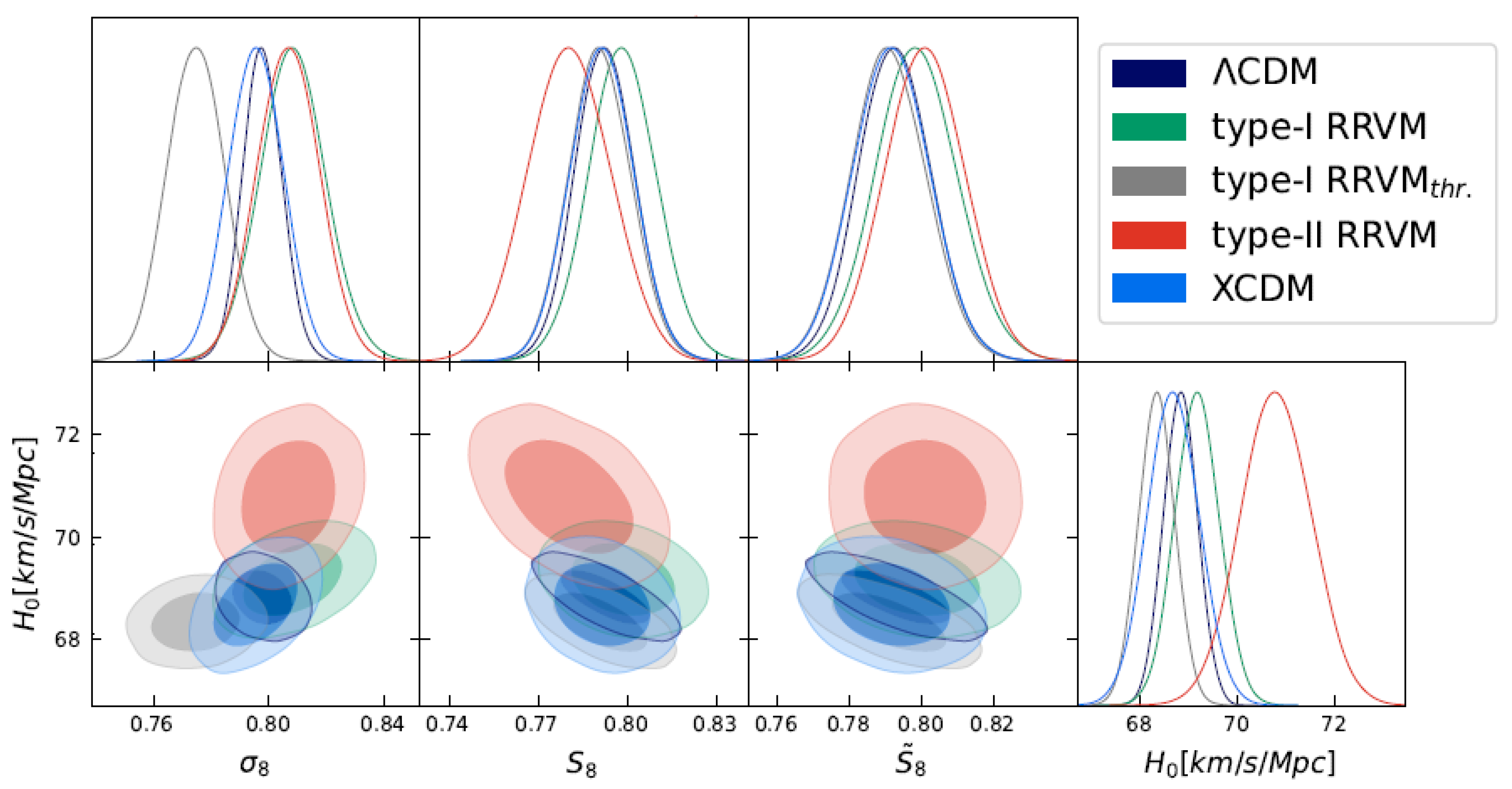

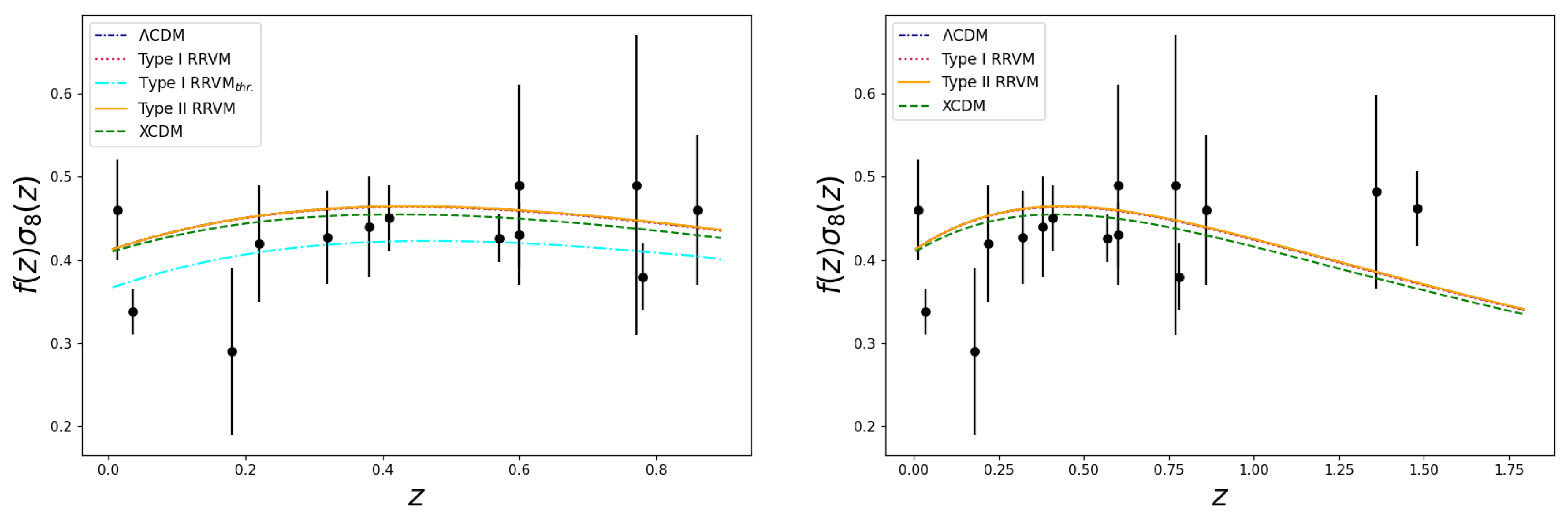
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Additional Tables
| Baseline | |||||
|---|---|---|---|---|---|
| Experiment | CDM | Type-I RRVM | Type-I RRVMthr. | Type-II RRVM | XCDM |
| CMB | |||||
| SNIa | |||||
| BAO- (correl.) | |||||
| BAO | |||||
| Baseline+SH0ES | |||||
|---|---|---|---|---|---|
| Experiment | CDM | Type-I RRVM | Type-I RRVMthr. | Type-II RRVM | XCDM |
| CMB | |||||
| SNIa | |||||
| BAO- (correl.) | |||||
| BAO | |||||
| Baseline (No pol.) | |||||
|---|---|---|---|---|---|
| Experiment | CDM | Type-I RRVM | Type-I RRVMthr. | Type-II RRVM | XCDM |
| CMB | |||||
| SNIa | |||||
| BAO- (correl.) | |||||
| BAO | |||||
| 1 | https://lesgourg.github.io/class_public/class.html, accessed on 22 May 2023. |
| 2 | In practice this means that we have first fitted the value of as one more free parameter in our analysis. Subsequently, we have assumed that the threshold point remains fixed at that point; see also [107,108,109,110] for a binned/tomographic approach to the DE. In our case, we have just one threshold whose existence might be motivated by QFT calculations [30,31]. |
| 3 | If (dark) matter is not conserved but G remains constant, we retrieve of course our previous scenario (16). In general, we may expect a mixture of both situations, but we shall refrain from dealing with the general case since it would introduce extra parameters; see, however, [111,112] for additional discussions that can be relevant for studies on the possible variation in the fundamental constants of nature. |
| 4 | It should be clear that is not a dynamical degree of freedom, in contradistinction to Brans–Dicke-type theories of gravitation [113], and therefore does not mediate any sort of long-range interaction that should be subdued by screening mechanisms. |
| 5 | Let us emphasize that Equation (56) is valid only in the MDE, and we have also pointed out that const. in the DE epoch. This means that G becomes more and more rigid when it transits from the MDE to the DE epoch, and therefore the actual limits on are weaker than those that we have roughly estimated. This works to our benefit of course. In fact, a detailed calculation would require computing in the DE epoch, but it proves unnecessary once we have shown that even in the most unfavorable case (i.e., when evolves more rapidly than it actually does in the DE epoch) the obtained limits on are nonetheless preserved by our fits. Notice that type-I models are totally unaffected by these limits, since G is in this case constant, so can be, in principle, larger for them. |
| 6 | https://gitlab.com/mmoresco/CCcovariance/-/blob/master/examples/CC_covariance.ipynb, accessed on 22 May 2023. |
| 7 | While it is common to rescale the measured values of by a factor to account for the Alcock–Paczynski (AP) effect [157] (in which the tildes denote the quantities computed in the fiducial cosmology employed by the galaxy surveys), there does not not seem to exist a general consensus on the exact correction to apply; see, e.g., [158] and references therein. In this sense, the above formula should be considered as just a rough estimate. We have checked that the AP-rescaling introduces negligible shifts in our fitting results, a conclusion that is well in accordance with previous analyses in the literature [38,39,158]. For this reason, we have opted to not include this correction in our work. |
| 8 | This region is also preferred by late-time dynamical DE models when fitted to a very wide variety of background data that are independent from the direct cosmic distance ladder and CMB, km/s/Mpc [161]. See [162,163,164,165] for measurements of more in accordance with SH0ES obtained also with the tip of the red giant branch method. |
| 9 | https://baudren.github.io/montepython.html, accessed on 22 May 2023. |
| 10 | https://getdist.readthedocs.io/en/latest/, accessed on 22 May 2023. |
| 11 | See Section 3.3 for the practical implementation. |
| 12 | |
| 13 | |
| 14 | Noticeably, the central values of , , and the absolute magnitude of SNIa, M, obtained for the type-II RRVM when the CMB polarization data are excluded in the fitting analysis are in very good agreement with the model-independent measurements from low-z data reported in [152], which are also independent from the main drivers of the tension. For the Hubble constant, these authors find km/s/Mpc. However, these measurements still have large uncertainties and cannot arbitrate the Hubble tension yet; see also [179]. |
| 15 |
References
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Peebles, P.J.E. Tests of Cosmological Models Constrained by Inflation. Astrophys. J. 1984, 284, 439–444. [Google Scholar] [CrossRef]
- Turner, M.S. The Road to Precision Cosmology. Annu. Rev. Nucl. Part. Sci. 2022, 72, 1–35. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T. Cosmological constant: The Weight of the vacuum. Phys. Rept. 2003, 380, 235–320. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Tonry, J.; Jha, C.J.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- de Bernardis, P.; Ade, P.A.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; Vittorio, N.; De Gasperis, G.; et al. A Flat universe from high resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955–959. [Google Scholar] [CrossRef] [Green Version]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.-J.; Tegmark, M.; York, D.G.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef] [Green Version]
- Tegmark, M.; Eisenstein, D.J.; Strauss, M.A.; Weinberg, D.H.; Blanton, M.R.; Frieman, J.A.; Blanton, M.R.; Frieman, J.A.; Fukugita, M.; York, D.G.; et al. Cosmological Constraints from the SDSS Luminous Red Galaxies. Phys. Rev. D 2006, 74, 123507. [Google Scholar] [CrossRef] [Green Version]
- Komatsu, E.; Dunkley, J.; Nolta, M.R.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Limon, M.; Wright, E.L.; et al. Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2009, 180, 330–376. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Macri, L.; Casertano, S.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R. A 3% Solution: Determination of the Hubble Constant with the Hubble Space Telescope and Wide Field Camera 3. Astrophys. J. 2011, 730, 119, Erratum in Astrophys. J. 2011, 732, 129. [Google Scholar] [CrossRef] [Green Version]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Roudier, G.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Roudier, G.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Solà, J. Cosmological constant and vacuum energy: Old and new ideas. J. Phys. Conf. Ser. 2013, 453, 012015. [Google Scholar] [CrossRef]
- Steinhardt, P.J. A quintessential introduction to dark energy. Phil. Trans. Roy. Soc. Lond. A 2003, 361, 2497–2513. [Google Scholar] [CrossRef] [Green Version]
- Solà, J.; Gómez-Valent, A. The CDM cosmology: From inflation to dark energy through running Λ. Int. J. Mod. Phys. D 2015, 24, 1541003. [Google Scholar] [CrossRef] [Green Version]
- Solà Peracaula, J. The cosmological constant problem and running vacuum in the expanding universe. Phil. Trans. Roy. Soc. Lond. A 2022, 380, 20210182. [Google Scholar] [CrossRef]
- Lemaître, G. Evolution of the expanding universe. Proc. Natl. Acad. Sci. USA 1934, 20, 12–17. [Google Scholar] [CrossRef] [Green Version]
- Grøn, O.G. A hundred years with the cosmological constant. Eur. J. Phys. 2018, 39, 043001. [Google Scholar] [CrossRef]
- Zel’dovich, Y. Cosmological constant and elementary particles. Sov. Phys. JETP. Lett. 1967, 6, 3167. [Google Scholar] [CrossRef]
- Zel’dovich, Y. The cosmological constant and the theory of elementary particles. Sov. Phys. Ups. 1968, 11, 381. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef] [Green Version]
- Tsujikawa, S. Quintessence: A Review. Class. Quant. Grav. 2013, 30, 214003. [Google Scholar] [CrossRef] [Green Version]
- Grøn, O. Repulsive Gravitation and Inflationary Universe Models. Am. J. Phys. 1986, 54, 46–52. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Z.; Unruh, W.G. How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe. Phys. Rev. D 2017, 95, 103504. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Pulido, C.; Solà, J. Running vacuum in quantum field theory in curved spacetime: Renormalizing ρvac without ∼m4 terms. Eur. Phys. J. C 2020, 80, 692. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Solà Peracaula, J. Renormalizing the vacuum energy in cosmological spacetime: Implications for the cosmological constant problem. Eur. Phys. J. C 2022, 82, 551. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Solà Peracaula, J. Equation of state of the running vacuum. Eur. Phys. J. C 2022, 82, 1137. [Google Scholar] [CrossRef]
- Moreno-Pulido, C.; Solà Peracaula, J.; Cheraghchi, S. Running vacuum in QFT in FLRW spacetime: The dynamics of ρvac(H) from the quantized matter fields. arXiv 2023, arXiv:2301.05205. [Google Scholar]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, Ö.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Yang, W.; et al. Snowmass2021—Letter of interest cosmology intertwined II: The hubble constant tension. Astropart. Phys. 2021, 131, 102605. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yang, T. Running Hubble Tension and a H0 Diagnostic. Phys. Rev. D 2021, 103, 103509. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble constant tension in the SNe Ia Pantheon sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, Ö.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Arendse, N.; Asgari, M.; Ballardini, M.; Yang, W.; et al. Cosmology Intertwined III: fσ8 and S8. Astropart. Phys. 2021, 131, 102604. [Google Scholar] [CrossRef]
- Macaulay, E.; Wehus, I.K.; Eriksen, H.K. Lower Growth Rate from Recent Redshift Space Distortion Measurements than Expected from Planck. Phys. Rev. Lett. 2013, 111, 161301. [Google Scholar] [CrossRef]
- Nesseris, S.; Pantazis, G.; Perivolaropoulos, L. Tension and constraints on modified gravity parametrizations of Geff(z) from growth rate and Planck data. Phys. Rev. 2017, D96, 023542. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.; Ishak, M. Cosmological discordances II: Hubble constant, Planck and large-scale-structure data sets. Phys. Rev. D 2017, 96, 083532. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Valent, A.; Solà Peracaula, J. Density perturbations for running vacuum: A successful approach to structure formation and to the σ8-tension. Mon. Not. Roy. Astron. Soc. 2018, 478, 126–145. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Quintero, C.; Ishak, M.; Fox, L.; Lin, W. Cosmological discordances. III. More on measure properties, large-scale-structure constraints, the Hubble constant and Planck data. Phys. Rev. D 2019, 100, 123538. [Google Scholar] [CrossRef] [Green Version]
- Asgari, M.; Lin, C.A.; Joachimi, B.; Giblin, B.; Heymans, C.; Hildebrandt, H.; Kannawadi, A.; Stolzner, B.; Troster, T.; Valentijn, E.; et al. KiDS-1000 Cosmology: Cosmic shear constraints and comparison between two point statistics. Astron. Astrophys. 2021, 645, A104. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Smith, M.; et al. Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Nguyen, N.M.; Huterer, D.; Wen, Y. Evidence for suppression of structure growth in the concordance cosmological model. arXiv 2023, arXiv:2302.01331. [Google Scholar]
- Adil, S.A.; Akarsu, O.; Malekjani, M.; Colgáin, E.O.; Pourojaghi, S.; Sen, A.A.; Sheikh-Jabbari, M.M. S8 increases with effective redshift in ΛCDM cosmology. arXiv 2023, arXiv:2303.06928. [Google Scholar]
- Heisenberg, L.; Villarrubia-Rojo, H.; Zosso, J. Can late-time extensions solve the H0 and σ8 tensions? Phys. Rev. D 2022, 106, 043503. [Google Scholar] [CrossRef]
- Marra, V.; Perivolaropoulos, L. Rapid transition of Geff at zt≃0.01 as a possible solution of the Hubble and growth tensions. Phys. Rev. D 2021, 104, L021303. [Google Scholar] [CrossRef]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. w-M phantom transition at zt < 0.1 as a resolution of the Hubble tension. Phys. Rev. D 2021, 103, 083517. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Hubble tension or a transition of the Cepheid SnIa calibrator parameters? Phys. Rev. D 2021, 104, 123511. [Google Scholar] [CrossRef]
- Alestas, G.; Camarena, D.; Di Valentino, E.; Kazantzidis, L.; Marra, V.; Nesseris, S.; Perivolaropoulos, L. Late-transition versus smooth H(z)-deformation models for the resolution of the Hubble crisis. Phys. Rev. D 2022, 105, 063538. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. A Reanalysis of the Latest SH0ES Data for H0: Effects of New Degrees of Freedom on the Hubble Tension. Universe 2022, 8, 502. [Google Scholar] [CrossRef]
- Grande, J.; Solà, J.; Stefancic, H. LXCDM: A Cosmon model solution to the cosmological coincidence problem? JCAP 2006, 8, 11. [Google Scholar] [CrossRef] [Green Version]
- Grande, J.; Pelinson, A.; Solà, J. Dark energy perturbations and cosmic coincidence. Phys. Rev. D 2009, 79, 043006. [Google Scholar] [CrossRef] [Green Version]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Pettorino, V.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar] [CrossRef]
- Dainotti, M.; De Simone, B.; Montani, G.; Schiavone, T.; Lambiase, G. The Hubble constant tension: Current status and future perspectives through new cosmological probes. arXiv 2023, arXiv:2301.10572. [Google Scholar]
- Shapiro, I.L.; Solà, J. Scaling behavior of the cosmological constant: Interface between quantum field theory and cosmology. JHEP 2002, 2, 6. [Google Scholar] [CrossRef] [Green Version]
- Babic, A.; Guberina, B.; Horvat, R.; Stefancic, H. Renormalization-group running cosmologies. A Scale-setting procedure. Phys. Rev. 2005, D71, 124041. [Google Scholar] [CrossRef] [Green Version]
- Alvarez, P.D.; Koch, B.; Laporte, C.; Rincón, A. Can scale-dependent cosmology alleviate the H0 tension? JCAP 2021, 6, 19. [Google Scholar] [CrossRef]
- Ozer, M.; Taha, M. A Solution to the Main Cosmological Problems. Phys. Lett. B 1986, 171, 363–365. [Google Scholar] [CrossRef]
- Bertolami, O. Time dependent cosmological term. Nuovo Cim. B 1986, 93, 36–42. [Google Scholar] [CrossRef]
- Freese, K.; Adams, F.C.; Frieman, J.A.; Mottola, E. Cosmology with Decaying Vacuum Energy. Nucl. Phys. B 1987, 287, 797–814. [Google Scholar] [CrossRef] [Green Version]
- Peebles, P.J.E.; Ratra, B. Cosmology with a Time Variable Cosmological Constant. Astrophys. J. 1988, 325, L17. [Google Scholar] [CrossRef]
- Chen, W.; Wu, Y.S. Implications of a cosmological constant varying as R-2. Phys. Rev. D 1992, 41, 695–698, Erratum in Phys. Rev. D 1992, 45, 4728. [Google Scholar] [CrossRef]
- Abdel-Rahman, A.M.M. Singularity–free decaying vacuum cosmologies. Phys. Rev. D 1992, 45, 3497–3511. [Google Scholar] [CrossRef]
- Carvalho, J.; Lima, J.; Waga, I. On the cosmological consequences of a time dependent lambda term. Phys. Rev. D 1992, 46, 2404–2407. [Google Scholar] [CrossRef]
- Arcuri, R.C.; Waga, I. Growth of density inhomogeneities in Newtonian cosmological models with variable Lambda. Phys. Rev. D 1994, 50, 2928–2931. [Google Scholar] [CrossRef] [PubMed]
- Waga, I. Decaying vacuum flat cosmological models: Expressions for some observable quantities and their properties. Astrophys. J. 1993, 414, 436–448. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Maia, J.M.F. Deflationary cosmology with decaying vacuum energy density. Phys. Rev. D 1994, 49, 5597–5600. [Google Scholar] [CrossRef] [PubMed]
- Lima, J.A.S.; Trodden, M. Decaying vacuum energy and deflationary cosmology in open and closed universes. Phys. Rev. D 1996, 53, 4280–4286. [Google Scholar] [CrossRef] [Green Version]
- Arbab, A.I. Cosmological models with variable cosmological and gravitational constants and bulk viscous models. Gen. Rel. Grav. 1997, 29, 61–74. [Google Scholar] [CrossRef]
- Espana-Bonet, C.; Ruiz-Lapuente, P.; Shapiro, I.L.; Sola, J. Testing the running of the cosmological constant with type Ia supernovae at high z. JCAP 2004, 2, 6. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Meng, X.H. Can vacuum decay in our universe? Class. Quant. Grav. 2005, 22, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Borges, H.A.; Carneiro, S. Friedmann cosmology with decaying vacuum density. Gen. Rel. Grav. 2005, 37, 1385–1394. [Google Scholar] [CrossRef] [Green Version]
- Alcaniz, J.S.; Lima, J.A.S. Interpreting cosmological vacuum decay. Phys. Rev. D 2005, 72, 063516. [Google Scholar] [CrossRef] [Green Version]
- Barrow, J.D.; Clifton, T. Cosmologies with energy exchange. Phys. Rev. D 2006, 73, 103520. [Google Scholar] [CrossRef] [Green Version]
- Costa, F.E.M.; Alcaniz, J.S. Cosmological consequences of a possible Λ-dark matter interaction. Phys. Rev. D 2010, 81, 043506. [Google Scholar] [CrossRef] [Green Version]
- Bessada, D.; Miranda, O.D. Probing a cosmological model with a Λ = Λ0+3βH2 decaying vacuum. Phys. Rev. D 2013, 88, 083530. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Valent, A.; Solà, J. Vacuum models with a linear and a quadratic term in H: Structure formation and number counts analysis. Mon. Not. Roy. Astron. Soc. 2015, 448, 2810–2821. [Google Scholar] [CrossRef]
- Overduin, J.; Cooperstock, F. Evolution of the scale factor with a variable cosmological term. Phys. Rev. D 1998, 58, 043506. [Google Scholar] [CrossRef] [Green Version]
- Basilakos, S.; Mavromatos, N.E.; Solà Peracaula, J. Gravitational and Chiral Anomalies in the Running Vacuum Universe and Matter-Antimatter Asymmetry. Phys. Rev. 2020, D101, 045001. [Google Scholar] [CrossRef] [Green Version]
- Basilakos, S.; Mavromatos, N.E.; Solà Peracaula, J. Quantum Anomalies in String-Inspired Running Vacuum Universe: Inflation and Axion Dark Matter. Phys. Lett. 2020, B803, 135342. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Solà Peracaula, J. Stringy-running-vacuum-model inflation: From primordial gravitational waves and stiff axion matter to dynamical dark energy. Eur. Phys. J. Spec. Top. 2021, 230, 2077–2110. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Solà Peracaula, J. Inflationary physics and trans-Planckian conjecture in the stringy running vacuum model: From the phantom vacuum to the true vacuum. Eur. Phys. J. Plus 2021, 136, 1152. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Running vacuum against the H0 and σ8 tensions. EPL 2021, 134, 19001. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J. The H0 tension in light of vacuum dynamics in the Universe. Phys. Lett. 2017, B774, 317–324. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Solà, J. Relaxing the σ8-tension through running vacuum in the Universe. EPL 2017, 120, 39001. [Google Scholar] [CrossRef] [Green Version]
- Solà Peracaula, J.; de Cruz Pérez, J.; Gómez-Valent, A. Dynamical dark energy vs. Λ = const in light of observations. EPL 2018, 121, 39001. [Google Scholar] [CrossRef] [Green Version]
- Solà, J. Cosmological constant vis-a-vis dynamical vacuum: Bold challenging the ΛCDM. Int. J. Mod. Phys. A 2016, 31, 1630035. [Google Scholar] [CrossRef] [Green Version]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. First evidence of running cosmic vacuum: Challenging the concordance model. Astrophys. J. 2017, 836, 43. [Google Scholar] [CrossRef] [Green Version]
- Solà Peracaula, J.; de Cruz Pérez, J.; Gómez-Valent, A. Possible signals of vacuum dynamics in the Universe. Mon. Not. Roy. Astron. Soc. 2018, 478, 4357–4373. [Google Scholar] [CrossRef] [Green Version]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. Hints of dynamical vacuum energy in the expanding Universe. Astrophys. J. 2015, 811, L14. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Valent, A.; Solà, J.; Basilakos, S. Dynamical vacuum energy in the expanding Universe confronted with observations: A dedicated study. JCAP 2015, 1, 4. [Google Scholar] [CrossRef] [Green Version]
- Solà Peracaula, J. Running Vacuum and the ΛCDM tensions. In Proceedings of the Corfu Summer Institute 2021 “School and Workshops on Elementary Particle Physics and Gravity" (CORFU2021), Corfu, Greece, 29 August–9 October 2022; p. 106. [Google Scholar] [CrossRef]
- Solà Peracaula, J. Tensions in the ΛCDM and vacuum dynamics. Int. J. Mod. Phys. 2018, A33, 1844009. [Google Scholar] [CrossRef]
- Solà, J. Dark energy: A Quantum fossil from the inflationary Universe? J. Phys. 2008, A41, 164066. [Google Scholar] [CrossRef]
- Basilakos, S.; Polarski, D.; Solà, J. Generalizing the running vacuum energy model and comparing with the entropic-force models. Phys. Rev. D 2012, 86, 043010. [Google Scholar] [CrossRef] [Green Version]
- Basilakos, S.; Solà, J. Entropic-force dark energy reconsidered. Phys. Rev. D 2014, 90, 023008. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Valent, A.; Karimkhani, E.; Solà, J. Background history and cosmic perturbations for a general system of self-conserved dynamical dark energy and matter. JCAP 2015, 12, 048. [Google Scholar] [CrossRef]
- Rezaei, M.; Malekjani, M.; Solà, J. Can dark energy be expressed as a power series of the Hubble parameter? Phys. Rev. D 2019, 100, 023539. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, M.; Solà Peracaula, J. Running vacuum versus holographic dark energy: A cosmographic comparison. Eur. Phys. J. C 2022, 82, 765. [Google Scholar] [CrossRef]
- Lesgourgues, J. The Cosmic Linear Anisotropy Solving System (CLASS) I: Overview. arXiv 2011, arXiv:1104.2932. [Google Scholar]
- Blas, D.; Lesgourgues, J.; Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS) II: Approximation schemes. JCAP 2011, 1107, 34. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.P.; Bertschinger, E. Cosmological perturbation theory in the synchronous and conformal Newtonian gauges. Astrophys. J. 1995, 455, 7–25. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wands, D.; Xu, L.; De-Santiago, J.; Hojjati, A. Cosmological constraints on a decomposed Chaplygin gas. Phys. Rev. D 2013, 87, 083503. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wands, D.; Zhao, G.B.; Xu, L. Post-Planck constraints on interacting vacuum energy. Phys. Rev. D 2014, 90, 023502. [Google Scholar] [CrossRef] [Green Version]
- Salvatelli, V.; Said, N.; Bruni, M.; Melchiorri, A.; Wands, D. Indications of a late-time interaction in the dark sector. Phys. Rev. Lett. 2014, 113, 181301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martinelli, M.; Hogg, N.B.; Peirone, S.; Bruni, M.; Wands, D. Constraints on the interacting vacuum–geodesic CDM scenario. Mon. Not. Roy. Astron. Soc. 2019, 488, 3423–3438. [Google Scholar] [CrossRef] [Green Version]
- Hogg, N.B.; Bruni, M.; Crittenden, R.; Martinelli, M.; Peirone, S. Latest evidence for a late time vacuum–geodesic CDM interaction. Phys. Dark Univ. 2020, 29, 100583. [Google Scholar] [CrossRef]
- Goh, L.W.K.; Gómez-Valent, A.; Pettorino, V.; Kilbinger, M. Constraining constant and tomographic coupled dark energy with low-redshift and high-redshift probes. Phys. Rev. D 2023, 107, 083503. [Google Scholar] [CrossRef]
- Fritzsch, H.; Solà, J. Matter Non-conservation in the Universe and Dynamical Dark Energy. Class. Quant. Grav. 2012, 29, 215002. [Google Scholar] [CrossRef] [Green Version]
- Fritzsch, H.; Solà, J. Fundamental constants and cosmic vacuum: The micro and macro connection. Mod. Phys. Lett. A 2015, 30, 1540034. [Google Scholar] [CrossRef] [Green Version]
- Brans, C.; Dicke, R. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev 1961, 124, 925. [Google Scholar] [CrossRef]
- Uzan, J.P. Varying Constants, Gravitation and Cosmology. Living Rev. Rel. 2011, 14, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Theureau, G.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Zhu, W.W.; Desvignes, G.; Wex, N.; Caballero, R.N.; Champion, D.J.; Demorest, P.B.; Ellis, J.A.; Janssen, G.H.; Tiburzi, C.; Kramer, M.; et al. Tests of Gravitational Symmetries with Pulsar Binary J1713+0747. Mon. Not. Roy. Astron. Soc. 2018, 482, 3249–3260. [Google Scholar] [CrossRef] [Green Version]
- Genova, A.; Mazarico, E.; Goossens, S.; Lemoine, F.G.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Solar system expansion and strong equivalence principle as seen by the NASA MESSENGER mission. Nat. Commun. 2018, 9, 289. [Google Scholar] [CrossRef] [Green Version]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Brans–Dicke Gravity with a Cosmological Constant Smoothes Out ΛCDM Tensions. Astrophys. J. Lett. 2019, 886, L6. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Brans–Dicke cosmology with a Λ-term: A possible solution to ΛCDM tensions. Class. Quant. Grav. 2020, 37, 245003. [Google Scholar] [CrossRef]
- de Cruz Pérez, J.; Solà Peracaula, J.; Singh, C.P. Running vacuum in Brans-Dicke theory: A possible cure for the σ8 and H0 tensions. arXiv 2023, arXiv:2302.04807. [Google Scholar]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rept. 2012, 513, 1–189. [Google Scholar] [CrossRef] [Green Version]
- Avilez, A.; Skordis, C. Cosmological constraints on Brans-Dicke theory. Phys. Rev. Lett. 2014, 113, 11101. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Valent, A.; Hassan Puttasiddappa, P. Difficulties in reconciling non-negligible differences between the local and cosmological values of the gravitational coupling in extended Brans-Dicke theories. JCAP 2021, 09, 40. [Google Scholar] [CrossRef]
- Shapiro, I.L.; Sola, J.; Stefancic, H. Running G and Lambda at low energies from physics at M(X): Possible cosmological and astrophysical implications. JCAP 2005, 2005, 12. [Google Scholar] [CrossRef] [Green Version]
- Carter, P.; Beutler, F.; Percival, W.J.; Blake, C.; Koda, J.; Ross, A.J. Low Redshift Baryon Acoustic Oscillation Measurement from the Reconstructed 6-degree Field Galaxy Survey. Mon. Not. Roy. Astron. Soc. 2018, 481, 2371–2383. [Google Scholar] [CrossRef] [PubMed]
- Kazin, E.A.; Koda, J.; Blake, C.; Padmanabhan, N.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Yee, H.K.; Croom, S.; et al. The WiggleZ Dark Energy Survey: Improved distance measurements to z = 1 with reconstruction of the baryonic acoustic feature. Mon. Not. Roy. Astron. Soc. 2014, 441, 3524–3542. [Google Scholar] [CrossRef] [Green Version]
- Gil-Marín, H.; Percival, W.J.; Verde, L.; Brownstein, J.R.; Chuang, C.H.; Kitaura, F.S.; Rodríguez-Torres, S.A.; Olmstead, M.D. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: RSD measurement from the power spectrum and bispectrum of the DR12 BOSS galaxies. Mon. Not. Roy. Astron. Soc. 2017, 465, 1757–1788. [Google Scholar] [CrossRef] [Green Version]
- Abbott, T.M.C.; Aguena, M.; Allam, S.; Amon, A.; Andrade-Oliveira, F.; Asorey, J.; Avila, S.; Bernstein, G.M.; Bertin, E.; Brandao-Souza, A.; et al. Dark Energy Survey Year 3 results: A 2.7% measurement of baryon acoustic oscillation distance scale at redshift 0.835. Phys. Rev. D 2022, 105, 043512. [Google Scholar] [CrossRef]
- Hou, J.; Sánchez, A.G.; Ross, A.J.; Smith, A.; Neveux, R.; Bautista, J.; Burtin, E.; Zhao, C.; Scoccimarro, R.; Vivek, M.; et al. The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: BAO and RSD measurements from anisotropic clustering analysis of the Quasar Sample in configuration space between redshift 0.8 and 2.2. Mon. Not. Roy. Astron. Soc. 2020, 500, 1201–1221. [Google Scholar] [CrossRef]
- Des Bourboux, H.D.M.; Rich, J.; Font-Ribera, A.; de Sainte Agathe, V.; Farr, J.; Etourneau, T.; Le Goff, J.-M.; Cuceu, A.; Youles, S.; Balland, C.; et al. The Completed SDSS-IV Extended Baryon Oscillation Spectroscopic Survey: Baryon Acoustic Oscillations with Lyα Forests. Astrophys. J. 2020, 901, 153. [Google Scholar] [CrossRef]
- Moresco, M.; Jimenez, R.; Verde, L.; Cimatti, A.; Pozzetti, L. Setting the Stage for Cosmic Chronometers. II. Impact of Stellar Population Synthesis Models Systematics and Full Covariance Matrix. Astrophys. J. 2020, 898, 82. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, S.; Zhang, T.J.; Sun, Y.C. Four new observational H(z) data from luminous red galaxies in the Sloan Digital Sky Survey data release seven. Res. Astron. Astrophys. 2014, 14, 1221–1233. [Google Scholar] [CrossRef] [Green Version]
- Jiménez, R.; Verde, L.; Treu, T.; Stern, D. Constraints on the equation of state of dark energy and the Hubble constant from stellar ages and the CMB. Astrophys. J. 2003, 593, 622–629. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jiménez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. 2005, D71, 123001. [Google Scholar] [CrossRef] [Green Version]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Welikala, N.; et al. Improved constraints on the expansion rate of the Universe up to z 1.1 from the spectroscopic evolution of cosmic chronometers. JCAP 2012, 1208, 6. [Google Scholar] [CrossRef] [Green Version]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jiménez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. JCAP 2016, 1605, 14. [Google Scholar] [CrossRef] [Green Version]
- Ratsimbazafy, A.; Loubser, S.; Crawford, S.; Cress, C.; Bassett, B.; Nichol, R.; Väisänen, P. Age-dating Luminous Red Galaxies observed with the Southern African Large Telescope. Mon. Not. Roy. Astron. Soc. 2017, 467, 3239–3254. [Google Scholar] [CrossRef] [Green Version]
- Stern, D.; Jiménez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic Chronometers: Constraining the Equation of State of Dark Energy. I: H(z) Measurements. JCAP 2010, 1002, 8. [Google Scholar] [CrossRef] [Green Version]
- Borghi, N.; Moresco, M.; Cimatti, A. Toward a Better Understanding of Cosmic Chronometers: A New Measurement of H(z) at z ∼ 0.7. Astrophys. J. Lett. 2022, 928, L4. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z∼2. Mon. Not. Roy. Astron. Soc. 2015, 450, L16–L20. [Google Scholar] [CrossRef] [Green Version]
- Avila, F.; Bernui, A.; de Carvalho, E.; Novaes, C.P. The growth rate of cosmic structures in the local Universe with the ALFALFA survey. Mon. Not. Roy. Astron. Soc. 2021, 505, 3404–3413. [Google Scholar] [CrossRef]
- Said, K.; Colless, M.; Magoulas, C.; Lucey, J.R.; Hudson, M.J. Joint analysis of 6dFGS and SDSS peculiar velocities for the growth rate of cosmic structure and tests of gravity. Mon. Not. Roy. Astron. Soc. 2020, 497, 1275–1293. [Google Scholar] [CrossRef]
- Simpson, F.; Blake, C.; Peacock, J.A.; Baldry, I.; Bland-Hawthorn, J.; Heavens, A.; Heymans, C.; Loveday, J.; Norberg, P. Galaxy and mass assembly: Redshift space distortions from the clipped galaxy field. Phys. Rev. 2016, D93, 023525. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Davis, T.; Drinkwater, M.J.; Forster, K.; Yee, H.K.C.; et al. Galaxy And Mass Assembly (GAMA): Improved cosmic growth measurements using multiple tracers of large-scale structure. Mon. Not. Roy. Astron. Soc. 2013, 436, 3089. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Davis, T.; Drinkwater, M.J.; Forster, K.; Yee, H.K.C.; et al. The WiggleZ Dark Energy Survey: The growth rate of cosmic structure since redshift z=0.9. Mon. Not. Roy. Astron. Soc. 2011, 415, 2876. [Google Scholar] [CrossRef]
- Mohammad, F.G.; Bianchi, D.; Percival, W.J.; de La Torre, S.; Guzzo, L.; Granett, B.R.; Branchini, E.; Bolzonella, M.; Garilli, B.; Moutard, T.; et al. The VIMOS Public Extragalactic Redshift Survey (VIPERS): Unbiased clustering estimate with VIPERS slit assignment. Astron. Astrophys. 2018, 619, A17. [Google Scholar] [CrossRef] [Green Version]
- Guzzo, L.; Pierleoni, M.; Meneux, B.; Branchini, E.; Le Fèvre, O.; Marinoni, C.; Garilli, B.; Blaizot, J.; De Lucia, G.; Zucca, E.; et al. A test of the nature of cosmic acceleration using galaxy redshift distortions. Nature 2008, 451, 541–545. [Google Scholar] [CrossRef]
- Song, Y.S.; Percival, W.J. Reconstructing the history of structure formation using Redshift Distortions. JCAP 2009, 910, 4. [Google Scholar] [CrossRef]
- Okumura, T.; Hikage, C.; Totani, T.; Tonegawa, M.; Okada, H.; Glazebrook, K.; Blake, C.; Ferreira, P.G.; Yoshida, N.; More, S.; et al. The Subaru FMOS galaxy redshift survey (FastSound). IV. New constraint on gravity theory from redshift space distortions at z∼1.4. Publ. Astron. Soc. Jap. 2016, 68, 38. [Google Scholar] [CrossRef] [Green Version]
- Turner, M.S.; White, M.J. CDM models with a smooth component. Phys. Rev. 1997, D56, R4439. [Google Scholar] [CrossRef] [Green Version]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Zheng, W.; Charvu, P.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Favale, A.; Gómez-Valent, A.; Migliaccio, M. Cosmic chronometers to calibrate the ladders and measure the curvature of the Universe. A model-independent study. arXiv 2023, arXiv:2301.09591. [Google Scholar]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Zheng, W.; Murakami, Y.; Anand, G.S.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Wiseman, P.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Vielva, P.; Basak, K.; et al. Planck 2018 results. VIII. Gravitational lensing. Astron. Astrophys. 2020, 641, A8. [Google Scholar] [CrossRef] [Green Version]
- Jiménez, R.; Loeb, A. Constraining cosmological parameters based on relative galaxy ages. Astrophys. J. 2002, 573, 37–42. [Google Scholar] [CrossRef]
- Alcock, C.; Paczynski, B. An evolution free test for non-zero cosmological constant. Nature 1979, 281, 358–359. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Evolution of the fσ8 tension with the Planck15/ΛCDM determination and implications for modified gravity theories. Phys. Rev. 2018, D97, 103503. [Google Scholar] [CrossRef] [Green Version]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Seibert, M. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astrophys. J. 2019, 882, 34. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Cao, S.; Ratra, B. H0=69.8±1.3 km s−1 Mpc−1, Ωm0 = 0.288 ± 0.017, and other constraints from lower-redshift, non-CMB and non-distance-ladder, expansion-rate data. Phys. Rev. 2023, D107, 103521. [Google Scholar]
- Yuan, W.; Riess, A.G.; Macri, L.M.; Casertano, S.; Scolnic, D. Consistent Calibration of the Tip of the Red Giant Branch in the Large Magellanic Cloud on the Hubble Space Telescope Photometric System and a Re-determination of the Hubble Constant. Astrophys. J. 2019, 886, 61. [Google Scholar] [CrossRef] [Green Version]
- Soltis, J.; Casertano, S.; Riess, A.G. The Parallax of ω Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant. Astrophys. J. Lett. 2021, 908, L5. [Google Scholar] [CrossRef]
- Anand, G.S.; Tully, R.B.; Rizzi, L.; Riess, A.G.; Yuan, W. Comparing Tip of the Red Giant Branch Distance Scales: An Independent Reduction of the Carnegie-Chicago Hubble Program and the Value of the Hubble Constant. Astrophys. J. 2022, 932, 15. [Google Scholar] [CrossRef]
- Scolnic, D.; Riess, A.G.; Wu, J.; Li, S.; Anand, G.S.; Beaton, R.; Casertano, S.; Anderson, R.; Dhawan, S.; Ke, X. CATS: The Hubble Constant from Standardized TRGB and Type Ia Supernova Measurements. arXiv 2023, arXiv:2304.06693. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Hastings, W. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Audren, B.; Lesgourgues, J.; Benabed, K.; Prunet, S. Conservative Constraints on Early Cosmology: An illustration of the Monte Python cosmological parameter inference code. JCAP 2013, 02, 1. [Google Scholar] [CrossRef] [Green Version]
- Brinckmann, T.; Lesgourgues, J. MontePython 3: Boosted MCMC sampler and other features. Phys. Dark Univ. 2019, 24, 100260. [Google Scholar] [CrossRef] [Green Version]
- Brooks, S.; Gelman, A. General Methods for Monitoring Convergence of Iterative Simulations. J. Comput. Graph. Stat. 1997, 7, 434. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Rubin, D. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457. [Google Scholar] [CrossRef]
- Lewis, A. GetDist: A Python Package for Analysing Monte Carlo Samples. arXiv 2019, arXiv:1910.13970. Available online: https://getdist.readthedocs.io (accessed on 22 May 2023).
- Fixsen, D.J. The Temperature of the Cosmic Microwave Background. Astrophys. J. 2009, 707, 916–920. [Google Scholar] [CrossRef] [Green Version]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; van der Linde, A. Bayesian measures of model complexity and fit. J. Roy. Stat. Soc. 2002, 64, 583. [Google Scholar] [CrossRef] [Green Version]
- Liddle, A.R. Information criteria for astrophysical model selection. Mon. Not. Roy. Astron. Soc. 2007, 377, L74–L78. [Google Scholar] [CrossRef] [Green Version]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Zheng, Z.; Amendola, L.; Pettorino, V.; Wetterich, C. Early dark energy in the pre- and postrecombination epochs. Phys. Rev. D 2021, 104, 083536. [Google Scholar] [CrossRef]
- Poulin, V.; Bernal, J.L.; Kovetz, E.; Kamionkowski, M. The Sigma-8 Tension is a Drag. arXiv 2022, arXiv:2209.06217. [Google Scholar]
- Gómez-Valent, A. Measuring the sound horizon and absolute magnitude of SNIa by maximizing the consistency between low-redshift data sets. Phys. Rev. D 2022, 105, 43528. [Google Scholar] [CrossRef]
- Benevento, G.; Kable, J.A.; Addison, G.E.; Bennett, C.L. An Exploration of an Early Gravity Transition in Light of Cosmological Tensions. Astrophys. J. 2022, 935, 156. [Google Scholar] [CrossRef]
- Ballesteros, G.; Notari, A.; Rompineve, F. The H0 tension: ΔGN vs. ΔNeff. JCAP 2020, 11, 24. [Google Scholar] [CrossRef]
- Braglia, M.; Ballardini, M.; Emond, W.T.; Finelli, F.; Gumrukcuoglu, A.E.; Koyama, K.; Paoletti, D. Larger value for H0 by an evolving gravitational constant. Phys. Rev. D 2020, 102, 23529. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J. Dynamical dark energy: Scalar fields and running vacuum. Mod. Phys. Lett. 2017, A32, 1750054. [Google Scholar] [CrossRef] [Green Version]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J. Signs of Dynamical Dark Energy in Current Observations. Phys. Dark Univ. 2019, 25, 100311. [Google Scholar] [CrossRef]
- Solà, J. Cosmologies with a time dependent vacuum. J. Phys. Conf. Ser. 2011, 283, 12033. [Google Scholar] [CrossRef]
- Solà, J. Vacuum energy and cosmological evolution. In Proceedings of the AIP Conference Proceedings, St. Petersburg, Russia, 1–4 October 2013; Volume 1606, pp. 19–37. [Google Scholar] [CrossRef] [Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Running Vacuum in the Universe: Phenomenological Status in Light of the Latest Observations, and Its Impact on the σ8 and H0 Tensions. Universe 2023, 9, 262. https://doi.org/10.3390/universe9060262
Solà Peracaula J, Gómez-Valent A, de Cruz Pérez J, Moreno-Pulido C. Running Vacuum in the Universe: Phenomenological Status in Light of the Latest Observations, and Its Impact on the σ8 and H0 Tensions. Universe. 2023; 9(6):262. https://doi.org/10.3390/universe9060262
Chicago/Turabian StyleSolà Peracaula, Joan, Adrià Gómez-Valent, Javier de Cruz Pérez, and Cristian Moreno-Pulido. 2023. "Running Vacuum in the Universe: Phenomenological Status in Light of the Latest Observations, and Its Impact on the σ8 and H0 Tensions" Universe 9, no. 6: 262. https://doi.org/10.3390/universe9060262
APA StyleSolà Peracaula, J., Gómez-Valent, A., de Cruz Pérez, J., & Moreno-Pulido, C. (2023). Running Vacuum in the Universe: Phenomenological Status in Light of the Latest Observations, and Its Impact on the σ8 and H0 Tensions. Universe, 9(6), 262. https://doi.org/10.3390/universe9060262








