Excitation Functions of Related Temperatures of η and η0 Emission Sources from Squared Momentum Transfer Spectra in High-Energy Collisions
Abstract
1. Introduction
2. Picture and Formalism
2.1. The Erlang Distribution
2.2. The Tsallis–Levy Function
2.3. Average Transverse Momentum and Initial-State Temperature
2.4. The Squared Momentum Transfer
2.5. The Process of Monte Carlo Calculations
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Caines, H. What’s interesting about strangeness production? An overview of recent results. J. Phys. G 2005, 31, S101–S117. [Google Scholar] [CrossRef]
- Shuryak, E.V. Quantum chromodynamics and the theory of superdense matter. Phys. Rep. 1980, 61, 71–158. [Google Scholar] [CrossRef]
- Digal, S.; Petreczky, P.; Satz, H. Quarkonium feed-down and sequential suppression. Phys. Rev. D 2001, 64, 094015. [Google Scholar] [CrossRef]
- Karsch, F.; Kharzeev, D.; Satz, H. Sequential charmonium dissociation. Phys. Lett. B 2006, 637, 75–80. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J. The quest for the quark-gluon plasma. Nature 2007, 448, 302–309. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.-H.; Ma, Y.-G.; Zhang, S. Charm hadron azimuthal angular correlations in Au+Au collisions at = 200 GeV from parton scatterings. Nucl. Sci. Tech. 2019, 30, 185. [Google Scholar] [CrossRef]
- Yan, T.-Z.; Li, S.; Wang, Y.-N.; Xie, F.; Yan, T.-F. Yield ratios and directed flows of light particles from proton-rich nuclei-induced collisions. Nucl. Sci. Tech. 2019, 30, 15. [Google Scholar] [CrossRef]
- Fisli, M.; Mebarki, N. Top quark pair-production in noncommutative standard model. Adv. High Energy Phys. 2020, 2020, 7279627. [Google Scholar] [CrossRef]
- He, X.-W.; Wu, F.-M.; Wei, H.-R.; Hong, B.-H. Energy-dependent chemical potentials of light hadrons and quarks based on transverse momentum spectra and yield ratios of negative to positive particles. Adv. High Energy Phys. 2020, 2020, 1265090. [Google Scholar] [CrossRef]
- Waqas, M.; Li, B.-C. Kinetic freeze-out temperature and transverse flow velocity in Au-Au collisions at RHIC-BES energies. Adv. High Energy Phys. 2020, 2020, 1787183. [Google Scholar] [CrossRef]
- Tang, Z.-B.; Zha, W.-M.; Zhang, Y.-F. An experimental review of open heavy flavor and quarkonium production at RHIC. Nucl. Sci. Tech. 2020, 31, 81. [Google Scholar] [CrossRef]
- Shen, C.; Yan, L. Recent development of hydrodynamic modeling in heavy-ion collisions. Nucl. Sci. Tech. 2020, 31, 122. [Google Scholar] [CrossRef]
- Yu, H.; Fang, D.-Q.; Ma, Y.-G. Investigation of the symmetry energy of nuclear matter using isospin-dependent quantum molecular dynamics. Nucl. Sci. Tech. 2020, 31, 61. [Google Scholar] [CrossRef]
- Bhaduri, S.; Bhaduri, A.; Ghosh, D. Study of di-muon production process in pp collision in CMS data from symmetry scaling perspective. Adv. High Energy Phys. 2020, 2020, 4510897. [Google Scholar] [CrossRef]
- Tawfik, A.N. Out-of-equilibrium transverse momentum spectra of pions at LHC energies. Adv. High Energy Phys. 2019, 2019, 4604608. [Google Scholar] [CrossRef]
- Nayak, J.K.; Alam, J.; Sarkar, S.; Sinha, B. Measuring initial temperature through a photon to dilepton ratio in heavy-ion collisions. J. Phys. G 2008, 35, 104161. [Google Scholar] [CrossRef]
- Adare, A. et al. [PHENIX Collaboration] Enhanced production of direct photons in Au+Au collisions at = 200 GeV and implications for the initial temperature. Phys. Rev. Lett. 2010, 104, 132301. [Google Scholar] [CrossRef]
- Csanád, M.; Májer, I. Initial temperature and EoS of quark matter via direct photons. Phys. Part. Nuclei Lett. 2011, 8, 1013–1015. [Google Scholar] [CrossRef]
- Csanád, M.; Májer, I. Equation of state and initial temperature of quark gluon plasma at RHIC. Cent. Eur. J. Phys. 2012, 10, 850–857. [Google Scholar] [CrossRef]
- Soltz, R.A.; Garishvili, I.; Cheng, M.; Abelev, B.; Glenn, A.; Newby, J.; Levy, L.A.L.; Pratt, S. Constraining the initial temperature and shear viscosity in a hybrid hydrodynamic model of = 200 GeV Au+Au collisions using pion spectra, elliptic flow, and femtoscopic radii. Phys. Rev. C 2013, 87, 044901. [Google Scholar] [CrossRef]
- Waqas, M.; Liu, F.-H. Initial, effective, and kinetic freeze-out temperatures from transverse momentum spectra in high-energy proton(deuteron)-nucleus and nucleus-nucleus collisions. Eur. Phys. J. Plus 2020, 135, 147. [Google Scholar] [CrossRef]
- Cleymans, J.; Paradza, M.W. Tsallis statistics in high energy physics: Chemical and thermal freeze-outs. Physics 2020, 2, 654–664. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, F.-H. Kinetic freeze-out properties from transverse momentum spectra of pions in high energy proton-proton collisions. Physics 2020, 2, 277–308. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, F.-H.; Olimov, K.K. Initial- and final-state temperatures of emission source from differential cross-section in squared momentum transfer in high-energy collisions. Adv. High Energy Phys. 2021, 2021, 6677885. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, F.-H.; Olimov, K.K. Initial-state temperature of light meson emission source From squared momentum transfer spectra in high-energy collisions. Front. Phys. 2021, 9, 792039. [Google Scholar] [CrossRef]
- Liu, F.-H.; Li, J.-S. Isotopic production cross section of fragments in 56Fe+p and 136Xe (124Xe)+Pb reactions over an energy range from 300A to 1500A MeV. Phys. Rev. C 2008, 78, 044602. [Google Scholar] [CrossRef]
- Liu, F.-H. Unified description of multiplicity distributions of final-state particles produced in collisions at high energies. Nucl. Phys. A 2008, 810, 159–172. [Google Scholar] [CrossRef]
- Liu, F.-H.; Gao, Y.-Q.; Tian, T.; Li, B.-C. Unified description of transverse momentum spectrums contributed by soft and hard processes in high-energy nuclear collisions. Eur. Phys. J. A 2014, 50, 94. [Google Scholar] [CrossRef]
- Hagedorn, R. Multiplicities, pT distributions and the expected hadron → quark-gluon phase transition. Riv. Nuovo Cim. 1983, 6, 1–50. [Google Scholar] [CrossRef]
- Abelev, B. et al. [ALICE Collaboration] Production of Σ(1385)± and Ξ(1530)0 in proton-proton collisions at = 7 TeV. Eur. Phys. J. C 2015, 75, 1–19. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Abelev, B.I. et al. [STAR Collaboration] Strange particle production in p+p collisions at = 200 GeV. Phys. Rev. C 2007, 75, 064901. [Google Scholar] [CrossRef]
- Zhang, N.-S. Particle Physics (Volume I); Science Press: Beijing, China, 1986. [Google Scholar]
- Hu, T. et al. [CLAS Collaboration] Photoproduction of η mesons off the proton for 1.2<Eγ<4.7 GeV using CLAS at Jefferson Laboratory. Phys. Rev. C 2020, 102, 065203. [Google Scholar]
- Bussey, P.J.; Raine, C.; Rutherglen, J.G.; Booth, P.S.L.; Carroll, L.J.; Daniel, P.R.; Edwards, A.W.; Hardwick, C.J.; Holt, J.R.; Jackson, J.N. et al. The polarized beam asymmetry in photoproduction of eta mesons from protons at 2.5 GeV and 3.0 GeV. Phys. Lett. B 1976, 61, 479–482. [Google Scholar] [CrossRef]
- Bellenger, D.; Deutsch, S.; Luckey, D.; Osborne, L.S.; Schwitters, R. Photoproduction of η0 mesons at 4 GeV. Phys. Rev. Lett. 1968, 21, 1205–1208. [Google Scholar] [CrossRef]
- Anderson, R.; Gustavson, D.; Johnson, J.; Ritson, D.; Jones, W.G.; Kreinick, D.; Murphy, F.; Weinstein, R. Measurements of π0 and η0 photoproduction at incident gamma-ray energies of 6.0-17.8 GeV. Phys. Rev. Lett. 1968, 21, 384–386. [Google Scholar] [CrossRef]
- Braunschweig, W.; Erlewein, W.; Frese, H.; Lübelsmeyer, K.; Meyer-Wachsmuth, H.; Schmitz, D.; Schultz von Dratzig, A.; Wessels, G. Single photoproduction of η-mesons of hydrogen in the forward direction at 4 and 6 GeV. Phys. Lett. B 1970, 33, 236–240. [Google Scholar] [CrossRef]
- Dewire, J.; Gittelman, B.; Loe, R.; Loh, E.C.; Ritchie, D.J.; Lewis, R.A. Photoproduction of eta mesons from hydrogen. Phys. Lett. B 1971, 37, 326–328. [Google Scholar] [CrossRef]
- Gutay, L.J.; Hirsch, A.S.; Scharenberg, R.P.; Srivastava, B.K.; Pajares, C. De-confinement in small systems: Clustering of color sources in high multiplicity p¯p collisions at = 1.8 TeV. Int. J. Mod. Phys. E 2015, 24, 1550101. [Google Scholar] [CrossRef]
- Scharenberg, R.P.; Srivastava, B.K.; Pajares, C. Exploring the initial stage of high multiplicity proton-proton collisions by determining the initial temperature of the quark-gluon plasma. Phys. Rev. D 2019, 100, 114040. [Google Scholar] [CrossRef]
- Sahoo, P.; De, S.; Tiwari, S.K.; Sahoo, R. Energy and centrality dependent study of deconfinement phase transition in a color string percolation approach at RHIC energies. Eur. Phys. J. A 2018, 54, 136. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, F.-H. Excitation function of initial temperature of heavy flavor quarkonium emission source in high energy collisions. Adv. High Energy Phys. 2020, 2020, 5031494. [Google Scholar] [CrossRef]
- Aaron, F.D. et al. [H1 Collaboration] Diffractive electroproduction of ρ and ϕ mesons at HERA. J. High Energy Phys. 2010, 2010, 032. [Google Scholar] [CrossRef]
- Aktas, A. et al. [H1 Collaboration] Elastic J/ψ production at HERA. Eur. Phys. J. C 2006, 46, 585–603. [Google Scholar] [CrossRef]
- Chekanov, S. et al. [ZEUS Collaboration] Exclusive ρ0 production in deep inelastic scattering at HERA. PMC Phys. A 2007, 1, 6. [Google Scholar] [CrossRef]
- Derrick, M. et al. [ZEUS Collaboration] Measurement of elastic ω photoproduction at HERA ZEUS Collaboration. Z. Phys. C 1997, 73, 73–84. [Google Scholar]
- Chekanov, S. et al. [ZEUS Collaboration] Exclusive electroproduction of ϕ mesons at HERA. Nucl. Phys. B 2005, 718, 3–31. [Google Scholar] [CrossRef]
- Chekanov, S. et al. [ZEUS Collaboration] Exclusive electroproduction of J/ψ mesons at HERA. Nucl. Phys. B 2004, 695, 3–37. [Google Scholar] [CrossRef]
- Barberis, D. et al. [WA102 Collaboration] A coupled channel analysis of the centrally produced K+K− and π+π− final states in pp interactions at 450 GeV/c. Phys. Lett. B 1999, 462, 462–470. [Google Scholar] [CrossRef]
- Barberis, D. et al. [WA102 Collaboration] A measurement of the branching fractions of the f1(1285) and f1(1420) produced in central pp interactions at 450 GeV/c. Phys. Lett. B 1998, 440, 225–232. [Google Scholar] [CrossRef]
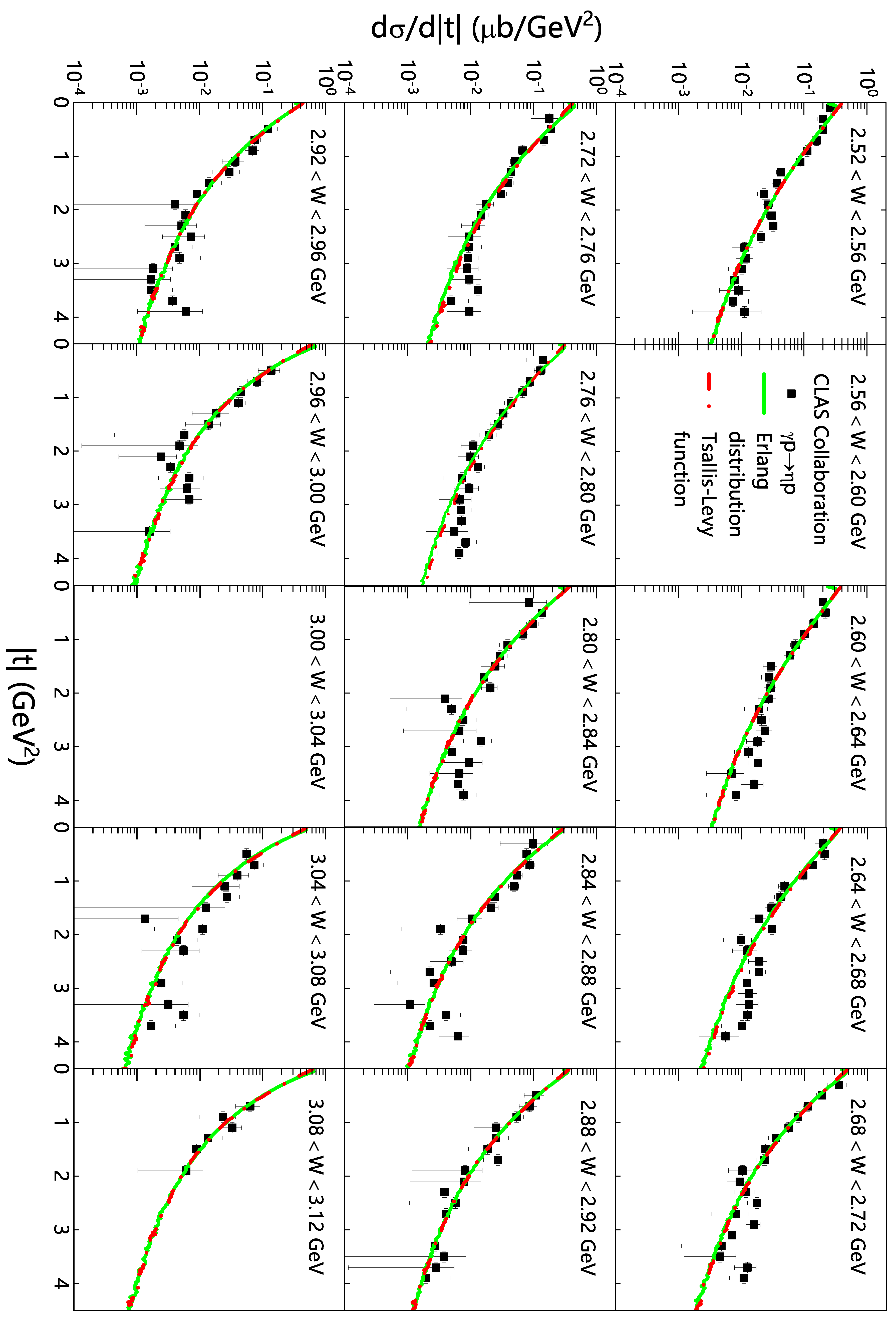
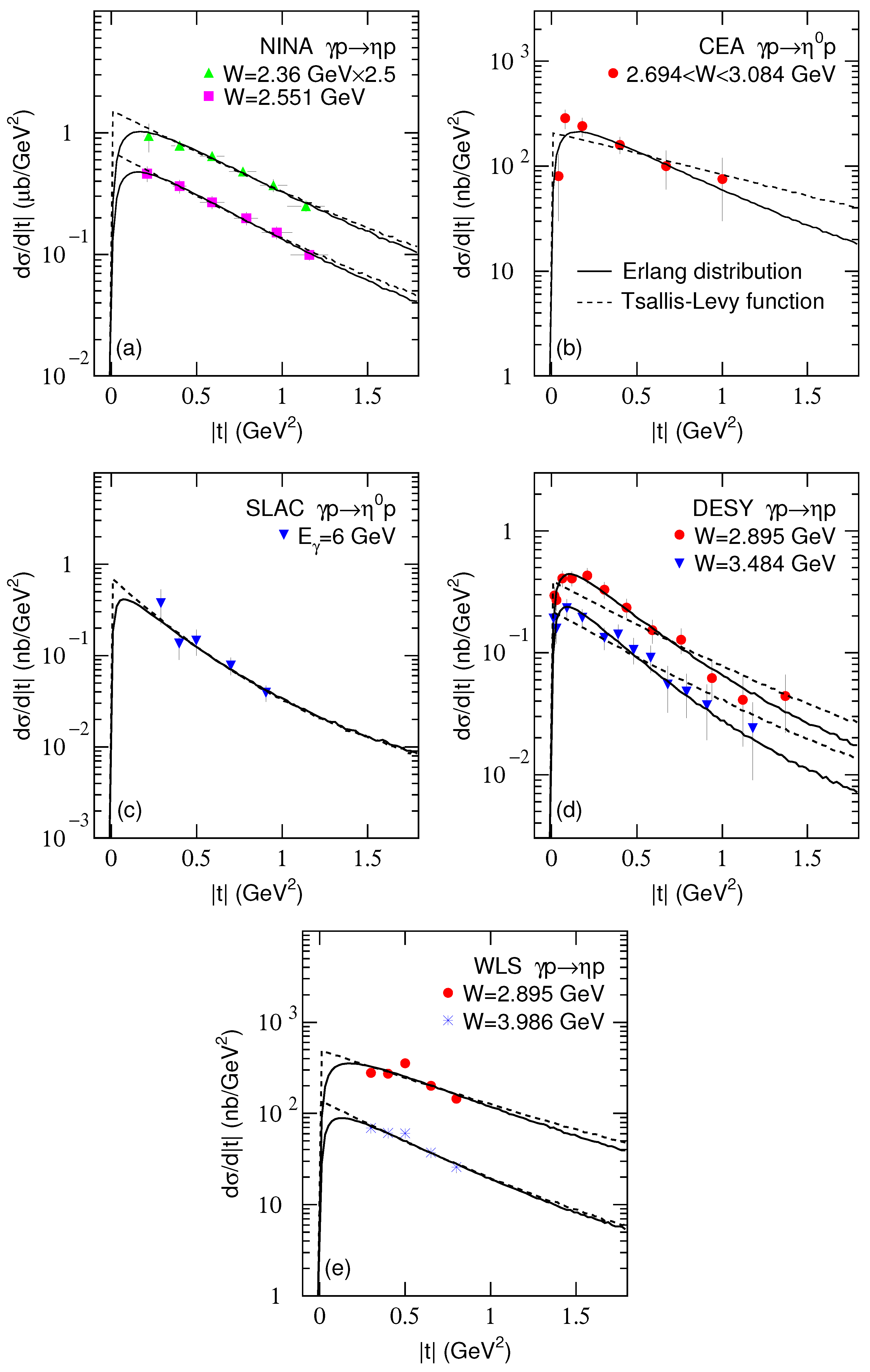
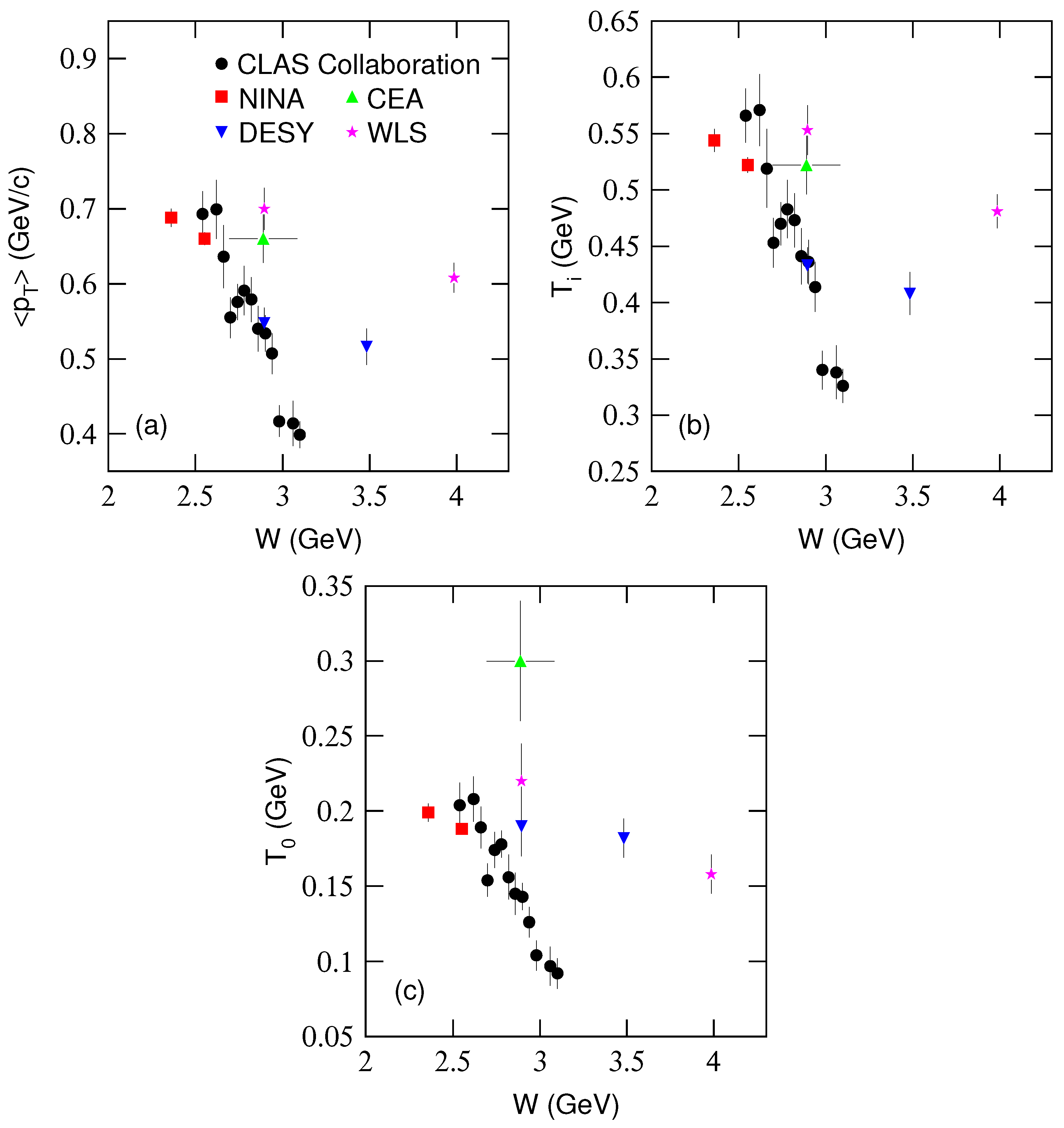
| Figure | W, (GeV) | (GeV/c) | (GeV) | /ndof | T (GeV) | /ndof | |
|---|---|---|---|---|---|---|---|
| Figure 1 | 3 | ||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| 3 | |||||||
| Figure 2a | 4 | ||||||
| 4 | |||||||
| Figure 2b | 4 | ||||||
| Figure 2c | 6 | 4 | |||||
| Figure 2d | 4 | ||||||
| 4 | |||||||
| Figure 2e | 4 | ||||||
| 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Liu, F.-H.; Olimov, K.K. Excitation Functions of Related Temperatures of η and η0 Emission Sources from Squared Momentum Transfer Spectra in High-Energy Collisions. Universe 2023, 9, 342. https://doi.org/10.3390/universe9070342
Wang Q, Liu F-H, Olimov KK. Excitation Functions of Related Temperatures of η and η0 Emission Sources from Squared Momentum Transfer Spectra in High-Energy Collisions. Universe. 2023; 9(7):342. https://doi.org/10.3390/universe9070342
Chicago/Turabian StyleWang, Qi, Fu-Hu Liu, and Khusniddin K. Olimov. 2023. "Excitation Functions of Related Temperatures of η and η0 Emission Sources from Squared Momentum Transfer Spectra in High-Energy Collisions" Universe 9, no. 7: 342. https://doi.org/10.3390/universe9070342
APA StyleWang, Q., Liu, F.-H., & Olimov, K. K. (2023). Excitation Functions of Related Temperatures of η and η0 Emission Sources from Squared Momentum Transfer Spectra in High-Energy Collisions. Universe, 9(7), 342. https://doi.org/10.3390/universe9070342








