Anisotropy of Self-Correlation Level Contours in Three-Dimensional Magnetohydrodynamic Turbulence
Abstract
:1. Introduction
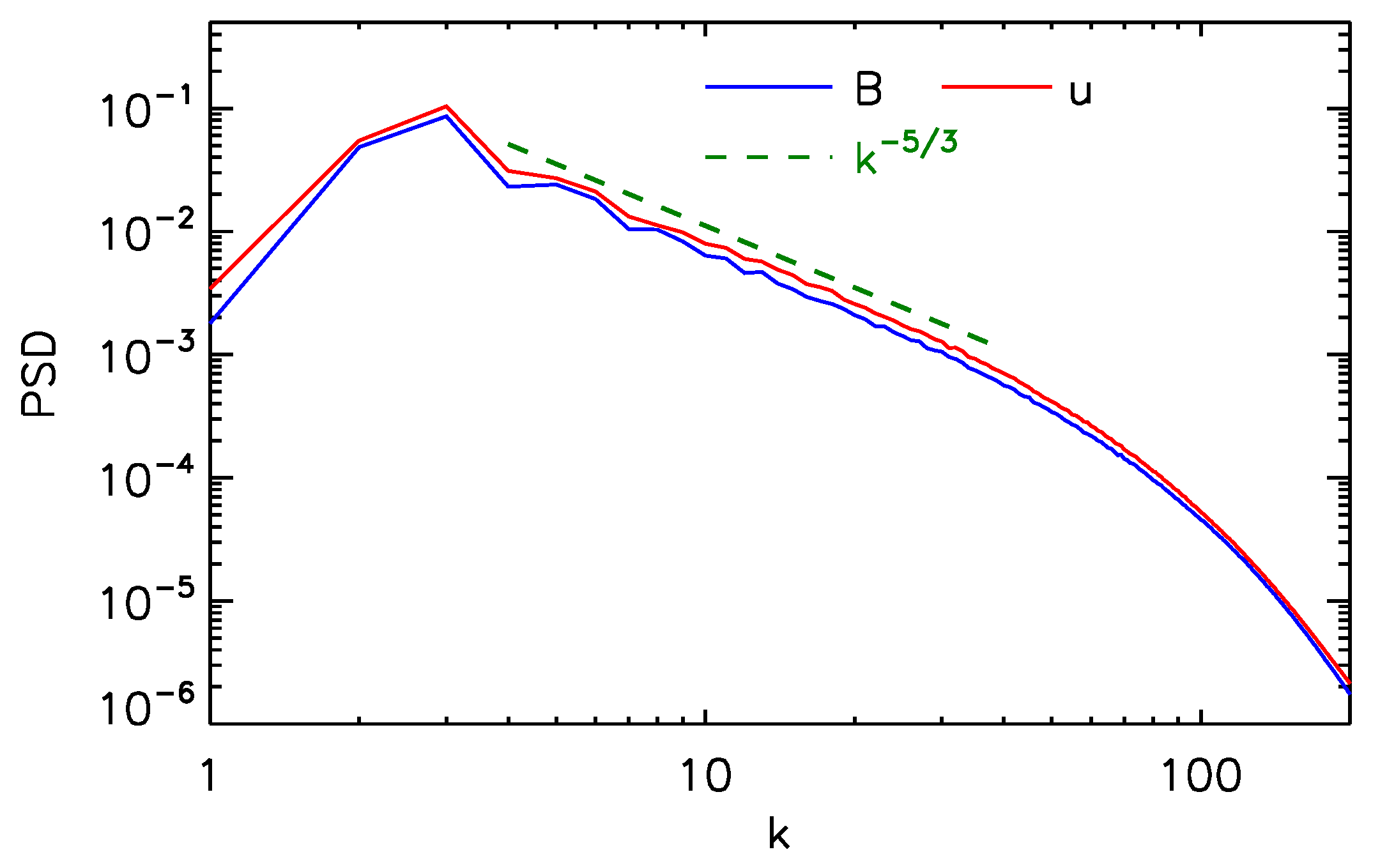
2. Numerical Mhd Model
3. Numerical Results
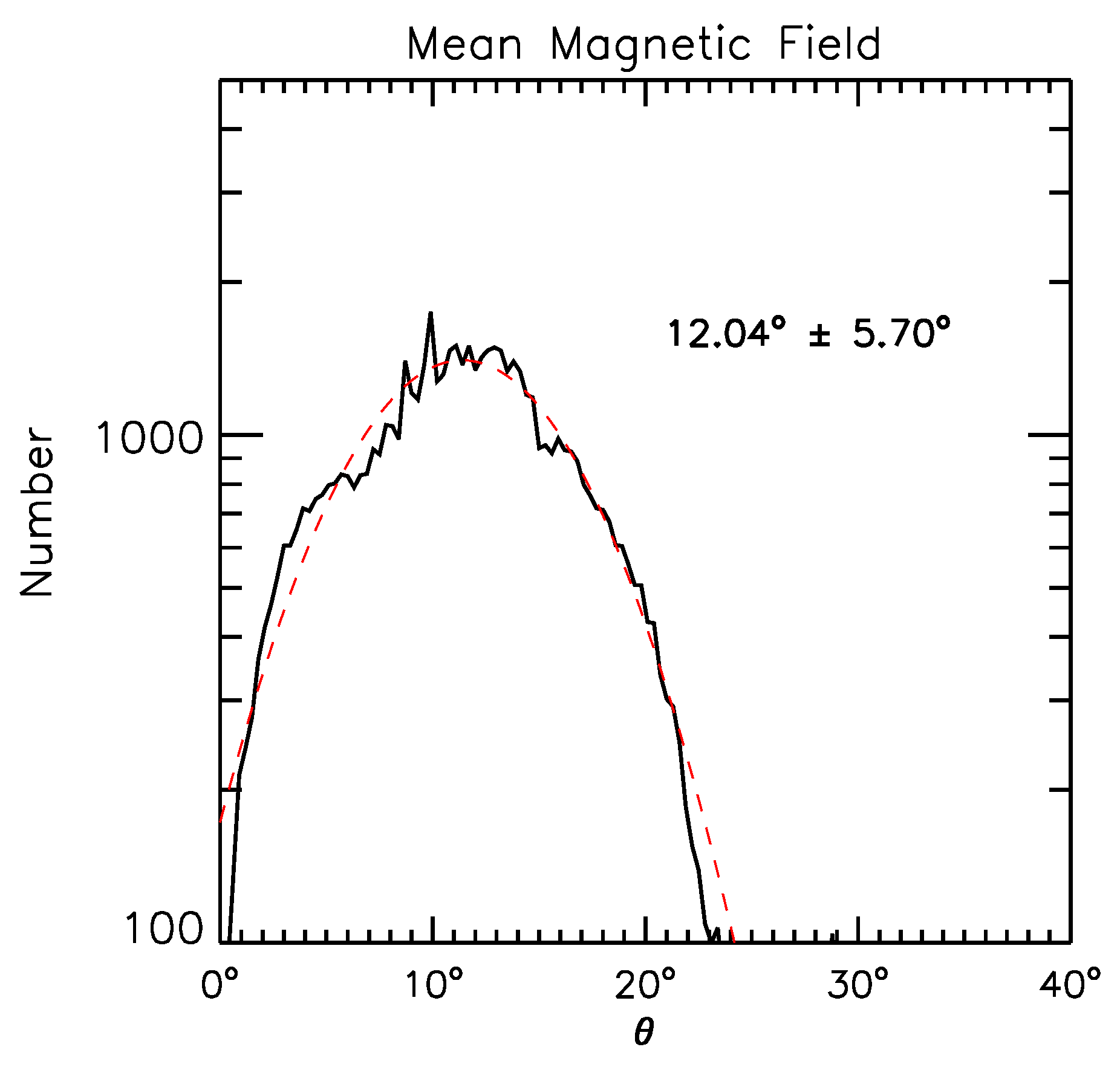
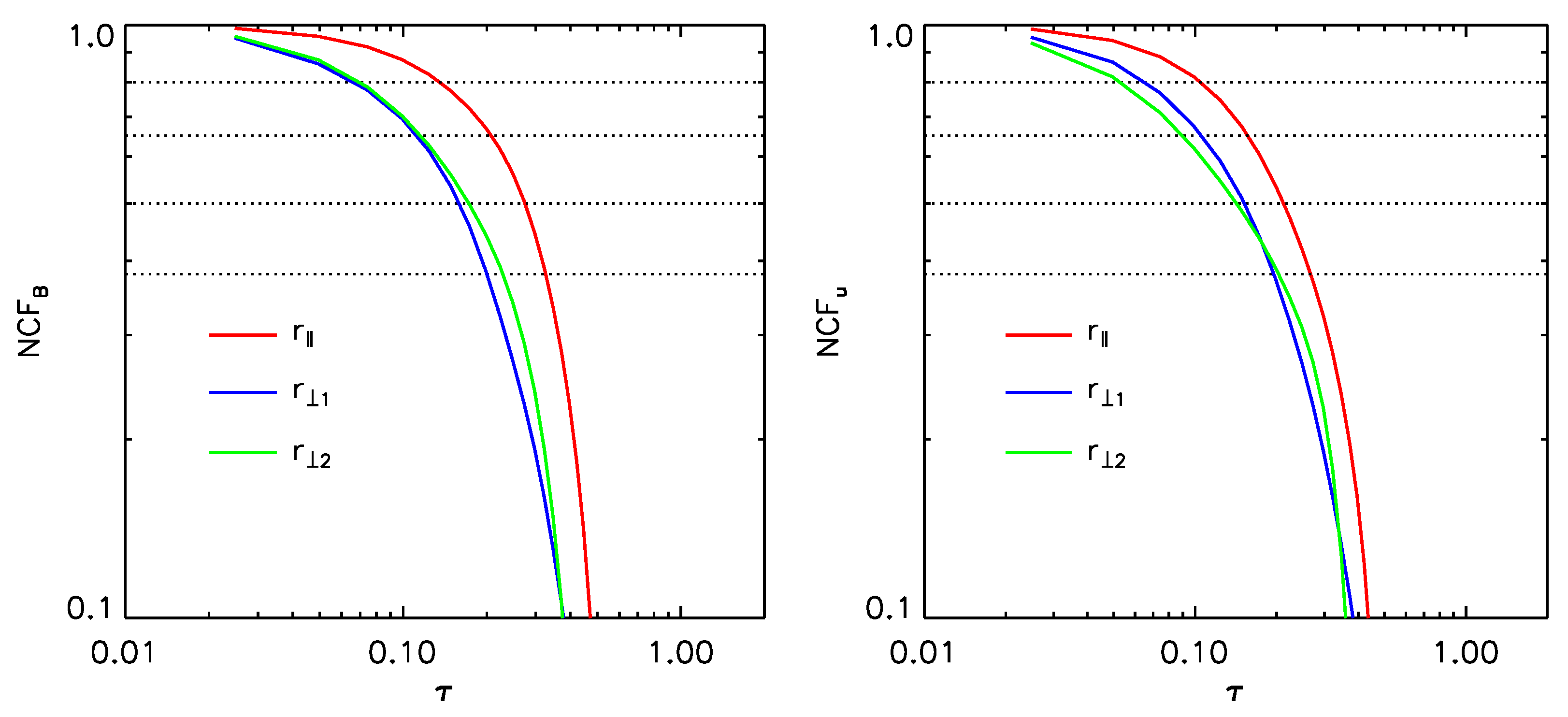
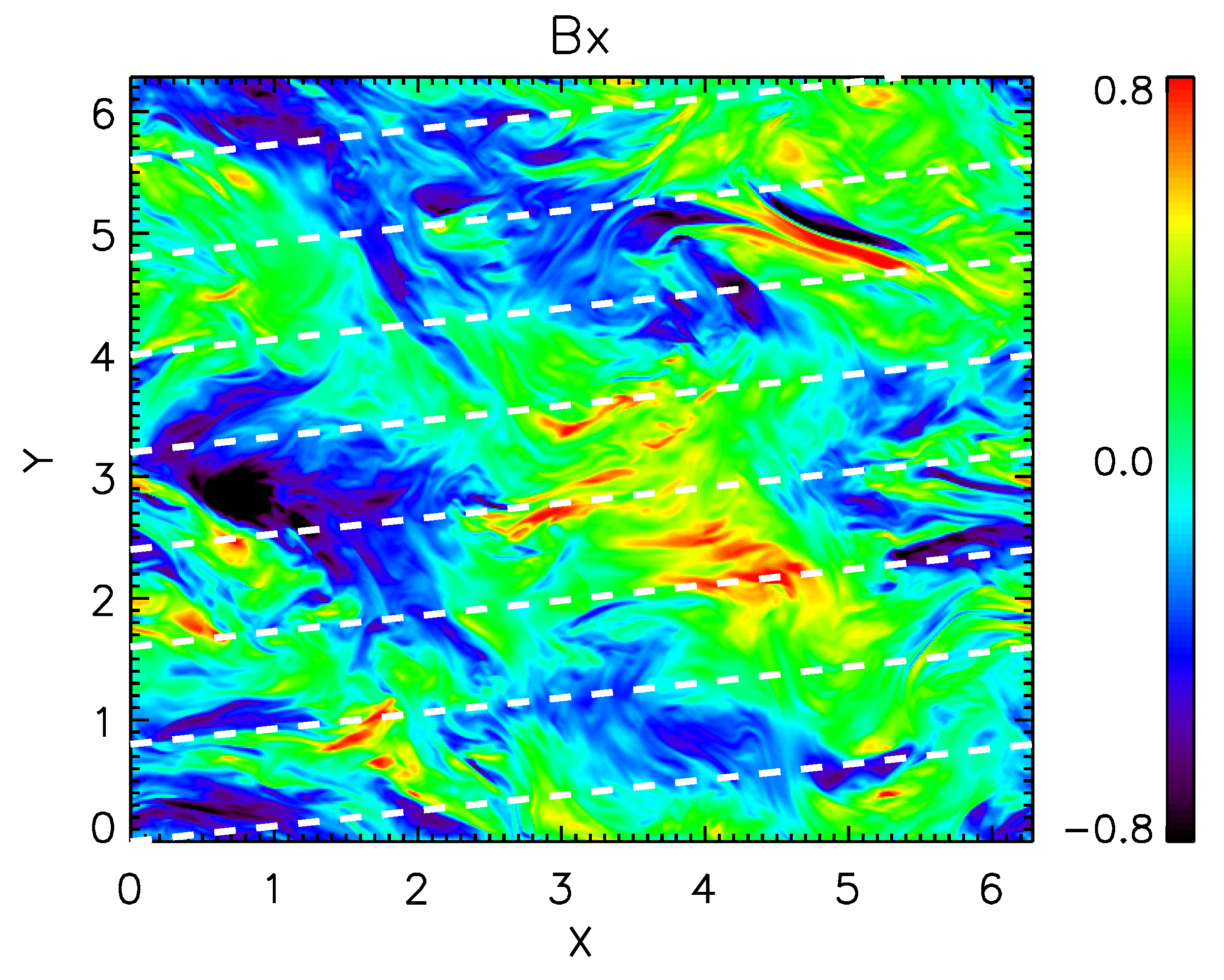
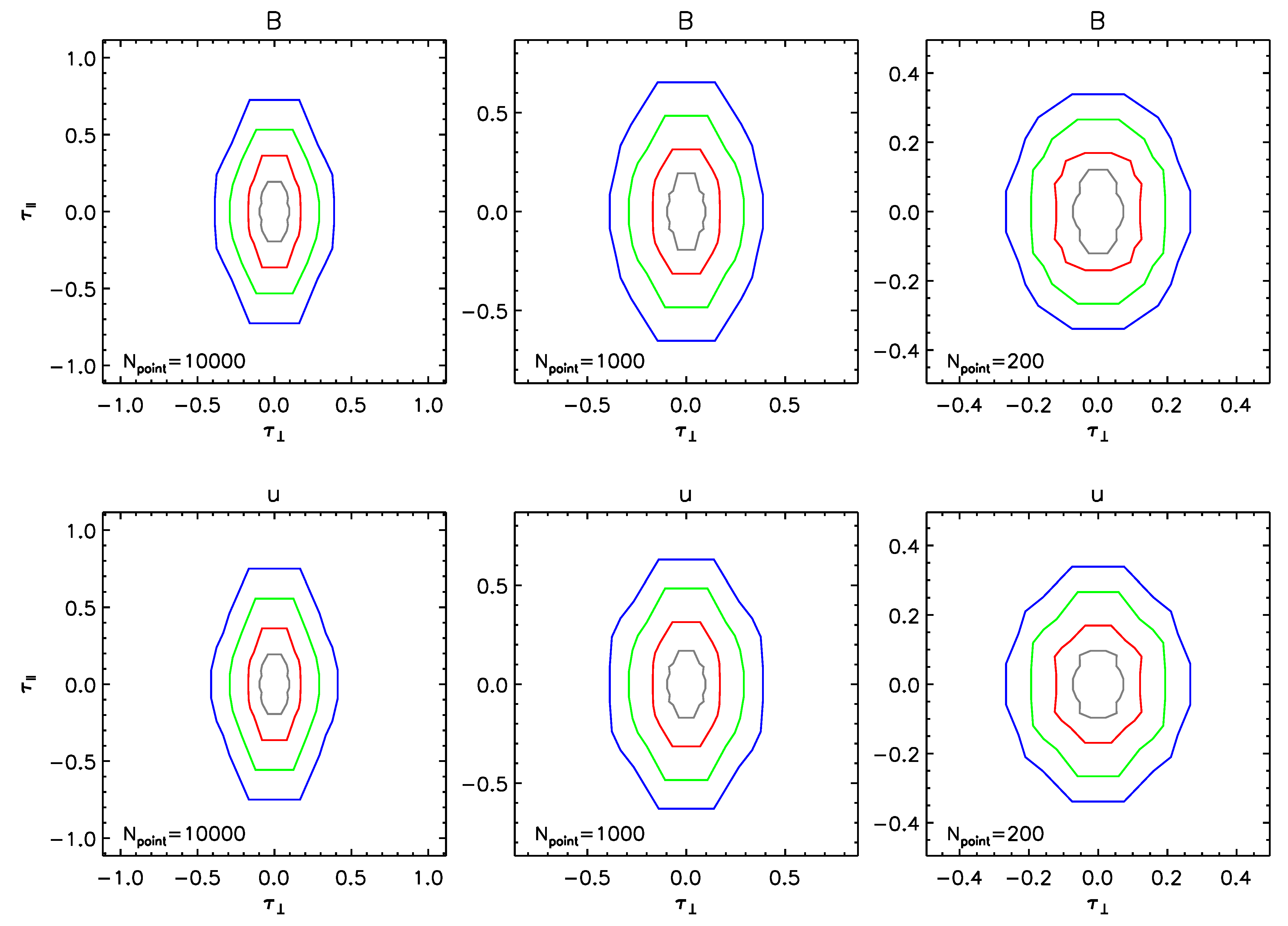
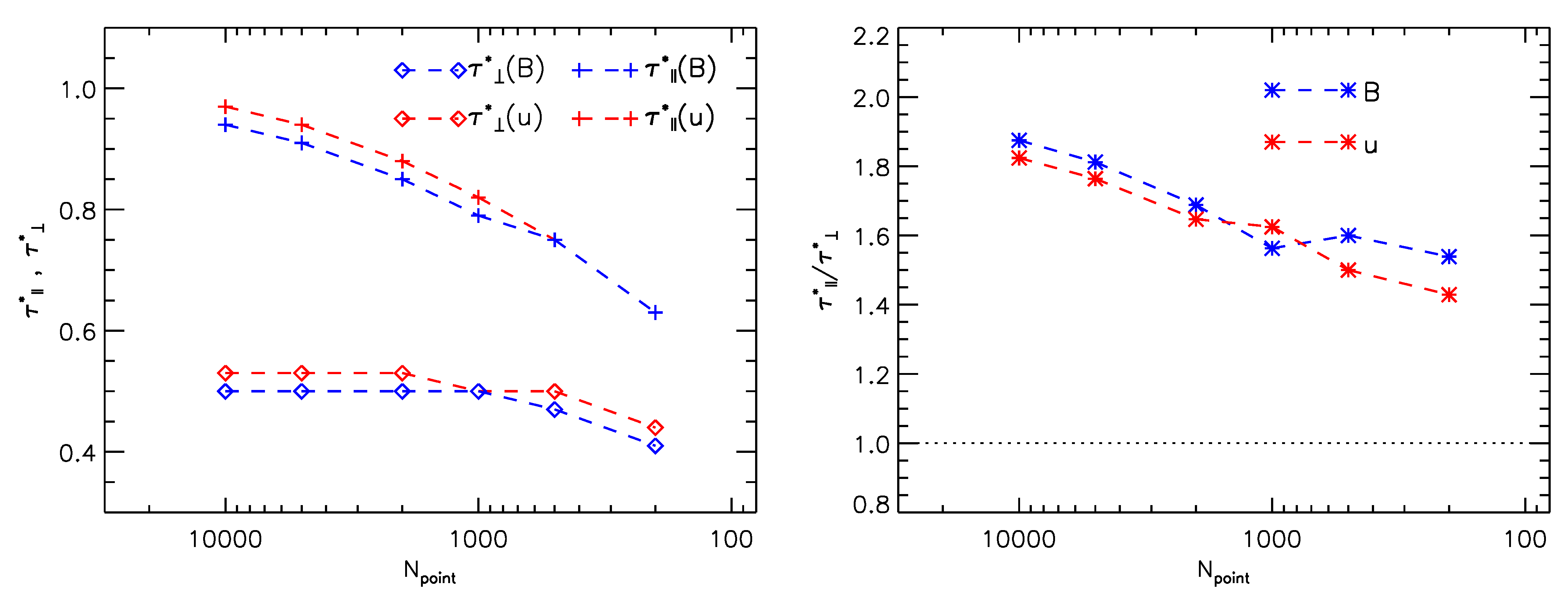
3.1. Anisotropy of the NCF’s Level Contours
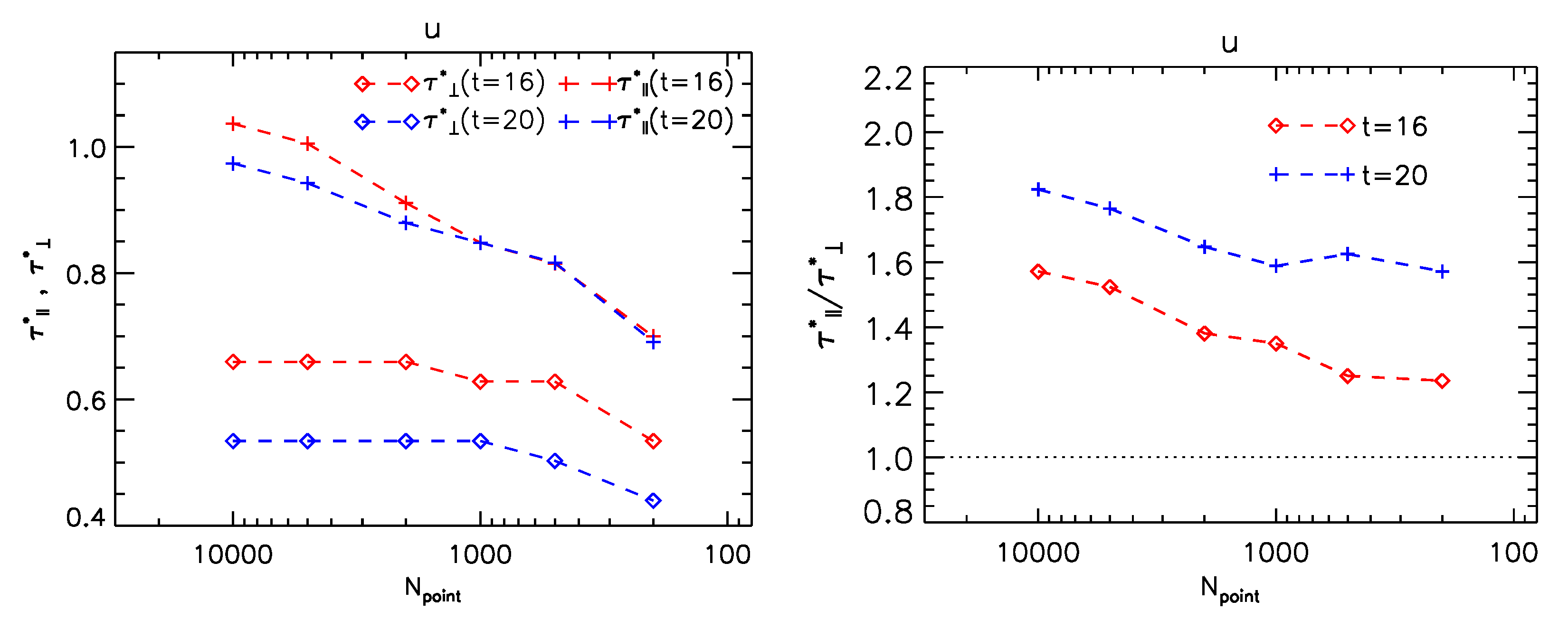
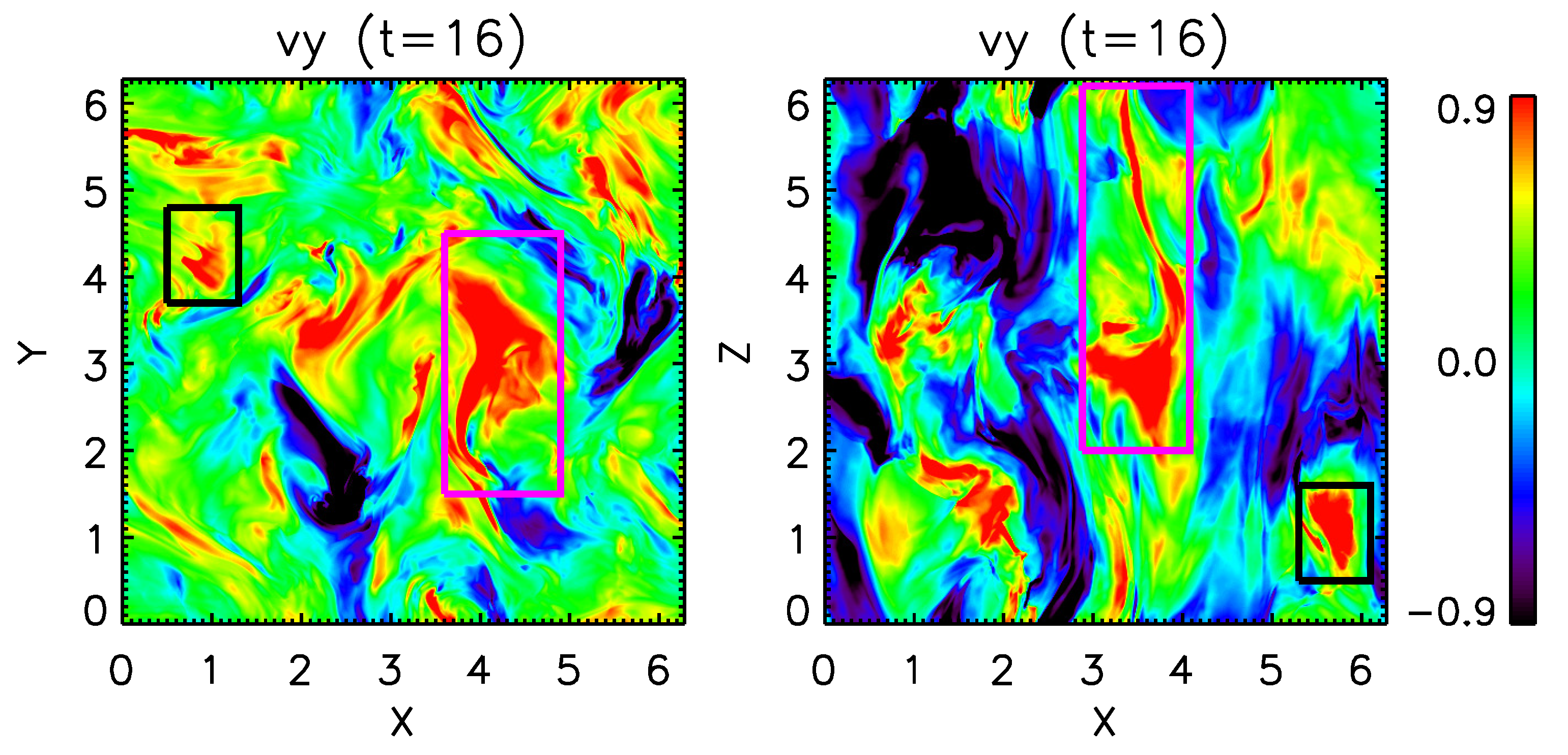
3.2. Evolution of the NCF’s Level Contours
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Three-Dimensional NCF’s Level Contours




References
- Shebalin, J.V.; Matthaeus, W.H.; Montgomery, D. Anisotropy in MHD turbulence due to a mean magnetic field. J. Plasma Phys. 1983, 29, 525–547. [Google Scholar] [CrossRef]
- Goldstein, M.L.; Roberts, D.A.; Matthaeus, W.H. Magnetohydrodynamic Turbulence In The Solar Wind. Annu. Rev. Astron. Astrophys. 1995, 33, 283–326. [Google Scholar] [CrossRef]
- Boldyrev, S. Spectrum of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2006, 96, 115002. [Google Scholar] [CrossRef] [PubMed]
- Zank, G.P.; Adhikari, L.; Hunana, P.; Shiota, D.; Bruno, R.; Telloni, D. Theory and Transport of Nearly Incompressible Magnetohydrodynamic Turbulence. Astrophys. J. 2017, 835, 147. [Google Scholar] [CrossRef]
- Horbury, T.S.; Wicks, R.T.; Chen, C.H.K. Anisotropy in Space Plasma Turbulence: Solar Wind Observations. Space Sci. Rev. 2012, 172, 325–342. [Google Scholar] [CrossRef]
- Oughton, S.; Matthaeus, W.H.; Wan, M.; Osman, K.T. Anisotropy in solar wind plasma turbulence. Philos. Trans. R. Soc. Lond. Ser. A 2015, 373, 20140152. [Google Scholar] [CrossRef]
- Chen, C.H.K. Recent progress in astrophysical plasma turbulence from solar wind observations. J. Plasma Phys. 2016, 82, 535820602. [Google Scholar] [CrossRef]
- Crooker, N.U.; Siscoe, G.L.; Russell, C.T.; Smith, E.J. Factors controlling degree of correlation between ISEE 1 and ISEE 3 interplanetary magnetic field measurements. J. Geophys. Res. Space Phys. 1982, 87, 2224–2230. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Goldstein, M.L.; Roberts, D.A. Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind. J. Geophys. Res. Space Phys. 1990, 95, 20673–20683. [Google Scholar] [CrossRef]
- Bieber, J.W.; Wanner, W.; Matthaeus, W.H. Dominant two-dimensional solar wind turbulence with implications for cosmic ray transport. J. Geophys. Res. Space Phys. 1996, 101, 2511–2522. [Google Scholar] [CrossRef]
- Dasso, S.; Milano, L.J.; Matthaeus, W.H.; Smith, C.W. Anisotropy in Fast and Slow Solar Wind Fluctuations. Astrophys. J. Lett. 2005, 635, L181–L184. [Google Scholar] [CrossRef]
- Osman, K.T.; Horbury, T.S. Multispacecraft Measurement of Anisotropic Correlation Functions in Solar Wind Turbulence. Astrophys. J. Lett. 2007, 654, L103–L106. [Google Scholar] [CrossRef]
- Weygand, J.M.; Matthaeus, W.H.; Dasso, S.; Kivelson, M.G.; Kistler, L.M.; Mouikis, C. Anisotropy of the Taylor scale and the correlation scale in plasma sheet and solar wind magnetic field fluctuations. J. Geophys. Res. Space Phys. 2009, 114, A07213. [Google Scholar] [CrossRef]
- Németh, Z.; Facskó, G.; Lucek, E.A. Correlation Functions of Small-Scale Fluctuations of the Interplanetary Magnetic Field. Sol. Phys. 2010, 266, 149–158. [Google Scholar] [CrossRef]
- He, J.S.; Marsch, E.; Tu, C.Y.; Zong, Q.G.; Yao, S.; Tian, H. Two-dimensional correlation functions for density and magnetic field fluctuations in magnetosheath turbulence measured by the Cluster spacecraft. J. Geophys. Res. 2011, 116, A06207. [Google Scholar] [CrossRef]
- Wang, X.; Tu, C.; He, J. 2D Isotropic Feature of Solar Wind Turbulence as Shown by Self-correlation Level Contours at Hour Timescales. Astrophys. J. 2019, 871, 93. [Google Scholar] [CrossRef]
- Wu, H.; Tu, C.; Wang, X.; He, J.; Wang, L. 3D Feature of Self-correlation Level Contours at 1010 cm Scale in Solar Wind Turbulence. Astrophys. J. 2019, 882, 21. [Google Scholar] [CrossRef]
- Wu, H.; Tu, C.; Wang, X.; He, J.; Wang, L. Dependence of 3D Self-correlation Level Contours on the Scales in the Inertial Range of Solar Wind Turbulence. Astrophys. J. Lett. 2019, 883, L9. [Google Scholar] [CrossRef]
- Luo, Q.Y.; Wu, D.J. Observations of Anisotropic Scaling of Solar Wind Turbulence. Astrophys. J. Lett. 2010, 714, L138–L141. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Mallet, A.; Yousef, T.A.; Schekochihin, A.A.; Horbury, T.S. Anisotropy of Alfvénic turbulence in the solar wind and numerical simulations. Mon. Not. R. Astron. Soc. 2011, 415, 3219–3226. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Mallet, A.; Schekochihin, A.A.; Horbury, T.S.; Wicks, R.T.; Bale, S.D. Three-dimensional Structure of Solar Wind Turbulence. Astrophys. J. 2012, 758, 120. [Google Scholar] [CrossRef]
- He, J.; Tu, C.; Marsch, E.; Bourouaine, S.; Pei, Z. Radial Evolution of the Wavevector Anisotropy of Solar Wind Turbulence between 0.3 and 1 AU. Astrophys. J. 2013, 773, 72. [Google Scholar] [CrossRef]
- Pei, Z.; He, J.; Wang, X.; Tu, C.; Marsch, E.; Wang, L.; Yan, L. Influence of intermittency on the anisotropy of magnetic structure functions of solar wind turbulence. J. Geophys. Res. Space Phys. 2016, 121, 911–924. [Google Scholar] [CrossRef]
- Verdini, A.; Grappin, R.; Alexandrova, O.; Lion, S. 3D Anisotropy of Solar Wind Turbulence, Tubes, or Ribbons? Astrophys. J. 2018, 853, 85. [Google Scholar] [CrossRef]
- Verdini, A.; Grappin, R.; Alexandrova, O.; Franci, L.; Landi, S.; Matteini, L.; Papini, E. Three-dimensional local anisotropy of velocity fluctuations in the solar wind. Mon. Not. R. Astron. Soc. 2019. [Google Scholar] [CrossRef]
- Horbury, T.S.; Forman, M.; Oughton, S. Anisotropic Scaling of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2008, 101, 175005. [Google Scholar] [CrossRef]
- Podesta, J.J. Dependence of Solar-Wind Power Spectra on the Direction of the Local Mean Magnetic Field. Astrophys. J. 2009, 698, 986–999. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Wicks, R.T.; Horbury, T.S.; Schekochihin, A.A. Interpreting Power Anisotropy Measurements in Plasma Turbulence. Astrophys. J. Lett. 2010, 711, L79–L83. [Google Scholar] [CrossRef]
- Wicks, R.T.; Horbury, T.S.; Chen, C.H.K.; Schekochihin, A.A. Power and spectral index anisotropy of the entire inertial range of turbulence in the fast solar wind. Mon. Not. R. Astron. Soc. 2010, 407, L31–L35. [Google Scholar] [CrossRef]
- Wicks, R.T.; Horbury, T.S.; Chen, C.H.K.; Schekochihin, A.A. Anisotropy of Imbalanced Alfvénic Turbulence in Fast Solar Wind. Phys. Rev. Lett. 2011, 106, 045001. [Google Scholar] [CrossRef]
- Wang, X.; Tu, C.; He, J.; Marsch, E.; Wang, L. The Influence of Intermittency on the Spectral Anisotropy of Solar Wind Turbulence. Astrophys. J. Lett. 2014, 783, L9. [Google Scholar] [CrossRef]
- Tu, C.Y.; Marsch, E. MHD structures, waves and turbulence in the solar wind: Observations and theories. Space Sci. Rev. 1995, 73, 1–210. [Google Scholar] [CrossRef]
- Goldreich, P.; Sridhar, S. Magnetohydrodynamic Turbulence Revisited. Astrophys. J. 1997, 485, 680–688. [Google Scholar] [CrossRef]
- Oughton, S.; Priest, E.R.; Matthaeus, W.H. The influence of a mean magnetic field on three-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 1994, 280, 95–117. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Ghosh, S.; Oughton, S.; Roberts, D.A. Anisotropic three-dimensional MHD turbulence. J. Geophys. Res. Space Phys. 1996, 101, 7619–7630. [Google Scholar] [CrossRef]
- Ghosh, S.; Goldstein, M.L. Anisotropy in Hall MHD turbulence due to a mean magnetic field. J. Plasma Phys. 1997, 57, 129–154. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Oughton, S.; Ghosh, S.; Hossain, M. Scaling of Anisotropy in Hydromagnetic Turbulence. Phys. Rev. Lett. 1998, 81, 2056–2059. [Google Scholar] [CrossRef]
- Cho, J.; Vishniac, E.T. The Anisotropy of Magnetohydrodynamic Alfvénic Turbulence. Astrophys. J. 2000, 539, 273–282. [Google Scholar] [CrossRef]
- Maron, J.; Goldreich, P. Simulations of Incompressible Magnetohydrodynamic Turbulence. Astrophys. J. 2001, 554, 1175–1196. [Google Scholar] [CrossRef]
- Cho, J.; Lazarian, A. Compressible Sub-Alfvénic MHD Turbulence in Low- β Plasmas. Phys. Rev. Lett. 2002, 88, 245001. [Google Scholar] [CrossRef]
- Müller, W.C.; Biskamp, D.; Grappin, R. Statistical anisotropy of magnetohydrodynamic turbulence. Phys. Rev. 2003, 67, 066302. [Google Scholar] [CrossRef]
- Müller, W.C.; Grappin, R. Spectral Energy Dynamics in Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2005, 95, 114502. [Google Scholar] [CrossRef]
- Mason, J.; Cattaneo, F.; Boldyrev, S. Numerical measurements of the spectrum in magnetohydrodynamic turbulence. Phys. Rev. 2008, 77, 036403. [Google Scholar] [CrossRef]
- Perez, J.C.; Boldyrev, S. Role of Cross-Helicity in Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 2009, 102, 025003. [Google Scholar] [CrossRef]
- Grappin, R.; Müller, W.C. Scaling and anisotropy in magnetohydrodynamic turbulence in a strong mean magnetic field. Phys. Rev. 2010, 82, 026406. [Google Scholar] [CrossRef]
- Boldyrev, S.; Perez, J.C.; Borovsky, J.E.; Podesta, J.J. Spectral Scaling Laws in Magnetohydrodynamic Turbulence Simulations and in the Solar Wind. Astrophys. J. Lett. 2011, 741, L19. [Google Scholar] [CrossRef]
- Beresnyak, A. Spectra of Strong Magnetohydrodynamic Turbulence from High-resolution Simulations. Astrophys. J. Lett. 2014, 784, L20. [Google Scholar] [CrossRef]
- Verdini, A.; Grappin, R. Imprints of Expansion on the Local Anisotropy of Solar Wind Turbulence. Astrophys. J. Lett. 2015, 808, L34. [Google Scholar] [CrossRef]
- Mallet, A.; Schekochihin, A.A.; Chandran, B.D.G.; Chen, C.H.K.; Horbury, T.S.; Wicks, R.T.; Greenan, C.C. Measures of three-dimensional anisotropy and intermittency in strong Alfvénic turbulence. Mon. Not. R. Astron. Soc. 2016, 459, 2130–2139. [Google Scholar] [CrossRef]
- Mallet, A.; Schekochihin, A.A. A statistical model of three-dimensional anisotropy and intermittency in strong Alfvénic turbulence. Mon. Not. R. Astron. Soc. 2017, 466, 3918–3927. [Google Scholar] [CrossRef]
- Yang, L.; He, J.; Tu, C.; Li, S.; Zhang, L.; Wang, X.; Marsch, E.; Wang, L. Influence of Intermittency on the Quasi-perpendicular Scaling in Three-dimensional Magnetohydrodynamic Turbulence. Astrophys. J. 2017, 846, 49. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, L.; He, J.; Tu, C.; Li, S.; Wang, X.; Wang, L. Disappearance of Anisotropic Intermittency in Large-amplitude MHD Turbulence and Its Comparison with Small-amplitude MHD Turbulence. Astrophys. J. 2018, 855, 69. [Google Scholar] [CrossRef]
- Yang, L.; He, J.; Tu, C.; Li, S.; Zhang, L.; Marsch, E.; Wang, L.; Wang, X.; Feng, X. Multiscale Pressure-Balanced Structures in Three-Dimensional Magnetohydrodynamic Turbulence. Astrophys. J. 2017, 836, 69. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, L.; He, J.; Tu, C.; Li, S.; Wang, X.; Wang, L. Coexistence of Slow-mode and Alfven-mode Waves and Structures in 3D Compressive MHD Turbulence. Astrophys. J. 2018, 866, 41. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, L.; He, J.; Tu, C.; Li, S.; Wang, X.; Wang, L. Formation and Properties of Tangential Discontinuities in Three-dimensional Compressive MHD Turbulence. Astrophys. J. 2017, 851, 121. [Google Scholar] [CrossRef]
- Yang, L.P.; Li, H.; Li, S.T.; Zhang, L.; He, J.S.; Feng, X.S. Energy occupation of waves and structures in 3D compressive MHD turbulence. Mon. Not. R. Astron. Soc. 2019, 488, 859–867. [Google Scholar] [CrossRef]
- Taylor, G.I. The Spectrum of Turbulence. Proc. R. Soc. Lond. Ser. A 1938, 164, 476–490. [Google Scholar] [CrossRef]
- Yan, L.; He, J.; Zhang, L.; Tu, C.; Marsch, E.; Chen, C.H.K.; Wang, X.; Wang, L.; Wicks, R.T. Spectral Anisotropy of Elsässer Variables in Two-dimensional Wave-vector Space as Observed in the Fast Solar Wind Turbulence. Astrophys. J. Lett. 2016, 816, L24. [Google Scholar] [CrossRef]
- Adhikari, L.; Zank, G.P.; Telloni, D.; Hunana, P.; Bruno, R.; Shiota, D. Theory and Transport of Nearly Incompressible Magnetohydrodynamics Turbulence. III. Evolution of Power Anistropy in Magnetic Field Fluctuations throughout the Heliosphere. Astrophys. J. 2017, 851, 117. [Google Scholar] [CrossRef]
- Sonnerup, B.U.O.; Cahill, L.J., Jr. Magnetopause Structure and Attitude from Explorer 12 Observations. J. Geophys. Res. Space Phys. 1967, 72, 171. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; He, J.; Wang, X.; Wu, H.; Zhang, L.; Feng, X. Anisotropy of Self-Correlation Level Contours in Three-Dimensional Magnetohydrodynamic Turbulence. Universe 2023, 9, 395. https://doi.org/10.3390/universe9090395
Yang L, He J, Wang X, Wu H, Zhang L, Feng X. Anisotropy of Self-Correlation Level Contours in Three-Dimensional Magnetohydrodynamic Turbulence. Universe. 2023; 9(9):395. https://doi.org/10.3390/universe9090395
Chicago/Turabian StyleYang, Liping, Jiansen He, Xin Wang, Honghong Wu, Lei Zhang, and Xueshang Feng. 2023. "Anisotropy of Self-Correlation Level Contours in Three-Dimensional Magnetohydrodynamic Turbulence" Universe 9, no. 9: 395. https://doi.org/10.3390/universe9090395




