Sequence-Dependent Correlated Segments in the Intrinsically Disordered Region of ChiZ
Abstract
:1. Introduction
2. Materials and Methods
2.1. Protein Expression and Purification
2.2. Small Angle X-ray Scattering
2.3. NMR Spectroscopy
2.4. Molecular Dynamics Simulations
2.5. Calculation of SAXS Profiles
2.6. Calculation of Chemical Shifts
2.7. Radius of Gyration, Secondary Structures, and Hydrogen Bonds
2.8. Dihedral Principal Component Analysis
2.9. Contact Maps
2.10. NMR Relaxation Properties
2.11. Data Availability
3. Results
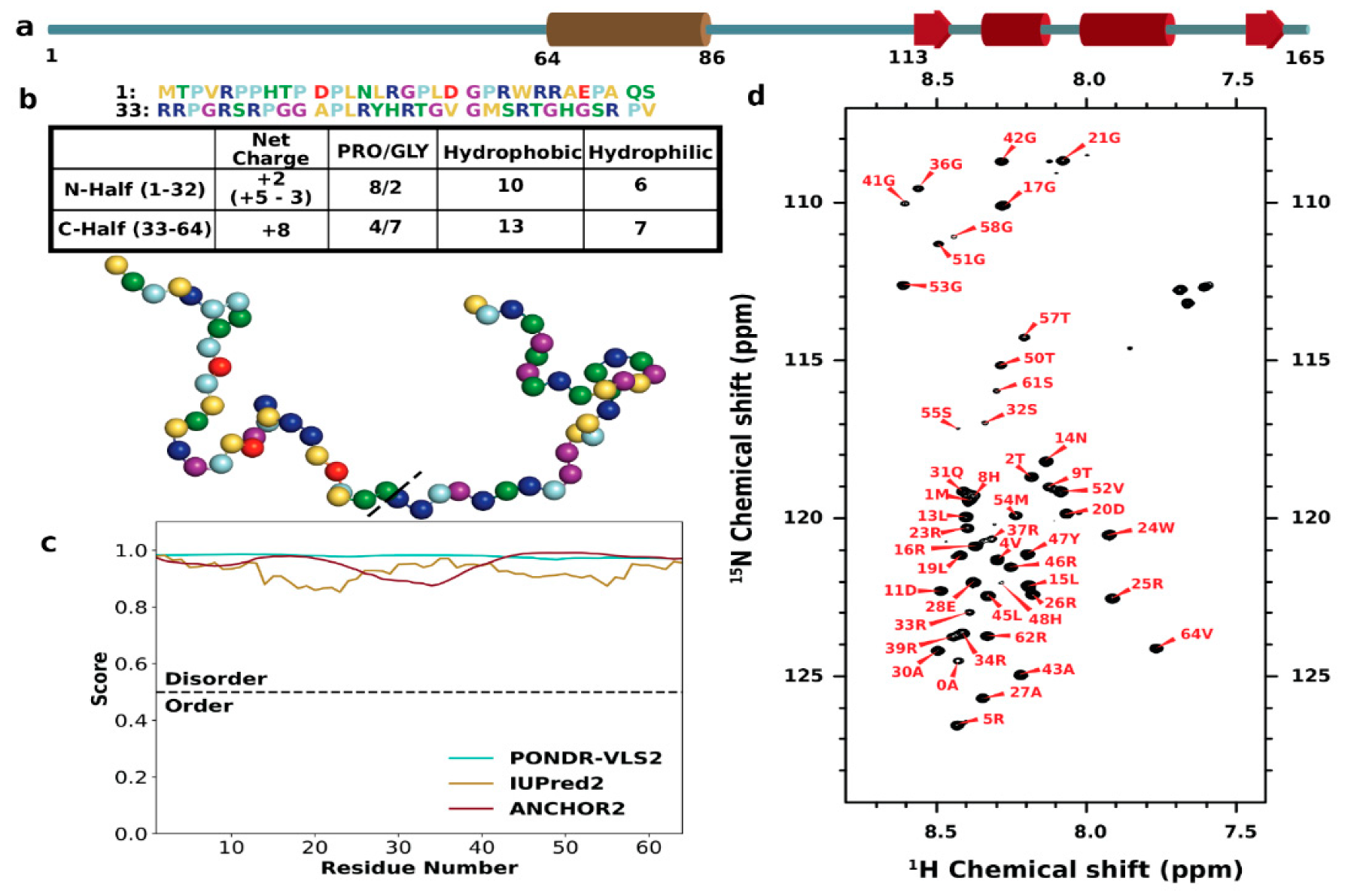
3.1. Sequence Characteristics and Disorder of ChiZ1-64
3.2. SAXS Profile and Secondary Chemical Shifts
3.3. Force Field Validation
3.4. High Poly-Proline II Propensities
3.5. Flat Energy Landscape in Conformational Space
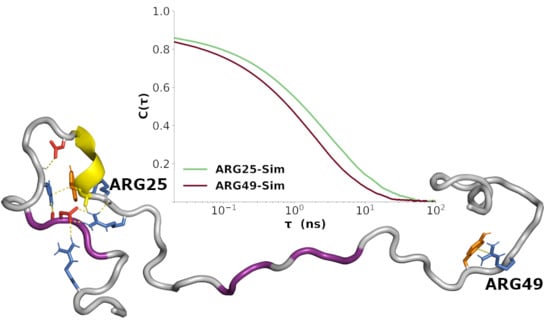
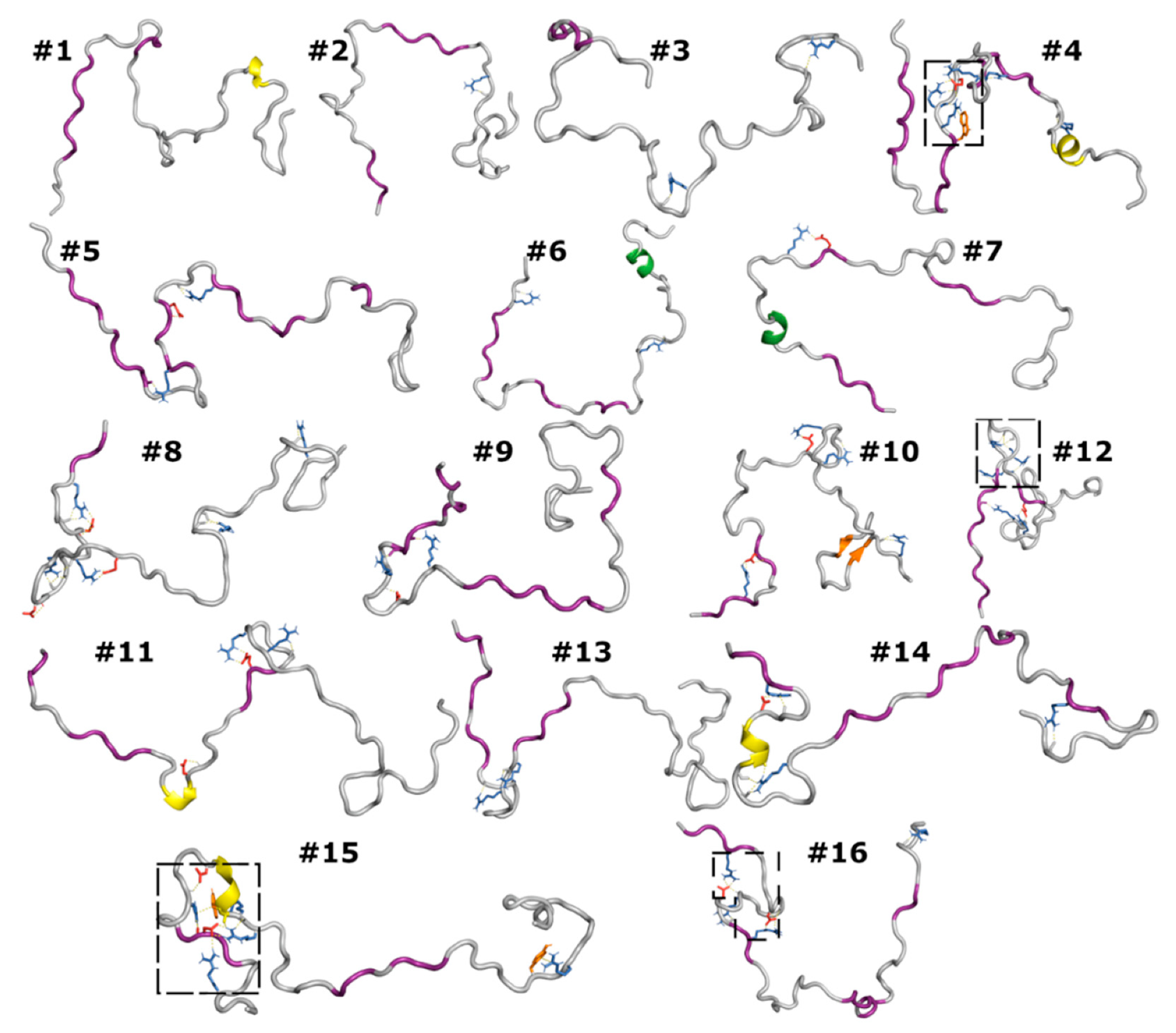
3.6. Correlated Segments Revealed by Contact Maps
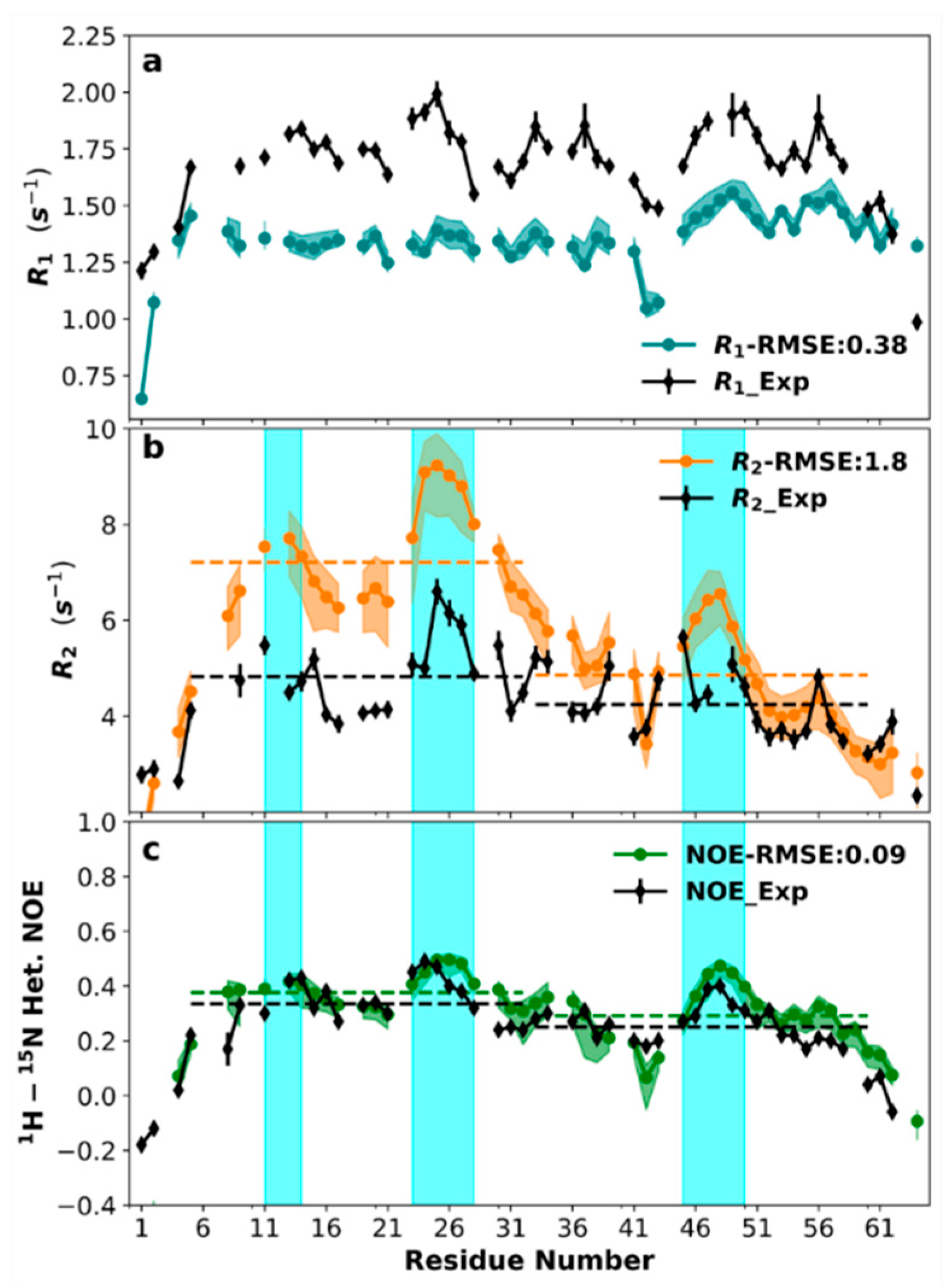
3.7. Sequence-Specific Backbone Dynamics
3.8. Amplitudes of Backbone Dynamics on Different Timescales
3.9. Non-Uniform Amide Proton Exchange Rates along the Sequence
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xue, B.; Dunker, A.K.; Uversky, V.N. Orderly order in protein intrinsic disorder distribution: Disorder in 3500 proteomes from viruses and the three domains of life. J. Biomol. Struct. Dyn. 2012, 30, 137–149. [Google Scholar] [CrossRef] [PubMed]
- Wright, P.E.; Dyson, H.J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Boil. 2014, 16, 18–29. [Google Scholar] [CrossRef] [PubMed]
- Kjaergaard, M.; Kragelund, B.B. Functions of intrinsic disorder in transmembrane proteins. Cell. Mol. Life Sci. 2017, 74, 3205–3224. [Google Scholar] [CrossRef]
- Babu, M.M.; van der Lee, R.; de Groot, N.S.; Gsponer, J. Intrinsically disordered proteins: Regulation and disease. Curr. Opin. Struct. Boil. 2011, 21, 432–440. [Google Scholar] [CrossRef] [PubMed]
- Martinelli, A.H.S.; Lopes, F.C.; John, E.B.D.O.; Carlini, C.R.; Ligabue-Braun, R. Modulation of Disordered Proteins with a Focus on Neurodegenerative Diseases and Other Pathologies. Int. J. Mol. Sci. 2019, 20, 1322. [Google Scholar] [CrossRef] [Green Version]
- Cook, E.C.; Sahu, D.; Bastidas, M.; Showalter, S.A. Solution Ensemble of the C-Terminal Domain from the Transcription Factor Pdx1 Resembles an Excluded Volume Polymer. J. Phys. Chem. B 2018, 123, 106–116. [Google Scholar] [CrossRef]
- Morgan, J.L.; Jensen, M.R.; Ozenne, V.; Blackledge, M.; Barbar, E. The LC8 Recognition Motif Preferentially Samples Polyproline II Structure in Its Free State. Biochemistry 2017, 56, 4656–4666. [Google Scholar] [CrossRef]
- Schneider, R.; Maurin, D.; Communie, G.; Kragelj, J.; Hansen, D.F.; Ruigrok, R.W.H.; Jensen, M.R.; Blackledge, M. Visualizing the Molecular Recognition Trajectory of an Intrinsically Disordered Protein Using Multinuclear Relaxation Dispersion NMR. J. Am. Chem. Soc. 2015, 137, 1220–1229. [Google Scholar] [CrossRef] [Green Version]
- Arai, M.; Sugase, K.; Dyson, H.J.; Wright, P.E. Conformational propensities of intrinsically disordered proteins influence the mechanism of binding and folding. Proc. Natl. Acad. Sci. USA 2015, 112, 9614–9619. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, E.; Andersson, E.; Dogan, J.; Gianni, S.; Jemth, P.; Camilloni, C. A structurally heterogeneous transition state underlies coupled binding and folding of disordered proteins. J. Boil. Chem. 2018, 294, 1230–1239. [Google Scholar] [CrossRef] [Green Version]
- Ou, L.; Matthews, M.; Pang, X.; Zhou, H.-X. The dock-and-coalesce mechanism for the association of a WASP disordered region with the Cdc42 GTPase. FEBS J. 2017, 284, 3381–3391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berlow, R.; Martinez-Yamout, M.A.; Dyson, H.J.; Wright, P.E. Role of Backbone Dynamics in Modulating the Interactions of Disordered Ligands with the TAZ1 Domain of the CREB-Binding Protein. Biochemistry 2019, 58, 1354–1362. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.-X. Intrinsic disorder: Signaling via highly specific but short-lived association. Trends Biochem. Sci. 2011, 37, 43–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borgia, A.; Borgia, M.B.; Bugge, K.; Kissling, V.M.; Heidarsson, P.O.; Fernandes, C.B.; Sottini, A.; Soranno, A.; Buholzer, K.J.; Nettels, D.; et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66. [Google Scholar] [CrossRef] [Green Version]
- Pang, X.; Zhou, H.-X. Rate Constants and Mechanisms of Protein-Ligand Binding. Annu. Rev. Biophys. 2017, 46, 105–130. [Google Scholar] [CrossRef] [Green Version]
- Uversky, V.N.; Gillespie, J.R.; Fink, A.L. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins Struct. Funct. Bioinform. 2000, 41, 415–427. [Google Scholar] [CrossRef]
- Das, R.K.; Pappu, R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA 2013, 110, 13392–13397. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.-X.; Pang, X. Electrostatic Interactions in Protein Structure, Folding, Binding, and Condensation. Chem. Rev. 2018, 118, 1691–1741. [Google Scholar] [CrossRef]
- Baul, U.; Chakraborty, D.; Mugnai, M.L.; Straub, J.E.; Thirumalai, D. Sequence Effects on Size, Shape, and Structural Heterogeneity in Intrinsically Disordered Proteins. J. Phys. Chem. B 2019, 123, 3462–3474. [Google Scholar] [CrossRef]
- Kikhney, A.G.; Svergun, D.I. A practical guide to small angle X-ray scattering (SAXS) of flexible and intrinsically disordered proteins. FEBS Lett. 2015, 589, 2570–2577. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, H.; Soranno, A.; Borgia, A.; Gast, K.; Nettels, D.; Schuler, B. Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy. Proc. Natl. Acad. Sci. USA 2012, 109, 16155–16160. [Google Scholar] [CrossRef] [Green Version]
- Soranno, A.; Stucki-Buchli, B.; Nettels, D.; Cheng, R.R.; Müller-Späth, S.; Pfeil, S.H.; Hoffmann, A.; Lipman, E.A.; Makarov, D.E.; Schuler, B. Quantifying internal friction in unfolded and intrinsically disordered proteins with single-molecule spectroscopy. Proc. Natl. Acad. Sci. USA 2012, 109, 17800–17806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soranno, A.; Holla, A.; Dingfelder, F.; Nettels, D.; Makarov, D.E.; Schuler, B. Integrated view of internal friction in unfolded proteins from single-molecule FRET, contact quenching, theory, and simulations. Proc. Natl. Acad. Sci. USA 2017, 114, E1833–E1839. [Google Scholar] [CrossRef] [Green Version]
- Jensen, M.R.; Zweckstetter, M.; Huang, J.-R.; Blackledge, M. Exploring Free-Energy Landscapes of Intrinsically Disordered Proteins at Atomic Resolution Using NMR Spectroscopy. Chem. Rev. 2014, 114, 6632–6660. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B. Computational, and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Boil. 2017, 42, 147–154. [Google Scholar] [CrossRef]
- Banks, A.; Qin, S.; Weiss, K.; Stanley, C.; Zhou, H.-X. Intrinsically Disordered Protein Exhibits Both Compaction and Expansion under Macromolecular Crowding. Biophys. J. 2018, 114, 1067–1079. [Google Scholar] [CrossRef]
- Sturzenegger, F.; Zosel, F.; Holmstrom, E.D.; Buholzer, K.J.; Makarov, D.E.; Nettels, D.; Schuler, B. Transition path times of coupled folding and binding reveal the formation of an encounter complex. Nat. Commun. 2018, 9, 4708. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-Y.; Meng, F.; Yoo, J.; Chung, H.S. Diffusion-limited association of disordered protein by non-native electrostatic interactions. Nat. Commun. 2018, 9, 4707. [Google Scholar] [CrossRef]
- Dyson, H.J.; Wright, P.E. Equilibrium NMR studies of unfolded and partially folded proteins. Nat. Genet. 1998, 5, 499–503. [Google Scholar] [CrossRef]
- Marsh, J.A.; Singh, V.K.; Jia, Z.; Forman-Kay, J.D. Sensitivity of secondary structure propensities to sequence differences between α- and γ-synuclein: Implications for fibrillation. Protein Sci. 2006, 15, 2795–2804. [Google Scholar] [CrossRef] [Green Version]
- Mittag, T.; Forman-Kay, J.D. Atomic-level characterization of disordered protein ensembles. Curr. Opin. Struct. Boil. 2007, 17, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Dass, R.; Corlianò, E.; Mulder, F.A.A. Measurement of Very Fast Exchange Rates of Individual Amide Protons in Proteins by NMR Spectroscopy. ChemPhysChem 2018, 20, 231–235. [Google Scholar] [CrossRef] [PubMed]
- McAllister, R.G.; Konermann, L. Challenges in the Interpretation of Protein H/D Exchange Data: A Molecular Dynamics Simulation Perspective. Biochemistry 2015, 54, 2683–2692. [Google Scholar] [CrossRef] [PubMed]
- Croke, R.L.; Sallum, C.O.; Watson, E.; Watt, E.D.; Alexandrescu, A.T. Hydrogen exchange of monomeric α-synuclein shows unfolded structure persists at physiological temperature and is independent of molecular crowding in Escherichia coli. Protein Sci. 2008, 17, 1434–1445. [Google Scholar] [CrossRef] [Green Version]
- Palmer, A.G. NMR Characterization of the Dynamics of Biomacromolecules. Chem. Rev. 2004, 104, 3623–3640. [Google Scholar] [CrossRef]
- Lipari, G.; Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982, 104, 4546–4559. [Google Scholar] [CrossRef]
- Khan, S.N.; Charlier, C.; Augustyniak, R.; Salvi, N.; Déjean, V.; Bodenhausen, G.; Lequin, O.; Pelupessy, P.; Ferrage, F. Distribution of Pico- and Nanosecond Motions in Disordered Proteins from Nuclear Spin Relaxation. Biophys. J. 2015, 109, 988–999. [Google Scholar] [CrossRef] [Green Version]
- Abyzov, A.; Salvi, N.; Schneider, R.; Maurin, D.; Ruigrok, R.W.H.; Jensen, M.R.; Blackledge, M. Identification of Dynamic Modes in an Intrinsically Disordered Protein Using Temperature-Dependent NMR Relaxation. J. Am. Chem. Soc. 2016, 138, 6240–6251. [Google Scholar] [CrossRef]
- Gill, M.; Byrd, R.A.; Palmer, A.G. Dynamics of GCN4 facilitate DNA interaction: A model-free analysis of an intrinsically disordered region. Phys. Chem. Chem. Phys. 2016, 18, 5839–5849. [Google Scholar] [CrossRef] [Green Version]
- Nettels, D.; Müller-Späth, S.; Küster, F.; Hofmann, H.; Haenni, M.; Rüegger, S.; Reymond, L.; Hoffmann, A.; Kubelka, J.; Heinz, B.; et al. Single-molecule spectroscopy of the temperature-induced collapse of unfolded proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 20740–20745. [Google Scholar] [CrossRef] [Green Version]
- Rauscher, S.; Gapsys, V.; Gajda, M.J.; Zweckstetter, M.; de Groot, B.L.; Grubmüller, H. Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524. [Google Scholar] [CrossRef] [Green Version]
- Best, R.B.; Zheng, W.; Mittal, J. Balanced Protein–Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput. 2014, 10, 5113–5124. [Google Scholar] [CrossRef] [Green Version]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef] [PubMed]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2016, 14, 71–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, Y.; Skrynnikov, N.R. Motion of a Disordered Polypeptide Chain as Studied by Paramagnetic Relaxation Enhancements,15N Relaxation, and Molecular Dynamics Simulations: How Fast Is Segmental Diffusion in Denatured Ubiquitin? J. Am. Chem. Soc. 2011, 133, 14614–14628. [Google Scholar] [CrossRef] [PubMed]
- Salvi, N.; Abyzov, A.; Blackledge, M. Multi-Timescale Dynamics in Intrinsically Disordered Proteins from NMR Relaxation and Molecular Simulation. J. Phys. Chem. Lett. 2016, 7, 2483–2489. [Google Scholar] [CrossRef]
- Salvi, N.; Abyzov, A.; Blackledge, M. Analytical Description of NMR Relaxation Highlights Correlated Dynamics in Intrinsically Disordered Proteins. Angew. Chem. Int. Ed. 2017, 56, 14020–14024. [Google Scholar] [CrossRef]
- Rezaei-Ghaleh, N.; Parigi, G.; Soranno, A.; Holla, A.; Becker, S.; Schuler, B.; Luchinat, C.; Zweckstetter, M. Local and Global Dynamics in Intrinsically Disordered Synuclein. Angew. Chem. Int. Ed. 2018, 57, 15262–15266. [Google Scholar] [CrossRef]
- Rezaei-Ghaleh, N.; Parigi, G.; Zweckstetter, M. Reorientational Dynamics of Amyloid-β from NMR Spin Relaxation and Molecular Simulation. J. Phys. Chem. Lett. 2019, 10, 3369–3375. [Google Scholar] [CrossRef] [Green Version]
- Salvi, N.; Abyzov, A.; Blackledge, M. Solvent-dependent segmental dynamics in intrinsically disordered proteins. Sci. Adv. 2019, 5, eaax2348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kämpf, K.; Izmailov, S.A.; Rabdano, S.O.; Groves, A.T.; Podkorytov, I.S.; Skrynnikov, N.R. What Drives 15N Spin Relaxation in Disordered Proteins? Combined NMR/MD Study of the H4 Histone Tail. Biophys. J. 2018, 115, 2348–2367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwalbe, H.; Fiebig, K.M.; Buck, M.; Jones, J.A.; Grimshaw, S.B.; Spencer, A.; Glaser, S.J.; Smith, L.J.; Dobson, C.M. Structural and Dynamical Properties of a Denatured Protein. Heteronuclear 3D NMR Experiments and Theoretical Simulations of Lysozyme in 8 M Urea. Biochemistry 1997, 36, 8977–8991. [Google Scholar] [CrossRef]
- Klein-Seetharaman, J. Long-Range Interactions Within a Nonnative Protein. Science 2002, 295, 1719–1722. [Google Scholar] [CrossRef] [Green Version]
- Martin, E.W.; Holehouse, A.S.; Peran, I.; Farag, M.; Incicco, J.J.; Bremer, A.; Grace, C.R.; Soranno, A.; Pappu, R.V.; Mittag, T. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science 2020, 367, 694–699. [Google Scholar] [CrossRef]
- Kieser, K.J.; Rubin, E.J. How sisters grow apart: Mycobacterial growth and division. Nat. Rev. Genet. 2014, 12, 550–562. [Google Scholar] [CrossRef]
- Das, N.; Dai, J.; Hung, I.; Rajagopalan, M.R.; Zhou, H.-X.; Cross, T.A. Structure of CrgA, a cell division structural and regulatory protein from Mycobacterium tuberculosis, in lipid bilayers. Proc. Natl. Acad. Sci. USA 2014, 112, E119–E126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chauhan, A.; Lofton, H.; Maloney, E.; Moore, J.; Fol, M.; Madiraju, M.V.V.S.; Rajagopalan, M. Interference of Mycobacterium tuberculosis cell division by Rv2719c, a cell wall hydrolase. Mol. Microbiol. 2006, 62, 132–147. [Google Scholar] [CrossRef] [PubMed]
- Escobar, C.A.; Cross, T.A. False positives in using the zymogram assay for identification of peptidoglycan hydrolases. Anal. Biochem. 2018, 543, 162–166. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, A.; Madiraju, M.V.V.S.; Fol, M.; Lofton, H.; Maloney, E.; Reynolds, R.; Rajagopalan, M. Mycobacterium tuberculosis Cells Growing in Macrophages Are Filamentous and Deficient in FtsZ Rings. J. Bacteriol. 2006, 188, 1856–1865. [Google Scholar] [CrossRef] [Green Version]
- Vadrevu, I.S.; Lofton, H.; Sarva, K.; Blasczyk, E.; Plocinska, R.; Chinnaswamy, J.; Madiraju, M.; Rajagopalan, M. ChiZ levels modulate cell division process in mycobacteria. Tuberculosis 2011, 91, S128–S135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Franke, D.; Petoukhov, M.V.; Konarev, P.V.; Panjkovich, A.; Tuukkanen, A.; Mertens, H.D.T.; Kikhney, A.G.; Hajizadeh, N.R.; Franklin, J.M.; Jeffries, C.M.; et al. ATSAS 2.8: A comprehensive data analysis suite for small-angle scattering from macromolecular solutions. J. Appl. Crystallogr. 2017, 50, 1212–1225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hwang, T.-L.; van Zijl, P.C.; Mori, S. Accurate quantitation of water-amide proton exchange rates using the phase-modulated CLEAN chemical EXchange (CLEANEX-PM) approach with a Fast-HSQC (FHSQC) detection scheme. J. Biomol. NMR 1998, 11, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-Z. Protein and Peptide Structure and Interactions Studied by Hydrogen Exchanger and NMR. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 1995. [Google Scholar]
- Bai, Y.; Milne, J.S.; Mayne, L.; Englander, S.W. Primary structure effects on peptide group hydrogen exchange. Proteins Struct. Funct. Bioinform. 1993, 17, 75–86. [Google Scholar] [CrossRef] [Green Version]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [Green Version]
- Debiec, K.T.; Cerutti, D.S.; Baker, L.R.; Gronenborn, A.M.; Case, D.A.; Chong, L.T. Further along the Road Less Traveled: AMBER ff15ipq, an Original Protein Force Field Built on a Self-Consistent Physical Model. J. Chem. Theory Comput. 2016, 12, 3926–3947. [Google Scholar] [CrossRef]
- Case, D.A.; Betz, R.M.; Cerutti, D.S.; Cheatham, T.E.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; et al. AMBER 2016; University of California: Oakland, CA, USA, 2016. [Google Scholar]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E.; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K.; et al. AMBER 2018; University of California: Oakland, CA, USA, 2018. [Google Scholar]
- Abraham, M.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Crowley, M.F.; Williamson, M.J.; Walker, R.C. CHAMBER: Comprehensive support for CHARMM force fields within the AMBER software. Int. J. Quantum Chem. 2009, 109, 3767–3772. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef] [PubMed]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Schneidman-Duhovny, D.; Hammel, M.; Sali, A. FoXS: A web server for rapid computation and fitting of SAXS profiles. Nucleic Acids Res. 2010, 38, W540–W544. [Google Scholar] [CrossRef] [PubMed]
- Henriques, J.; Arleth, L.; Lindorff-Larsen, K.; Skepö, M. On the Calculation of SAXS Profiles of Folded and Intrinsically Disordered Proteins from Computer Simulations. J. Mol. Boil. 2018, 430, 2521–2539. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Liu, Y.; Ginzinger, S.W.; Wishart, D.S. SHIFTX2: Significantly improved protein chemical shift prediction. J. Biomol. NMR 2011, 50, 43–57. [Google Scholar] [CrossRef] [Green Version]
- Tamiola, K.; Acar, B.; Mulder, F.A.A. Sequence-Specific Random Coil Chemical Shifts of Intrinsically Disordered Proteins. J. Am. Chem. Soc. 2010, 132, 18000–18003. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef]
- Mansiaux, Y.; Joseph, A.P.; Gelly, J.-C.; de Brevern, A.G. Assignment of PolyProline II Conformation and Analysis of Sequence—Structure Relationship. PLoS ONE 2011, 6, e18401. [Google Scholar] [CrossRef]
- Mu, Y.; Nguyen, P.H.; Stock, G. Energy landscape of a small peptide revealed by dihedral angle principal component analysis. Proteins Struct. Funct. Bioinform. 2004, 58, 45–52. [Google Scholar] [CrossRef] [PubMed]
- Altis, A.; Hegger, R.; Nguyen, P.H.; Stock, G. Dihedral angle principal component analysis of molecular dynamics simulations. J. Chem. Phys. 2007, 126, 244111. [Google Scholar] [CrossRef] [Green Version]
- Best, R.B.; Hummer, G.; Eaton, W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17874–17879. [Google Scholar] [CrossRef] [Green Version]
- McGibbon, R.T.; Beauchamp, K.A.; Harrigan, M.; Klein, C.; Swails, J.M.; Hernández, C.X.; Schwantes, C.R.; Wang, L.-P.; Lane, T.; Pande, V.S. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, B.; Dunbrack, R.L.; Williams, R.W.; Dunker, A.K.; Uversky, V.N. PONDR-FIT: A Meta-Predictor of Intrinsically Disordered Amino Acids. Biochim. Biophys. Acta Proteins Proteom. 2010, 1804, 996–1010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mészáros, B.; Erdos, G.; Dosztányi, Z. IUPred2A: Context-dependent prediction of protein disorder as a function of redox state and protein binding. Nucleic Acids Res. 2018, 46, W329–W337. [Google Scholar] [CrossRef] [PubMed]
- Dosztányi, Z.; Mészáros, B.; Simon, I. ANCHOR: Web server for predicting protein binding regions in disordered proteins. Bioinformatics 2009, 25, 2745–2746. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernadó, P.; Blackledge, M. A Self-Consistent Description of the Conformational Behavior of Chemically Denatured Proteins from NMR and Small Angle Scattering. Biophys. J. 2009, 97, 2839–2845. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cho, M.-K.; Kim, H.-Y.; Bernadó, P.; Fernández, C.O.; Blackledge, M.; Zweckstetter, M. Amino Acid Bulkiness Defines the Local Conformations and Dynamics of Natively Unfolded α-Synuclein and Tau. J. Am. Chem. Soc. 2007, 129, 3032–3033. [Google Scholar] [CrossRef]
- Maiti, S.; Acharya, B.; Boorla, V.S.; Manna, B.; Ghosh, A.; De, S. Dynamic Studies on Intrinsically Disordered Regions of Two Paralogous Transcription Factors Reveal Rigid Segments with Important Biological Functions. J. Mol. Boil. 2019, 431, 1353–1369. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hicks, A.; Escobar, C.A.; Cross, T.A.; Zhou, H.-X. Sequence-Dependent Correlated Segments in the Intrinsically Disordered Region of ChiZ. Biomolecules 2020, 10, 946. https://doi.org/10.3390/biom10060946
Hicks A, Escobar CA, Cross TA, Zhou H-X. Sequence-Dependent Correlated Segments in the Intrinsically Disordered Region of ChiZ. Biomolecules. 2020; 10(6):946. https://doi.org/10.3390/biom10060946
Chicago/Turabian StyleHicks, Alan, Cristian A. Escobar, Timothy A. Cross, and Huan-Xiang Zhou. 2020. "Sequence-Dependent Correlated Segments in the Intrinsically Disordered Region of ChiZ" Biomolecules 10, no. 6: 946. https://doi.org/10.3390/biom10060946
APA StyleHicks, A., Escobar, C. A., Cross, T. A., & Zhou, H.-X. (2020). Sequence-Dependent Correlated Segments in the Intrinsically Disordered Region of ChiZ. Biomolecules, 10(6), 946. https://doi.org/10.3390/biom10060946