Human Eye Optics within a Non-Euclidian Geometrical Approach and Some Implications in Vision Prosthetics Design
Abstract
:1. Introduction
2. Results
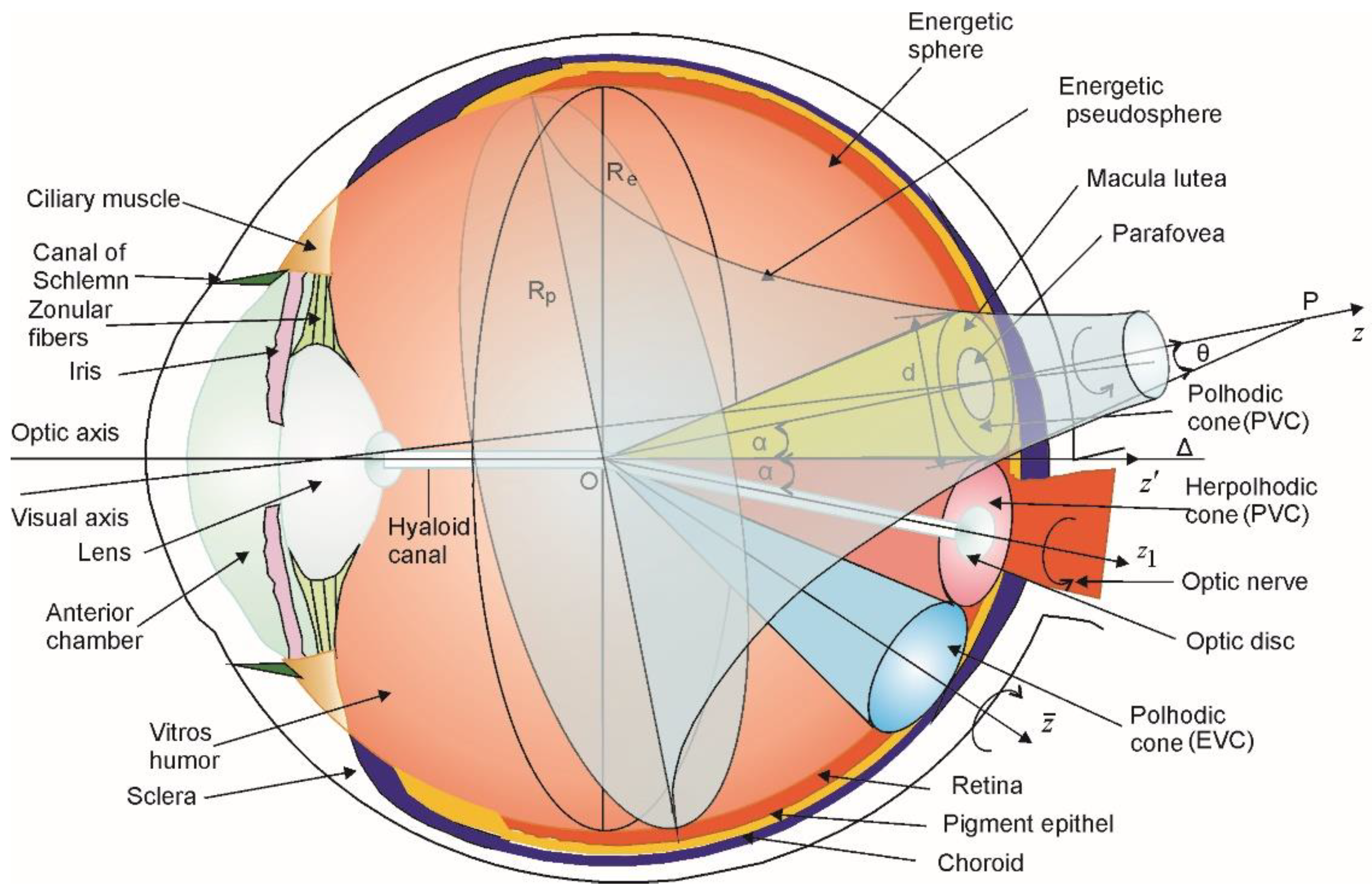
2.1. Vitreous Humor Charge Vortices Model for Eye Globe Morphology Emergence
- There are three vortices: two polhodic vortices (one associated with PVCs and the other with EVCs) and one herpolhodic vortex associated with a PVC (which will be described below).The polhodic vortices have the mobile directions Oz and as symmetry axis, while the herpolhodic one has Oz1 direction along the hyaloid channel as symmetry axis.
- The PVC polhodic cone (represented in yellow) rotates counter-clockwise with angular speed ω around the Oz axis;
- The PVC herpolhodic cone (represented in red) rotates counter-clockwise with angular speed ω1 around the Oz1 axis;
- The EVC polhodic cone (represented in blue) rotates clockwise with angular speed ω′ around the axis .
- The polhodic and herpolhodic vortices are tangent upon a common generatrix Δ, which is in fact the ocular optical axis (Figure 1).
- The angles between the axis of the herpolhodic () and polhodic cones (Oz și Oz1) are 2α = 22°44′. The optical axis Oz′ (Δ) is the bisectrix of the angle between Oz and Oz1.
2.2. Macula Representation as an Elliptical Pseudosphere
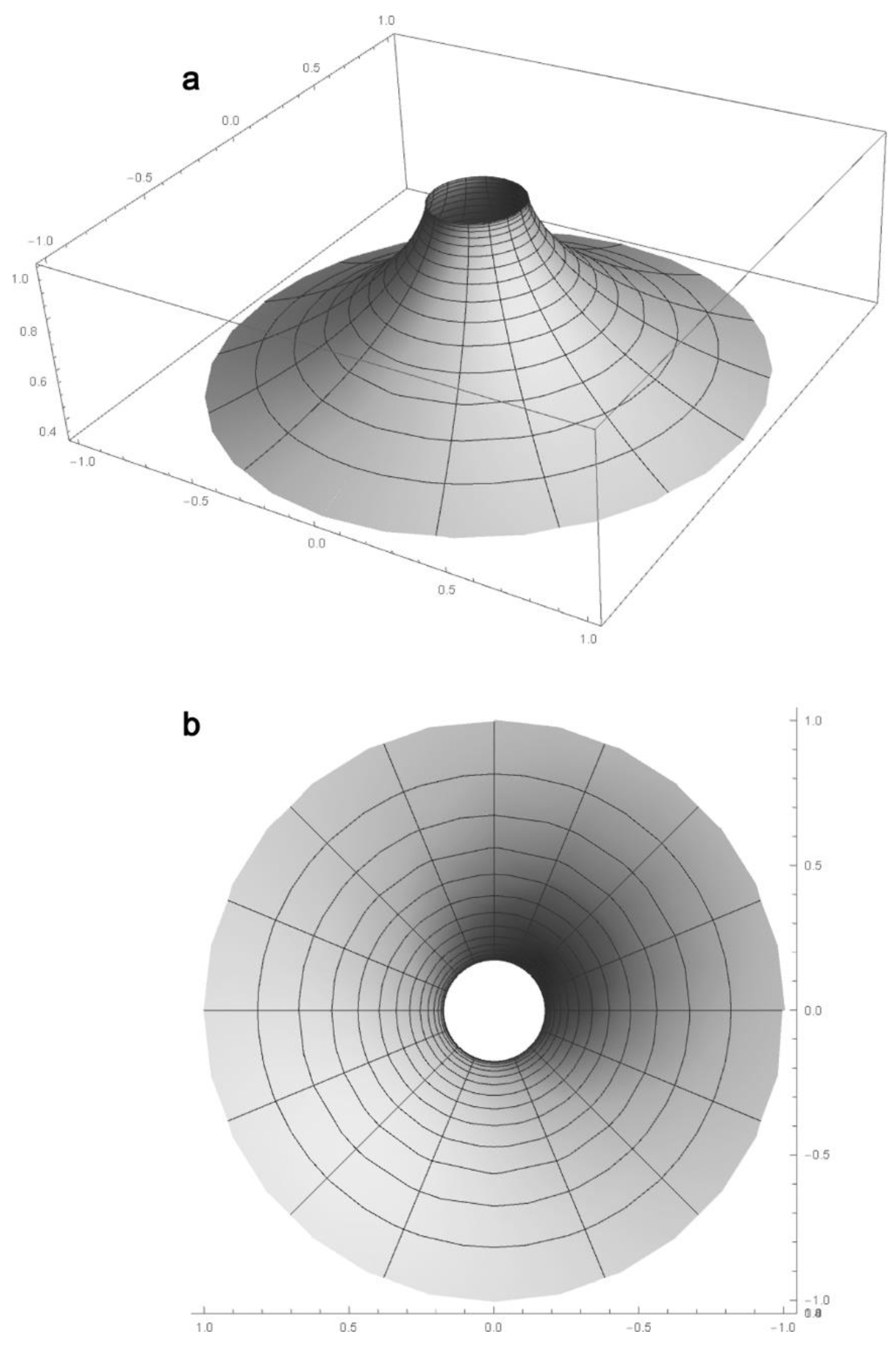
2.3. Macula Zones Generation within Klein–Beltrami Model
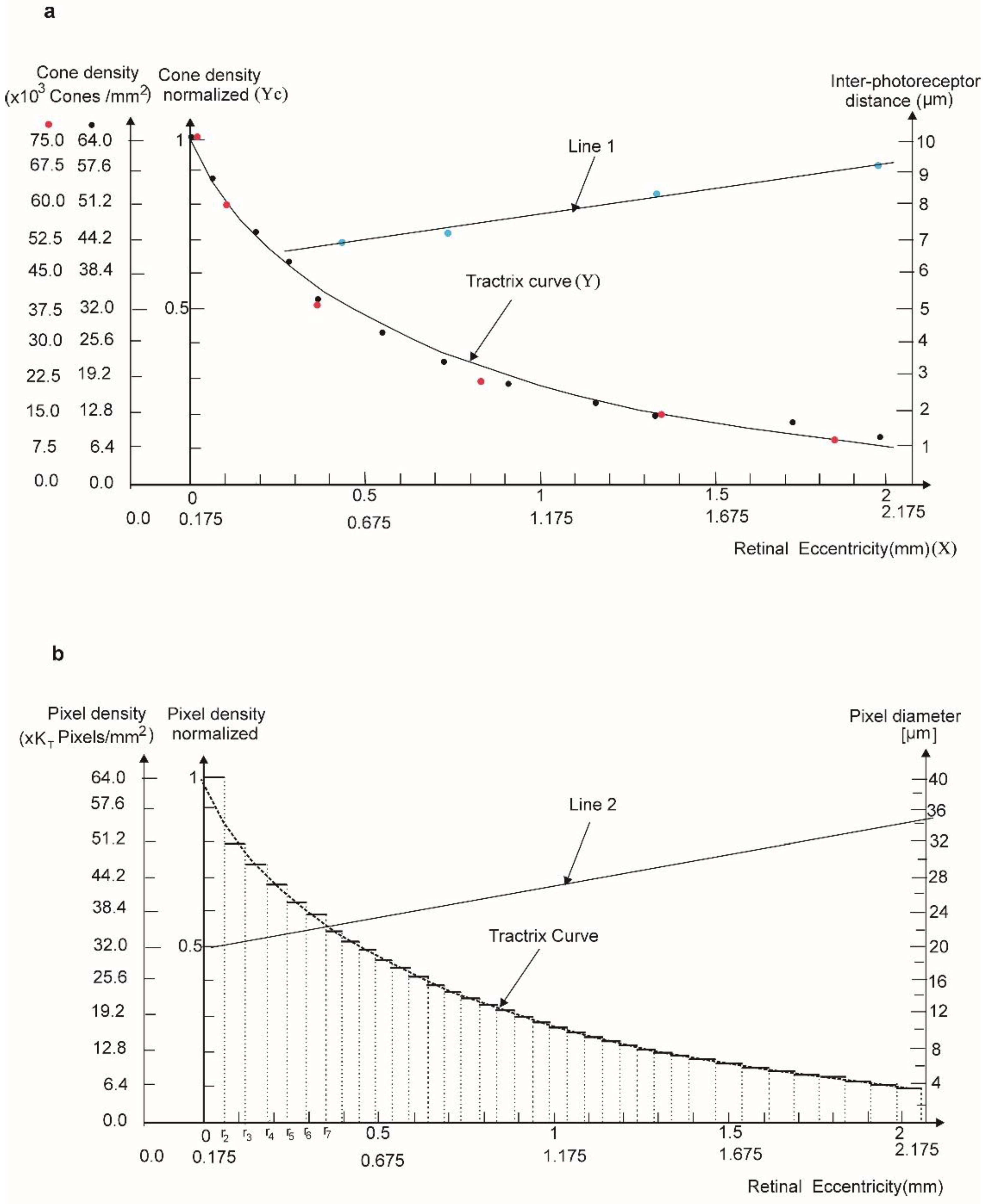
2.4. Discrete Model for Artificial Photo-Receptor Cell Distribution
2.4.1. Photoreceptor Cell Zones on Artificial Human Macula Surface
2.4.2. Fibonacci Mathematical Model for Color Pixel Optimized Paving
2.4.3. Photoreceptor Cell Positions in the Annular Hyperbolic Zones
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Bovolenta, P.; Cisneros, E. Retinitis pigmentosa: Cone photoreceptors starving to death. Nat. Neurosci. 2009, 12, 5–6. [Google Scholar] [CrossRef]
- Chader, G.J.; Weiland, J.; Humayun, M.S. Artificial vision: Needs, functioning, and testing of a retinal elec-tronic prosthesis. Prog. Brain Res. 2009, 175, 317–332. [Google Scholar] [PubMed]
- Stone, J.L.; Barlow, W.E.; Humayun, M.S.; de Juan, E.; Milam, A.H. Morphometric analysis of macular photoreceptors and ganglion cells in retinas with retinitis pigmentosa. Arch. Ophthalmol. 1992, 110, 1634–1639. [Google Scholar] [CrossRef]
- MacLaren, R.E.; Pearson, R.A.; MacNeil, A.; Douglas, R.H.; Salt, T.E.; Akimoto, M.; Swaroop, A.; Sowden, J.C.; Ali, R.R. Retinal repair by transplantation of photoreceptor precursors. Nat. Cell Biol. 2006, 444, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Dagnelie, G.; Schuchard, R.A. The state of visual prosthetics--hype or promise? J. Rehabil. Res. Dev. 2007, 44, 11–14. [Google Scholar] [CrossRef]
- Fariss, R.N.; Li, Z.-Y.; Milam, A.H. Abnormalities in rod photoreceptors, amacrine cells, and horizontal cells in human retinas with retinitis pigmentosa. Am. J. Ophthalmol. 2000, 129, 215–223. [Google Scholar] [CrossRef]
- Caspi, A.; Roy, A.; Dorn, J.D.; Greenberg, R.J. Retinotopic to Spatiotopic mapping in blind patients implanted with the argus ii retinal prosthesis. Investig. Opthalmol. Vis. Sci. 2017, 58, 119–127. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.H.-L.; Da Cruz, L. The Argus® II retinal prosthesis system. Prog. Retin. Eye Res. 2016, 50, 89–107. [Google Scholar] [CrossRef]
- Sabbah, N.; Authié, C.N.; Sanda, N.; Mohand-Said, S.; Sahel, J.-A.; Safran, A.B. Importance of eye position on spatial localization in blind subjects wearing an argus ii retinal prosthesis. Investig. Opthalmol. Vis. Sci. 2014, 55, 8259–8266. [Google Scholar] [CrossRef] [Green Version]
- Stingl, K.; Bartz-Schmidt, K.U.; Besch, D.; Chee, C.K.; Cottriall, C.L.; Gekeler, F.; Groppe, M.; Jackson, T.L.; MacLaren, R.E.; Koitschev, A.; et al. Subretinal visual implant alpha IMS—Clinical trial interim report. Vis. Res. 2015, 111, 149–160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuehlewein, L.; Kitiratschky, V.; Gosheva, M.; Edwards, T.L.; MacLaren, R.E.; Groppe, M.; Kusnyerik, A.; Soare, C.; Jackson, T.L.; Sun, C.H.; et al. Optical coherence tomography in patients with the subretinal implant retina implant Alpha IMS. Ophthalmic Surg. Lasers Imaging Retina 2017, 48, 993–999. [Google Scholar] [CrossRef] [PubMed]
- Kitiratschky, V.B.; Stingl, K.; Wilhelm, B.; Peters, T.; Besch, D.; Sachs, H.; Gekeler, F.; Bartz-Schmidt, K.U.; Zrenner, E. Safety evaluation of “retina implant alpha IMS”—A prospective clinical trial. Graefe’s Arch. Clin. Exp. Ophthalmol. 2014, 253, 381–387. [Google Scholar] [CrossRef] [PubMed]
- Stingl, K.; Bartz-Schmidt, K.U.; Besch, D.; Braun, A.; Bruckmann, A.R.; Gekeler, F.; Greppmaier, U.; Hipp, S.; Hörtdörfer, G.; Kernstock, C.; et al. Artificial vision with wirelessly powered subretinal electronic implant alpha-IMS. Proc. R. Soc. B Boil. Sci. 2013, 280, 20130077. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chuang, A.T.; Margo, C.E.; Greenberg, P.B. Retinal implants: A systematic review: Table 1. Br. J. Ophthalmol. 2014, 98, 852–856. [Google Scholar] [CrossRef]
- Fernandes, R.A.B.; Diniz, B.; Ribeiro, R.; Humayun, M. Artificial vision through neuronal stimulation. Neurosci. Lett. 2012, 519, 122–128. [Google Scholar] [CrossRef]
- Ghezzi, D. Retinal prostheses: Progress toward the next generation implants. Front. Neurosci. 2015, 9, 290. [Google Scholar] [CrossRef] [Green Version]
- Gautam, V.; Narayan, K.S. Polymer optoelectronic structures for retinal prosthesis. Organogenesis 2013, 10, 9–12. [Google Scholar] [CrossRef] [Green Version]
- Serban, A.I.; Geicu, O.I.; Serban, F. Geophysicochemical model of an ionospheric auroral gyroscope. Earth Space Sci. 2016, 3, 15–33. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Chui, T.Y.P.; Zhong, Z.; Elsner, A.E.; Burns, S.A. Variation of Cone photoreceptor packing density with retinal eccentricity and age. Investig. Opthalmol. Vis. Sci. 2011, 52, 7376–7384. [Google Scholar] [CrossRef] [Green Version]
- Muthiah, M.N.; Gias, C.; Chen, F.K.; Zhong, J.; McClelland, Z.; Sallo, F.B.; Peto, T.; Coffey, P.J.; da Cruz, L. Cone photoreceptor definition on adaptive optics retinal imaging. Br. J. Ophthalmol. 2014, 98, 1073–1079. [Google Scholar] [CrossRef]
- Tumahai, P.; Moureaux, C.; Meillat, M.; Debellemanière, G.; Flores, M.; Delbosc, B.; Saleh, M. High-resolution imaging of photoreceptors in healthy human eyes using an adaptive optics retinal camera. Eye 2018, 32, 1723–1730. [Google Scholar] [CrossRef]
- Cooper, R.F.; Aguirre, G.K.; Morgan, J.I.W. Fully automated estimation of spacing and density for retinal mosaics. Transl. Vis. Sci. Technol. 2019, 8, 26. [Google Scholar] [CrossRef]
- Del Guidice, E.; Vitiello, G. Role of the electromagnetic field in the formation of domains in the process of symmetry-breaking phase transitions. Phys. Rev. A 2006, 74, 022105. [Google Scholar] [CrossRef] [Green Version]
- Montagnier, L.; Aissa, J.; Del Giudice, E.; Lavallee, C.; Tedeschi, A.; Vitiello, G. DNA waves and water. J. Phys. Conf. Ser. 2011, 306, 012007. [Google Scholar] [CrossRef]
- Czerlinski, G.; Ryba, R. Trevor coherence domains in living systems. J. Vortex Sci. Technol. 2015, 2, 110. [Google Scholar] [CrossRef]
- Del Giudice, E.; Spinetti, P.R.; Tedeschi, A. Water dynamics at the root of metamorphosis in living organisms. Water 2010, 2, 566–586. [Google Scholar] [CrossRef] [Green Version]
- Mogi, I.; Morimoto, R.; Aogaki, R.; Watanabe, K. Surface chirality induced by rotational electrodeposition in magnetic fields. Sci. Rep. 2013, 3, srep02574. [Google Scholar] [CrossRef] [Green Version]
- Van De Graaff, K.M. Sensory Organs. In Human Anatomy, 6th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2001; p. 500. [Google Scholar]
- Millodot, M. Dictionary of Optometry and Visual Science, 7th ed.; Elsevier: London, UK, 2009. [Google Scholar]
- Small, R.G. The Clinical Handbook of Ophthalmology; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Luneburg, R.K. The metric of binocular visual space. J. Opt. Soc. Am. 1950, 40, 627–640. [Google Scholar] [CrossRef]
- Finikov, S.P. A Course in Differential Geometry; Gostehizdat: Moscow, Russia, 1952. [Google Scholar]
- Serban, A.I.; Serban, F. Biomorphomatics; Ceres: Bucharest, Romania, 2013. [Google Scholar]
- Modèle hyperbolique de Klein-Beltrami. Available online: http://www.cabri.net/abracadabri/GeoNonE/GeoHyper/KBModele/Biss3KB.html (accessed on 3 August 2020).
- Vranceanu, G. Analytical, Projective and Differential Geometry; Didactică şi Pedagogică: Bucuresti, Romania, 1962. [Google Scholar]
- Hirsch, R.L.; Holzer, J.R.; Finnin, M.S.; Cazares, S.M. Significance of Retinal Lession Potentially Caused by Dazzling Lasers; Technical Report; Joint Non-Lethal Weapons Directorate: Alexandria, VA, USA, 2015. [Google Scholar]
- Franco, E.C.S.; Finlay, B.L.; Silveira, L.C.L.; Yamada, E.; Crowley, J.C. Conservation of absolute foveal area in new world monkeys. Brain Behav. Evol. 2000, 56, 276–286. [Google Scholar] [CrossRef] [PubMed]
- Mersereau, R.M. The processing of hexagonally sampled two-dimensional signals. Proc. Inst. Electr. Electron. Eng. 1979, 67, 930–949. [Google Scholar] [CrossRef]
- Veni, S.; Narayanankutty, K.A. Vision-based hexagonal image processing using Hex-Gabor. Signal Image Video Process. 2012, 8, 317–326. [Google Scholar] [CrossRef]
- Curcio, C.A.; Sloan, K.R.; Kalina, R.E.; Hendrickson, A.E. Human photoreceptor topography. J. Comp. Neurol. 1990, 292, 497–523. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dickau, R. Fibonacci Numbers Count Domino Tilings. Available online: http://demonstrations.wolfram.com/FibonacciNumbersCountDominoTilings/ (accessed on 3 April 2020).
- Bowmaker, J.K.; Dartnall, H.J. Visual pigments of rods and cones in a human retina. J. Physiol. 1980, 298, 501–511. [Google Scholar] [CrossRef] [PubMed]
- Agoston, G.A. Color Theory and Its Application in Art and Design; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Hofer, H.; Carroll, J.; Neitz, J.; Neitz, M.; Williams, D.R. Organization of the human trichromatic cone mosaic. J. Neurosci. 2005, 25, 9669–9679. [Google Scholar] [CrossRef]
- Brainard, D.H. Color and the cone mosaic. Annu. Rev. Vis. Sci. 2015, 1, 519–546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Curcio, C.A.; Allen, K.A.; Sloan, K.R.; Lerea, C.L.; Hurley, J.B.; Klock, I.B.; Milam, A.H. Distribution and morphology of human cone photoreceptors stained with anti-blue opsin. J. Comp. Neurol. 1991, 312, 610–624. [Google Scholar] [CrossRef]
- Sawides, L.; de Castro, A.; Burns, S.A. The organization of the cone photoreceptor mosaic measured in the living human retina. Vis. Res. 2017, 132, 34–44. [Google Scholar] [CrossRef] [PubMed]
- Nathans, J. The evolution and physiology of human color vision: Insights from molecular genetic studies of visual pigments. Neuron 1999, 24, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Lenz, R.; Carmona, P.L.; Meer, P. The hyperbolic geometry of illumination-induced chromaticity changes. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–6. [Google Scholar]
- Bacher, R. On geodesics of phyllotaxis. Conflu. Math. 2014, 6, 3–30. [Google Scholar] [CrossRef]
- Parker, A.C.; Azar, A.N. A hierarchical artificial retina architecture. SPIE Eur. Microtech. New Millenn. 2009, 7365, 736503. [Google Scholar] [CrossRef]
- Koenderink, J.J.; van Doorn, A.J.; Lappin, J.S. Direct measurement of the curvature of visual space. Perception 2000, 29, 69–79. [Google Scholar] [CrossRef] [Green Version]
- Chossat, P.; Faugeras, O. Hyperbolic Planforms in Relation to Visual Edges and Textures Perception. PLoS Comput. Biol. 2009, 5, e1000625. [Google Scholar] [CrossRef]
- Poggio, G.F.; Poggio, T. The analysis of stereopsis. Annu. Rev. Neurosci. 1984, 7, 379–412. [Google Scholar] [CrossRef]
- Lappin, J.S. What is binocular disparity? Front. Psychol. 2014, 5, 870. [Google Scholar] [CrossRef] [Green Version]
- Trotter, Y.; Celebrini, S.; Durand, J.B. Evidence for implication of primate area V1 in neural 3-D spatial lo-calization processing. J. Physiol. Paris 2004, 98, 125–134. [Google Scholar] [CrossRef]
- Gonzalez, F.; Perez, R. Neural mechanisms underlying stereoscopic vision. Prog. Neurobiol. 1998, 55, 191–224. [Google Scholar] [CrossRef]
- Mandel, Y.; Goetz, G.; Lavinsky, D.; Huie, P.; Mathieson, K.; Wang, L.; Kamins, T.; Galambos, L.; Manivanh, R.; Harris, J.; et al. Cortical responses elicited by photovoltaic subretinal prostheses exhibit similarities to visually evoked potentials. Nat. Commun. 2013, 4, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mathieson, K.; Loudin, J.; Goetz, G.; Huie, P.; Wang, L.; Kamins, T.I.; Galambos, L.; Smith, R.; Harris, J.S.; Sher, A.; et al. Photovoltaic retinal prosthesis with high pixel density. Nat. Photonics 2012, 6, 391–397. [Google Scholar] [CrossRef] [PubMed]
- Chow, Y.A.; Chow, V.Y.; Packo, K.H.; Pollack, J.S.; Peyman, G.A.; Schuchard, R. The artificial silicon retina microchip for the treatment of visionloss from retinitis pigmentosa. Arch. Ophthalmol. 2004, 122, 460–469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chow, A.Y.; Bittner, A.K.; Pardue, M.T. The artificial silicon retina in retinitis pigmentosa patients. Trans. Am. Ophthalmol. Soc. 2010, 108, 120–154. [Google Scholar]
- Zrenner, E.; Bartz-Schmidt, K.U.; Benav, H.; Besch, D.; Bruckmann, A.; Gabel, V.-P.; Gekeler, F.; Greppmaier, U.; Harscher, A.; Kibbel, S.; et al. Subretinal electronic chips allow blind patients to read letters and combine them to words. Proc. R. Soc. B Boil. Sci. 2010, 278, 1489–1497. [Google Scholar] [CrossRef] [PubMed]
- Palanker, D.; Vankov, A.; Huie, P.; Baccus, S. Design of a high-resolution optoelectronic retinal prosthesis. J. Neural Eng. 2005, 2, S105–S120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ayton, L.N.; Barnes, N.; Dagnelie, G.; Fujikado, T.; Goetz, G.; Hornig, R.; Jones, B.W.; Muqit, M.M.K.; Rathbun, D.L.; Stingl, K.; et al. An update on retinal prostheses. Clin. Neurophysiol. 2020, 131, 1383–1398. [Google Scholar] [CrossRef] [PubMed]
- Humayun, M.S.; Weiland, J.D.; Fujii, G.Y.; Greenberg, R.; Williamson, R.; Little, J.; Mech, B.; Cimmarusti, V.; Van Boemel, G.; Dagnelie, G.; et al. Visual perception in a blind subject with a chronic microelectronic retinal prosthesis. Vis. Res. 2003, 43, 2573–2581. [Google Scholar] [CrossRef] [Green Version]
- Stingl, K.; Schippert, R.; Bartz-Schmidt, K.U.; Besch, D.; Cottriall, C.L.; Edwards, T.L.; Gekeler, F.; Greppmaier, U.; Kiel, K.; Koitschev, A.; et al. Interim results of a multicenter trial with the new electronic subretinal implant alpha ams in 15 patients blind from inherited retinal degenerations. Front. Neurosci. 2017, 11, 445. [Google Scholar] [CrossRef] [Green Version]
- Ayton, L.N.; Blamey, P.J.; Guymer, R.H.; Luu, C.D.; Nayagam, D.A.X.; Sinclair, N.C.; Shivdasani, M.N.; Yeoh, J.; McCombe, M.F.; Briggs, R.J.; et al. First-in-human trial of a novel suprachoroidal retinal prosthesis. PLoS ONE 2014, 9, e115239. [Google Scholar] [CrossRef] [Green Version]
- Tong, W.; Meffin, H.; Garrett, D.J.; Ibbotson, M.R. Stimulation Strategies for improving the resolution of retinal prostheses. Front. Neurosci. 2020, 14, 262. [Google Scholar] [CrossRef] [PubMed]
- Copson, E.T.; Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Le Floch, A.; Ropars, G.; Enoch, J.; Lakshminarayananan, V. The polarization sense in human vision. Vis. Res. 2010, 50, 2048–2054. [Google Scholar] [CrossRef]
- Singh, M.; Haverinen, H.M.; Dhagat, P.; Jabbour, G.E. Inkjet printing-process and its applications. Adv. Mater. 2010, 22, 673–685. [Google Scholar] [CrossRef]
- Ghezzi, D.; Antognazza, M.R.; Dal Maschio, M.; Lanzarini, E.; Benfenati, F.; Lanzani, G. A hybrid bioorganic interface for neuronal photoactivation. Nat. Commun. 2011, 2, 1–7. [Google Scholar] [CrossRef]
- Cheng, Y.-J.; Yang, S.-H.; Hsu, C.-S. Synthesis of conjugated polymers for organic solar cell applications. Chem. Rev. 2009, 109, 5868–5923. [Google Scholar] [CrossRef]
- Maya-Vetencourt, J.F.; Ghezzi, D.; Antognazza, M.R.; Colombo, E.; Mete, M.; Feyen, P.; Desii, A.; Buschiazzo, A.; Di Paolo, M.; Di Marco, S.; et al. A fully organic retinal prosthesis restores vision in a rat model of degenerative blindness. Nat. Mater. 2017, 16, 681–689. [Google Scholar] [CrossRef] [PubMed]
- McElroy, N.; Cadirci, M.; Al-Otaify, A.; Page, R.; Binks, D.J. Increasing efficiency with multiple exciton generation. In Quantum Dot Solar Cells; Wu, J., Wang, Z.M., Eds.; Springer: New York, NY, USA, 2014. [Google Scholar]
- European Commission. Active Implantable Medical Devices. Available online: http://ec.europa.eu/enterprise/policies/european-standards/harmonisedstandards/implantable-medical-devices/ (accessed on 6 July 2020).
- Bareket-Keren, L.; Hanein, Y. Carbon nanotube-based multi electrode arrays for neuronal interfacing: Progress and prospects. Front. Neural Circuits 2013, 6, 122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bareket-Keren, L.; Hanein, Y. Novel interfaces for light directed neuronal stimulation: Advances and challenges. Int. J. Nanomed. 2014, 9, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Schneider, J.J. Vertically Aligned carbon nanotubes as platform for biomimetically inspired mechanical sensing, bioactive surfaces, and electrical cell interfacing. Adv. Biosyst. 2017, 1, 1700101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nash, J. Photovoltaic properties and solar cell applications of colloidal quantum dots. Aisthesis 2018, 9, 36–41. [Google Scholar]
- Xu, Y.; Munday, J.N. Light trapping in a polymer solar cell by tailored quantum dot emission. Opt. Express 2014, 22, A259–A267. [Google Scholar] [CrossRef] [Green Version]
- Goodwin, H.; Jellicoe, T.C.; Davis, N.J.L.K.; Böhm, M.L. Multiple exciton generation in quantum dot-based solar cells. Nanophotonics 2017, 7, 111–126. [Google Scholar] [CrossRef]
- Beard, M.C.; Johnson, J.C.; Luther, J.M.; Nozik, A. Multiple exciton generation in quantum dots versus singlet fission in molecular chromophores for solar photon conversion. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140412. [Google Scholar] [CrossRef] [Green Version]
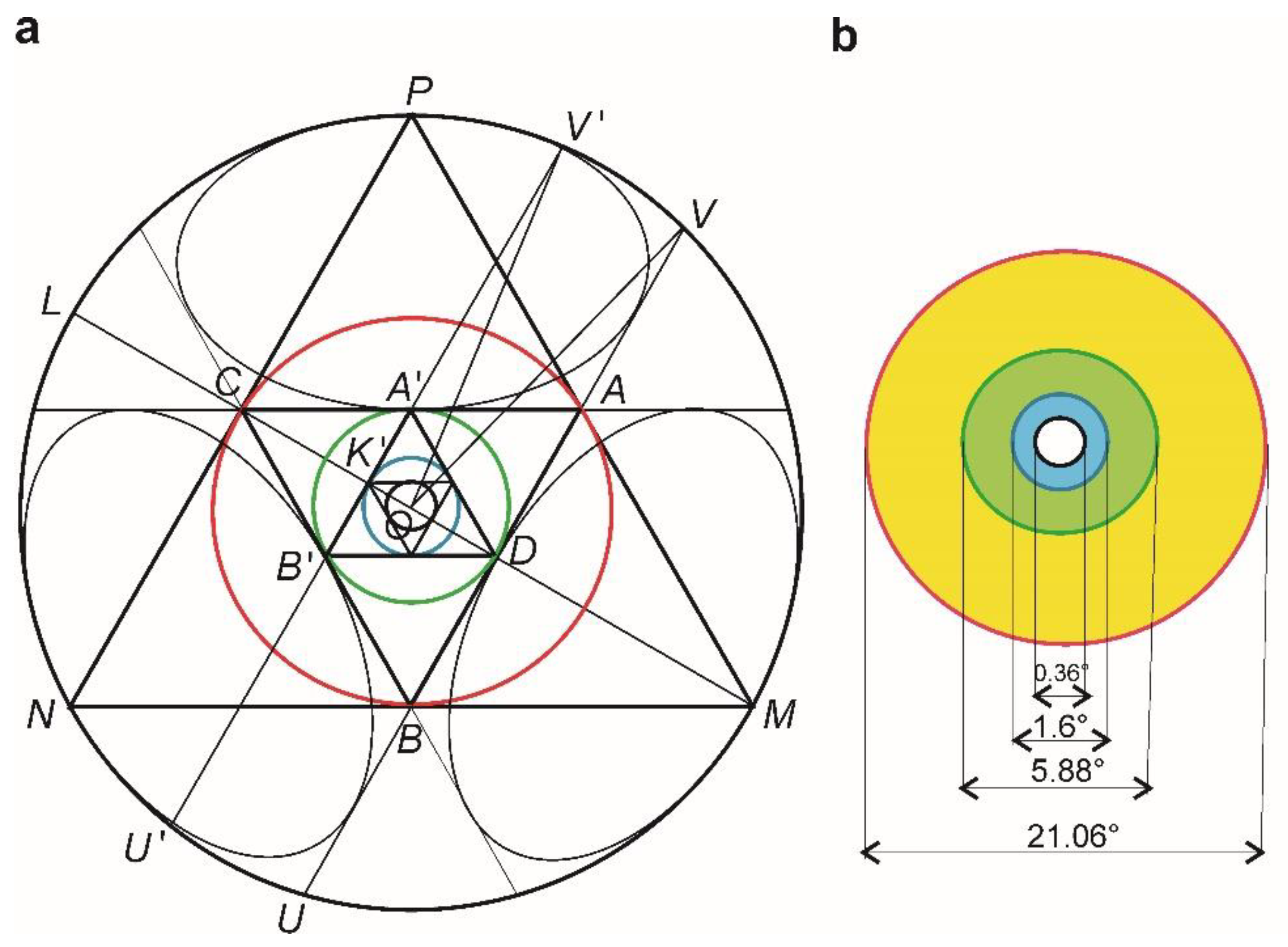


| Macula | Fovea | FAZ ** | Umbo | |
|---|---|---|---|---|
| Calculated values of ′ angles complementary to 60° | ||||
| 21.06° | 5.88° | 1.6° | 0.36° | |
| Values of the angular eccentricities * | 18.20° | 5.0° | 1.4° | 0.35° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilteanu, L.; Geicu, O.I.; Stanca, L.; Pisoschi, A.M.; Serban, F.; Serban, A.I.; Calu, V. Human Eye Optics within a Non-Euclidian Geometrical Approach and Some Implications in Vision Prosthetics Design. Biomolecules 2021, 11, 215. https://doi.org/10.3390/biom11020215
Bilteanu L, Geicu OI, Stanca L, Pisoschi AM, Serban F, Serban AI, Calu V. Human Eye Optics within a Non-Euclidian Geometrical Approach and Some Implications in Vision Prosthetics Design. Biomolecules. 2021; 11(2):215. https://doi.org/10.3390/biom11020215
Chicago/Turabian StyleBilteanu, Liviu, Ovidiu I. Geicu, Loredana Stanca, Aurelia M. Pisoschi, Florea Serban, Andreea I. Serban, and Valentin Calu. 2021. "Human Eye Optics within a Non-Euclidian Geometrical Approach and Some Implications in Vision Prosthetics Design" Biomolecules 11, no. 2: 215. https://doi.org/10.3390/biom11020215
APA StyleBilteanu, L., Geicu, O. I., Stanca, L., Pisoschi, A. M., Serban, F., Serban, A. I., & Calu, V. (2021). Human Eye Optics within a Non-Euclidian Geometrical Approach and Some Implications in Vision Prosthetics Design. Biomolecules, 11(2), 215. https://doi.org/10.3390/biom11020215









