The Budapest Amyloid Predictor and Its Applications
Abstract
1. Introduction
- (i)
- Simplicity: we used solely a linear SVM in its construction;
- (ii)
- Transparency: no prefiltering and data manipulation were used in the construction of the predictor;
- (iii)
- (iv)
- Free online availability, together with automatic prediction of the neighboring hexapeptides;
- (v)
- Easy applicability for inferring location-dependent amyloidogenic properties of amino acids, as we describe below.
2. Methods
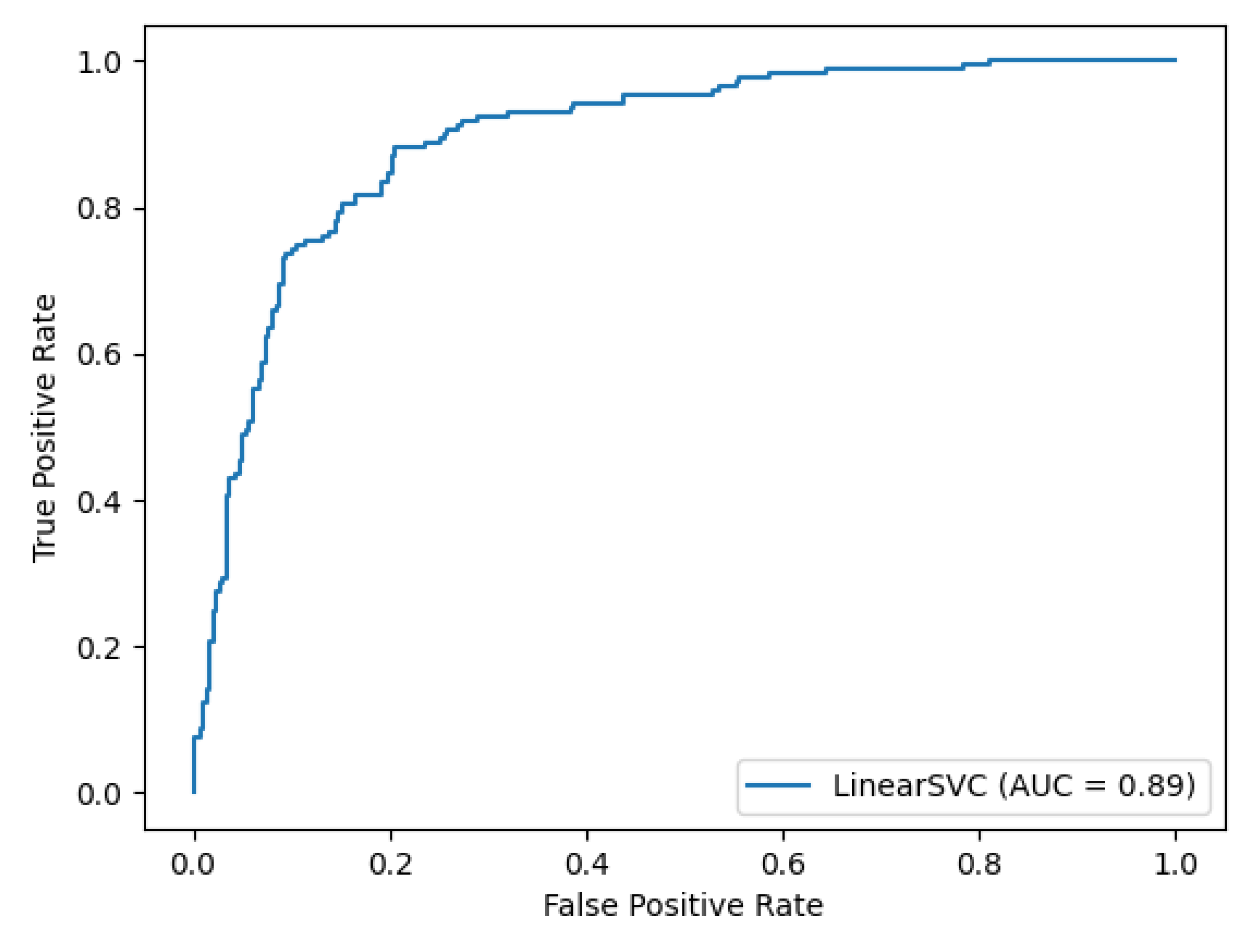
3. Discussion and Results
Comparison with Earlier Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Horváth, D.; Menyhárd, D.K.; Perczel, A. Protein aggregation in a nutshell: The splendid molecular architecture of the dreaded amyloid fibrils. Curr. Protein Pept. Sci. 2019, 20, 1077–1088. [Google Scholar] [CrossRef] [PubMed]
- Taricska, N.; Horvath, D.; Menyhard, D.K.; Akontz-Kiss, H.; So, M.; Goto, Y.; Fujiwara, T.; Perczel, A. The route from the folded to the amyloid state: Exploring the potential energy surface of a drug-like miniprotein. Chem. Eur. J. 2020, 26, 1968–1978. [Google Scholar] [CrossRef] [PubMed]
- Takács, K.; Varga, B.; Grolmusz, V. PDB _Amyloid: An extended live amyloid structure list from the PDB. FEBS Open Bio 2019, 9, 185–190. [Google Scholar] [CrossRef]
- Takacs, K.; Grolmusz, V. On the border of the amyloidogenic sequences: Prefix analysis of the parallel beta sheets in the PDB_Amyloid collection. arXiv 2020, arXiv:2003.02942. [Google Scholar]
- Maji, S.K.; Perrin, M.H.; Sawaya, M.R.; Jessberger, S.; Vadodaria, K.; Rissman, R.A.; Riek, R. Functional amyloids as natural storage of peptide hormones in pituitary secretory granules. Science 2009, 325, 328–332. [Google Scholar] [CrossRef]
- Falabella, P.; Riviello, L.; Pascale, M.; Di Lelio, I.; Tettamanti, G.; Grimaldi, A.; Pennacchio, F. Functional amyloids in insect immune response. Insect Biochem. Mol. Biol. 2012, 42, 203–211. [Google Scholar] [CrossRef]
- Iconomidou, V.A.; Hamodrakas, S.J. Natural protective amyloids. Curr. Protein Pept. Sci. 2008, 9, 291–309. [Google Scholar] [CrossRef]
- Soto, C.; Estrada, L.; Castilla, J. Amyloids, prions and the inherent infectious nature of misfolded protein aggregates. Trends Biochem. Sci. 2006, 31, 150–155. [Google Scholar] [CrossRef]
- Emiel, M.; Kenny, R.; Rodrigo, G.; Ladan, K.; Laleh, K.; van der Kant, R.; Maxime, S.; Bert, H.; Meine, R.; Hannah, W.; et al. Reverse engineering synthetic antiviral amyloids. Nat. Commun. 2020, 11, 2832. [Google Scholar] [CrossRef]
- Santos, J.; Pujols, J.; Pallarès, I.; Iglesias, V.; Ventura, S. Computational prediction of protein aggregation: Advances in proteomics, conformation-specific algorithms and biotechnological applications. Comput. Struct. Biotechnol. J. 2020, 18, 1403–1413. [Google Scholar] [CrossRef] [PubMed]
- Conchillo-Sole, O.; de Groot, N.S.; Aviles, F.X.; Vendrell, J.; Daura, X.; Ventura, S. Aggrescan: A server for the prediction and evaluation of “hot spots” of aggregation in polypeptides. BMC Bioinform. 2007, 8, 65. [Google Scholar] [CrossRef]
- Gian Gaetano Tartaglia and Michele Vendruscolo. The zyggregator method for predicting protein aggregation propensities. Chem. Soc. Rev. 2008, 37, 1395–1401. [Google Scholar] [CrossRef]
- Kim, C.; Choi, J.; Lee, S.J.; Welsh, W.J.; Yoon, S. Netcssp: web application for predicting chameleon sequences and amyloid fibril formation. Nucleic Acids Res. 2009, 37, W469–W473. [Google Scholar] [CrossRef]
- Familia, C.; Dennison, S.R.; Quintas, A.; Phoenix, D.A. Prediction of peptide and protein propensity for amyloid formation. PLoS ONE 2015, 10, e0134679. [Google Scholar] [CrossRef] [PubMed]
- Beerten, J.; Van Durme, J.; Gallardo, R.; Capriotti, E.; Serpell, L.; Rousseau, F.; Schymkowitz, J. WALTZ-DB: A benchmark database of amyloidogenic hexapeptides. Bioinformatics 2015, 31, 1698–1700. [Google Scholar] [CrossRef]
- Louros, N.; Konstantoulea, K.; De Vleeschouwer, M.; Ramakers, M.; Schymkowitz, J.; Rousseau, F. WALTZ-DB 2.0: An updated database containing structural information of experimentally determined amyloid-forming peptides. Nucleic Acids Res. 2020, 48, D389–D393. [Google Scholar] [CrossRef] [PubMed]
- Louros, N.; Orlando, G.; De Vleeschouwer, M.; Rousseau, F.; Schymkowitz, J. Structure-based machine-guided mapping of amyloid sequence space reveals uncharted sequence clusters with higher solubilities. Nat. Commun. 2020, 11, 3314. [Google Scholar] [CrossRef] [PubMed]
- Hauser, C.A.; Deng, R.; Mishra, A.; Loo, Y.; Khoe, U.; Zhuang, F.; Hauser, U.A. Natural tri-to hexapeptides self-assemble in water to amyloid β-type fiber aggregates by unexpected α-helical intermediate structures. Proc. Natl. Acad. Sci. USA 2011, 108, 1361–1366. [Google Scholar] [CrossRef] [PubMed]
- Tenidis, K.; Waldner, M.; Bernhagen, J.; Fischle, W.; Bergmann, M.; Weber, M.; Kapurniotu, A. Identification of a penta-and hexapeptide of islet amyloid polypeptide (iapp) with amyloidogenic and cytotoxic properties. J. Mol. Biol. 2000, 295, 1055–1071. [Google Scholar] [CrossRef] [PubMed]
- Reches, M.; Gazit, E. Amyloidogenic hexapeptide fragment of medin: homology to functional islet amyloid polypeptide fragments. Amyloid Int. J. Exp. Clin. Investig. Off. J. Int. Soc. Amyloidosis 2004, 11, 81–89. [Google Scholar] [CrossRef]
- Iconomidou, V.A.; Chryssikos, G.D.; Gionis, V.; Galanis, A.S.; Cordopatis, P.; Hoenger, A.; Hamodrakas, S.J. Amyloid fibril formation propensity is inherent into the hexapeptide tandemly repeating sequence of the central domain of silkmoth chorion proteins of the a-family. J. Struct. Biol. 2006, 156, 480–488. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Keresztes, L.; Szogi, E.; Varga, B.; Grolmusz, V. Identifying super-feminine, super-masculine and sex-defining connections in the human braingraph. arXiv 2019, arXiv:1912.02291. [Google Scholar]
- Kawashima, S.; Pokarowski, P.; Pokarowska, M.; Kolinski, A.; Katayama, T.; Kanehisa, M. Aaindex: Amino acid index database, progress report 2008. Nucleic Acids Res. 2008, 36, D202–D205. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, E. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Thangakani, A.M.; Kumar, S.; Velmurugan, D.; Gromiha, M.M. Distinct position-specific sequence features of hexa-peptides that form amyloid-fibrils: Application to discriminate between amyloid fibril and amorphous ?-aggregate forming peptide sequences. BMC Bioinform. 2013, 14 (Suppl. 8), S6. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Wu, N.; Guo, J.; Fan, Y. Prediction of amyloid fibril-forming segments based on a support vector machine. BMC Bioinform. 2009, 10, S45. [Google Scholar] [CrossRef]
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| A | −0.26 | −0.32 | −0.27 | −0.14 | −0.43 | −0.22 |
| R | −0.45 | −0.41 | −0.46 | −0.33 | −0.52 | −0.35 |
| N | −0.40 | −0.34 | −0.49 | −0.27 | −0.46 | −0.30 |
| D | −0.49 | −0.43 | −0.56 | −0.41 | −0.56 | −0.36 |
| C | −0.09 | −0.21 | 0.03 | −0.05 | −0.17 | −0.05 |
| Q | −0.37 | −0.30 | −0.36 | −0.34 | −0.48 | −0.32 |
| E | −0.51 | −0.41 | −0.43 | −0.30 | −0.61 | −0.39 |
| G | −0.23 | −0.37 | −0.46 | −0.37 | −0.30 | −0.33 |
| H | −0.32 | −0.26 | −0.26 | −0.30 | −0.35 | −0.25 |
| I | −0.06 | −0.08 | 0.26 | 0.09 | −0.06 | −0.07 |
| L | −0.10 | −0.18 | 0.02 | 0.04 | −0.22 | −0.13 |
| K | −0.39 | −0.45 | −0.51 | −0.35 | −0.59 | −0.32 |
| M | −0.17 | −0.25 | −0.02 | −0.10 | −0.19 | −0.18 |
| F | −0.13 | −0.11 | 0.05 | −0.03 | −0.13 | −0.11 |
| P | −0.56 | −0.38 | −0.56 | −0.51 | −0.42 | −0.45 |
| S | −0.37 | −0.35 | −0.41 | −0.30 | −0.48 | −0.23 |
| T | −0.34 | −0.33 | −0.28 | −0.23 | −0.40 | −0.23 |
| W | −0.17 | −0.17 | −0.09 | −0.06 | −0.12 | −0.16 |
| Y | −0.23 | −0.11 | −0.13 | −0.06 | −0.18 | −0.15 |
| V | −0.05 | −0.14 | 0.19 | 0.14 | −0.19 | 0.01 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | V | I | C | L | F | M | W | G | Y | A | H | T | S | Q | K | N | R | D | E | P |
| 2 | I | F | Y | V | W | L | C | M | H | Q | A | T | N | S | G | P | R | E | D | K |
| 3 | I | V | F | C | L | M | W | Y | H | A | T | Q | S | E | R | G | N | K | D | P |
| 4 | V | I | L | F | C | W | Y | M | A | T | N | H | E | S | R | Q | K | G | D | P |
| 5 | I | W | F | C | Y | M | V | L | G | H | T | P | A | N | Q | S | R | D | K | E |
| 6 | V | C | I | F | L | Y | W | M | A | T | S | H | N | Q | K | G | R | D | E | P |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keresztes, L.; Szögi, E.; Varga, B.; Farkas, V.; Perczel, A.; Grolmusz, V. The Budapest Amyloid Predictor and Its Applications. Biomolecules 2021, 11, 500. https://doi.org/10.3390/biom11040500
Keresztes L, Szögi E, Varga B, Farkas V, Perczel A, Grolmusz V. The Budapest Amyloid Predictor and Its Applications. Biomolecules. 2021; 11(4):500. https://doi.org/10.3390/biom11040500
Chicago/Turabian StyleKeresztes, László, Evelin Szögi, Bálint Varga, Viktor Farkas, András Perczel, and Vince Grolmusz. 2021. "The Budapest Amyloid Predictor and Its Applications" Biomolecules 11, no. 4: 500. https://doi.org/10.3390/biom11040500
APA StyleKeresztes, L., Szögi, E., Varga, B., Farkas, V., Perczel, A., & Grolmusz, V. (2021). The Budapest Amyloid Predictor and Its Applications. Biomolecules, 11(4), 500. https://doi.org/10.3390/biom11040500







