Bifurcations and Proarrhythmic Behaviors in Cardiac Electrical Excitations
Abstract
:1. Introduction
2. Ionic Mechanisms of Excitations in Cardiomyocytes
2.1. Mechanisms for Maintenance of Ion Homeostasis
2.2. Ionic Mechanisms of Cardiac Action Potentials
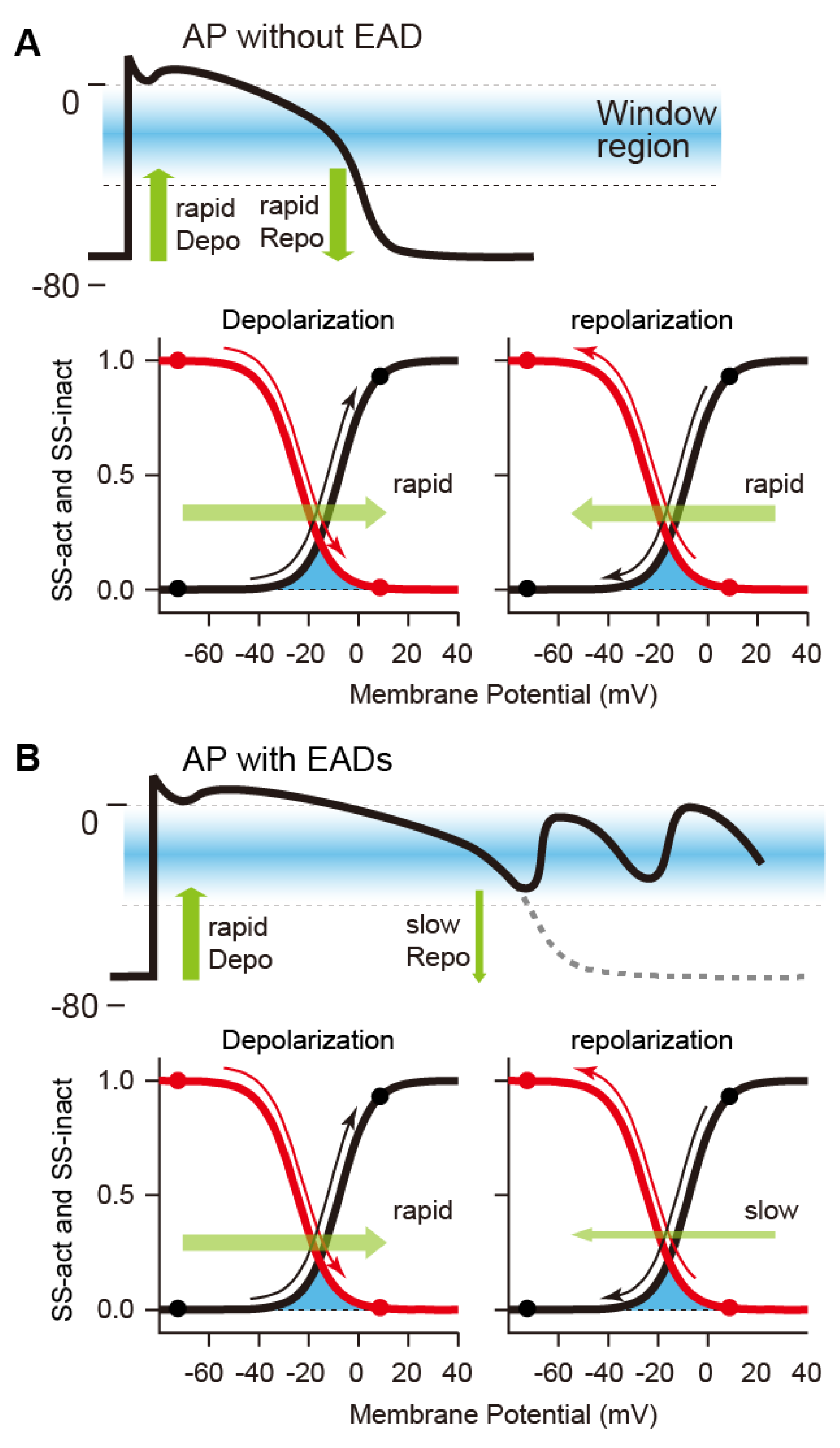
2.3. Mechanisms of Abnormal Action Potentials (Afterdepolarization)
3. Mathematical Cardiomyocyte Models and Bifurcation Phenomena
3.1. Mathematical Models of Action Potential in Cardiomyocytes
3.2. Bifurcations in Nonlinear Dynamical Systems
3.2.1. Definitions of Dynamical Systems
3.2.2. Hopf Bifurcation
3.2.3. Saddle-Node Bifurcation
3.2.4. Homoclinic Bifurcation
3.2.5. Period-Doubling Bifurcation
3.2.6. Neimark–Sacker Bifurcation
3.2.7. Bifurcation Analysis
4. Bifurcation Analyses of Proarrhythmic Behaviors
4.1. Bifurcation Analyses of Cardiac Cell Models
4.2. Bifurcation Analyses of Early Afterdepolarizations
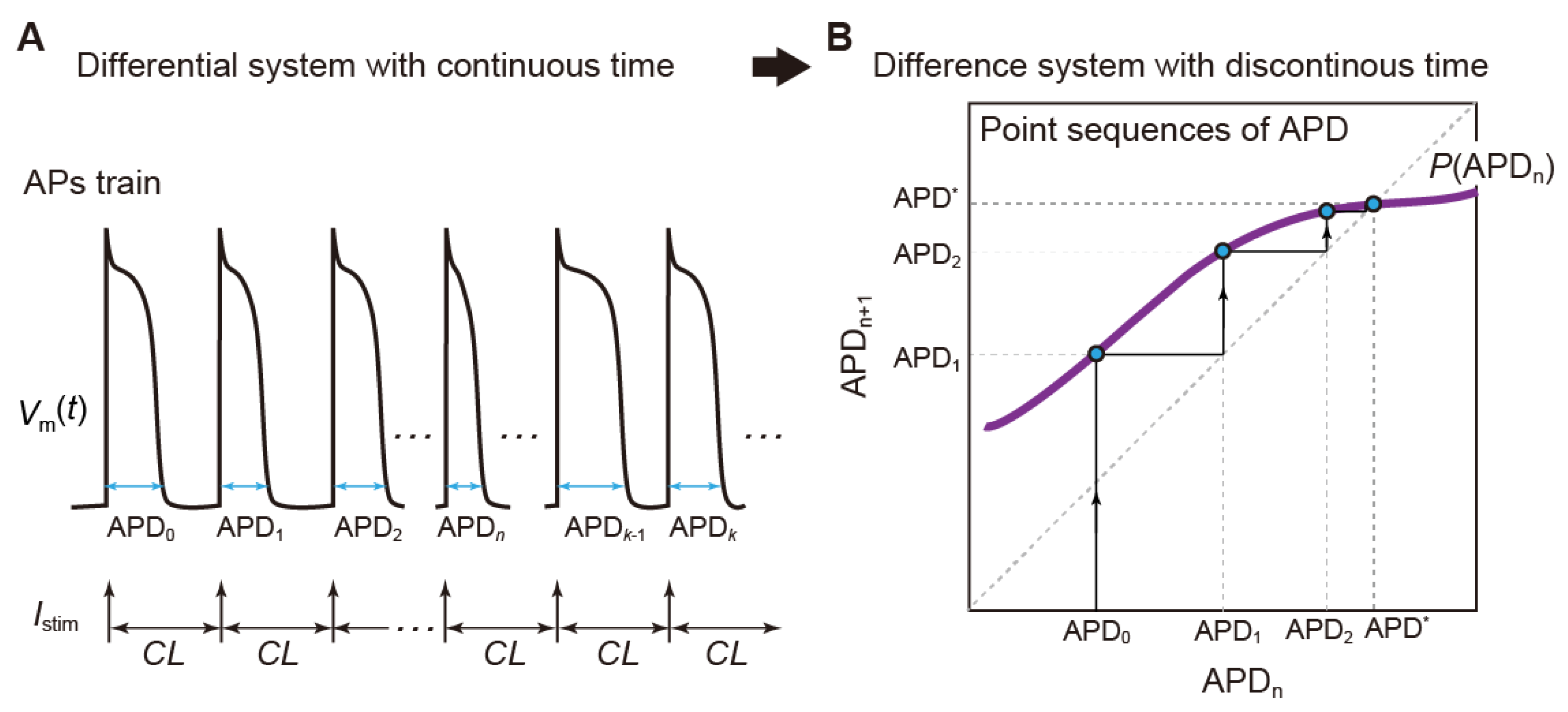
4.3. Slow–Fast Decomposition Analyses of Dynamic AP Responses with EADs
5. Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guckenheimer, J.M.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1986; p. 453. [Google Scholar]
- Nusse, H.E.; Yorke, J.A.; Kostelich, Y.J. Dynamics: Numerical Explorations; Springer: New York, NY, USA, 1994; p. 484. [Google Scholar]
- Noble, D. The Music of Life: Biology beyond the Genome; Oxford University Press: Oxford, UK, 2006; 153p. [Google Scholar]
- Noble, D. A theory of biological relativity: No privileged level of causation. Interface Focus 2012, 2, 55–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Furutani, K.; Tsumoto, K.; Kurachi, Y. HD Physiology Project-Japanese efforts to promote multilevel integrative systems biology and physiome research. NPJ Syst. Biol. Appl. 2017, 3, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sperelakis, N. Cell Physiology Source Book: Essentials of Membrane Biophysics, 4th ed.; Sperelakis, N., Ed.; Academic Press: San Diego, CA, USA, 2012; p. 996. [Google Scholar]
- Belair, J.; Glass, L.; An Der Heiden, U.; Milton, J. Dynamical disease: Identification, temporal aspects and treatment strategies of human illness. Chaos 1995, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Glass, L. Dynamics of Cardiac Arrhythmias. Phys. Today 1996, 49, 40–45. [Google Scholar] [CrossRef]
- Glass, L. Synchronization and rhythmic processes in physiology. Nature 2001, 410, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019; 513p. [Google Scholar]
- Arnold, V.I. Geometrical Methods in the Theory of Ordinary Differential Equations; Springer: New York, NY, USA, 1983; p. 334. [Google Scholar]
- Hale, J.K.; Hüseyin, K. Dynamics and Bifurcations; Springer: New York, NY, USA, 1991; p. 568. [Google Scholar]
- Matsumoto, T.; Komuro, M.; Kokubu, H.; Tokunaga, R. Bifurcations: Sights, Sounds, and Mathematics; Springer: Tokyo, Japan, 1993; p. 468. [Google Scholar]
- Bers, D.M. Excitation-Contraction Coupling and Cardiac Contractile Force, 2nd ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 2001; Volume 237, 427p. [Google Scholar]
- Bers, D.M. Cardiac excitation-contraction coupling. Nature 2002, 415, 198–205. [Google Scholar] [CrossRef] [PubMed]
- Bers, D.M. Calcium cycling and signaling in cardiac myocytes. Annu. Rev. Physiol. 2008, 70, 23–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eisner, D.A.; Caldwell, J.L.; Trafford, A.W.; Hutchings, D.C. The Control of Diastolic Calcium in the Heart: Basic Mechanisms and Functional Implications. Circ. Res. 2020, 126, 395–412. [Google Scholar] [CrossRef]
- Kistamás, K.; Veress, R.; Horváth, B.; Bányász, T.; Nánási, P.P.; Eisner, D.A. Calcium Handling Defects and Cardiac Arrhythmia Syndromes. Front. Pharmacol. 2020, 11, 72. [Google Scholar] [CrossRef]
- Skou, J.C. The influence of some cations on an adenosine triphosphatase from peripheral nerves. Biochim. Biophys. Acta 1957, 23, 394–401. [Google Scholar] [CrossRef]
- Reyes, N.; Gadsby, D.C. Ion permeation through the Na+,K+-ATPase. Nature 2006, 443, 470–474. [Google Scholar] [CrossRef] [PubMed]
- Pavlovic, D.; Fuller, W.; Shattock, M.J. Novel regulation of cardiac Na pump via phospholemman. J. Mol. Cell. Cardiol. 2013, 61, 83–93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shattock, M.J.; Ottolia, M.; Bers, D.M.; Blaustein, M.P.; Boguslavskyi, A.; Bossuyt, J.; Bridge, J.H.; Chen-Izu, Y.; Clancy, C.E.; Edwards, A.; et al. Na+/Ca2+ exchange and Na+/K+-ATPase in the heart. J. Physiol. 2015, 593, 1361–1382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matchkov, V.V.; Krivoi, I.I. Specialized Functional Diversity and Interactions of the Na,K-ATPase. Front. Physiol. 2016, 7, 179. [Google Scholar] [CrossRef] [Green Version]
- Berry, R.G.; Despa, S.; Fuller, W.; Bers, D.M.; Shattock, M.J. Differential distribution and regulation of mouse cardiac Na+/K+-ATPase alpha1 and alpha2 subunits in T-tubule and surface sarcolemmal membranes. Cardiovasc. Res. 2007, 73, 92–100. [Google Scholar] [CrossRef] [Green Version]
- Kimura, J.; Noma, A.; Irisawa, H. Na-Ca exchange current in mammalian heart cells. Nature 1986, 319, 596–597. [Google Scholar] [CrossRef]
- Lytton, J. Na+/Ca2+ exchangers: Three mammalian gene families control Ca2+ transport. Biochem. J. 2007, 406, 365–382. [Google Scholar] [CrossRef]
- Fliegel, L.; Dyck, J.R.; Wang, H.; Fong, C.; Haworth, R.S. Cloning and analysis of the human myocardial Na+/H+ exchanger. Mol. Cel. Biochem. 1993, 125, 137–143. [Google Scholar] [CrossRef]
- Schwinger, R.H.; Wang, J.; Frank, K.; Müller-Ehmsen, J.; Brixius, K.; McDonough, A.A.; Erdmann, E. Reduced sodium pump alpha1, alpha3, and beta1-isoform protein levels and Na+,K+-ATPase activity but unchanged Na+-Ca2+ exchanger protein levels in human heart failure. Circulation 1999, 99, 2105–2112. [Google Scholar] [CrossRef] [Green Version]
- Lingrel, J.; Moseley, A.; Dostanic, I.; Cougnon, M.; He, S.; James, P.; Woo, A.; O’Connor, K.; Neumann, J. Functional roles of the alpha isoforms of the Na,K-ATPase. Ann. N. Y. Acad. Sci. 2003, 986, 354–359. [Google Scholar] [CrossRef]
- Li, Z.; Langhans, S.A. Transcriptional regulators of Na,K-ATPase subunits. Front. Cell. Dev. Biol. 2015, 3, 66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hensley, C.B.; Azuma, K.K.; Tang, M.J.; McDonough, A.A. Thyroid hormone induction of rat myocardial Na(+)-K(+)-ATPase: Alpha 1-, alpha 2-, and beta 1-mRNA and -protein levels at steady state. Am. J. Physiol. 1992, 262, C484–C492. [Google Scholar] [CrossRef]
- Sweadner, K.J.; Herrera, V.L.; Amato, S.; Moellmann, A.; Gibbons, D.K.; Repke, K.R. Immunologic identification of Na+,K(+)-ATPase isoforms in myocardium. Isoform change in deoxycorticosterone acetate-salt hypertension. Circ. Res. 1994, 74, 669–678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shamraj, O.I.; Melvin, D.; Lingrel, J.B. Expression of Na,K-ATPase isoforms in human heart. Biochem. Biophys. Res. Commun. 1991, 179, 1434–1440. [Google Scholar] [CrossRef]
- Zahler, R.; Gilmore-Hebert, M.; Baldwin, J.C.; Franco, K.; Benz, E.J., Jr. Expression of alpha isoforms of the Na,K-ATPase in human heart. Biochim. Biophys. Acta 1993, 1149, 189–194. [Google Scholar] [CrossRef]
- Quednau, B.D.; Nicoll, D.A.; Philipson, K.D. Tissue specificity and alternative splicing of the Na+/Ca2+ exchanger isoforms NCX1, NCX2, and NCX3 in rat. Am. J. Physiol. 1997, 272, C1250–C1261. [Google Scholar] [CrossRef] [PubMed]
- Eisner, D.A.; Caldwell, J.L.; Kistamás, K.; Trafford, A.W. Calcium and Excitation-Contraction Coupling in the Heart. Circ. Res. 2017, 121, 181–195. [Google Scholar] [CrossRef] [PubMed]
- Hurtado, C.; Prociuk, M.; Maddaford, T.G.; Dibrov, E.; Mesaeli, N.; Hryshko, L.V.; Pierce, G.N. Cells expressing unique Na+/Ca2+ exchange (NCX1) splice variants exhibit different susceptibilities to Ca2+ overload. Am. J. Physiol. Heart Circ. Physiol. 2006, 290, H2155–H2162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nicoll, D.A.; Longoni, S.; Philipson, K.D. Molecular cloning and functional expression of the cardiac sarcolemmal Na+-Ca2+ exchanger. Science 1990, 250, 562–565. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.L.; Yu, A.S.; Lytton, J. Tissue-specific expression of Na+-Ca2+ exchanger isoforms. J. Biol. Chem. 1994, 269, 14849–14852. [Google Scholar] [CrossRef]
- Hibino, H.; Inanobe, A.; Furutani, K.; Murakami, S.; Findlay, I.; Kurachi, Y. Inwardly rectifying potassium channels: Their structure, function, and physiological roles. Physiol. Rev. 2010, 90, 291–366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reilly, L.; Eckhardt, L.L. Cardiac potassium inward rectifier Kir2: Review of structure, regulation, pharmacology, and arrhythmogenesis. Heart Rhythm. 2021, 18, 1423–1434. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Banh, R.; Gamal El-Din, T.M.; Tonggu, L.; Lenaeus, M.J.; Pomès, R.; Zheng, N.; Catterall, W.A. Open-state structure and pore gating mechanism of the cardiac sodium channel. Cell 2021, 184, 5151–5162.e5111. [Google Scholar] [CrossRef] [PubMed]
- Rook, M.B.; Evers, M.M.; Vos, M.A.; Bierhuizen, M.F. Biology of cardiac sodium channel Nav1.5 expression. Cardiovasc. Res. 2012, 93, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Dixon, J.E.; McKinnon, D. Quantitative analysis of potassium channel mRNA expression in atrial and ventricular muscle of rats. Circ. Res. 1994, 75, 252–260. [Google Scholar] [CrossRef] [Green Version]
- Dixon, J.E.; Shi, W.; Wang, H.S.; McDonald, C.; Yu, H.; Wymore, R.S.; Cohen, I.S.; McKinnon, D. Role of the Kv4.3 K+ channel in ventricular muscle. A molecular correlate for the transient outward current. Circ. Res. 1996, 79, 659–668. [Google Scholar] [CrossRef]
- Gaborit, N.; Le Bouter, S.; Szuts, V.; Varro, A.; Escande, D.; Nattel, S.; Demolombe, S. Regional and tissue specific transcript signatures of ion channel genes in the non-diseased human heart. J. Physiol. 2007, 582, 675–693. [Google Scholar] [CrossRef]
- Näbauer, M.; Beuckelmann, D.J.; Uberfuhr, P.; Steinbeck, G. Regional differences in current density and rate-dependent properties of the transient outward current in subepicardial and subendocardial myocytes of human left ventricle. Circulation 1996, 93, 168–177. [Google Scholar] [CrossRef]
- Kääb, S.; Dixon, J.; Duc, J.; Ashen, D.; Näbauer, M.; Beuckelmann, D.J.; Steinbeck, G.; McKinnon, D.; Tomaselli, G.F. Molecular basis of transient outward potassium current downregulation in human heart failure: A decrease in Kv4.3 mRNA correlates with a reduction in current density. Circulation 1998, 98, 1383–1393. [Google Scholar] [CrossRef] [Green Version]
- Reuter, H. The dependence of slow inward current in Purkinje fibres on the extracellular calcium-concentration. J. Physiol. 1967, 192, 479–492. [Google Scholar] [CrossRef]
- Sanguinetti, M.C.; Jurkiewicz, N.K. Two components of cardiac delayed rectifier K+ current. Differential sensitivity to block by class III antiarrhythmic agents. J. Gen Physiol. 1990, 96, 195–215. [Google Scholar] [CrossRef] [PubMed]
- Mitra, R.; Morad, M. Two types of calcium channels in guinea pig ventricular myocytes. Proc. Natl. Acad. Sci. USA 1986, 83, 5340–5344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hirano, Y.; Fozzard, H.A.; January, C.T. Characteristics of L- and T-type Ca2+ currents in canine cardiac Purkinje cells. Am. J. Physiol. 1989, 256, H1478–H1492. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, F.; Lacinová, L.; Klugbauer, N. Voltage-dependent calcium channels: From structure to function. In Reviews of Physiology, Biochemistry and Pharmacology; Springer: Berlin/Heidelberg, Germany, 1999; Volume 139, pp. 33–87. [Google Scholar]
- Bohn, G.; Moosmang, S.; Conrad, H.; Ludwig, A.; Hofmann, F.; Klugbauer, N. Expression of T- and L-type calcium channel mRNA in murine sinoatrial node. FEBS Lett. 2000, 481, 73–76. [Google Scholar] [CrossRef] [Green Version]
- Sanguinetti, M.C.; Jiang, C.; Curran, M.E.; Keating, M.T. A mechanistic link between an inherited and an acquired cardiac arrhythmia: HERG encodes the IKr potassium channel. Cell 1995, 81, 299–307. [Google Scholar] [CrossRef] [Green Version]
- Trudeau, M.C.; Warmke, J.W.; Ganetzky, B.; Robertson, G.A. HERG, a human inward rectifier in the voltage-gated potassium channel family. Science 1995, 269, 92–95. [Google Scholar] [CrossRef]
- Sanguinetti, M.C.; Tristani-Firouzi, M. hERG potassium channels and cardiac arrhythmia. Nature 2006, 440, 463–469. [Google Scholar] [CrossRef]
- Stengl, M.; Volders, P.G.; Thomsen, M.B.; Spätjens, R.L.; Sipido, K.R.; Vos, M.A. Accumulation of slowly activating delayed rectifier potassium current (IKs) in canine ventricular myocytes. J. Physiol. 2003, 551, 777–786. [Google Scholar] [CrossRef]
- Nerbonne, J.M.; Kass, R.S. Molecular physiology of cardiac repolarization. Physiol. Rev. 2005, 85, 1205–1253. [Google Scholar] [CrossRef] [Green Version]
- Silva, J.R.; Pan, H.; Wu, D.; Nekouzadeh, A.; Decker, K.F.; Cui, J.; Baker, N.A.; Sept, D.; Rudy, Y. A multiscale model linking ion-channel molecular dynamics and electrostatics to the cardiac action potential. Proc. Natl. Acad. Sci. USA 2009, 106, 11102–11106. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Song, Z.; Di, Z.; Qu, Z. Stability of spatially discordant repolarization alternans in cardiac tissue. Chaos 2020, 30, 123141. [Google Scholar] [CrossRef] [PubMed]
- Vandenberg, J.I.; Perozo, E.; Allen, T.W. Towards a Structural View of Drug Binding to hERG K(+) Channels. Trends Pharm. Sci. 2017, 38, 899–907. [Google Scholar] [CrossRef] [PubMed]
- Vandenberg, J.I.; Torres, A.M.; Campbell, T.J.; Kuchel, P.W. The HERG K+ channel: Progress in understanding the molecular basis of its unusual gating kinetics. Eur. Biophys. J. 2004, 33, 89–97. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matsuda, H. Effects of external and internal K+ ions on magnesium block of inwardly rectifying K+ channels in guinea-pig heart cells. J. Physiol. 1991, 435, 83–99. [Google Scholar] [CrossRef] [PubMed]
- Ishihara, K. External K(+) dependence of strong inward rectifier K(+) channel conductance is caused not by K(+) but by competitive pore blockade by external Na+. J. Gen. Physiol. 2018, 150, 977–989. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shimizu, W. Update of diagnosis and management of inherited cardiac arrhythmias. Circ. J. 2013, 77, 2867–2872. [Google Scholar] [CrossRef] [Green Version]
- Obeyesekere, M.N.; Antzelevitch, C.; Krahn, A.D. Management of ventricular arrhythmias in suspected channelopathies. Circ. Arrhythm. Electrophysiol. 2015, 8, 221–231. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sicouri, S.; Antzelevitch, C. Mechanisms Underlying the Actions of Antidepressant and Antipsychotic Drugs That Cause Sudden Cardiac Arrest. Arrhythm. Electrophysiol. Rev. 2018, 7, 199–209. [Google Scholar] [CrossRef] [Green Version]
- Wilders, R.; Verkerk, A.O. Long QT Syndrome and Sinus Bradycardia-A Mini Review. Front. Cardiovasc. Med. 2018, 5, 106. [Google Scholar] [CrossRef]
- Roden, D.M. Taking the “idio” out of “idiosyncratic”: Predicting torsades de pointes. Pacing Clin. Electrophysiol. 1998, 21, 1029–1034. [Google Scholar] [CrossRef]
- Nattel, S.; Maguy, A.; Le Bouter, S.; Yeh, Y.H. Arrhythmogenic ion-channel remodeling in the heart: Heart failure, myocardial infarction, and atrial fibrillation. Physiol. Rev. 2007, 87, 425–456. [Google Scholar] [CrossRef] [PubMed]
- Roden, D.M. Predicting drug-induced QT prolongation and torsades de pointes. J. Physiol. 2016, 594, 2459–2468. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wit, A.L. Afterdepolarizations and triggered activity as a mechanism for clinical arrhythmias. Pacing Clin. Electrophysiol. 2018, 41, 883–896. [Google Scholar] [CrossRef] [PubMed]
- Schlotthauer, K.; Bers, D.M. Sarcoplasmic reticulum Ca(2+) release causes myocyte depolarization. Underlying mechanism and threshold for triggered action potentials. Circ. Res. 2000, 87, 774–780. [Google Scholar] [CrossRef] [Green Version]
- Pogwizd, S.M.; Schlotthauer, K.; Li, L.; Yuan, W.; Bers, D.M. Arrhythmogenesis and contractile dysfunction in heart failure: Roles of sodium-calcium exchange, inward rectifier potassium current, and residual beta-adrenergic responsiveness. Circ. Res. 2001, 88, 1159–1167. [Google Scholar] [CrossRef] [Green Version]
- Maruyama, M.; Joung, B.; Tang, L.; Shinohara, T.; On, Y.K.; Han, S.; Choi, E.K.; Kim, D.H.; Shen, M.J.; Weiss, J.N.; et al. Diastolic intracellular calcium-membrane voltage coupling gain and postshock arrhythmias: Role of purkinje fibers and triggered activity. Circ. Res. 2010, 106, 399–408. [Google Scholar] [CrossRef] [Green Version]
- Marban, E.; Robinson, S.W.; Wier, W.G. Mechanisms of arrhythmogenic delayed and early afterdepolarizations in ferret ventricular muscle. J. Clin. Investig. 1986, 78, 1185–1192. [Google Scholar] [CrossRef]
- January, C.T.; Riddle, J.M.; Salata, J.J. A model for early afterdepolarizations: Induction with the Ca2+ channel agonist Bay K 8644. Circ. Res. 1988, 62, 563–571. [Google Scholar] [CrossRef] [Green Version]
- January, C.T.; Riddle, J.M. Early afterdepolarizations: Mechanism of induction and block. A role for L-type Ca2+ current. Circ. Res. 1989, 64, 977–990. [Google Scholar] [CrossRef] [Green Version]
- Milberg, P.; Fink, M.; Pott, C.; Frommeyer, G.; Biertz, J.; Osada, N.; Stypmann, J.; Mönnig, G.; Koopmann, M.; Breithardt, G.; et al. Blockade of I(Ca) suppresses early afterdepolarizations and reduces transmural dispersion of repolarization in a whole heart model of chronic heart failure. Br. J. Pharm. 2012, 166, 557–568. [Google Scholar] [CrossRef] [Green Version]
- Zeng, J.; Rudy, Y. Early afterdepolarizations in cardiac myocytes: Mechanism and rate dependence. Biophys. J. 1995, 68, 949–964. [Google Scholar] [CrossRef] [Green Version]
- Qu, Z.; Xie, L.H.; Olcese, R.; Karagueuzian, H.S.; Chen, P.S.; Garfinkel, A.; Weiss, J.N. Early afterdepolarizations in cardiac myocytes: Beyond reduced repolarization reserve. Cardiovasc. Res. 2013, 99, 6–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gonano, L.A.; Mattiazzi, A. Targeting late ICaL to close the window to ventricular arrhythmias. J. Gen. Physiol. 2021, 153. [Google Scholar] [CrossRef] [PubMed]
- Madhvani, R.V.; Angelini, M.; Xie, Y.; Pantazis, A.; Suriany, S.; Borgstrom, N.P.; Garfinkel, A.; Qu, Z.; Weiss, J.N.; Olcese, R. Targeting the late component of the cardiac L-type Ca2+ current to suppress early afterdepolarizations. J. Gen. Physiol. 2015, 145, 395–404. [Google Scholar] [CrossRef] [Green Version]
- Kurata, Y.; Tsumoto, K.; Hayashi, K.; Hisatome, I.; Tanida, M.; Kuda, Y.; Shibamoto, T. Dynamical mechanisms of phase-2 early afterdepolarizations in human ventricular myocytes: Insights from bifurcation analyses of two mathematical models. Am. J. Physiol. Heart Circ. Physiol. 2017, 312, H106–H127. [Google Scholar] [CrossRef] [Green Version]
- Nagy, Z.A.; Virág, L.; Tóth, A.; Biliczki, P.; Acsai, K.; Bányász, T.; Nánási, P.; Papp, J.G.; Varró, A. Selective inhibition of sodium-calcium exchanger by SEA-0400 decreases early and delayed after depolarization in canine heart. Br. J. Pharm. 2004, 143, 827–831. [Google Scholar] [CrossRef] [Green Version]
- Milberg, P.; Pott, C.; Frommeyer, G.; Fink, M.; Ruhe, M.; Matsuda, T.; Baba, A.; Klocke, R.; Quang, T.H.; Nikol, S.; et al. Acute inhibition of the Na(+)/Ca(2+) exchanger reduces proarrhythmia in an experimental model of chronic heart failure. Heart Rhythm. 2012, 9, 570–578. [Google Scholar] [CrossRef]
- Pott, C.; Muszynski, A.; Ruhe, M.; Bögeholz, N.; Schulte, J.S.; Milberg, P.; Mönnig, G.; Fabritz, L.; Goldhaber, J.I.; Breithardt, G.; et al. Proarrhythmia in a non-failing murine model of cardiac-specific Na+/Ca2+ exchanger overexpression: Whole heart and cellular mechanisms. Basic Res. Cardiol. 2012, 107, 247. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Liao, Z.; Grandi, E.; Shiferaw, Y.; Bers, D.M. Slow [Na]i Changes and Positive Feedback Between Membrane Potential and [Ca]i Underlie Intermittent Early Afterdepolarizations and Arrhythmias. Circ. Arrhythm. Electrophysiol. 2015, 8, 1472–1480. [Google Scholar] [CrossRef] [Green Version]
- Ton, A.T.; Nguyen, W.; Sweat, K.; Miron, Y.; Hernandez, E.; Wong, T.; Geft, V.; Macias, A.; Espinoza, A.; Truong, K.; et al. Arrhythmogenic and antiarrhythmic actions of late sustained sodium current in the adult human heart. Sci. Rep. 2021, 11, 12014. [Google Scholar] [CrossRef]
- Priori, S.G.; Corr, P.B. Mechanisms underlying early and delayed afterdepolarizations induced by catecholamines. Am. J. Physiol. 1990, 258, H1796–H1805. [Google Scholar] [CrossRef]
- Volders, P.G.; Vos, M.A.; Szabo, B.; Sipido, K.R.; de Groot, S.H.; Gorgels, A.P.; Wellens, H.J.; Lazzara, R. Progress in the understanding of cardiac early afterdepolarizations and torsades de pointes: Time to revise current concepts. Cardiovasc. Res. 2000, 46, 376–392. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Wen, H.; Fefelova, N.; Allen, C.; Baba, A.; Matsuda, T.; Xie, L.H. Revisiting the ionic mechanisms of early afterdepolarizations in cardiomyocytes: Predominant by Ca waves or Ca currents? Am. J. Physiol. Heart Circ. Physiol. 2012, 302, H1636–H1644. [Google Scholar] [CrossRef]
- Choi, B.R.; Burton, F.; Salama, G. Cytosolic Ca2+ triggers early afterdepolarizations and Torsade de Pointes in rabbit hearts with type 2 long QT syndrome. J. Physiol. 2002, 543, 615–631. [Google Scholar] [CrossRef] [PubMed]
- Chang, P.C.; Wo, H.T.; Lee, H.L.; Lin, S.F.; Wen, M.S.; Chu, Y.; Yeh, S.J.; Chou, C.C. Role of sarcoplasmic reticulum calcium in development of secondary calcium rise and early afterdepolarizations in long QT syndrome rabbit model. PLoS ONE 2015, 10, e0123868. [Google Scholar] [CrossRef] [PubMed]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Noble, D. Cardiac action and pacemaker potentials based on the Hodgkin-Huxley equations. Nature 1960, 188, 495–497. [Google Scholar] [CrossRef]
- Luo, C.H.; Rudy, Y. A dynamic model of the cardiac ventricular action potential. II. Afterdepolarizations, triggered activity, and potentiation. Circ. Res. 1994, 74, 1097–1113. [Google Scholar] [CrossRef] [Green Version]
- Luo, C.H.; Rudy, Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ. Res. 1994, 74, 1071–1096. [Google Scholar] [CrossRef] [Green Version]
- Clancy, C.E.; Rudy, Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature 1999, 400, 566–569. [Google Scholar] [CrossRef]
- Matsuoka, S.; Sarai, N.; Kuratomi, S.; Ono, K.; Noma, A. Role of individual ionic current systems in ventricular cells hypothesized by a model study. Jpn. J. Physiol. 2003, 53, 105–123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shannon, T.R.; Wang, F.; Puglisi, J.; Weber, C.; Bers, D.M. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 2004, 87, 3351–3371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahajan, A.; Shiferaw, Y.; Sato, D.; Baher, A.; Olcese, R.; Xie, L.H.; Yang, M.J.; Chen, P.S.; Restrepo, J.G.; Karma, A.; et al. A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophys. J. 2008, 94, 392–410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bondarenko, V.E.; Szigeti, G.P.; Bett, G.C.; Kim, S.J.; Rasmusson, R.L. Computer model of action potential of mouse ventricular myocytes. Am. J. Physiol. Heart Circ. Physiol. 2004, 287, H1378–H1403. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.J.; Sobie, E.A. Mathematical model of the neonatal mouse ventricular action potential. Am. J. Physiol. Heart Circ. Physiol. 2008, 294, H2565–H2575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Demir, S.S. Computational modeling of cardiac ventricular action potentials in rat and mouse: Review. Jpn. J. Physiol. 2004, 54, 523–530. [Google Scholar] [CrossRef] [Green Version]
- Rozier, K.; Bondarenko, V.E. Mathematical modeling physiological effects of the overexpression of β(2)-adrenoceptors in mouse ventricular myocytes. Am. J. Physiol. Heart Circ. Physiol. 2018, 314, H643–H658. [Google Scholar] [CrossRef]
- Asfaw, T.N.; Tyan, L.; Glukhov, A.V.; Bondarenko, V.E. A compartmentalized mathematical model of mouse atrial myocytes. Am. J. Physiol. Heart Circ. Physiol. 2020, 318, H485–H507. [Google Scholar] [CrossRef]
- Hund, T.J.; Rudy, Y. Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model. Circulation 2004, 110, 3168–3174. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Rudy, Y. A model of canine purkinje cell electrophysiology and Ca(2+) cycling: Rate dependence, triggered activity, and comparison to ventricular myocytes. Circ. Res. 2011, 109, 71–79. [Google Scholar] [CrossRef] [Green Version]
- Decker, K.F.; Heijman, J.; Silva, J.R.; Hund, T.J.; Rudy, Y. Properties and ionic mechanisms of action potential adaptation, restitution, and accommodation in canine epicardium. Am. J. Physiol. Heart Circ. Physiol. 2009, 296, H1017–H1026. [Google Scholar] [CrossRef] [Green Version]
- Kurata, Y.; Hisatome, I.; Matsuda, H.; Shibamoto, T. Dynamical mechanisms of pacemaker generation in IK1-downregulated human ventricular myocytes: Insights from bifurcation analyses of a mathematical model. Biophys. J. 2005, 89, 2865–2887. [Google Scholar] [CrossRef] [Green Version]
- Courtemanche, M.; Ramirez, R.J.; Nattel, S. Ionic mechanisms underlying human atrial action potential properties: Insights from a mathematical model. Am. J. Physiol. 1998, 275, H301–H321. [Google Scholar] [CrossRef] [PubMed]
- ten Tusscher, K.H.; Noble, D.; Noble, P.J.; Panfilov, A.V. A model for human ventricular tissue. Am. J. Physiol. Heart Circ. Physiol. 2004, 286, H1573–H1589. [Google Scholar] [CrossRef] [PubMed]
- ten Tusscher, K.H.; Panfilov, A.V. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H1088–H1100. [Google Scholar] [CrossRef] [PubMed]
- Grandi, E.; Pasqualini, F.S.; Bers, D.M. A novel computational model of the human ventricular action potential and Ca transient. J. Mol. Cell. Cardiol. 2010, 48, 112–121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Hara, T.; Virág, L.; Varró, A.; Rudy, Y. Simulation of the undiseased human cardiac ventricular action potential: Model formulation and experimental validation. PLoS Comput. Biol. 2011, 7, e1002061. [Google Scholar] [CrossRef] [Green Version]
- Tomek, J.; Bueno-Orovio, A.; Passini, E.; Zhou, X.; Minchole, A.; Britton, O.; Bartolucci, C.; Severi, S.; Shrier, A.; Virag, L.; et al. Development, calibration, and validation of a novel human ventricular myocyte model in health, disease, and drug block. eLife 2019, 8, e48890. [Google Scholar] [CrossRef]
- Noble, D.; Garny, A.; Noble, P.J. How the Hodgkin-Huxley equations inspired the Cardiac Physiome Project. J. Physiol. 2012, 590, 2613–2628. [Google Scholar] [CrossRef]
- Amuzescu, B.; Airini, R.; Epureanu, F.B.; Mann, S.A.; Knott, T.; Radu, B.M. Evolution of mathematical models of cardiomyocyte electrophysiology. Math. Biosci. 2021, 334, 108567. [Google Scholar] [CrossRef]
- Minorsky, N. Nonlinear Oscillations; Van Nostrand: Princeton, NJ, USA, 1962; p. 714. [Google Scholar]
- Pontryagin, L.S. Ordinary Differential Equations; Addison-Wesley: Reading, MA, USA, 1962; p. 298. [Google Scholar]
- Kuznetsov, Y. Elements of Applied Bifurcation Theory, 3rd ed.; Springer: New York, NY, USA, 2004; p. 631. [Google Scholar]
- Yehia, A.R.; Jeandupeux, D.; Alonso, F.; Guevara, M.R. Hysteresis and bistability in the direct transition from 1:1 to 2:1 rhythm in periodically driven single ventricular cells. Chaos 1999, 9, 916–931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michaels, D.C.; Chialvo, D.R.; Matyas, E.P.; Jalife, J. Chaotic activity in a mathematical model of the vagally driven sinoatrial node. Circ. Res. 1989, 65, 1350–1360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Okamoto, Y.; Takano, M.; Ohba, T.; Ono, K. Arrhythmogenic coupling between the Na+-Ca2+ exchanger and inositol 1,4,5-triphosphate receptor in rat pulmonary vein cardiomyocytes. J. Mol. Cell. Cardiol. 2012, 52, 988–997. [Google Scholar] [CrossRef]
- Okamoto, Y.; Kawamura, K.; Nakamura, Y.; Ono, K. Pathological impact of hyperpolarization-activated chloride current peculiar to rat pulmonary vein cardiomyocytes. J. Mol. Cell. Cardiol. 2014, 66, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Haïssaguerre, M.; Jaïs, P.; Shah, D.C.; Takahashi, A.; Hocini, M.; Quiniou, G.; Garrigue, S.; Le Mouroux, A.; Le Métayer, P.; Clémenty, J. Spontaneous Initiation of Atrial Fibrillation by Ectopic Beats Originating in the Pulmonary Veins. N. Engl. J. Med. 1998, 339, 659–666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Umehara, S.; Tan, X.; Okamoto, Y.; Ono, K.; Noma, A.; Amano, A.; Himeno, Y. Mechanisms Underlying Spontaneous Action Potential Generation Induced by Catecholamine in Pulmonary Vein Cardiomyocytes: A Simulation Study. Int. J. Mol. Sci. 2019, 20, 2913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsumoto, K.; Kurata, Y.; Furutani, K.; Kurachi, Y. Hysteretic Dynamics of Multi-Stable Early Afterdepolarisations with Repolarisation Reserve Attenuation: A Potential Dynamical Mechanism for Cardiac Arrhythmias. Sci. Rep. 2017, 7, 10771. [Google Scholar] [CrossRef] [Green Version]
- Barrio, R.; Martínez, M.; Pueyo, E.; Serrano, S. Dynamical analysis of early afterdepolarization patterns in a biophysically detailed cardiac model. Chaos 2021, 31, 073137. [Google Scholar] [CrossRef]
- Gadsby, D.C.; Cranefield, P.F. Two levels of resting potential in cardiac Purkinje fibers. J. Gen Physiol. 1977, 70, 725–746. [Google Scholar] [CrossRef]
- Cranefield, P.F. Action potentials, afterpotentials, and arrhythmias. Circ. Res. 1977, 41, 415–423. [Google Scholar] [CrossRef] [Green Version]
- Jalife, J.; Antzelevitch, C. Phase resetting and annihilation of pacemaker activity in cardiac tissue. Science 1979, 206, 695–697. [Google Scholar] [CrossRef] [PubMed]
- Walker, M.L.; Wan, X.; Kirsch, G.E.; Rosenbaum, D.S. Hysteresis effect implicates calcium cycling as a mechanism of repolarization alternans. Circulation 2003, 108, 2704–2709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, R.; Patwardhan, A. Restitution of action potential duration during sequential changes in diastolic intervals shows multimodal behavior. Circ. Res. 2004, 94, 634–641. [Google Scholar] [CrossRef] [PubMed]
- Berger, R.D. Electrical restitution hysteresis: Good memory or delayed response? Circ. Res. 2004, 94, 567–569. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arnol’d, V.I. Loss of stability of self-oscillations close to resonance and versal deformations of equivariant vector fields. Funct. Anal. Its Appl. 1977, 11, 85–92. [Google Scholar] [CrossRef]
- Miake, J.; Marbán, E.; Nuss, H.B. Biological pacemaker created by gene transfer. Nature 2002, 419, 132–133. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Neural excitability, spiking and bursting. Int. J. Bifurc. Chaos 2000, 10, 1171–1266. [Google Scholar] [CrossRef] [Green Version]
- Kitajima, H.; Ioka, E.; Yazawa, T. Generation Mechanism of Alternans in Luo–Rudy Model. Int. J. Bifurc. Chaos 2016, 26, 1650075. [Google Scholar] [CrossRef]
- Guevara, M.R.; Glass, L.; Shrier, A. Phase locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cardiac cells. Science 1981, 214, 1350–1353. [Google Scholar] [CrossRef]
- Landaw, J.; Qu, Z. Bifurcations Caused by Feedback between Voltage and Intracellular Ion Concentrations in Ventricular Myocytes. Phys. Rev. Lett. 2019, 123, 218101. [Google Scholar] [CrossRef]
- Sun, J.; Amellal, F.; Glass, L.; Billette, J. Alternans and period-doubling bifurcations in atrioventricular nodal conduction. J. Theor. Biol. 1995, 173, 79–91. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsumoto, K.; Ashihara, T.; Naito, N.; Shimamoto, T.; Amano, A.; Kurata, Y.; Kurachi, Y. Specific decreasing of Na(+) channel expression on the lateral membrane of cardiomyocytes causes fatal arrhythmias in Brugada syndrome. Sci. Rep. 2020, 10, 19964. [Google Scholar] [CrossRef] [PubMed]
- Tsumoto, K.; Ashihara, T.; Haraguchi, R.; Nakazawa, K.; Kurachi, Y. Ischemia-related subcellular redistribution of sodium channels enhances the proarrhythmic effect of class I antiarrhythmic drugs: A simulation study. PLoS ONE 2014, 9, e109271. [Google Scholar] [CrossRef] [PubMed]
- Chialvo, D.R.; Gilmour, R.F., Jr.; Jalife, J. Low dimensional chaos in cardiac tissue. Nature 1990, 343, 653–657. [Google Scholar] [CrossRef] [PubMed]
- Frame, L.H.; Simson, M.B. Oscillations of conduction, action potential duration, and refractoriness. A mechanism for spontaneous termination of reentrant tachycardias. Circulation 1988, 78, 1277–1287. [Google Scholar] [CrossRef] [Green Version]
- Qu, Z.; Xie, F.; Garfinkel, A.; Weiss, J.N. Origins of spiral wave meander and breakup in a two-dimensional cardiac tissue model. Ann. Biomed. Eng. 2000, 28, 755–771. [Google Scholar] [CrossRef]
- Qu, Z.; Hu, G.; Garfinkel, A.; Weiss, J.N. Nonlinear and Stochastic Dynamics in the Heart. Phys. Rep. 2014, 543, 61–162. [Google Scholar] [CrossRef] [Green Version]
- AUTO. Available online: http://indy.cs.concordia.ca/auto/ (accessed on 1 November 2021).
- Doedel, E.; Kernévez, J. AUTO: Software for Continuation Problems in Ordinary Differential Equations with Applications; Applied Mathematics Technical Report; California Institute of Technology: Pasadena, CA, USA, 1986. [Google Scholar]
- XPP-AUT. Available online: http://www.math.pitt.edu/~bard/xpp/xpp.html (accessed on 1 November 2021).
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A. MATCONT: A MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans. Math. Softw. 2003, 29, 141–164. [Google Scholar] [CrossRef]
- Kawakami, H. Bifurcation of periodic responses in forced dynamic nonlinear circuits: Computation of bifurcation values of the system parameters. IEEE Trans. Circuits Syst. 1984, 31, 248–260. [Google Scholar] [CrossRef]
- Tsumoto, K.; Ueta, T.; Yoshinaga, T.; Kawakami, H. Bifurcation analyses of nonlinear dynamical systems: From theory to numerical computations. Nonlinear Theory Its Appl. IEICE 2012, 3, 458–476. [Google Scholar] [CrossRef] [Green Version]
- Parker, T.S.; Chua, L. Practical Numerical Algorithms for Chaotic Systems; Springer: New York, NY, USA, 1989; p. 348. [Google Scholar]
- Glass, L.; Mackey, M.C. From Clocks to Chaos: The Rhythms of Life; Princeton University Press: Princeton, NJ, USA, 1988; p. 248. [Google Scholar]
- Shrier, A.; Dubarsky, H.; Rosengarten, M.; Guevara, M.R.; Nattel, S.; Glass, L. Prediction of complex atrioventricular conduction rhythms in humans with use of the atrioventricular nodal recovery curve. Circulation 1987, 76, 1196–1205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keener, J.P. On cardiac arrythmias: AV conduction block. J. Math. Biol. 1981, 12, 215–225. [Google Scholar] [CrossRef]
- Guevara, M.R.; Shrier, A.; Glass, L. Phase resetting of spontaneously beating embryonic ventricular heart cell aggregates. Am. J. Physiol. 1986, 251, H1298–H1305. [Google Scholar] [CrossRef] [PubMed]
- Guevara, M.R.; Shrier, A.; Glass, L. Phase-locked rhythms in periodically stimulated heart cell aggregates. Am. J. Physiol. 1988, 254, H1–H10. [Google Scholar] [CrossRef] [PubMed]
- Keener, J.P.; Glass, L. Global bifurcations of a periodically forced nonlinear oscillator. J. Math. Biol. 1984, 21, 175–190. [Google Scholar] [CrossRef]
- Jalife, J.; Moe, G.K. Phasic effects of vagal stimulation on pacemaker activity of the isolated sinus node of the young cat. Circ. Res. 1979, 45, 595–608. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, N.; Yoshizawa, S.; Sato, T. Difference equation model of ventricular parasystole as an interaction between cardiac pacemakers based on the phase response curve. J. Theor. Biol. 1983, 103, 439–465. [Google Scholar] [CrossRef]
- Glass, L.; Goldberger, A.L.; Bélair, J. Dynamics of pure parasystole. Am. J. Physiol. 1986, 251, H841–H847. [Google Scholar] [CrossRef] [Green Version]
- Landau, M.; Lorente, P.; Michaels, D.; Jalife, J. Bistabilities and annihilation phenomena in electrophysiological cardiac models. Circ. Res. 1990, 66, 1658–1672. [Google Scholar] [CrossRef] [Green Version]
- Guevara, M.R.; Jongsma, H.J. Phase resetting in a model of sinoatrial nodal membrane: Ionic and topological aspects. Am. J. Physiol. 1990, 258, H734–H747. [Google Scholar] [CrossRef]
- Guevara, M.R.; Jongsma, H.J. Three ways of abolishing automaticity in sinoatrial node: Ionic modeling and nonlinear dynamics. Am. J. Physiol. 1992, 262, H1268–H1286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurata, Y.; Hisatome, I.; Imanishi, S.; Shibamoto, T. Roles of L-type Ca2+ and delayed-rectifier K+ currents in sinoatrial node pacemaking: Insights from stability and bifurcation analyses of a mathematical model. Am. J. Physiol. Heart Circ. Physiol. 2003, 285, H2804–H2819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurata, Y.; Matsuda, H.; Hisatome, I.; Shibamoto, T. Regional difference in dynamical property of sinoatrial node pacemaking: Role of Na+ channel current. Biophys. J. 2008, 95, 951–977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurata, Y.; Matsuda, H.; Hisatome, I.; Shibamoto, T. Roles of hyperpolarization-activated current If in sinoatrial node pacemaking: Insights from bifurcation analysis of mathematical models. Am. J. Physiol. Heart Circ. Physiol. 2010, 298, H1748–H1760. [Google Scholar] [CrossRef] [PubMed]
- Kurata, Y.; Hisatome, I.; Shibamoto, T. Roles of sarcoplasmic reticulum Ca2+ cycling and Na+/Ca2+ exchanger in sinoatrial node pacemaking: Insights from bifurcation analysis of mathematical models. Am. J. Physiol. Heart Circ. Physiol. 2012, 302, H2285–H2300. [Google Scholar] [CrossRef] [PubMed]
- Kurata, Y.; Hisatome, I.; Tanida, M.; Shibamoto, T. Effect of hyperpolarization-activated current If on robustness of sinoatrial node pacemaking: Theoretical study on influence of intracellular Na(+) concentration. Am. J. Physiol. Heart Circ. Physiol. 2013, 304, H1337–H1351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, Z.; Yamaguchi, R.; Doi, S. Bifurcation analysis and effects of changing ionic conductances on pacemaker rhythm in a sinoatrial node cell model. Biosystems 2011, 106, 9–18. [Google Scholar] [CrossRef]
- Pan, Z.; Doi, S. Global bifurcation structure and variability of pacemaker rhythm in a detailed model of cardiac sinoatrial node cells. Electron. Commun. Jpn. 2012, 95, 28–39. [Google Scholar] [CrossRef]
- Bouchard, S.; Jacquemet, V.; Vinet, A. Automaticity in acute ischemia: Bifurcation analysis of a human ventricular model. Phys. Rev. E Stat Nonlin Soft Matter Phys. 2011, 83, 011911. [Google Scholar] [CrossRef]
- Chay, T.R.; Lee, Y.S. Phase resetting and bifurcation in the ventricular myocardium. Biophys. J. 1985, 47, 641–651. [Google Scholar] [CrossRef] [Green Version]
- Vinet, A.; Chialvo, D.R.; Michaels, D.C.; Jalife, J. Nonlinear dynamics of rate-dependent activation in models of single cardiac cells. Circ. Res. 1990, 67, 1510–1524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurata, Y.; Matsuda, H.; Hisatome, I.; Shibamoto, T. Effects of pacemaker currents on creation and modulation of human ventricular pacemaker: Theoretical study with application to biological pacemaker engineering. Am. J. Physiol. Heart Circ. Physiol. 2007, 292, H701–H718. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gibb, W.J.; Wagner, M.B.; Lesh, M.D. Effects of simulated potassium blockade on the dynamics of triggered cardiac activity. J. Theor. Biol. 1994, 168, 245–257. [Google Scholar] [CrossRef] [PubMed]
- Sato, D.; Xie, L.H.; Nguyen, T.P.; Weiss, J.N.; Qu, Z. Irregularly appearing early afterdepolarizations in cardiac myocytes: Random fluctuations or dynamical chaos? Biophys. J. 2010, 99, 765–773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sato, D.; Xie, L.H.; Sovari, A.A.; Tran, D.X.; Morita, N.; Xie, F.; Karagueuzian, H.; Garfinkel, A.; Weiss, J.N.; Qu, Z. Synchronization of chaotic early afterdepolarizations in the genesis of cardiac arrhythmias. Proc. Natl. Acad. Sci. USA 2009, 106, 2983–2988. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, C.H.; Rudy, Y. A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circ. Res. 1991, 68, 1501–1526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landaw, J.; Qu, Z. Memory-induced nonlinear dynamics of excitation in cardiac diseases. Phys. Rev. E 2018, 97, 042414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, X.; Song, Z.; Qu, Z. Determinants of early afterdepolarization properties in ventricular myocyte models. PLoS Comput. Biol. 2018, 14, e1006382. [Google Scholar] [CrossRef] [Green Version]
- Qu, Z. Chaos in the genesis and maintenance of cardiac arrhythmias. Prog. Biophys. Mol. Biol. 2011, 105, 247–257. [Google Scholar] [CrossRef] [Green Version]
- Kimrey, J.; Vo, T.; Bertram, R. Canard analysis reveals why a large Ca2+ window current promotes early afterdepolarizations in cardiac myocytes. PLoS Comput. Biol. 2020, 16, e1008341. [Google Scholar] [CrossRef]
- Amuzescu, B.; Georgescu, A.; Nistor, G.; Popescu, M.; Svab, I.; Flonta, M.L.; Corlan, A.D. Stability and sustained oscillations in a ventricular cardiomyocyte model. Interdiscip Sci. 2012, 4, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.X.; Sato, D.; Yochelis, A.; Weiss, J.N.; Garfinkel, A.; Qu, Z. Bifurcation and chaos in a model of cardiac early afterdepolarizations. Phys. Rev. Lett. 2009, 102, 258103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asakura, K.; Cha, C.Y.; Yamaoka, H.; Horikawa, Y.; Memida, H.; Powell, T.; Amano, A.; Noma, A. EAD and DAD mechanisms analyzed by developing a new human ventricular cell model. Prog. Biophys. Mol. Biol. 2014, 116, 11–24. [Google Scholar] [CrossRef] [PubMed]
- Himeno, Y.; Asakura, K.; Cha, C.Y.; Memida, H.; Powell, T.; Amano, A.; Noma, A. A human ventricular myocyte model with a refined representation of excitation-contraction coupling. Biophys. J. 2015, 109, 415–427. [Google Scholar] [CrossRef] [Green Version]
- Iyer, V.; Mazhari, R.; Winslow, R.L. A computational model of the human left-ventricular epicardial myocyte. Biophys. J. 2004, 87, 1507–1525. [Google Scholar] [CrossRef] [Green Version]
- Heijman, J.; Volders, P.G.; Westra, R.L.; Rudy, Y. Local control of β-adrenergic stimulation: Effects on ventricular myocyte electrophysiology and Ca(2+)-transient. J. Mol. Cell. Cardiol. 2011, 50, 863–871. [Google Scholar] [CrossRef] [Green Version]
- Morotti, S.; Edwards, A.G.; McCulloch, A.D.; Bers, D.M.; Grandi, E. A novel computational model of mouse myocyte electrophysiology to assess the synergy between Na+ loading and CaMKII. J. Physiol. 2014, 592, 1181–1197. [Google Scholar] [CrossRef]
- Hegyi, B.; Morotti, S.; Liu, C.; Ginsburg, K.S.; Bossuyt, J.; Belardinelli, L.; Izu, L.T.; Chen-Izu, Y.; Bányász, T.; Grandi, E.; et al. Enhanced Depolarization Drive in Failing Rabbit Ventricular Myocytes: Calcium-Dependent and β-Adrenergic Effects on Late Sodium, L-Type Calcium, and Sodium-Calcium Exchange Currents. Circ. Arrhythm. Electrophysiol. 2019, 12, e007061. [Google Scholar] [CrossRef]
- Kurata, Y.; Tanida, M.; Kuda, Y.; Shibamoto, T. Dynamical mechanisms underlying abnormal electrical activities of cardiac myocytes: Insights from bifurcation analyses of mathematical models for human ventricular myocytes. J. Kanazawa Med. Univ. 2014, 39, 59–66. [Google Scholar]
- Kurata, Y.; Tsumoto, K.; Hayashi, K.; Hisatome, I.; Kuda, Y.; Tanida, M. Multiple Dynamical Mechanisms of Phase-2 Early Afterdepolarizations in a Human Ventricular Myocyte Model: Involvement of Spontaneous SR Ca(2+) Release. Front. Physiol. 2019, 10, 1545. [Google Scholar] [CrossRef]
- Kitajima, H.; Yazawa, T. Bifurcation Analysis on a Generation of Early Afterdepolarization in a Mathematical Cardiac Model. Int. J. Bifurc. Chaos 2021, 31, 2150179. [Google Scholar] [CrossRef]
- Ten Tusscher, K.H.; Bernus, O.; Hren, R.; Panfilov, A.V. Comparison of electrophysiological models for human ventricular cells and tissues. Prog. Biophys. Mol. Biol. 2006, 90, 326–345. [Google Scholar] [CrossRef] [PubMed]
- Roden, D.M.; Hoffman, B.F. Action potential prolongation and induction of abnormal automaticity by low quinidine concentrations in canine Purkinje fibers. Relationship to potassium and cycle length. Circ. Res. 1985, 56, 857–867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jost, N.; Virág, L.; Bitay, M.; Takács, J.; Lengyel, C.; Biliczki, P.; Nagy, Z.; Bogáts, G.; Lathrop, D.A.; Papp, J.G.; et al. Restricting excessive cardiac action potential and QT prolongation: A vital role for IKs in human ventricular muscle. Circulation 2005, 112, 1392–1399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takanaka, C.; Singh, B.N. Barium-induced nondriven action potentials as a model of triggered potentials from early afterdepolarizations: Significance of slow channel activity and differing effects of quinidine and amiodarone. J. Am. Coll Cardiol. 1990, 15, 213–221. [Google Scholar] [CrossRef] [Green Version]
- Burashnikov, A.; Antzelevitch, C. Acceleration-induced action potential prolongation and early afterdepolarizations. J. Cardiovasc. Electrophysiol. 1998, 9, 934–948. [Google Scholar] [CrossRef]
- Viswanathan, P.C.; Rudy, Y. Cellular arrhythmogenic effects of congenital and acquired long-QT syndrome in the heterogeneous myocardium. Circulation 2000, 101, 1192–1198. [Google Scholar] [CrossRef] [Green Version]
- Silva, J.; Rudy, Y. Subunit interaction determines IKs participation in cardiac repolarization and repolarization reserve. Circulation 2005, 112, 1384–1391. [Google Scholar] [CrossRef] [Green Version]
- Britton, O.J.; Bueno-Orovio, A.; Virág, L.; Varró, A.; Rodriguez, B. The Electrogenic Na(+)/K(+) Pump Is a Key Determinant of Repolarization Abnormality Susceptibility in Human Ventricular Cardiomyocytes: A Population-Based Simulation Study. Front. Physiol. 2017, 8, 278. [Google Scholar] [CrossRef] [Green Version]
- Kügler, P.; Bulelzai, M.A.; Erhardt, A.H. Period doubling cascades of limit cycles in cardiac action potential models as precursors to chaotic early Afterdepolarizations. BMC Syst. Biol. 2017, 11, 42. [Google Scholar] [CrossRef] [Green Version]
- Furutani, K.; Tsumoto, K.; Chen, I.S.; Handa, K.; Yamakawa, Y.; Sack, J.T.; Kurachi, Y. Facilitation of I Kr current by some hERG channel blockers suppresses early afterdepolarizations. J. Gen. Physiol. 2019, 151, 214–230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fitzhugh, R. Thresholds and plateaus in the Hodgkin-Huxley nerve equations. J. Gen. Physiol. 1960, 43, 867–896. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erhardt, A.H. Early Afterdepolarisations Induced by an Enhancement in the Calcium Current. Processes 2019, 7, 20. [Google Scholar] [CrossRef] [Green Version]
- Sato, D.; Clancy, C.E.; Bers, D.M. Dynamics of sodium current mediated early afterdepolarizations. Heliyon 2017, 3, e00388. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kügler, P.; Erhardt, A.H.; Bulelzai, M.A.K. Early afterdepolarizations in cardiac action potentials as mixed mode oscillations due to a folded node singularity. PLoS ONE 2018, 13, e0209498. [Google Scholar] [CrossRef]
- Erhardt, A.H.; Solem, S. On complex dynamics in a Purkinje and a ventricular cardiac cell model. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105511. [Google Scholar] [CrossRef]
- Vo, T.; Bertram, R. Why pacing frequency affects the production of early afterdepolarizations in cardiomyocytes: An explanation revealed by slow-fast analysis of a minimal model. Phys Rev. E 2019, 99, 052205. [Google Scholar] [CrossRef] [Green Version]
- Doi, S.; Nabetani, S.; Kumagai, S. Complex nonlinear dynamics of the Hodgkin-Huxley equations induced by time scale changes. Biol. Cybern 2001, 85, 51–64. [Google Scholar] [CrossRef]
- Song, Z.; Ko, C.Y.; Nivala, M.; Weiss, J.N.; Qu, Z. Calcium-voltage coupling in the genesis of early and delayed afterdepolarizations in cardiac myocytes. Biophys. J. 2015, 108, 1908–1921. [Google Scholar] [CrossRef] [Green Version]
- Borowski, P.; Kuske, R.; Li, Y.X.; Cabrera, J.L. Characterizing mixed mode oscillations shaped by noise and bifurcation structure. Chaos 2010, 20, 043117. [Google Scholar] [CrossRef] [Green Version]
- Yaru, L.; Shenquan, L. Characterizing mixed-mode oscillations shaped by canard and bifurcation structure in a three-dimensional cardiac cell model. Nonlinear Dyn. 2021, 103, 2881–2902. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsumoto, K.; Kurata, Y. Bifurcations and Proarrhythmic Behaviors in Cardiac Electrical Excitations. Biomolecules 2022, 12, 459. https://doi.org/10.3390/biom12030459
Tsumoto K, Kurata Y. Bifurcations and Proarrhythmic Behaviors in Cardiac Electrical Excitations. Biomolecules. 2022; 12(3):459. https://doi.org/10.3390/biom12030459
Chicago/Turabian StyleTsumoto, Kunichika, and Yasutaka Kurata. 2022. "Bifurcations and Proarrhythmic Behaviors in Cardiac Electrical Excitations" Biomolecules 12, no. 3: 459. https://doi.org/10.3390/biom12030459
APA StyleTsumoto, K., & Kurata, Y. (2022). Bifurcations and Proarrhythmic Behaviors in Cardiac Electrical Excitations. Biomolecules, 12(3), 459. https://doi.org/10.3390/biom12030459





