SynerGNet: A Graph Neural Network Model to Predict Anticancer Drug Synergy
Abstract
1. Introduction
2. Materials and Methods
2.1. Protein–Protein Interaction Network
2.2. Node Features
2.2.1. Genomic Alterations
2.2.2. Gene Ontology Terms
2.2.3. Drug–Protein Associations
2.3. Graph Statistics
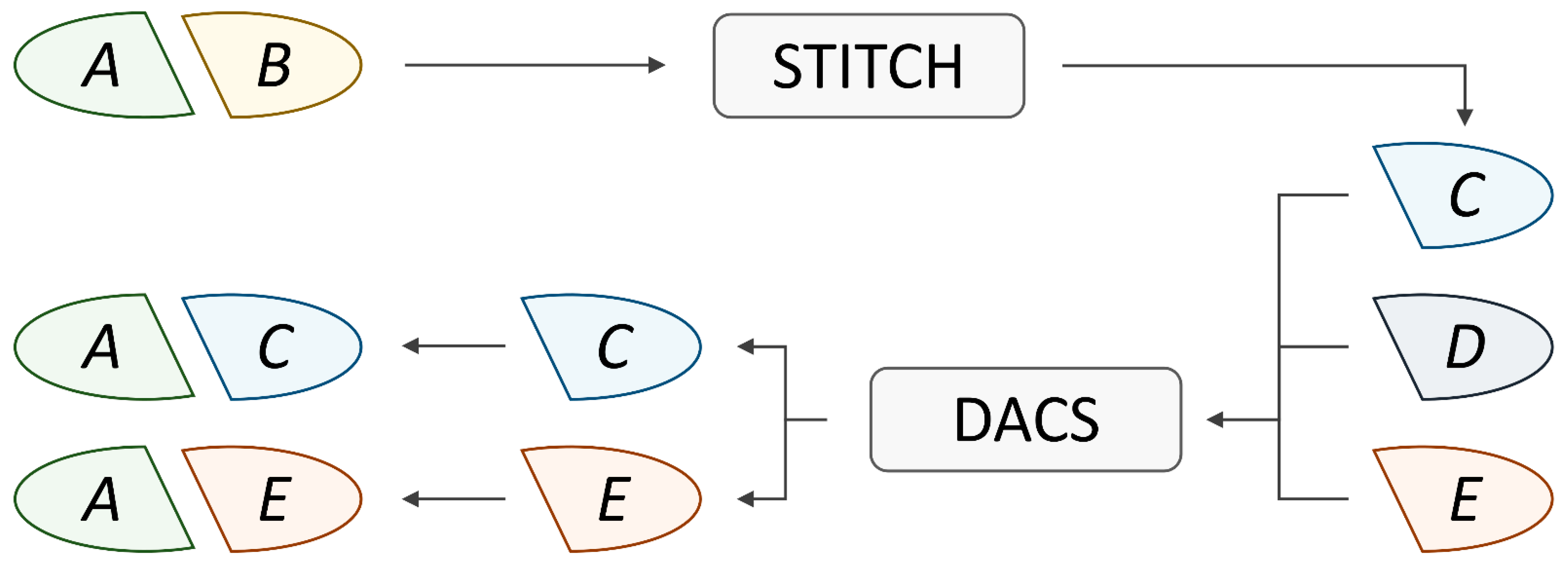
2.4. Drug Action/Chemical Similarity Score
2.5. Graph Data Vectorization
2.6. Training and Validation
2.7. Evaluation Metrics
3. Results
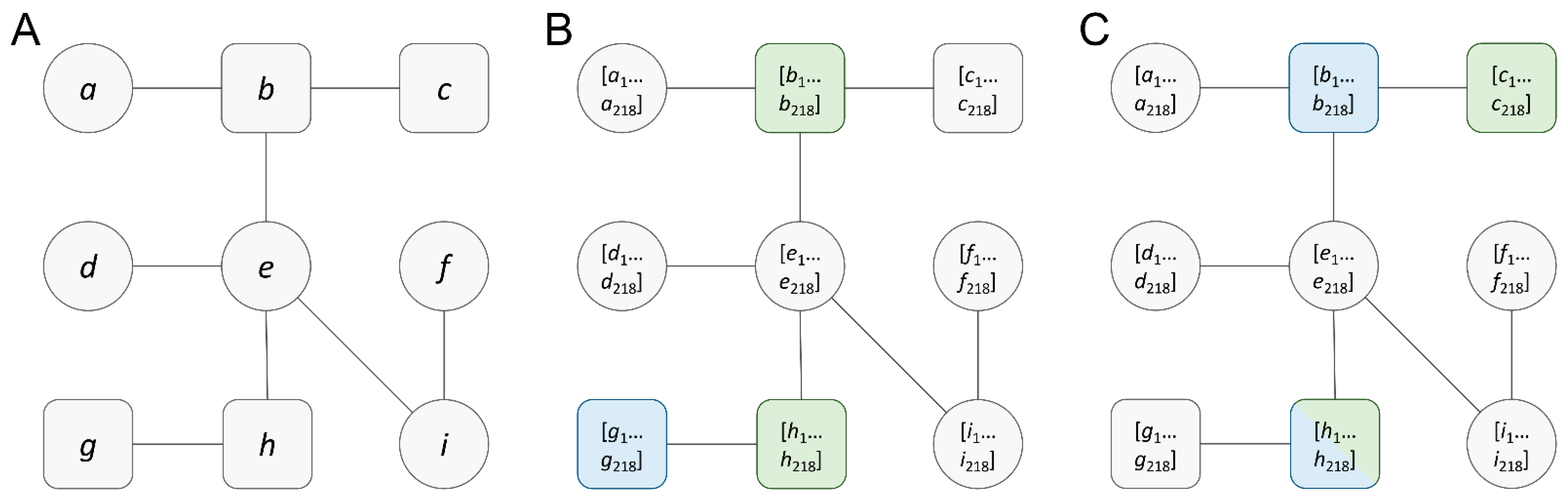
3.1. Cancer-Specific Featured Graphs
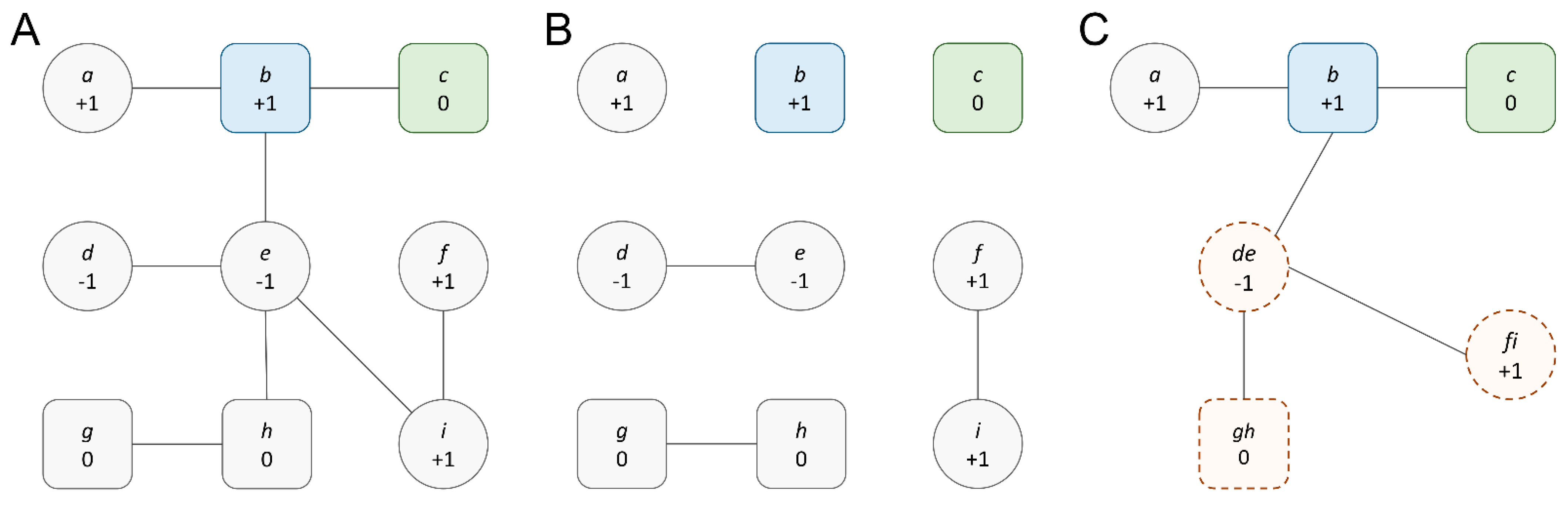
3.2. Graph Reduction to Create Topological Diversity
3.3. Analysis of Reduced Cancer-Specific Networks
3.4. Data Augmentation
3.5. SynerGNet to Predict Drug Synergy
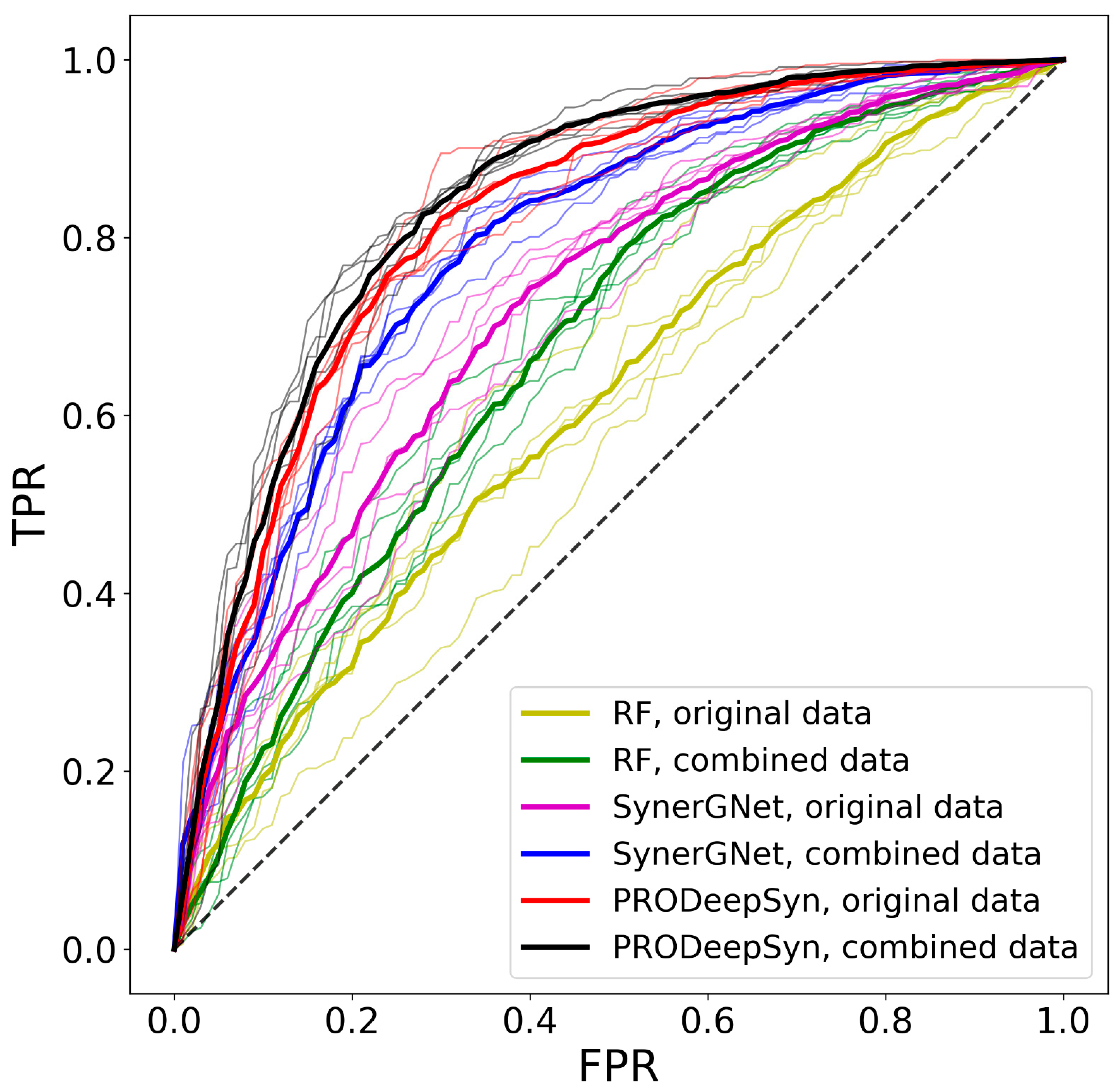
3.6. Performance of Drug Synergy Predictors
3.7. Independent Validation of SynerGNet
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef]
- Chabner, B.A.; Roberts, T.G. Timeline: Chemotherapy and the war on cancer. Nat. Rev. Cancer 2005, 5, 65–72. [Google Scholar] [CrossRef] [PubMed]
- Smith, C.E.P.; Prasad, V. Targeted Cancer Therapies. Am. Fam. Physician 2021, 103, 155–163. [Google Scholar] [PubMed]
- Baxevanis, C.N.; Perez, S.A.; Papamichail, M. Cancer immunotherapy. Crit. Rev. Clin. Lab. Sci. 2009, 46, 167–189. [Google Scholar] [CrossRef]
- Holohan, C.; Van Schaeybroeck, S.; Longley, D.B.; Johnston, P.G. Cancer drug resistance: An evolving paradigm. Nat. Rev. Cancer 2013, 13, 714–726. [Google Scholar] [CrossRef] [PubMed]
- Mokhtari, R.B.; Homayouni, T.S.; Baluch, N.; Morgatskaya, E.; Kumar, S.; Das, B.; Yeger, H. Combination therapy in combating cancer. Oncotarget 2017, 8, 38022. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.X.; Wong, H.L.; Xue, H.Y.; Eoh, J.Y.; Wu, X.Y. Nanomedicine of synergistic drug combinations for cancer therapy–Strategies and perspectives. J. Control. Release 2016, 240, 489–503. [Google Scholar] [CrossRef] [PubMed]
- Fisusi, F.A.; Akala, E.O. Drug combinations in breast cancer therapy. Pharm. Nanotechnol. 2019, 7, 3–23. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, H. Predicting synergistic effects between compounds through their structural similarity and effects on transcriptomes. Bioinformatics 2016, 32, 3782–3789. [Google Scholar] [CrossRef]
- Rafique, R.; Islam, S.R.; Kazi, J.U. Machine learning in the prediction of cancer therapy. Comput. Struct. Biotechnol. J. 2021, 19, 4003–4017. [Google Scholar] [CrossRef]
- Besharatifard, M.; Vafaee, F. A Review on Graph Neural Networks for Predicting Synergistic Drug Combinations. Artif. Intell. Rev. 2023, 57, 49. [Google Scholar] [CrossRef]
- Wu, L.; Wen, Y.; Leng, D.; Zhang, Q.; Dai, C.; Wang, Z.; Liu, Z.; Yan, B.; Zhang, Y.; Wang, J. Machine learning methods, databases and tools for drug combination prediction. Brief. Bioinform. 2022, 23, bbab355. [Google Scholar] [CrossRef]
- Von Winterfeldt, D.; Edwards, W. Decision Analysis and Behavioral Research; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 278–282. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rendle, S. Factorization machines. In Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 995–1000. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S.; Cook, E. Applied Logistic Regression, 2nd ed.; John Wiley Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Webb, G.I.; Keogh, E.; Miikkulainen, R. Naïve Bayes. Encycl. Mach. Learn. 2010, 15, 713–714. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Menden, M.P.; Wang, D.; Mason, M.J.; Szalai, B.; Bulusu, K.C.; Guan, Y.; Yu, T.; Kang, J.; Jeon, M.; Wolfinger, R. Community assessment to advance computational prediction of cancer drug combinations in a pharmacogenomic screen. Nat. Commun. 2019, 10, 2674. [Google Scholar] [CrossRef]
- Shi, J.-Y.; Li, J.-X.; Mao, K.-T.; Cao, J.-B.; Lei, P.; Lu, H.-M.; Yiu, S.-M. Predicting combinative drug pairs via multiple classifier system with positive samples only. Comput. Methods Programs Biomed. 2019, 168, 1–10. [Google Scholar] [CrossRef]
- Wildenhain, J.; Spitzer, M.; Dolma, S.; Jarvik, N.; White, R.; Roy, M.; Griffiths, E.; Bellows, D.S.; Wright, G.D.; Tyers, M. Prediction of synergism from chemical-genetic interactions by machine learning. Cell Syst. 2015, 1, 383–395. [Google Scholar] [CrossRef] [PubMed]
- Preuer, K.; Lewis, R.P.; Hochreiter, S.; Bender, A.; Bulusu, K.C.; Klambauer, G. DeepSynergy: Predicting anti-cancer drug synergy with Deep Learning. Bioinformatics 2018, 34, 1538–1546. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Huang, S.; Jiang, P.; Hu, P. DTF: Deep tensor factorization for predicting anticancer drug synergy. Bioinformatics 2020, 36, 4483–4489. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Zhang, L.; Payne, P.R.; Li, F. Synergistic drug combination prediction by integrating multiomics data in deep learning models. Transl. Bioinform. Ther. Dev. 2021, 2194, 223–238. [Google Scholar]
- Zhang, X.-M.; Liang, L.; Liu, L.; Tang, M.-J. Graph neural networks and their current applications in bioinformatics. Front. Genet. 2021, 12, 690049. [Google Scholar] [CrossRef]
- Jiang, P.; Huang, S.; Fu, Z.; Sun, Z.; Lakowski, T.M.; Hu, P. Deep graph embedding for prioritizing synergistic anticancer drug combinations. Comput. Struct. Biotechnol. J. 2020, 18, 427–438. [Google Scholar] [CrossRef]
- Li, H.; Zou, L.; Kowah, J.A.; He, D.; Wang, L.; Yuan, M.; Liu, X. Predicting Drug Synergy and Discovering New Drug Combinations Based on a Graph Autoencoder and Convolutional Neural Network. Interdiscip. Sci. Comput. Life Sci. 2023, 15, 316–330. [Google Scholar] [CrossRef]
- Wang, T.; Wang, R.; Wei, L. AttenSyn: An Attention-Based Deep Graph Neural Network for Anticancer Synergistic Drug Combination Prediction. J. Chem. Inf. Model. 2023. Online ahead of print. [Google Scholar] [CrossRef]
- Numcharoenpinij, N.; Termsaithong, T.; Phunchongharn, P.; Piyayotai, S. Predicting Synergistic Drug Interaction with DNN and GAT. In Proceedings of the 2022 IEEE 5th International Conference on Knowledge Innovation and Invention (ICKII), Hualien, Taiwan, 22–24 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 24–29. [Google Scholar]
- Xu, M.; Zhao, X.; Wang, J.; Feng, W.; Wen, N.; Wang, C.; Wang, J.; Liu, Y.; Zhao, L. DFFNDDS: Prediction of synergistic drug combinations with dual feature fusion networks. J. Cheminformatics 2023, 15, 33. [Google Scholar] [CrossRef] [PubMed]
- Mazandu, G.K.; Hooper, C.; Opap, K.; Makinde, F.; Nembaware, V.; Thomford, N.E.; Chimusa, E.R.; Wonkam, A.; Mulder, N.J. IHP-PING—Generating integrated human protein–protein interaction networks on-the-fly. Brief. Bioinform. 2021, 22, bbaa277. [Google Scholar] [CrossRef]
- Szklarczyk, D.; Kirsch, R.; Koutrouli, M.; Nastou, K.; Mehryary, F.; Hachilif, R.; Gable, A.L.; Fang, T.; Doncheva, N.T.; Pyysalo, S. The STRING database in 2023: Protein–protein association networks and functional enrichment analyses for any sequenced genome of interest. Nucleic Acids Res. 2023, 51, D638–D646. [Google Scholar] [CrossRef]
- Stark, C.; Breitkreutz, B.-J.; Reguly, T.; Boucher, L.; Breitkreutz, A.; Tyers, M. BioGRID: A general repository for interaction datasets. Nucleic Acids Res. 2006, 34 (Suppl. S1), D535–D539. [Google Scholar] [CrossRef] [PubMed]
- Xenarios, I.; Rice, D.W.; Salwinski, L.; Baron, M.K.; Marcotte, E.M.; Eisenberg, D. DIP: The database of interacting proteins. Nucleic Acids Res. 2000, 28, 289–291. [Google Scholar] [CrossRef] [PubMed]
- Keshava Prasad, T.; Goel, R.; Kandasamy, K.; Keerthikumar, S.; Kumar, S.; Mathivanan, S.; Telikicherla, D.; Raju, R.; Shafreen, B.; Venugopal, A. Human protein reference database—2009 update. Nucleic Acids Res. 2009, 37 (Suppl. S1), D767–D772. [Google Scholar] [CrossRef]
- Orchard, S.; Ammari, M.; Aranda, B.; Breuza, L.; Briganti, L.; Broackes-Carter, F.; Campbell, N.H.; Chavali, G.; Chen, C.; Del-Toro, N. The MIntAct project—IntAct as a common curation platform for 11 molecular interaction databases. Nucleic Acids Res. 2014, 42, D358–D363. [Google Scholar] [CrossRef]
- Licata, L.; Briganti, L.; Peluso, D.; Perfetto, L.; Iannuccelli, M.; Galeota, E.; Sacco, F.; Palma, A.; Nardozza, A.P.; Santonico, E. MINT, the molecular interaction database: 2012 update. Nucleic Acids Res. 2012, 40, D857–D861. [Google Scholar] [CrossRef]
- Mewes, H.W.; Ruepp, A.; Theis, F.; Rattei, T.; Walter, M.; Frishman, D.; Suhre, K.; Spannagl, M.; Mayer, K.F.; Stümpflen, V. MIPS: Curated databases and comprehensive secondary data resources in 2010. Nucleic Acids Res. 2011, 39 (Suppl. S1), D220–D224. [Google Scholar] [CrossRef]
- Consortium, U. UniProt: A hub for protein information. Nucleic Acids Res. 2015, 43, D204–D212. [Google Scholar] [CrossRef]
- Barretina, J.; Caponigro, G.; Stransky, N.; Venkatesan, K.; Margolin, A.A.; Kim, S.; Wilson, C.J.; Lehar, J.; Kryukov, G.V.; Sonkin, D.; et al. The Cancer Cell Line Encyclopedia enables predictive modelling of anticancer drug sensitivity. Nature 2012, 483, 603–607. [Google Scholar] [CrossRef]
- Harris, M.A.; Clark, J.; Ireland, A.; Lomax, J.; Ashburner, M.; Foulger, R.; Eilbeck, K.; Lewis, S.; Marshall, B.; Mungall, C.; et al. The Gene Ontology (GO) database and informatics resource. Nucleic Acids Res. 2004, 32, D258–D261. [Google Scholar] [CrossRef]
- Edera, A.A.; Milone, D.H.; Stegmayer, G. Anc2vec: Embedding gene ontology terms by preserving ancestors relationships. Brief. Bioinform. 2022, 23, bbac003. [Google Scholar] [CrossRef] [PubMed]
- Szklarczyk, D.; Santos, A.; Von Mering, C.; Jensen, L.J.; Bork, P.; Kuhn, M. STITCH 5: Augmenting protein–chemical interaction networks with tissue and affinity data. Nucleic Acids Res. 2016, 44, D380–D384. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Srivast, G.; Ramanujam, J.; Brylinski, M. Augmented drug combination dataset to improve the performance of machine learning models predicting synergistic anticancer effects. Sci. Rep. 2024, 14, 1668. [Google Scholar] [CrossRef] [PubMed]
- Lyu, J.; Irwin, J.J.; Shoichet, B.K. Modeling the expansion of virtual screening libraries. Nat. Chem. Biol. 2023, 19, 712–718. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis for Special Types of Data; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Liu, H.; Zhang, W.; Zou, B.; Wang, J.; Deng, Y.; Deng, L. DrugCombDB: A comprehensive database of drug combinations toward the discovery of combinatorial therapy. Nucleic Acids Res. 2020, 48, D871–D881. [Google Scholar] [PubMed]
- Pu, L.; Singha, M.; Wu, H.-C.; Busch, C.; Ramanujam, J.; Brylinski, M. An integrated network representation of multiple cancer-specific data for graph-based machine learning. NPJ Syst. Biol. Appl. 2022, 8, 14. [Google Scholar] [CrossRef]
- Gross, J.L.; Yellen, J.; Anderson, M. Graph Theory and Its Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Li, G.; Xiong, C.; Thabet, A.; Ghanem, B. Deepergcn: All you need to train deeper gcns. arXiv 2020, arXiv:2006.07739. [Google Scholar]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.-I.; Jegelka, S. Representation learning on graphs with jumping knowledge networks. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5453–5462. [Google Scholar]
- Wang, X.; Zhu, H.; Jiang, Y.; Li, Y.; Tang, C.; Chen, X.; Li, Y.; Liu, Q.; Liu, Q. PRODeepSyn: Predicting anticancer synergistic drug combinations by embedding cell lines with protein–protein interaction network. Brief. Bioinform. 2022, 23, bbab587. [Google Scholar] [CrossRef]
- Pu, L.; Singha, M.; Ramanujam, J.; Brylinski, M. CancerOmicsNet: A multi-omics network-based approach to anti-cancer drug profiling. Oncotarget 2022, 13, 695. [Google Scholar] [CrossRef]

| Graph Property | Full-Size Graphs | Reduced Graphs |
|---|---|---|
| Number of nodes | 18,997 | 1372 ± 195 |
| Number of edges | 697,185 | 4204 ± 3083 |
| Average node degree | 73.40 | 5.78 ± 2.90 |
| Graph density | 0.00386 | 0.00408 ± 0.00135 |
| Graph diameter | 9 | 6 |
| Ratio of druggable/non-druggable nodes | 3.1 | 0.29 ± 0.15 |
| Classifier | Dataset | AUC | BAC | PPV | FPR | MCC | ΔBAC |
|---|---|---|---|---|---|---|---|
| RF | Original | 0.612 | 0.572 | 0.800 | 0.635 | 0.142 | 0.222 |
| Combined | 0.678 | 0.599 | 0.807 | 0.711 | 0.243 | 0.336 | |
| SynerGNet | Original | 0.721 | 0.676 | 0.863 | 0.380 | 0.313 | 0.032 |
| Combined | 0.790 | 0.734 | 0.892 | 0.307 | 0.423 | 0.075 | |
| PRODeepSyn | Original | 0.819 | 0.724 | 0.927 | 0.156 | 0.379 | 0.066 |
| Combined | 0.838 | 0.730 | 0.931 | 0.147 | 0.389 | 0.089 |
| Tissue | AUC | BAC | PPV | FPR | MCC |
|---|---|---|---|---|---|
| Breast | 0.778 | 0.698 | 0.869 | 0.418 | 0.375 |
| Digestive system | 0.683 | 0.637 | 0.807 | 0.473 | 0.265 |
| Excretory system | 0.793 | 0.710 | 0.831 | 0.288 | 0.402 |
| Respiratory system | 0.768 | 0.653 | 0.908 | 0.593 | 0.297 |
| Other | 0.843 | 0.720 | 0.883 | 0.140 | 0.518 |
| Classifier | Training Set | AUC | BAC | PPV | FPR | MCC |
|---|---|---|---|---|---|---|
| SynerGNet | Original | 0.595 | 0.485 | 0.103 | 0.531 | −0.019 |
| Combined | 0.748 | 0.633 | 0.143 | 0.735 | 0.195 | |
| PRODeepSyn | Original | 0.159 | 0.308 | 0.036 | 0.551 | −0.239 |
| Combined | 0.092 | 0.437 | 0.096 | 0.959 | −0.172 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Srivastava, G.; Ramanujam, J.; Brylinski, M. SynerGNet: A Graph Neural Network Model to Predict Anticancer Drug Synergy. Biomolecules 2024, 14, 253. https://doi.org/10.3390/biom14030253
Liu M, Srivastava G, Ramanujam J, Brylinski M. SynerGNet: A Graph Neural Network Model to Predict Anticancer Drug Synergy. Biomolecules. 2024; 14(3):253. https://doi.org/10.3390/biom14030253
Chicago/Turabian StyleLiu, Mengmeng, Gopal Srivastava, J. Ramanujam, and Michal Brylinski. 2024. "SynerGNet: A Graph Neural Network Model to Predict Anticancer Drug Synergy" Biomolecules 14, no. 3: 253. https://doi.org/10.3390/biom14030253
APA StyleLiu, M., Srivastava, G., Ramanujam, J., & Brylinski, M. (2024). SynerGNet: A Graph Neural Network Model to Predict Anticancer Drug Synergy. Biomolecules, 14(3), 253. https://doi.org/10.3390/biom14030253







