A Novel Error Sensitivity Analysis Method for a Parallel Spindle Head
Abstract
:1. Introduction
2. Configuration and Error Modeling
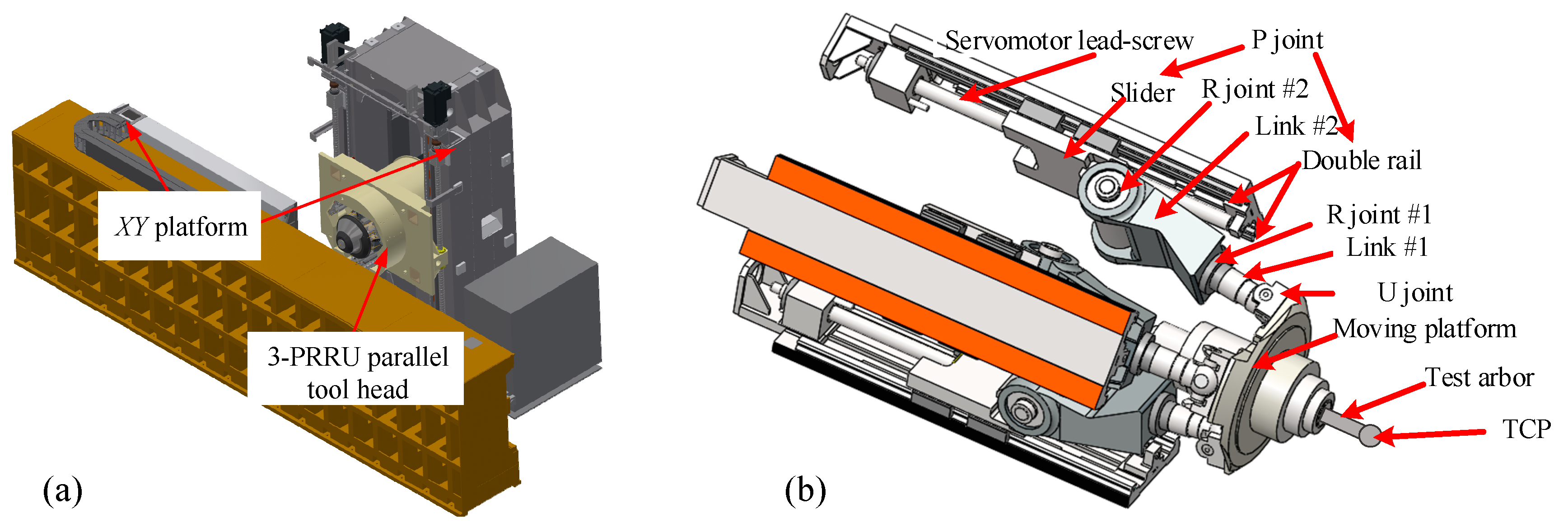
2.1. Configuration
2.2. TCP Position Error Modeling
3. Definition of Sensitivity Indices
3.1. Introduction of the Sensitivity Indices
3.2. Definition of the Sensitivity Indices
| Algorithm 1: LSI solving algorithm based on Monte Carlo method |
| INPUT: dr, L, Le, N, q |
| Begin |
| Step 1. Solve the coordinates of the points A1, B1, A2, and B2 corresponding to dr and q based on the error kinematic model. |
| Step 2. Solve for n, a, and b according to Equations (12)–(15). |
| Step 3. Randomly generate N points inside the least outer cuboid according to Equation (16). |
| Step 4. Determine the number m of points within Ω1 and the number n of points in the region where Ω1 intersects with Ω2 among the N points according to Equations (18) and (19). |
| Step 5. Then, the LSI corresponding to the error parameter dr and input vector q can be expressed as wi = 1 − n/m. |
4. Error Sensitivity Analysis of the 3-DOF Parallel Spindle Head
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Slamani, M.; Mayer, R.; Balazinski, M.; Zargarbashi, S.H.; Engin, S.; Lartigue, C. Dynamic and geometric error assessment of an XYC axis subset on five-axis high-speed machine tools using programmed end point constraint measurements. Int. J. Adv. Manuf. Technol. 2010, 50, 1063–1073. [Google Scholar] [CrossRef]
- Lee, R.S.; She, C.H. Developing a postprocessor for three types of five-axis machine tools. Int. J. Adv. Manuf. Technol. 1997, 13, 658–665. [Google Scholar] [CrossRef]
- El-Khasawneh, B.S.; Ferreira, P.M. Computation of stiffness and stiffness bounds for parallel link manipulators. Int. J. Mach. Tools Manuf. 1999, 39, 321–342. [Google Scholar] [CrossRef]
- Briot, S.; Bonev, I.A. Accuracy analysis of 3-DOF planar parallel robots. Mech. Mach. Theory 2008, 43, 445–458. [Google Scholar] [CrossRef]
- Laliberté, T.; Gosselin, C.M.; Jean, M. Static balancing of 3-DOF planar parallel mechanisms. IEEE-ASME Trans. Mechatron. 1999, 4, 363–377. [Google Scholar] [CrossRef]
- Burghardt, A.; Szybicki, D.; Kurc, K.; Muszyñska, M.; Mucha, J. Experimental study of Inconel 718 surface treatment by edge robotic deburring with force control. Strength Mater. 2017, 49, 594–604. [Google Scholar] [CrossRef]
- Khanghah, S.P.; Boozarpoor, M.; Lotfi, M.; Teimouri, R. Optimization of micro-milling parameters regarding burr size minimization via RSM and simulated annealing algorithm. Trans. Indian Inst. Met. 2015, 68, 897–910. [Google Scholar] [CrossRef]
- Burghardt, A.; Szybicki, D.; Kurc, K.; Muszyńska, M. Optimization of process parameters of edge robotic deburring with force control. Int. J. Appl. Mech. Eng. 2016, 21, 987–995. [Google Scholar] [CrossRef]
- Ramesh, R.; Mannan, M.A.; Poo, A.N. Error compensation in machine tools—A review: Part I: Geometric, cutting-force induced and fixture-dependent errors. Int. J. Mach. Tools Manuf. 2000, 40, 1235–1256. [Google Scholar] [CrossRef]
- Ramesh, R.; Mannan, M.A.; Poo, A.N. Error compensation in machine tools—A review: Part II: Thermal errors. Int. J. Mach. Tools Manuf. 2000, 40, 1257–1284. [Google Scholar] [CrossRef]
- Khan, A.W.; Chen, W. A methodology for systematic geometric error compensation in five-axis machine tools. Int. J. Adv. Manuf. Technol. 2011, 53, 615–628. [Google Scholar] [CrossRef]
- Chanal, H.; Duc, E.; Ray, P.; Hascoet, J.Y. A new approach for the geometrical calibration of parallel kinematics machines tools based on the machining of a dedicated part. Int. J. Mach. Tools Manuf. 2007, 47, 1151–1163. [Google Scholar] [CrossRef]
- Majarena, A.C.; Santolaria, J.; Samper, D.; Aguilar, J.J. An overview of kinematic and calibration models using internal/external sensors or constraints to improve the behavior of spatial parallel mechanisms. Sensors 2010, 10, 10256–10297. [Google Scholar] [CrossRef]
- Li, Q.; Wang, W.; Jiang, Y.; Li, H.; Zhang, J.; Jiang, Z. A sensitivity method to analyze the volumetric error of five-axis machine tool. Int. J. Adv. Manuf. Technol. 2018, 98, 1791–1805. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Wang, S.; Du, H.; Chai, B.; Hu, S.J. Active precision design for complex machine tools: Methodology and case study. Int. J. Adv. Manuf. Technol. 2015, 80, 581–590. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Yu, G.; Li, W. A new calibration method for hybrid machine tools using virtual tool center point position constraint. Measurement 2021, 181, 109582. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Yu, G.; Li, W.; Kong, X. A multiple test arbors-based calibration method for a hybrid machine tool. Robot. Comput.-Integr. Manuf. 2023, 80, 102480. [Google Scholar] [CrossRef]
- Tian, W.; Gao, W.; Zhang, D.; Huang, T. A general approach for error modeling of machine tools. Int. J. Mach. Tools Manuf. 2014, 79, 17–23. [Google Scholar] [CrossRef]
- Lee, S.; Zeng, Q.; Ehmann, K.F. Error modeling for sensitivity analysis and calibration of the tri-pyramid parallel robot. Int. J. Adv. Manuf. Technol. 2017, 93, 1319–1332. [Google Scholar] [CrossRef]
- Cui, H.; Zhu, Z.; Gan, Z.; Brogardh, T. Kinematic analysis and error modeling of TAU parallel robot. Robot. Comput.-Integr. Manuf. 2005, 21, 497–505. [Google Scholar] [CrossRef]
- Tian, W.; Mou, M.; Yang, J.; Yin, F. Kinematic calibration of a 5-DOF hybrid kinematic machine tool by considering the ill-posed identification problem using regularisation method. Robot. Comput.-Integr. Manuf. 2019, 60, 49–62. [Google Scholar] [CrossRef]
- Sun, T.; Zhai, Y.; Song, Y.; Zhang, J. Kinematic calibration of a 3-DoF rotational parallel manipulator using laser tracker. Robot. Comput.-Integr. Manuf. 2016, 41, 78–91. [Google Scholar] [CrossRef]
- Vischer, P.; Clavel, R. Kinematic calibration of the parallel Delta robot. Robotica 1998, 16, 207–218. [Google Scholar] [CrossRef]
- Huang, P.; Wang, J.; Wang, L.; Yao, R. Kinematical calibration of a hybrid machine tool with regularization method. Int. J. Mach. Tools Manuf. 2011, 51, 210–220. [Google Scholar] [CrossRef]
- Niu, P.; Cheng, Q.; Liu, Z.; Chu, H. A machining accuracy improvement approach for a horizontal machining center based on analysis of geometric error characteristics. Int. J. Adv. Manuf. Technol. 2021, 112, 2873–2887. [Google Scholar] [CrossRef]
- Sun, Y.; Lueth, T.C. Safe manipulation in robotic surgery using compliant constant-force mechanism. IEEE Trans. Med. Robot. Bionics 2023, 5, 486–495. [Google Scholar] [CrossRef]
- Zhang, S.; He, C.; Liu, X.; Xu, J.; Sun, Y. Kinematic chain optimization design based on deformation sensitivity analysis of a five-axis machine tool. Int. J. Precis. Eng. Manuf. 2020, 21, 2375–2389. [Google Scholar] [CrossRef]
- Guo, S.; Mei, X.; Jiang, G. Geometric accuracy enhancement of five-axis machine tool based on error analysis. Int. J. Adv. Manuf. Technol. 2019, 105, 137–153. [Google Scholar] [CrossRef]
- Patel, A.J.; Ehmann, K.F. Volumetric error analysis of a Stewart platform-based machine tool. CIRP Ann. 1997, 46, 287–290. [Google Scholar] [CrossRef]
- Fan, K.C.; Wang, H.; Zhao, J.W.; Chang, T.H. Sensitivity analysis of the 3-PRS parallel kinematic spindle platform of a serial-parallel machine tool. Int. J. Mach. Tools Manuf. 2003, 43, 1561–1569. [Google Scholar] [CrossRef]
- Jiang, S.; Chi, C.; Fang, H.; Tang, T.; Zhang, J. A minimal-error-model based two-step kinematic calibration methodology for redundantly actuated parallel manipulators: An application to a 3-DOF spindle head. Mech. Mach. Theory 2022, 167, 104532. [Google Scholar] [CrossRef]
- Du, X.; Wang, B.; Zheng, J. Geometric Error Analysis of a 2UPR-RPU Over-Constrained Parallel Manipulator. Machines 2022, 10, 990. [Google Scholar] [CrossRef]
- Chen, G.; Liang, Y.; Sun, Y.; Chen, W.; Wang, B. Volumetric error modeling and sensitivity analysis for designing a five-axis ultra-precision machine tool. Int. J. Adv. Manuf. Technol. 2013, 68, 2525–2534. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhao, H.; Zhang, G.; Gu, P.; Cai, L. An analytical approach for crucial geometric errors identification of multi-axis machine tool based on global sensitivity analysis. Int. J. Adv. Manuf. Technol. 2014, 75, 107–121. [Google Scholar] [CrossRef]
- Cheng, Q.; Sun, B.; Liu, Z.; Li, J.; Dong, X.; Gu, P. Key geometric error extraction of machine tool based on extended Fourier amplitude sensitivity test method. Int. J. Adv. Manuf. Technol. 2017, 90, 3369–3385. [Google Scholar] [CrossRef]
- Li, T.; Li, F.; Jiang, Y.; Wang, H.; Zhang, J. Error modeling and sensitivity analysis of a 3-P (Pa) S parallel type spindle head with parallelogram structure. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417715012. [Google Scholar] [CrossRef]
- Bonev, I.A. Geometric Analysis of Parallel Mechanisms; Université Laval: Québec, QC, Canada, 2002. [Google Scholar]
- Xie, F.; Liu, X.J.; Wang, J. A 3-DOF parallel manufacturing module and its kinematic optimization. Robot. Comput.-Integr. Manuf. 2012, 28, 334–343. [Google Scholar] [CrossRef]
- Guo, S.; Jiang, G. Investigation of sensitivity analysis and compensation parameter optimization of geometric error for five-axis machine tool. Int. J. Adv. Manuf. Technol. 2017, 93, 3229–3243. [Google Scholar] [CrossRef]
- Li, J.; Xie, F.; Liu, X.J. Geometric error modeling and sensitivity analysis of a five-axis machine tool. Int. J. Adv. Manuf. Technol. 2016, 82, 2037–2051. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, G.; Chen, W.; Sun, Y.; Chen, J. Analysis of volumetric error of machine tool based on Monte Carlo method. J. Comput. Theor. Nanosci. 2013, 10, 1290–1295. [Google Scholar] [CrossRef]








| Case | Critical Geometric Errors | Other Geometric Errors |
|---|---|---|
| 1 | Keep the initial value unchanged | Keep the initial value unchanged |
| 2 | Reduce by half | Keep the initial value unchanged |
| 3 | Keep the initial value unchanged | Reduce by half |
| 4 | Reduce by half | Reduce by half |
| Case | R/mm | Le/mm |
|---|---|---|
| a | 6 | 25 |
| b | 6 | 45 |
| c | 8 | 25 |
| d | 8 | 45 |
| e | 12 | 25 |
| f | 12 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Li, M.; Yu, G. A Novel Error Sensitivity Analysis Method for a Parallel Spindle Head. Robotics 2023, 12, 129. https://doi.org/10.3390/robotics12050129
Wang L, Li M, Yu G. A Novel Error Sensitivity Analysis Method for a Parallel Spindle Head. Robotics. 2023; 12(5):129. https://doi.org/10.3390/robotics12050129
Chicago/Turabian StyleWang, Liping, Mengyu Li, and Guang Yu. 2023. "A Novel Error Sensitivity Analysis Method for a Parallel Spindle Head" Robotics 12, no. 5: 129. https://doi.org/10.3390/robotics12050129
APA StyleWang, L., Li, M., & Yu, G. (2023). A Novel Error Sensitivity Analysis Method for a Parallel Spindle Head. Robotics, 12(5), 129. https://doi.org/10.3390/robotics12050129





