Instantaneous Kinematics and Free-from-Singularity Workspace of 3-XXRRU Parallel Manipulators
Abstract
1. Introduction
- (i)
- Identification of singularity conditions without the need to reference a specific actuation system;
- (ii)
- Introduction of two dimensionless performance indices ranging from 0 to 1;
- (iii)
- Determination of the optimal actuation system;
- (iv)
- Demonstration that suitably sized and actuated 3-XXRRU PMs offer a broad, singularity-free workspace that is fully isotropic.
2. Materials and Methods
2.1. Input–Output Instantaneous Relationship
2.2. Singularity Analysis
2.3. Evaluation of Kinetostatic Performance
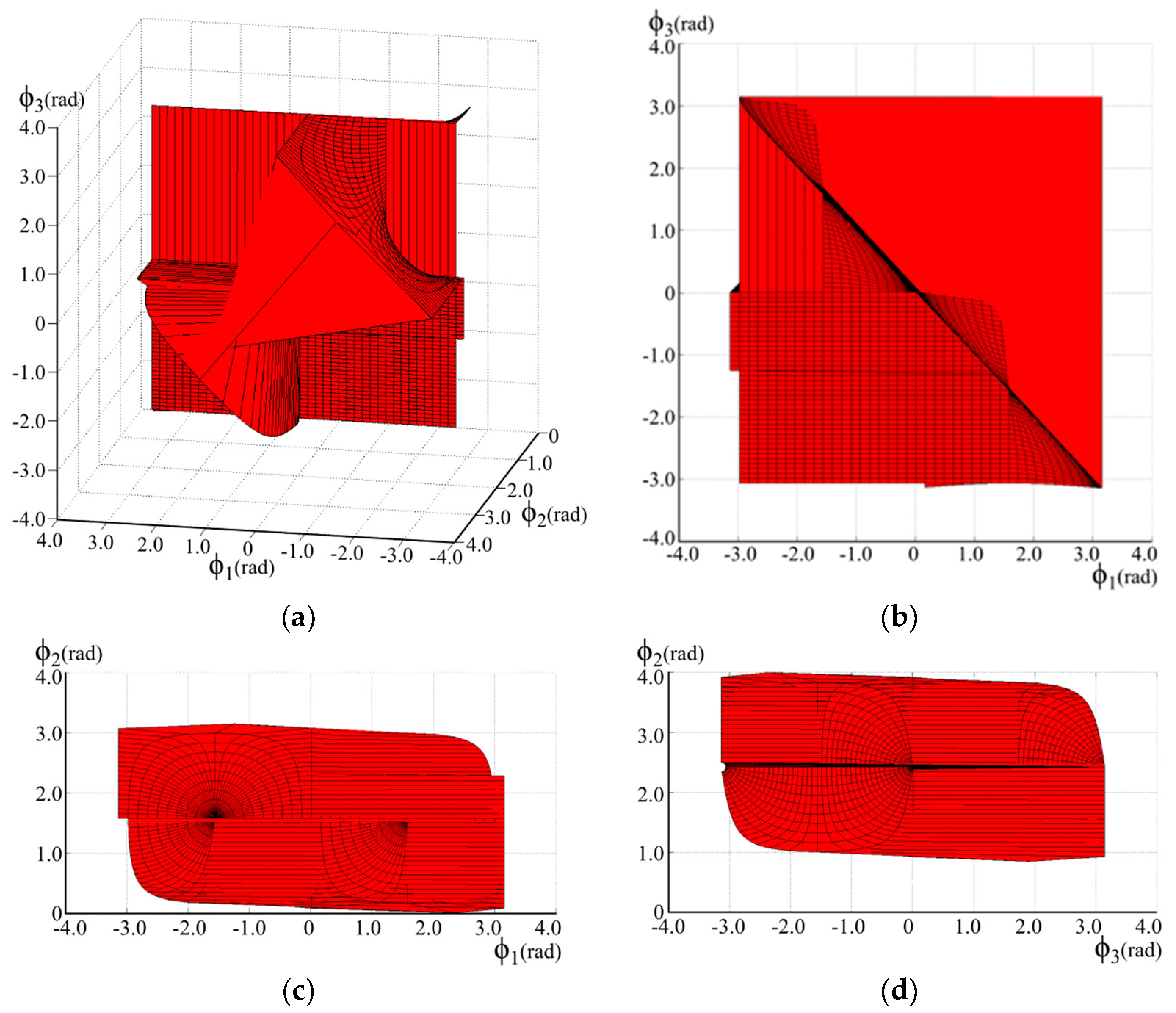
3. Results
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Merlet, J.-P. Parallel Robots; Springer: Berlin/Heidelberg, Germany, 2000; ISBN 978-1-4020-0385-1. [Google Scholar]
- Tsai, L.-W. Mechanism Design: Enumeration of Kinematic Structures According to Function; CRC Press: London, UK, 2001; ISBN 978-0-8493-0901-4. [Google Scholar]
- Tsai, L.-W. Robot Analysis: The Mechanics of Serial and Parallel Manipulators; John Wiley & Sons: New York, NY, USA, 1999; ISBN 978-0-4713-2593-2. [Google Scholar]
- Meng, J.; Liu, G.; Li, Z. A geometric theory for analysis and synthesis of sub-6 DoF parallel manipulators. IEEE Trans. Robot. 2007, 23, 625–649. [Google Scholar] [CrossRef]
- Lin, R.; Guo, W.; Gao, F. Type Synthesis of a Family of Novel Four, Five, and Six Degrees-of-Freedom Sea Lion Ball Mechanisms With Three Limbs. ASME J. Mech. Robot. 2016, 8, 021023. [Google Scholar] [CrossRef]
- Cleary, K.; Brooks, T. Kinematic analysis of a novel 6-DOF parallel manipulator. In Proceedings of the 1993 IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; Volume 1, pp. 708–713. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, I.-M.; Yang, G. Kinematic design of a family of 6-DOF partially decoupled parallel manipulators. Mech. Mach. Theory 2009, 44, 912–922. [Google Scholar] [CrossRef]
- Coppola, G.; Zhang, D.; Liu, K. A 6-DOF reconfigurable hybrid parallel manipulator. Robot. Comput. Integr. Manuf. 2014, 30, 99–106. [Google Scholar] [CrossRef]
- Monsarrat, B.; Gosselin, C.M. Workspace analysis and optimal design of a 3-leg 6-DOF parallel platform mechanism. IEEE Trans. Robot. Autom. 2003, 19, 954–966. [Google Scholar] [CrossRef]
- Angeles, J.; Yang, G.; Chen, I.-M. Singularity analysis of three-legged, six-dof platform manipulators with URS legs. IEEE/ASME Trans. Mechatron. 2003, 8, 469–475. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, D. Novel Design of a 3-RRUU 6-DOF Parallel Manipulator. IOP Conf. Ser. Mater. Sci. Eng. 2019, 491, 012006. [Google Scholar] [CrossRef]
- Fu, J.; Gao, F. Optimal design of a 3-leg 6-DOF parallel manipulator for a specific workspace. Chin. J. Mech. Eng. 2016, 29, 659–668. [Google Scholar] [CrossRef]
- Seward, N.; Bonev, I.A. A new 6-DOF parallel robot with simple kinematic model. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4061–4066. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, P.; Hou, Z.; Hu, B.; Sui, C.; Han, J. Kinetostatic analysis of a novel 6-DoF 3UPS parallel manipulator with multi-fingers. Mech. Mach. Theory 2014, 78, 36–50. [Google Scholar] [CrossRef]
- Simas, H.; Meneghini, L.; Di Gregorio, R.; Simoni, R. Position Analysis of a Novel Family of three-legged 6-DOF Parallel Manipulators of type 3-XXRRU. In Advances in Mechanism and Machine Science: Proceedings of the 16th IFToMM World Congress 2023 [WC2023], Tokyo, Japan, 5–10 November 2023; Okada, M., Ed.; Paper No.: 147; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Gosselin, C.M.; Angeles, J. Singularity analysis of closed-loop kinematic chains. IEEE Trans. Robot. Automat. 1990, 6, 281–290. [Google Scholar] [CrossRef]
- Ma, O.; Angeles, J. Architecture singularities of platform manipulators. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 1542–1547. [Google Scholar]
- Zlatanov, D.; Fenton, R.G.; Benhabib, B. A unifying framework for classification and interpretation of mechanism singularities. ASME J. Mech. Des. 1995, 117, 566–572. [Google Scholar] [CrossRef]
- Zlatanov, D.; Bonev, I.A.; Gosselin, C.M. Constraint Singularities as C-Space Singularities. In Proceedings of the 8th International Symposium on Advances in Robot Kinematics (ARK 2002), Caldes de Malavella, Spain, 24–28 June 2002. [Google Scholar]
- Zlatanov, D.; Bonev, I.A.; Gosselin, C.M. Constraint singularities of parallel mechanisms. In Proceedings of the 2002 IEEE International Conference On Robotics & Automation, Washington, DC, USA, 11–15 May 2002; pp. 496–502. [Google Scholar]
- Hunt, K.H. Kinematic Geometry of Mechanisms; Oxford University Press: Oxford, UK, 1978. [Google Scholar]
- Davidson, J.K.; Hunt, K.H. Robots and Screw Theory: Applications of Kinematics and Statics to Robotics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Uicker, J., Jr.; Pennock, G.; Shigley, J. Theory of Machines and Mechanisms, 5th ed.; Oxforf University Press: Oxford, UK, 2016. [Google Scholar]
- Kim, H.S.; Tsai, L.-W. Evaluation of a Cartesian parallel manipulator. In Advances in Robot Kinematics; Lenarcic, J., Thomas, F., Eds.; Kluwer Academic Publishers: London, UK, 2002; pp. 21–28. [Google Scholar]
- Kim, H.S.; Tsai, L.-W. Design Optimization of a Cartesian Parallel Manipulator. ASME J. Mech. Des. 2003, 125, 43–51. [Google Scholar] [CrossRef]
- Silvester, J.R. Determinants of block matrices. Math. Gaz. 2000, 84, 460–467. [Google Scholar] [CrossRef]
- Sothanaphan, N. Determinants of block matrices with noncommuting blocks. Linear Algebra Its Appl. 2017, 512, 202–218. [Google Scholar] [CrossRef][Green Version]
- Angeles, J. Fundamentals of Robotic Mechanical Systems, 4th ed.; Springer: Cham, Switzerland, 2014; ISBN 978-3-319-30762-6. [Google Scholar]
- Hervé, J.M. Uncoupled actuation of pan-tilt wrists. IEEE Trans. Robot. 2006, 22, 56–64. [Google Scholar] [CrossRef]
- Li, Q.; Hervé, J.M.; Ye, W. Geometric Method for Type Synthesis of Parallel Manipulators; Springer: Singapore, 2020; pp. 223–238. ISBN 978-981-13-8754-8. [Google Scholar] [CrossRef]
| 1 | The sequence of capital letters indicates the types of joints or sub-mechanisms encountered by moving from the base to the platform along the limb. |
| 2 | It is worth noting that the input–output instantaneous relationship (IOR) of manipulators is always linear and homogeneous both in the actuated-joint rates (inputs) and in the platform twist (output) [16,18] since it is the time derivative of the mechanism constraint-equation system which is holonomic and time independent for manipulators. |
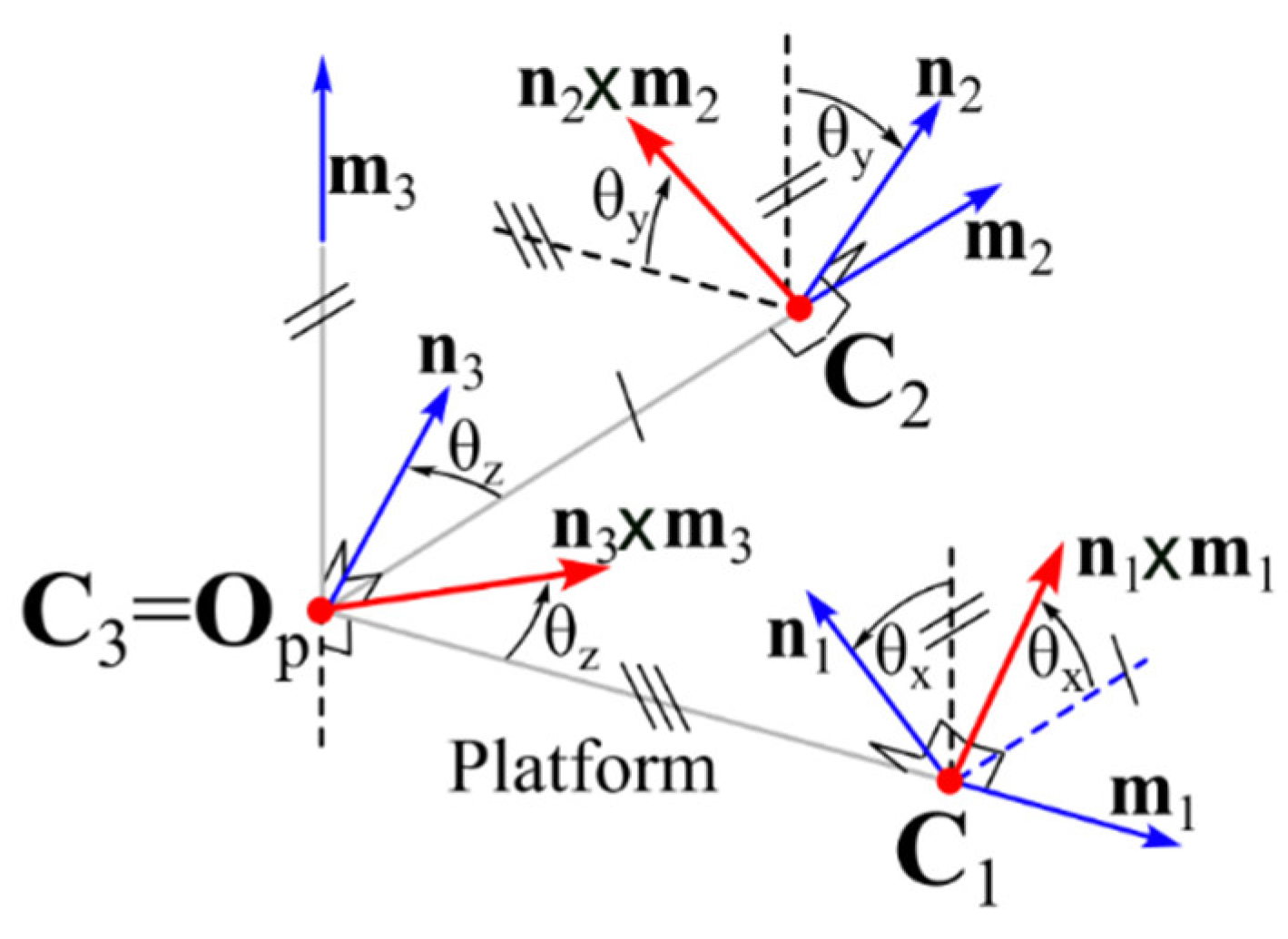
| 3 | It is worth noting that a U joint consists of two R-pairs in series with mutually orthogonal axes, which intersect one another at a point, named the center of the U joint. |
| 4 | The connectivity of a limb is by definition the DOF number of the kinematic chain constituted by platform and base uniquely connected by that limb. |
| 5 | Such a criterion counts the DOF number, l, of a spatial mechanism through the formula l = 6(m − 1) − (6 − i)ci where m is the number of rigid bodies and ci is the number of constraints with i DOF among the m bodies. |
| 6 | Hereafter, a line will be denoted (P, u) where P is a point belonging to the line and u is a unit vector parallel to the line. |
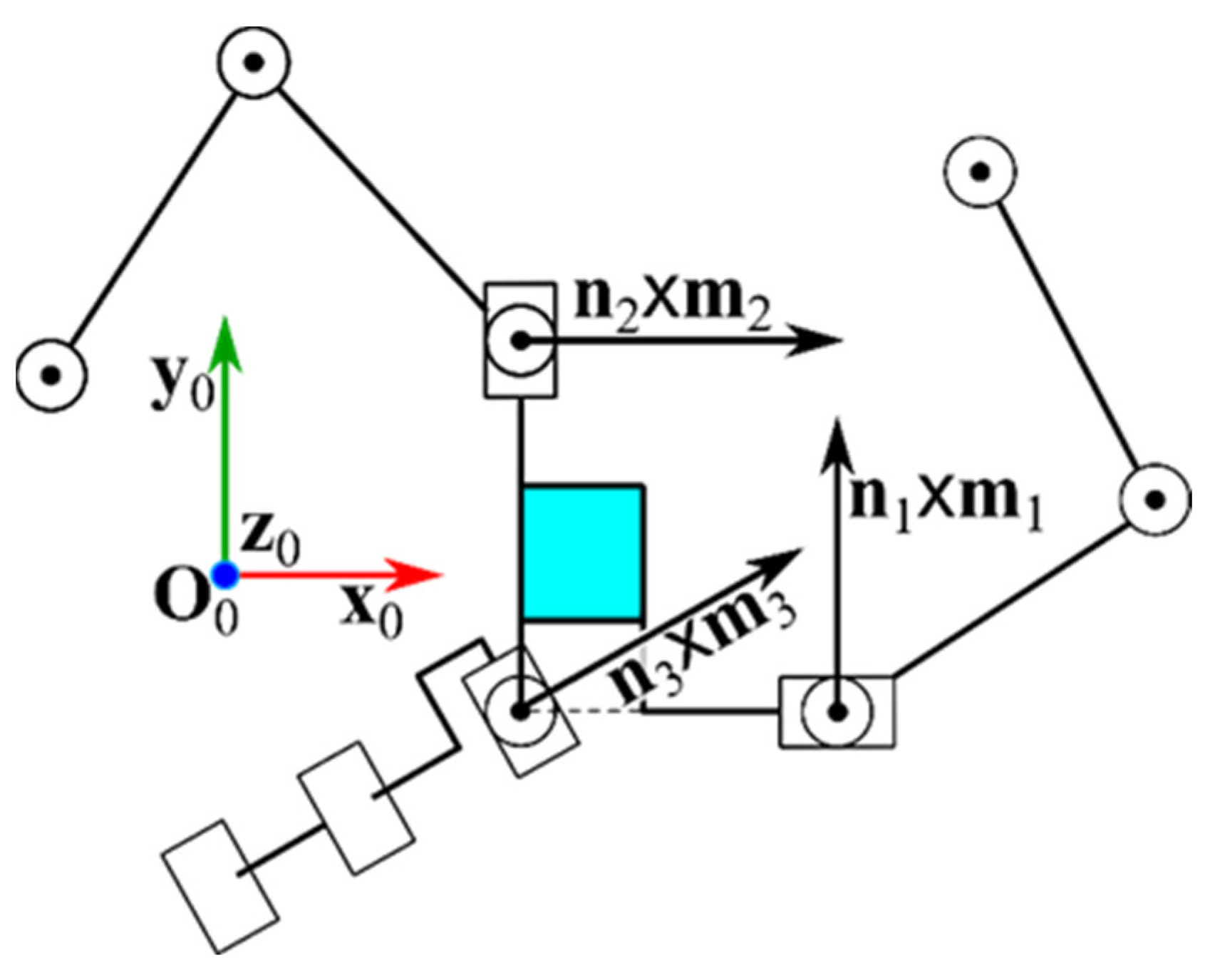
| 7 | With reference to Figure 1b, it is worth stressing that the positive direction, toward which the unit vectors ni and mi, for i = 1, 2, 3, point, is arbitrarily chosen and that it does not affect the values of jn and jn×m. |
| 8 | A PPS is a 2-DOF PM that is able to freely orientate one line fixed to its platform by keeping one point of the line fixed to the base. They are employed in many applications like the motion of a telescope or of a parabolic antenna, etc. |
| 9 | It is worth noting that a C-pair can be obtained by putting in series a prismatic (P) pair and an R-pair whose axis is parallel to the sliding direction of the P-pair and that such a PR chain is easy to actuate. In such a PR chain, the R-pair will be the first non-actuated R-pair of the remaining RRU chain of the XXRRU limb. |
| 10 | The spherical five-bar linkage is a particular PPS consisting of five binary links sequentially connected, to form a single-loop, through R-pairs whose axes share a common intersection point. This R-pair axes’ arrangement guarantees that their intersection point is fixed to the frame (i.e., the links’ motion is spherical) and that any line, which is fixed to a mobile link and passes through the above-mentioned intersection point, keeps that point at rest during the link motion. In Figure 10, the blue lines are the R-pair axes. |







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simas, H.; Di Gregorio, R.; Simoni, R. Instantaneous Kinematics and Free-from-Singularity Workspace of 3-XXRRU Parallel Manipulators. Robotics 2023, 12, 138. https://doi.org/10.3390/robotics12050138
Simas H, Di Gregorio R, Simoni R. Instantaneous Kinematics and Free-from-Singularity Workspace of 3-XXRRU Parallel Manipulators. Robotics. 2023; 12(5):138. https://doi.org/10.3390/robotics12050138
Chicago/Turabian StyleSimas, Henrique, Raffaele Di Gregorio, and Roberto Simoni. 2023. "Instantaneous Kinematics and Free-from-Singularity Workspace of 3-XXRRU Parallel Manipulators" Robotics 12, no. 5: 138. https://doi.org/10.3390/robotics12050138
APA StyleSimas, H., Di Gregorio, R., & Simoni, R. (2023). Instantaneous Kinematics and Free-from-Singularity Workspace of 3-XXRRU Parallel Manipulators. Robotics, 12(5), 138. https://doi.org/10.3390/robotics12050138







