Design and Characterization of a Self-Aligning End-Effector Robot for Single-Joint Arm Movement Rehabilitation

Abstract

Traditional end-effector robots for arm rehabilitation are usually attached at the hand, primarily focusing on coordinated multi-joint training. Therapy at an individual joint level of the arm for severely impaired stroke survivors is not always possible with existing end-effector robots. The Arm Rehabilitation Robot (AREBO)—an end-effector robot—was designed to provide both single and multi-joint assisted training while retaining the advantages of traditional end-effector robots, such as ease of use, compactness and portability, and potential cost-effectiveness (compared to exoskeletons). This work presents the design, optimization, and characterization of AREBO for training single-joint movements of the arm. AREBO has three actuated and three unactuated degrees of freedom, allowing it to apply forces in any arbitrary direction at its endpoint and self-align to arbitrary orientations within its workspace. AREBO’s link lengths were optimized to maximize its workspace and manipulability. AREBO provides single-joint training in both unassisted and adaptive weight support modes using a human arm model to estimate the human arm’s kinematics and dynamics without using additional sensors. The characterization of the robot’s controller and the algorithm for estimating the human arm parameters were performed using a two degrees of freedom mechatronic model of the human shoulder joint. The results demonstrate that (a) the movements of the human arm can be estimated using a model of the human arm and robot’s kinematics, (b) AREBO has similar transparency to that of existing arm therapy robots in the literature, and (c) the adaptive weight support mode control can adapt to different levels of impairment in the arm. This work demonstrates how an appropriately designed end-effector robot can be used for single-joint training, which can be easily extended to multi-joint training. Future work will focus on the evaluation of the system on patients with any neurological condition requiring arm training.

1. Introduction

Every year, around 12.2 million people suffer from stroke worldwide [1]. It is estimated that 82% of the needs of stroke survivors are unmet due to multiple reasons, including poor access to rehabilitation services and limited healthcare resources [2]. Increased focus on mobility soon after a stroke limits the amount of upper limb rehabilitation for recovery during the early sensitive period. Furthermore, 40% of stroke survivors are left with chronic upper limb impairments and activity limitations that impact their quality of life [3].

Rehabilitation robots were introduced to overcome some of these barriers by providing semi-supervised high-intensity training. Rehabilitation robots for the upper limb fall under two categories: (1) exoskeletons and (2) end-effectors. Exoskeletons, as the name suggests, are exterior skeletons that resemble the human limb segment’s anatomical structure to which they are attached. They are attached at multiple points on the arm to support both single and multi-joint training in a 3D space. Despite these advantages, exoskeletons are bulkier, can be more expensive because of the need for more actuators, and require a longer set-up time than end-effectors due to the strict alignment constraints of the human and the robot axes of rotation [4]. Some popular examples of upper limb exoskeletons include Anyexo [5], ARMin [6], Harmony [7], NESM-$\gamma$ [8], CURER [9], BiEXO [10], AGREE [11], and FLOAT [12].

End-effectors, however, are simpler robots than exoskeletons. They are attached to the arm only at one point (usually at the hand) and hence are easy to set up. However, most end-effectors are fully gravity-support planar robots (e.g., MIT Manus [13] and H-man [14] making them unsuitable for training 3D movements in a non-gravity-eliminated environment. Unlike exoskeletons, most end-effectors cannot

(a)

be used for providing assisted training in single-joint movements, which may be relevant for severely impaired patients;

(b)

track human limb kinematics while interacting with a human subject during therapy without the use of additional sensors. Previous work has demonstrated that RGB+D cameras [15] or body-worn inertial measurement units [16] can be used to track human limb kinematics by fusing information with the robot’s endpoint kinematics data.

Although both types of robots have their pros and cons, end-effector-based solutions have been more popular than exoskeletons owing to their simpler structure, potentially reduced cost due to fewer actuators, and ease of use [17]. The clinical utility of end-effector robots can be further improved if an end-effector robot with the following features can be developed:

(a)

capable of adaptive training of single- and multi-joint arm movements in 3D with titrated gravity support; single-joint movements would be suitable for severely affected patients, while coordinated multi-joint movements would be suitable for moderately impaired patients with sufficient strength but poor coordination.

(b)

ability to track the joint kinematics of the human arm to provide feedback and track progress.

Such a robot would be a versatile tool for administering a wide range of arm-therapy activities.

Recent work along this line is the EMU robot [18], which has a six degrees of freedom (DOFs) end-effector kinematic structure with two actuated and four unactuated DOFs. EMU was designed for assisted training of 3D arm movements with varying levels of gravity support, and the amount of weight support was estimated using a four DOFs model of the human arm. It is designed to assist 3D multi-joint arm movements against gravity using its two-actuated DOFs, which makes it unsuitable for single-joint movement training. Safe single-joint assisted training requires at least three actuated DOFs to apply force in any direction to cause the desired rotary movement of the (arbitrarily oriented) human limb while avoiding undesirable forces that push or pull the limb segment from the joint. We recently proposed the design of a self-aligning six DOFs end-effector robot, AREBO (Arm Rehabilitation Robot), which has three actuated and three unactuated DOFs [19]. The three actuated DOFs allow the robot to apply safe forces at its endpoint that result in pure rotational movements around a joint. The three unactuated DOFs allow it to align to arbitrary orientations within its workspace, which reduces the constraints on the relative position and orientation of the human subject with respect to the robot. This previous work focused on the exposition of the kinematic structure, its optimization, and the algorithm for estimating the human arm parameters for single-joint movements.

Physical human–robot interaction plays a crucial role in rehabilitation as it must promote recovery while ensuring safety. The control modes for this interaction can be broadly classified into three categories [20]: (1) assistive, (2) corrective, and (3) resistive modes. In the assistive mode, the robot’s controller compensates for the weakness in the arm and helps the user to complete the task. In the corrective mode, the robot’s control law restricts the abnormal movement patterns (due to synergy) observed in stroke subjects, thus enforcing a desired movement pattern. When the robot controller opposes the voluntary movements of the user, then it is operating in a resistive control mode. Any control mode that maximizes the patient’s voluntary participation is likely to be conducive to recovery; however, there is currently no strong evidence in support of any one control mode [21]. The choice of a control mode for training is based on the clinician’s decision, which is based on the nature of the patient’s sensorimotor impairments and needs. But a robot must at least have (a) a mode that allows patients to make voluntary movements without any hindrance (unassisted mode), and (b) an assistive mode that adapts to the patient’s capabilities.

In the current study, we present work on developing an end-effector robot to train single-joint movements with adaptive gravity support while tracking human joint kinematics without the use of additional sensors. This work extends our previous work [19] by (a) proposing a simplification to the previous kinematic structure, (b) designing, fabricating, and assembling a physical prototype of AREBO (Figure 1), and (c) developing and characterizing the robot controller for human–robot interaction during assisted training of the single-joint movements of the arm.

2. Methods

2.1. Kinematics

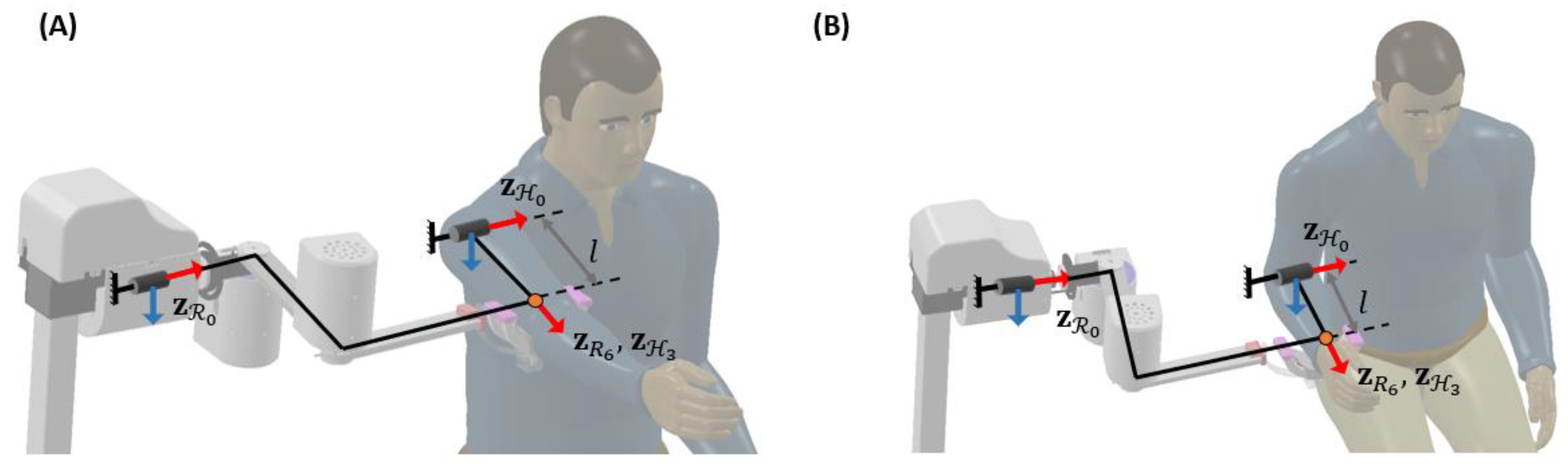
2.1.1. AREBO’s Kinematic Chain

AREBO was designed to have a six DOF kinematic chain (Figure 2) to provide flexibility in attaching the arm to the robot. The three proximal DOFs are actuated, which can control the 3D position of the robot’s endpoint, while the three distal DOFs of the robot are unactuated, forming a spherical joint centered around the robot’s endpoint, which forms the robot’s unactuated segment (Figure 2). Let ${\mathcal{R}}_0$ be the base frame of the robot that is fixed to the earth and let ${\mathcal{R}}_1, {\mathcal{R}}_2, \dots , {\mathcal{R}}_6$ represent the local reference frames attached to each DOF of the robot. AREBO has six generalized coordinates corresponding to its six DOF, $\mathsf{\theta }={\left[\begin{array}{cccc}{\theta }_1& {\theta }_2& \dots & {\theta }_6\end{array}\right]}^T\in {[-\pi , \pi )}^6$. Figure 2 depicts AREBO’s kinematic chain along with its Denavit–Hartenberg (DH) parameters for the transformation between subsequent local reference frames. The origin of the ${\mathcal{R}}_6$ reference frame $\left({\mathbf{p}}_r\in R^3\right)$ is referred to as the robot’s endpoint, which is a function of the first three generalized coordinates (${\theta }_1, {\theta }_2,{\theta }_3$) and the link lengths ($r_1, r_2$). The ${\mathcal{R}}_6$ reference frame’s orientation ${\mathbf{R}}_{{\mathcal{R}}_6}^{{\mathcal{R}}_0}\in SO(3)$ depends on all six generalized coordinates $\mathsf{\theta }$. Refer to the Supplementary Material for the detailed forward and inverse kinematics of the robot.

The current design has the same kinematic structure as the one proposed by [19], except for one modification to the unactuated segment of the robot. In [19], the axes of the three unactuated DOFs (${\mathcal{R}}_4, {\mathcal{R}}_5, {\mathcal{R}}_6$) did not coincide, which led to translations of the arm that cannot be controlled by the robot. Thus, this was modified in the current design to form a spherical joint at the endpoint, as shown in Figure 2, which addresses this issue.

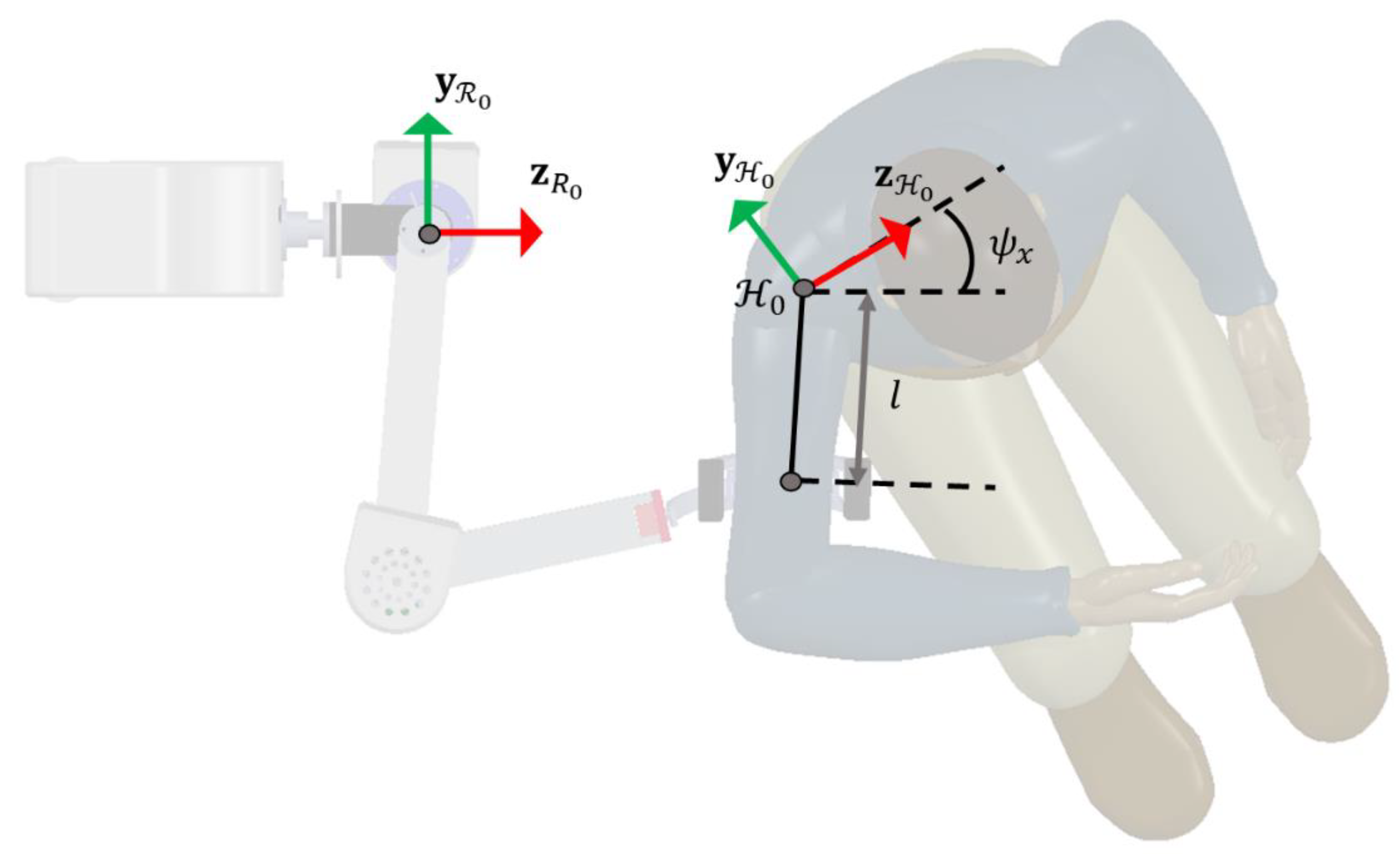
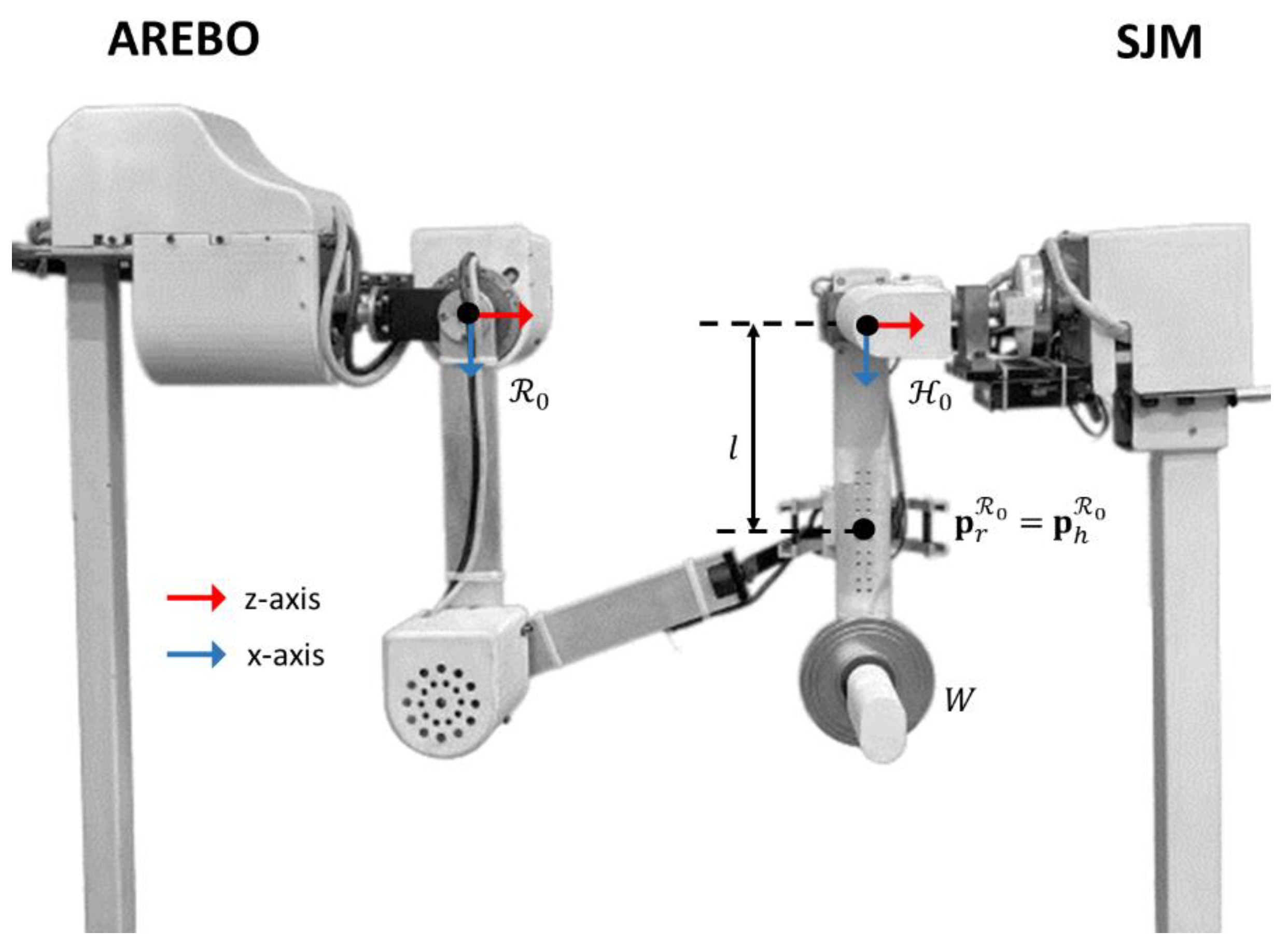
2.1.2. Human–Robot Closed Loop Kinematic Chain

A closed-loop kinematic chain is formed by rigidly attaching the robot to the human arm (the upper arm or the forearm as shown in Figure 3). The human shoulder was modeled as a spherical joint replicating the shoulder articulation as shown in Figure 4. The reference frame ${\mathcal{H}}_0$ is the human base frame (attached to the trunk or the upper arm as shown in Figure 3), while the three reference frames ${\mathcal{H}}_1$, ${\mathcal{H}}_2$, and ${\mathcal{H}}_3$ are the local reference frames corresponding to the three DOFs of the human arm. The three generalized coordinates of the human arm are given by $\mathsf{\varphi }={\left[\begin{array}{ccc}{\varphi }_1& {\varphi }_2& {\varphi }_3\end{array}\right]}^T\in {[-\pi , \pi )}^3$. The origin of the ${\mathcal{H}}_3$ reference frame is referred to as the endpoint of the arm $\left({\mathbf{p}}_h\in {\mathbb{R}}^3\right),$ and its orientation is given by ${\mathbf{R}}_{{\mathcal{H}}_3}^{{\mathcal{H}}_0}\in SO(3)$.

We make the following assumptions on how the robot is connected to the human arm:

• The human base frame ${\mathcal{H}}_0$ is located close enough to the robot’s base frame ${\mathcal{R}}_0$ such that the intersection between the robot and human arm workspaces has a non-zero area.
• The endpoint of the arm is attached to the spherical joint at the robot’s endpoint, such that ${\mathbf{p}}_r^{{\mathcal{R}}_0}={\mathbf{p}}_h^{{\mathcal{R}}_0}$, where ${\mathbf{p}}_r^{{\mathcal{R}}_0}$ and ${\mathbf{p}}_h^{{\mathcal{R}}_0}$ are the positions of the robot and arm endpoints with respect to the robot’s base reference frame ${\mathcal{R}}_0$.
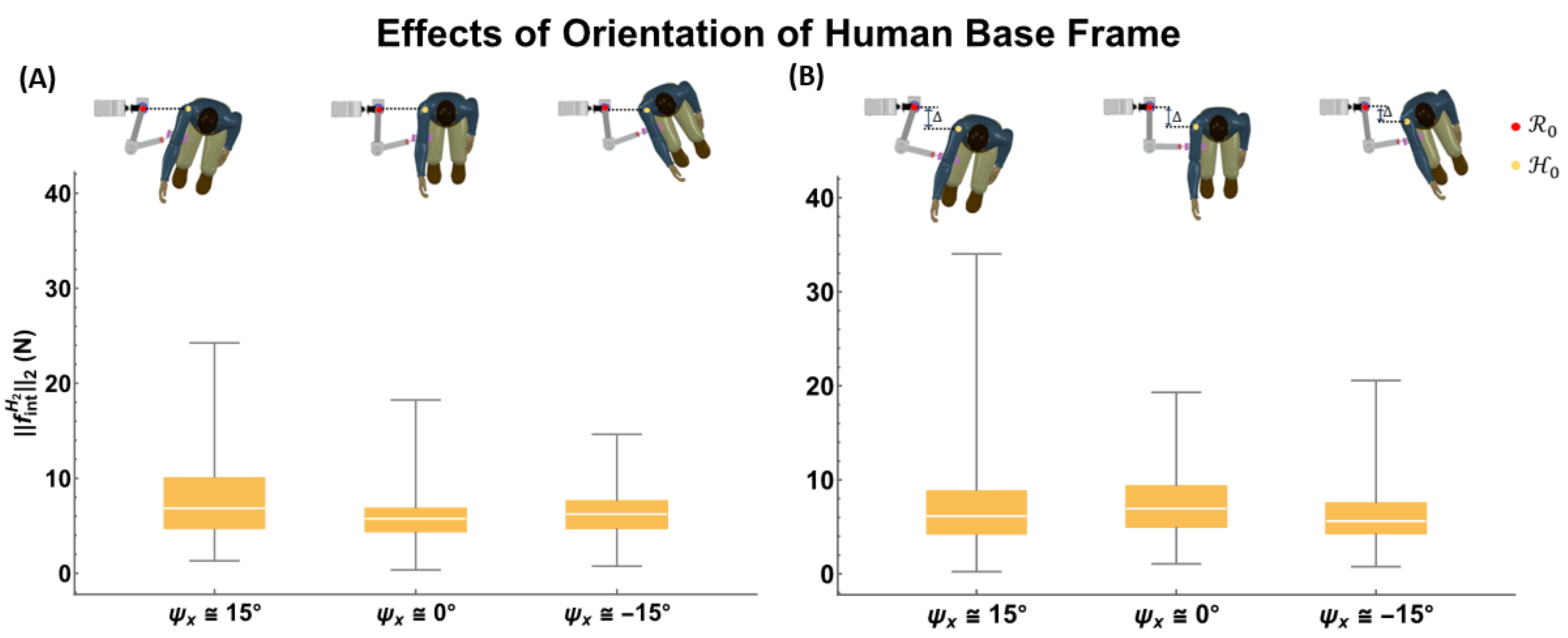
• The orientation of the human base frame with respect to the robot’s base frame; ${\mathbf{R}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}$ is assumed to be rotated around the ${\mathbf{x}}_{{\mathcal{R}}_0}$-axis.

This type of connection between the arm and AREBO allows the robot to measure and support two DOFs movements of the human arm (${\varphi }_1, {\varphi }_2$), namely, (a) shoulder flexion/extension and shoulder abduction/adduction if AREBO is attached to the upper arm, or (b) shoulder internal/external rotation and elbow flexion/extension if AREBO is attached to the forearm. In the rest of this paper, we assume that (a) the upper arm is connected to the robot while detailing the different features of the system and its evaluation, and (b) the elbow and the trunk are fixed. However, all these can be implemented for the forearm as well, with slight modifications.

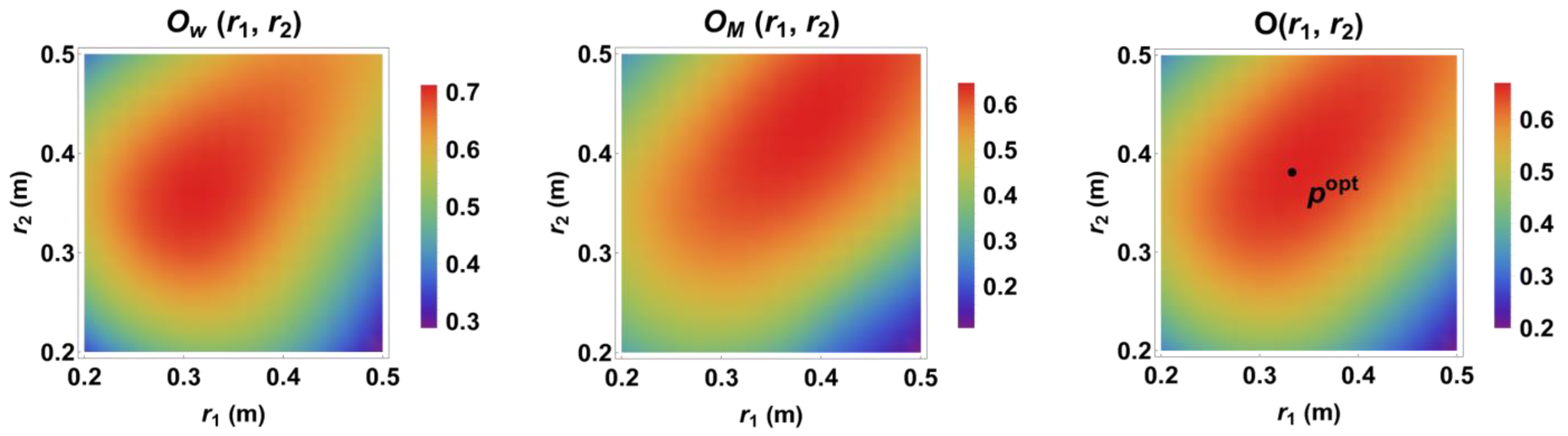
2.1.3. Optimization of Link Lengths

The robot link lengths ($r_1, r_2$) were optimized (like in [19]) for single-joint movements of the arm by maximizing the robot’s workspace and manipulability in a plane orthogonal to the longitudinal axis of the attached arm segment (${\mathbf{z}}_{{\mathcal{H}}_3}$ in Figure 4). A brute force search was implemented to find the optimal link lengths for the robot for different combinations of the arm parameters, namely, the arm lengths, positions, and orientations of the human joint $\left({\mathcal{H}}_0\right)$ with respect to the robot $\left({\mathcal{R}}_0\right)$. An initial coarse search with link lengths $(r_1, r_2)$ ranging between 20 and 50 cm was conducted to locate the region near which the optimum point exists (2 cm increments). After that, a fine search with 1 mm increments in the link lengths revealed the optimum link lengths.

Table 1. Parameter values and range for the coarse and fine search used in the optimization of the robot link lengths $r_1, r_2$. CS—coarse search, FS—fine search, $l$—distance between human joint and AREBO’s attachment point, ${\mathit{o}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}={\left[\begin{array}{ccc}{o}_x& o_y& o_z\end{array}\right]}^T$—origin of the human joint, ${\psi }_x$—rotation of the human around the $x_{{\mathcal{H}}_0}$-axis.

Parameter		Values (cm)	No of Values
$r_1$	CS	{20, 22, …, 50}	16
	FS	{33.1, 33.2, …, 34.9}	19
$r_2$	CS	{20, 22, …, 50}	16
	FS	{37.1, 37.2, …, 38.9}	19
$l$		{15, 17.5, 20}	3
$o_x, o_y$		{−10, 0, 10}	3
$o_z$		{20, 30, 40}	3
${\psi }_x$ (deg)		{−30, 0, 30}	3

provides the details of the parameter ranges and step sizes used for the optimization procedure. The objective function for the optimization procedure was defined as follows:

$$O\left(r_1,r_2\right)=\frac{1}{2}\left(O_W\left(r_1,r_2\right)+O_M\left(r_1,r_2\right)\right)$$

where the workspace component of the objective function $O_W\left(r_1,r_2\right)$ quantifies the relative intersection between the robot’s and human’s workspaces averaged across combinations of the human parameters; $O_M\left(r_1,r_2\right)$ is the manipulability of the robot in a plane orthogonal to the arm. The details of these two components are provided in the Supplementary Material.

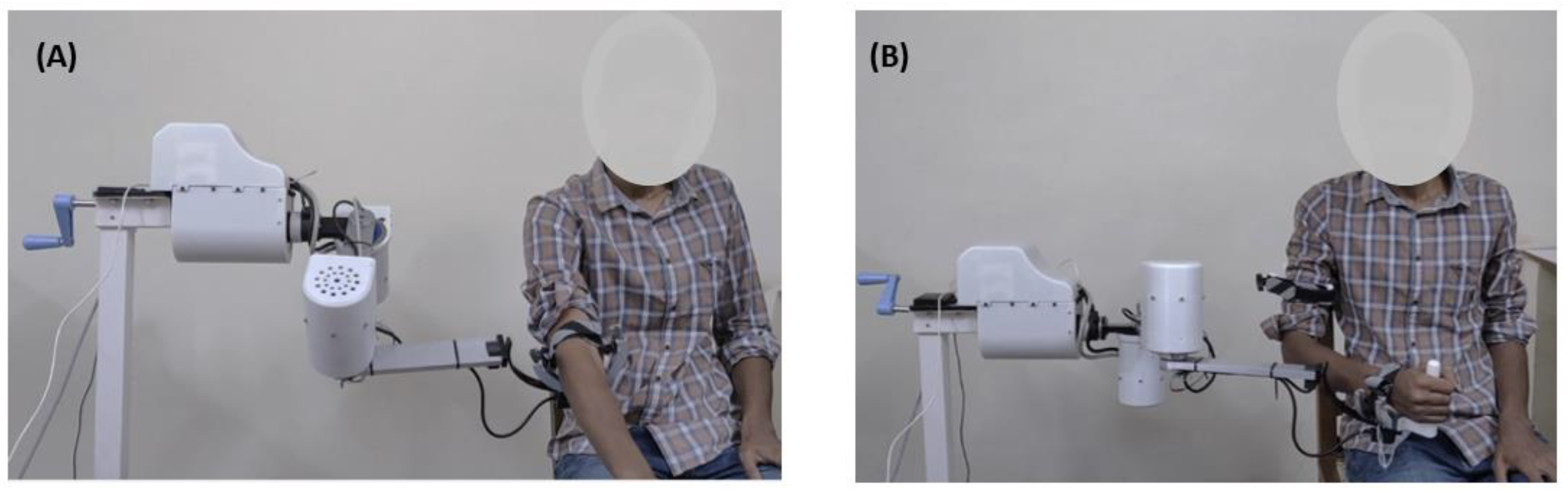
2.2. Robot Hardware

2.2.1. Mechanical Design

The three proximal joints with the motor and torque sensor assembly were interconnected by two aluminium links and three custom-designed flange couplings with keyways. The tapped hole and key on the motor shaft were utilized to prevent relative motion between the coupling and actuator. The couplings and the links were fabricated with IS 2062 plain carbon steel and 6061 aluminium alloy, respectively. The 3D model of the distal spherical joint formed by the robot’s three unactuated DOFs is shown in Figure 5. An elliptical plate with a shaft at one end connects the cuff with the rest of the robot (Figure 5C). The dimensions of the ellipse were calculated to allow a range of motion of 90 degrees for ${\theta }_5$. The 5th joint (${\mathcal{R}}_5$) was formed by a circular segment placed over a shaft. Twelve ball bearings (four on each side and four at the bottom) were strategically placed to clone the behavior of a hinge joint at ${\mathcal{R}}_6$. Two C-shaped semi-circular aluminium profiles held together by three spacers formed the sixth DOF.

The robot’s kinematic chain is mounted on a manually adjustable telescopic mechanism to change the height of ${\mathcal{R}}_0$ from the ground. This height is varied by rotating the handle that is attached to a bevel gear and lead screw arrangement and has a 260 mm stroke length. This telescopic mechanism is mounted on a plus-shaped chassis constructed from four beams made from $40 \mathrm{m}\mathrm{m}\times 40 \mathrm{m}\mathrm{m}$ 6063 aluminium profiles with an IS 2062 plain carbon steel stiffener at its base. Four caster wheels with brakes bestow portability to the entire assembly.

2.2.2. Joint Actuation and Sensing

For a person of a height of 185 mm (95th percentile) and a weight of 100 kg, the torque required to hold the arm flexed at $90°$ against gravity is found to be 15.8 Nm [22]. Considering the dynamics of the human–robot system, the actuator requirement for the first DOF was conservatively chosen to be around 40 Nm. The second and third actuator torque was found to be 20 Nm using similar calculations for the arm abducted at 45$°$. The maximum angular velocity required for training activities of daily living considering both shoulder and elbow joints is around $180$ deg/s [23]. Actuators were shortlisted based on these torque and speed requirements, and the most compact actuator among them was integrated into AREBO. AREBO’s three actuated DOFs use individual brushless DC motors (details in

Table 2. Specification of actuators and torque sensors used in AREBO. The actuators are from Maxon International Ltd. (London, UK), and the torque sensors are from Forsentek Co., Ltd. (Shenzhen, China). Three Escon 70/10 ec motor controllers are used along with each actuator.

	Motor	Gearbox	Torque Sensor	Encoder
1st Joint	EC Flat 90, Nominal torque—0.953 Nm, part no. 607950	GP 52 C, Gear ratio: 53:1, part no. 223090	FTHC, Range—40 Nm	MILE, 4096 CPT, Part no., 651168
2nd Joint	EC Flat 60, Nominal torque—0.563 Nm, part no. 614649	GP 52 C, Gear ratio: 43:1, part no. 223089	FTHC, Range—20 Nm	MILE, 4096 CPT, Part no., 651168
3rd Joint	EC Flat 60, Nominal torque—0.563 Nm, part no. 614649	GP 52 C, Gear ratio: 43:1, part no. 223089	FTHC, Range—20 Nm	MILE, 4096 CPT, Part no., 651168
4th Joint	Unactuated joint			Calt, 1000 CPT, Model no. PD30-08G1000BST5
5th Joint	Unactuated joint			Calt, 1000 CPT, Model no. PD30-08G1000BST5
6th Joint	Unactuated and not instrumented

) configured through individual controllers to operate in a current control mode. A three-stage planetary gearbox is used along with electric motors to obtain the torque requirements at the three actuated DOFs.

Each actuated joint consists of a reaction-type joint torque sensor that is sandwiched between the actuator’s body and the proximal segment of the joint (Figure 6); the torque sensors are used to implement an outer torque control loop around each joint. The rotary encoder on each brushless DC motor senses the joint position of the three actuated DOFs $\left({\theta }_1,{\theta }_2, {\theta }_3\right)$; two additional rotary encoders were fitted to sense ${\theta }_4$ and ${\theta }_5.$ These encoders allow us to compute ${\mathbf{x}}_{{\mathcal{R}}_6}$ and the orientation of ${\mathcal{R}}_5$ (${\mathbf{R}}_{{\mathcal{R}}_5}$) since we do not measure ${\theta }_6$ (Figure 2). The specifications of the actuators and sensors are given in Table 2.

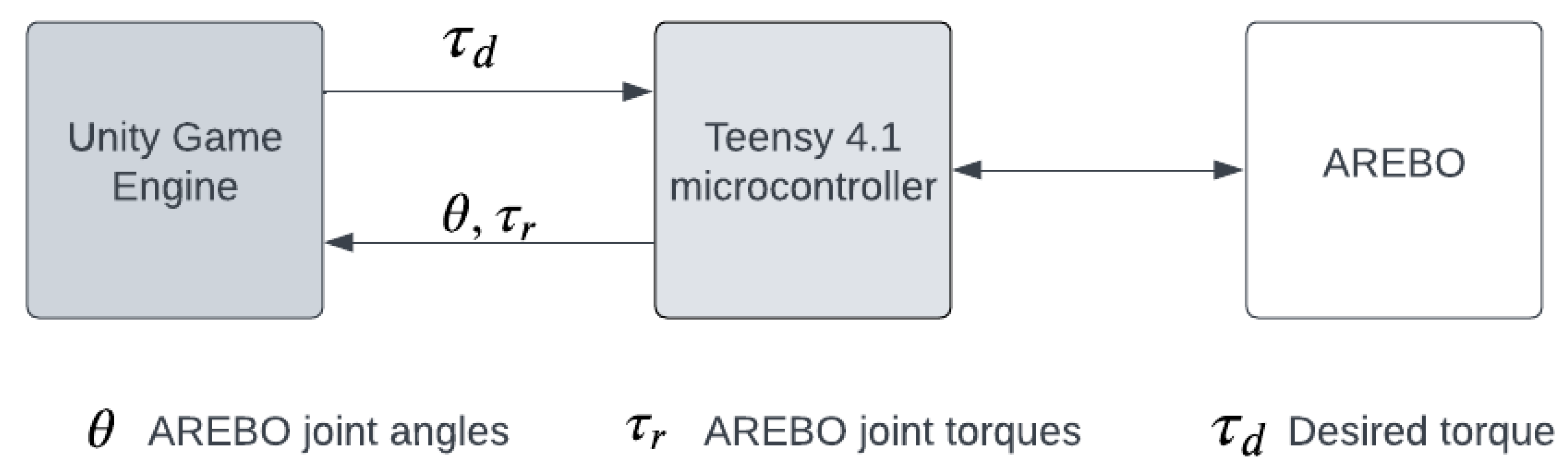
2.2.3. Firmware and Software

A Teensy 4.1 (PJRC.com, LLC, USA) microcontroller performs the low-level hardware interfacing AREBO’s actuators and sensors. The three actuators are controlled through individual pulse width modulation (PWM) lines from the microcontroller to the ESCON 70/10 motor controllers operating in the current control mode. The five encoders are connected to ten digital lines (channel A and channel B for each encoder). Each torque sensor is connected to an HX711 (dual-channel 24-bit precision A/D weight pressure sensor) load cell amplifier, which connects to the microcontroller through two digital lines (two-wire interface). The firmware on the microcontroller runs at 200 Hz, with each iteration of the firmware code performing sensor reading, control law execution, and data communication with the PC. The different components of the firmware/software system interfacing the robot are depicted in Figure 7.

The software to communicate with the robot was written using the Unity Game Engine (Unity Technologies, Bellevue, WA, USA). The graphical user interface communicates with the robot for reading data and setting control modes and controller parameters. This software reads the sensor data from the firmware via a USB serial link and logs it to the PC at 200 Hz. The software eventually contains the games used when training arm movements with AREBO.

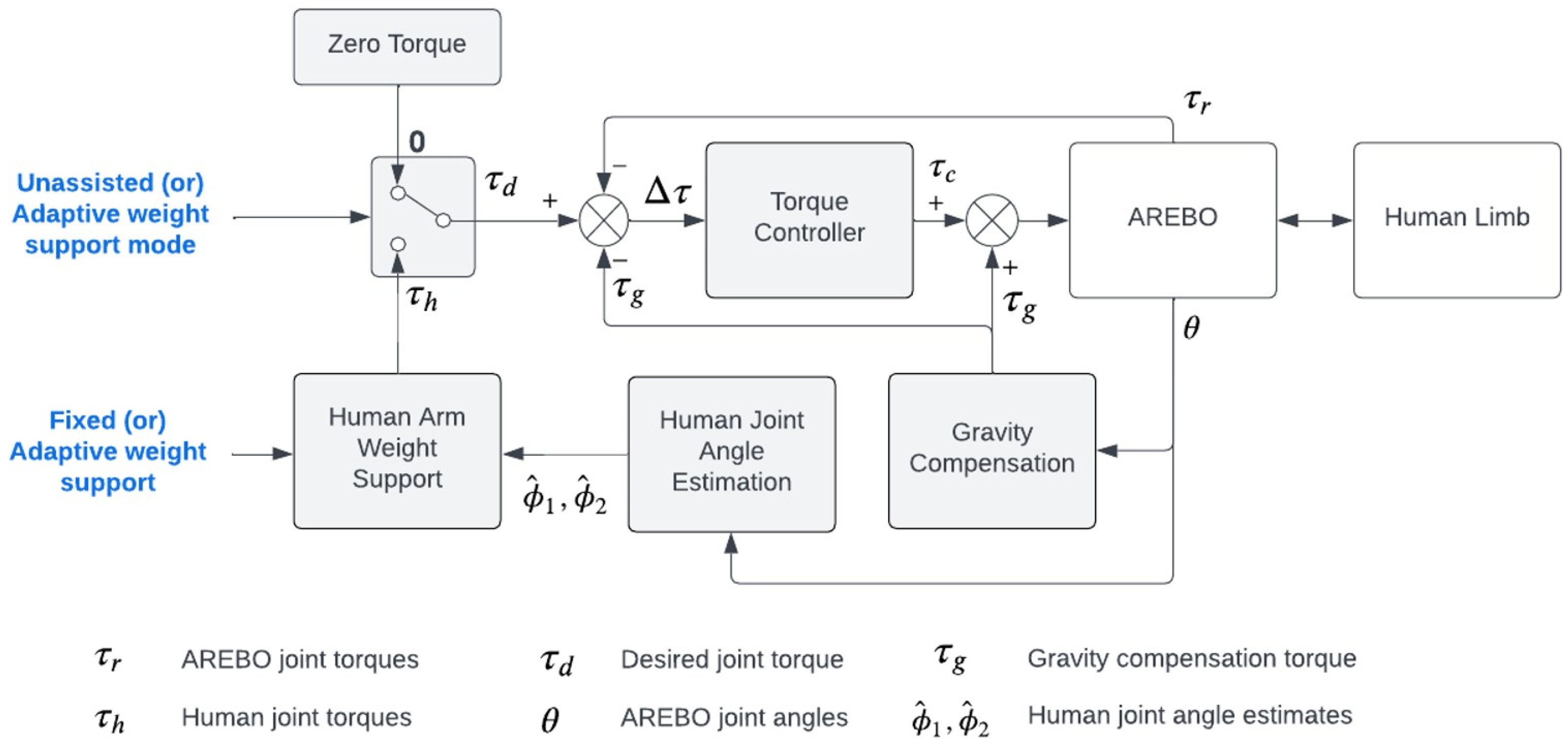
2.3. AREBO Human–Robot Physical Interaction: Controller Details

As a rehabilitation robot designed for measuring and assisting arm movements, two types of human–robot physical interactions are supported by AREBO, which are defined as two modes of operation of the robot:

(a)

Unassisted mode (UAM): This mode allows subjects to perform voluntary active movements with no physical robotic assistance and minimal interaction forces from the robot’s mechanical structure, which is necessary to actively engage patients during training and assess their residual ability.

(b)

Adaptive weight support mode (WSM): In this control mode, the robot and user work together to complete a task. While the user voluntarily moves the arm, the robot provides just the amount of weight support needed to compensate for the weakness in the arm. The support from the robot can be fixed or adaptive depending on the training type desired by the user.

AREBO’s controller architecture that allows the implementation of UAM and WSM is depicted in Figure 8. The controller has the following components:

(a)

Low-level current control loop: At the lowest level, a current control loop is implemented by the Maxon motor controllers for each individual motor.

(b)

High-level torque control loop: A high-level torque control loop is implemented for each actuated robot using the joint torque sensors to control the interaction force $\left({\mathbf{f}}_{int}^{{\mathcal{R}}_0}={\left[f_{int,x}, f_{int,y}, f_{int,z}\right]}^T\right)$ between the arm and AREBO applied at the robot’s endpoint.

(c)

Gravity compensation module: A gravity compensation module that computes the torques required at the robot joints to hold the robot in a particular joint configuration against gravity.

(d)

Human joint estimation module: This module allows the estimation of the human joint angle from the robot’s joint angles without the need for any additional sensor on the arm.

(e)

Human arm weight support module: This module estimates the torque required to provide a given level of weight support to the arm based on the estimate of the arm’s joint angles.

This controller is used to implement the two modes of training (UAM and WSM) with the robot. The details of each of these modules are provided in the rest of this section.

2.3.1. High-Level Torque Control Loop

The purpose of this loop is to control the interaction force ${\mathbf{f}}_{int}^{{\mathcal{R}}_0}\in R^3$ between the robot and arm, which is represented in the robot’s base frame ${\mathcal{R}}_0$. This interaction force could be due to the subject applying a force on the robot, i.e., the subject attempting to move voluntarily while connected to the robot, or the robot applying a force on the arm for assisting or resisting movements. The joint torques due to this interaction force $\left({\mathsf{\tau }}_{int}\in {\mathbb{R}}^6\right)$ is given by the following:

$${\mathsf{\tau }}_{int}\left[n\right]=\left[\begin{array}{cccc}{\tau }_{int,1}\left[n\right]& {\tau }_{int,2}\left[n\right]& \dots & {\tau }_{int,6}\left[n\right]\end{array}\right]={\mathbf{J}}^T\left(\mathsf{\theta }\left[n\right]\right)·{\mathbf{f}}_{int}^{{\mathcal{R}}_0}\left[n\right]$$

where, $\mathbf{J}\left(·\right)\in {\mathbb{R}}^{3\times 6}$ is the robot’s Jacobian matrix (details in the Supplementary Material). AREBO’s kinematic structure will result in zero torques in the last three robot DOFs, i.e., ${\mathsf{\tau }}_{int,4}\left[n\right]={\mathsf{\tau }}_{int,5}\left[n\right]={\mathsf{\tau }}_{int,6}\left[n\right]=0$.

The torque controller for each of the three actuated joints of AREBO is a PD controller, with the discrete-time control law for the $i^{th}$ DOF given by the following:

$${\tau }_{c,i}\left[n\right]=k_{i,1}∆{\tau }_i\left[n\right]+k_{i,2}∆{\tau }_i\left[n-1\right]$$

$${∆\tau }_i\left[n\right]={\tau }_{d,i}\left[n\right]-{\tau }_{r,i}\left[n\right]-{\tau }_{g,i}\left[n\right]$$

where,

• $n$ is the current time instant.
• The subscript $i$ indicates that these are variables associated with $i^{th}$ DOF.
• ${\tau }_{c,i}\left[n\right]$ is the output of the PD controller at the time instant $n$.
• ${\tau }_{g,i}\left[n\right]$ is the torque required to fully compensate for the weight of the robot at the current joint configuration $\mathsf{\theta }\left[n\right]$.
• ${\tau }_{d,i}\left[n\right]$ is the desired torque, which is manipulated for implementing the unassisted and adaptive weight support control modes.
• ${\tau }_{r,i}\left[n\right]={\tau }_{int,i}\left[n\right]+{\tau }_{g,i}\left[n\right]$ is the torque read by the robot’s joint torque sensor, which contains the torque required to hold the robot in the current configuration $\left({\tau }_{g,i}\left[n\right]\right)$, and ${\tau }_{int,i}\left[n\right]$ the torque due to the interaction force ${\mathbf{f}}_{int}^{{\mathcal{R}}_0}$.
• $k_{i,1}$ and $k_{i,2}$ are the parameters of the PD controllers. The same fixed controller parameters are used for the 2nd and 3rd DOFs of the robot, while these two parameters are piecewise constant functions of the interaction torque ${\tau }_{int,i}\left[n\right]={\tau }_{r,i}\left[n\right]-{\tau }_{g,i}\left[n\right]$ for the 1st DOF (details in the Supplementary Material).

The maximum possible bandwidth of the torque controller used was experimentally determined to be around 2.75 Hz (details in the Supplementary Material).

2.3.2. Gravity Compensation

The gravity compensation module ensures that the robot’s actuators automatically take care of the robot’s weight for any possible robot joint configuration $\mathsf{\theta }\left[n\right]$. This module uses the current robot joint angles $\mathsf{\theta }\left[n\right]$ to compute the torques required to maintain the robot in that configuration against gravity using the following expression:

$${\mathbb{R}}^3\ni \mathbf{g}\left(\mathsf{\theta }\right)=\left[\begin{array}{c}{\tau }_{g,1}\left(\mathsf{\theta }\right)\\ {\tau }_{g,2}\left(\mathsf{\theta }\right)\\ {\tau }_{g,3}\left(\mathsf{\theta }\right)\end{array}\right]$$

where ${\tau }_{g,i}\left(\mathsf{\theta }\right)$ is the torque required at the joint $i$ to maintain the robot in the joint configuration $\mathsf{\theta }$.

The parameters of the gravity term $\mathbf{g}\left(\mathsf{\theta }\right)$ were estimated through a calibration procedure, where a PD position controller moved and held the robot at joint configurations, while the static joint torques at the first three joints were recorded. The details of the calibration procedure and the parameter estimation procedure are provided in the Supplementary Material.

2.3.3. Human Joint Angle Estimation

The kinematics of the arm can be estimated from AREBO’s joint kinematics if three parameters of the arm are known, namely, the length of the human arm $\left(l\right)$, the relative orientation $\left({\mathbf{R}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}\right)$, and the origin $\left({\mathbf{r}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}\right)$ of the human base frame $\left({\mathcal{H}}_0\right)$ with respect to the robot base frame $\left({\mathcal{R}}_0\right)$ as indicated in Figure 9. The problem of estimating these parameters around the arm can be split into two sub-problems, which can be solved through simple calibration procedures: estimating the (a) orientation ${\mathbf{R}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}$ and (b) origin ${\mathbf{r}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}$ and the arm length $l$.

The orientation of the human base joint with respect to the robot’s base joint is assumed to be rotated around the ${\mathbf{x}}_{{\mathcal{R}}_0}$-axis, i.e., ${\mathbf{R}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}$ is parametrized by a single scalar ${\psi }_x$. This parameter can be estimated from the knowledge of the plane of shoulder flexion/extension movements with zero abduction. The calibration procedure for estimating ${\psi }_x$ will require the user to perform flexion/extension movements while attached to the robot, which records its kinematics during the procedure. The endpoint kinematics of the robot can be used to estimate the equation of the plane that contains the flexion/extension plane and, thus, the orientation parameter ${\psi }_x$. The algorithm for this estimation process is provided in the Supplementary Material (Algorithm S1).

Once the orientation parameter ${\psi }_x$ is estimated, then ${\mathbf{R}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos {\psi }_x& -\sin {\psi }_x\\ 0& \sin {\psi }_x& \cos {\psi }_x\end{array}\right]$. With this information, we can estimate the origin ${\mathbf{r}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}$ and the arm length $l$ parameters through another simple calibration procedure. This is achieved by having the robot perform small random movements of the arm while recording the robot’s kinematics; here, we assume that the human base frame does not undergo any translation or rotation during the calibration procedure. The endpoint kinematics of the robot can be used to estimate ${\mathbf{r}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}$ and $l$. The algorithm for this procedure is provided in the Supplementary Material (Algorithm S2).

2.3.4. Human Arm Weight Support

AREBO provides adaptive weight support during movements by modulating the amount of de-weighting of the subject’s arm. The de-weighting parameter is a scalar $\alpha \in \left[\mathrm{0,1}\right]$, where $0$ indicates no weight support and $1$ indicates 100% weight support. Arm de-weighting requires an estimate of the torque required for holding the arm against gravity, which is achieved using a model of the arm. The details of this model and the procedure for estimating the model parameters are discussed in the Supplementary Material.

This arm model provides the torques ${\mathsf{\tau }}_h\left(\mathsf{\varphi }\right)={\left[\begin{array}{ccc}{\tau }_{h,1}\left(\mathsf{\varphi }\right)& {\tau }_{h,2}\left(\mathsf{\varphi }\right)& 0\end{array}\right]}^T$ required to hold the arm against gravity in the current orientation $\mathsf{\varphi }$. Let the interaction force on the arm to generate this moment around the human joints be ${\mathbf{f}}_h^{{\mathcal{H}}_0}\in {\mathbb{R}}^3$, acting at the point of AREBO’s attachment with the arm, which is given by the following expression:

$${\mathbf{f}}_h^{{\mathcal{H}}_0}\left(\mathsf{\varphi }\right)={\mathbf{J}}_h^{-T}\left(\mathsf{\varphi }\right)·{\mathsf{\tau }}_h\left(\mathsf{\varphi }\right),\hspace{1em}\hspace{0.17em}{\varphi }_2\ne \pm 90°$$

where, ${\mathbf{J}}_h\left(\mathsf{\varphi }\right)\in {\mathbb{R}}^{3\times 3}$ is the Jacobian matrix of the arm’s kinematic chain at the arm orientation $\mathsf{\varphi }$. The abduction angle ${\varphi }_2$ of the human limb is limited to be within $\pm 45°$, which prevents it from going into singularity, ensuring that ${\mathbf{J}}_h^{-T}\left(\mathsf{\varphi }\right)$ always exists. Partial de-weighting can be provided by the robot when the human–robot interaction force is set to some fraction of ${\mathbf{f}}_h^{{\mathcal{H}}_0}$,

$${\mathbf{f}}_{int}^{{\mathcal{R}}_0}\left(\mathsf{\varphi }\right)=\mathsf{\alpha }{\mathbf{R}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}·{\mathbf{f}}_h^{{\mathcal{H}}_0}\left(\mathsf{\varphi }\right)$$

where ${\mathbf{R}}_{{\mathcal{H}}_0}^{{\mathcal{R}}_0}$ is the rotation matrix representing the human base frame ${\mathcal{H}}_0$ in the robot’s base frame ${\mathcal{R}}_0.$

The torques at the three joints of the robot to generate this interaction force ${\mathbf{f}}_{int}^{{\mathcal{R}}_0}\left(\mathsf{\varphi }\right)$ are given by the following:

$${\mathsf{\tau }}_{int}\left(\mathsf{\theta },\mathsf{\varphi }\right)={\mathbf{J}}^T\left(\mathsf{\theta }\right)·{\mathbf{f}}_{int}^{{\mathcal{R}}_0}\left(\mathsf{\varphi }\right)$$

where $\mathbf{J}\left(\mathsf{\theta }\right)\in {\mathbb{R}}^{3\times 6}$ is the robot’s Jacobian matrix at the robot joint orientation $\mathsf{\theta }$. This ${\mathsf{\tau }}_{int}\left(\mathsf{\theta },\mathsf{\varphi }\right)$ is set as the desired torque ${\mathsf{\tau }}^{\mathbf{d}}$ to the torque controller (Figure 8).

The level of assistance or de-weighting is decided by the de-weighting parameter $\alpha$, which could be either fixed or adaptive. In the case of fixed support, $\alpha$ is constant throughout the session and its value is decided by the clinician. In the case of adaptive support, the value of $\alpha$ is modulated within a therapy session depending on the success or failure of movements performed by the subject on a trial-by-trial basis.

$$\alpha \left[k+1\right]=F\left(S\left[k\right],\alpha \left[k\right]\right)\alpha \left[k\right]+∆\left(S\left[k\right]\right), k\in Z_{>0}$$

where,

• $k$ is the trial number (an integer greater than 0).
• $S\left[k\right]$ is a binary variable indicating the success or failure of trial $k$.
• $F(S\left[k\right],\alpha [k])=\left\{\begin{array}{cc}1,& S\left[k\right]=0\\ 0.95,& S\left[k\right]=1,\alpha \left[k\right]\le 0.5 \\ 0.98,& S\left[K\right]=1,\alpha \left[k\right]>0.5\end{array}\right.$ is the forgetting factor that reduces the amount of arm support following successful trials.
• $∆\left(S\left[k\right]\right)=\left\{\begin{array}{cc}0.02,& S\left[k\right]=0\\ 0& S\left[k\right]=1\end{array}\right.$ is the learning factor that increases the amount of de-weighting following a failed trial.

2.4. Experiments with AREBO

The AREBO controller and its different components were tested to evaluate its performance during physical human–robot interaction. To make the development and testing process controlled and repeatable, we developed a mechatronic human shoulder joint simulator, which we refer to as the shoulder joint model (SJM). The SJM was used for carrying out all the experiments to characterize the AREBO controller, which is described in the rest of this section.

2.4.1. Shoulder Joint Model (SJM)

This physical model of the shoulder joint was fabricated to develop, tune, and test the AREBO controller. SJM is a two DOFs setup that has a kinematic structure like that of the human shoulder joint, without the last DOF (${\mathcal{H}}_3$ in Figure 3 for internal–external rotations). The two DOFs of the SJM are actuated by two brushless DC motors and have individual joint torque sensors (details in the Supplementary Material). Figure 10 depicts the attachment of SJM with AREBO, where the SJM’s link is attached to AREBO’s cuff through a three-axis load cell (Forsentek Ltd., Shenzhen, China, range: 100 N along each axis) sandwiched between them; this load cell measures the interaction force in the local reference frame ${\mathcal{H}}_2$, i.e., ${\mathbf{f}}_{int}^{{\mathcal{H}}_2}$. The SJM link has multiple threaded holes to attach the robot’s cuff at different distances from the two DOFs (i.e., changing $l$). The SJM also has provisions on its link for attaching weights to simulate different arm weights (Figure 10).

Except for its height adjustment mechanism, the two DOFs SJM assembly is rigidly mounted on a frame like that of AREBO’s. The frame contacts the ground through four castor wheels that enable rotation of SJM around ${\mathbf{x}}_{{\mathcal{H}}_0}$ to set ${\psi }_x$ and translate the origin of the human base frame ${\mathcal{H}}_0$ with respect to the robot’s base frame, ${\mathcal{R}}_0$. The brakes on the wheels are physically engaged each time the setup is brought to its experimental position.

A linear PD position controller with a feedforward gravity compensation term was implemented to control the movements of the SJM; the individual motor controllers were operated in a current control mode. The details of this controller are provided in the Supplementary Material.

The experimental characterization of AREBO described in this section was carried out by connecting the SJM to AREBO as shown in Figure 10 and by fixing different parameters associated with this connection, which is described in Figure 9.

2.4.2. Demonstration of Self-Aligning Feature of AREBO

AREBO’s three unactuated DOFs enable flexibility in the relative positioning of the human subject with respect to the robot during therapy. To demonstrate this feature, SJM is placed at five different locations ($p_1-p_4$ corners of a square with 30 cm sides and center $p_5$ Figure 11A) and is connected to AREBO. AREBO is set to operate in the unassisted mode with gravity compensation, while the SJM’s movements are implemented through position control. The SJM performs the same 120 s of random movements (${\varphi }_1\in \left[0°,90°\right]$ and ${\varphi }_2\in \left[-30°,30°\right]$) at each of these five positions, while the joint angles of AREBO are recorded.

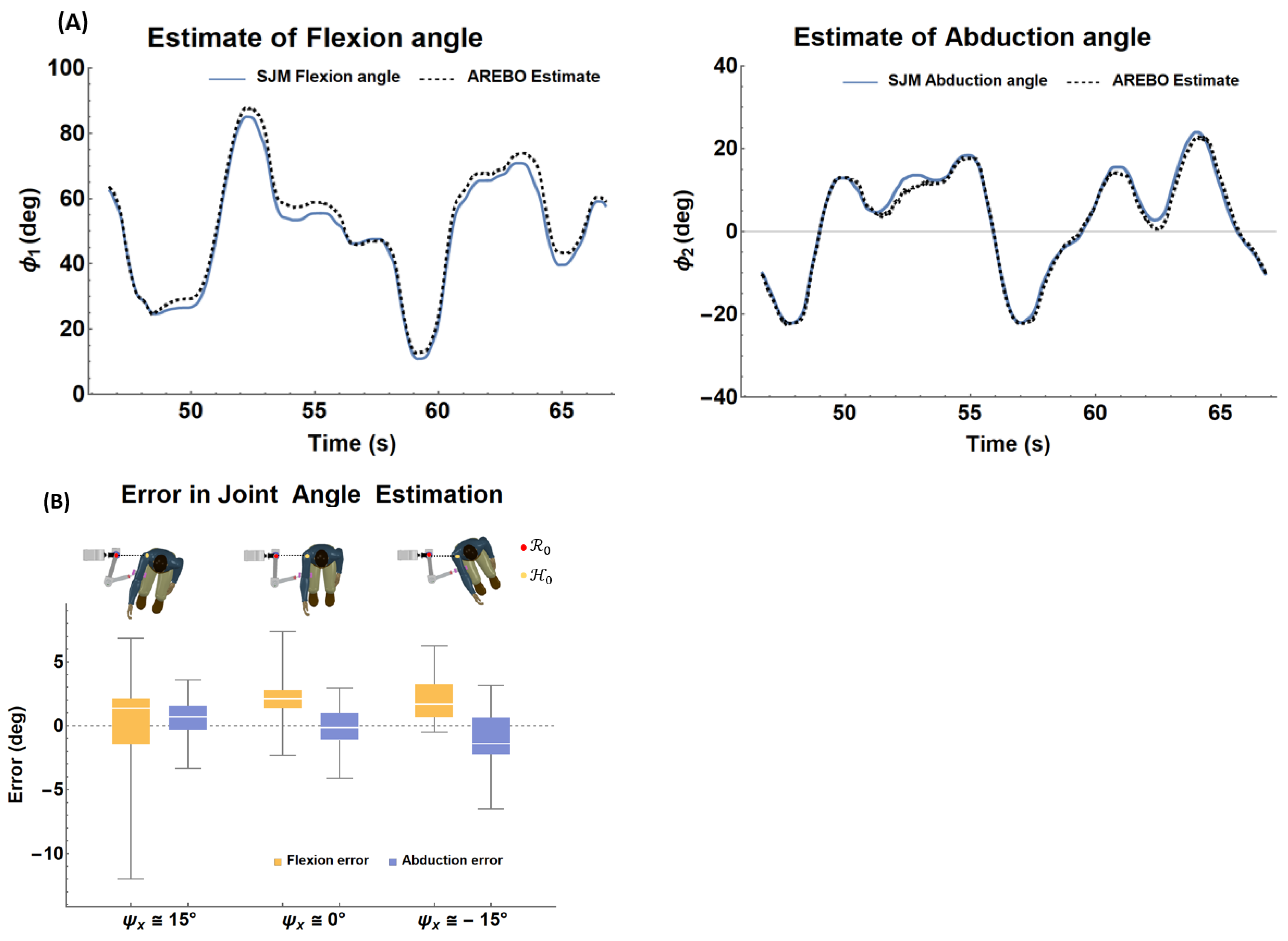
2.4.3. Accuracy of Human Joint Angle Estimation

To evaluate how well the human joint angles can be estimated using AREBO’s joint angles, an experiment was performed with the SJM connected to AREBO. The estimate of the human joint angle requires information around the arm parameters, namely, the arm length $\left(l\right)$ and the human base frame’s orientation $\left({\mathbf{R}}_{{\mathcal{R}}_0}^{{\mathcal{H}}_0}\right)$. The SJM was first programmed to perform three sinusoidal flexion/extension movements in the range of 0–90° within 15 s while connected to AREBO. The data from this movement was used to estimate the arm parameters. Following this, the SJM was programmed to move in a random polysine trajectory given by the following:

$${\varphi }_j\left(t\right)=\sum _{i=1}^4{A}_{j,i}\sin \left(2\pi f_{i}t+{\nu }_i\right)+A_{j,0},\hspace{0.17em} j=\left\{1, 2\right\}$$

where ${\varphi }_j\left(t\right)$ is the human joint angles simulated by the SJM, $f_i=\{0.1, 0.2, 0.35, 0.3\}\mathrm{H}\mathrm{z}$, and ${\nu }_i$ is sampled from a uniform distribution between $0$ and $2\pi$. The values of ${\left\{A_{j,i}\right\}}_{1\le i\le \mathrm{4,1}\le j\le 2}$ are chosen such that the flexion/extension movements are between $0 \mathrm{a}\mathrm{n}\mathrm{d} 90°$ and the abduction/adduction movements are between $-30$ and $+30°$. During this polysine movement, the joint angles of AREBO $\mathsf{\theta }\left(t\right)$ were recorded, which were then used to estimate the human joint angles $\widehat{\mathsf{\varphi }}\left(t\right)$. This was achieved by first computing the forward kinematics for AREBO to obtain the endpoint kinematics, which was then used to solve the inverse kinematics for the arm using the arm parameters $l,{\psi }_x$. The estimate of the human joint angles is compared with the ground truth from the SJM’s joint angles $\mathsf{\varphi }\left(t\right)$ obtained from its encoders. The magnitude of the error $\widehat{\mathsf{\varphi }}\left(t\right)-\mathsf{\varphi }\left(t\right)$ provides a measure of the accuracy of the human joint angle estimation procedure, which also includes the procedure for estimating the human arm parameters. The experiment was performed for three different arm parameter combinations. There are several possible sources of error in this estimation procedure, one of which is to evaluate its effect on the joint angle estimation accuracy, which is discussed in the Supplementary Material.

2.4.4. Transparency of the Unassisted Mode (UAM)

The UAM was designed to make the robot transparent to a subject’s voluntary movements when they are connected to the robot. The transparency can be quantified by the magnitude of the interaction force ${‖{\mathbf{f}}_{int}^{{\mathcal{H}}_2}‖}_2$ between the robot and arm. The UAM’s transparency in AREBO was tested using the SJM by programming it to re-perform random (polysine) movements under different conditions, while AREBO’s joint angles $\left(\mathsf{\theta }\right)$ and SJM’s joint angles $\left(\mathsf{\varphi }\right)$, along with the interaction force ${\mathbf{f}}_{int}^{{\mathcal{H}}_2}$ from the SJM’s three-axis load cell, were recorded. The three different conditions that were tested include the effect of the (a) different components of the AREBO controller, (b) misalignment between the human and robot joint axes, and (c) different orientations of the human base frame $\left({\psi }_x\right)$.

Effect of the different components of the AREBO controller: In this experiment, the following conditions were tested to evaluate the effects of the different components of the AREBO controller:

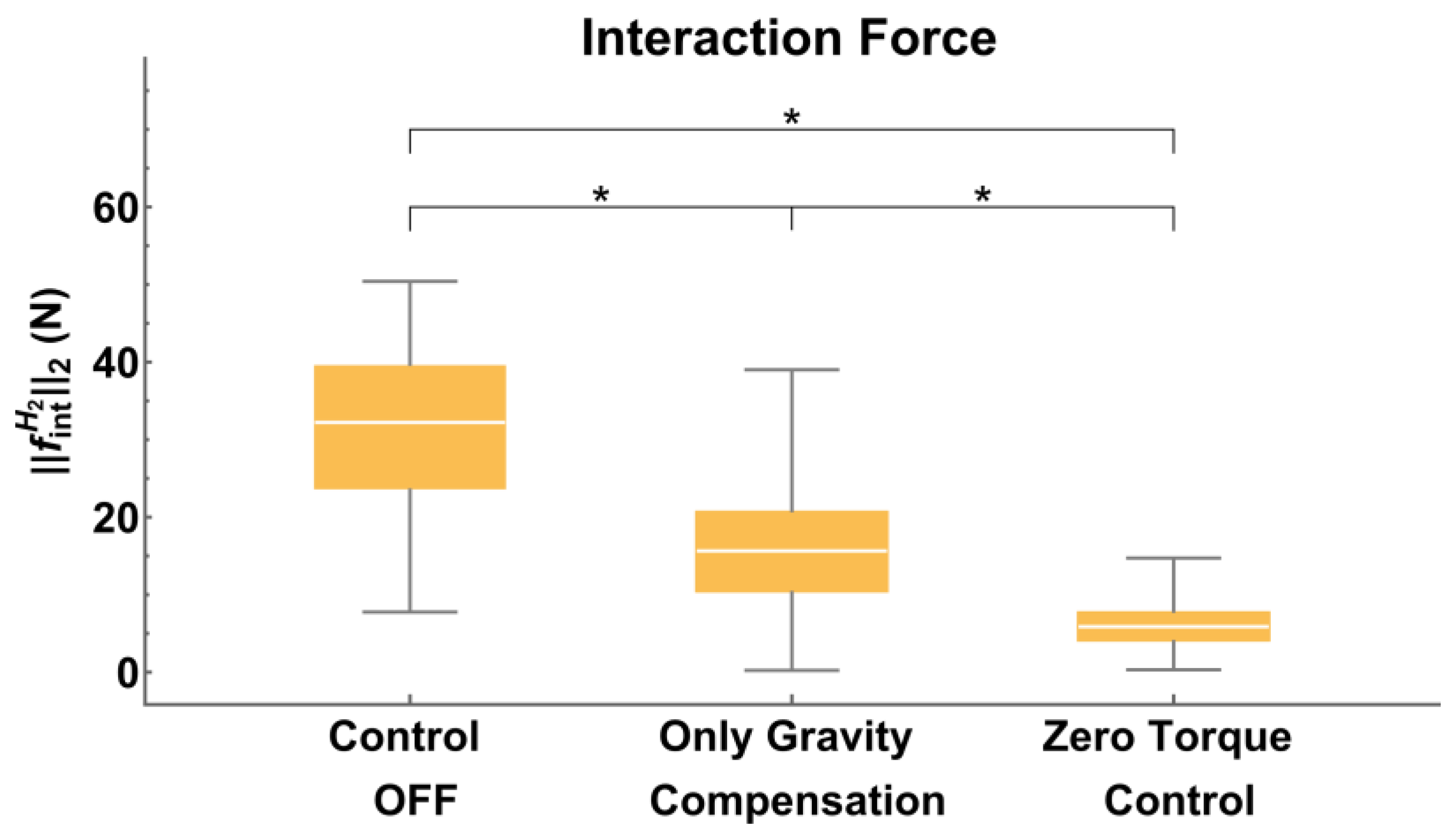
• Control OFF: The actuators of the robot were switched off, which requires the SJM to work against AREBO’s inertia, weight, and friction. This condition provides a measure of the forces required to move AREBO with zero actuation.
• Only Gravity Compensation: The gravity compensation module alone is switched on, and the output of the torque controller is set to zero, i.e., ${\mathsf{\tau }}^c=\mathbf{0}$. In this condition, AREBO’s weight is fully compensated, and the SJM must only work against AREBO’s inertia and friction.
• Zero Torque Control: The entire controller is enabled with the weight support parameter set to zero $\alpha =0$, i.e., no weight support for the arm is provided. In this mode, the AREBO controller works to keep the interaction force zero. The lower the magnitude of ${\mathbf{f}}_{int}^{{\mathcal{H}}_2}$, the better the robot’s transparency.

In this experiment, the SJM was placed such that the origin of the SJM’s base frame coincided with the z-axis of the robot’s base frame ${\mathit{z}}_{{\mathcal{R}}_0}$, and the orientation of the SJM’s base frame with respect to the robot’s base frame was zero, i.e., ${\psi }_x\cong 0°$.

Effect of misalignment of human and robot joint axes: In this experiment, AREBO’s transparency was evaluated using the zero-torque controller, while the SJM was located at different positions with respect to the robot. The SJM was placed approximately at the corners of a square with 30 cm sides, with the center of the square coinciding with the z-axis of the robot’s base frame (Figure 11A). The SJM was programmed to perform random polysine movements during the experiment for all five positions of the SJM. The orientation of the SJM’s base frame with respect to the robot’s base frame was zero, i.e., ${\psi }_x\cong 0°$.

Effects of different orientations of the human base frame: To evaluate the effect of different trunk orientations on the robot’s transparency, the SJM was placed at different combinations of three orientations ${\psi }_x~(-15°, 0°, 15°$) and at (0 cm, −15 cm) displacements along the y-axis of the robot’s base frame. The SJM performed the same polysine movement during the six takes, while AREBO was set in the zero-torque control mode.

2.4.5. Effect of the Adaptive Weight Support (WSM)

AREBO’s controller can provide either fixed arm weight support or adaptive support by modulating the de-weighting parameter $\alpha$. To test the adaptive capability of the WSM control, the SJM was programmed to simulate arm weakness by limiting the torques produced by the SJM’s motors by an impairment factor $\xi \in \left[\mathrm{0,1}\right]$, where $\xi =0$ corresponds to a healthy arm and $\xi =1$ corresponds to a fully flaccid arm. The output of the linear PD position controller and the gravity compensation module is multiplied by $\left(1-\xi \right)$ before it is sent to the motors. The details of the SJM controller are given in the Supplementary Material.

The first step in this experiment was identifying the human arm model parameters for computing torques required to hold the arm against gravity at different joint positions. Following this, SJM was programmed to perform a series of 300 discrete point-to-point reaching movements consisting of 3 s movement followed by 2 s of rest. The joint trajectory for the $k^{th}$ trial is given by the following:

$$\begin{array}{c}{\varphi }_j\left(t;k\right)=\left\{\begin{array}{cc}{\lambda }_{j,i}\left[k\right]+\left({\lambda }_{j,f}\left[k\right]-{\lambda }_{j,i}\left[k\right]\right)·u\left(t-5·\overline{k-1}\right)& 5\left(k-1\right)\le t<5\left(k-2\right)\\ {\lambda }_{j,f}\left[k\right]& 5\left(k-2\right)\le t<5k\end{array}\right.,\\ k\in \left\{\mathrm{1,2},\dots 300\right\}\\ u\left(l\right)=\frac{10l^3}{3^3}-\frac{15l^4}{3^4}+\frac{6l^5}{3^5},\hspace{0.17em} l\in \left[\mathrm{0,3}\right]\end{array}$$

where ${\lambda }_{j,i}\left[k\right]$ and ${\lambda }_{j,f}\left[k\right]$ are the initial and final positions of the joint $j$ of the SJM for the $k^{th}$ trial, $u\left(·\right)$ is the normalized 3 s long minimum jerk trajectory, and $t$ is the current time instant of the experiment. Note that the final position of the $k^{th}$ trial will be the initial position for the ${\left(k+1\right)}^{th}$ trial, i.e., ${\lambda }_{j,i}\left[k+1\right]={\lambda }_{j,f}\left[k\right]$. The initial and final angles for the flexion/extension and abduction/adduction movements were chosen so that these movements are between $0$–$60°$ and $0$–$30°$, respectively.

The joint angle profile ${\varphi }_j(t;k)$ is input as the desired angle to the position controller of the SJM to compute the torque to be commanded from the SJM motor in joint $j$. To simulate impairment of the SJM, the impairment factor was set to the following:

$$\xi [k]=\left\{\begin{array}{cc}0.6& 1\le k\le 100\\ 0.2& 100<k\le 200\\ 0& 200<k\le 300\end{array}\right.$$

The different levels of impairment are used to evaluate how the de-weighting parameter adapts to the varying impairment levels. The torque commanded from the SJM for each trial is multiplied by $\left(1-\xi \left[k\right]\right)$.

The de-weighting parameter is adapted on a trial-by-trial basis depending on the success or failure of the current trial. A trial was considered successful if the SJM reaches within $\pm 5°$ of the target location. In this experiment, the de-weighting parameter for the first trial is chosen to be 0.3, i.e., $\alpha \left[1\right]=0.3$.

3. Results

3.1. Optimum Link Lengths

Figure 12 shows the heat map for the distribution of objective function $O(r_1,r_2)$ as a function of the robot link lengths $r_1$ and $r_2$ along with its workspace $O_w(r_1,r_2)$ and manipulability $O_M(r_1,r_2)$ components. All three variables showed a similar distribution trend with a single maximum within the range of values searched for $r_1$ and $r_2$, which occurred at $r_1=333 \mathrm{m}\mathrm{m}$ and $r_2=381 \mathrm{m}\mathrm{m}$. The physical prototype of the robot was fabricated with these optimal link lengths for the study’s experiments.

3.2. Self-Aligning Feature of AREBO

Figure 11B illustrates the variation of the threeactuated DOFs $\left({\theta }_4, {\theta }_5\right)$ at the five different locations of SJM (Figure 11A), while the SJM performed the same movement. One-way ANOVA on ${\theta }_4$ and ${\theta }_5$ revealed a statistically significant difference for both of the angles due to the different locations of the SJM (For ${\theta }_4:F=\mathrm{73,426.1}, p=0.0$; for ${\theta }_5:F=\mathrm{12,363.4}, p=0.0$). This shows that AREBO’s unactuated segment allows the robot to automatically align to the different orientations of the robot; the absence of this feature will result in undesirable forces on the human limb when it is connected to the robot. Post-hoc analysis with Bonferroni correction indicated that all pairwise comparisons were statistically significant.

3.3. Accuracy of Human Joint Angle Estimation

The plot of the actual angle of the SJM $\mathsf{\varphi }\left(t\right)$ and the estimated joint angle $\widehat{\mathsf{\varphi }}\left(t\right)$ for the flexion/extension and abduction/adduction joints for a particular trial is shown in Figure 13A. The overall difference between the actual and estimated angles is summarized by the accompanying boxplot (Figure 13B) for the different orientations of the SJM with respect to the robot. The estimation error was similar across almost all the different orientation conditions for the flexion/extension and abduction/adduction angles. The only exception was the flexion/extension angle estimation error for the case when the SJM was rotated towards the robot ${\psi }_x\cong +15°$, where the spread of the error was a little wider; the instantaneous error in flexion/extension could be as large at $~10°$. The absolute median error for flexion/extension and abduction/adduction joints were $2.10$ and $1.30°$, respectively.

3.4. Transparency of the Unassisted Mode

The magnitude of the interaction force ${\Vert {\mathbf{f}}_{int}^{{\mathcal{H}}_2}\Vert }_2$ measured using the loadcell sandwiched between the endpoints of AREBO and SJM demonstrating the effect of the different components of the robot’s controller are shown in Figure 14. As expected, the interaction force magnitude reduces significantly with the use of the gravity compensation module and the zero-torque controller. With the zero-torque controller, the magnitude of the interaction force had a median value of 5.88 N with an interquartile range (IQR) of 3.52 N, compared to a median of 32.21 N and IQR of 15.76 N when the controller was switched off. One-way ANOVA revealed that the interaction forces ${\Vert {\mathbf{f}}_{int}^{{\mathcal{H}}_2}\Vert }_2$ were significantly different $(F=\mathrm{30,431.4}, p=0.0)$ in the three cases (Control OFF, Only Gravity Compensation, Zero Torque Control). The post hoc test with Bonferroni correction found all pairwise comparisons to be significantly different.

The experiment on the effects of the position of the human joint with respect to the robot on transparency revealed that higher interaction forces (Figure 15A) are encountered when the SJM is behind the robot (points $p_1$ and $p_2$ in Figure 11A whose y-coordinates are greater than 0) compared to the points that are in line and in front of the robot (points $p_3$, $p_4$, and $p_5$ in Figure 11A whose y-coordinates are less than or equal to 0). One-way ANOVA showed that SJM location had a significant effect on the magnitude of the interaction forces (Figure 15A; $F=6642.25, p=0.0$); all pairwise comparisons were significant except between $p_4$ and $p_5$. The high interaction force for the SJM positions $p_1$ and $p_2$ is due to larger displacements required from the robot’s first joint ${\theta }_1$ when the SJM is behind the robot (as shown in Figure 15B); larger accelerations required around this joint resulted in larger interaction forces.

In the experiment on the effects of the orientation of the human base frame (Figure 16), the median value of the interaction force was similar in almost all cases, although the interaction forces at all the orientations were significantly different ($F=659.5, p=0.0$ in oneway ANOVA). The spread of the interaction force values was slightly higher when the SJM was rotated towards the robot (${\psi }_x>0)$, as seen in the two boxplots corresponding to different values of displacement along the y-axis of the robot’s base frame. The post hoc test with Bonferroni correction revealed that except for the two interaction forces at ${\psi }_x\cong -15°$, all the other interaction forces were significantly different from each other.

3.5. Training with the Adaptive Weight Support Mode

The adaptive de-weighting feature of AREBO was tested by simulating impairments with the SJM at different levels of weakness in the joints. The amount of weakness was held constant for 100 trials to evaluate how AREBO’s controller adapted to the impairment level. The adaptation of the de-weighting parameter $\alpha \left[k\right]$ as a function of the trial number $k$ is shown in Figure 17A. The value of $\alpha \left[1\right]=0.3$, slowly rises to 0.6 within the first 30 trials to compensate for the 60% impairment simulated in the SJM. After the 100th trial, $\alpha \left[k\right]$ decays toward 0.2 to account for the 20% simulated impairment. After the 200th trial, the de-weighting factor slowly decays to 0 as the SJM was simulated to behave like a healthy arm (Figure 17A). This adaptation of the de-weighting parameter helps maintain the trial success rate at around 70% whenever there is some residual impairment in the arm. This is depicted in Figure 17B, which shows the success rate in the past 20 trials as a function of the trial number; the success rate is between 60 and 80% when there is residual weakness in the SJM, and it is 100% for a healthy arm (Figure 17B).

4. Discussion

This paper presents the physical realization, optimization, and characterization of the end-effector robot—AREBO—introduced in our earlier work [19]. The present work’s novelty is the demonstration of using an end-effector robot for sensing and safe training of 3D single-joint movements against gravity. AREBO was designed to allow training in both unassisted and adaptive weight support modes. The robot’s capabilities were characterized using a mechatronic shoulder joint model (SJM).

The self-aligning feature of AREBO enabled by the three distal unactuated DOFs ensures freedom in where the subject sits with respect to the robot, unlike the case of the exoskeleton, which has strict requirements. We firmly believe that this feature is necessary for the robot’s usability for routine clinical use.

The pre-requisite to providing single-joint training using an end-effector robot is the ability to estimate the movement kinematics of the arm. Although this could be achieved by placing additional sensors on the arm, AREBO uses a model of the human arm to estimate the kinematics of the arm. Knowledge of the estimation error is important in setting safety limits for the arm when using the robot for assisted movement training. AREBO’s human arm kinematics estimation algorithm resulted in an angle error that was mostly in the range of $\pm 5°$. The $~1°$ backlash of the ceramic gearboxes with a three-stage planetary reduction in AREBO’s (and SJM’s) actuators is likely to be a major source of this error. The presence of load-dependent play in AREBO’s unactuated DOFs is also a potential contributing factor. This angle estimation error of $\pm 5°$ might be acceptable for training purposes in neurorehabilitation. However, if desired, it could be made much smaller by using harmonic drives and reducing the backlash in the unactuated structures, which will inflate the device cost.

The use of compensation strategies (such as trunk movements) is commonly observed in stroke survivors with arm impairments, in which case the shoulder joint position will not be fixed. However, in upper limb rehabilitation robots, it is a common practice to assume the trunk is fixed to avoid compensatory movements [6,9,11,24] and promote true recovery by breaking abnormal synergies [25]. Thus, the current work used a kinematic model of the human arm where the shoulder position and the elbow joint are assumed to be fixed; the elbow joint can be fixed using an orthotic device during single-joint training of the shoulder. However, to gauge the amount of error in shoulder joint estimation due to unconstrained trunk movements, a theoretical analysis with a five DOFs kinematic model of the trunk was performed (see Supplementary Material). As expected, the results of this analysis indicate that the shoulder joint estimation error is of similar magnitude to the amount of trunk movement (95th percentile absolute error, ~20° in flexion and ~27° in abduction, for random trunk movements of ~20°). Thus, when the trunk is unconstrained, the robot data alone cannot provide an accurate estimate of the shoulder joint kinematics. One would need to employ additional sensors on the human limb for accurate estimation. However, the optimal choice for the sensing modality and the number of such sensors are unknown.

The physical human–robot interaction is implemented through two control modalities: unassisted and adaptive weight support modes. In the unassisted mode, AREBO remains transparent to the movements of the human subject. A robot’s transparency is often quantified through the interaction forces/torques while a subject interacts with the robot performing different movements. The RehabExos [26,27] and ABLE [27] robots measured the interaction forces at the points of connection between the user and the robot, while the Armin [28] and ANYexo [5] robots measured the peak and mean interaction torque at each joint. In all the above cases, healthy subjects interacted with the robots while performing movements with constraints in velocity (angular velocity in the major joint < $30°/\mathrm{s}$ and/or the trajectory, e.g., straight, or circular path [5,28], or a pointing task [27]). In the current study, AREBO’s transparency was quantified by measuring the interaction force and joint torques between the robot and the SJM. AREBO’s mean interaction force was around $~6 \mathrm{N}$, which was lower than that of the ABLE exoskeleton $\left(~10 \mathrm{N}\right)$, but AREBO’s peak interaction force $\left(~15 \mathrm{N}\right)$ was higher than the ABLE exoskeleton $\left(~12 \mathrm{N}\right)$ [27]. In terms of joint interaction torques, the peak interaction torque along the flexion/extension axis in ARMin and ANYexo was 2.30 Nm and 2.31 Nm, respectively. The peak interaction joint torque for AREBO is 2.67 Nm at the 1st joint for random movements in the range of $0–90°$ with a 95th percentile angular speed of $~50°/\mathrm{s}$ and an absolute peak speed of $~120°/\mathrm{s}$. These results show that AREBO is comparable with existing non-backdriveable robots in terms of transparency. There can, however, be slightly higher interaction forces when the subject is seated behind the robot, due to the larger movement amplitudes and accelerations required from the robot. Such seating positions must be avoided when interacting with the robot to maximize transparency. Thus, when appropriately seated (in line or in front of the robot), the safety and perception of the physical interaction with AREBO are likely to be similar to that of the existing robots that have been evaluated with patients. It might be possible to further lower the interaction torques by other means, including reducing the inertia of the kinematic chain, opting for a lower speed reduction-ratio gearbox with higher torque rating electric motors, and cable-driven transmission for the robot’s third joint by moving the actuator closer to the base. These modifications can be explored for future design revisions of AREBO.

The adaptive weight support training mode compensates for the arm’s weight depending on the user’s impairment. By reducing the effort to lift the arm against gravity, the arm’s residual capacity can now be allocated to move the arm and experience an increased range of motion. In stroke, there is evidence to show that supporting the shoulder against gravity not only increases the range of motion in the shoulder joint but also facilitates elbow extension [29], finger extension, and gross hand opening and closing [30]. Previous studies have also shown that training arm movements with gradual loading of the shoulder can increase the work area of the upper limb by breaking abnormal joint coupling [25]. Such training protocols can be easily implemented with AREBO. The adaptive algorithm used in this study adjusts the weight support based on the success/failure of movements performed by the subject. The parameters of this algorithm $\left(F\left(S\left[k\right],\alpha \left[k\right]\right), ∆\left(S\left[k\right]\right)\right)$ were tuned empirically to have a success rate of around 70%, which is based on the challenge point hypothesis [31] to increase motivation in therapy.

The stability of the robot controller interacting with the human subject is another crucial factor for the safety and comfortable interaction between the robot and the human. The experimental evaluations with the robot have found that the controller is stable in both the unassisted and assisted modes. A mathematical proof of the stability of the controllers might not be feasible without major simplifying assumptions about the feedback controller representing the human subject. However, if the human subject is modeled as a purely passive or a feedforward control system, a mathematical proof of stability might be demonstrable. This study did not seek such a mathematical demonstration.

The single-joint training regimes proposed here could easily be extended for assisted coordinated multi-joint training of the arm for less severely affected patients. This can be achieved by taking an approach like that of the Emu robot [24] where a model of the human arm (shoulder and elbow) can be employed, along with an appropriate calibration procedure. One could employ a vision-based pose tracking system to estimate human arm kinematics, which can simplify the calibration procedure for estimating the parameters of the human arm model.

The current study presented the engineering design and characterization of AREBO, which is only the first crucial step towards realizing this system as a useful clinical tool for arm rehabilitation. This work has shown how an end-effector robot can be used for training single-joint movements in 3D with adaptive gravity support, along with tracking human limb movements without the use of additional sensors on the human limb. The characterization of the system with a mechatronic model of the shoulder joint has provided information about the best possible relative positioning of the robot and the human for the most transparent interaction between them. Further work is necessary to build on the outcomes of the current study to get the system ready for use by clinicians and patients:

• Extension of the algorithms for multi-joint shoulder-elbow arm training, along with exploring the feasibility of using vision-based methods for tracking trunk, shoulder, and elbow kinematics [32].
• Characterizing the different components of the robot with healthy subjects, including the algorithm for estimating human joint angles, the unassisted mode for evaluating the transparency, and the adaptive weight support mode.
• Development of therapy games for unassisted and adaptive weight support training with the robot.
• Evaluation of the usability of the robot for arm rehabilitation on different neuromusculoskeletal conditions.

Our current and future work is focused on addressing these issues to get AREBO ready for evaluating its usefulness as a clinical tool for arm rehabilitation.