Double-Layer RRT* Objective Bias Anytime Motion Planning Algorithm
Abstract
:1. Introduction
- (1)
- This paper proposes a double-layer RRT* tree structure. In the first layer, initial path information is provided. In the second layer, an iterative optimization process is used to update the selected path and improve the path selection accuracy.
- (2)
- A new feedback-based objective bias strategy is used to obtain the initial path, and the initial path is smoothed by removing redundant processing through segmentation forward pruning.
- (3)
- The second layer of the RRT* scheme optimizes the selected path using the heuristic information provided by the spanning tree structure of the initial path.
2. Motion Planning Problem Statements
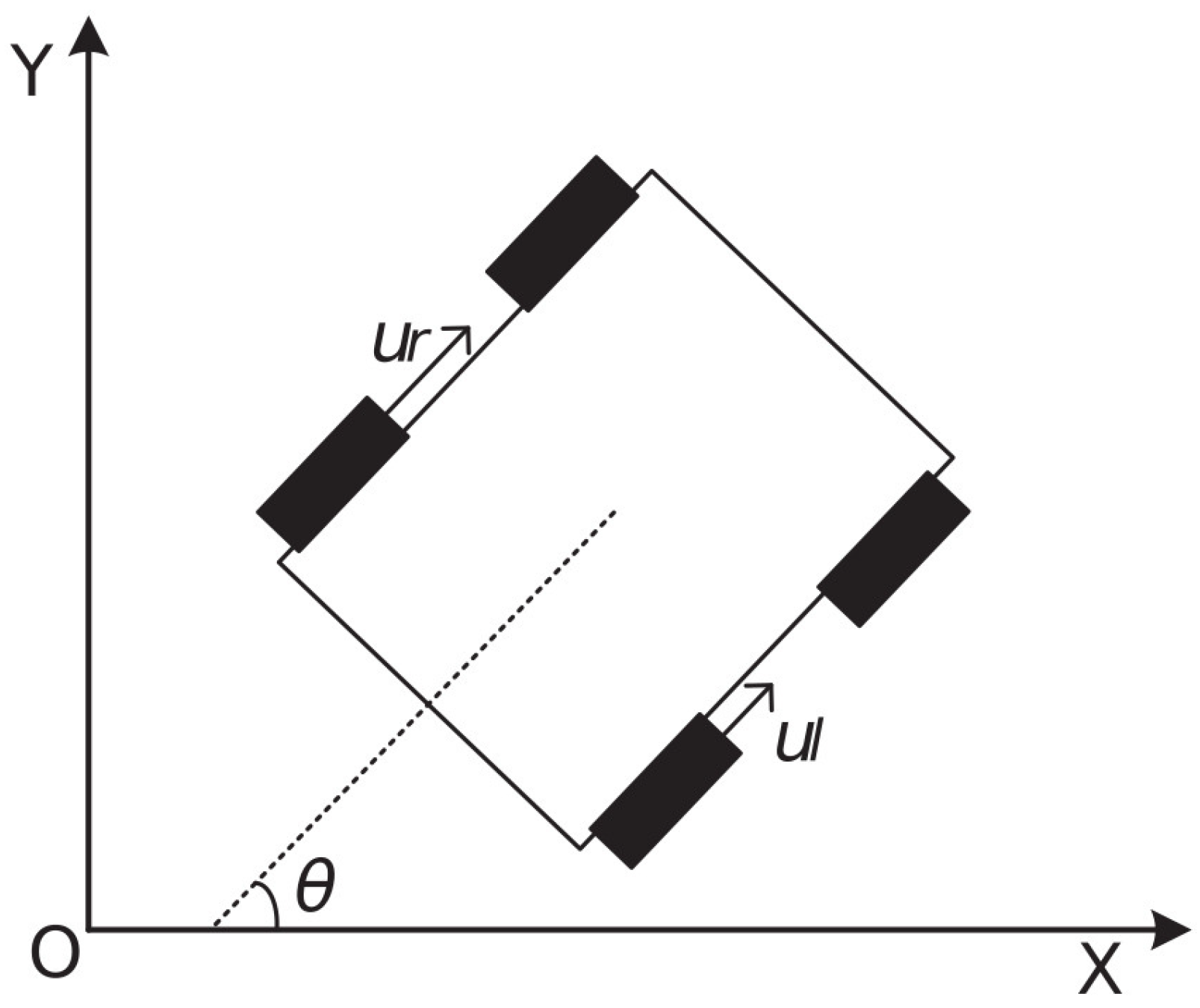
2.1. Robot Model and Control Input
2.2. Problem Statement
3. Initial Path Generation Algorithm
3.1. Initial Path Generation
| Algorithm 1. Build Initial Path . |
| 1: 2: for from to do 3: 4: ; 5: ; 6: if then 7: ; 8: else 9: ; 10: end if 11: ; 12: for do 13: ; 14: ; 15: end for 16: ; 17: if then 18: return ; 19: end if 20: end for 21: ; |
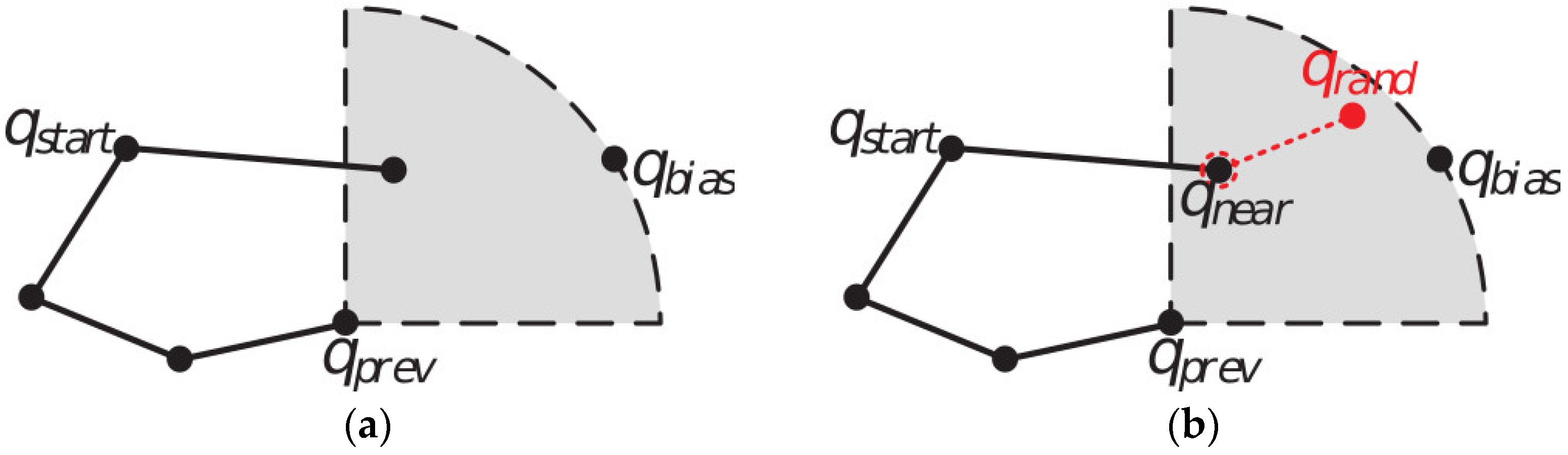
3.2. Objective-Biased Sampling Strategy
3.3. Segmented Forward Pruning
4. Optimization Algorithm
4.1. Optimization Algorithm
| Algorithm 2. Optimization . |
| 1: 2: ; 3: while do 4: ; 5: ; 6: ; 7: ; 8: if then 9: ; 10: else 11: ; 12: end if 13: ; 14: for do 15: ; 16: ; 17: end for 18: ; 19: if then 20: ; 21: ; 22: end if 23: end while |
4.2. Reverse Maintenance Strategy
5. Simulation and Experimental Results
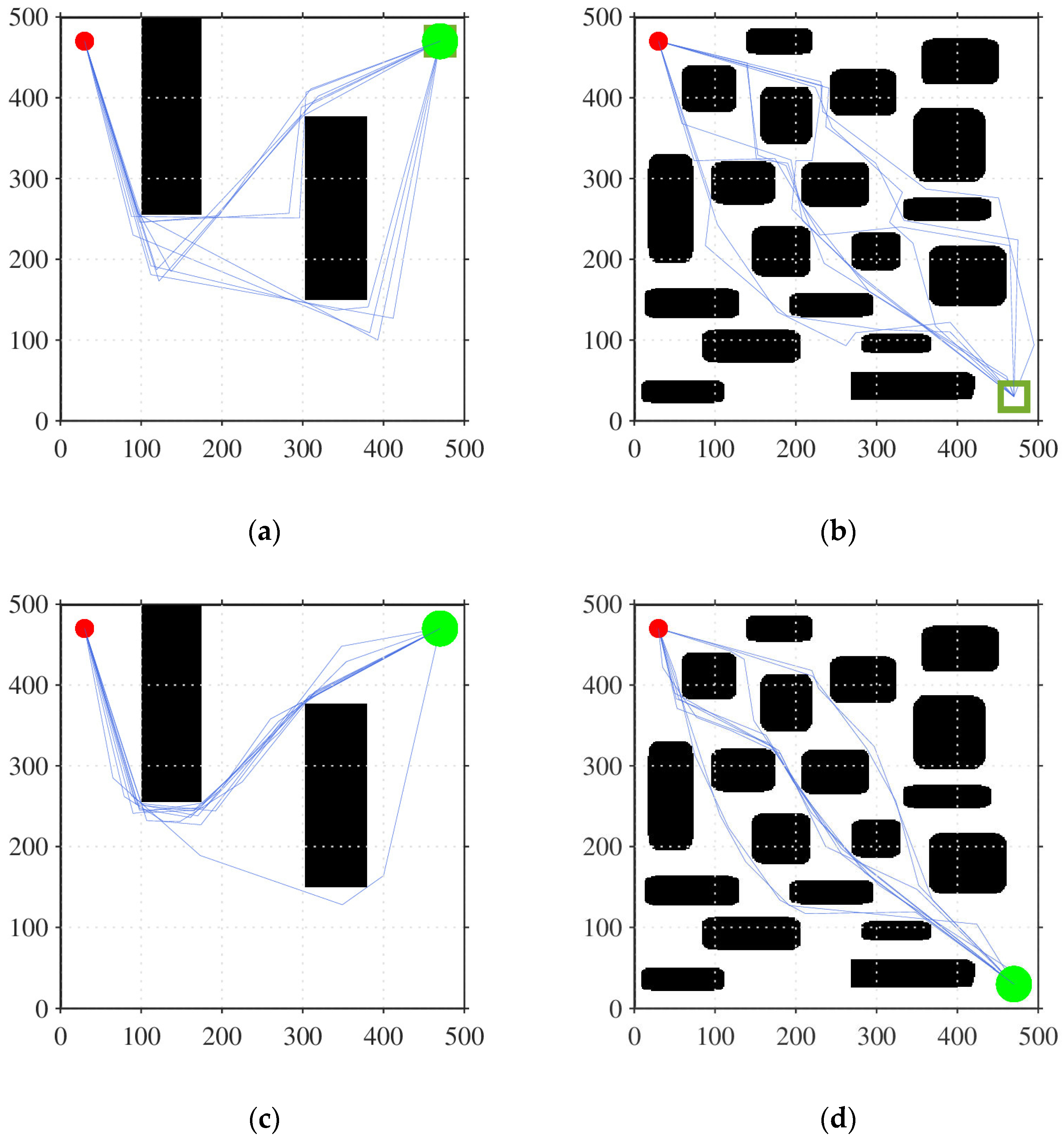
5.1. Initial Path Generation Simulation
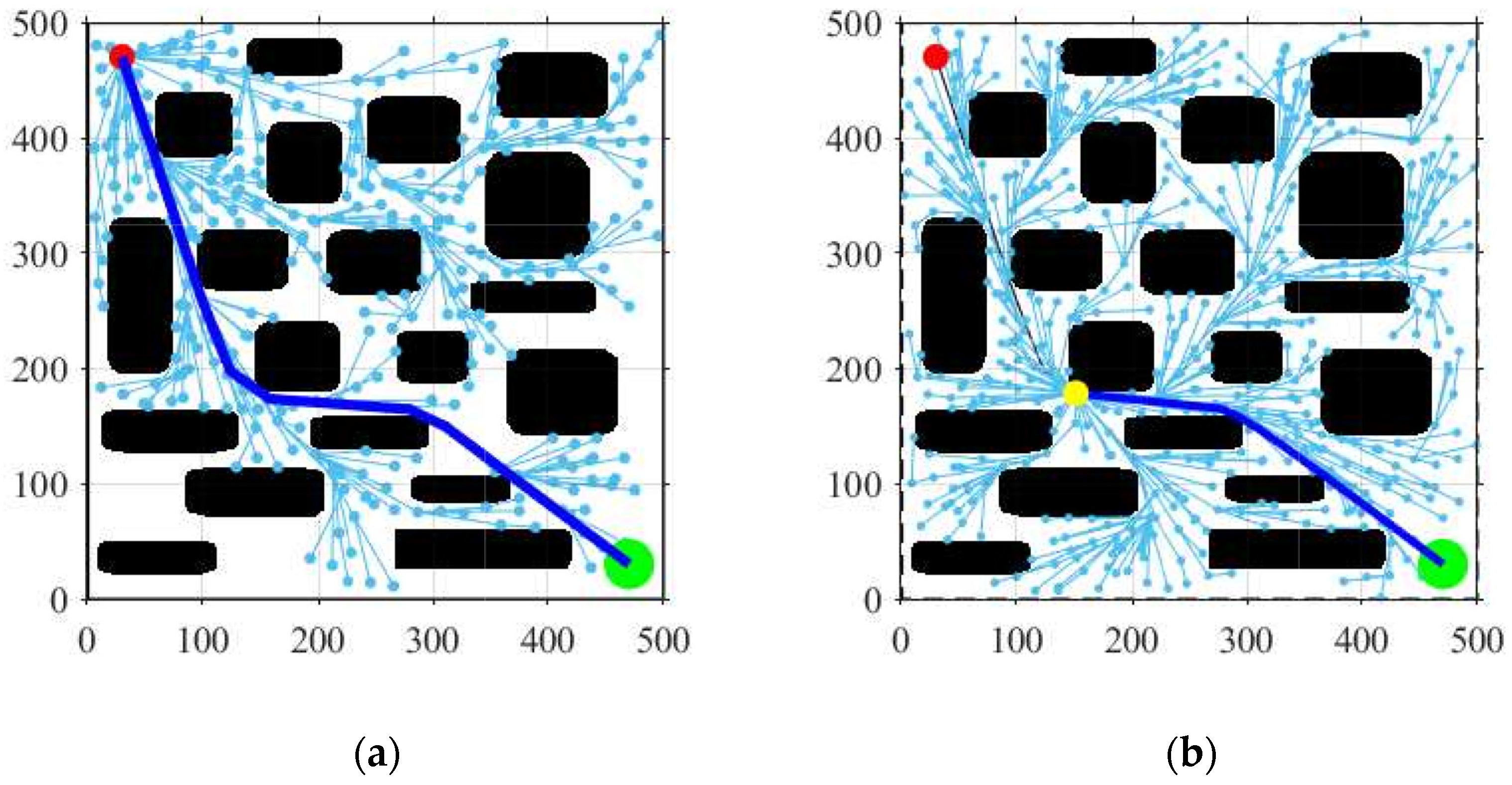
5.2. Optimization Simulation
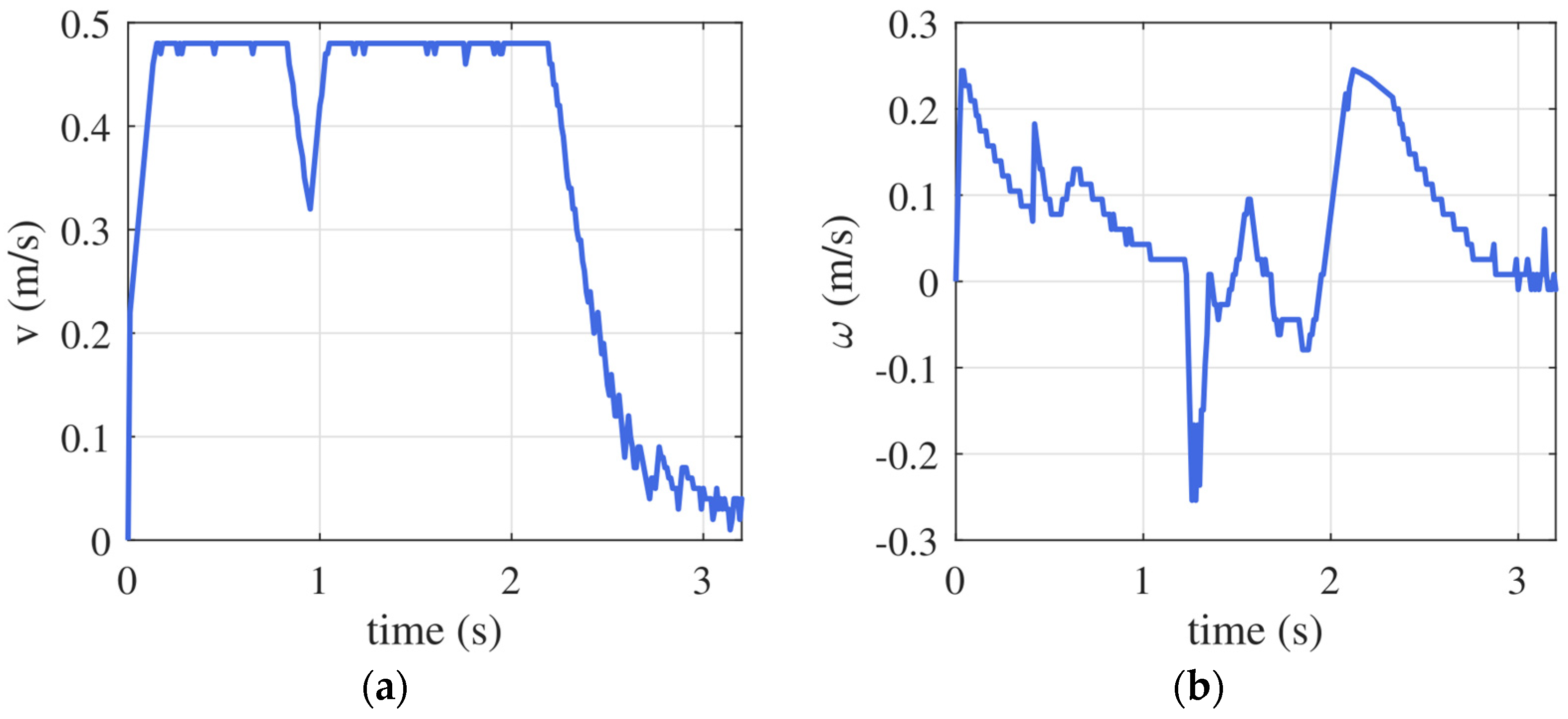
6. DOB-RRT* Evaluations in Real Environment
6.1. Experimental Environment Configuration
6.2. Mobile Robot Applications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Latombe, J.-C. Motion planning: A journey of robots, molecules, digital actors, and other artifacts. Int. J. Robot. Res. 1999, 18, 1119–1128. [Google Scholar] [CrossRef]
- Gao, H.; Hou, X.; Xu, J.; Guan, B. Quad-Rotor Unmanned Aerial Vehicle Path Planning Based on the Target Bias Extension and Dynamic Step Size RRT* Algorithm. World Electr. Veh. J. 2024, 15, 29. [Google Scholar] [CrossRef]
- Liu, Y.; Badler, N.I. Real-time reach planning for animated characters using hardware acceleration. In Proceedings of the 11th IEEE International Workshop on Program Comprehension, New Brunswick, NJ, USA, 8–9 May 2003; pp. 86–93. [Google Scholar]
- Thompson, B.; Yoon, H.-S. Efficient path planning algorithm for additive manufacturing systems. IEEE Trans. Compon. Packag. Manuf. Technol. 2014, 4, 1555–1563. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Li, Z.; Song, S.; Lim, C.M.; Wang, Y.; Ren, H. Safety-enhanced motion planning for flexible surgical manipulator using neural dynamics. IEEE Trans. Control Syst. Technol. 2016, 25, 1711–1723. [Google Scholar] [CrossRef]
- LaValle, S. Planning Algorithms. Camb. Univ. Press Google Sch. 2006, 2, 3671–3678. [Google Scholar]
- Huang, Y.; Lee, H.-H. Adaptive Informed RRT*: Asymptotically Optimal Path Planning With Elliptical Sampling Pools in Narrow Passages. Int. J. Control Autom. Syst. 2024, 22, 241–251. [Google Scholar] [CrossRef]
- Huang, Y.; Tsao, C.-T.; Lee, H.-H. Efficiency Improvement to Neural-Network-Driven Optimal Path Planning via Region and Guideline Prediction. IEEE Robot. Autom. Lett. 2024, 9, 1851–1858. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-exploring random trees: A new tool for path planning. Research Report 9811 1998. [Google Scholar]
- Hsu, D.; Kindel, R.; Latombe, J.-C.; Rock, S. Randomized kinodynamic motion planning with moving obstacles. Int. J. Robot. Res. 2002, 21, 233–255. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Cheng, P. Sampling-Based Motion Planning with Differential Constraints; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2005. [Google Scholar]
- Iehl, R.; Cortés, J.; Simeon, T. Costmap planning in high dimensional configuration spaces. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kaohsiung, Taiwan, 11–14 July 2012; pp. 166–172. [Google Scholar]
- Shkolnik, A.; Walter, M.; Tedrake, R. Reachability-guided sampling for planning under differential constraints. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 2–17 May 2009; pp. 2859–2865. [Google Scholar]
- Yang, K.; Jung, D.; Sukkarieh, S. Continuous curvature path-smoothing algorithm using cubic B zier spiral curves for non-holonomic robots. Adv. Robot. 2013, 27, 247–258. [Google Scholar] [CrossRef]
- Yang, K.; Sukkarieh, S. An analytical continuous-curvature path-smoothing algorithm. IEEE Trans. Robot. 2010, 26, 561–568. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. Randomized bidirectional B-spline parameterization motion planning. IEEE Trans. Intell. Transp. Syst. 2015, 17, 406–419. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Karaman, S.; Walter, M.R.; Perez, A.; Frazzoli, E.; Teller, S. Anytime motion planning using the RRT. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1478–1483. [Google Scholar]
- Qi, J.; Yang, H.; Sun, H. MOD-RRT*: A sampling-based algorithm for robot path planning in dynamic environment. IEEE Trans. Ind. Electron. 2020, 68, 7244–7251. [Google Scholar] [CrossRef]
- Salzman, O.; Halperin, D. Asymptotically near-optimal RRT for fast, high-quality motion planning. IEEE Trans. Robot. 2016, 32, 473–483. [Google Scholar] [CrossRef]
- Otte, M.; Frazzoli, E. RRTX: Asymptotically optimal single-query sampling-based motion planning with quick replanning. Int. J. Robot. Res. 2016, 35, 797–822. [Google Scholar] [CrossRef]
- Chen, L.; Shan, Y.; Tian, W.; Li, B.; Cao, D. A fast and efficient double-tree RRT*-like sampling-based planner applying on mobile robotic systems. IEEE/ASME Trans. Mechatron. 2018, 23, 2568–2578. [Google Scholar] [CrossRef]
- Merat, F. Introduction to robotics: Mechanics and control. IEEE J. Robot. Autom. 1987, 3, 166. [Google Scholar] [CrossRef]
- Geraerts, R.; Overmars, M.H. Creating high-quality paths for motion planning. Int. J. Robot. Res. 2007, 26, 845–863. [Google Scholar] [CrossRef]









| Mean | Min | Max | ||
|---|---|---|---|---|
| RRT | Path Time | 0.23 | 0.13 | 0.41 |
| Plan Length | 749.52 | 697.15 | 958.43 | |
| RRT* | Path Time (s) | 3.81 | 1.51 | 9.22 |
| Plan Length | 694.15 | 673.88 | 888.41 | |
| DOB-RRT* | Path Time (s) | 0.42 | 0.26 | 1.13 |
| Plan Length | 697.91 | 674.29 | 892.13 |
| Mean | Min | Max | ||
|---|---|---|---|---|
| RRT | Path Time (s) | 0.48 | 0.26 | 0.98 |
| Plan Length | 711.71 | 656.1 | 811.21 | |
| RRT* | Path Time (s) | 3.81 | 1.51 | 9.22 |
| Plan Length | 664.71 | 640.94 | 721.05 | |
| DOB-RRT* | Path Time (s) | 0.68 | 0.44 | 1.24 |
| Plan Length | 660.21 | 642.47 | 726.72 |
| RRT* | 2.71 | 2.33 |
| DOB-RRT* | 0.53 | 0.38 |
| Plan Time (s) | Path Length (m) | ||
|---|---|---|---|
| 0.34 | 2.57 | 2.24 | 3.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmaiel, H.; Zhao, G.; Qasem, Z.A.H.; Qi, J.; Sun, H. Double-Layer RRT* Objective Bias Anytime Motion Planning Algorithm. Robotics 2024, 13, 41. https://doi.org/10.3390/robotics13030041
Esmaiel H, Zhao G, Qasem ZAH, Qi J, Sun H. Double-Layer RRT* Objective Bias Anytime Motion Planning Algorithm. Robotics. 2024; 13(3):41. https://doi.org/10.3390/robotics13030041
Chicago/Turabian StyleEsmaiel, Hamada, Guolin Zhao, Zeyad A. H. Qasem, Jie Qi, and Haixin Sun. 2024. "Double-Layer RRT* Objective Bias Anytime Motion Planning Algorithm" Robotics 13, no. 3: 41. https://doi.org/10.3390/robotics13030041
APA StyleEsmaiel, H., Zhao, G., Qasem, Z. A. H., Qi, J., & Sun, H. (2024). Double-Layer RRT* Objective Bias Anytime Motion Planning Algorithm. Robotics, 13(3), 41. https://doi.org/10.3390/robotics13030041







