A Review of the Literature on the Lower-Mobility Parallel Manipulators of 3-UPU or 3-URU Type

Abstract

Various 3-UPU architectures feature two rigid bodies connected to one another through three kinematic chains (limbs) of universal–prismatic–universal (UPU) type. They were first proposed in the last decade of the 20th century and have animated discussions among researchers for more-or-less two decades. Such discussions brought to light many features of lower-mobility parallel manipulators (PMs) that were unknown until then. The discussions also showed that such architectures may be sized into translational PMs, parallel wrists, or even reconfigurable (metamorphic) PMs. Even though commercial robots with these architectures have not yet been built, the interest in them remains. Consequently, a review of the literature on these architectures, highlighting their contribution to the progress of lower-mobility PM design, is still of interest for the scientific community. This paper aims at presenting a critical review of the results that have been obtained up until now.

1. Introduction

The most common parallel manipulators with three degrees of freedom (DOF) are constituted by two rigid bodies, the end effector (platform) and the frame (base), joined by three kinematic chains (limbs) with the same topology and connectivity1 equal to five. Among these parallel manipulators (PMs), 3-UPU architectures2 (Figure 1) are those with three limbs of UPU type. Such architectures are special cases of the 3-UTU ones, where T denotes a generic single-DOF kinematic pair that makes the axes of the two intermediate R-pairs of the limb translate with respect to one another. A T pair, over a P pair, could be, for instance, an R-pair with axis parallel to the two that have to translate with respect to one another (see Figure 2). Even though most of the literature refers to 3-UPU, the presented results hold for any 3-UTU.

In 1996, Tsai [2] proposed a translational 3-UPU. The Tsai 3-UPU (Figure 1c) had the three R-pair axes fixed in the base (in the platform) in a coplanar arrangement. In [2], Tsai solved, in explicit form, the direct (DPA) and inverse (IPA) position analyses of this translational PM (TPM), which gave two DPA solutions and one IPA solution. Such results made him conclude that the translational 3-UPU was simple to manufacture and to control.

Following Tsai’s proposal, Park built a prototype, named SNU 3-UPU [3,4,5] (Figure 1d), which had the three R-pair axes fixed in the base (in the platform) in a coplanar arrangement and with a common intersection point. In 2001 [3], he presented the prototype and highlighted that the SNU 3-UPU exhibited an unforeseen extra mobility at the home position, which made the platform orientation change. Such strange behavior started animated discussions [3,4,5,6,7,8,9] that, in 2002, identified the constraint singularities [3,6] as the main cause of the strange behavior and as a negative feature that occurs in most of the lower-mobility PMs.

In the meantime, Parenti-Castelli et al. [10,11,12,13,14,15,16] studied more general families of TPMs that included both the Tsai 3-UPU and the SNU 3-UPU. In 1998, Di Gregorio and Parenti-Castelli [10] showed that a PM of 3-RRPRR type becomes a TPM if it is manufactured and assembled out of particular singular configurations (later called constraint singularities [6]), so that, in each RRPRR limb,

(i)

the axes of the two intermediate R-pairs are parallel to one another, and

(ii)

the axes of the two ending R-pairs are parallel to each other.

Then, from 1999 to 2000, together with Bubani, Di Gregorio and Parenti-Castelli studied in depth the whole family of translational 3-UPUs with the three R-pair axes fixed in the base (in the platform) in a coplanar arrangement. In [11], Di Gregorio and Parenti-Castelli presented the general expressions of the singularity loci of any translational 3-UPU and demonstrated that, in the above-mentioned case of coplanar axes, the rotation (constraint) singularity locus is constituted by a right circular cylinder (Figure 3), which could degenerate [11,12] (Figure 4) for particular platform (base) geometries, and a plane. In the SNU 3-UPU (Figure 1d), the cylinder equation, reported in [11], becomes the equation of a line perpendicular to the base plane and passing through the home position, which explains the strange behavior found by Park. These results were exploited by Parenti-Castelli et al. to build a prototype [13,14] of the Tsai 3-UPU that worked correctly. Later, the same results together with an in-depth analysis of the joint-clearance effects allowed for Bhutani and Dwarakanath [17,18] to build a “high-precision” Tsai 3-UPU that could be used as a measuring machine.

In 2000, Karouia and Hervè [19] identified the geometric conditions that make a 3-UPU architecture become a parallel wrist3 (PW). In particular, by using group theory, they demonstrated that, out of singular configurations, a 3-UPU architecture is a PW (Figure 1b), if

(a)

the platform and the base are manufactured so that the three R-pair axes embedded in them have a common intersection point;

(b)

each UPU limb (Figure 5) is manufactured and assembled so that the axes of the two intermediate R-pairs are parallel to one another; and

(c)

the 3-UPU is assembled so that the axes of the six R-pairs adjacent to the base or to the platform share a common intersection point (such point becomes the spherical motion center).

Karouia and Hervè [19] also advised that such conditions do not exclude the existence of singular configurations where the platform locally acquires an additional translational DOF. Later, Di Gregorio [20,21], by analyzing statics and kinematics of 3-UPU wrists, provided both the geometric (Figure 6) and the analytic conditions that identify the translation (constraint) singularities of these wrists. In [22], Ashith-Shyam and Ghosal presented a 3-UPU wrist prototype for sun tracking; and, in [23,24], Huda and Takeda presented the prototype of a 3-URU wrist for a machine tool and the adopted design methodology.

The consideration that translational 3-UPUs have rotation singularities and 3-UPU wrists have translation singularities pushed Zlatanov et al. [6] to introduce the concept of “constraint singularity” and to highlight that these singularities may occur in any lower-mobility PMs. A constraint singularity is a configuration where a lower-mobility PM may change its operating mode. They may occur when the limbs’ connectivity is higher than the DOF number of the PM. Also, Zlatanov et al. [25] illustrated this concept through the DYMO 3-URU prototype (Figure 7), which exploited its constraint singularities to change its operating mode: It was able to become a TPM, a PW, or a 3-DOF planar PM. DYMO showed for the first time that a 3-UTU can be a reconfigurable machine.

In particular, a 3-UTU can switch from TPM to PW and vice versa if it satisfies conditions (a) and (b) from Karouia and Hervè [19] as stated above; whereas, it can switch from TPM or PW to 3-DOF planar PM and vice versa, if in addition to satisfying conditions (a) and (b), the three R-pair axes fixed in the base (in the platform) are coplanar. The central issue for actually getting a reconfigurable 3-UTU is how to manage the passage through a singular configuration? In [26], Carbonari et al. bypassed the problem by proposing a reconfigurable 3-URU (Figure 8) that could switch from TPM to PW and vice versa at a given non-singular configuration through an ad-hoc-conceived device, which modifies the geometry of the U-joints adjacent to the base. In the same line, Sarabandi et al. [27] presented a particular 3-UPU geometry that can switch from TPM to PW and vice versa by simply turning the platform assembly upside down. This 3-UPU could do the same switch by passing through a singular configuration without disassembling the platform, but the authors did not propose any strategy to go through the singularity.

Eventually, structural singularities of 3-UPU architectures were used to ideate a Shoenflies motion generator [28] of 4-UPU type [29,30,31,32], and a rolling mechanism [33].

This review paper aims at summarizing the relevant analytic and geometric aspects of the above-mentioned results in a unique framework that should be useful for designers and researchers. The paper is organized as follows. Section 2 gives some background concepts and presents the adopted notations together with some general comments. Section 3 and Section 4 analyze translational and wrist architectures, respectively. Then, Section 5 analyzes reconfigurable and structurally singular architectures, and Section 6 draws the conclusions.

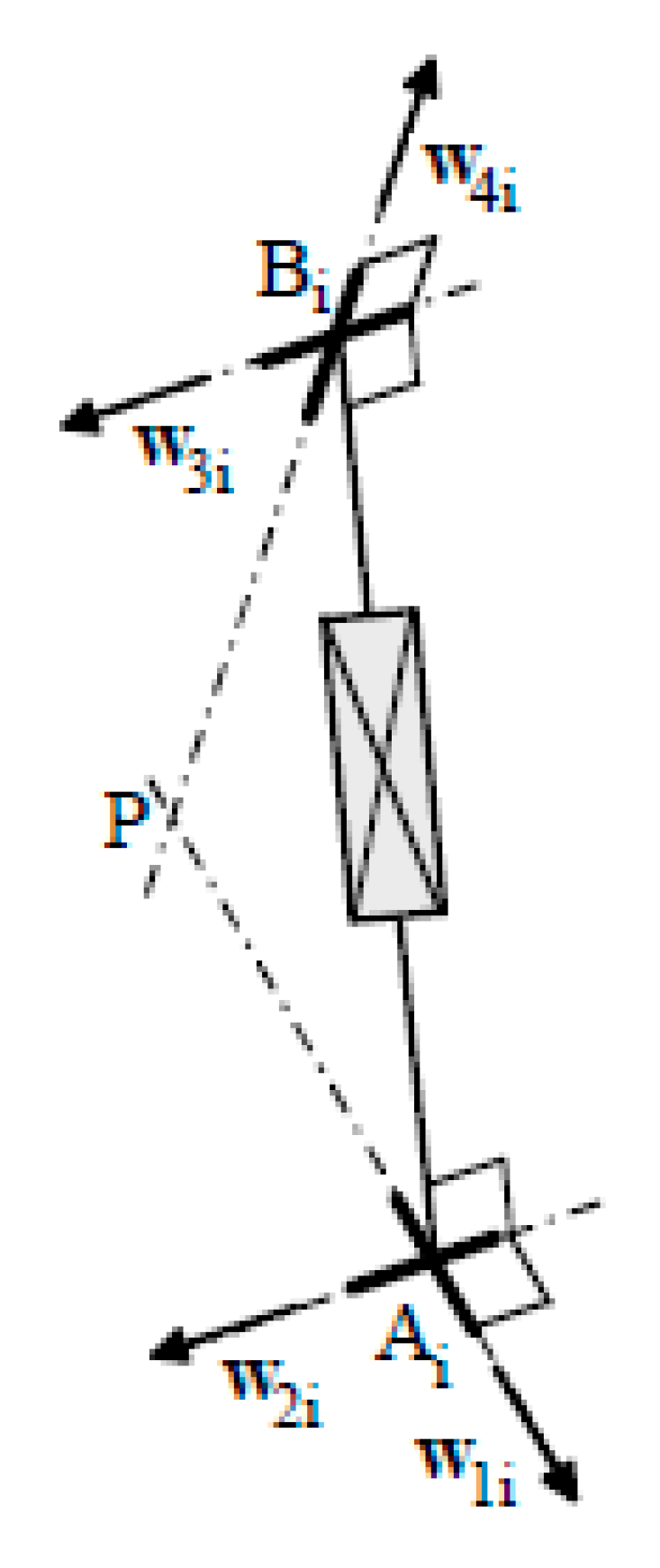
2. Background, Notations, and General Comments

The instantaneous input–output relationship of a PM is a linear and homogeneous system that relates the platform twist and the actuated-joint rates. In this relationship, the two coefficient matrices (Jacobians) that multiply the platform twist, and the actuated-joint rates depend only on the PM configuration. Singularities are PM configurations that makes either or both these Jacobians rank-deficient. The PM configuration is not controllable at a singularity. In particular, singularities of the Jacobian that multiplies the platform twist (named parallel singularities) occur inside the reachable workspace, and make the platform gain one or more instantaneous DOFs locally (i.e., they are a particular type of uncertainty configurations [1]). From a statics’ point of view [21], at a parallel singularity, the platform is not able to carry external loads, even small ones, without overloading at least one link (i.e., without breaking down at least one link). Consequently, parallel singularities must be identified during design and avoided during operation by locating the useful workspace in free-from-singularity regions of the operational space.

That is why the possibility of building a particular type of 3-UPU is related to the identification of those geometries that provide wide free-from-singularity regions where the platform can perform only one type of motion (spatial translation (TPMs) or spherical motion (PWs) or planar motion). The following part of this paper illustrates the main results reported in the literature by analyzing the input–output instantaneous relationships of these architectures.

Figure 1a shows a general 3-UPU architecture together with the adopted notations. With reference to Figure 1a,

-

Ox_by_bz_b and Px_py_pz_p are two Cartesian references fixed to the base and the platform, respectively;

-

A_i (B_i) for i = 1, 2, 3 are the centers of the U joints adjacent to the base (platform);

-

in each UPU limb, the four R-pairs are numbered with an index, j, that increases by moving from the base toward the platform;

-

w_ji, for j = 1, …, 4, is the j-th R-pair axis’ unit vector of the i-th UPU limb, i = 1, 2, 3;

-

w_2i and w_3i are perpendicular to the axis of the i-th limb (i.e., the line through A_i and B_i), for i = 1, 2, 3.

Moreover, the following parameters/vectors are defined:

-

θ_ji, for j = 1, …,4, is the angular joint variable, counterclockwise with respect to w_ji, of the j-th R-pair of the i-th UPU limb, i = 1, 2, 3;

-

d_i = |B_i − A_i| is the linear joint variable of the P-pair (hereafter named “limb length”) of the i-th UPU limb, i = 1, 2, 3;

-

p = (P − O); b_i = (B_i − O) = p + b_0i with b_0i = (B_i − P), for i = 1, 2, 3;

-

a_i = (A_i − O), for i = 1, 2, 3; c_i = (b_0i − a_i) for i = 1, 2, 3; g_i = (b_i − a_i)/d_i for i = 1, 2, 3;

-

r_i = w_1i × w_2i for i = 1, 2, 3; h_i = w_3i × w_4i for i = 1, 2, 3; n_i = [(b_i − a_i)⋅r_i] h_i for i = 1, 2, 3.

With these notations, the following instantaneous relationships can be written:

$${\dot{b}}_{\mathrm{i}}={\dot{\mathrm{d}}}_{\mathrm{i}}{g}_{\mathrm{i}}+{\mathrm{d}}_{\mathrm{i}}{(\dot{\mathsf{\theta }}}_{1\mathrm{i}}{w}_{1\mathrm{i}}+{\dot{\mathsf{\theta }}}_{2\mathrm{i}}{w}_{2\mathrm{i}})\times g_{\mathrm{i}}\hspace{1em}\mathrm{i}=1,2,3,$$

(1a)

$${\dot{b}}_{\mathrm{i}}=\dot{p}+\mathsf{\omega }\times (b_{\mathrm{i}}-p)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3,$$

(1b)

$$\mathsf{\omega }={\displaystyle \sum _{\mathrm{j}=1,4}{\dot{\mathsf{\theta }}}_{\mathrm{ji}}{w}_{\mathrm{ji}}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3,$$

(1c)

where ω is the angular velocity of the platform, and $\dot{x}$ denotes the time derivative of x. Equations (1a), (1b), and (1c) are formally the same that appeared in [34] for the 3-nSPU manipulator and, with the same algebraic manipulations reported in [34], they yield the following instantaneous input–output relationship:

$$\left[\begin{array}{c}1\\ 0\end{array}\right]\dot{d}=\left[\begin{array}{cc}G& K\\ S& J\end{array}\right]\left(\begin{array}{c}\dot{p}\\ \mathsf{\omega }\end{array}\right),$$

(2)

where 1 and 0 are the 3 × 3 identity and null matrices, respectively; $\dot{d}={({\dot{\mathrm{d}}}_1,{\dot{\mathrm{d}}}_2,{\dot{\mathrm{d}}}_3)}^{\mathrm{T}}$ is the vector collecting the P-pairs’ joint rates, which are the instantaneous inputs, and

G^T = (g₁, g₂, g₃), K^T = (k₁, k₂, k₃), S^T = (s₁, s₂, s₃), J^T = (j₁, j₂, j₃)

(3)

with

k_i = (b_i − p) × g_i, s_i = h_i × r_i − [g_i⋅(h_i × r_i)] g_i, j_i = (b_i − p) × s_i − [(b_i − a_i)⋅r_i] h_i,  i = 1, 2, 3.

(4)

System (2) holds for any 3-UPU no matter if it is a TPM or a PW. It becomes specific when the above-mentioned geometric conditions that make the 3-UPU a TPM or a PW are inserted into it. The last three equations of system (2) do not involve the input-joint rates and are general no matter which input variables (i.e., the chosen actuated joints) are used; when their coefficient matrix (i.e., the 3 × 6 matrix [S J]) is rank-deficient, a constraint singularity occurs.

The first three equations of system (2) relate the input-joint rates to the platform twist; in these equations, when the coefficient matrix that multiplies the platform twist (i.e., the 3 × 6 matrix [G K]) is rank deficient, the platform can perform elementary motions without changing its operating mode, even though the actuated joints are locked. These three equations vary together with the associated singularity conditions if the input variables are changed. Nevertheless, if the actuated joints just control the limb lengths, the changes involve only the left-hand sides of these equations, leaving the 3 × 6 matrix [G K] unchanged together with the associated singularities. For instance, with reference to Figure 2, if the actuated P-pair of the i-th limb is replaced by an actuated R-pair with an axis parallel to w_2i and w_3i, the following relationships hold

$${\mathrm{d}}_{\mathrm{i}}^2={\mathrm{e}}_{\mathrm{i}}^2+{\mathrm{f}}_{\mathrm{i}}^2-2{\mathrm{e}}_{\mathrm{i}}^{}{\mathrm{f}}_{\mathrm{i}}^{}\cos {\mathsf{\phi }}_{\mathrm{i}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3$$

(5)

whose 1st time derivatives are

$${\dot{\mathrm{d}}}_{\mathrm{i}}^{}=\frac{{\mathrm{e}}_{\mathrm{i}}^{}{\mathrm{f}}_{\mathrm{i}}^{}\sin {\mathsf{\phi }}_{\mathrm{i}}}{\sqrt{{\mathrm{e}}_{\mathrm{i}}^2+{\mathrm{f}}_{\mathrm{i}}^2-2{\mathrm{e}}_{\mathrm{i}}^{}{\mathrm{f}}_{\mathrm{i}}^{}\cos {\mathsf{\phi }}_{\mathrm{i}}}}{\dot{\mathsf{\phi }}}_{\mathrm{i}}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3.$$

(6)

Thus, the simple substitution of the right-hand side of Equation (6) for ${\dot{\mathrm{d}}}_{\mathrm{i}}$, i = 1, 2, 3 into the left-hand side of system (2) transforms the instantaneous input–output relationship of a 3-UPU into the one of a 3-URU.

3. Translational 3-UTU

The geometric conditions, (i) and (ii), for getting a TPM, with the adopted notations, become (i) w_2i = ±w_3i and (ii) w_1i = ±w_4i for i = 1, 2, 3, which yield h_i = ±r_i, s_i = 0 and j_i = ±[(b_i − a_i)⋅h_i] h_i. Consequently, the instantaneous input–output relationship (2) becomes

$$\left[\begin{array}{c}1\\ 0\end{array}\right]\dot{d}=\left[\begin{array}{cc}G& K\\ 0& J\end{array}\right]\left(\begin{array}{c}\dot{p}\\ \mathsf{\omega }\end{array}\right).$$

(7)

3.1. Rotation (Constraint) Singularities

By canceling the coefficients ±[(b_i − a_i)⋅h_i]4 the last three equations of system (7) become [12]

h_i⋅ω = 0  i = 1, 2, 3.

(8)

Equation (8) admits a non-null solution for ω (i.e., a rotation (constraint) singularity occurs) if and only if

h₁⋅(h₂ × h₃) = 0.

(9)

From a geometric point of view, Equation (9) is satisfied when the three vectors h_i, for i = 1, 2, 3, are coplanar (i.e., when all the intersections among the planes parallel to the U-joints’ cross links are parallel lines). Consequently, if the unit vectors w_1i (w_4i), for i = 1, 2, 3, are all parallel, this geometric condition is always satisfied5 and a structural rotation (constraint) singularity occurs [29,30,31].

From an analytic point of view [11], Equation (9) is an algebraic equation, whose unknowns are the coordinates of a platform point6 measured in Ox_by_bz_b, which represents a surface (rotation (constraint) singularity locus) in Ox_by_bz_b (the operational space) whose points locate the singular configurations where the platform can rotate. The deduction of this algebraic equation is as follows7:

$$w_{3\mathrm{i}}=\frac{w_{4\mathrm{i}}\times (b_{\mathrm{i}}-a_{\mathrm{i}})}{\left|w_{4\mathrm{i}}\times (b_{\mathrm{i}}-a_{\mathrm{i}})\right|}=\frac{w_{1\mathrm{i}}\times [p+(b_{0\mathrm{i}}-a_{\mathrm{i}})]}{\left|w_{1\mathrm{i}}\times [p+(b_{0\mathrm{i}}-a_{\mathrm{i}})]\right|}=\frac{w_{1\mathrm{i}}\times p+c_{\mathrm{i}}}{\left|w_{1\mathrm{i}}\times p+c_{\mathrm{i}}\right|}\mathrm{i}=1,2,3$$

(10)

which yields

$$h_{\mathrm{i}}=w_{3\mathrm{i}}\times w_{4\mathrm{i}}=\frac{(w_{1\mathrm{i}}\times p+c_{\mathrm{i}})\times w_{1\mathrm{i}}}{\left|w_{1\mathrm{i}}\times p+c_{\mathrm{i}}\right|}=\frac{p-(w_{1\mathrm{i}}\cdot p)w_{1\mathrm{i}}+c_{\mathrm{i}}\times w_{1\mathrm{i}}}{\left|w_{1\mathrm{i}}\times p+c_{\mathrm{i}}\right|}\hspace{1em}\mathrm{i}=1,2,3$$

(11)

and

$$h_1\cdot (h_2\times h_3)=\frac{[p-(w_{11}\cdot p)w_{11}+c_1\times w_{11}]\cdot \{[p-(w_{12}\cdot p)w_{12}+c_2\times w_{12}]\times [p-(w_{13}\cdot p)w_{13}+c_3\times w_{13}]\}}{\left|w_{11}\times p+c_1\right|\left|w_{12}\times p+c_2\right|\left|w_{13}\times p+c_3\right|}.$$

(12)

Since the denominator of expression (12) is constituted by the product of vector magnitudes, it does not provide zeros of Equation (9); hence, in Equation (9), it can be eliminated to give the following algebraic equation of the singularity locus:

$$[p-(w_{11}\cdot p)w_{11}+c_1\times w_{11}]\cdot \{[p-(w_{12}\cdot p)w_{12}+c_2\times w_{12}]\times [p-(w_{13}\cdot p)w_{13}+c_3\times w_{13}]\}=0$$

(13a)

whose expansion yields

(w₁₂ ⋅ p) (w₁₃ ⋅ p) [(w₁₂ × w₁₃) ⋅ p] − (w₁₂ ⋅ p){[w₁₂ × (c₃ × w₁₃)] ⋅ p} − (w₁₃ ⋅ p) {[(c₂ × w₁₂) × w₁₃] ⋅ p} +
+ {[(c₂ × w₁₂) × (c₃ × w₁₃)] ⋅ p} + (w₁₁ ⋅ p) {[(w₁₃ ⋅ p)w₁₃ − (w₁₂ ⋅ p)w₁₂ − (c₃ × w₁₃) + c₂ × w₁₂] × w₁₁} ⋅ p +
− (w₁₁ ⋅ p) (w₁₂ ⋅ p) (w₁₃ ⋅ p) [(w₁₂ × w₁₃) ⋅ w₁₁] + (w₁₁ ⋅ p) (w₁₂ ⋅ p) [w₁₂ × (c₃ × w₁₃)] ⋅ w₁₁ +
+ (w₁₁ ⋅ p) (w₁₃ ⋅ p) [(c₂ × w₁₂) × w₁₃] ⋅ w₁₁ – (w₁₁ ⋅ p) [(c₂ × w₁₂) × (c₃ × w₁₃)] ⋅ w₁₁ − {[(w₁₃ ⋅ p)w₁₃ +
− (w₁₂ ⋅ p)w₁₂ − (c₃ × w₁₃) + c₂ × w₁₂] × (c₁ × w₁₁)} ⋅ p + (w₁₂ ⋅ p) (w₁₃ ⋅ p) [(w₁₂ × w₁₃) ⋅ (c₁ × w₁₁)] +
− (w₁₂ ⋅ p) {[w₁₂ × (c₃ × w₁₃)] ⋅ (c₁ × w₁₁)} − (w₁₃ ⋅ p) {[(c₂ × w₁₂) × w₁₃] ⋅ (c₁ × w₁₁)} +
+ [(c₂ × w₁₂) × (c₃ × w₁₃)] ⋅ (c₁ × w₁₁) = 0.

(13b)

Equation (13) is cubic in the coordinates of point P (see Figure 1a). Since the coefficients that appear in Equation (13) depend on the shape of the platform and base, the rotation (constraint) singularity locus depends only on the platform and base geometries.

In the SNU 3-UPU (Figure 1d), the base (platform) triangle A₁A₂A₃ (B₁B₂B₃) is an equilateral triangle, and the unit vectors w_1i (w_4i), i = 1, 2, 3, lie on three R-pair axes that have the center of this triangle as a common intersection. By choosing this center as origin O (P), and the triangle plane as the x_by_b (x_py_p) coordinate plane for Ox_by_bz_b (Px_py_pz_p), it is easy to realize that, in Equation (13a), the vectors c_i × w_1i, for i = 1, 2, 3, are all null vectors since c_i is parallel to w_1i. Consequently, when P lies on the line through O perpendicular to the base triangle A₁A₂A₃ (i.e., the SNU 3-UPU is at its home position), the dot products (w_1i ⋅ p), for i = 1, 2, 3, are equal to zero and the left-hand side of Equation (13a), which becomes p ⋅(p × p), is identically equal to zero, that is, the platform can rotate.

In the Tsai 3-UPU (Figure 1c), the base (platform) triangle A₁A₂A₃ (B₁B₂B₃) is an equilateral triangle, but the i-th unit vector w_1i (w_4i), i = 1, 2, 3, is parallel to the base-triangle (platform-triangle) side opposite to the vertex A_i (B_i), which the corresponding R-pair axis passes through. For this geometry, Equation (13) yields, as a singularity locus, a cubic surface (see [14]), that is the product of the base-triangle plane by a right circular cylinder whose generatrix is a line perpendicular to the base-triangle plane. The analytic expression of this cylinder is reported in [14].

The set of all the 3-UPUs with the axes of the three R-pairs, adjacent to the base (platform), that lie on the plane of the base (platform) triangle contains both SNU and Tsai 3-UPUs. This set was studied in [12]. The introduction of the geometric conditions that identify this set into Equation (13) shows that [12] the rotation (constraint) singularity locus of all these 3-UPUs is always the product of the base-triangle plane by a right circular cylinder whose generatrix is a line perpendicular to the base-triangle plane. By choosing A₁ (B₁) as origin O (P), and the base-triangle (platform-triangle) plane as x_by_b (x_py_p) coordinate plane for Ox_by_bz_b (Px_py_pz_p), the analytic expression of this cylinder is reported in [12] together with the simple geometric construction shown in Figure 3, which allows to draw immediately the singularity cylinder. The construction of Figure 3 relies on the fact that three points are sufficient to identify a circle, and that three singularities, B₁’, B₁’’ and B₁’’’ in Figure 3, are easy to find. The same construction highlights (Figure 4) that, when any two R-pair axes (together with the corresponding unit vectors w_1i) are parallel, the singularity cylinder degenerates into a singularity plane (see [12] for details).

3.2. Translation Singularities

Out of rotation singularities, the platform angular velocity, ω, is a null vector. Thus, the first three equations of system (7) become [12]:

$${\mathbf{g}}_{\mathrm{i}}\cdot \dot{p}={\dot{\mathrm{d}}}_{\mathrm{i}}\hspace{1em}\mathrm{i}=1,2,3.$$

(14)

When the actuators are locked, Equations (14) admit a non-null solution for $\dot{p}$ (i.e., a translation singularity occurs) if and only if

g₁⋅(g₂ × g₃) = 0.

(15)

From a geometric point of view, Equation (15) is satisfied when the three unit vectors g_i, for i = 1, 2, 3, are parallel to a plane (i.e., when all the limb axes are parallel to a unique plane). If the base and platform triangles are equal, this condition is always satisfied and a structural translation singularity occurs [2,12].

From an analytic point of view [11], Equation (15) is an algebraic equation, whose unknowns are the coordinates of a platform point measured in Ox_by_bz_b, which represents a surface (translation singularity locus) in Ox_by_bz_b whose points locate the singular configurations where the platform translation is not controllable by the actuators. The deduction of this algebraic equation is as follows:

$$g_1\cdot (g_2\times g_3)=\frac{(p+b_{01}-a_1)\cdot [(p+b_{02}-a_2)\times (p+b_{03}-a_3)]}{{\mathrm{d}}_1{\mathrm{d}}_2{\mathrm{d}}_3}.$$

(16)

Since the denominator of expression (16) is constituted by the product of the limb lengths, it does not provides zeros of Equation (15); hence, in Equation (15), it can be eliminated to give the following algebraic equation of the singularity locus

$$(p+b_{01}-a_1)\cdot [(p+b_{02}-a_2)\times (p+b_{03}-a_3)]=0$$

(17a)

whose expansion is

p⋅{[(b₀₃ − a₃) × (b₀₁ − a₁)] + [(b₀₁ − a₁) × (b₀₂ − a₂)] + [(b₀₂ − a₂) × (b₀₃ − a₃)]} + (b₀₁ − a₁) ⋅ [(b₀₂ − a₂) × (b₀₃ − a₃)] = 0.

(17b)

Equation (17b) is linear in the coordinates of P. Therefore, the translation singularity locus is always a plane [11], which is perpendicular to the vector in curly brackets that dot multiplies p in Equation (17b). By choosing A₁ (B₁) as origin O (P), and the base-triangle (platform-triangle) plane as the x_by_b (x_py_p) coordinate plane for Ox_by_bz_b (Px_py_pz_p), it is easy to realize that, if the base and platform triangles are equal, the vectors (b_0i − a_i), for i = 1, 2, 3, are all null vectors. Consequently, the left-hand side of Equation (17b) is identically null (i.e., a structural singularity occurs). Also, in the case of the 3-UPUs with the axes of the three R-pairs, adjacent to the base (platform), that lie on the plane of the base (platform) triangle, it is easy to realize that the singularity plane is the base-triangle plane [12]. Indeed, in this case, the vectors (b_0i − a_i), for i = 1, 2, 3, are all parallel to the base plane, which implies that, in Equation (17b), the mixed product (b₀₁ − a₁) ⋅ [(b₀₂ − a₂) × (b₀₃ − a₃)] is equal to zero and the vector in curly brackets is perpendicular to the base-triangle plane.

4. 3-UTU Wrist

The geometric condition (a) for getting a PW, allows for the choice of the point O (P), see Figure 1a,b, coincident with the common intersection point of the three axes of the R-pairs adjacent to the base (platform). Such a choice makes a_i (b_i) parallel to w_1i (w_4i), for i = 1, 2, 3. In addition, condition (b) yields w_2i = ±w_3i; whereas, condition (c) implies that O coincides with P (i.e., p = 0). Consequently, k_i = b_i × g_i, s_i = h_i × r_i since g_i is perpendicular to h_i × r_i, and j_i = 0, for i = 1, 2, 3 (see Equation (4)). These formulas allow for the conclusion that k_i and s_i are both parallel to w_2i and w_3i (see Figure 5), which are unit vectors perpendicular to the plane of the triangle A_iB_iP.

Therefore, the instantaneous input–output relationship (2) for the 3-UPU wrist becomes

$$\left[\begin{array}{c}1\\ 0\end{array}\right]\dot{d}=\left[\begin{array}{cc}G& K\\ S& 0\end{array}\right]\left(\begin{array}{c}\dot{p}\\ \mathsf{\omega }\end{array}\right).$$

(18)

4.1. Translation (Constraint) Singularities

The last three equations of system (18) become

$${\mathbf{s}}_{\mathrm{i}}\cdot \dot{p}=0\hspace{1em}\mathrm{i}=1,2,3.$$

(19)

Equations (19) admit a non-null solution for $\dot{p}$ (i.e., a translation (constraint) singularity occurs) if and only if

s₁ ⋅ (s₂ × s₃) = 0,

(20a)

which, since s_i is parallel to w_2i for i = 1, 2, 3, can be simplified as follows [20,21]:

w₂₁ ⋅ (w₂₂ × w₂₃) = 0.

(20b)

Equation (20b) is satisfied when the three vectors w_2i, for i = 1, 2, 3, are all parallel to a unique plane, that is, when the planes of the three triangles A_iB_iP, for i = 1, 2, 3, have a line as a common intersection (Figure 6) [20]. Also, it is worth noting that each unit vector w_2i is indeterminate when the triangle A_iB_iP is flattened (i.e., the points A_i, B_i, and P are aligned); in this case (see Figure 5), a simple inspection of the flattened limb reveals that the i-th limb can freely rotate around its axis.

A general analytic expression of Equation (20b) has been deduced in [21] where, by using the Rodrigues parameters [35] to parameterize the platform orientation, a fourth-degree polynomial equation in the three Rodrigues parameters has been obtained.

4.2. Rotation Singularities

Out of the translation singularities, $\dot{p}$ is a null vector. Thus, the first three equations of system (18) become [20]:

$${\mathbf{k}}_{\mathrm{i}}\cdot \mathsf{\omega }={\dot{\mathrm{d}}}_{\mathrm{i}}\hspace{1em}\hspace{1em}\mathrm{i}=1,2,3.$$

(21)

When the actuators are locked, Equation (21) admit a non-null solution for ω (i.e., a rotation singularity occurs) if and only if

k₁⋅(k₂ × k₃) = 0,

(22a)

which, since k_i is parallel to w_2i for i = 1, 2, 3, can be simplified as follows [20,21]:

w₂₁ ⋅ (w₂₂ × w₂₃) = 0.

(22b)

Equation (22b) coincides with Equation (20b). Thus, the locus of the rotation singularities coincides with that of the translation (constraint) singularities in a 3-UPU wrist.

5. Reconfigurable and Structurally Singular 3-6UTUs

The presence of constraint singularities in 3-UTUs allows for the building of reconfigurable PMs, that is, machines that can change their operating mode. In [25], Zlatanov et al. presented DYMO (Figure 7a), a 3-URU that is able to become a TPM (Figure 7b), a PW (Figure 7c), or a 3-DOF planar PM (Figure 7d). DYMO (Figure 7a) satisfies geometric conditions (a) and (b), and has the three R-pair axes fixed in the base (in the platform) in a coplanar arrangement. So, the constraint singularity that occurs when the intersection of the three R-pair axes fixed in the platform coincides with the intersection of the three R-pair axes fixed in the base is present in all the three operating modes and can be exploited to change the operating mode.

Unfortunately, the platform pose is out of control at a constraint singularity, and this simple method for reconfiguring the machine cannot be implemented. Carbonari et al. [26] bypassed the problem by proposing a reconfigurable 3-URU that could switch from TPM to PW and vice versa at a given non-singular configuration. Their 3-URU (Figure 8) satisfies conditions (a) and (b), and adopts an ad-hoc-conceived device, which modifies the geometry of the U-joints adjacent to the base. In the same line, Sarabandi et al. [27] presented a particular 3-UPU geometry that satisfies conditions (a) and (b) and can switch from TPM to PW and vice versa by simply turning the platform assembly upside down.

The rotation (constraint) structural singularity (see Section 3.1) that occurs in translational 3-UPUs when (Figure 1) the unit vectors w_1i (w_4i), for i = 1, 2, 3, are all parallel makes the platform able to rotate around axes parallel to these unit vectors. Such additional finite DOF allows for the introduction of one more UPU limb to control the platform rotation. The resulting 4-UPU is a Shoenflies motion generator [28]. It was presented in [29] and studied in [30,31,32].

Eventually, in a translational 3-UPU, if, over the above-mentioned structural singularity, the structural translation singularity (see Section 3.2) that occurs when the platform and base triangles are equal is introduced, the resulting 3-UPU acquires two additional finite DOFs: one rotation and one translation. Such a geometry has been used in [33] to conceive a 5-DOF rolling mechanism able to move on the floor.

6. Conclusions

A critical review of the extensive literature on 3-UTU architectures has been presented. The presented review allows for the following conclusions: The study of these architectures contributed to the mechanism theory by revealing the presence of “constraint singularities” in most of the lower-mobility PMs. All the design tools have been developed for both translational 3-UPUs and 3-UPU wrists. Even though commercial robots with these architectures are not present on the market, prototypes that work correctly have been built, and the structural singularities of these architectures have been exploited. The majority of the published works on the translational 3-UTUs refer to the set of 3-UTUs with coplanar axes of the three R-pairs adjacent to the base (platform).

Possible future research on these architectures should investigate translational 3-UTUs with base and platform geometries in which the R-pair axes are not coplanar and strategies to pass through a constraint singularity.