FloorVLoc: A Modular Approach to Floorplan Monocular Localization
Abstract
1. Introduction
- does not require the environment to be previously explored
- incorporates prior information which is readily available and easy to obtain
- effectively resolves the metric scale ambiguity
- provides a means to handle and correct drift in all degrees of freedom
- utilizes geometric map information of the environment structure which is stable and stationary (without photometric reliance) and
- keeps the prior map information required at a minimum.
- A modular core methodology which can integrate any monocular-based local scene reconstruction with a floorplan to perform global localization, including automatic scale calibration.
- A theoretical and experimental analysis of the conditions on the visual features associated with the walls necessary for the localization to be uniquely recovered.
- Two full global positioning systems based on this methodology which perform continuous positioning at real-time computation rates. One approach utilizes visual odometry in between Floorplan Vision Vehicle Localization (FloorVLoc) linear optimization localization updates; another approach formulates the system in a Monte Carlo Localization (MCL) framework with a FloorVLoc measurement model, correcting motion based on whatever wall information is present shown in Figure 2.
- Experimental evaluation of the global positioning systems for indoor search and rescue applications in a challenging real-world environment, as well as real and simulation testing for a focused study of various aspects of the methodology.
2. Literature Review
3. Global Localization: The FloorVLoc Core
3.1. Optimization Framework (FloorVLoc-OPT)
3.2. Planar Motion
3.2.1. Data Association
3.2.2. Initialization
3.2.3. Uniqueness Criteria
3.3. Monte Carlo Localization Framework (FloorVLoc-MCL)
3.3.1. Motion Model
3.3.2. Measurement Model
4. Experimental Evaluation
4.1. Comparison to Related Methods
4.2. Ablation Study
4.2.1. FloorVLoc-MCL
4.2.2. FloorVLoc-OPT
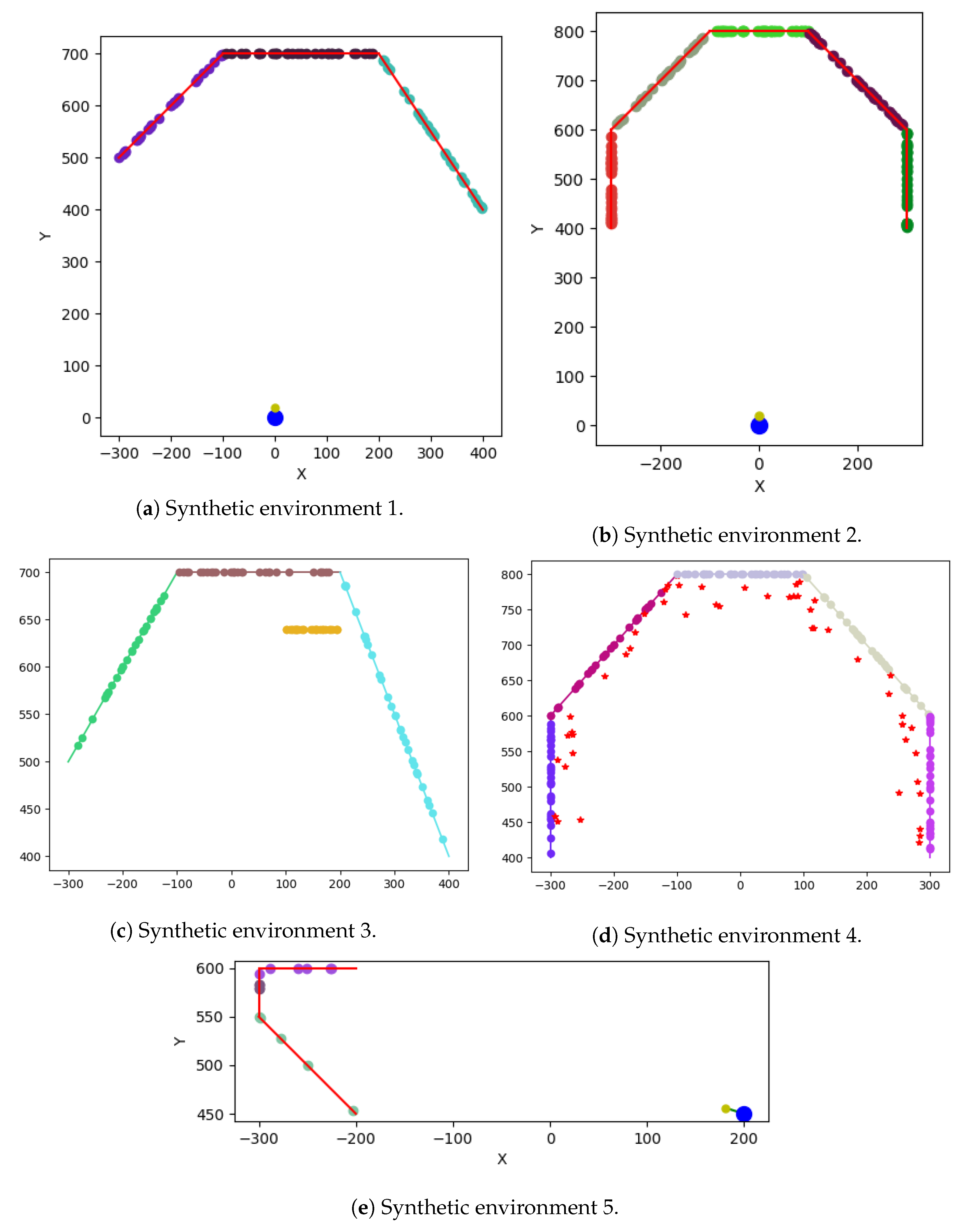
4.2.3. Test 1—Scale Perturbation
4.2.4. Test 2—Initial Orientation Perturbation
4.2.5. Test 3—Initial Position Perturbation
4.2.6. Test 4—All Perturbation
4.3. Runtime
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix B. Proof of Lemma 2
Appendix C. Process for Obtaining Ground Truth for the Tech-R-2 Dataset

References
- Mouradian, C.; Yangui, S.; Glitho, R.H. Robots as-a-service in cloud computing: Search and rescue in large-scale disasters case study. In Proceedings of the 15th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 12–15 January 2018; pp. 1–7. [Google Scholar]
- Whitman, J.; Zevallos, N.; Travers, M.; Choset, H. Snake robot urban search after the 2017 mexico city earthquake. In Proceedings of the 2018 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Philadelphia, PA, USA, 6–8 August 2018; pp. 1–6. [Google Scholar]
- Martell, A.; Lauterbach, H.A.; Nuchtcer, A. Benchmarking structure from motion algorithms of urban environments with applications to reconnaissance in search and rescue scenarios. In Proceedings of the 2018 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Philadelphia, PA, USA, 6–8 August 2018; pp. 1–7. [Google Scholar]
- Sun, W.; Xue, M.; Yu, H.; Tang, H.; Lin, A. Augmentation of Fingerprints for Indoor WiFi Localization Based on Gaussian Process Regression. IEEE Trans. Veh. Technol. 2018, 67, 10896–10905. [Google Scholar] [CrossRef]
- Zhao, X.; Ruan, L.; Zhang, L.; Long, Y.; Cheng, F. An Analysis of the Optimal Placement of Beacon in Bluetooth-INS Indoor Localization. In Proceedings of the 14th International Conference on Location Based Services (LBS 2018), Zurich, Switzerland, 15–17 January 2018; pp. 50–55. [Google Scholar]
- Großwindhager, B.; Stocker, M.; Rath, M.; Boano, C.A.; Römer, K. SnapLoc: An ultra-fast UWB-based indoor localization system for an unlimited number of tags. In Proceedings of the 18th ACM/IEEE International Conference on Information Processing in Sensor Networks (IPSN), Montreal, QC, Canada, 16–18 April 2019; pp. 61–72. [Google Scholar]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A Novel NLOS Mitigation Algorithm for UWB Localization in Harsh Indoor Environments. IEEE Trans. Veh. Technol. 2019, 68, 686–699. [Google Scholar] [CrossRef]
- Di Felice, M.; Bocanegra, C.; Chowdhury, K.R. WI-LO: Wireless indoor localization through multi-source radio fingerprinting. In Proceedings of the 10th International Conference on Communication Systems & Networks (COMSNETS), Bengaluru, India, 3–7 January 2018; pp. 305–311. [Google Scholar]
- Cheng, W.; Lin, W.; Chen, K.; Zhang, X. Cascaded parallel filtering for memory-efficient image-based localization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 1032–1041. [Google Scholar]
- Speciale, P.; Schonberger, J.L.; Kang, S.B.; Sinha, S.N.; Pollefeys, M. Privacy preserving image-based localization. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 5493–5503. [Google Scholar]
- Thoma, J.; Paudel, D.P.; Chhatkuli, A.; Probst, T.; Gool, L.V. Mapping, Localization and Path Planning for Image-Based Navigation Using Visual Features and Map. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7383–7391. [Google Scholar]
- Piasco, N.; Sidibé, D.; Gouet-Brunet, V.; Demonceaux, C. Learning Scene Geometry for Visual Localization in Challenging Conditions. In Proceedings of the IEEE 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9094–9100. [Google Scholar]
- Brachmann, E.; Krull, A.; Nowozin, S.; Shotton, J.; Michel, F.; Gumhold, S.; Rother, C. Dsac-differentiable ransac for camera localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6684–6692. [Google Scholar]
- Brachmann, E.; Rother, C. Learning less is more-6d camera localization via 3d surface regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4654–4662. [Google Scholar]
- Cavallari, T.; Golodetz, S.; Lord, N.A.; Valentin, J.; Di Stefano, L.; Torr, P.H. On-the-fly adaptation of regression forests for online camera relocalisation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4457–4466. [Google Scholar]
- Meng, L.; Chen, J.; Tung, F.; Little, J.J.; Valentin, J.; de Silva, C.W. Backtracking regression forests for accurate camera relocalization. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6886–6893. [Google Scholar]
- Schönberger, J.L.; Pollefeys, M.; Geiger, A.; Sattler, T. Semantic visual localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6896–6906. [Google Scholar]
- Taira, H.; Okutomi, M.; Sattler, T.; Cimpoi, M.; Pollefeys, M.; Sivic, J.; Pajdla, T.; Torii, A. InLoc: Indoor visual localization with dense matching and view synthesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7199–7209. [Google Scholar]
- Camposeco, F.; Cohen, A.; Pollefeys, M.; Sattler, T. Hybrid scene compression for visual localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–21 June 2019; pp. 7653–7662. [Google Scholar]
- Sattler, T.; Maddern, W.; Toft, C.; Torii, A.; Hammarstrand, L.; Stenborg, E.; Safari, D.; Okutomi, M.; Pollefeys, M.; Sivic, J.; et al. Benchmarking 6dof outdoor visual localization in changing conditions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8601–8610. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Brahmbhatt, S.; Gu, J.; Kim, K.; Hays, J.; Kautz, J. Geometry-aware learning of maps for camera localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2616–2625. [Google Scholar]
- Cai, M.; Shen, C.; Reid, I.D. A Hybrid Probabilistic Model for Camera Relocalization. BMVC 2018, 1, 8. [Google Scholar]
- Kendall, A.; Cipolla, R. Geometric loss functions for camera pose regression with deep learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5974–5983. [Google Scholar]
- Melekhov, I.; Ylioinas, J.; Kannala, J.; Rahtu, E. Image-based localization using hourglass networks. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 879–886. [Google Scholar]
- Naseer, T.; Burgard, W. Deep regression for monocular camera-based 6-dof global localization in outdoor environments. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1525–1530. [Google Scholar]
- Walch, F.; Hazirbas, C.; Leal-Taixe, L.; Sattler, T.; Hilsenbeck, S.; Cremers, D. Image-based localization using lstms for structured feature correlation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 627–637. [Google Scholar]
- Wu, J.; Ma, L.; Hu, X. Delving deeper into convolutional neural networks for camera relocalization. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5644–5651. [Google Scholar]
- Sattler, T.; Zhou, Q.; Pollefeys, M.; Leal-Taixe, L. Understanding the limitations of cnn-based absolute camera pose regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–21 June 2019; pp. 3302–3312. [Google Scholar]
- Feng, G.; Ma, L.; Tan, X.; Qin, D. Drift-Aware Monocular Localization Based on a Pre-Constructed Dense 3D Map in Indoor Environments. ISPRS Int. J. Geo-Inf. 2018, 7, 299. [Google Scholar] [CrossRef]
- Feng, G.; Ma, L.; Tan, X. Line Model-Based Drift Estimation Method for Indoor Monocular Localization. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2019; pp. 1–5. [Google Scholar]
- Munoz-Salinas, R.; Marin-Jimenez, M.J.; Medina-Carnicer, R. SPM-SLAM: Simultaneous localization and mapping with squared planar markers. Pattern Recognit. 2019, 86, 156–171. [Google Scholar] [CrossRef]
- Munoz-Salinas, R.; Marin-Jimenez, M.J.; Yeguas-Bolivar, E.; Medina-Carnicer, R. Mapping and localization from planar markers. Pattern Recognit. 2018, 73, 158–171. [Google Scholar] [CrossRef]
- Romero-Ramirez, F.J.; Muñoz-Salinas, R.; Medina-Carnicer, R. Speeded up detection of squared fiducial markers. Image Vis. Comput. 2018, 76, 38–47. [Google Scholar] [CrossRef]
- Shipitko, O.S.; Abramov, M.P.; Lukoyanov, A.S.; Panfilova, E.I.; Kunina, I.A.; Grigoryev, A.S. Edge detection based mobile robot indoor localization. In Eleventh International Conference on Machine Vision (ICMV 2018); International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11041, p. 110412V. [Google Scholar]
- Unicomb, J.; Ranasinghe, R.; Dantanarayana, L.; Dissanayake, G. A monocular indoor localiser based on an extended kalman filter and edge images from a convolutional neural network. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar]
- Torii, A.; Taira, H.; Sivic, J.; Pollefeys, M.; Okutomi, M.; Pajdla, T.; Sattler, T. Are Large-Scale 3D Models Really Necessary for Accurate Visual Localization? IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Caselitz, T.; Steder, B.; Ruhnke, M.; Burgard, W. Monocular camera localization in 3d lidar maps. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 1926–1931. [Google Scholar] [CrossRef]
- Ito, S.; Endres, F.; Kuderer, M.; Tipaldi, G.D.; Stachniss, C.; Burgard, W. W-rgb-d: Floor-plan-based indoor global localization using a depth camera and wifi. In Proceedings of the 2014 IEEE international conference on robotics and automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 417–422. [Google Scholar]
- Winterhalter, W.; Fleckenstein, F.; Steder, B.; Spinello, L.; Burgard, W. Accurate indoor localization for RGB-D smartphones and tablets given 2D floor plans. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 3138–3143. [Google Scholar]
- Ma, L.; Kerl, C.; Stückler, J.; Cremers, D. CPA-SLAM: Consistent plane-model alignment for direct RGB-D SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 15–20 September 2016; pp. 1285–1291. [Google Scholar]
- Chu, H.; Ki Kim, D.; Chen, T. You are here: Mimicking the human thinking process in reading floor-plans. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2210–2218. [Google Scholar]
- Mendez, O.; Hadfield, S.; Pugeault, N.; Bowden, R. SeDAR: Reading floorplans like a human. Int. J. Comput. Vis. 2019. [Google Scholar] [CrossRef]
- Mendez, O.; Hadfield, S.; Pugeault, N.; Bowden, R. SeDAR-Semantic Detection and Ranging: Humans can localise without LiDAR, can robots? In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–8. [Google Scholar]
- Wang, S.; Fidler, S.; Urtasun, R. Lost shopping! monocular localization in large indoor spaces. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2695–2703. [Google Scholar]
- Boniardi, F.; Caselitz, T.; Kümmerle, R.; Burgard, W. A pose graph-based localization system for long-term navigation in CAD floor plans. Robot. Auton. Syst. 2019, 112, 84–97. [Google Scholar] [CrossRef]
- Boniardi, F.; Caselitz, T.; Kummerle, R.; Burgard, W. Robust LiDAR-based localization in architectural floor plans. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3318–3324. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Cvišić, I.; Ćesić, J.; Marković, I.; Petrović, I. SOFT-SLAM: Computationally efficient stereo visual simultaneous localization and mapping for autonomous unmanned aerial vehicles. J. Field Robot. 2018, 35, 578–595. [Google Scholar] [CrossRef]
- Gao, X.; Wang, R.; Demmel, N.; Cremers, D. LDSO: Direct sparse odometry with loop closure. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2198–2204. [Google Scholar]
- Pascoe, G.; Maddern, W.; Tanner, M.; Piniés, P.; Newman, P. Nid-slam: Robust monocular slam using normalised information distance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1435–1444. [Google Scholar]
- Buczko, M.; Willert, V. Monocular outlier detection for visual odometry. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 739–745. [Google Scholar]
- Siam, S.M.; Zhang, H. Fast-SeqSLAM: A fast appearance based place recognition algorithm. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5702–5708. [Google Scholar]
- Forster, C.; Zhang, Z.; Gassner, M.; Werlberger, M.; Scaramuzza, D. SVO: Semidirect visual odometry for monocular and multicamera systems. IEEE Trans. Robot. 2016, 33, 249–265. [Google Scholar] [CrossRef]
- Gomez-Ojeda, R.; Briales, J.; Gonzalez-Jimenez, J. Pl-svo: Semi-direct monocular visual odometry by combining points and line segments. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4211–4216. [Google Scholar]
- Indelman, V.; Roberts, R.; Dellaert, F. Incremental light bundle adjustment for structure from motion and robotics. Robot. Auton. Syst. 2015, 70, 63–82. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Probabilistic Semi-Dense Mapping from Highly Accurate Feature-Based Monocular SLAM. In Proceedings of the Robotics: Science and Systems, Rome, Italy, 13–17 July 2015; Volume 2015. [Google Scholar]
- Salehi, A.; Gay-Bellile, V.; Bourgeois, S.; Chausse, F. Improving constrained bundle adjustment through semantic scene labeling. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 133–142. [Google Scholar]
- Urban, S.; Wursthorn, S.; Leitloff, J.; Hinz, S. MultiCol bundle adjustment: A generic method for pose estimation, simultaneous self-calibration and reconstruction for arbitrary multi-camera systems. Int. J. Comput. Vis. 2017, 121, 234–252. [Google Scholar]
- Zhao, L.; Huang, S.; Sun, Y.; Yan, L.; Dissanayake, G. Parallaxba: Bundle adjustment using parallax angle feature parametrization. Int. J. Robot. Res. 2015, 34, 493–516. [Google Scholar] [CrossRef]
- Godard, C.; Mac Aodha, O.; Firman, M.; Brostow, G.J. Digging into self-supervised monocular depth estimation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019; pp. 3828–3838. [Google Scholar]
- Chen, P.Y.; Liu, A.H.; Liu, Y.C.; Wang, Y.C.F. Towards Scene Understanding: Unsupervised Monocular Depth Estimation With Semantic-Aware Representation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; pp. 2619–2627. [Google Scholar]
- Wang, R.; Pizer, S.M.; Frahm, J.M. Recurrent Neural Network for (Un-)Supervised Learning of Monocular Video Visual Odometry and Depth. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; pp. 5550–5559. [Google Scholar]
- Chen, W.; Qian, S.; Deng, J. Learning Single-Image Depth From Videos Using Quality Assessment Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; pp. 5604–5613. [Google Scholar]
- Gur, S.; Wolf, L. Single Image Depth Estimation Trained via Depth From Defocus Cues. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; pp. 7675–7684. [Google Scholar]
- Frost, D.; Prisacariu, V.; Murray, D. Recovering Stable Scale in Monocular SLAM Using Object-Supplemented Bundle Adjustment. IEEE Trans. Robot. 2018, 34, 736–747. [Google Scholar] [CrossRef]
- Parkhiya, P.; Khawad, R.; Murthy, J.K.; Bhowmick, B.; Krishna, K.M. Constructing Category-Specific Models for Monocular Object-SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar] [CrossRef]
- Gálvez-López, D.; Salas, M.; Tardós, J.D.; Montiel, J. Real-time monocular object slam. Robot. Auton. Syst. 2016, 75, 435–449. [Google Scholar] [CrossRef]
- Murthy, J.K.; Sharma, S.; Krishna, K.M. Shape priors for real-time monocular object localization in dynamic environments. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1768–1774. [Google Scholar]
- Pillai, S.; Leonard, J. Monocular slam supported object recognition. arXiv 2015, arXiv:1506.01732. Available online: https://arxiv.org/abs/1506.01732 (accessed on 6 September 2020).
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Wang, X.; Zhang, H.; Yin, X.; Du, M.; Chen, Q. Monocular Visual Odometry Scale Recovery Using Geometrical Constraint. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 988–995. [Google Scholar] [CrossRef]
- Bullinger, S.; Bodensteiner, C.; Arens, M.; Stiefelhagen, R. 3d vehicle trajectory reconstruction in monocular video data using environment structure constraints. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 35–50. [Google Scholar]
- Song, S.; Chandraker, M. Robust scale estimation in real-time monocular SFM for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1566–1573. [Google Scholar]
- Zhou, D.; Dai, Y.; Li, H. Reliable scale estimation and correction for monocular visual odometry. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gotenburg, Sweden, 19–22 June 2016; pp. 490–495. [Google Scholar]
- Dragon, R.; Van Gool, L. Ground plane estimation using a hidden markov model. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 4026–4033. [Google Scholar]
- Liu, H.; Chen, M.; Zhang, G.; Bao, H.; Bao, Y. Ice-ba: Incremental, consistent and efficient bundle adjustment for visual-inertial slam. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1974–1982. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Von Stumberg, L.; Usenko, V.; Cremers, D. Direct Sparse Visual-Inertial Odometry using Dynamic Marginalization. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar] [CrossRef]
- Quan, M.; Piao, S.; Tan, M.; Huang, S.S. Map-Based Visual-Inertial Monocular SLAM using Inertial assisted Kalman Filter. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar]
- Shin, Y.S.; Park, Y.S.; Kim, A. Direct visual SLAM using sparse depth for camera-lidar system. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–8. [Google Scholar]
- Graeter, J.; Wilczynski, A.; Lauer, M. Limo: Lidar-monocular visual odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7872–7879. [Google Scholar]
- Giubilato, R.; Chiodini, S.; Pertile, M.; Debei, S. Scale Correct Monocular Visual Odometry Using a LiDAR Altimeter. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3694–3700. [Google Scholar]
- Alatise, M.B.; Hancke, G.P. Pose estimation of a mobile robot based on fusion of IMU data and vision data using an extended Kalman filter. Sensors 2017, 17, 2164. [Google Scholar] [CrossRef] [PubMed]
- Bloesch, M.; Burri, M.; Omari, S.; Hutter, M.; Siegwart, R. Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback. Int. J. Robot. Res. 2017, 36, 1053–1072. [Google Scholar] [CrossRef]
- Gamage, D.; Drummond, T. Reduced dimensionality extended kalman filter for slam in a relative formulation. In Proceedings of the 2015 IEEE/RSJ international conference on intelligent robots and systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1365–1372. [Google Scholar]
- Ko, N.Y.; Youn, W.; Choi, I.H.; Song, G.; Kim, T.S. Features of invariant extended Kalman filter applied to unmanned aerial vehicle navigation. Sensors 2018, 18, 2855. [Google Scholar] [CrossRef]
- Teng, C.H. Enhanced outlier removal for extended Kalman filter based visual inertial odometry. In Proceedings of the 2018 IEEE International Conference on Applied System Invention (ICASI), Chiba, Japan, 13–17 April 2018; pp. 74–77. [Google Scholar]
- Wen, S.; Zhang, Z.; Ma, C.; Wang, Y.; Wang, H. An extended Kalman filter-simultaneous localization and mapping method with Harris-scale-invariant feature transform feature recognition and laser mapping for humanoid robot navigation in unknown environment. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417744747. [Google Scholar] [CrossRef]
- Jo, H.; Cho, H.M.; Jo, S.; Kim, E. Efficient Grid-Based Rao–Blackwellized Particle Filter SLAM With Interparticle Map Sharing. IEEE/ASME Trans. Mechatronics 2018, 23, 714–724. [Google Scholar] [CrossRef]
- Ma, K.; Schirru, M.M.; Zahraee, A.H.; Dwyer-Joyce, R.; Boxall, J.; Dodd, T.J.; Collins, R.; Anderson, S.R. Robot mapping and localisation in metal water pipes using hydrophone induced vibration and map alignment by dynamic time warping. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2548–2553. [Google Scholar]
- Rormero, A.R.; Borges, P.V.K.; Pfrunder, A.; Elfes, A. Map-aware particle filter for localization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2018; pp. 2940–2947. [Google Scholar]
- Taniguchi, A.; Hagiwara, Y.; Taniguchi, T.; Inamura, T. Online spatial concept and lexical acquisition with simultaneous localization and mapping. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 811–818. [Google Scholar]
- Valls, M.I.; Hendrikx, H.F.; Reijgwart, V.J.; Meier, F.V.; Sa, I.; Dubé, R.; Gawel, A.; Bürki, M.; Siegwart, R. Design of an autonomous racecar: Perception, state estimation and system integration. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2048–2055. [Google Scholar]
- Noonan, J.; Rotstein, H.; Geva, A.; Rivlin, E. Vision-Based Indoor Positioning of a Robotic Vehicle with a Floorplan. In Proceedings of the 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 1–8. [Google Scholar]
- Noonan, J.; Rotstein, H.; Geva, A.; Rivlin, E. Global Monocular Indoor Positioning of a Robotic Vehicle with a Floorplan. Sensors 2019, 19, 634. [Google Scholar] [CrossRef]
- Geva, A. Sensory Routines for Indoor Autonomous Quad-Copter. Ph.D. Thesis, Technion, Israel Institute of Technology, Haifa, Israel, 2019. [Google Scholar]
- Slavcheva, M.; Kehl, W.; Navab, N.; Ilic, S. Sdf-2-sdf registration for real-time 3d reconstruction from RGB-D data. Int. J. Comput. Vis. 2018, 126, 615–636. [Google Scholar]
- Whelan, T.; Salas-Moreno, R.F.; Glocker, B.; Davison, A.J.; Leutenegger, S. ElasticFusion: Real-time dense SLAM and light source estimation. Int. J. Robot. Res. 2016, 35, 1697–1716. [Google Scholar] [CrossRef]
- Kähler, O.; Prisacariu, V.A.; Murray, D.W. Real-time large-scale dense 3D reconstruction with loop closure. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 500–516. [Google Scholar]
- Dai, A.; Nießner, M.; Zollhöfer, M.; Izadi, S.; Theobalt, C. Bundlefusion: Real-time globally consistent 3d reconstruction using on-the-fly surface reintegration. ACM Trans. Graph. (ToG) 2017, 36, 76a. [Google Scholar] [CrossRef]
- Xie, X.; Yang, T.; Li, J.; Ren, Q.; Zhang, Y. Fast and Seamless Large-scale Aerial 3D Reconstruction using Graph Framework. In Proceedings of the ACM 2018 International Conference on Image and Graphics Processing, Hong Kong, China, 24–26 February 2018; pp. 126–130. [Google Scholar]
- Dellaert, F.; Fox, D.; Burgard, W.; Thrun, S. Monte carlo localization for mobile robots. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 2, pp. 1322–1328. [Google Scholar]
- Sun, Y.; Liu, M.; Meng, M.Q.H. Motion removal for reliable RGB-D SLAM in dynamic environments. Robot. Auton. Syst. 2018, 108, 115–128. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, M.; Meng, M.Q.H. Improving RGB-D SLAM in dynamic environments: A motion removal approach. Robot. Auton. Syst. 2017, 89, 110–122. [Google Scholar] [CrossRef]
- Torr, P.H.; Zisserman, A. MLESAC: A new robust estimator with application to estimating image geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]



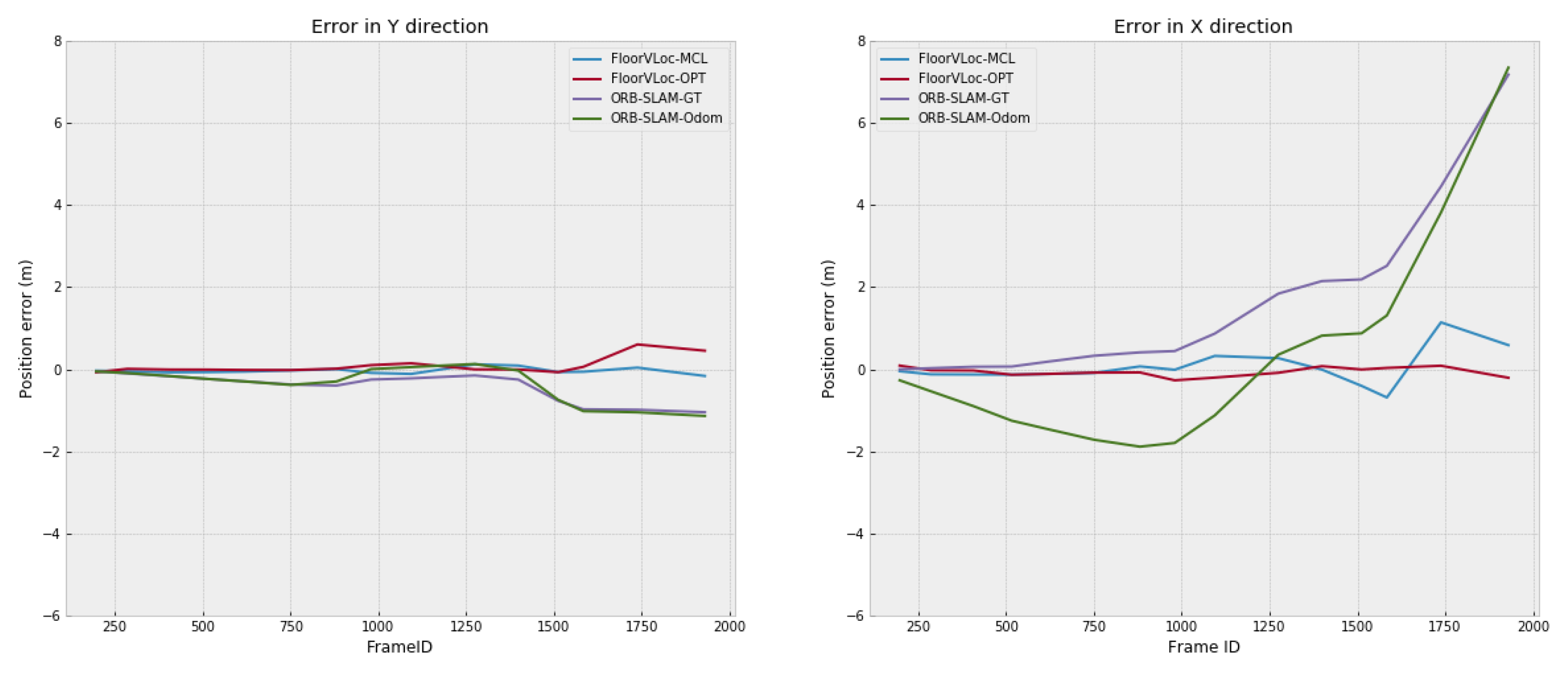







| Method | (cm) | (cm) | (rad) | (rad) |
|---|---|---|---|---|
| ORB-SLAM with Odometry Scale | (151.31, 43.66) | (202.65, 34.58) | 0.0088 | 0.019 |
| ORB-SLAM with GT Scale | (23.67, 37.46) | (249.59, 42.24) | 0.0088 | 0.019 |
| FloorVLoc-OPT | (5.86, 8.00) | (10.90, 19.34) | 0.00035 | 0.046 |
| FloorVLoc-MCL | (5.92, 3.37) | (40.10, 7.86) | 0.00066 | 0.080 |
| Parameters | Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | Test 6 | Test 7 | Test 8 | Test 9 |
|---|---|---|---|---|---|---|---|---|---|
| Synthetic Environment | 1 | 1 | 1 | 5 | 2 | 2 | 4 | 1 | 3 |
| Init Ori Error (rad) | 0 | 0 | 0 | 0.04 | 0 | 0.02 | 0 | 0 | 0 |
| Incorrect Correspondences | 0 | 1 | 1 | 1 | 53.3% | 53.3% | 50 | 40% | 30 |
| Single Incorrect Corres. Error (cm) | - | 3.6 | 193.2 | - | - | - | - | - | - |
| Num Planes | 3 | 3 | 3 | 3 | 5 | 5 | 5 | 3 | 4 |
| Num Points/Plane | 30 | 30 | 30 | 5 | 30 | 30 | 30 | 30 | 30 |
| Robust Estimation | - | - | - | - | ✓ | ✓ | ✓ | ✓ | ✓ |
| Pixel Noise [–0.5, 0.5] px | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Scale Factor Noise | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Position Error (cm) | (–0.05, –0.15) | (–0.19, 0.49) | (–23.2, 31.2) | (0.267, 6.36) | (0.88, 0.49) | (–0.49, 0.62) | (0.05, –0.07) | (0.32, 7.6) | (0.44, 0.16) |
| Orientation Error (rad) | 0.0001 | 0.0006 | 0.074 | 0.01468 | 0.0016 | 0.001 | 0.0041 | 0.0002 | 0.0017 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noonan, J.; Rivlin, E.; Rotstein, H. FloorVLoc: A Modular Approach to Floorplan Monocular Localization. Robotics 2020, 9, 69. https://doi.org/10.3390/robotics9030069
Noonan J, Rivlin E, Rotstein H. FloorVLoc: A Modular Approach to Floorplan Monocular Localization. Robotics. 2020; 9(3):69. https://doi.org/10.3390/robotics9030069
Chicago/Turabian StyleNoonan, John, Ehud Rivlin, and Hector Rotstein. 2020. "FloorVLoc: A Modular Approach to Floorplan Monocular Localization" Robotics 9, no. 3: 69. https://doi.org/10.3390/robotics9030069
APA StyleNoonan, J., Rivlin, E., & Rotstein, H. (2020). FloorVLoc: A Modular Approach to Floorplan Monocular Localization. Robotics, 9(3), 69. https://doi.org/10.3390/robotics9030069




