Next Article in Journal
Quantitative Analysis of Land Subsidence and Its Effect on Vegetation in Xishan Coalfield of Shanxi Province
Previous Article in Journal
Spatial Patterns of the Spread of COVID-19 in Singapore and the Influencing Factors
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJGI
Volume 11
Issue 3
10.3390/ijgi11030153
ijgi-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Use of Spatial Interpolation to Improve the Quality of Corn Silage Data in Case of Presence of Extreme or Missing Values

by
Thomas M. Koutsos
*,
Georgios C. Menexes
and
Ilias G. Eleftherohorinos
School of Agriculture, Faculty of Agriculture, Forestry and Natural Environment, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
*
Author to whom correspondence should be addressed.
ISPRS Int. J. Geo-Inf. 2022, 11(3), 153; https://doi.org/10.3390/ijgi11030153
Submission received: 3 January 2022 / Revised: 13 February 2022 / Accepted: 21 February 2022 / Published: 22 February 2022
Browse Figures
Review Reports Versions Notes

Abstract

:
Agricultural spatial analysis has the potential to offer new ways of analyzing crop data considering the spatial information of the measurements. Moving from farmers’ estimates and crop-cuts techniques to interpolation is a new challenge, and a promising path to achieving more reliable results, especially in the case of field data with extreme or missing values. By comparing the main descriptive statistics of three types of crop parameters (fresh weight, dry weight, and ear weight) in three randomly taken maize plots, we found that the issue of missing values can be addressed by using interpolation to calculate estimated values of given parameters in non-sampling locations. Moreover, based on the descriptive statistics, the implementation of interpolation can reduce crop field variability (extreme values) and achieve an improvement of coefficient of variation (CV) values up to 30%, compared with other methods used, such as the replacing of missing values by the average of all data, or the average of the row or column, with an improvement of only up to 15%. These findings strongly suggest that the implementation of an interpolation method in case of extreme or missing values in crop data is an effective process for improving their quality, and consequently, their reliability. As a result, the application of spatial interpolation to existing crop data can provide more dependable estimations of average crop parameters values, compared to the usual farmers’ estimates.

1. Introduction

Crop yield and other crop parameters such as fresh and dry weight are the most commonly computed estimates to provide productivity metrics in both plot-level analysis, and in larger scale design. However, although a wide variety of methodological protocols and sampling methods was used for the estimation of crop parameters, no improvements were observed, and in some cases, the estimated accuracy is not clearly understood or clarified [1,2,3,4,5,6,7]. Among these methods, the crop-cutting techniques have been regarded as the most reliable and objective for estimating crop yield and other crop parameters, although they are usually dependent on a number of factors, such as administrative setup, type and size of field staff, farmer cooperation, land configuration, field shape, soil differences and harvest time, crop type, cropping pattern, available skills, and resources [6,8,9,10,11,12,13]. Furthermore, the existence of missing values and outliers, along with the arbitrary process of removing measurements from field areas with no adequate plant density, are the most important issues that further affect the expected shortcomings in the field estimates.
Data quality issues, such as completeness, consistency, accuracy, and validity [14,15,16,17,18], are needed before the analysis, because data with low quality lead to poor decision-making, and consequently, to misleading conclusions, and, in some cases, do not reflect actual or real-world situations. Completeness is mainly related to the presence of missing values in a data set, which, from a statistical point of view, reduce the representativeness of the sample, and can therefore falsify parameter estimates and inferences about the parent statistical population. In addition, the statistical analysis of data with many missing values becomes complicated and risky, since, according to [19,20], the analysis and the imputation of missing values in a data set derived from an experiment are not easy tasks, even in cases where only one observation is missing. Based on this, [21] reported that there are several ways to overcome the issues of missing values, such as (a) imputation by filling the “gaps” with other values (e.g., mean or median values), (b) omission by discarding cases with missing values from further statistical analyses, and (c) the use of specialized statistical methods that are rather robust and unaffected by the presence of missing values.
The prediction of missing values at non-sampled points, using existing measured data, is of great interest in many scientific disciplines, and is highly appreciated as the best linear unbiased prediction (BLUP) method for delivering accurate predictions at non-sampling locations [22,23,24]. Among the most successful statistical methods, Kriging, a geostatistical interpolation gridding method, has been proven useful and popular in many fields, producing visually appealing contour maps from irregularly spaced data. Regarding agriculture, Kriging is highly recommended as an effective method to derive single-year yield maps, such as durum wheat yield data [25], sugarcane data [26], corn grain and corn silage yield data [24], or multi-year crop yield data, including both spatial and temporal variation in yield. Kriging has also been successfully applied to soil parameter mapping [27], such as iron content, alone or via Co-Kriging, to explore the spatial cross-correlation of soil parameters and pH or electrical conductivity [28].
The main idea of using the effective interpolation Kriging method is to obtain more weight in the prediction of missing data (missing values) near sample points. Kriging is based on the knowledge of the spatial structure of data via the use of variogram or covariance with the calculation of the weighted average of data. New values can be estimated either in non-sampled locations (missing values) or in locations with extreme values (outliers). The estimation of the interpolated value is given as the linearly weighted sum of the values of its surrounding points. The calculation of the weighting factors is done by minimizing the error variance of the model of the spatial continuity for the data regarding the spatial distribution of the data. Therefore, the final aim of the Kriging interpolation method is to always achieve the best linear unbiased prediction based on the calculation of prediction variance, such as the variance of the difference of the linear predictor and the measured data. In general, interpolation has been thoroughly examined for its importance in precision crop production [29] to explore the drivers of the within-field spatial and temporal variability of crop yield [30], or to predict the spatial patterns of within-field crop yield variability [31]. Recently, a new, interesting approach has been proposed for locating and removing extreme values from crop field data using spatial analysis [32].
This work aims to examine whether the implementation of a spatial interpolation technique can improve crop data quality by reducing crop field variability. We also aim to explore the way in which interpolation can manage extreme and missing values in experimental plot data, and therefore its potential to provide more reliable and representative mean values as productivity metrics for crop parameters. The main idea is to take advantage of the power of an exact interpolator, such as Kriging, to transform the measurements taken in the field into a surface of new estimated values throughout the area of interest. If interpolation can improve data quality, then estimates can be more accurate, and therefore, the calculation of mean values as crop metrics can be more dependable, reliable, and representative for the statistical population of any crop parameter under consideration. Therefore, given the most commonly measured maize parameters (fresh weight—FW, dry weight—DW, and ear weight—EW) of three randomly taken experimental plots, we examined the benefit of applying an interpolation method to the original set of measurements and how safe it is to draw conclusions for larger cultivating areas based on small experimental plots.
Therefore, the main objectives of this work are the following:
–
Examine whether an interpolation method can improve field data quality by reducing the expected crop field variability, and to what extent this can be achieved.
–
Examine whether an interpolation method can effectively address the problems of extreme or missing values in data.

2. Materials and Methods

A maize (hybrid AGN720, Italy) crop was established in a three-ha field area of the AUTH Farm (latitude 40°32′1.75″ N and longitude 22°59′26.98″ (A) during the 2016 growing season. The seedbed was prepared according to agricultural practices applied in the area, and fertilization was made with 200 and 100 kg N and P/ha, respectively. In late April (27 April 2016), the field was sown with a 4-row pneumatic sowing machine Gaspardo. Weed control was achieved with the recommended rate of the early post-emergence applied herbicide Modett 25/28 SE (25% terbuthylazine + 28% dimethenamid-p), whereas irrigation was performed according to the requirements of the crop plants. After crop emergence, three randomly taken plots (4 m × 4.25 m) with six rows per plot were marked. The distance between the crop rows was 80 cm, and the distance between plants in the same row was 17 cm. Therefore, there were 25–26 plants/row, 150 plants/plot, and 450 plants in total. The distance between the three plots was 20 m. The individual plants in the three plots (Figure 1), for the purpose of the study, were considered as the units of the target statistical population from which samples had been extracted. A grid of 25 (rows) × 6 (columns) was used for the representation of the harvested plants (Figure 1) in each plot (where: row is x dimension and column is y dimension). A unique ID was assigned to each measurement/plant based on the row and column of each plant in each plot. IDs were also assigned in places where no measurement was available (the missing values appear as places with no dots in Figure 1), to be filled in later with an average value of either the total average of all measurements (RT method), an average of the measurements in the same row (RR method), or an average of the measurements in the same column (RC method).
At the silage stage (when the kernels began to glaze) of maize (14 weeks after sowing), all plants were harvested from each subplot, and the silage yield (fresh weight—FW, dry weight—DW, and ear weight—EW) of each plant was recorded. The silage stage was determined by breaking the ears of maize and visually evaluating the kernels’ stage of development. The silage yield data (measurements for fresh weight, dry weight, ear weight) were then entered in Excel, and organized in one table containing all information available, such as the plot and the exact position of each record (column: x dimension, row: y dimension) based on a 25 (rows) × 6 (columns) grid that represents the harvested plants in each plot (Figure 1). For achieving better visual results, we used the centers of the squares of the grid of each plot, instead of the absolute numbers of rows and columns of the measurements (i.e., for the plant located in the first row and first column, we assigned dimensions x = 0.5 and y = 0.5 instead of x = 1 and y = 1).
The measurements of the three determined crop parameters (FW, DW, EW) obtained from the three field plots were finally used to construct the corresponding Kriging grids and contour maps to perform comparisons and present the spatial variability of data. For each plot and crop parameter (fresh weight, dry weight, and ear weight), a grid of the new estimated values (software used: Surfer for Windows), with size: 100 rows × 24 columns, was constructed using Ordinary Kriging.
For each plot and each crop parameter, contour maps were created based on these new grids (Figure 2). Estimated values were then extracted from each grid to an ascii format file (.grd convert to .dat file), to be used in Excel to calculate metrics for the descriptive analysis and for the boxplots, to present statistics for each distribution, and make the comparison between them easier.
The implementation of Kriging and the production of the new grids of estimated data were done through ‘Surfer for Windows’, a very popular and effective Windows program from Golden Software. Surfer for Windows is one of the best modelling geo-spatial tools for data interpolation, producing accurate grids for several interpolation methods. The aim of using the Kriging interpolation method is to achieve the best linear unbiased prediction, based on the calculation of prediction variance as the variance of the difference of the linear predictor and the measured data. Therefore, through the implementation of Kriging, the value of the random function Z = Z ( x ) at any arbitrary location of interest x0 can be estimated based on the nearest measured observations z ( x i ) of Z ( x ) at the n   ∈ ℕ sample points x i . Kriging uses a weighted average of the nearest measured observations at the sample points x i to reveal the spatial structure of data and calculate weights based on the assumptions on μ ( x ) and on the variogram or covariance function of Z ( x ) . As this prediction variance decreases, the accuracy of the linear predictor increases, and the best linear prediction is achieved.
Concerning the general information about the gridding process, the following parameters were used (all the default settings in creating a grid using Surfer, the gridding software used): no trend removal was used, and the automatic variogram fitting mode was selected, which attempts to find a better set of parameters for the current model. Regarding the values used by the autofit feature, the fit criterion was set to “Least Squares” with maximum iterations set to 50, target precision (%) set to 0.0001, and maximum distance set to 1 × 1038. Concerning the experimental variogram, the lag size was set to 0.5, the number of lags was 15, the direction equaled 0, and tolerance equaled 90. For the semi-variogram model: the variogram component type selected was linear for all grids created (anisotropy angle set to 0 and anisotropy ratio set to 1). Concerning the Kriging parameters and gridding rules, Kriging type was set to point (point weight measurements for fresh, dry and ear weight corresponding to plants). Regarding the “search neighborhood”, all data were used for the estimation of the values of the new grids. The main descriptive statistics were calculated for the selected three types of crop parameters (FW, DW, EW) for all the plants harvested in the three plots for three different cases: (a) measured data or data for all harvested plants (M); (b) data without the measurements from the excluded area (MC) due to reduced plant density; (c) data after interpolation (I). The descriptive statistics for the FW, DW, and EW are shown in Table 1, Table 2 and Table 3, respectively.
Among other descriptive statistics, the main metric used to compare the performance (reduction of data variability—improved mean values) of the above sampling methods was the coefficient of variation (CV), which also indicates the degree of precision with which the treatments are compared, and generally is a good index of the reliability of the experiment [19]. Average CV was calculated for each of the three types of crop weights, and for each of the three plots, to explore and compare the variation of the different weights type level per sampling method, parameter, and plot. Suppose that there is n set of co-ordinates, z1, z2, …, zn, Y ( z n ) their weight values in a single plot, where Y ¯ the mean value. CV can be defined as (Equation (1)):
C V = 1 n − 1 ∑ i = 1 n ( Y ( z i ) − Y ¯ ) 2 Y ¯
The CV represents the experimental error as a percentage of the total mean, and therefore, the lower the CV, the higher the reliability of the experiment. The performance of each sampling method under consideration was assessed based on the descriptive statistics, and mainly on the mean values and the corresponding CV values in each case.

3. Results

The Kriging contour maps (Figure 2) offer a great representation of the variability of the crop parameter values under consideration, where outliers are easily located (either visually by the red color area or through analyzing the estimated values from the corresponding grids). Based on the different color area pattern of Figure 2, it is clear that the fresh weight in all plots has a similar color areas pattern (estimated data) to that of ear weight, but different than that of dry weight. However, the Kriging standard deviations derived from the implementation of spatial interpolation on the fresh weight were similar in plots 1, 2, and 3, with respective standard deviations of dry weight and ear weight (Figure 3).
Regarding the coefficient of variation (CV) in all data from three plots, the fresh weight, dry weight and ear weight, CV values in most cases of applying interpolation were almost three times as good (CV lower values) as in any other sampling method. Interpolation performed better in all plots and for all types of crop weight, with the only exception for the RR method in plot 3 for dry weight, while for fresh and ear weights, the CV values were lower, but close to those of the RR (missing values replaced by the average of the row where the missing value belongs) method (Table 1, Table 2 and Table 3). In plot 1, the CV values for the interpolation were better than in any other method, and specifically twice as good as those for RT (missing values replaced by the total average of all values) and RC (missing values replaced by the average of the column where the missing value belongs) method, while CV values for MC (data measured cutting off the measurements from the lines 21 to 25), and RR was no different to the CV values in measured data (M). In plot 2, the CV values for the interpolation were also better than in any other method (MC, RT, RC, RR). The CV values for RT and RC were better than those in plot 1, but even so, the CV values for the interpolation were twice as good. The CV values for MC and RR methods were very close to those in measured data (M) that showed no improvement. In plot 3, the CV values for the RR method were (surprisingly) slightly better than those for the interpolation, and markedly better than in the rest of the methods. However, the CV values for the interpolation were still better than those for MC, RT, and RC methods. In general, the improvements in CV values of fresh weight, dry weight, and ear weight data derived from (Kriging) interpolation were 26.3–33.7% (range: 7.4%), 30.0–31.1% (range: 1.1%), and 25.2–33.2% (range: 8%), respectively, compared with the measured data (Table 4). The corresponding min–max values for CVs in RR were from 0.5 to 39.5% (range: 39%) for the fresh weight, 1.4% up to 44.9% (range: 43.5%) for the dry weight, and 1.4%, up to 34.9% (range: 33.5%) for the ear weight (Table 4). Therefore, although the RR method performed better in plot 3 than the interpolation approach, overall, the range of CV values was significantly lower in CV values from the interpolation, which shows a much more robust improvement.
Kriging, compared to the sampling methods under consideration (RT, RC, RR) in all plots, showed a better performance in handling the outliers issue (Table 1) for the types of weight (FW, DW, EW) under consideration, and for all three plots, with the only exception the RR method in plot 1 and 2. For all the data of three plots, the upper and lower outliers % for fresh weight, dry weight, and ear weight in most cases of interpolation were better than in any other method (RT, RC, RR). More specifically, in plot 1 and plot 2, the upper outliers % for the interpolation approach were better than those for RT and RC method, and only the RR method performed better than the interpolation. However, in plot 2 for the lower outliers %, the interpolation approach performed better than RT and RC, and the same as the RR method for all three types of weight. In plot 3, the upper outliers % were better for the interpolation compared to RT, RC, and RR methods, and the lower outliers % were also better for the interpolation, with the only exception being those that correspond to the RC method for the fresh weight. In a nutshell, the fresh weight upper outliers % for the interpolation ranged from 0.3 to 1.5% (range: 1.2%), while for the RT method, it was 2.1 to 5.3% (range: 3.2%), for the RC method, it was 1.4 to 4.0% (range: 2.6%), and for the RR method, it was 0 to 6.3% (range: 6.3%). Respectively, for the dry weight, the upper outliers % for the interpolation ranged from 0.5 to 1.6% (range: 1.1%), while for the RT method, it was 3.3% in all plots, and for the RC method, it was 2.0 to 3.3% (range: 1.3%), and for the RR method, it was 1.3 to 4.7% (range: 3.4%). Moreover, for the ear weight, the upper outliers % for the interpolation ranged from 0 to 0.1% (range: 0.1%), for the RT method, it ranged from 0 to 2.7% (range: 2.7%), for the RC method, it also ranged from 0 to 2.7% (range: 2.7%), and for the RR method, it ranged from 0 to 0.7% (range: 0.7%). Therefore, the above findings indicate that interpolation improved CV values (lower values), replaced missing values, and lowered the number of both upper and lower outliers (%), in most cases compared to the rest of the sampling methods (RT, RC, and RR).
Since the coefficient of variation (CV) values have been improved (lower values), missing values have been replaced by estimated values via interpolation, and the number of both upper and lower outliers (%) was lower compared to the rest of the sampling methods (RT, RC, and RR), we can conclude that the mean values after the implementation of Kriging are more dependable and reliable, and thus, the overall quality of crop data has been improved.
The differences in CV values (%) between all measured data and those derived from the sampling methods MC, RT, RC, RR, and I (Table 4) clearly show the efficiency of each sampling method compared to interpolation (I). It is notable that implementation achieved up to 30% lower CV values (column: I diff% from M), whereas the other sampling methods (RT, RC, RR) of replacing missing values with an average value (total average, row or column average value) achieved only up to 15% lower CV values (Figure 4). Thus, interpolation performed twice as well in reducing data variability than other commonly used methods. It must also be noted that, despite the changes in CV values due to interpolation, mean values were not affected (Figure 5), proving the efficiency of the method.
Concerning the mean values of fresh weight, dry weight, and ear weight, they were more or less similar between the methods used (Table 5), and only the RR showed an overestimation (plot 2 for all weights) or underestimation (plot 3 for all weights). The MC approach (“cutting off” the area with low data density) showed similar mean values to the measured data (mean values ranged from −0.9 to 1.9%), while the RT and RC methods performed quite similarly, with mean values ranging from −2.5 to 3.1%, and −2.2 to 3.0%, respectively. The RR method performed worse than any other method with mean values ranging from −8.5 to 11.7%, whereas the mean values of interpolation method were slightly higher than the RT and RC methods. In a nutshell, for all data of three plots, the RT method had no difference compared to the measured data (M), while MC, RC, and RR methods had similar mean values to the measured data in plot 1, same or slightly overestimated in plot 2, and the same or slightly underestimated in plot 3. For the total values from all plots, the interpolation approach had slightly higher mean values (ranging from 0.5% to 1.5%) compared to the rest of the methods (0 to 0.4%), while, based on handling missing and extreme values, this difference is considered to be a “correction” of the measured mean values. More specifically, in plot 1, the interpolation had same mean values compared to the measured data, in plot 2, slightly overestimated mean values, and in plot 3, the mean values were almost similar to the measured data for the fresh weight, slightly underestimated for the dry weight, and slightly overestimated for the ear weight.
The boxplots (Figure 4, Figure 5 and Figure 6) for the different sampling methods (MC, RT, RC, RR, I) indicated that the approach of excluding areas of measurements with low data density (MC) has no great effect on the data variability (the boxes and lower/upper whiskers are almost identical) compared to the corresponding boxplot resulting from all measured data (M). In addition, the other approaches (RT, RR, RC) to replacing the missing values seem to provide better overall performance (the boxes are shrunken). However, replacing the missing values with the row average (RR) can be unsafe due to the limited number of observations (less than six). This is confirmed in the case of ear weight for plot 3, where the RR approach performed quite well, but for plot 2, the results lead to an increased data variability. Finally, Kriging interpolation (I), for the three crop parameters and for all plots, shows a better performance (more shrunken boxes compared to the corresponding boxplots from all measured data) compared to the previous approaches of replacing missing values by an average (either row, column, or total). In addition, the variability and the symmetry of the distributions in each case (three types of weight, three plots and data from all plots) remain almost stable and consistent.

4. Discussion

The similar estimated CV values for all crop parameters, using either all the measured data (M) of the three plots or those obtained after the removal of the measurements at the upper part of the plots due to low plant density (MC approach, “cutting-off” an area with reduced plant density/measurements), strongly suggests that this approach is not adequate to improve data variability, and it is rather a biased and unsafe method. In addition, these results indicate that the common practice (for agro-scientists and farmers) of excluding areas with low density data to address the issue of the missing values cannot safely lead to improved results.
The reduction in CV values by 7.9–15.8% or 7.8–15.3% in the case of replacing the missing values with the total average value of all the data in the plot or with the total average value of the column (where the missing value belongs to) shows that these two approaches could be safely used for the improvement of the data quality before their statistical analyses. However, the reduction in CV values by 0.5–44.9% in the case of replacing the missing values with the total average value of the row (which the missing value belongs to) indicates that this method is less safe than the other two methods due to the wide percentage range of improvement. This is confirmed by the fact that, for plots 1 and 2, the replacement of the missing values with row average improved CV values by only 0.5–3.7%, while in plot 3, the respective improvement for the three crop parameters was much higher and ranged from 34.9 to 39.6%.
The improvement of CV values by 25.2 to 33.7%, in the case of addressing the issue of missing values through the implementation of an interpolation method such as Kriging, shows a much more solid approach. In particular, the range difference % in CV values was similar for all the plots, and for all the crop parameters, it was 1.3–1.8% in all cases, 1.1% in plot 1 (25.2 to 26.3%), 2.2% in plot 2 (27.6 to 29.8%), and 2.6% in plot 3 (31.1 to 33.7%). The fact that the overall average improvement in CV values for the MC approach is only 1.7%, for the RT 12%, for the RC 11.8%, for the RR 14.5%, and for I (interpolation) 29.8%, suggests that the implementation of Kriging was found to be the best method to reduce data variability as compared to other methods (MC, RT, RC, and RR). In a nutshell, Kriging performed at least twice as well in achieving better CV values compared to all other sampling methods.
The best improvement of CV values in the case of interpolation can be explained by the fact that this process aims to create a grid of estimated data as close as possible to the original measurements at non-sampled locations (Figure 7). This is because Kriging can achieve an accurate and precise prediction of the missing values as it calculates them, by considering the rest of the data, depending on their values and distance (weight) from the estimated value location. The effectiveness of this approach is also confirmed by comparing the Kriging results with those obtained from the other sampling methods that are based on the replacement of missing values with an average (total, row, or column average). Based on these, Kriging performed at least twice as well (up to 30% lower CV values) compared to the other sampling methods that achieved an improvement in CV values of only up to 15%. Therefore, after the implementation of Kriging, the dispersion of data is limited, and the variability is reduced, providing a remarkable improvement in interquartile range (IQR), standard deviation (SD), and coefficient of variation (CV) values, which lead to more consistent means, and make the predictions more dependable than those without spatial interpolation. In general, based on the comparison between measured data and data derived from the interpolation process, it is clear that the implementation of Kriging is a solid way to both estimate values at non-sampling locations, and to abate the impact of outliers, while the process offers an overall improvement on data quality.
The results of this study indicated that the Kriging implementation provides a visual and very useful way of understanding the existing variability of the three types of weight (fresh, dry, and ear weight) measured for all the harvested plants in each plot, through the construction of contour maps for each crop parameter. The Kriging contour maps, apart from the great representation of the spatial variability of crop parameters, have the potential to offer a basis for the further analysis and interpretation of this variability, and to provide insights into a possible decision support making for the delineation of management zones. The differences in variability spotted for the same parameter between plots show that the spatial information of the measurements cannot be ignored, and should be considered before the calculation of crop mean values as metrics for larger areas. The high variability in the values of the crop parameters between the adjacent plants, either within the same plot or between plots, is contrary to the expected, since the crop cultivar used was hybrid and all seeds have the same genotype. These differences in variability, which could be attributed to soil and climatic conditions prevailing during the growing season, along with the agricultural practices applied, were also identified and confirmed by the Kriging contour maps.

5. Conclusions

The results of this study indicated that the quality of experimental data can be improved before the calculation of mean values via the implementation of Kriging interpolation. More specifically, Kriging managed to refine data suffering from missing values by estimating values in non-sampled locations (plants that did not emerge). Moreover, the Kriging spatial interpolation method managed to balance the outliers by estimating new values in these locations based on the value and weight (distance) of their neighboring values that reduced the effect of the existing extreme values. As a result of this process, crop field variability (CV values) in crop parameters measurements was reduced up to 30% compared to other sampling methods (based on the replacement of missing values by an average value) that achieved lower CV values of only up to 15%.
Based on this significant reduction in crop data variability and the effective way of handling the missing values and outliers, we can conclude that the implementation of Kriging can lead to much more reliable and representative crop mean values, that can be used as crop metrics for further calculations and estimates. In addition, the lower CV values provide a greater precision in the data available for decision-making, supporting the vital role of applying interpolation in crop field data for profitability estimates.

Author Contributions

Conceptualization, Thomas M. Koutsos; methodology, Thomas M. Koutsos, Georgios C. Menexes and Ilias G. Eleftherohorinos; software, Thomas M. Koutsos; validation, Thomas M. Koutsos, Georgios C. Menexes and Ilias G. Eleftherohorinos; formal analysis, Thomas M. Koutsos and Georgios C. Menexes; investigation, Thomas M. Koutsos; resources, Thomas M. Koutsos; data curation, Koutsos Thomas; writing—original draft preparation, Thomas M. Koutsos; writing—review and editing, Thomas M. Koutsos, Georgios C. Menexes, Ilias G. Eleftherohorinos; visualization, Thomas M. Koutsos. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

We would like to thank the university students A. Pesios and A. Chatzopoulos for providing the data, and the staff of the A.U.Th. Farm for their assistance throughout the experiment.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kosmowski, F.; Chamberlin, J.; Ayalew, H.; Sida, T.; Abay, K.; Graufurd, P. How accurate are yield estimates from crop cuts? Evidence from smallholder maze farms in Ethiopia. Food Policy 2021, 102, 102122. [Google Scholar] [CrossRef] [PubMed]
  2. Wahab, I.; Jirstrom, M.; Hall, O. An Integrated Approach to Unravelling Smallholder Yield Levels: The Case of Small Family Farms, Eastern Region, Ghana. Agriculture 2020, 19, 206. [Google Scholar] [CrossRef]
  3. Wahab, I. In-season plot area loss and implications for yield estimation in smallholder rainfed farming systems at the village level in Sub-Saharan Africa. GeoJournal 2020, 85, 1553–1572. [Google Scholar] [CrossRef] [Green Version]
  4. Abay, K.A.; Abate, G.T.; Barrett, C.B.; Bernard, T. Correlated non-classical measurement errors, ‘Second best’ policy inference, and the inverse size-productivity relationship in agriculture. J. Dev. Econ. 2019, 139, 171–184. [Google Scholar] [CrossRef] [Green Version]
  5. Carletto, C.; Gourlay, S. A thing of the past? Household surveys in a rapidly evolving (agricultural) data landscape: Insights from the LSMS-ISA. Agric. Econ. 2019, 50 (Suppl. S1), 51–62. [Google Scholar] [CrossRef]
  6. Casley Dennis, J.; Kumar, K. The Collection, Analysis, and Use of Monitoring and Evaluation Data. In Third World Planning Review; Liverpool University Press: Liverpool, UK, 1988; p. 91. [Google Scholar] [CrossRef]
  7. Verma, V.; Marchant, T.; Scott, C. Evaluation of Crop-Cut Methods and Farmer Reports for Estimating Crop Production: Results of a Methodological Study in Five African Countries; Longacre Agricultural Development Centre Limited: London, UK, 1988; p. 75. [Google Scholar] [CrossRef]
  8. Lobell, D.B.; Azzari, G.; Burke, M.; Gourlay, S.; Jin, Z.; Kilic, T.; Murray, S. Eyes in the Sky, Boots on the Ground: Assessing Satellite- and Ground-Based Approaches to Crop Yield Measurement and Analysis. Am. J. Agric. Econ. 2020, 102, 202–219. [Google Scholar] [CrossRef]
  9. FAO—Food and Agriculture Organization of the United Nations. Methodology for Estimation of Crop Area and Crop Yield under Mixed and Continuous Cropping. In Publication Prepared in the Framework of the Global Strategy to Improve Agricultural and Rural Statistics; FAO: Rome, Italy, 2017. [Google Scholar]
  10. Piepho, H.P.; Mohring, J.; Williams, E.R. Why Randomize Agricultrural Experiments? J. Agron. Crop Sci. 2013, 199, 374–383. [Google Scholar] [CrossRef]
  11. Fermont, A.; Benson, T. Estimating Yield of Food Crops Grown by Smallholder Farmers: A Review in the Uganda Context; IFPRI Discuss Pap. 01097; IFPRI: Washington, DC, USA, 2011; pp. 1–57. [Google Scholar]
  12. Hagblad, L. Crop Cutting Versus Farmer Reports–Review of Swedish Findings. In Statistik Rapport 1998, 2; Statistics Sweden: Örebro, Sweden, 1988. [Google Scholar]
  13. Murphy, J.; Casley, D.J.; Curry, J.J. Farmers’ estimations as a source of production data. In World Bank Technical Paper 132; World Bank Publication: Washington, DC, USA, 1991. [Google Scholar]
  14. Liu, Q.; Feng, G.; Zheng, W.; Tian, J. Managing data quality of cooperative information systems: Model and algorithm. Expert Syst. Appl. 2022, 189, 116074. [Google Scholar] [CrossRef]
  15. Srinath, Y.; Vijayakumar, K.; Revathy, S.M.; Rangaraj, A.G.; Sheelarani, N.; Boopathi, K.; Balaraman, K. Automated Data Quality Mechanism and Analysis of Meteorological Data Obtained from Wind-Monitoring Stations of India. In Data Management, Analytics and Innovation; Lecture Notes on Data Engineering and Communications Technologies; Springer: Singapore, 2022; pp. 237–262. [Google Scholar]
  16. Taleb, I.; Serhani, M.A.; Bouhaddioui, C.; Dssouli, R. Big data quality framework: A holistic approach to continuous quality management. J. Big Data 2021, 8, 76. [Google Scholar] [CrossRef]
  17. Desiere, S.; Jolliffe, D. Land productivity and plot size: Is measurement error driving the inverse relationship? J. Dev. Econ. 2018, 130, 84–98. [Google Scholar] [CrossRef] [Green Version]
  18. Kim, T.; Ko, W.; Kim, J. Analysis and Impact Evaluation of Missing Data Imputation in Day-ahead PV Generation Forecasting. Appl. Sci. 2018, 9, 204. [Google Scholar] [CrossRef] [Green Version]
  19. Gomez, K.; Gomez, A. Statistical Procedures for Agricultural Research, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1984; pp. 276–294. [Google Scholar]
  20. Steel, R.G.D.; Torrie, J.H.; Dickey, D.A. Principles and Procedures for Statistics: A Biometrical Approach, 3rd ed.; McGraw Hill: Boston, MA, USA, 1997; pp. 416–420. [Google Scholar]
  21. Li, T.; Hutfless, S.; Scharfstein, D.; Daniels, M.; Hogan, J.; Little, R.; Roy, J.; Law, A.; Diskersin, K. Standards in the Prevention and Handling of Missing Data for Patient Centered Outcomes Research—A Systematic Review and Expert Consensus. J. Clin. Epidemiol. 2014, 67, 15–32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; John Wiley & Sons Ltd.: West Sussex, UK, 2007. [Google Scholar]
  23. Wiens, D.P.; Zhou, Z. Robust estimators and designs for field experiments. J. Stat. Plan Inference 2008, 138, 93–104. [Google Scholar] [CrossRef]
  24. Cho, J.B.; Guinness, J.; Kharel, T.P.; Sunoj, S.; Kharel, D.; Oware, E.K.; van Aardt, J.; Ketterings, Q.M. Spatial estimation methods for mapping corn silage and grain yield monitor data. Precis. Agric. 2021, 22, 1501–1520. [Google Scholar] [CrossRef]
  25. Buttafuoco, G.; Castrignanò, A.; Cucci, G.; Lacolla, G.; Lucà, F. Geostatistical modelling of within-field soil and yield variability for management zones delineation: A case study in a durum wheat field. Prec. Agric. 2017, 18, 37–58. [Google Scholar] [CrossRef]
  26. Maldaner, L.F.; Molin, J.P. Data processing within rows for sugarcane yield mapping. Sci. Agric. 2020, 77, 1–8. [Google Scholar] [CrossRef]
  27. Guo-Shun, L.; Hou-Long, J.; Shu-Duan, L.; Xin-Zhong, W.; Hong-Zhi, S.; Yong-Feng, Y.; Xia-Meng, Y.; Hong-Chao, H.; Qing-Hua, L.; Jian-Guo, G. Comparison of Kriging Interpolation Precision With Different Soil Sampling Intervals for Precision Agriculture. Soil Sci. 2010, 175, 405–415. [Google Scholar] [CrossRef]
  28. Tziachris, P.; Metaxa, E.; Papadopoulos, F.; Papadopoulou, M. Spatial Modelling and Prediction Assessment of Soil Iron Using Kriging Interpolation with pH as Auxiliary Information. ISPRS Int. J. Geo-Inf. 2017, 6, 283. [Google Scholar] [CrossRef] [Green Version]
  29. Souza, E.G.; Bazzi, C.L.; Khosla, R.; Uribe-Opazo, M.A.; Reich, R.M. Interpolation type and data computation of crop yield maps is important for precision crop production. J. Plant Nutr. 2016, 39, 531–538. [Google Scholar] [CrossRef]
  30. Maestrini, B.; Basso, B. Drivers of within-feld spatial and temporal variability of crop yield across the US Midwest. Sci. Rep. 2018, 8, 106–112. [Google Scholar] [CrossRef]
  31. Maestrini, B.; Basso, B. Predicting spatial patterns of within-field crop yield variability. Field Crops Res. 2018, 219, 106–112. [Google Scholar] [CrossRef]
  32. Vega, A.; Córdoba, M.; Castro-Franco, M.; Balzarini, M. Protocol for automating error removal from yield maps. Precis. Agric. 2019, 20, 1033–1044. [Google Scholar] [CrossRef]
Ijgi 11 00153 g001 550
Figure 1. Schematic presentation of all the maize plants (dots) harvested in each plot (M). Τhe upper part of M plots was marked as “excluded” (MC plots) due to the limited number of plants (rows 21–25) in this area (some plants were not emerged) to be distinguished from the rest of the area, where measurements have adequate density, and to improve the overall quality of the mean estimates. Where: M: All measured (all sampled data); MC: Measured cut (without the measurements from the upper part area—lines 21 to 25).
Figure 1. Schematic presentation of all the maize plants (dots) harvested in each plot (M). Τhe upper part of M plots was marked as “excluded” (MC plots) due to the limited number of plants (rows 21–25) in this area (some plants were not emerged) to be distinguished from the rest of the area, where measurements have adequate density, and to improve the overall quality of the mean estimates. Where: M: All measured (all sampled data); MC: Measured cut (without the measurements from the upper part area—lines 21 to 25).
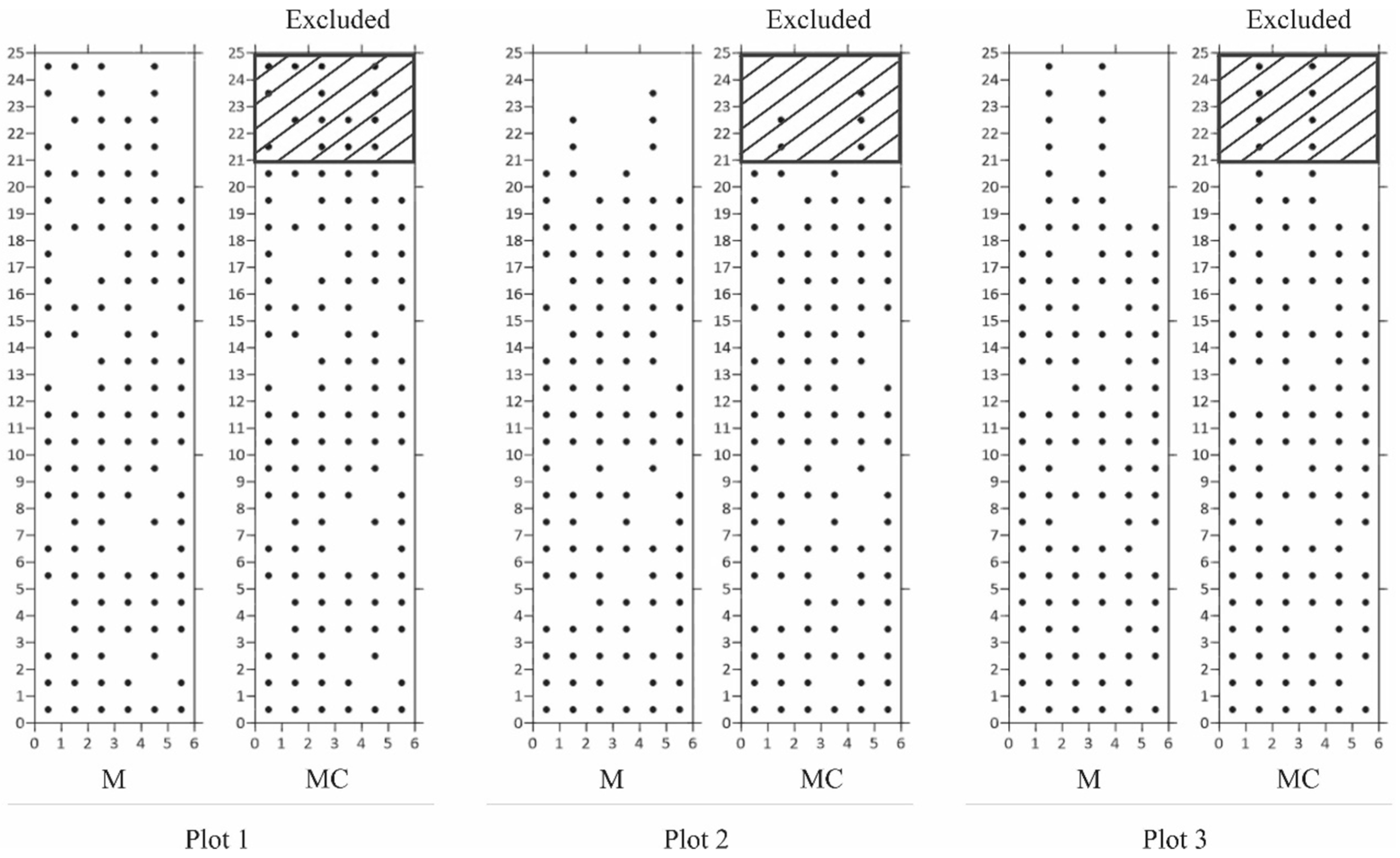
Ijgi 11 00153 g001
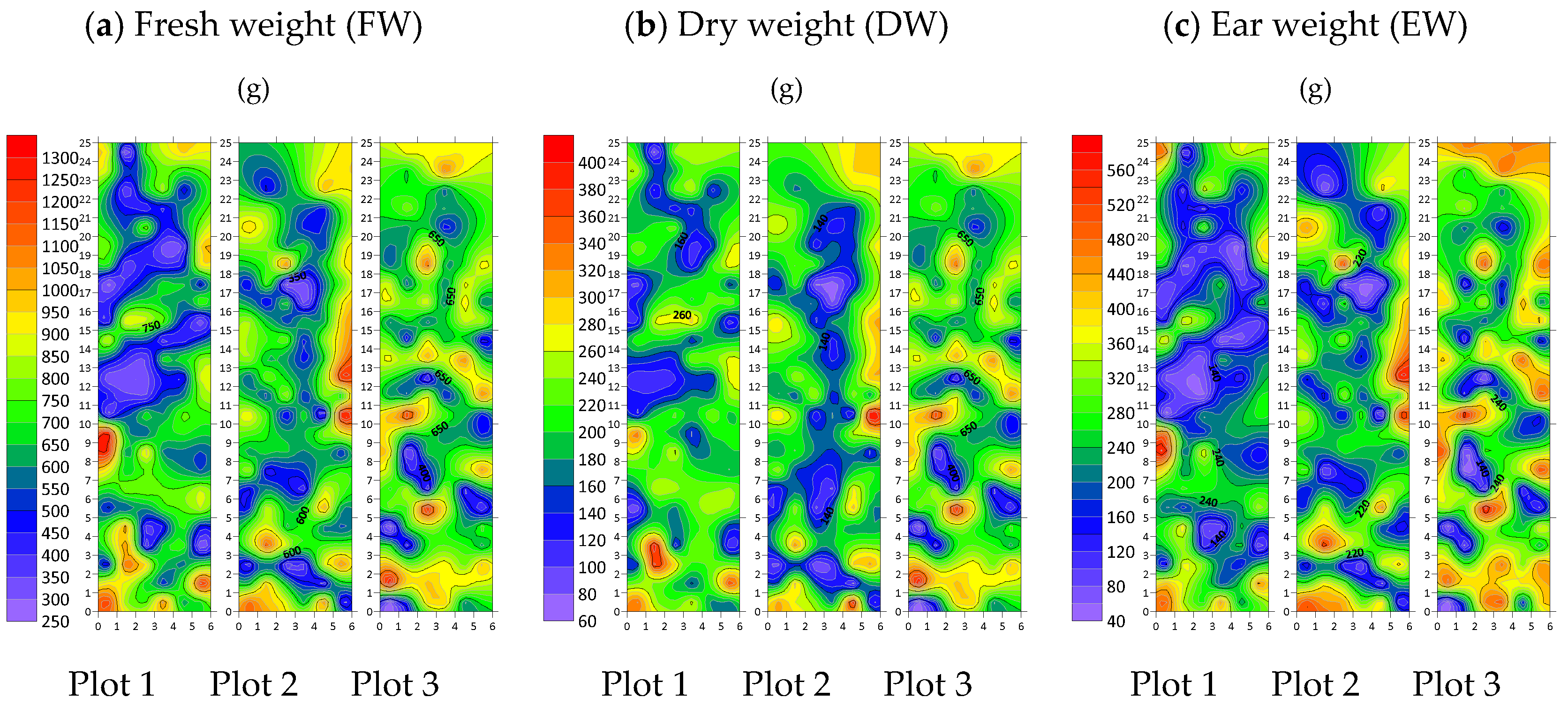
Ijgi 11 00153 g002 550
Figure 2. Spatial interpolation using Kriging on the three crop parameters: (a) Fresh weight (FW); (b) Dry weight (DW); (c) Ear weight (EW) of all harvested individual plants.
Figure 2. Spatial interpolation using Kriging on the three crop parameters: (a) Fresh weight (FW); (b) Dry weight (DW); (c) Ear weight (EW) of all harvested individual plants.
Ijgi 11 00153 g002
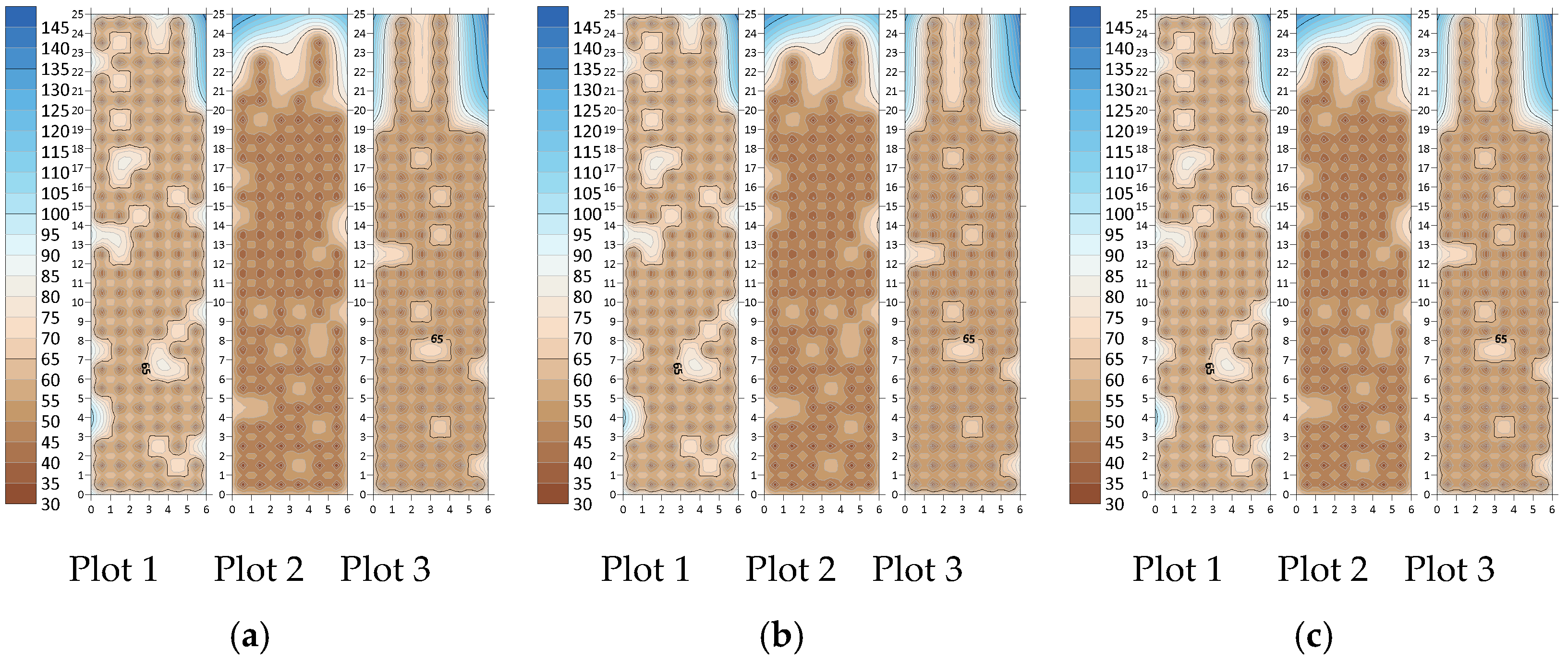
Ijgi 11 00153 g003 550
Figure 3. Kriging standard deviations derived from the implementation of spatial interpolation on the three crop parameters: (a) Fresh weight (FW); (b) Dried weight (DW); (c) Ear weight (EW) of all harvested individual plants. Areas with lower standard deviation (SD) values appear as “data holes” in the plots, and they correspond to the missing values. Areas with even lower data density (upper part of plots) have higher estimated standard deviation values concerning the implementation of Kriging.
Figure 3. Kriging standard deviations derived from the implementation of spatial interpolation on the three crop parameters: (a) Fresh weight (FW); (b) Dried weight (DW); (c) Ear weight (EW) of all harvested individual plants. Areas with lower standard deviation (SD) values appear as “data holes” in the plots, and they correspond to the missing values. Areas with even lower data density (upper part of plots) have higher estimated standard deviation values concerning the implementation of Kriging.
Ijgi 11 00153 g003
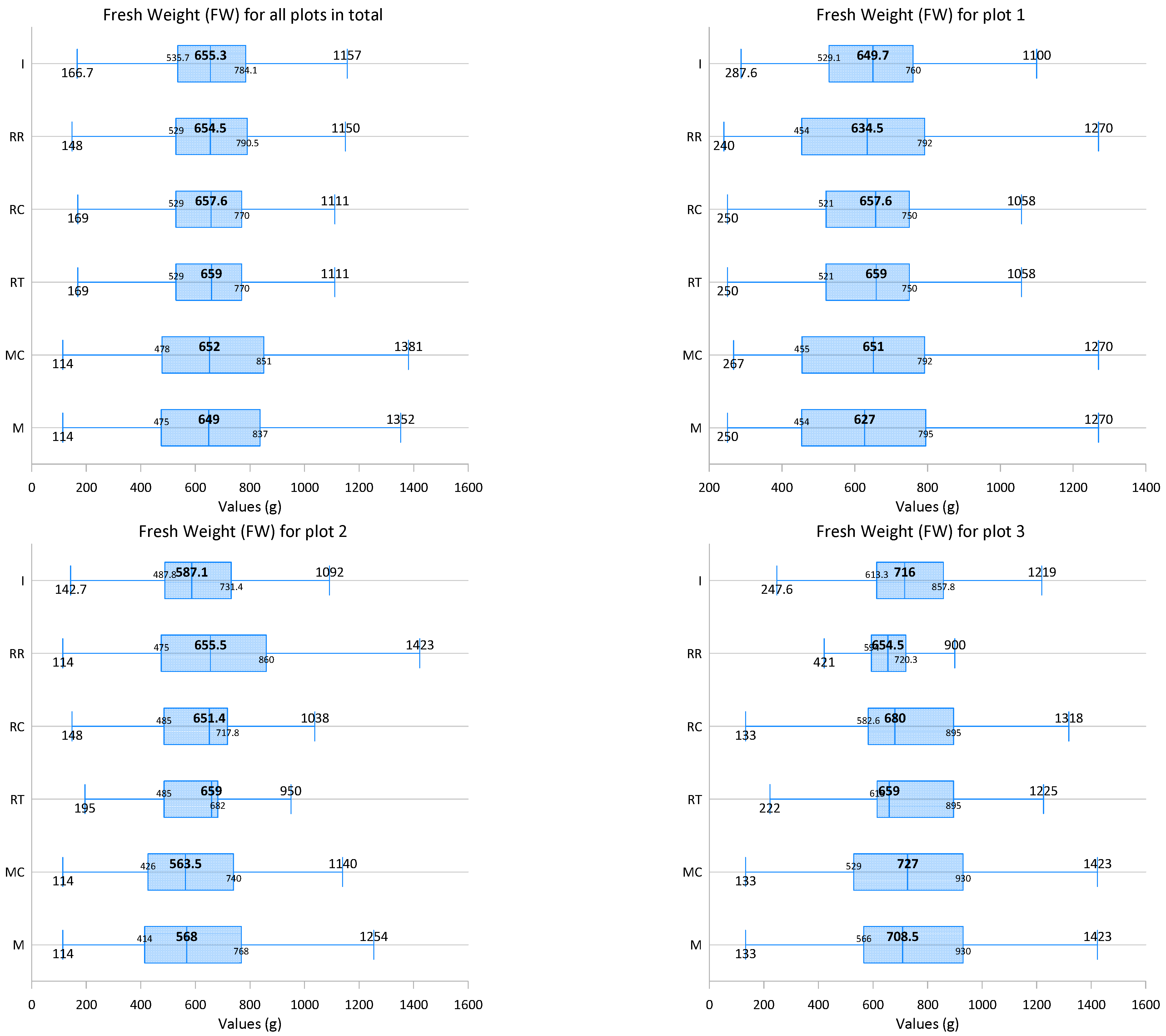
Ijgi 11 00153 g004 550
Figure 4. Fresh Weight (FW) descriptive statistics for the different sampling methods: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation.
Figure 4. Fresh Weight (FW) descriptive statistics for the different sampling methods: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation.
Ijgi 11 00153 g004
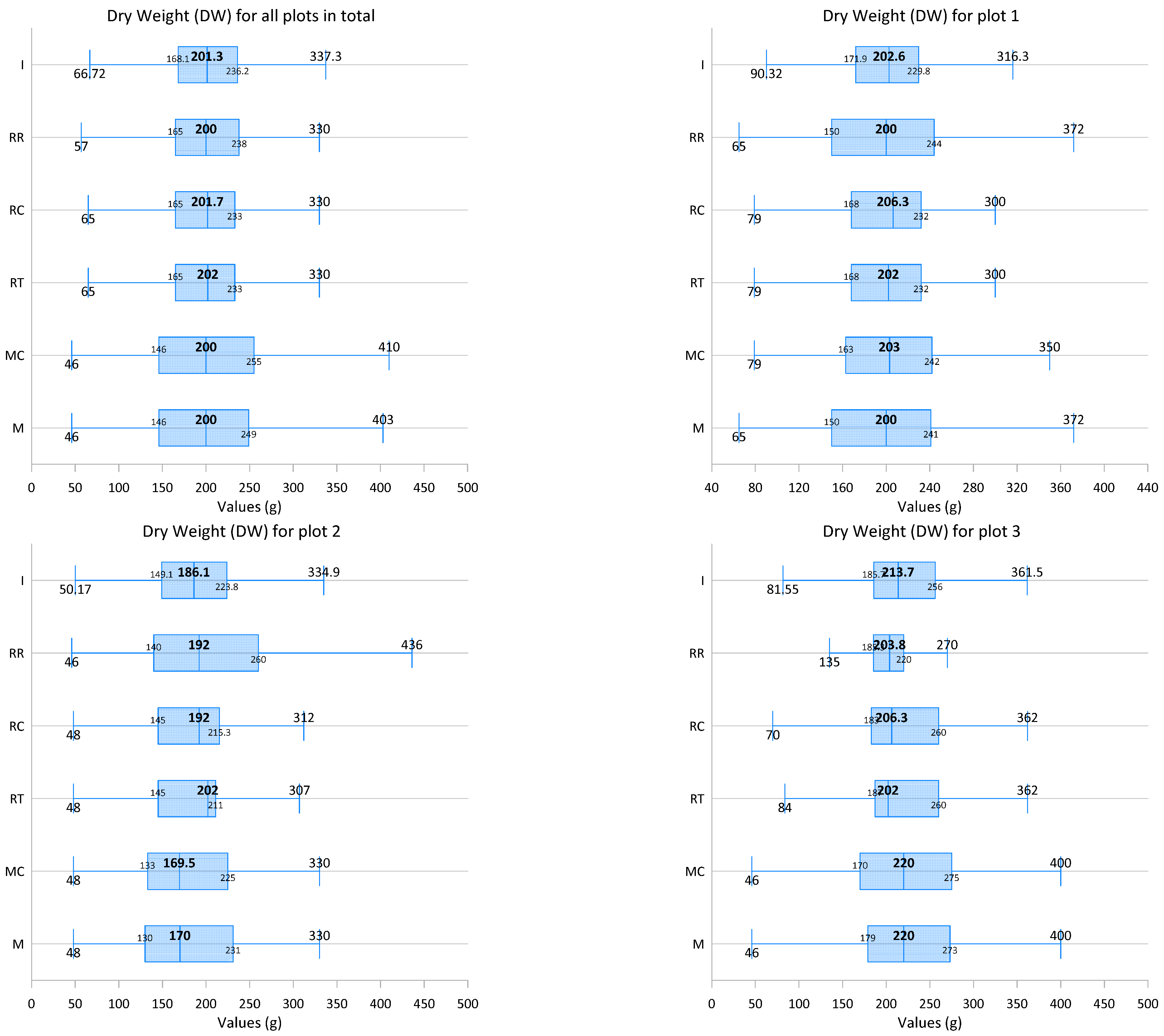
Ijgi 11 00153 g005 550
Figure 5. Dry weight (DW) descriptive statistics for the different sampling methods: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation.
Figure 5. Dry weight (DW) descriptive statistics for the different sampling methods: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation.
Ijgi 11 00153 g005
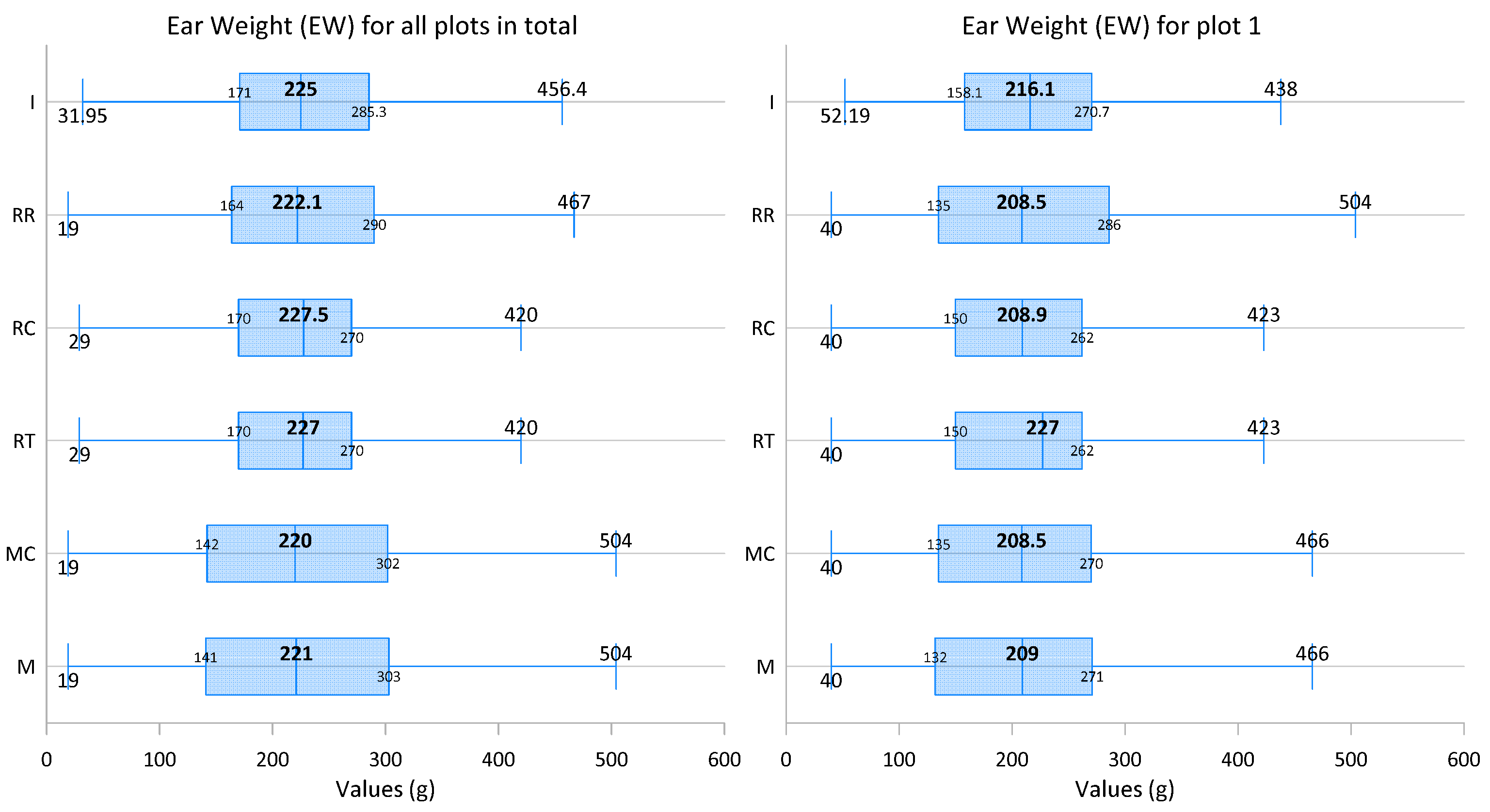
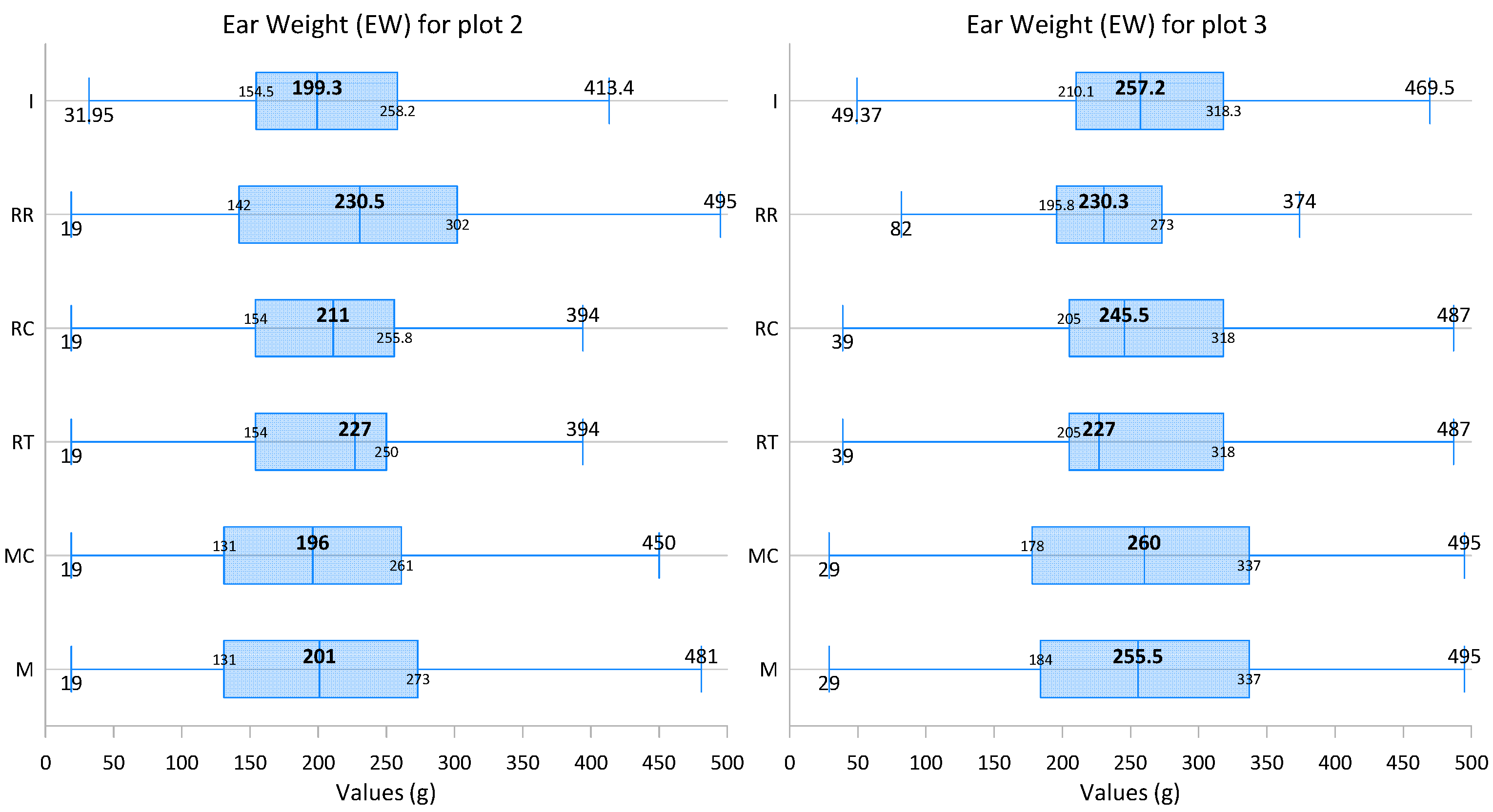
Ijgi 11 00153 g006a 550Ijgi 11 00153 g006b 550
Figure 6. Ear weight (EW) descriptive statistics for the different sampling methods: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation.
Figure 6. Ear weight (EW) descriptive statistics for the different sampling methods: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation.
Ijgi 11 00153 g006aIjgi 11 00153 g006b
Ijgi 11 00153 g007 550
Figure 7. Schematic illustration of the Kriging interpolating approach on how to address missing and extreme values in original experimental data. This is a real data section across plot 1 (section AB) comparing sampled and estimated (via Kriging interpolation) fresh weight (FW) values. Kriging calculates values at non-sampled locations (missing values) and applies a correction in case of outliers or extreme values (based on the neighboring data values).
Figure 7. Schematic illustration of the Kriging interpolating approach on how to address missing and extreme values in original experimental data. This is a real data section across plot 1 (section AB) comparing sampled and estimated (via Kriging interpolation) fresh weight (FW) values. Kriging calculates values at non-sampled locations (missing values) and applies a correction in case of outliers or extreme values (based on the neighboring data values).
Ijgi 11 00153 g007
Table
Table 1. Descriptive statistics for fresh weight (FW) (g).
Table 1. Descriptive statistics for fresh weight (FW) (g).
All PlotsPlot 1
MMCRTRCRRIMMCRTRCRRI
Min114.0114.0114.0114.0114.0142.7250.0267.0250.0250.0240.0287.6
Q1475.8479.5529.0529.0529.0535.7454.5459.3523.3523.3454.3529.1
Median649.0652.0659.0657.6654.5655.3627.0651.0659.0657.6634.5649.7
Q3834.5844.0770.0770.0790.5783.9793.5790.3747.5747.5790.5759.9
Max1423.01423.01423.01423.01423.01370.01337.01337.01337.01337.01337.01299.2
Mean659.5661.9659.4660.4660.0665.5648.6657.5650.7652.2646.2654.7
IQR358.8364.5241.0241.0261.5248.3339.0331.0224.3224.3336.3230.8
IQR/2179.4182.3120.5120.5130.8124.1169.5165.5112.1112.1168.1115.4
SD254.5260.3224.6225.5227.3182.7239.5245.1213.2214.2237.5178.3
CV38.639.334.134.134.427.536.937.332.832.836.827.2
KURT−0.1−0.10.70.60.5−0.10.00.10.70.6−0.10.3
SKEW0.30.30.40.40.40.30.50.60.60.60.50.4
Upper Outliers (%)0.60.33.43.42.30.80.81.14.04.00.71.5
Lower Outliers (%)0.00.00.90.90.50.00.00.00.00.00.00.0
For the Box
Q2-Q1173.3172.5130.0128.6125.5119.7172.5191.8135.8134.4180.3120.7
Q3-Q2185.5192.0111.0112.4136.0128.6166.5139.388.589.9156.0110.1
For the Whiskers
Q3+1.5*IQR1372.61390.81131.51131.51182.81156.41302.01286.81083.91083.91294.91106.1
Q1−1.5*IQR−62.4−67.3167.5167.5136.8163.3−54.0−37.3186.9186.9−50.1182.8
Upper Whisker1372.61390.81131.51131.51182.81156.41302.01286.81083.91083.91294.91106.1
Lower Whisker114.0114.0167.5167.5136.8163.3250.0267.0250.0250.0240.0287.6
Wupper-Q3538.1546.8361.5361.5392.3372.4508.5496.5336.4336.4504.4346.2
Q1-Wlower361.8365.5361.5361.5392.3372.4204.5192.3273.3273.3214.3241.5
Plot 2Plot 3
MMCRTRCRRIMMCRTRCRRI
Min114.0114.0114.0114.0114.0142.7133.0133.0133.0133.0281.0166.7
Q1420.0428.8489.0489.0475.8487.8564.0543.5611.0582.6593.5613.3
Median568.0563.5659.0651.4655.5587.1708.5727.0659.0680.0654.5716.0
Q3756.0737.8680.3717.8859.3731.0930.0930.0891.3891.3720.3857.6
Max1352.01352.01352.01352.01423.01251.11423.01423.01423.01423.01150.01370.0
Mean597.6593.3613.5614.6659.3613.6729.9731.1716.1716.6675.2728.1
IQR336.0309.0191.3228.8383.5243.2366.0386.5280.3308.7126.8244.4
IQR/2168.0154.595.6114.4191.8121.6183.0193.3140.1154.363.4122.2
SD248.7251.9215.4216.8276.7179.2259.8266.2234.7235.1145.2171.9
CV41.642.535.135.342.029.235.636.432.832.821.523.6
KURT0.10.31.00.9−0.10.2−0.1−0.10.60.62.30.1
SKEW0.50.50.30.30.30.50.00.00.20.20.80.0
Upper Outliers (%)0.92.05.34.00.01.00.00.02.11.46.30.3
Lower Outliers (%)0.00.03.30.70.00.00.00.02.10.03.50.4
For the Box
Q2-Q1148.0134.8170.0162.4179.899.4144.5183.548.097.461.0102.7
Q3-Q2188.0174.321.366.4203.8143.8221.5203.0232.3211.365.8141.6
For the Whiskers
Q3+1.5*IQR1260.01201.3967.11061.01434.51095.81479.01509.81311.61354.2910.41224.2
Q1−1.5*IQR−84.0−34.8202.1145.8−99.5122.915.0−36.3190.6119.6403.4246.8
Upper Whisker1260.01201.3967.11061.01423.01095.81423.01423.01311.61354.2910.41224.2
Lower Whisker114.0114.0202.1145.8114.0142.7133.0133.0190.6133.0403.4246.8
Wupper-Q3504.0463.5286.9343.2563.8364.8493.0493.0420.4463.0190.1366.5
Q1-Wlower306.0314.8286.9343.2361.8345.1431.0410.5420.4449.6190.1366.5
Where: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation; Q1-Q2-Q3: Quartiles; IQR: Intra-Quadratic Range; SD: Standard Deviation; CV: Coefficient of Variation. Note: numbers in bold highlight the parameters of interest.
Table
Table 2. Descriptive statistics for dry weight (DW) (g).
Table 2. Descriptive statistics for dry weight (DW) (g).
All PlotsPlot 1
MMCRTRCRRIMMCRTRCRRI
Min46.046.046.046.046.050.265.079.065.065.065.076.6
Q1146.5147.0165.0165.0165.0168.1150.0163.3168.5168.5150.0171.9
Median200.0200.0202.0201.7200.0201.3200.0203.0202.0206.3200.0202.6
Q3249.0253.5233.0233.0238.0236.2240.5241.8231.5231.5243.5229.7
Max464.0464.0464.0464.0464.0447.5410.0410.0410.0410.0410.0392.6
Mean202.0202.9202.0202.0202.1203.1201.3205.2201.5201.7200.4201.3
IQR102.5106.568.068.073.068.190.578.563.063.093.557.8
IQR/251.353.334.034.036.534.145.339.331.531.546.828.9
SD75.878.266.566.767.353.265.367.158.158.465.945.7
CV37.538.532.933.033.326.232.432.728.829.032.922.7
KURT0.40.41.51.41.30.40.70.71.61.50.30.7
SKEW0.50.50.50.50.50.30.50.60.50.50.40.3
Upper Outliers (%)1.41.03.33.33.31.21.73.23.33.31.31.6
Lower Outliers (%)0.00.01.61.61.30.30.00.00.70.70.00.0
For the Box
Q2-Q153.553.037.036.735.033.250.039.833.537.850.030.7
Q3-Q249.053.531.031.338.034.940.538.829.525.243.527.1
For the Whiskers
Q3+1.5*IQR402.8413.3335.0335.0347.5338.4376.3359.5326.0326.0383.8316.4
Q1−1.5*IQR−7.3−12.863.063.055.565.914.345.574.074.09.885.2
Upper Whisker402.8413.3335.0335.0347.5338.4376.3359.5326.0326.0383.8316.4
Lower Whisker46.046.063.063.055.565.965.079.074.074.065.085.2
Wupper-Q3153.8159.8102.0102.0109.5102.2135.8117.894.594.5140.386.7
Q1-Wlower100.5101.0102.0102.0109.5102.285.084.394.594.585.086.7
Plot 2Plot 3
MMCRTRCRRIMMCRTRCRRI
Min48.048.048.048.046.050.246.046.046.046.084.054.2
Q1131.5133.0145.3145.3140.0149.1177.0170.5187.8183.0185.3185.6
Median170.0169.5202.0192.0192.0186.1220.0220.0202.0206.3203.8213.7
Q3228.0225.0210.5215.3259.3223.8271.5274.0259.3259.3220.0256.0
Max436.0436.0436.0436.0464.0398.6464.0464.0464.0464.0362.0447.5
Mean180.4179.2186.0185.8201.5188.6223.5223.5218.6218.6204.4219.4
IQR96.592.065.370.0119.374.794.5103.571.576.334.870.3
IQR/248.346.032.635.059.637.347.351.835.838.117.435.2
SD75.477.065.565.887.454.380.883.171.571.740.754.6
CV41.843.035.235.443.428.836.137.232.732.819.924.9
KURT0.50.71.41.30.20.00.40.31.31.33.50.5
SKEW0.60.70.40.40.50.30.30.30.50.50.70.3
Upper Outliers (%)1.82.03.32.01.30.51.71.93.33.34.71.0
Lower Outliers (%)0.00.00.00.00.00.00.00.02.71.34.00.5
For the Box
Q2-Q138.536.556.846.852.037.043.049.514.323.318.528.0
Q3-Q258.055.58.523.367.337.751.554.057.353.016.242.3
For the Whiskers
Q3+1.5*IQR372.8363.0308.4320.3438.1335.8413.3429.3366.5373.6272.1361.5
Q1−1.5*IQR−13.3−5.047.440.2−38.937.135.315.380.568.6133.180.1
Upper Whisker372.8363.0308.4320.3438.1335.8413.3429.3366.5373.6272.1361.5
Lower Whisker48.048.048.048.046.050.246.046.080.568.6133.180.1
Wupper-Q3144.8138.097.9105.0178.9112.0141.8155.3107.3114.452.1105.5
Q1-Wlower83.585.097.397.394.098.9131.0124.5107.3114.452.1105.5
Where: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation; Q1-Q2-Q3: Quartiles; IQR: Intra-Quadratic Range; SD: Standard Deviation; CV: Coeffiecient of Variation. Note: numbers in bold highlight the parameters of interest.
Table
Table 3. Descriptive statistics for ear weight (EW) (g).
Table 3. Descriptive statistics for ear weight (EW) (g).
MMCRTRCRRIMMCRTRCRRI
Min19.019.019.019.019.032.040.040.040.040.040.052.2
Q1141.3144.0170.0170.0164.8171.0133.5135.3150.0150.0135.3158.1
Median221.0220.0227.0227.5222.1225.0209.0208.5227.0208.9208.5216.1
Q3302.8301.5270.0270.0290.0285.2270.5270.0261.5261.5285.0270.6
Max572.0572.0572.0572.0572.0562.3572.0572.0572.0572.0572.0562.3
Mean226.9226.5226.9227.9227.4230.3217.3216.6219.3219.7218.0221.1
IQR161.5157.5100.0100.0125.3114.3137.0134.8111.5111.5149.8112.5
IQR/280.878.850.050.062.657.168.567.455.855.874.956.3
SD111.4112.497.698.299.482.5115.3115.7102.7103.3112.387.7
CV49.149.643.043.143.735.853.153.446.847.051.539.7
KURT−0.4−0.40.40.30.2−0.10.10.30.80.70.00.6
SKEW0.30.30.30.30.30.30.70.70.70.60.60.6
Upper Outliers (%)0.30.34.04.01.60.53.43.24.04.00.72.1
Lower Outliers (%)0.00.00.40.40.00.00.00.00.00.00.00.0
For the Box
Q2-Q179.876.057.057.557.354.075.573.377.058.973.358.0
Q3-Q281.881.543.042.567.960.261.561.534.552.676.554.5
For the Whiskers
Q3+1.5*IQR545.0537.8420.0420.0477.9456.6476.0472.1428.8428.8509.6439.5
Q1−1.5*IQR−101.0−92.320.020.0−23.1−0.4−72.0−66.9−17.3−17.3−89.4−10.7
Upper Whisker545.0537.8420.0420.0477.9456.6476.0472.1428.8428.8509.6439.5
Lower Whisker19.019.020.020.019.032.040.040.040.040.040.052.2
Wupper-Q3242.3236.3150.0150.0187.9171.4205.5202.1167.3167.3224.6168.8
Q1-Wlower122.3125.0150.0150.0145.8139.093.595.3110.0110.095.3105.9
Plot 2Plot 3
MMCRTRCRRIMMCRTRCRRI
Min19.019.019.019.019.032.029.029.029.029.082.043.2
Q1131.5131.3154.3154.3144.0154.5183.5181.0205.5205.1195.8210.0
Median201.0196.0227.0211.0230.5199.3255.5260.0227.0245.5230.3257.2
Q3270.5260.8249.8255.8301.8258.0336.3336.5316.8316.8270.8318.2
Max481.0481.0481.0481.0495.0464.7495.0495.0495.0495.0439.0469.5
Mean207.1205.3212.3213.0227.7209.5255.7255.8249.2251.0236.5260.3
IQR139.0129.595.5101.5157.8103.5152.8155.5111.3111.775.0108.2
IQR/269.564.847.850.878.951.876.477.855.655.837.554.1
SD103.7103.989.590.4112.375.9109.5112.097.097.165.974.5
CV50.150.642.242.449.336.242.843.838.938.727.928.6
KURT−0.10.10.80.6−0.50.1−0.6−0.60.00.01.1−0.4
SKEW0.40.50.30.20.10.5−0.2−0.20.00.00.7−0.2
Upper Outliers (%)0.93.14.03.30.00.90.00.01.31.34.00.0
Lower Outliers (%)0.00.00.00.00.00.00.00.02.72.70.70.1
For the Box
Q2-Q169.564.872.856.886.544.872.079.021.540.434.547.2
Q3-Q269.564.822.844.871.358.780.876.589.871.340.461.0
For the Whiskers
Q3+1.5*IQR479.0455.0393.0408.0538.4413.3565.4569.8483.6484.2383.2480.5
Q1−1.5*IQR−77.0−63.011.02.0−92.6−0.8−45.6−52.338.637.683.347.8
Upper Whisker479.0455.0393.0408.0495.0413.3495.0495.0483.6484.2383.2469.5
Lower Whisker19.019.019.019.019.032.029.029.038.637.683.347.8
Wupper-Q3208.5194.3143.3152.3193.3155.3158.8158.5166.9167.5112.4151.3
Q1-Wlower112.5112.3135.3135.3125.0122.5154.5152.0166.9167.5112.4162.3
Where: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation; Q1-Q2-Q3: Quartiles; IQR: Intra-Quadratic Range; SD: Standard Deviation; CV: Coeffiecient of Variation. Note: numbers in bold highlight the parameters of interest.
Table
Table 4. Difference (Diff) in CV values (%) between the measured data (all data) (M) and those values derived from the sampling methods: MC, RT, RC, RR, and I, where: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation; FW: Fresh weight; DW: Dry weight; EW: Ear weight. Note: numbers in bold highlight the parameters of interest.
Table 4. Difference (Diff) in CV values (%) between the measured data (all data) (M) and those values derived from the sampling methods: MC, RT, RC, RR, and I, where: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 20 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation; FW: Fresh weight; DW: Dry weight; EW: Ear weight. Note: numbers in bold highlight the parameters of interest.
All PlotsMMCMC+
Diff% from M		RTRT
Diff% from M		RCRC
Diff% from M		RRRR
Diff% from M		II
Diff% from M
FW38.639.31.934.111.734.111.534.410.827.528.9
DW37.538.52.632.912.333.012.033.311.326.230.2
EW49.149.61.143.012.443.112.243.711.035.827.0
Plot 1MMCMC
Diff% from M		RTRT
Diff% from M		RCRC
Diff% from M		RRRR
Diff% from M		II
Diff% from M
FW36.937.31.032.811.332.811.036.80.527.226.3
DW32.432.70.828.811.129.010.732.91.422.730.0
EW53.153.40.746.811.847.011.451.52.939.725.2
Plot 2MMCMC
Diff% from M		RTRT
Diff% from M		RCRC
Diff% from M		RRRR
Diff% from M		II
Diff% from M
FW41.642.52.035.115.635.315.242.00.829.229.8
DW41.843.02.735.215.835.415.343.43.728.831.1
EW50.150.61.142.215.842.415.349.31.436.227.6
Plot 3MMCMC
Diff% from M		RTRT
Diff% from M		RCRC
Diff% from M		RRRR
Diff% from M		II
Diff% from M
FW35.636.42.332.87.932.87.821.539.623.633.7
DW36.137.22.932.79.532.89.219.944.924.931.1
EW42.843.82.238.99.238.79.727.934.928.633.2
Where Diff% = ((CV(MC or RT or RC or I) − CV(M))/(CV(MC or RT or RC or I)))*100.
Table
Table 5. Difference (Diff) in mean values (%) between the measured data (all data) (M) and the estimated mean values by the other sampling methods: MC, RT, RC, RR, and I, where: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 21 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation; FW: Fresh weight; DW: Dry weight; EW: Ear weight. Note: numbers in bold highlight the parameters of interest.
Table 5. Difference (Diff) in mean values (%) between the measured data (all data) (M) and the estimated mean values by the other sampling methods: MC, RT, RC, RR, and I, where: M: Measured (all data); MC: Measured cut (without the measurements from the upper part area—lines 21 to 25); RT: Missing values were replaced by the total average of all values; RC: Missing values were replaced by the average of the column, where the missing value belongs to; RR: Missing values were replaced by the average of the row, where the missing value belongs to; I: Interpolation; FW: Fresh weight; DW: Dry weight; EW: Ear weight. Note: numbers in bold highlight the parameters of interest.
All PlotsMMCDiff%RTDiff%RCDiff%RRDiff%IDiff%
FW659.5661.90.4659.40.0660.40.1660.00.1665.50.9
DW202.0202.90.4202.00.0202.00.0202.10.0203.10.5
EW226.9226.5−0.2226.90.0227.90.5227.40.2230.31.5
Plot 1MMCDiff%RTDiff%RCDiff%RRDiff%IDiff%
FW648.6657.51.4650.70.3652.20.6646.2−0.4654.70.9
DW201.3205.21.9201.50.1201.70.2200.4−0.4201.30.0
EW217.3216.6−0.3219.30.9219.71.1218.00.4221.11.8
Plot 2MMCDiff%RTDiff%RCDiff%RRDiff%IDiff%
FW597.6593.3−0.7613.52.7614.62.9659.310.3613.62.7
DW180.4179.2−0.7186.03.1185.83.0201.511.7188.64.5
EW207.1205.3−0.9212.32.5213.02.9227.79.9209.51.1
Plot 3MMCDiff%RTDiff%RCDiff%RRDiff%IDiff%
FW729.9731.10.2716.1−1.9716.6−1.8675.2−7.5728.1−0.2
DW223.5223.50.0218.6−2.2218.6−2.2204.4−8.5219.4−1.8
EW255.7255.80.1249.2−2.5251.0−1.8236.5−7.5260.31.8
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Koutsos, T.M.; Menexes, G.C.; Eleftherohorinos, I.G. The Use of Spatial Interpolation to Improve the Quality of Corn Silage Data in Case of Presence of Extreme or Missing Values. ISPRS Int. J. Geo-Inf. 2022, 11, 153. https://doi.org/10.3390/ijgi11030153

AMA Style

Koutsos TM, Menexes GC, Eleftherohorinos IG. The Use of Spatial Interpolation to Improve the Quality of Corn Silage Data in Case of Presence of Extreme or Missing Values. ISPRS International Journal of Geo-Information. 2022; 11(3):153. https://doi.org/10.3390/ijgi11030153

Chicago/Turabian Style

Koutsos, Thomas M., Georgios C. Menexes, and Ilias G. Eleftherohorinos. 2022. "The Use of Spatial Interpolation to Improve the Quality of Corn Silage Data in Case of Presence of Extreme or Missing Values" ISPRS International Journal of Geo-Information 11, no. 3: 153. https://doi.org/10.3390/ijgi11030153

APA Style

Koutsos, T. M., Menexes, G. C., & Eleftherohorinos, I. G. (2022). The Use of Spatial Interpolation to Improve the Quality of Corn Silage Data in Case of Presence of Extreme or Missing Values. ISPRS International Journal of Geo-Information, 11(3), 153. https://doi.org/10.3390/ijgi11030153

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop