Development Process, Quantitative Models, and Future Directions in Driving Analysis of Urban Expansion
Abstract
:1. Introduction
2. The Development Process of DAUE
2.1. The Booming of DAUE Study and Transition of Involved Research Institutions
2.1.1. Three Identified Development Stages of DAUE
2.1.2. Increasingly Multidisciplinary Subjects of DAUE
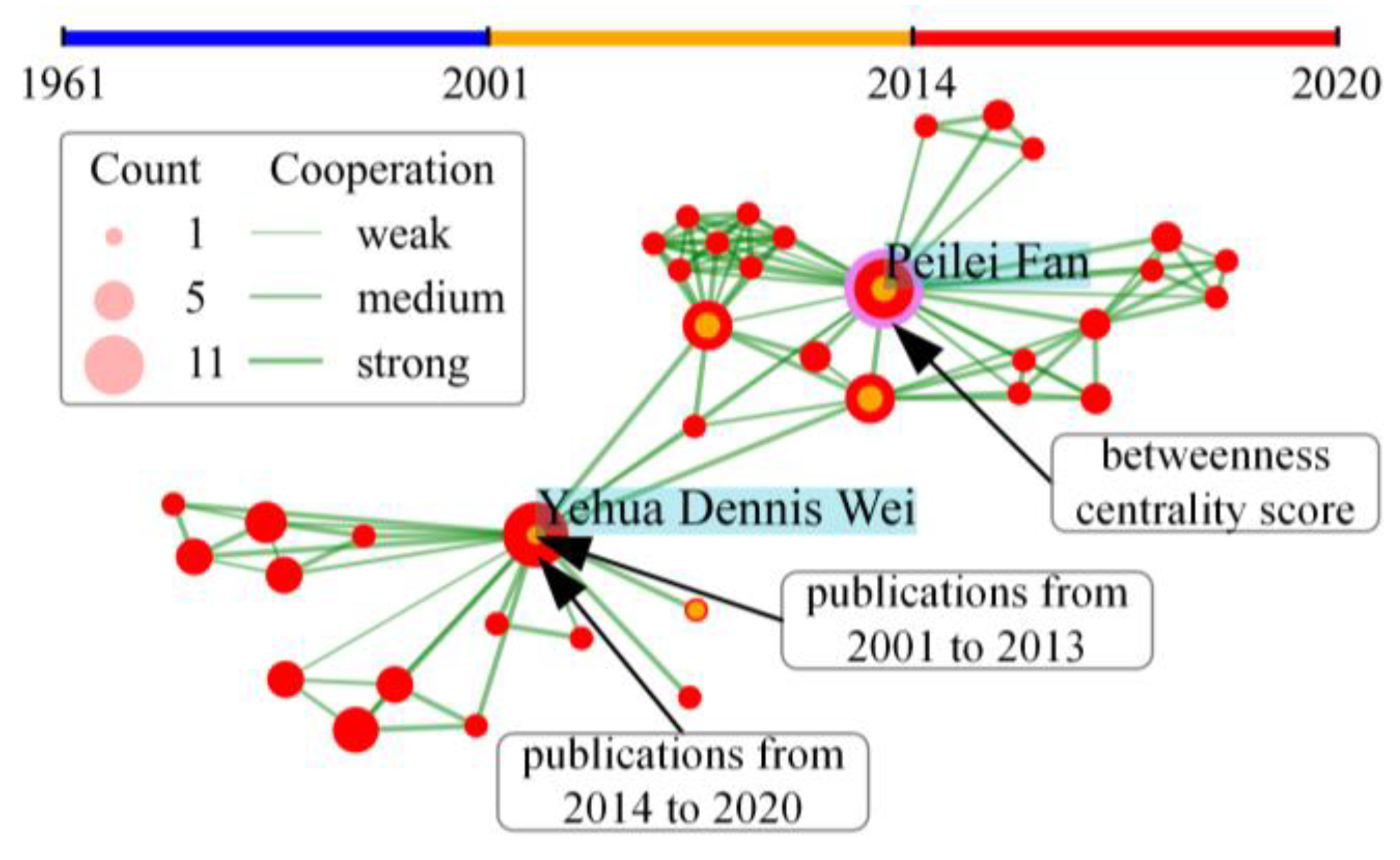
2.1.3. The Transition of Involved DAUE Research Institutions
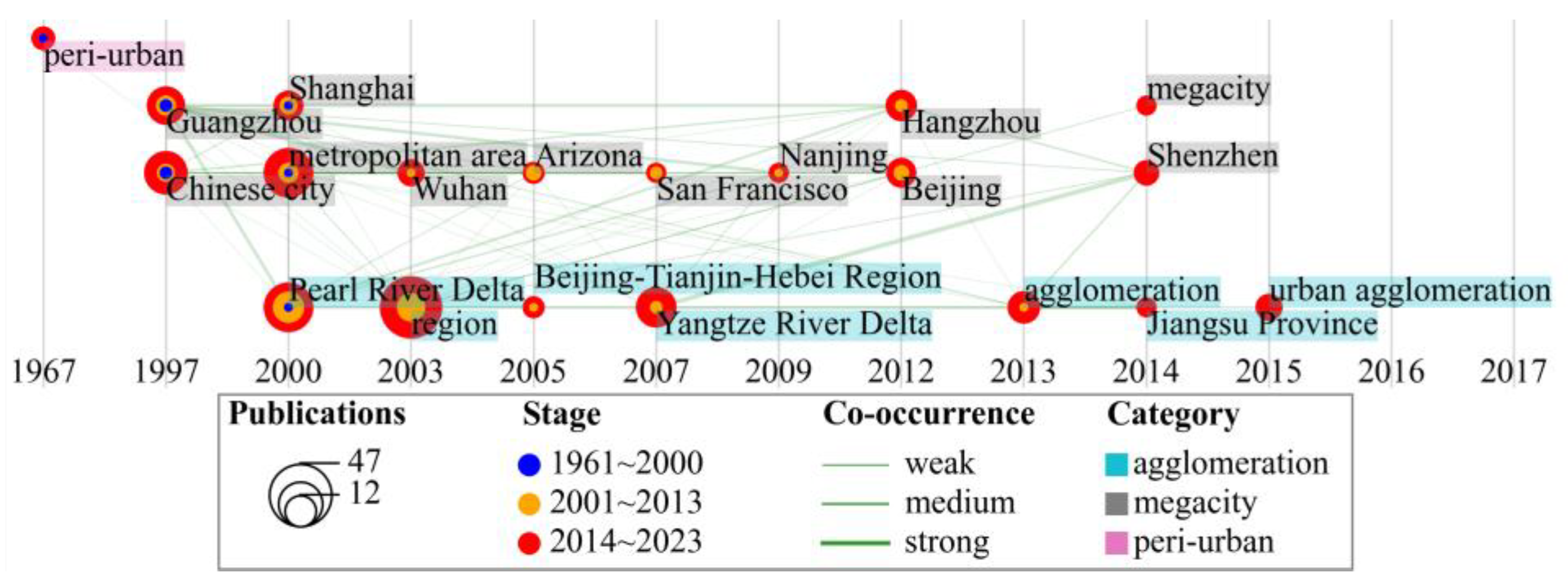
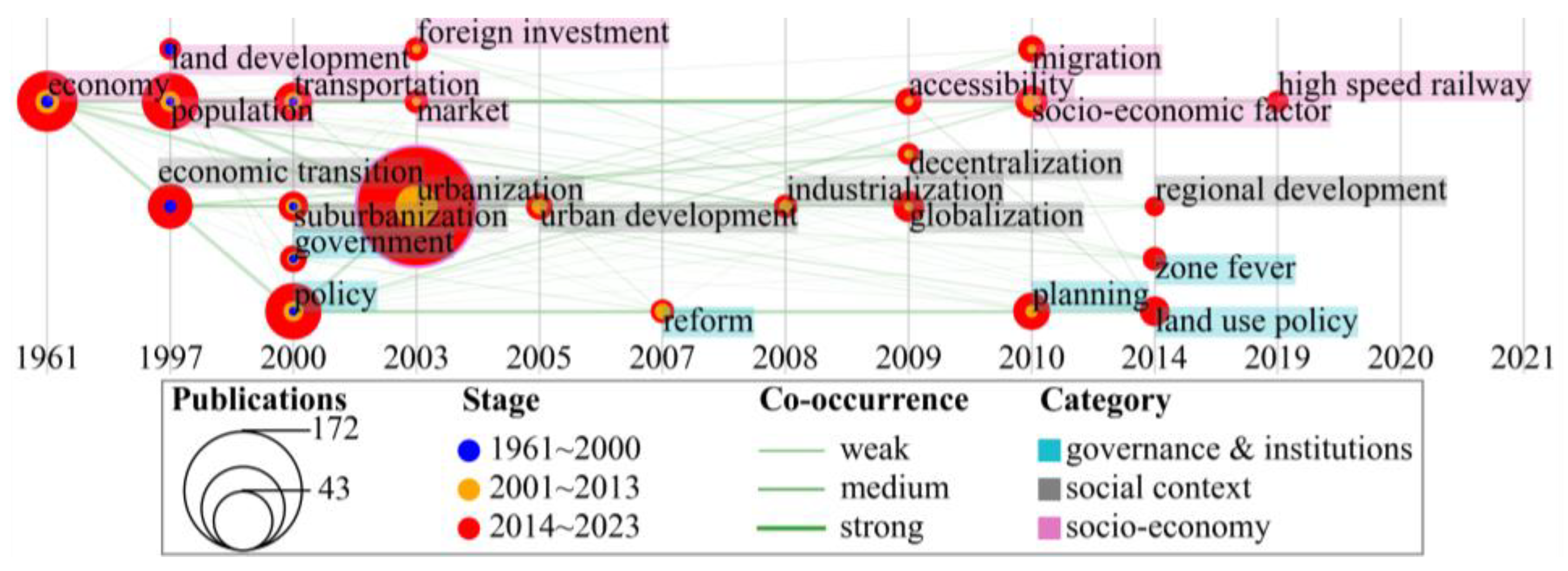
2.2. Evolution of DAUE Hot Themes
2.2.1. Hot Research Themes and Their Diachronic Extension
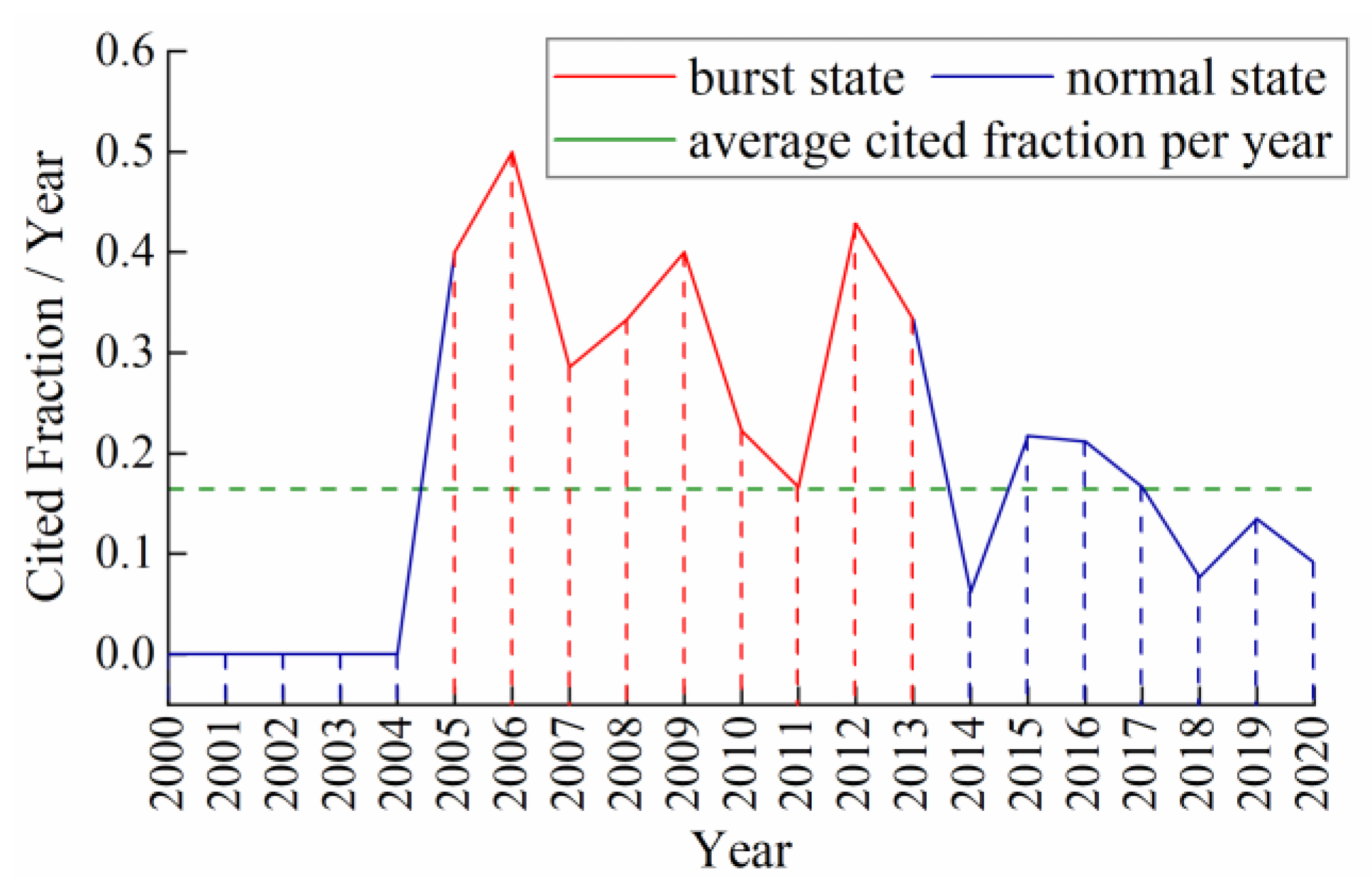
2.2.2. Burst Detection for Hot Themes
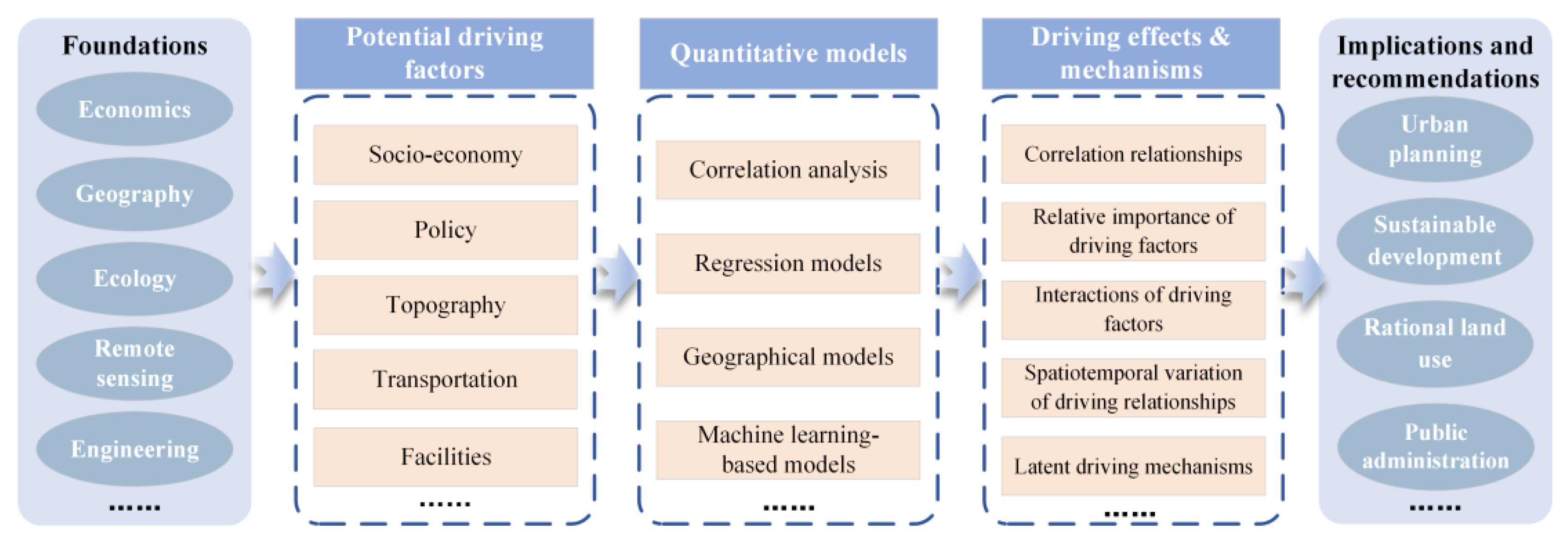
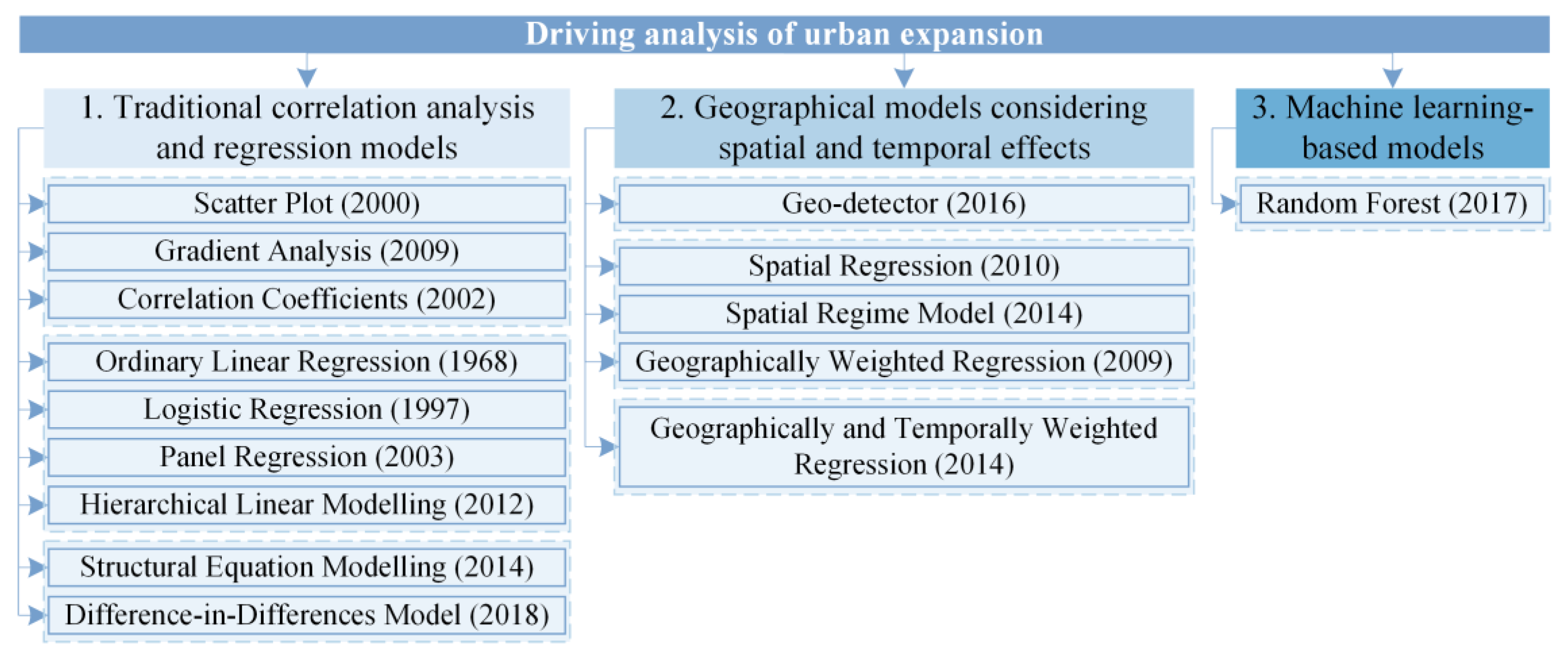
3. Quantification Models in DAUE
3.1. Traditional Correlation Analysis and Regression Models
3.1.1. Correlation Analysis
3.1.2. Classic Regression Models without Considering Spatiotemporal Effect
3.2. Geographical Models Considering Spatial and Temporal Effects
3.2.1. Geo-Detector: Model Considering Spatial Distribution
3.2.2. Spatial Regression Models: Models Considering Spatial Dependence
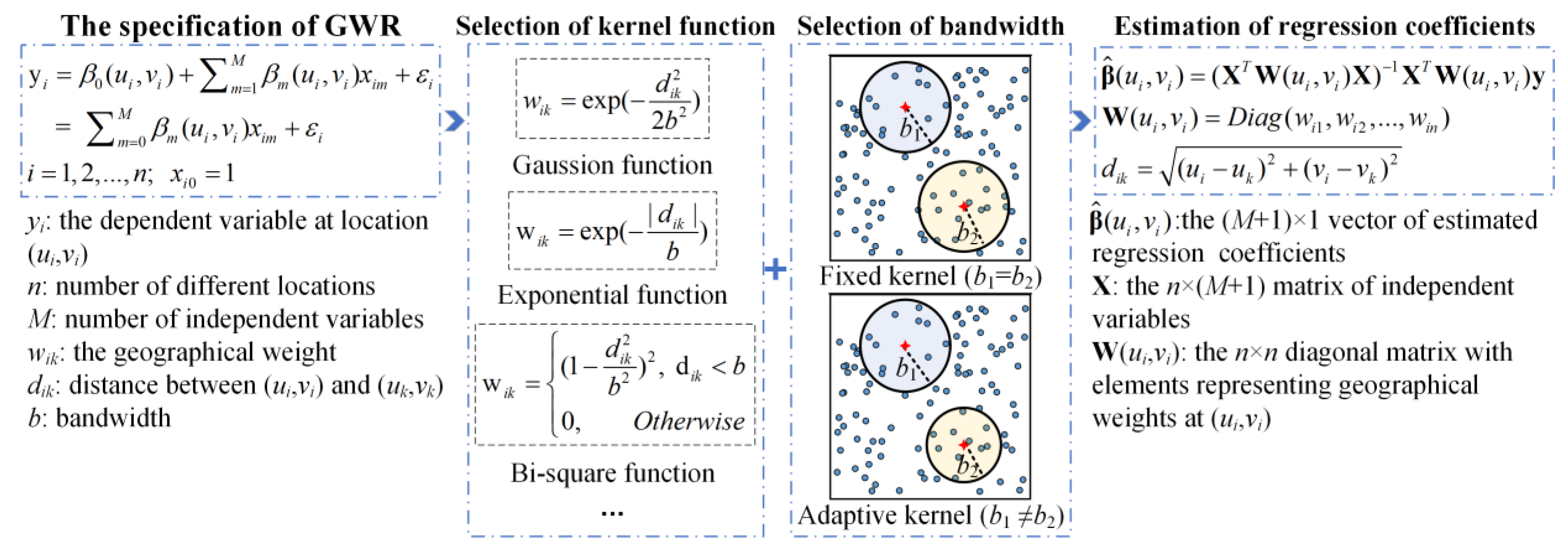
3.2.3. SRM and GWR: Models Considering Spatial Dependence and Spatial Heterogeneity
3.2.4. GTWR and GTWLR: Models Considering Both Spatial and Temporal Effects
3.3. Machine Learning-Based Models
3.4. Brief Model Summary
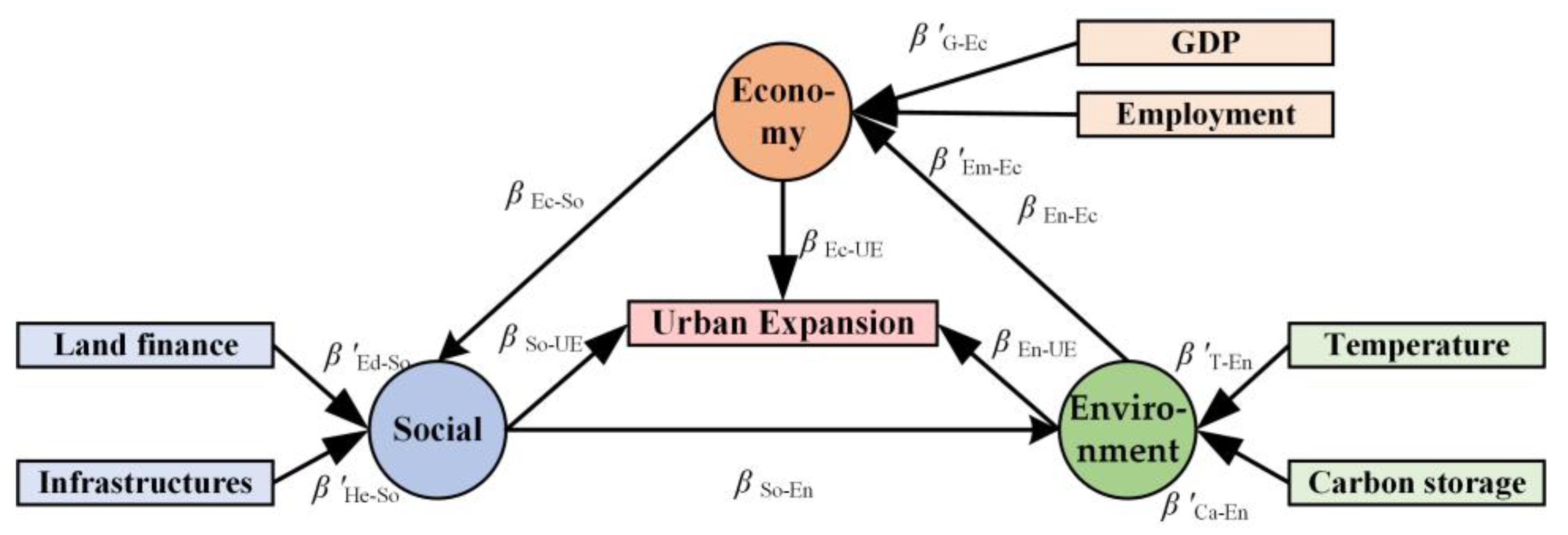
4. Discussion: Limitations and Future Research Directions
4.1. The Complement of Multi-Scale Interaction Research on Hierarchical Urban Systems
4.2. The Supplement of Remote Sensing-Derived Data and Assimilation of Multi-Source Spatiotemporal Big Data
4.3. The Performance Improvement of Quantitative Models Based on Interpretable Machine Learning
4.4. The Mutually Beneficial Integration of CA-Based Urban Expansion Simulation and DAUE
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Data Collection
| Term Indicates “Urban Expansion” | Term Indicates “Driving Mechanism Analysis” |
|---|---|
| Urban expansion | Driver |
| Urban extension | Driving force/factor |
| Urban growth | Influencing factor |
| Urban land growth | Determinant |
| Urban sprawl | Factor |
| Land expansion | Cause |
| Built-up expansion | Causal |
| Land take | Mechanism |
| Land development | |
| Urban land change |
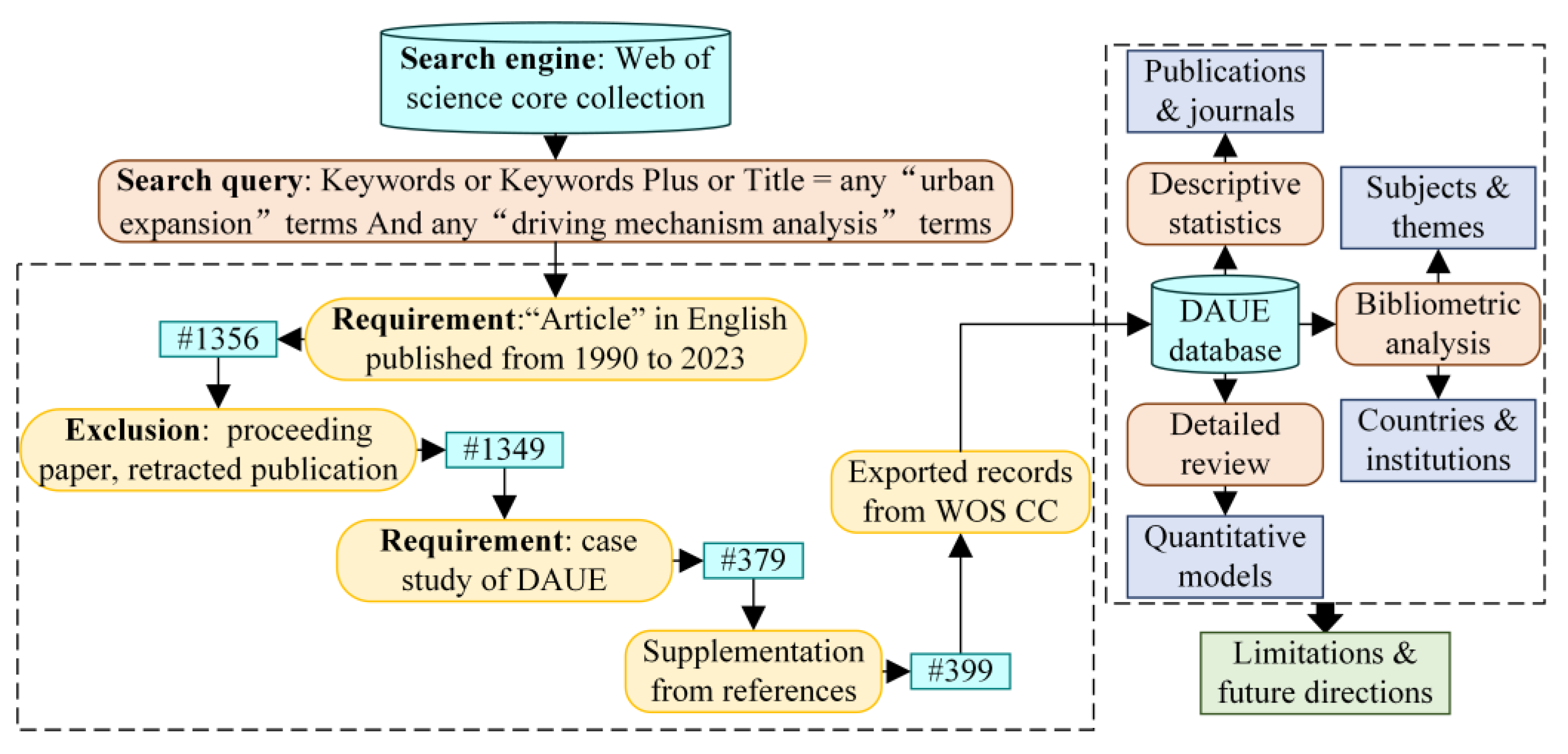
Appendix B. Research Methods
References
- Ritchie, H.; Roser, M. Urbanization. 2018. Available online: https://ourworldindata.org/urbanization (accessed on 16 May 2022).
- Deng, Y.; Fu, B.; Sun, C. Effects of urban planning in guiding urban growth: Evidence from Shenzhen, China. Cities 2018, 83, 118–128. [Google Scholar] [CrossRef]
- Li, G.; Li, F. Urban sprawl in China: Differences and socioeconomic drivers. Sci. Total Environ. 2019, 673, 367–377. [Google Scholar] [CrossRef] [PubMed]
- Fan, P.; Yue, W.; Zhang, J.; Huang, H.; Messina, J.; Verburg, P.H.; Qi, J.; Moore, N.; Ge, J. The spatial restructuring and determinants of industrial landscape in a mega city under rapid urbanization. Habitat Int. 2020, 95, 102099. [Google Scholar] [CrossRef]
- Pierri Daunt, A.B.; Sanna Freire Silva, T.; Bürgi, M.; Hersperger, A.M. Urban expansion and forest reserves: Drivers of change and persistence on the coast of São Paulo State (Brazil). Land Use Policy 2021, 101, 105189. [Google Scholar] [CrossRef]
- Park, H.; Fan, P.; John, R.; Chen, J. Urbanization on the Mongolian Plateau after economic reform: Changes and causes. Appl. Geogr. 2017, 86, 118–127. [Google Scholar] [CrossRef]
- Li, G.; Sun, S.; Fang, C. The varying driving forces of urban expansion in China: Insights from a spatial-temporal analysis. Landsc. Urban Plan. 2018, 174, 63–77. [Google Scholar] [CrossRef]
- Liang, X.; Guan, Q.; Clarke, K.C.; Liu, S.; Wang, B.; Yao, Y. Understanding the drivers of sustainable land expansion using a patch-generating land use simulation (PLUS) model: A case study in Wuhan, China. Comput. Environ. Urban Syst. 2021, 85, 101569. [Google Scholar] [CrossRef]
- Lambin, E.F.; Geist, H.J.; Lepers, E. Dynamics of land-use and land-cover change in tropical regions. Annu. Rev. Environ. Resour. 2003, 28, 205–241. [Google Scholar] [CrossRef]
- Van Vliet, J.; Magliocca, N.R.; Büchner, B.; Cook, E.; Rey Benayas, J.M.; Ellis, E.C.; Heinimann, A.; Keys, E.; Lee, T.M.; Liu, J.; et al. Meta-studies in land use science: Current coverage and prospects. Ambio 2016, 45, 15–28. [Google Scholar] [CrossRef]
- Shaw, B.J.; van Vliet, J.; Verburg, P.H. The peri-urbanization of Europe: A systematic review of a multifaceted process. Landsc. Urban Plan. 2020, 196, 103733. [Google Scholar] [CrossRef]
- Wahyudi, A.; Liu, Y. Cellular automata for urban growth modelling: A review on factors defining transition rules. Int. Rev. Spat. Plan. Sustain. Dev. 2016, 4, 60–75. [Google Scholar] [CrossRef]
- Hersperger, A.M.; Oliveira, E.; Pagliarin, S.; Palka, G.; Verburg, P.; Bolliger, J.; Grădinaru, S. Urban land-use change: The role of strategic spatial planning. Glob. Environ. Change 2018, 51, 32–42. [Google Scholar] [CrossRef]
- Kim YNewman, G.; Güneralp, B. A review of driving factors, scenarios, and topics in urban land change models. Land 2020, 9, 246. [Google Scholar]
- Dadashpoor, H.; Ahani, S. Explaining Objective Forces, Driving Forces, and Causal Mechanisms Affecting the Formation and Expansion of the Peri-Urban Areas: A Critical Realism Approach. Land Use Policy 2021, 102, 105232. [Google Scholar] [CrossRef]
- Colsaet, A.; Laurans, Y.; Levrel, H. What drives land take and urban land expansion? A systematic review. Land Use Policy 2018, 79, 339–349. [Google Scholar] [CrossRef]
- Kasraian, D.; Maat, K.; Stead, D.; van Wee, B. Long-term impacts of transport infrastructure networks on land-use change: An international review of empirical studies. Transp. Rev. 2016, 36, 772–792. [Google Scholar] [CrossRef]
- Seto, K.C.; Sánchez-Rodríguez, R.; Fragkias, M. The new geography of contemporary urbanization and the environment. Annu. Rev. Environ. Resour. 2010, 35, 167–194. [Google Scholar] [CrossRef]
- Seto, K.C.; Fragkias, M.; Güneralp, B.; Reilly, M.K. A meta-analysis of global urban land expansion. PLoS ONE 2011, 6, e23777. [Google Scholar] [CrossRef]
- Muth, R.F. Economic Change and Rural-Urban Land Conversions. Econometrica 1961, 29, 1. [Google Scholar] [CrossRef]
- Zhang, L.; Yue, W.; Liu, Y.; Fan, P.; Wei, Y.D. Suburban industrial land development in transitional China: Spatial restructuring and determinants. Cities 2018, 78, 96–107. [Google Scholar] [CrossRef]
- Harvey, R.O.; Clark, W.A.V. The Nature and Economics of Urban Sprawl. Land Econ. 1965, 41, 1. [Google Scholar] [CrossRef]
- Brueckner, J.K. Urban sprawl: Diagnosis and remedies. Int. Reg. Sci. Rev. 2000, 23, 160–171. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, T.; Sun, J.; Li, Y.; Li, W. Accelerated urban expansion in Lhasa City and the implications for sustainable development in a Plateau City. Sustainability 2017, 9, 1499. [Google Scholar] [CrossRef]
- Cao, Y.; Bai, Z.; Zhou, W.; Zhang, X. Analyses of traits and driving forces on urban land expansion in a typical coal-resource-based city in a loess area. Environ. Earth Sci. 2016, 75, 1191. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, X.; Ai, B.; Li, S. Capturing the varying effects of driving forces over time for the simulation of urban growth by using survival analysis and cellular automata. Landsc. Urban Plan. 2016, 152, 59–71. [Google Scholar] [CrossRef]
- Feng, Y.; Tong, X. Using exploratory regression to identify optimal driving factors for cellular automaton modeling of land use change. Environ. Monit. Assess. 2017, 189, 515. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.J.; Wang, R.; Tong, X.; Shafizadeh-Moghadam, H. How much can temporally stationary factors explain cellular automata-based simulations of past and future urban growth? Comput. Environ. Urban Syst. 2019, 76, 150–162. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Wu, X.; Yao, Y.; Wu, X.; Chen, Y. Multiple intra-urban land use simulations and driving factors analysis: A case study in Huicheng, China. GISci. Remote Sens. 2019, 56, 282–308. [Google Scholar] [CrossRef]
- Kuang, W.; Chi, W.; Lu, D.; Dou, Y. A comparative analysis of megacity expansions in China and the U.S.: Patterns, rates and driving forces. Landsc. Urban Plan. 2014, 132, 121–135. [Google Scholar] [CrossRef]
- Subasinghe, S.; Estoque, R.C.; Murayama, Y. Spatiotemporal analysis of urban growth using GIS and remote sensing: A case study of the Colombo metropolitan area, Sri Lanka. ISPRS Int. J. Geo-Inf. 2016, 5, 197. [Google Scholar] [CrossRef]
- Lu, D.; Li, L.; Li, G.; Fan, P.; Ouyang, Z.; Moran, E. Examining spatial patterns of urban distribution and impacts of physical conditions on urbanization in coastal and inland metropoles. Remote Sens. 2018, 10, 1101. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, H.; Liu, K.; Wu, Q. Research on the influence of site factors on the expansion of construction land in the Pearl River Delta, China: By using GIS and remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 366–373. [Google Scholar] [CrossRef]
- Kasraian, D.; Raghav, S.; Miller, E.J. A multi-decade longitudinal analysis of transportation and land use co-evolution in the Greater Toronto-Hamilton Area. J. Transp. Geogr. 2020, 84, 102696. [Google Scholar] [CrossRef]
- Lei, H.; Koch, J.; Shi, H. An analysis of spatio-temporal urbanization patterns in Northwest China. Land 2020, 9, 411. [Google Scholar] [CrossRef]
- Deng, Y.; Srinivasan, S. Urban land use change and regional access: A case study in Beijing, China. Habitat Int. 2016, 51, 103–113. [Google Scholar] [CrossRef]
- Azhdari, A.; Sasani, M.A.; Soltani, A. Exploring the relationship between spatial driving forces of urban expansion and socioeconomic segregation: The case of Shiraz. Habitat Int. 2018, 81, 33–44. [Google Scholar] [CrossRef]
- Arellano, M. Panel Data Econometrics; OUP Oxford: Oxford, UK, 2003. [Google Scholar]
- Baltagi, B.H. Econometric Analysis of Panel Data, 6th ed.; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Oueslati, W.; Alvanides, S.; Garrod, G. Determinants of urban sprawl in European cities. Urban Stud. 2015, 52, 1594–1614. [Google Scholar] [CrossRef]
- Chen, J.; Gao, J.; Chen, W. Urban land expansion and the transitional mechanisms in Nanjing, China. Habitat Int. 2016, 53, 274–283. [Google Scholar] [CrossRef]
- Jiang, L.; Deng, X.; Seto, K.C. Multi-level modeling of urban expansion and cultivated land conversion for urban hotspot counties in China. Landsc. Urban Plan. 2012, 108, 131–139. [Google Scholar] [CrossRef]
- Liao, C.; Dai, T.; Cai, H.; Zhang, W. Examining the driving factors causing rapid urban expansion in China: An analysis based on GlobeLand30 data. ISPRS Int. J. Geo-Inf. 2017, 6, 264. [Google Scholar] [CrossRef]
- Meyfroidt, P. Approaches and terminology for causal analysis in land systems science. J. Land Use Sci. 2016, 11, 501–522. [Google Scholar] [CrossRef]
- Thomas, H. Coming of age. In Chemical Engineer; Guilford Publications: New York, NY, USA, 2008; pp. 38–40. [Google Scholar]
- He, C.; Huang, Z.; Wang, R. Land use change and economic growth in urban China: A structural equation analysis. Urban Stud. 2014, 51, 2880–2898. [Google Scholar] [CrossRef]
- Wang, C.; Liu, H.; Zhang, M. Exploring the mechanism of border effect on urban land expansion: A case study of Beijing-Tianjin-Hebei region in China. Land Use Policy 2020, 92, 104424. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, L.; Wang, R. Administrative-Hierarchical Urban Land Expansion in China: Urban Agglomeration in the Yangtze River Delta. J. Urban Plan. Dev. 2018, 144, 05018018. [Google Scholar] [CrossRef]
- Deng, T.; Wang, D.; Hu, Y.; Liu, S. Did high-speed railway cause urban space expansion?—Empirical evidence from China’s prefecture-level cities. Res. Transp. Econ. 2020, 80, 100840. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Liu, X.; Chen, Y.; Ou, J.; Niu, N.; Jin, Y.; Shi, H. Will the Development of a High-Speed Railway Have Impacts on Land Use Patterns in China? Ann. Am. Assoc. Geogr. 2019, 109, 979–1005. [Google Scholar] [CrossRef] [PubMed]
- Angrist, J.D.; Pischke, J.-S. Parallel Worlds: Fixed Effects, Differences-in-differences, and Panel Data. In Mostly Harmless Econometrics: An Empiricist’s Companion; Princeton University Press: Princeton, NJ, USA, 2008; pp. 165–184. [Google Scholar]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Zhou, T.; Jiang, G.; Zhang, R.; Zheng, Q.; Ma, W.; Zhao, Q.; Li, Y. Addressing the rural in situ urbanization (RISU) in the Beijing–Tianjin–Hebei region: Spatio-temporal pattern and driving mechanism. Cities 2018, 75, 59–71. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, X.; Li, T. Identifying driving forces of built-up land expansion based on the geographical detector: A case study of pearl river delta urban agglomeration. Int. J. Environ. Res. Public Health 2020, 17, 1759. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Ju, H.; Zhang, S.; Jiang, W. Spatiotemporal patterns and driving forces of urban expansion in coastal areas: A study on urban agglomeration in the pearl river delta, China. Sustainability 2020, 12, 191. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, L.; Li, X.; Zhang, C.; Shi, T.; Wu, X.; Yang, C.; Gao, W.; Li, Q.; Wu, G. Exploring annual urban expansions in the Guangdong-Hong Kong-Macau Greater Bay Area: Spatiotemporal features and driving factors in 1986–2017. Remote Sens. 2020, 12, 2615. [Google Scholar] [CrossRef]
- Deng, X.; Huang, J.; Rozelle, S.; Uchida, E. Economic growth and the expansion of urban land in China. Urban Stud. 2010, 47, 813–843. [Google Scholar] [CrossRef]
- Feng, Y.C.; Wang, X.; Du, W.; Liu, J.; Li, Y. Spatiotemporal characteristics and driving forces of urban sprawl in China during 2003–2017. J. Clean. Prod. 2019, 241, 118061. [Google Scholar] [CrossRef]
- Gómez-Antonio, M.; Hortas-Rico, M.; Li, L. The Causes of Urban Sprawl in Spanish Urban Areas: A Spatial Approach. Spat. Econ. Anal. 2016, 11, 219–247. [Google Scholar] [CrossRef]
- Li, H.; Wei, Y.H.D.; Huang, Z. Urban land expansion and spatial dynamics in Globalizing Shanghai. Sustainability 2014, 6, 8856–8875. [Google Scholar] [CrossRef]
- Li, H.; Wei, Y.D.; Liao, F.H.; Huang, Z. Administrative hierarchy and urban land expansion in transitional China. Appl. Geogr. 2015, 56, 177–186. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46 (Suppl. S1), 234. [Google Scholar] [CrossRef]
- Luo, J.; Wei, Y.H.D. Modeling spatial variations of urban growth patterns in Chinese cities: The case of Nanjing. Landsc. Urban Plan. 2009, 91, 51–64. [Google Scholar] [CrossRef]
- Jing, S.; Yan, Y.; Niu, F.; Song, W. Urban Expansion in China: Spatiotemporal Dynamics and Determinants. Land 2022, 11, 356. [Google Scholar] [CrossRef]
- Liao, F.H.F.; Wei, Y.H.D. Modeling determinants of urban growth in Dongguan, China: A spatial logistic approach. Stoch. Environ. Res. Risk Assess. 2014, 28, 801–816. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Liu, Y.; Liu, Y.; Xu, S.; Zhao, Y.; Chen, Y.; Hong, S. Urban expansion patterns and their driving forces based on the center of gravity-GTWR model: A case study of the Beijing-Tianjin-Hebei urban agglomeration. J. Geogr. Sci. 2020, 30, 297–318. [Google Scholar] [CrossRef]
- Wrenn, D.H.; Sam, A.G. Geographically and temporally weighted likelihood regression: Exploring the spatiotemporal determinants of land use change. Reg. Sci. Urban Econ. 2014, 44, 60–74. [Google Scholar] [CrossRef]
- Gao, C.; Feng, Y.; Tong, X.; Lei, Z.; Chen, S.; Zhai, S. Modeling urban growth using spatially heterogeneous cellular automata models: Comparison of spatial lag, spatial error and GWR. Comput. Environ. Urban Syst. 2020, 81, 101459. [Google Scholar] [CrossRef]
- Wu, R.; Li, Z.G.; Wang, S.J. The varying driving forces of urban land expansion in China: Insights from a spatial-temporal analysis. Sci. Total Environ. 2021, 766, 142591. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and Temporal Weighted Regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăgu, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Huang, L.; Shahtahmassebi, A.R.; Gan, M.; Deng, J.; Wang, J.; Wang, K. Characterizing spatial patterns and driving forces of expansion and regeneration of industrial regions in the Hangzhou megacity, China. J. Clean. Prod. 2020, 253, 119959. [Google Scholar] [CrossRef]
- You, H.; Yang, X. Urban expansion in 30 megacities of China: Categorizing the driving force profiles to inform the urbanization policy. Land Use Policy 2017, 68, 531–551. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning. 2023. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 8 April 2023).
- Meyfroidt, P.; Chowdhury, R.R.; de Bremond, A.; Ellis, E.C.; Erb, K.-H.; Filatova, T.; Garrett, R.D.; Grove, J.M.; Heinimann, A.; Kuemmerle, T.; et al. Middle-range theories of land system change. Glob. Environ. Change 2018, 53, 52–67. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Wu, J. What drives urban growth in China? A multi-scale comparative analysis. Appl. Geogr. 2018, 98, 43–51. [Google Scholar] [CrossRef]
- Seto, K.C.; Reenberg, A.; Boone, C.G.; Fragkias, M.; Haase, D.; Langanke, T.; Marcotullio, P.; Munroe, D.K.; Olah, B.; Simon, D. Urban land teleconnections and sustainability. Proc. Natl. Acad. Sci. USA 2012, 109, 7687–7692. [Google Scholar] [CrossRef]
- Liu, J.; Hull, V.; Moran, E.; Nagendra, H.; Swaffield, S.R.; Turner, B.L. Applications of the telecoupling framework to land-change science. Rethink. Glob. Land Use Urban Era 2014, 14, 119–140. [Google Scholar]
- Li, Y.; Xiong, W. A spatial panel data analysis of China’s urban land expansion, 2004–2014. Pap. Reg. Sci. 2019, 98, 393–407. [Google Scholar] [CrossRef]
- Chen, B.; Wu, C.; Huang, X.; Yang, X. Examining the relationship between urban land expansion and economic linkage using coupling analysis: A case study of the Yangtze River Economic Belt, China. Sustainability 2020, 12, 1227. [Google Scholar] [CrossRef]
- Tan, R.; Zhou, K.; He, Q.; Xu, H. Analyzing the effects of spatial interaction among city clusters on urban growth-case of Wuhan Urban agglomeration. Sustainability 2016, 8, 759. [Google Scholar] [CrossRef]
- Wu, C.; Huang, X.; Chen, B. Telecoupling mechanism of urban land expansion based on transportation accessibility: A case study of transitional Yangtze River economic Belt, China. Land Use Policy 2020, 96, 104687. [Google Scholar] [CrossRef]
- Weiss, S.F.; Kaiser, E.J. A Quantitative Evaluation of Major Factors Influencing Urban Land Development in a Regional Cluster. Traffic Q. 1968, 22, 109–115. [Google Scholar]
- Mathews, A.J.; Frazier, A.E.; Nghiem, S.V.; Neumann, G.; Zhao, Y. Satellite scatterometer estimation of urban built-up volume: Validation with airborne lidar data. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 100–107. [Google Scholar] [CrossRef]
- Li, M.; Koks, E.; Taubenböck, H.; van Vliet, J. Continental-scale mapping and analysis of 3D building structure. Remote Sens. Environ. 2020, 245, 111859. [Google Scholar] [CrossRef]
- Shi, K.; Yu, B.; Huang, Y.; Hu, Y.; Yin, B.; Chen, Z.; Chen, L.; Wu, J. Evaluating the Ability of NPP-VIIRS Nighttime Light Data to Estimate the Gross Domestic Product and the Electric Power Consumption of China at Multiple Scales: A Comparison with DMSP-OLS Data. Remote Sens. 2014, 6, 1705–1724. [Google Scholar] [CrossRef]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating census data for population mapping using Random forests with remotely-sensed and ancillary data. PLoS ONE 2015, 10, e0107042. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Gao, S.; Gong, L.; Kang, C.; Zhi, Y. Social Sensing: A New Approach to Understanding Our Socioeconomic Environments. Ann. Assoc. Am. Geogr. 2015, 105, 512–530. [Google Scholar] [CrossRef]
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Tu, W.; Cao, J.; Gao, Q.; Cao, R.; Fang, Z.; Yue, Y.; Li, Q. Sensing Urban Dynamics by Fusing Multi-sourced Spatiotemporal Big Data. Wuhan Daxue Xuebao (Xinxi Kexue Ban)/Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 1875–1883. [Google Scholar]
- Shi, S.; Wong, S.K.; Zheng, C. Network capital and urban development: An inter-urban capital flow network analysis. Reg. Stud. 2022, 56, 406–419. [Google Scholar] [CrossRef]
- Wang, Q.; Phillips, N.E.; Small, M.L.; Sampson, R.J. Urban mobility and neighborhood isolation in America’s 50 largest cities. Proc. Natl. Acad. Sci. USA 2018, 115, 7735–7740. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, L.; Xiao, Y.; Lu, Y. Investigating the spatiotemporal pattern between the built environment and urban vibrancy using big data in Shenzhen, China. Comput. Environ. Urban Syst. 2022, 95, 101827. [Google Scholar] [CrossRef]
- Li, X.; Huang, X.; Li, D.; Xu, Y. Aggravated social segregation during the COVID-19 pandemic: Evidence from crowdsourced mobility data in twelve most populated U.S. metropolitan areas. Sustain. Cities Soc. 2022, 81, 103869. [Google Scholar] [CrossRef] [PubMed]
- Muneer, A.; Mohd Taib, S.; Mohamed Fati, S.O.; Balogun, A.; Abdul Aziz, I. A Hybrid Deep Learning-Based Unsupervised Anomaly Detection in High Dimensional Data. Comput. Mater. Contin. 2022, 70, 5363–5381. [Google Scholar] [CrossRef]
- Georgiou, T.; Liu, Y.; Chen, W.; Lew, M. A survey of traditional and deep learning-based feature descriptors for high dimensional data in computer vision. Int. J. Multimed. Inf. Retr. 2020, 9, 135–170. [Google Scholar] [CrossRef]
- Yao, H.; Tang, X.; Wei, H.; Zheng, G.; Li, Z. Revisiting spatial-temporal similarity: A deep learning framework for traffic prediction. Proc. AAAI Conf. Artif. Intell. 2019, 33, 5668–5675. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Wang, J.; Bretz, M.; Dewan, M.A.A.; Delavar, M.A. Machine learning in modelling land-use and land cover-change (LULCC): Current status, challenges and prospects. Sci. Total Environ. 2022, 822, 153559. [Google Scholar] [CrossRef]
- Molnar, C.; Casalicchio, G.; Bischl, B. Interpretable Machine Learning—A Brief History, State-of-the-Art and Challenges. Commun. Comput. Inf. Sci. 2020, 1323, 417–431. [Google Scholar]
- Du, M.; Liu, N.; Hu, X. Techniques for interpretable machine learning. Commun. ACM 2020, 63, 68–77. [Google Scholar] [CrossRef]
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Müller, K.R. Explaining Deep Neural Networks and Beyond: A Review of Methods and Applications. Proc. IEEE 2021, 109, 247–278. [Google Scholar] [CrossRef]
- Scholkopf, B.; Locatello, F.; Bauer, S.; Ke, N.R.; Kalchbrenner, N.; Goyal, A.; Bengio, Y. Toward Causal Representation Learning. Proc. IEEE 2021, 109, 612–634. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Li, F.; Zhu, Q.; Riley, W.J.; Zhao, L.; Xu, L.; Yuan, K.; Chen, M.; Wu, H.; Gui, Z.; Gong, J.; et al. AttentionFire_v1.0: Interpretable machine learning fire model for burned-Area predictions over tropics. Geosci. Model Dev. 2023, 16, 869–884. [Google Scholar] [CrossRef]
- Shu, B.; Zhu, S.; Qu, Y.; Zhang, H.; Li, X.; Carsjens, G.J. Modelling multi-regional urban growth with multilevel logistic cellular automata. Comput. Environ. Urban Syst. 2020, 80, 101457. [Google Scholar] [CrossRef]
- Veldkamp, A.; Fresco, L.O. CLUE: A conceptual model to study the conversion of land use and its effects. Ecol. Model. 1996, 85, 253–270. [Google Scholar] [CrossRef]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Clarke, K.C.; Gaydos, L.J. ; Gaydos, L.J. Loose-coupling a cellular automaton model and GIS: Long-term urban growth prediction for San Francisco and Washington/Baltimore. Int. J. Geogr. Inf. Sci. 1998, 12, 699–714. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Li, X.; Chen, Y. Simulation model of land use dynamics and application: Progress and prospects. Yaogan Xuebao/J. Remote Sens. 2017, 21, 329–340. [Google Scholar]
- Chen, Y.; Li, X. Applications and New Trends of Machine Learning in Urban Simulation Research. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 1884–1889. [Google Scholar]
- Xing, W.; Qian, Y.; Guan, X.; Yang, T.; Wu, H. A novel cellular automata model integrated with deep learning for dynamic spatio-temporal land use change simulation. Comput. Geosci. 2020, 137, 104430. [Google Scholar] [CrossRef]
- Chen, C. Science Mapping: A Systematic Review of the Literature. J. Data Inf. Sci. 2017, 2, 1–40. [Google Scholar] [CrossRef]
- Kleinberg, J. Bursty and hierarchical structure in streams. Data Min. Knowl. Discov. 2003, 7, 373–397. [Google Scholar] [CrossRef]
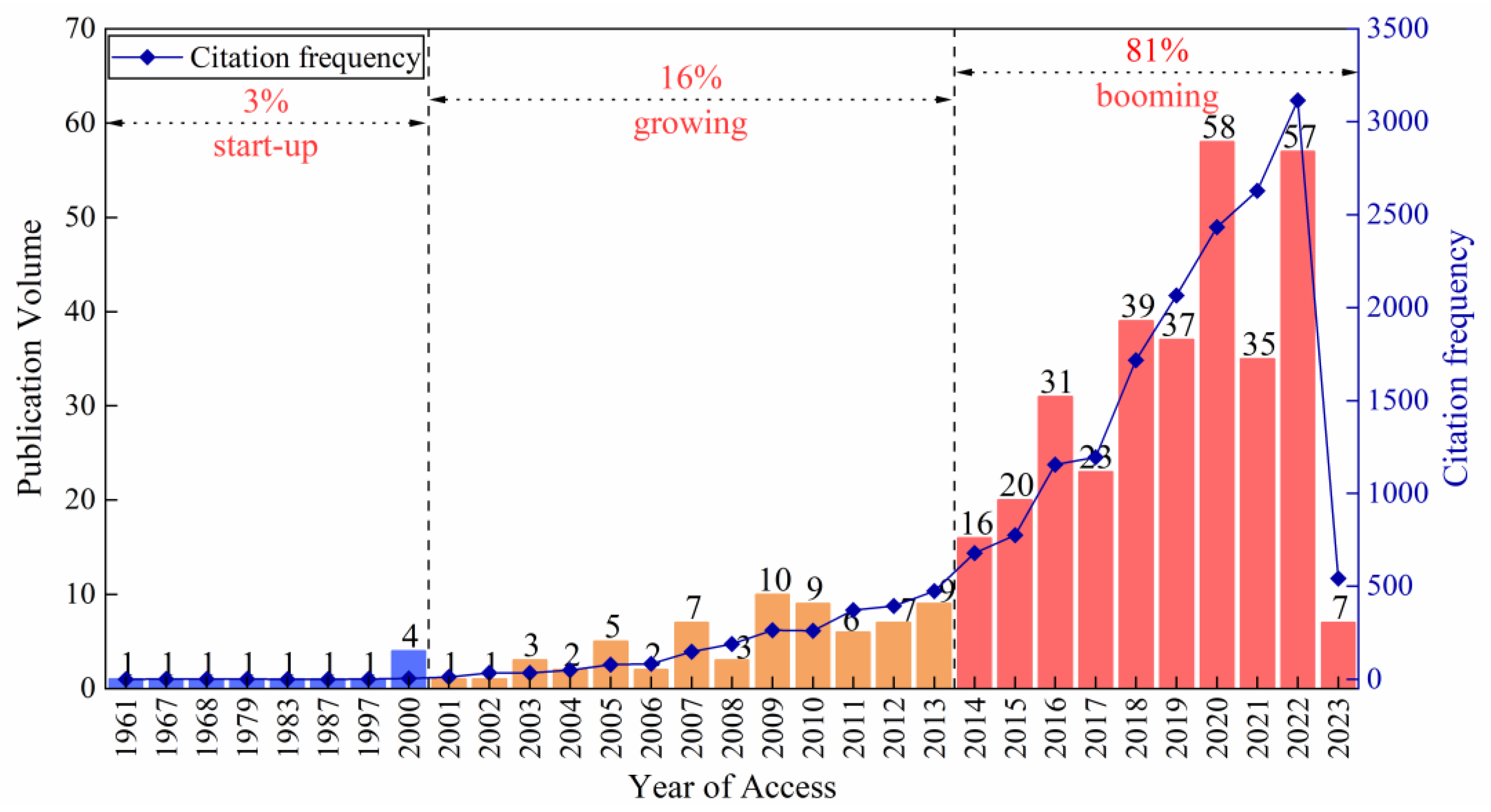


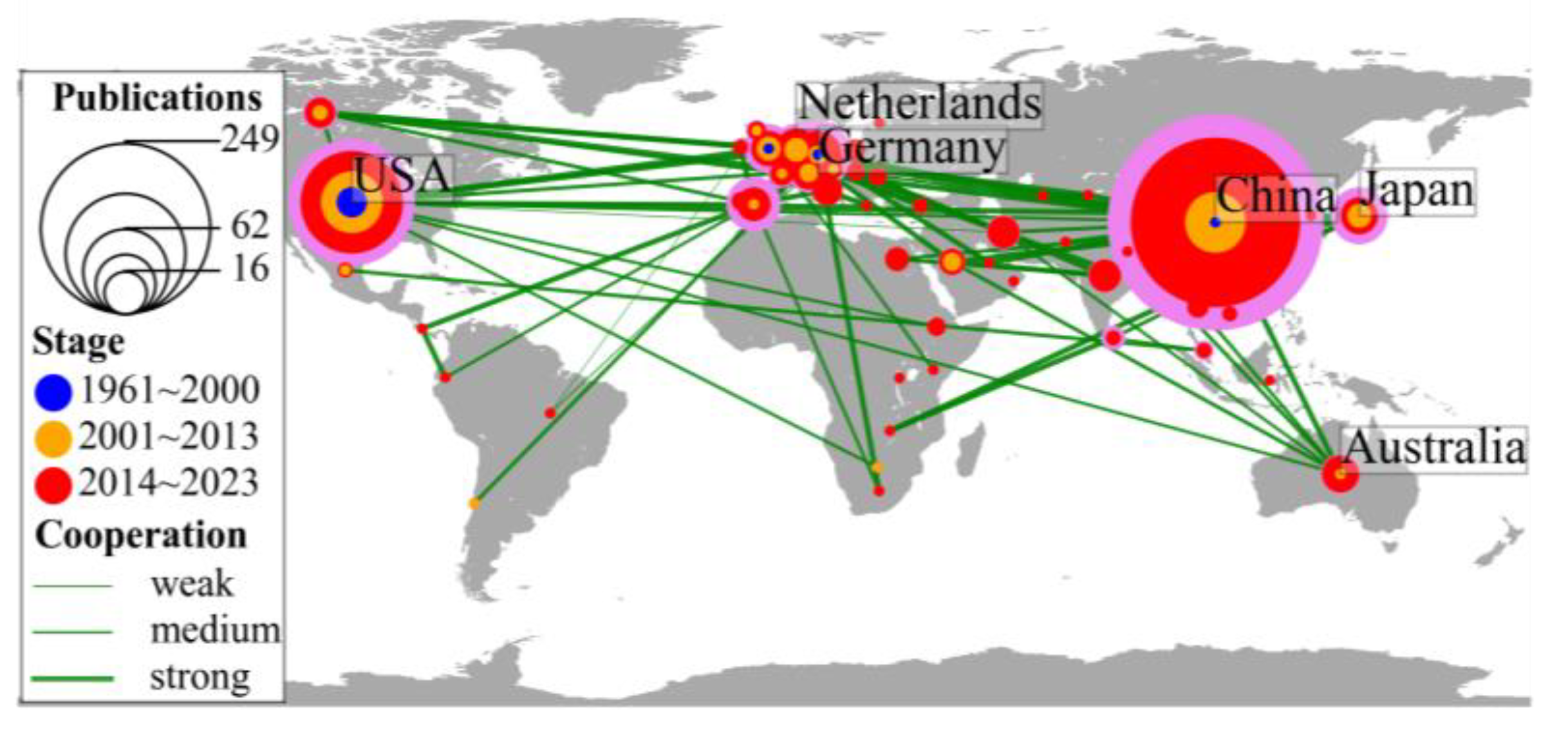
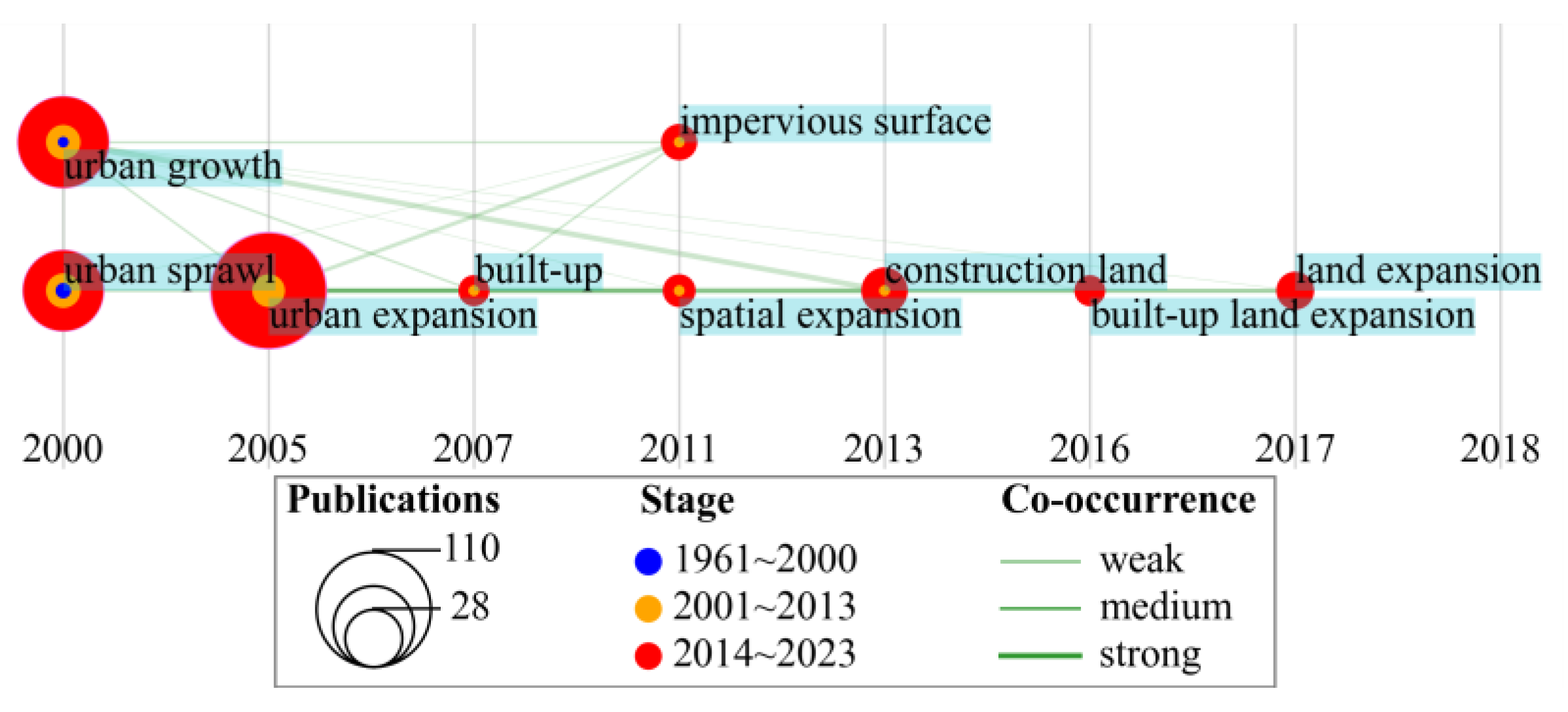
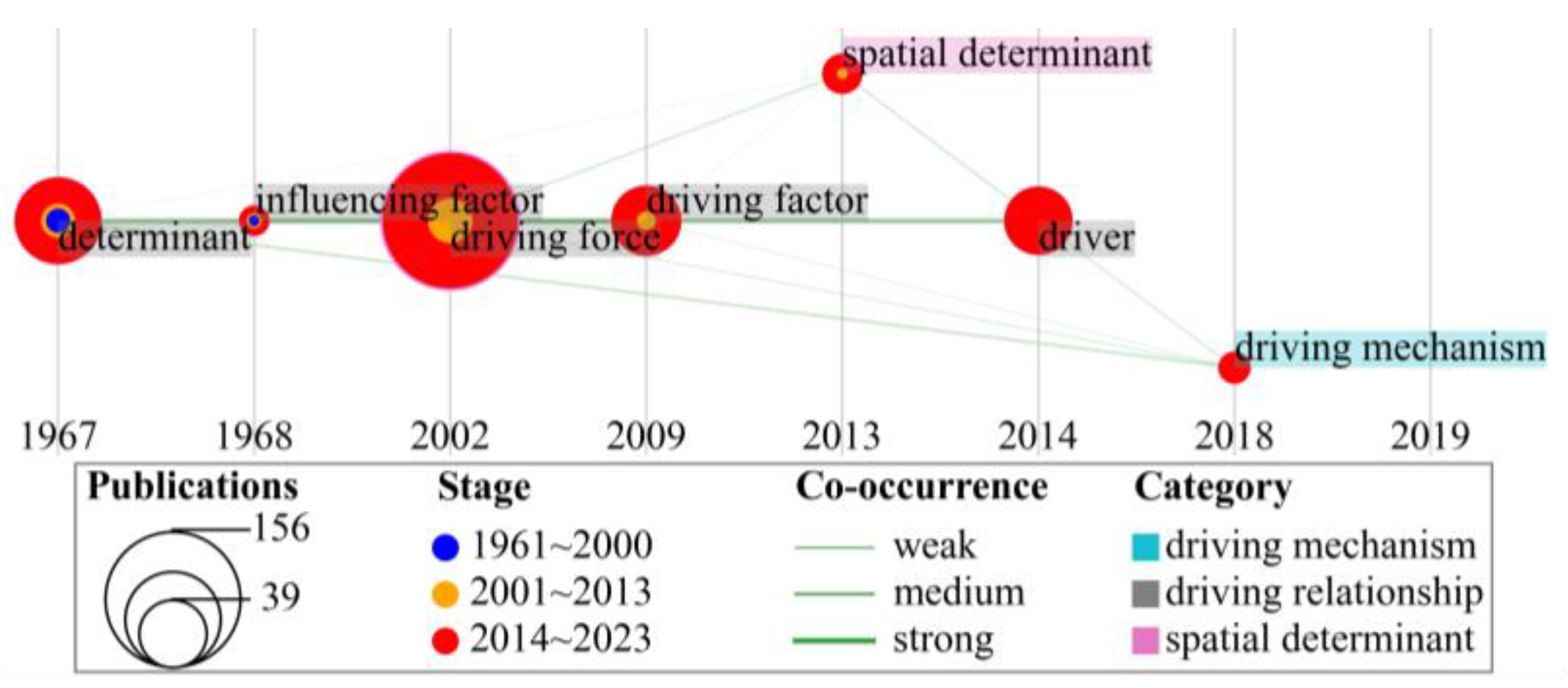


| Rank | Records | BC 1 | Year 2 | Institution | Country |
|---|---|---|---|---|---|
| 1 | 71 | 0.34 | 2002 | Chinese Academy of Sciences | China |
| 2 | 23 | 0.02 | 2014 | University of Chinese Academy of Sciences | China |
| 3 | 19 | 0.06 | 2005 | Beijing Normal University | China |
| 3 | 19 | 0.05 | 2011 | Zhejiang University | China |
| 5 | 18 | 0.07 | 2013 | Wuhan University | China |
| 6 | 15 | 0.07 | 2014 | Sun Yat-sen University | China |
| 6 | 15 | 0.09 | 2014 | Peking University | China |
| 8 | 12 | 0.05 | 2014 | Nanjing University | China |
| 9 | 11 | 0.05 | 2011 | Michigan State University | USA |
| 9 | 11 | 0.05 | 2015 | China University of Geosciences | China |
| Category | Theme | Records | Burst Strength | Burst Duration |
|---|---|---|---|---|
| Social Context | Economic Transition | 24 | 3.59 | 2015~2017 |
| Data Source | Remote Sensing | 33 | 3.93 | 2002~2013 |
| Analysis Tool | GIS | 48 | 4.40 | 2005~2013 |
| Application | Cellular Automata | 36 | 3.61 | 2017~2020 |
| Models | Formula | Levels of Involved Explanatory Variables | ||
|---|---|---|---|---|
| Level 1 | Level 2 | Level 1 | Level 2 | |
| Null model | ||||
| Random-coefficient regression model | | √ | ||
| Intercepts-and-slopes-as-outcomes model | √ | √ | ||
| Methods | Models | Advantages/Application Scenarios | Limitations/Requirements | |
|---|---|---|---|---|
| Traditional correlation analysis and regression models | Scatter plot |
|
| |
| Gradient analysis |
|
| ||
| Correlation coefficient | PCC 1 |
|
| |
| GRA 2 |
|
| ||
| OLR 1 |
|
| ||
| Logistic regression 1 |
| |||
| Panel regression 1 |
|
| ||
| HLM 1 |
| |||
| Structural equation modelling 1 |
|
| ||
| DID 1 |
|
| ||
| Geographic models considering spatial and temporal effects | Geo-detector 2 |
|
| |
| Spatial regression models 1 |
|
| ||
| SRM 1 |
|
| ||
| GWR 1 |
| |||
| GTWR, GTWLR 1 |
|
| ||
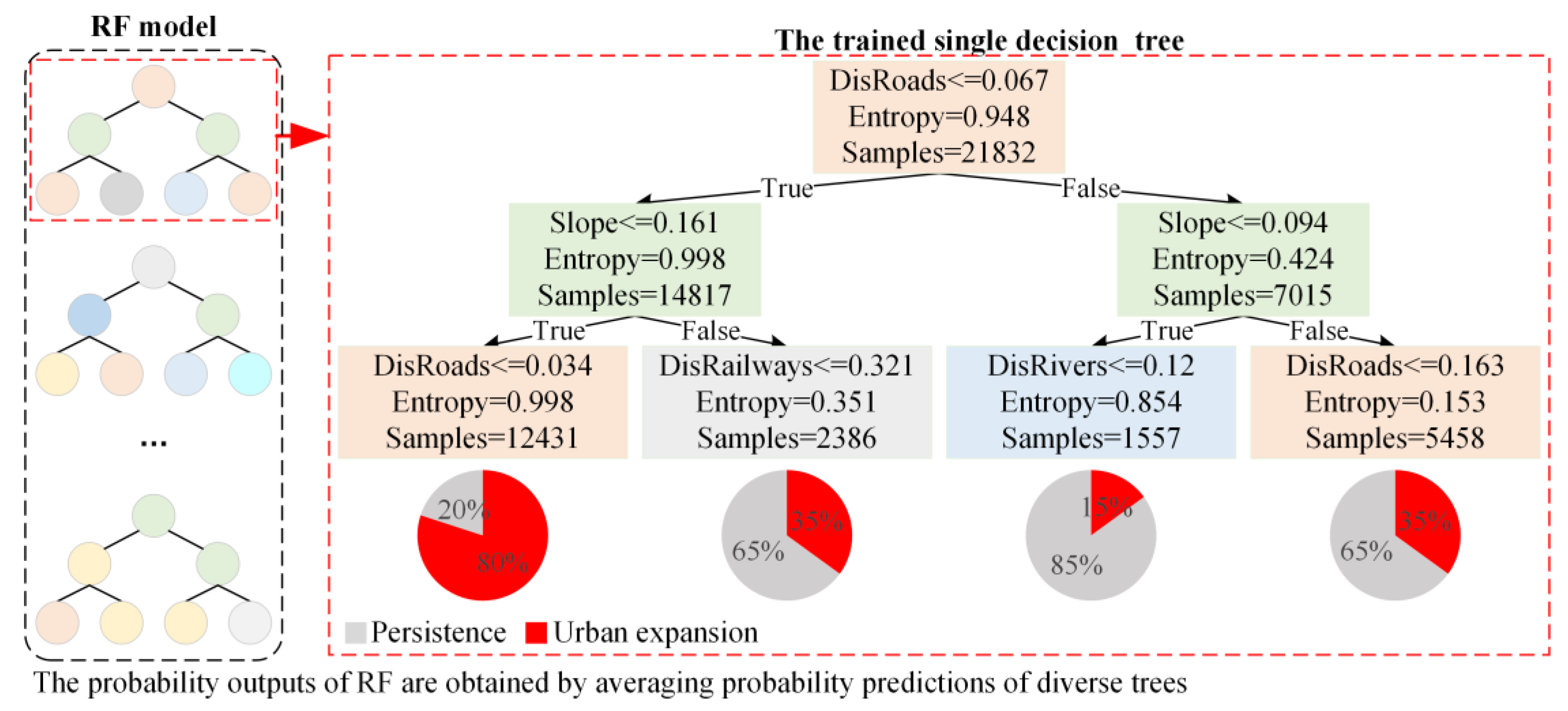
| Machine learning models | RF 2 |
|
| |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Li, J.; Yang, C.; Xing, W. Development Process, Quantitative Models, and Future Directions in Driving Analysis of Urban Expansion. ISPRS Int. J. Geo-Inf. 2023, 12, 174. https://doi.org/10.3390/ijgi12040174
Guan X, Li J, Yang C, Xing W. Development Process, Quantitative Models, and Future Directions in Driving Analysis of Urban Expansion. ISPRS International Journal of Geo-Information. 2023; 12(4):174. https://doi.org/10.3390/ijgi12040174
Chicago/Turabian StyleGuan, Xuefeng, Jingbo Li, Changlan Yang, and Weiran Xing. 2023. "Development Process, Quantitative Models, and Future Directions in Driving Analysis of Urban Expansion" ISPRS International Journal of Geo-Information 12, no. 4: 174. https://doi.org/10.3390/ijgi12040174
APA StyleGuan, X., Li, J., Yang, C., & Xing, W. (2023). Development Process, Quantitative Models, and Future Directions in Driving Analysis of Urban Expansion. ISPRS International Journal of Geo-Information, 12(4), 174. https://doi.org/10.3390/ijgi12040174







