Modeling Root Exudate Accumulation Gradients to Estimate Net Exudation Rates by Peatland Soil Depth
Abstract
:1. Introduction
2. Results
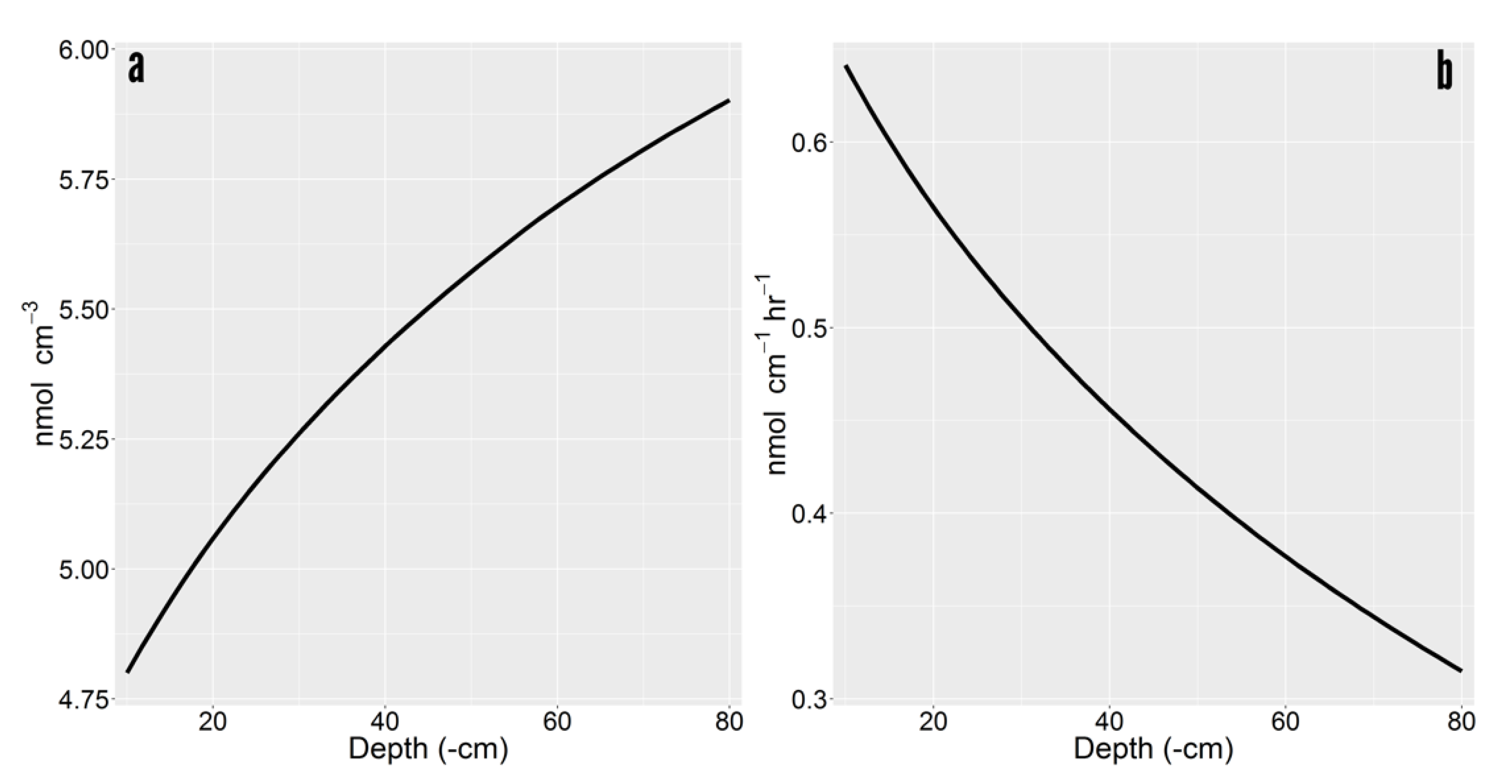
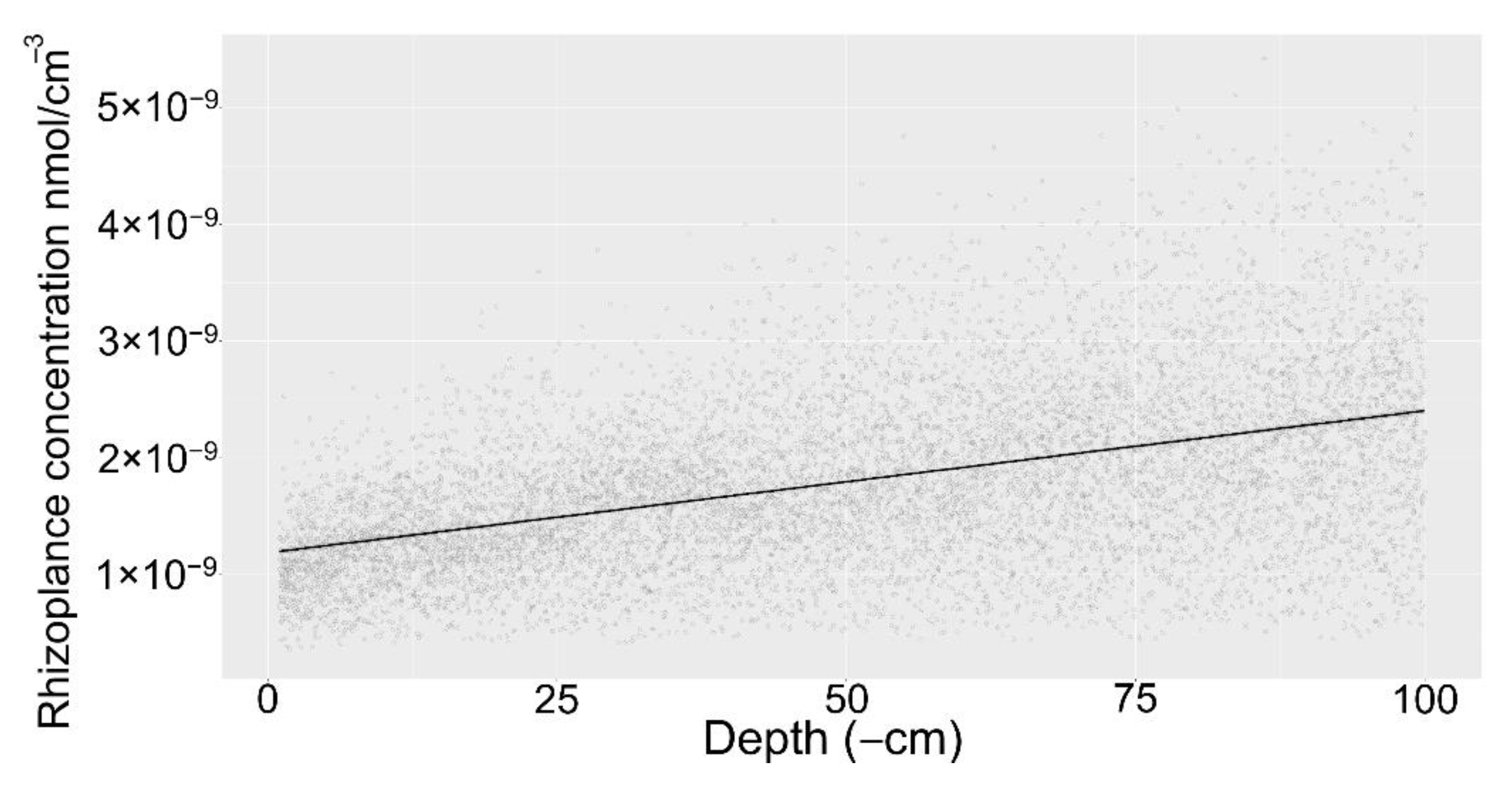
2.1. Rhizosphere Accumulation Gradients by Depth
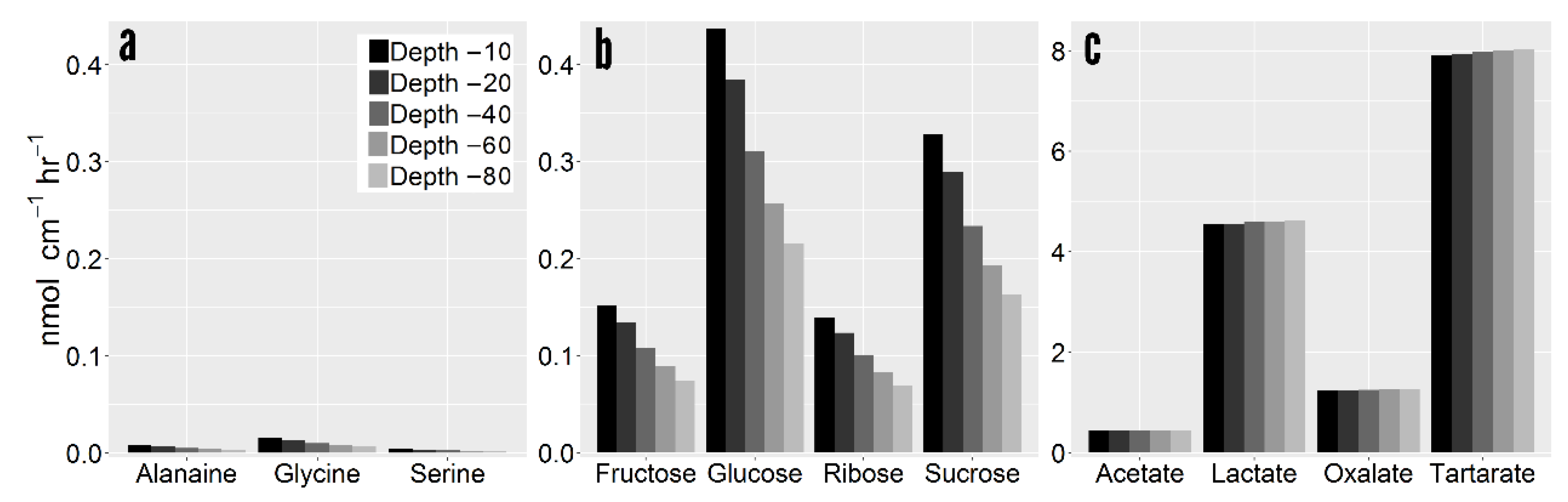
2.2. Compound Specific Exudation
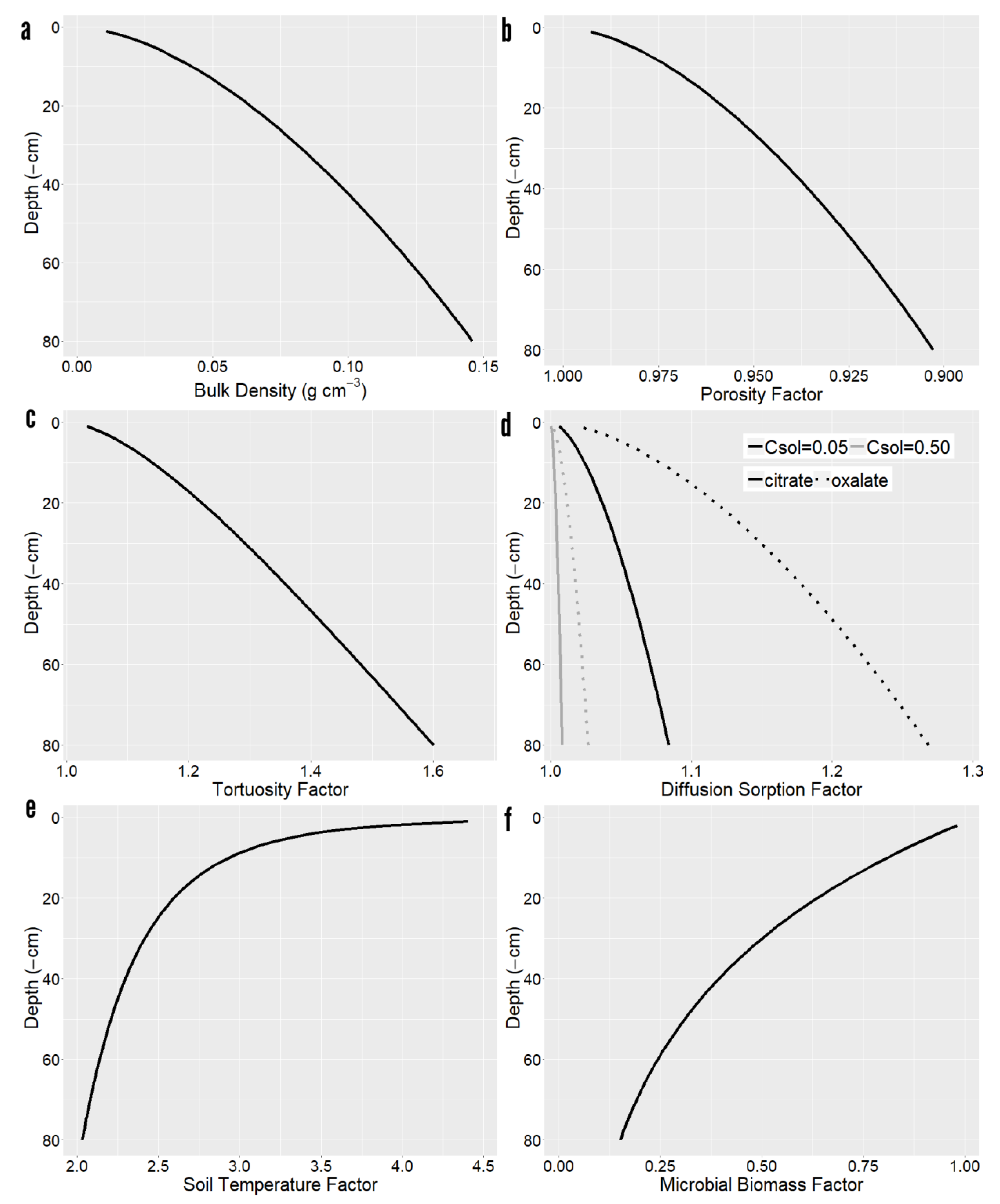
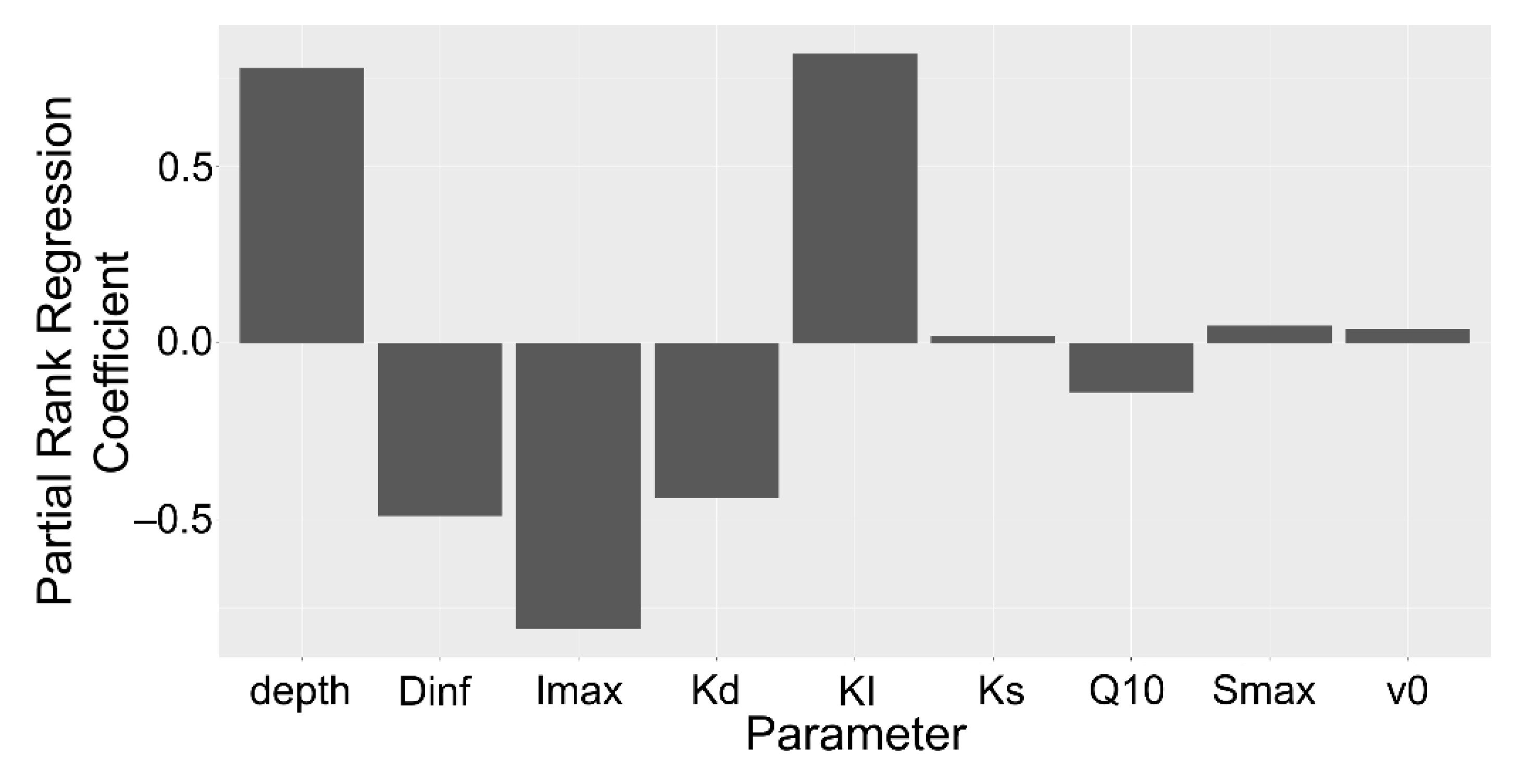
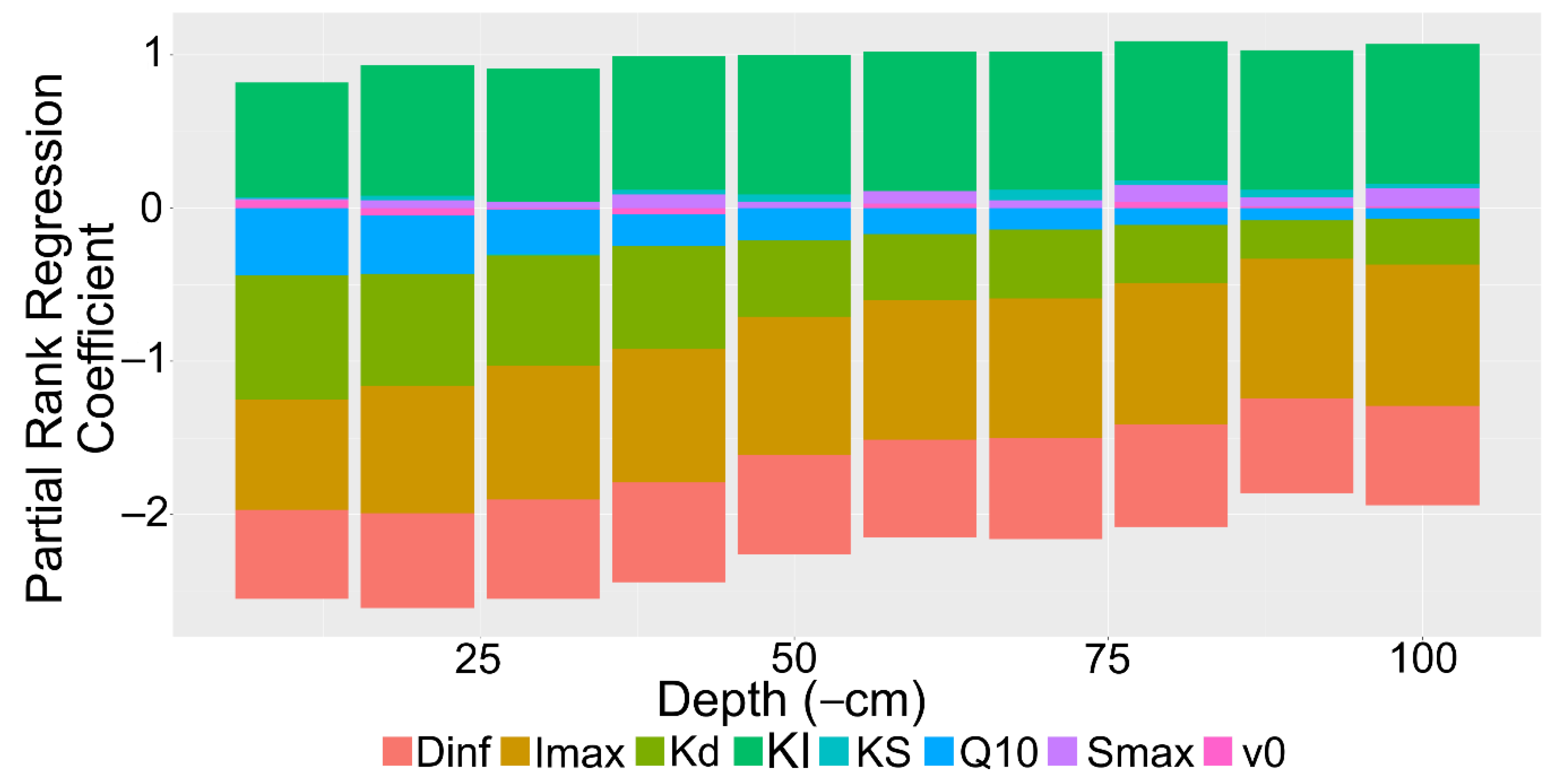
2.3. Sensitivity Analysis
3. Discussion
4. Materials and Methods
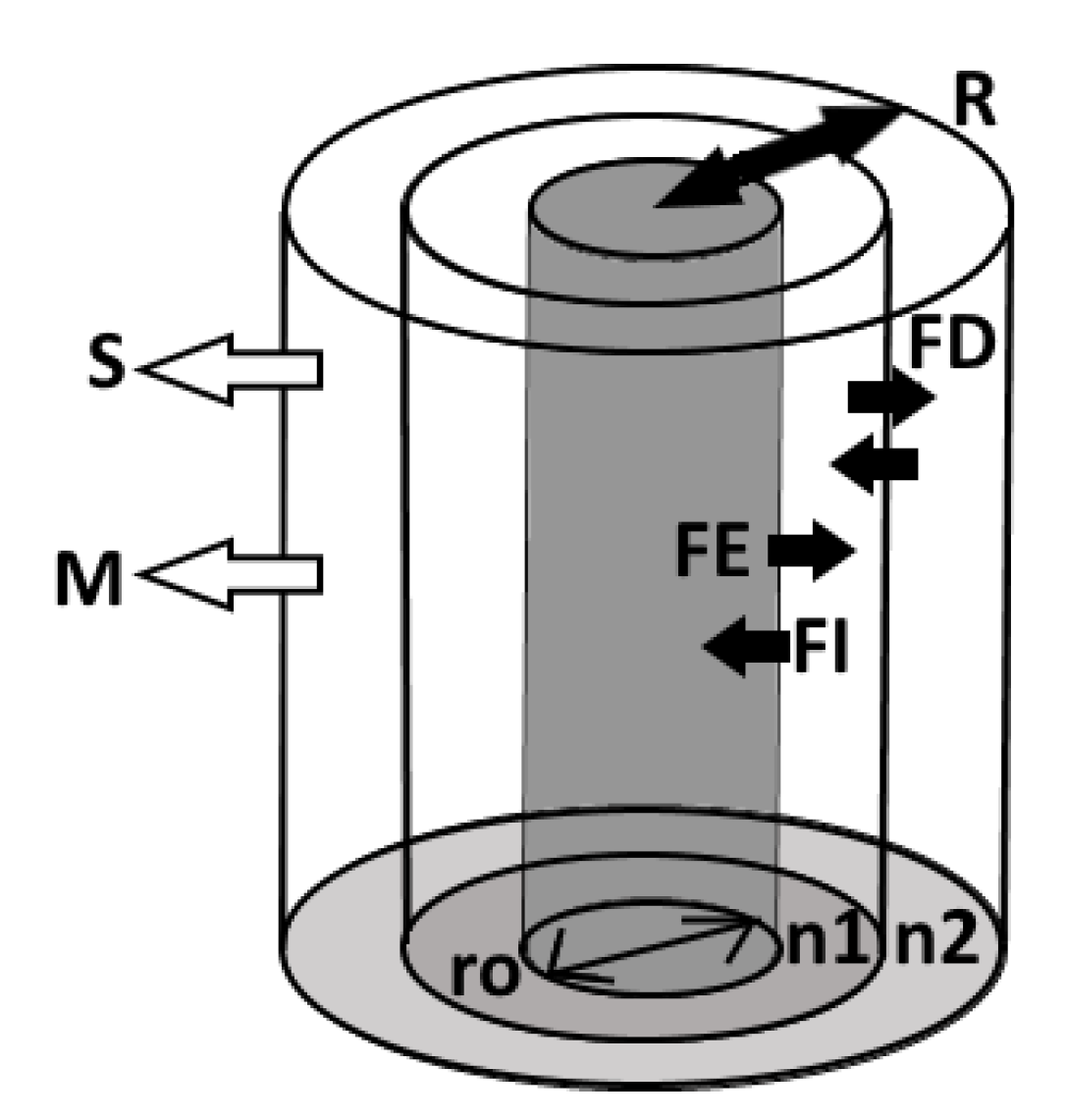
4.1. Root Exudation Modeling Approach
4.2. Diffusion Modeling Approach ()
4.3. Sorption Modeling Approach ()
4.4. Mineralization Modeling Approach ()
4.5. Numerical Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grayston, S.J.; Vaughan, D.; Jones, D. Rhizosphere carbon flow in trees, in comparison with annual plants: The importance of root exudation and its impact on microbial activity and nutrient availability. Appl. Soil Ecol. 1997, 5, 29–56. [Google Scholar] [CrossRef]
- Jones, D.L.; Hodge, A.; Kuzyakov, Y. Plant and mycorrhizal regulation of rhizodeposition. New Phytol. 2004, 163, 459–480. [Google Scholar] [CrossRef]
- Farrar, J.; Hawes, M.; Jones, D.; Lindow, S. How roots control the flux of carbon to the rhizosphere. Ecology 2003, 84, 827–837. [Google Scholar] [CrossRef]
- Fan, T.W.-M.; Lane, A.N.; Shenker, M.; Bartley, J.P.; Crowley, D.; Higashi, R.M. Comprehensive chemical profiling of gramineous plant root exudates using high-resolution NMR and MS. Phytochemistry 2001, 57, 209–221. [Google Scholar] [CrossRef]
- Neumann, G.; Römheld, V. Root excretion of carboxylic acids and protons in phosphorus-deficient plants. Plant Soil 1999, 211, 121–130. [Google Scholar] [CrossRef]
- Bekkara, F.; Jay, M.; Viricel, M.R.; Rome, S. Distribution of phenolic compounds within seed and seedlings of two Vicia faba cvs differing in their seed tannin content, and study of their seed and root phenolic exudations. Plant Soil 1998, 203, 27–36. [Google Scholar] [CrossRef]
- Xia, J.H.; Roberts, J.K.M. Improved Cytoplasmic pH Regulation, Increased Lactate Efflux, and Reduced Cytoplasmic Lactate Levels Are Biochemical Traits Expressed in Root Tips of Whole Maize Seedlings Acclimated to a Low-Oxygen Environment. Plant Physiol. 1994, 105, 651–657. [Google Scholar] [CrossRef] [Green Version]
- Kuzyakov, Y.; Razavi, B.S. Rhizosphere size and shape: Temporal dynamics and spatial stationarity. Soil Biol. Biochem. 2019, 135, 343–360. [Google Scholar] [CrossRef]
- Hinsinger, P.; Gobran, G.R.; Gregory, P.J.; Wenzel, W.W. Rhizosphere geometry and heterogeneity arising from root-mediated physical and chemical processes. New Phytol. 2005, 168, 293–303. [Google Scholar] [CrossRef]
- Mariano, E.D.; Jorge, R.A.; Keltjens, W.G.; Menossi, M. Metabolism and root exudation of organic acid anions under aluminium stress. Braz. J. Plant Physiol. 2005, 17, 157–172. [Google Scholar] [CrossRef]
- Jones, D.L.; Darrah, P.R. Role of root derived organic acids in the mobilization of nutrients from the rhizosphere. Plant Soil 1994, 166, 247–257. [Google Scholar] [CrossRef]
- Paynel, F.; Murray, P.J.; Cliquet, J.B. Root exudates: A pathway for short-term N transfer from clover and ryegrass. Plant Soil 2001, 229, 235–243. [Google Scholar] [CrossRef]
- Sundin, P.; Valeur, A.; Olsson, S.; Odham, G. Interactions between bacteria-feeding nematodes and bacteria in the rape rhizosphere: Effects on root exudation and distribution of bacteria. FEMS Microbiol. Lett. 1990, 73, 13–22. [Google Scholar] [CrossRef]
- Hertenberger, G.; Wanek, W. Evaluation of methods to measure differential 15N labeling of soil and root N pools for studies of root exudation. Rapid Commun. Mass Spectrom. 2004, 18, 2415–2425. [Google Scholar] [CrossRef] [PubMed]
- Warren, C.R. Wheat roots efflux a diverse array of organic N compounds and are highly proficient at their recapture. Plant Soil 2015, 397, 147–162. [Google Scholar] [CrossRef] [Green Version]
- Oburger, E.; Dell’mour, M.; Hann, S.; Wieshammer, G.; Puschenreiter, M.; Wenzel, W.W. Evaluation of a novel tool for sampling root exudates from soil-grown plants compared to conventional techniques. Environ. Exp. Bot. 2013, 87, 235–247. [Google Scholar] [CrossRef]
- Pinton, R.; Varanini, Z.; Nannipieri, P. (Eds.) The Rhizosphere: Biochemistry and Organic Substances at the Soil-Plant Interface, 2nd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2009; Volume 104, pp. 1095–8290. ISBN 0305-7364. [Google Scholar]
- Nguyen, C. Rhizodeposition of organic C by plants: Mechanisms and controls. Agronomie 2003, 23, 375–396. [Google Scholar] [CrossRef]
- Ryan, P.R.; Delhaize, E.; Randall, P.J. Characterisation of Al-stimulated efflux of malate from the apices of Al-tolerant wheat roots. Planta 1995, 196, 103–110. [Google Scholar] [CrossRef]
- Neumann, G.; Martinoia, E. Cluster roots—An underground adaptation for survival in extreme environments. Trends Plant Sci. 2002, 7, 162–167. [Google Scholar] [CrossRef]
- Kraffczyk, I.; Trolldenier, G.; Beringer, H. Soluble root exudates of maize: Influence of potassium supply and rhizosphere microorganisms. Soil Biol. Biochem. 1984, 16, 315–322. [Google Scholar] [CrossRef]
- Ryan, P.; Delhaize, E.; Jones, D. Function and Mechanism of organic anion exudation from plant roots. Annu. Rev. Plant Physiol. Plant Mol. Biol. 2001, 52, 527–560. [Google Scholar] [CrossRef] [PubMed]
- Lesuffleur, F.; Paynel, F.; Bataillé, M.-P.; Deunff, E.L.; Cliquet, J.-B. Root amino acid exudation: Measurement of high efflux rates of glycine and serine from six different plant species. Plant Soil 2007, 294, 235–246. [Google Scholar] [CrossRef]
- Svennerstam, H.; Jämtgård, S.; Ahmad, I.; Huss-Danell, K.; Näsholm, T.; Ganeteg, U. Transporters in arabidopsis roots mediating uptake of amino acids at naturally occurring concentrations. New Phytol. 2011, 191, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.J.; Jeong, S.E.; Kim, P.J.; Madsen, E.L.; Jeon, C.O. High resolution depth distribution of Bacteria, Archaea, methanotrophs, and methanogens in the bulk and rhizosphere soils of a flooded rice paddy. Front. Microbiol. 2015, 6, 639. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Artz, R.R.E.; Johnson, D. Species-specific effects of plants colonising cutover peatlands on patterns of carbon source utilisation by soil microorganisms. Soil Biol. Biochem. 2008, 40, 544–549. [Google Scholar] [CrossRef]
- Hafner, S.; Wiesenberg, G.L.B.; Stolnikova, E.; Merz, K.; Kuzyakov, Y. Spatial distribution and turnover of root-derived carbon in alfalfa rhizosphere depending on top- and subsoil properties and mycorrhization. Plant Soil 2014, 380, 101–115. [Google Scholar] [CrossRef]
- Tückmantel, T.; Leuschner, C.; Preusser, S.; Kandeler, E.; Angst, G.; Mueller, C.W.; Meier, I.C. Root exudation patterns in a beech forest: Dependence on soil depth, root morphology, and environment. Soil Biol. Biochem. 2017, 107, 188–197. [Google Scholar] [CrossRef]
- Luster, J.; Göttlein, A.; Nowack, B.; Sarret, G. Sampling, defining, characterising and modeling the rhizosphere-the soil science tool box. Plant Soil 2009, 321, 457–482. [Google Scholar] [CrossRef]
- Darrah, P.R. Measuring the diffusion coefficient of rhizosphere exudates in soil. I. The diffusion of non-sorbing compounds. J. Soil Sci. 1991, 42, 413–420. [Google Scholar] [CrossRef]
- Personeni, E.; Nguyen, C.; Marchal, P.; Pagès, L. Experimental evaluation of an efflux-influx model of C exudation by individual apical root segments. J. Exp. Bot. 2007, 58, 2091–2099. [Google Scholar] [CrossRef]
- Raynaud, X. Soil properties are key determinants for the development of exudate gradients in a rhizosphere simulation model. Soil Biol. Biochem. 2010, 42, 210–219. [Google Scholar] [CrossRef]
- Okutani, F.; Hamamoto, S.; Aoki, Y.; Nakayasu, M.; Nihei, N.; Nishimura, T.; Yazaki, K.; Sugiyama, A. Rhizosphere modelling reveals spatiotemporal distribution of daidzein shaping soybean rhizosphere bacterial community. Plant Cell Environ. 2020, 43, 1036–1046. [Google Scholar] [CrossRef] [PubMed]
- Horn, M.A.; Matthies, C.; Küsel, K.; Schramm, A.; Drake, H.L. Hydrogenotrophic methanogenesis by moderately acid-tolerant methanogens of a methane-emitting acidic peat. Appl. Environ. Microbiol. 2003, 69, 74–83. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Wang, Q.; Matsushita, B.; Fukushima, T.; Ouyang, Z.; Watanabe, M. A new method to define the VI-Ts diagram using subpixel vegetation and soil information: A case study over a semiarid agricultural region in the North China plain. Sensors 2008, 8, 6260–6279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phillips, R.P.; Erlitz, Y.; Bier, R.; Bernhardt, E.S. New approach for capturing soluble root exudates in forest soils. Funct. Ecol. 2008, 22, 990–999. [Google Scholar] [CrossRef]
- Aoki, M.; Fujii, K.; Kitayama, K. Environmental Control of Root Exudation of Low-Molecular Weight Organic Acids in Tropical Rainforests. Ecosystems 2012, 15, 1194–1203. [Google Scholar] [CrossRef]
- Raich, J.W.; Tufekcioglu, A. Vegetation and soil respiration: Correlations and controls. Biogeochemistry 2000, 48, 71–90. [Google Scholar] [CrossRef]
- Hao, X.; Zhang, R.; Kravchenko, A. Effects of root density distribution models on root water uptake and water flow under irrigation. Soil Sci. 2005, 170, 167–174. [Google Scholar] [CrossRef]
- Oburger, E.; Kirk, G.J.D.; Wenzel, W.W.; Puschenreiter, M.; Jones, D.L. Interactive effects of organic acids in the rhizosphere. Soil Biol. Biochem. 2009, 41, 449–457. [Google Scholar] [CrossRef]
- Glanville, H.; Rousk, J.; Golyshin, P.; Jones, D.L. Mineralization of low molecular weight carbon substrates in soil solution under laboratory and field conditions. Soil Biol. Biochem. 2012, 48, 88–95. [Google Scholar] [CrossRef]
- Wania, R.; Ross, I.; Prentice, I.C. Implementation and evaluation of a new methane model within a dynamic global vegetation model: LPJ-WHyMe v1.3.1. Geosci. Model Dev. 2010, 3, 565–584. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Blodau, C. PEATBOG: A biogeochemical model for analyzing coupled carbon and nitrogen dynamics in northern peatlands. Geosci. Model Dev. 2013, 6, 1173–1207. [Google Scholar] [CrossRef] [Green Version]
- Kristensen, E.; Ahmed, S.I.; Devol, A.H. Aerobic and anaerobic decomposition of organic matter in marine sediment: Which is fastest? Limnol. Oceanogr. 1995, 40, 1430–1437. [Google Scholar] [CrossRef]
- Rezanezhad, F.; Price, J.S.; Quinton, W.L.; Lennartz, B.; Milojevic, T.; Cappellen, P.V. Structure of peat soils and implications for water storage, flow and solute transport: A review update for geochemists. Chem. Geol. 2016, 429, 75–84. [Google Scholar] [CrossRef]
- Barber, S.; Cushman, J. Nutrient uptake model for agronomic crops. In Modelling Wastewater Renovation Land Treatment; Iskander, I., Ed.; Wiley: New York, NY, USA, 1981; Volume 1, pp. 382–409. [Google Scholar]
- Michaelis, L.; Menten, M. Die Kinetik der Invertinwirkung. Biochem. Z. 1913, 49, 333–369. [Google Scholar]
- Bresseleers, G.J.M.; Goderis, H.L.; Tobback, P.P. Measurement of the glucose permeation rate across phospholipid bilayers using small unilamellar vesicles Effect of membrane composition and temperature. BBA Biomembr. 1984, 772, 374–382. [Google Scholar] [CrossRef]
- Bertin, C.; Yang, X.; Weston, L.A. The role of root exudates and allelochemicals in the rhizosphere. Plant Soil 2003, 256, 67–83. [Google Scholar] [CrossRef]
- Jones, D.L. Organic acids in the rhizosphere—A critical review. Plant Soil 1998, 205, 25–44. [Google Scholar] [CrossRef]
- Jones, D.L.; Edwards, A.C. Influence of sorption on the biological utilization of two simple carbon substrates. Soil Biol. Biochem. 1998, 30, 1895–1902. [Google Scholar] [CrossRef]
- Tinker, P.B.; Nye, P.H. Solute Movement in the Rhizosphere; Oxford University Press: Oxford, UK, 2000; Volume 52, ISBN 1365-2389. [Google Scholar]
- Van Cappellen, P.; Gaillard, J.F. Biogeochemical dynamics in aquatic systems. In Reactive Transport in Porous Media, Reviews in Mineralogy; Lichtner, P., Steefel, C., Oelkers, E., Eds.; Mineralogical Society of America: Washington, DC, USA, 1996; Volume 34, pp. 335–376. [Google Scholar]
- Xia, J.H.; Saglio, P.H. Characterization of the Hexose Transport System in Maize Root Tips. Plant Physiol. 1988, 88, 1015–1020. [Google Scholar] [CrossRef] [Green Version]
- Hayward, P.M.; Clymo, R.S. Profiles of Water Content and Pore Size in Sphagnum and Peat, and their Relation to Peat Bog Ecology. Proc. R Soc. Lond. B Biol. Sci. 1982, 215, 299. [Google Scholar]
- Weiss, R.; Alm, J.; Laiho, R.; Laine, J. Modeling moisture retention in peat soils. Soil Sci. Soc. Am. J. 1998, 62, 305–313. [Google Scholar] [CrossRef]
- Dimitrov, D.D.; Grant, R.F.; Lafleur, P.M.; Humphreys, E.R. Modeling the effects of hydrology on ecosystem respiration at Mer Bleue bog. J. Geophys. Res. Biogeosci. 2010, 115, G04043. [Google Scholar] [CrossRef] [Green Version]
- Blodau, C.; Moore, T.R. Macroporosity affects water movement and pore water sampling in peat soils. Soil Sci. 2002, 167, 98–109. [Google Scholar] [CrossRef] [Green Version]
- Quinton, W.L.; Hayashi, M.; Chasmer, L.E. Peatland hydrology of discontinuous permafrost in the northwest territories: Overview and synthesis. Can. Water Resour. J. 2009, 34, 311–328. [Google Scholar] [CrossRef]
- Rezanezhad, F.; Quinton, W.L.; Price, J.S.; Elliot, T.R.; Elrick, D.; Shook, K.R. Influence of pore size and geometry on peat unsaturated hydraulic conductivity computed from 3D computed tomography image analysis. Hydrol. Process. 2010, 24, 2983–2994. [Google Scholar] [CrossRef]
- Quinton, W.L.; Hayashi, M.; Carey, S.K. Peat hydraulic conductivity in cold regions and its relation to pore size and geometry. Hydrol. Process. 2008, 22, 2829–2837. [Google Scholar] [CrossRef]
- Archie, G. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–67. [Google Scholar] [CrossRef]
- Shackelford, C.D.; Daniel, D.E. Diffusion in saturated soil. I: Background. J. Geotech. Eng. 1991, 117, 467–484. [Google Scholar] [CrossRef]
- Van Hees, P.; Vinogradoff, S.; Edwards, A.; Godbold, D.; Jones, D. Low molecular weight organic acid adsorption in forest soils: Effects on soil solution concentrations and biodegradation rates. Soil Biol. Biochem. 2003, 35, 1015–1026. [Google Scholar] [CrossRef]
- Jagadamma, S.; Mayes, M.A.; Zinn, Y.L.; Gisladottir, G.; Russell, A.E. Sorption of organic carbon compounds to the fine fraction of surface and subsurface soils. Geoderma 2014, 213, 79–86. [Google Scholar] [CrossRef]
- Strom, L.; Owen, A.G.; Godbold, D.L.; Jones, D.L. Organic acid behaviour in a calcareous soil: Sorption reactions and biodegradation rates. Soil Biol. Biochem. 2001, 33, 2125–2133. [Google Scholar] [CrossRef]
- Hees, P.A.W.V.; Jones, D.L.; Godbold, D.L. Biodegradation of low molecular weight organic acids in coniferous forest podzolic soils. Soil Biol. Biochem. 2002, 34, 1261–1272. [Google Scholar] [CrossRef]
- Jones, D.L.; Brassington, D.S. Sorption of organic acids in acid soils and its implications in the rhizosphere. Eur. J. Soil Sci. 1998, 49, 447–455. [Google Scholar] [CrossRef]
- Tate, R.L. Soil Microbiology, 2nd ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Jones, D.L.; Kemmitt, S.J.; Wright, D.; Cuttle, S.P.; Bol, R.; Edwards, A.C. Rapid intrinsic rates of amino acid biodegradation in soils are unaffected by agricultural management strategy. Soil Biol. Biochem. 2005, 37, 1267–1275. [Google Scholar] [CrossRef]
- Toerien, D.F.; Cavari, B. Effect of Temperature on Heterotrophic Glucose Uptake, Mineralization, and Turnover Rates in Lake Sediments. Appl. Environ. Microbiol. 1982, 43, 1–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C. Controls on organic carbon preservation: The use of stratified water bodies to compare intrinsic rates of decomposition in oxic and anoxic systems. Geochim. Cosmochim. Acta 1992, 56, 3323–3335. [Google Scholar] [CrossRef]
- Chidthaisong, A.; Rosenstock, B.; Conrad, R. Measurement of monosaccharides and conversion of glucose to acetate in anoxic rice field soil. Appl. Environ. Microbiol. 1999, 65, 2350–2355. [Google Scholar] [CrossRef] [Green Version]
- Christian, R.R.; Wiebe, W.J. Anaerobic microbial community metabolism in Spartina alterniflora soil. Limnol. Oceanogr. 1978, 23, 328–336. [Google Scholar] [CrossRef]
- Kuzyakov, Y.; Demin, V. CO2 efflux by rapid decomposition of low molecular organic substances in soils. Sci. Soils 1998, 3, 11–22. [Google Scholar] [CrossRef]
- Jones, D.L.; Murphy, D.V. Microbial response time to sugar and amino acid additions to soil. Soil Biol. Biochem. 2007, 39, 2178–2182. [Google Scholar] [CrossRef]
- Greenup, A.L.; Bradford, M.A.; Mcnamara, N.P.; Ineson, P.; Lee, J.A. The role of Eriophorum vaginatum in CH4 flux from an ombrotrophic peatland. Plant Soil 2000, 227, 265–272. [Google Scholar] [CrossRef]
- Grayston, S.J.; Wang, S.; Campbell, C.D.; Edwards, A.C. Selective influence of plant species on microbial diversity in the rhizosphere. Soil Biol. Biochem. 1998, 30, 369–378. [Google Scholar] [CrossRef]
- Marschner, P.; Marhan, S.; Kandeler, E. Microscale distribution and function of soil microorganisms in the interface between rhizosphere and detritusphere. Soil Biol. Biochem. 2012, 49, 174–183. [Google Scholar] [CrossRef]
- Johnson, D.; Booth, R.E.; Whiteley, A.S.; Bailey, M.J.; Read, D.J.; Grime, J.P.; Leake, J.R. Plant community composition affects the biomass, activity and diversity of microorganisms in limestone grassland soil. Eur. J. Soil Sci. 2003, 54, 671–677. [Google Scholar] [CrossRef]
- Hees, P.A.W.V.; Jones, D.L.; Finlay, R.; Godbold, D.L.; Lundström, U.S. The carbon we do not see—The impact of low molecular weight compounds on carbon dynamics and respiration in forest soils: A review. Soil Biol. Biochem. 2005, 37, 1–13. [Google Scholar] [CrossRef]
- Balba, M.T.; Nedwell, D.B. Microbial metabolism of acetate, propionate and butyrate in anoxic sediment from the Colne Point saltmarsh, Essex, U.K. J. Gen. Microbiol. 1982, 128, 1415–1422. [Google Scholar] [CrossRef] [Green Version]
- Moore, T.R.; Bubier, J.L.; Bledzki, L. Litter decomposition in temperate peatland ecosystems: The effect of substrate and site. Ecosystems 2007, 10, 949–963. [Google Scholar] [CrossRef] [Green Version]
- Frolking, S.; Roulet, N.T.; Moore, T.R.; Lafleur, P.M.; Bubier, J.L.; Crill, P.M. Modeling seasonal to annual carbon balance of Mer Bleue Bog, Ontario, Canada. Glob. Biogeochem. Cycles 2002, 16. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Trettin, C.C.; Li, H.; Sun, G. An integrated model of soil, hydrology, and vegetation for carbon dynamics in wetland ecosystems. Glob. Biogeochem. Cycles 2002, 16, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Lai, D.Y.F. Modelling the effects of climate change on methane emission from a northern ombrotrophic bog in Canada. Environ. Geol. 2009, 58, 1197–1206. [Google Scholar] [CrossRef]
- Scanlon, D.; Moore, T. Carbon dioxide production from peatland soil profiles: The influence of temperature, oxic/anoxic conditions and substrate. Soil Sci. 2000, 165, 153–160. [Google Scholar] [CrossRef]
- Walter, B.P.; Heimann, M. A process-based, climate-sensitive model to derive methane emissions from natural wetlands: Application to five wetland sites, sensitivity to model parameters, and climate. Glob. Biogeochem. Cycles 2000, 14, 745–765. [Google Scholar] [CrossRef] [Green Version]
- Vinolas, L.C.; Healey, J.R.; Jones, D.L. Kinetics of soil microbial uptake of free amino acids. Biol. Fertil. Soils 2001, 33, 67–74. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Bacour, C.; Jacquemoud, S.; Tourbier, Y.; Dechambre, M.; Frangi, J.P. Design and analysis of numerical experiments to compare four canopy reflectance models. Remote Sens. Environ. 2002, 79, 72–83. [Google Scholar] [CrossRef]
- Sobol, I. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. Engl. Transl 1993, 1, 407–414. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer, 1st ed.; John Wiley and Sons: West Sussex, UK, 2008. [Google Scholar]
- Pujol, G. Sensitivity: Sensitivity Analysis. R Package Version 1.3-0. 2007. Available online: www2.uaem.mx/r-mirror/web/packages/sensitivity/sensitivity.pdf (accessed on 2 November 2020).
- Schramke, J.A.; Murphy, S.F.; Doucette, W.J.; Hintze, W.D. Prediction of aqueous diffusion coefficients for organic compounds at 25 °C. Chemosphere 1999, 38, 2381–2406. [Google Scholar] [CrossRef]
- Buffle, J.; Zhang, Z.; Startchev, K. Metal flux and dynamic speciation at (Bio)interfaces. Part I: Critical evaluation and compilation of physicochemical parameters for complexes with simple ligands and fulvic/humic substances. Environ. Sci. Technol. 2007, 41, 7609–7620. [Google Scholar] [CrossRef]
- Uedaira, H.; Uedaira, H. Sugar-water interaction from diffusion measurements. J. Solut. Chem. 1985, 14, 27–34. [Google Scholar] [CrossRef]
- Kuzyakov, Y.; Jones, D.L. Glucose uptake by maize roots and its transformation in the rhizosphere. Soil Biol. Biochem. 2006, 38, 851–860. [Google Scholar] [CrossRef]
- Proctor, C.; He, Y. Quantifying root extracts and exudates of sedge and shrub in relation to root morphology. Soil Biol. Biochem. 2017, 114, 168–180. [Google Scholar] [CrossRef]
- Kielland, K. Amino acid absorption by Arctic plants: Implications for plant nutrition and nitrogen cycling. Ecology 1994, 75, 2373–2383. [Google Scholar] [CrossRef]
- Williams, M.; Yanai, R.D. Multi-dimensional sensitivity analysis and ecological implications of a nutrient uptake model. Plant Soil 1996, 180, 311–324. [Google Scholar] [CrossRef]
- Basiliko, N.; Moore, T.R.; Lafleur, P.M.; Roulet, N.T. Seasonal and inter-annual decomposition, microbial biomass, and nitrogen dynamics in a canadian bog. Soil Sci. 2005, 170, 902–912. [Google Scholar] [CrossRef]



| Symbol | Definition | Unit | Range | Ref. |
|---|---|---|---|---|
| Solute Parameters (* range is solute specific) | ||||
| Z | Charge of solute in solution * | −integer | −1 to −3 | |
| Diffusion coefficient of solute in H2O * | cm2 s−1 | 0.52–1.28 | [95,96,97] | |
| Maximum sorption * | µmol g−1 | 0.12–19.98 | [30,51,68,75,89,98] | |
| Sorption affinity coefficient * | Unitless | 0.145–4.3 | [30,51,68,75,89,98] | |
| kd | Mineralization rate * | hr−1 | 0.15–2.35 | [41,64,68,69,95,96] |
| Root Parameters (* Solute specific) | ||||
| l | Root length | cm | Constant | |
| r0 | Root radius | cm | Constant | |
| Ccyto | Root cell cytoplasm concentration * | µmol cm−3 | 0.5–40 | [99] |
| Perm | Membrane permeability coefficient * | cm hr−1 × 10−4 | 1.15–4.32 | [54] |
| Maximum uptake rate * | µmol cm−1 hr−1 | 0.006–0.07 | [24,54] | |
| Michaelis-Menten coefficient * | µmol cm−3 | 0.002–5.9 | [54,100] | |
| Membrane potential | mV | Constant | [83] | |
| v0 | Volume of water entering the root | cm3/s | 5.0 × 10−10–5.0 × 10−6 | [101] |
| Soil Parameters (all vary by depth) | ||||
| Tortuosity factor | unitless | 2–3 | [61] | |
| Bulk density | g cm−3 | 0.0107–0.146 | [58] | |
| Microbial biomass factor | unitless | 0–1 | [102] | |
| Soil temperature factor | unitless | 1.9–4.4 | ||
| Soil temperature | Celsius | 8–17.8 | ||
| ϵ(d) | Soil porosity | cm3/cm3 | 0–1 | |
| Sorption retardation factor per solute | unitless | >1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Proctor, C.; He, Y. Modeling Root Exudate Accumulation Gradients to Estimate Net Exudation Rates by Peatland Soil Depth. Plants 2021, 10, 106. https://doi.org/10.3390/plants10010106
Proctor C, He Y. Modeling Root Exudate Accumulation Gradients to Estimate Net Exudation Rates by Peatland Soil Depth. Plants. 2021; 10(1):106. https://doi.org/10.3390/plants10010106
Chicago/Turabian StyleProctor, Cameron, and Yuhong He. 2021. "Modeling Root Exudate Accumulation Gradients to Estimate Net Exudation Rates by Peatland Soil Depth" Plants 10, no. 1: 106. https://doi.org/10.3390/plants10010106
APA StyleProctor, C., & He, Y. (2021). Modeling Root Exudate Accumulation Gradients to Estimate Net Exudation Rates by Peatland Soil Depth. Plants, 10(1), 106. https://doi.org/10.3390/plants10010106





