Sampling Variation of RAD-Seq Data from Diploid and Tetraploid Potato (Solanum tuberosum L.)
Abstract
:1. Introduction
2. Results
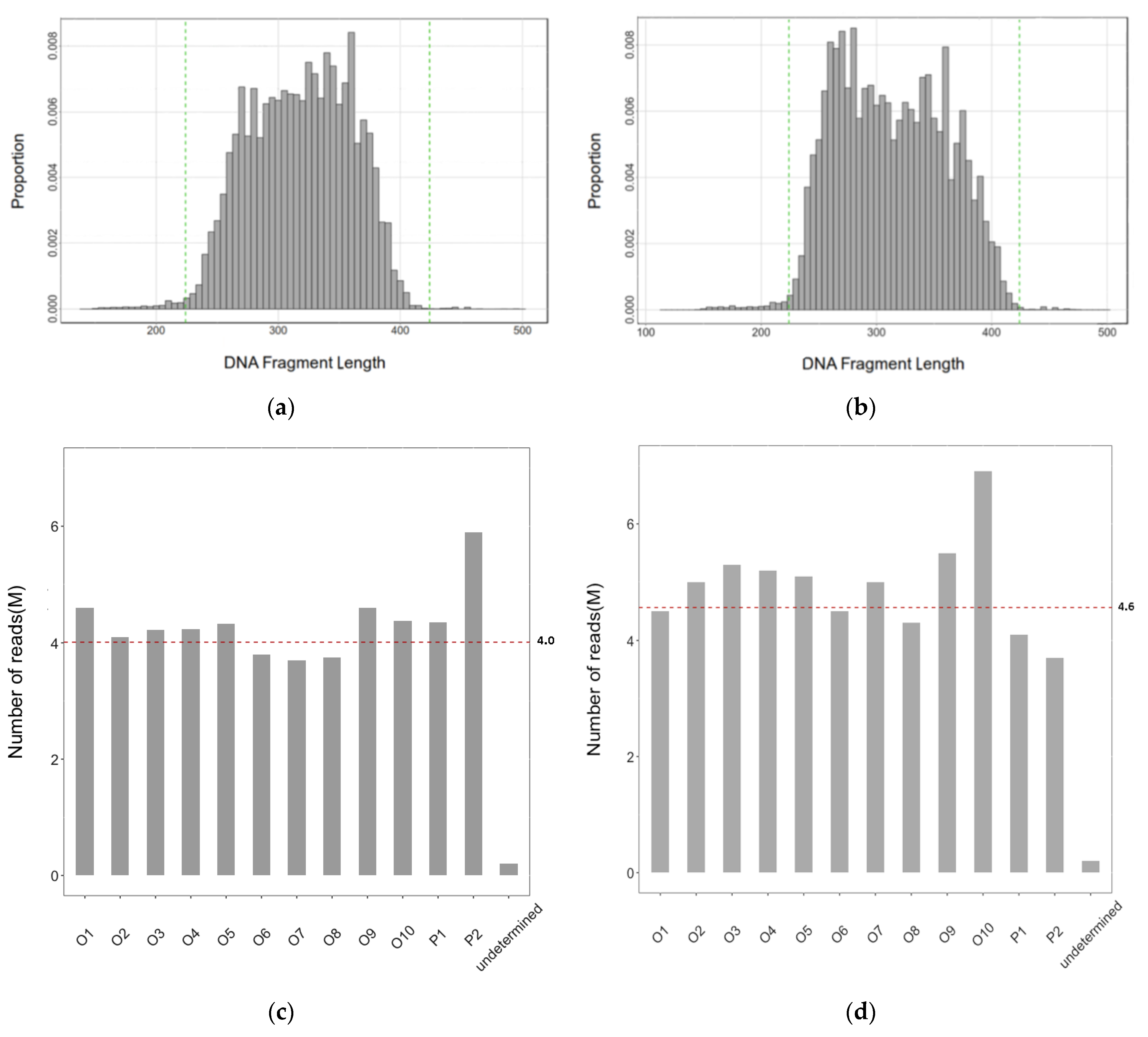
2.1. Sequence Data Collected
2.2. The Efficiency of the RAD-Seq Protocol to Remove the Chloroplast and Ribosomal RNA (rRNA) DNA Fragments
2.3. Preliminary Bioinformatic Analysis of the RAD-Seq Data
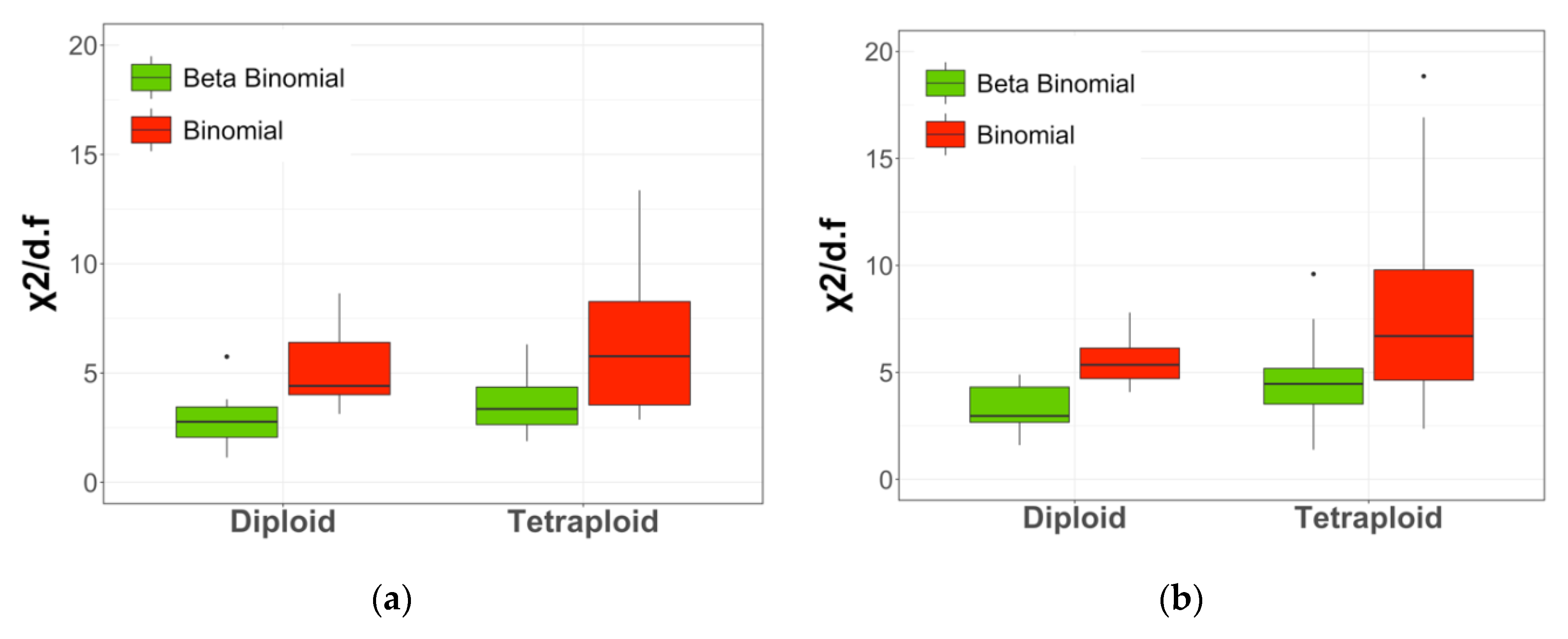
2.4. Sampling Distribution Fitting
3. Discussion
4. Materials and Methods
4.1. Creation of Diploid and Tetraploid Segregation Populations of Solanum tuberosum L.
4.2. Construction of RAD-Seq Libraries
4.3. Preliminary Processing of the Sequence Data
4.4. Identifying SNPs from the Sequence Data
4.5. Calling Polymorphic Sites and Genotype at the Identified Sites
4.6. Sampling Distributions of Sequence Data
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davey, J.W.; Hohenlohe, P.A.; Etter, P.D.; Boone, J.Q.; Catchen, J.M.; Blaxter, M.L. Genome-wide genetic marker discovery and genotyping using next-generation sequencing. Nat. Rev. Genet. 2011, 12, 499–510. [Google Scholar] [CrossRef] [PubMed]
- Blischak, P.D.; Kubatko, L.S.; Wolfe, A.D. SNP genotyping and parameter estimation in polyploids using low-coverage sequencing data. Bioinformatics 2018, 34, 407–415. [Google Scholar] [CrossRef]
- Poland, J.A.; Rife, T.W. Genotyping-by-Sequencing for Plant Breeding and Genetics. Plant Genome 2012, 5, 92–102. [Google Scholar] [CrossRef] [Green Version]
- Hackett, C.A.; Bradshaw, J.E.; Bryan, G.J. QTL mapping in autotetraploids using SNP dosage information. Theor. Appl. Genet. 2014, 127, 1885–1904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van de Geijn, B.; McVicker, G.; Gilad, Y.; Pritchard, J.K. WASP: Allele-specific software for robust molecular quantitative trait locus discovery. Nat. Methods 2015, 12, 1061–1063. [Google Scholar] [CrossRef] [Green Version]
- Uitdewilligen, J.G.; Wolters, A.M.; D’Hoop, B.B.; Borm, T.J.; Visser, R.G.; Van Eck, H.J. A next-generation sequencing method for genotyping-by-sequencing of highly heterozygous autotetraploid potato. PLoS ONE 2013, 8, e62355. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wall, J.D.; Tang, L.F.; Zerbe, B.; Kvale, M.N.; Kwok, P.Y.; Schaefer, C.; Risch, N. Estimating genotype error rates from high-coverage next-generation sequence data. Genome Res. 2014, 24, 1734–1739. [Google Scholar] [CrossRef] [Green Version]
- Degner, J.F.; Marioni, J.C.; Pai, A.A.; Pickrell, J.K.; Nkadori, E.; Gilad, Y.; Pritchard, J.K. Effect of read-mapping biases on detecting allele-specific expression from RNA-sequencing data. Bioinformatics 2009, 25, 3207–3212. [Google Scholar] [CrossRef]
- Heinrich, V.; Stange, J.; Dickhaus, T.; Imkeller, P.; Kruger, U.; Bauer, S.; Mundlos, S.; Robinson, P.N.; Hecht, J.; Krawitz, P.M. The allele distribution in next-generation sequencing data sets is accurately described as the result of a stochastic branching process. Nucleic Acids Res. 2012, 40, 2426–2431. [Google Scholar] [CrossRef] [Green Version]
- Li, H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics 2011, 27, 2987–2993. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.H.; Schwartz, R.S.; Winter, D.J.; Conrad, D.F.; Cartwright, R.A. Estimating error models for whole genome sequencing using mixtures of Dirichlet-multinomial distributions. Bioinformatics 2017, 33, 2322–2329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gerard, D.; Ferrao, L.F.V.; Garcia, A.A.F.; Stephens, M. Genotyping polyploids from messy sequencing data. Genetics 2018, 210, 789–807. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baird, N.A.; Etter, P.D.; Atwood, T.S.; Currey, M.C.; Shiver, A.L.; Lewis, Z.A.; Selker, E.U.; Cresko, W.A.; Johnson, E.A. Rapid SNP discovery and genetic mapping using sequenced RAD markers. PLoS ONE 2008, 3, e3376. [Google Scholar] [CrossRef]
- Langmead, B.; Salzberg, S.L. Fast gapped-read alignment with Bowtie 2. Nat. Methods 2012, 9, 357–359. [Google Scholar] [CrossRef] [Green Version]
- Garrison, E.; Marth, G. Haplotype-based variant detection from short-read sequencing. arXiv 1207, arXiv:1207.3907. [Google Scholar]
- Nielsen, R.; Paul, J.S.; Albrechtsen, A.; Song, Y.S. Genotype and SNP calling from next-generation sequencing data. Nat. Rev. Genet. 2011, 12, 443–451. [Google Scholar] [CrossRef]
- Chen, N.; Van Hout, C.V.; Gottipati, S.; Clark, A.G. Using mendelian inheritance to improve high-throughput SNP discovery. Genetics 2014, 198, 847–857. [Google Scholar] [CrossRef] [Green Version]
- Griffin, P.C.; Robin, C.; Hoffmann, A.A. A next-generation sequencing method for overcoming the multiple gene copy problem in polyploid phylogenetics, applied to Poa grasses. BMC Biol. 2011, 9, 19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Margarido, G.R.A.; Pastina, M.M.; Souza, A.P.; Garcia, A.A.F. Multi-trait multi-environment quantitative trait loci mapping for a sugarcane commercial cross provides insights on the inheritance of important traits. Mol. Breed. 2015, 35, 175. [Google Scholar] [CrossRef] [Green Version]
- Booth, C.S.; Pienaar, E.; Termaat, J.R.; Whitney, S.E.; Louw, T.M.; Viljoen, H.J. Efficiency of the polymerase chain reaction. Chem. Eng. Sci. 2010, 65, 4996–5006. [Google Scholar] [CrossRef] [Green Version]
- Aksyonov, S.A.; Bittner, M.; Bloom, L.B.; Reha-Krantz, L.J.; Gould, I.R.; Hayes, M.A.; Kiernan, U.A.; Niederkofler, E.E.; Pizziconi, V.; Rivera, R.S.; et al. Multiplexed DNA sequencing-by-synthesis. Anal. Biochem. 2006, 348, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Hackett, C.A.; Boskamp, B.; Vogogias, A.; Preedy, K.F.; Milne, I. TetraploidSNPMap: Software for linkage analysis and QTL mapping in autotetraploid populations using SNP dosage data. J. Hered. 2017, 108, 438–442. [Google Scholar] [CrossRef]
- Chen, Z.J.; Sreedasyam, A.; Ando, A.; Song, Q.; De Santiago, L.M.; Hulse-Kemp, A.M.; Ding, M.; Ye, W.; Kirkbride, R.C.; Jenkins, J.; et al. Genomic diversifications of five Gossypium allopolyploid species and their impact on cotton improvement. Nat. Genet. 2020, 52, 525–533. [Google Scholar] [CrossRef] [Green Version]
- Jiang, N.; Zhang, F.; Wu, J.; Chen, Y.; Hu, X.; Fang, O.; Leach, L.J.; Wang, D.; Luo, Z. A highly robust and optimized sequence-based approach for genetic polymorphism discovery and genotyping in large plant populations. Theor. Appl. Genet. 2016, 129, 1739–1757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zych, K.; Gort, G.; Maliepaard, C.A.; Jansen, R.C.; Voorrips, R.E. FitTetra 2.0-improved genotype calling for tetraploids with multiple population and parental data support. BMC Bioinform. 2019, 20, 148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kvam, P.; Day, D. The multivariate Polya distribution in combat modeling. Nav. Res. Logist. 2001, 48, 1–17. [Google Scholar] [CrossRef]
- Yang, Z.H.; Tian, J.F. An accurate approximation formula for gamma function. J. Inequal. Appl. 2018, 2018, 56. [Google Scholar] [CrossRef]


| Mapped Regions | Without Removing Chloroplast and rRNA Fragments | With Removing Chloroplast and rRNA Fragments | ||
|---|---|---|---|---|
| Diploid | Tetraploid | Diploid | Tetraploid | |
| Genomic DNA | 27.0 | 30.3 | 85.5 | 84.8 |
| Chloroplast DNA | 64.5 | 61.1 | 6.5 | 4.4 |
| rRNA genes | 0.7 | 1.2 | 0.3 | 0.3 |
| Unmapped | 7.8 | 7.4 | 7.7 | 10.5 |
| Individuals | Diploids | Tetraploids | ||||||
|---|---|---|---|---|---|---|---|---|
| AA | Aa | aa | AAAA | AAAa | AAaa | Aaaa | aaaa | |
| P1 | 6369 | 16,109 | 20,837 | 6355 | 12,420 | 7389 | 4776 | 17,905 |
| P2 | 6314 | 12,992 | 25,866 | 6104 | 12,129 | 7804 | 5232 | 20,150 |
| O1 | 6190 | 9712 | 15,781 | 6330 | 11,007 | 6747 | 5122 | 20,605 |
| O2 | 5756 | 8471 | 16,875 | 5719 | 9556 | 6294 | 4549 | 18,086 |
| O3 | 5657 | 8024 | 16,292 | 8779 | 13,662 | 8297 | 6727 | 24,261 |
| O4 | 5843 | 10,034 | 15,295 | 6398 | 9618 | 6664 | 4131 | 21,851 |
| O5 | 5812 | 9257 | 15,803 | 6609 | 11,194 | 7071 | 5152 | 21,951 |
| O6 | 5181 | 5843 | 15,410 | 6508 | 10,303 | 6886 | 5137 | 19,245 |
| O7 | 4904 | 8329 | 17,343 | 6965 | 10,571 | 7877 | 5145 | 20,327 |
| O8 | 5294 | 10,134 | 19,844 | 6149 | 9854 | 6936 | 4444 | 18,988 |
| O9 | 5562 | 10,918 | 23,296 | 5692 | 9535 | 6300 | 3968 | 15,634 |
| O10 | 5450 | 7459 | 18,270 | 6999 | 12,306 | 7714 | 5269 | 21,468 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, Z.; Yang, J.; Wang, L.; Tao, Q.; Zhang, F.; Zhang, Y.; Luo, Z. Sampling Variation of RAD-Seq Data from Diploid and Tetraploid Potato (Solanum tuberosum L.). Plants 2021, 10, 319. https://doi.org/10.3390/plants10020319
Dang Z, Yang J, Wang L, Tao Q, Zhang F, Zhang Y, Luo Z. Sampling Variation of RAD-Seq Data from Diploid and Tetraploid Potato (Solanum tuberosum L.). Plants. 2021; 10(2):319. https://doi.org/10.3390/plants10020319
Chicago/Turabian StyleDang, Zhenyu, Jixuan Yang, Lin Wang, Qin Tao, Fengjun Zhang, Yuxin Zhang, and Zewei Luo. 2021. "Sampling Variation of RAD-Seq Data from Diploid and Tetraploid Potato (Solanum tuberosum L.)" Plants 10, no. 2: 319. https://doi.org/10.3390/plants10020319






