Validating a Simple Mechanistic Model That Describes Weather Impact on Pasture Growth
Abstract
:1. Introduction
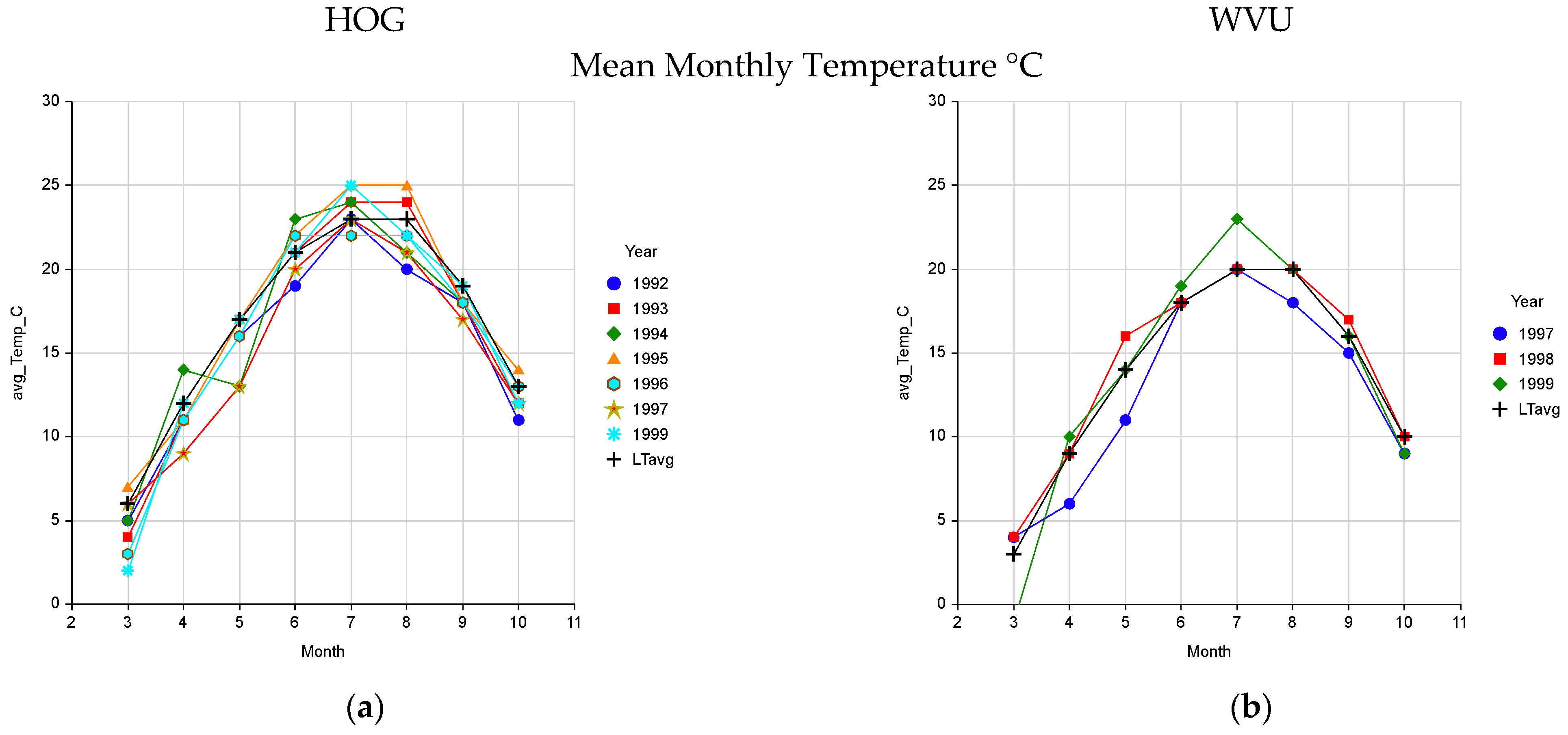
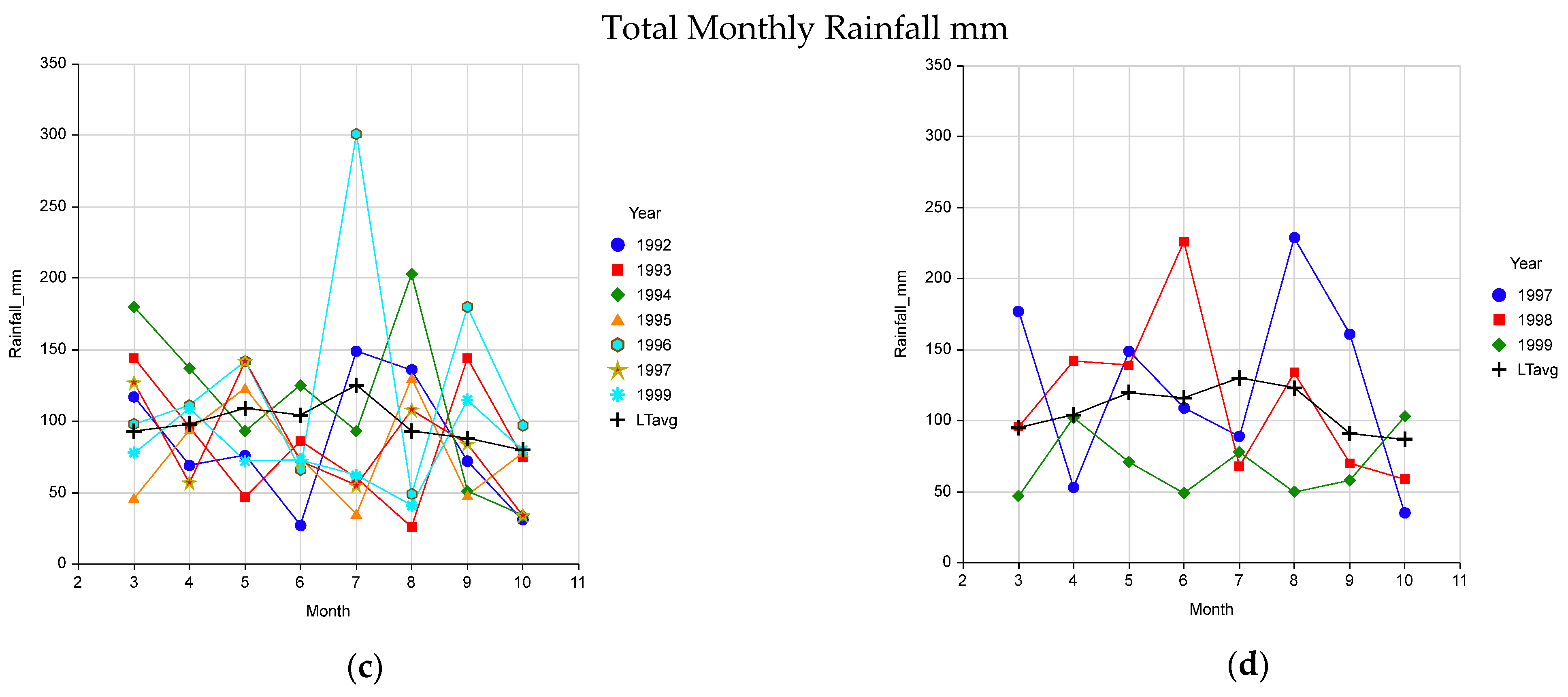
2. Results
3. Discussion
4. Materials and Methods
4.1. Pasture Growth Model Description
4.2. Plant and Soil Biology Response to ASW
4.3. Plant Response to Temperature
4.4. Plant Response to Daylength
4.5. Field Measurement of Pasture Growth
4.6. Forage Growth Measurement
4.7. Testing the Model
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| # Pasture Growth Model programmed using the Python language (version 3) import os import math # description of location and soil # latitude, degrees North lat_deg = 40.0 # latitude in radians lat_rad = math.radians(lat_deg) # available soil water maximum, a function of soil texture and rooting depth HOG = 9.0 #WVU = 5.0 asw_max = 9.0 # asw today set to maximum at start of year asw_d = asw_max print(‘Latitude’, lat_deg, ‘,’, ‘asw_max’, asw_max) # Maximum Pasture Growth Rate, function of plant species and soil fertility pgr_max = 100 et_pe_c3 = 0.80 # evapotranspiration/pan evaporation, cool-season (C3)plants et_pe_c4 = 0.73 # evapotranspiration/pan evaporation, warm-season (C4)plants # Temperature effect on cool-season plant growth adapted from Fick, 1980 # Temperature in degrees F as reported locally low_min_pgt = 32.0 # low minimum plant growth temperature, 0 °C low_op_pgt = 50.0 # low optimum plant growth temperature, 10 °C high_op_pgt = 68.0 # high optimum plant growth temperature, 20 °C high_max_pgt = 86.0 # high maximum plant growth temperature, 30 °C # Day length effect on plant growth rate Fick 1980, Figure 3, p. 148. dl_spring_crit = 8.0 dl_spring_opt = 12.0 dl_fall_opt = 13.0 dl_fall_crit = 8.0 # Initialize relative growth rates, ET and pan evaporation rgr_asw = 1.0 # relative growth rate due to plant available soil water rgr_dl = 0.0 # relative growth rate due to day length rgr_temp = 0.0 # relative growth rate due to average air temperature rgr_env = 0.0 # relative growth rate due to total environment eff_et = 0.0 # effective evapotranspiration pan_evap = 0.0 # pan evaporation t_sum_300 = 0.0 # t_sum_300 used to start summing cum_rgr_env # Start Annual Loop # WVU weather data # weather_data = open(‘wvu_weather.csv’, ‘r’) # HOG weather data weather_data = open(‘HOG 7 yr weather.csv’, ‘r’) header = weather_data.readline() header = header.split(‘,’) #output_file = open(‘wvu_rgr_asw.csv’,’w’) # WVU PGR output file output_file = open(‘HOG_rgr_obs_vs_pred_test.csv’,’w’) # HOG output file #header at top of output file doy_data_output = (‘year,month,day,doy,rgr_dl,rgr_temp,rgr_asw,rgr_env,cum_rgr_env\n’) output_file.write(doy_data_output) # Header on terminal print(‘ Year Month Day rgr_dl rgr_temp rgr_asw rgr_env cum_rgr_env’) year = 1997 # initialize year while year<=1999: # loop from 1992 to 1999 t_sum_300 = 0.0 cum_rgr_env = 0.0 month = 1 while month <= 12: # loop to run through days of the year by month days_weather = weather_data.readline() days_weather = days_weather.split(‘,’) month = int(days_weather[0]) day = int(days_weather[1]) year = int(days_weather[2]) doy = int(days_weather [3]) precip = float(days_weather[4]) t_max = float(days_weather[5]) t_min = float(days_weather[6]) precip = precip/100 # precipitation in hundreds of an inch converting to inches t_avg = (t_max + t_min)/2 # calculate average air temperature t_avg_c = (t_avg - 32) * (100/180) if t_avg_c < 0: t_sum_300 = t_sum_300 else: t_sum_300 = t_sum_300 + t_avg_c # Calculate daily solar variables # equations from: Global Radiation in West Virginia. 1979. WVU Agriculture # and Forestry Experiment Station Bul. 665T solar_dec = 0.41015 * math.sin(0.01721 * doy - 1.389) # a close estimate of solar declination in radians solar_dec_deg = math.degrees(solar_dec) day_length = 24 * math.acos(-math.tan(lat_rad) * math.tan(solar_dec))/math.pi H = math.pi * (day_length/2)/12 # hour angle between sun rise and solar noon d = (doy - 80) # number of days off set to align doy with spring equinox and summer solstice if(d > 186): solar_l = (d - 186) else: solar_l = (180 * d/186) # this is solar “lambda” but in Python needed to be renamed solar_r = (1 - 0.01672 ** 2)/(1 + 0.01672 * math.cos(math.pi * (77.5 + solar_l)/180)) # solar_r is the solar radius vector the ratio of earth-sun distance and its mean # e is the eccentricity of the earth’s orbit = 0.01672 # sp – solar potential radiation at the top of the atmosphere sp = 889.23/solar_r ** 2 * (math.cos(lat_rad) * math.cos(solar_dec) * (math.sin(H) - H * math.cos(H))) #print(“DOY “, doy, “Declination “, ‘{:.1f}’.format(solar_dec_deg), “Day length “, ‘{:.1f}’.format(day_length), “hr”) # Calculate pan evaporation and plant evapotranspiration in last 24 h pan_evap = -0.2345 - 0.0326 * precip + 0.002188 * t_avg + 0.0002088 * sp + 0.004202 * (t_max - t_min) # print(‘pan evap’,’{:.2f}’.format(pan_evap)) if pan_evap < 0: pan_evap_d = 0 # pan evaporation allowed today else: pan_evap_d = pan_evap # asw_max – maximum plant available soil water in rooting zone at field capacity # asw_d - plant available soil water in rooting zone today # asw_pct - asw_d as a fraction (decimal percent) of asw_max eff_et = pan_evap_d * et_pe_c3 * rgr_asw asw_d = (asw_d + precip - eff_et) if asw_d < 0.0: asw_d = 0.0 elif asw_d > asw_max: asw_d = asw_max else: asw_d = asw_d # Calculate relative growth rate factors # Calculate relative growth rate due to plant available soil water - rgr_asw if (asw_d/asw_max) < 0: rgr_asw = 0.0 elif (asw_d/asw_max) < 0.50: rgr_asw = (2.0 * asw_d/asw_max) else: rgr_asw = 1.0 # Calculate relative growth rate due to the day’s air temperature - rgr_temp if t_avg <= low_min_pgt: rgr_temp = 0.0 elif t_avg < low_op_pgt: rgr_temp = ((t_avg - low_min_pgt) * (1/(low_op_pgt - low_min_pgt))) elif t_avg < high_op_pgt: rgr_temp = 1.0 elif t_avg < high_max_pgt: rgr_temp = 1 + ((t_avg - high_op_pgt) * (1/(high_op_pgt - high_max_pgt))) else: rgr_temp = 0.0 # Calculate relative growth rate due to daylength - rgr_dl if doy < 172: if day_length < dl_spring_crit: rgr_dl = 0.0 elif day_length < dl_spring_opt: rgr_dl = (1/(dl_spring_opt - dl_spring_crit)) * (day_length - dl_spring_crit) else: rgr_dl = 1.0 elif day_length > dl_fall_opt: rgr_dl = 1.0 elif day_length > dl_fall_crit: rgr_dl = 1.0 + (1/(dl_fall_opt - dl_fall_crit)) * (day_length - dl_fall_opt) else: rgr_dl = 0.0 # Relative growth rate due to soil biological activity “soil health” rgr_sbio = rgr_asw # Calculate relative growth rate due to the environment - rgr_env rgr_env = rgr_asw * rgr_sbio * rgr_temp * rgr_dl # relative growth rate due to all environmental factors if rgr_env < 0.0: rgr_env = 0.0 else: rgr_env = rgr_env if t_sum_300 < 300: cum_rgr_env = cum_rgr_env else: cum_rgr_env = cum_rgr_env + rgr_env if doy < 365: cum_rgr_env = cum_rgr_env else: cum_rgr_env = 0.0 t_sum_300 = 0.0 # End calculate relative growth rate due to the environment print(year,’ ‘, month,’ ‘,day,’ ‘, ‘{:.3f}’.format(rgr_dl),’ ‘, ‘{:.3f}’.format(rgr_temp),’ ‘, ‘{:.3f}’.format(rgr_asw),’ ‘, ‘{:.3f}’.format(rgr_env), ‘ ‘, ‘{:.3f}’.format(cum_rgr_env)) doy_data_output = (str(year) + ‘,’ + str(month) + ‘,’ + str(day)+’,’+str(doy) + ‘,’ + str(‘{:.3f}’.format(rgr_dl)) + ‘,’ + str(‘{:.3f}’.format(rgr_temp)) + ‘,’ + str(‘{:.3f}’.format(rgr_asw)) + ‘,’ + str(‘{:.3f}’.format(rgr_env)) + ‘,’ + str(‘{:.3f}’.format(cum_rgr_env)) + ‘\n’) output_file.write(doy_data_output) # End annual loop # End multi-year loop weather_data.close() output_file.close() |
Appendix B
- doy is Julian day of the year
- precip is in 100th of an inch as reported by NOAA
- t_max is daily maximum temperature
- t_min is daily minimum temperature
- temperatures are °F as used by livestock producers in the United States
| Month | Day | Year | Doy | Precip | t_max | t_min | Station |
| 1 | 1 | 1992 | 1 | 0 | 45 | 19 | Hart Field |
| 1 | 2 | 1992 | 2 | 0 | 54 | 21 | Hart Field |
| 1 | 3 | 1992 | 3 | 3 | 52 | 43 | Hart Field |
| 1 | 4 | 1992 | 4 | 0 | 52 | 45 | Hart Field |
| 1 | 5 | 1992 | 5 | 1 | 45 | 36 | Hart Field |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| 12 | 27 | 1999 | 361 | 0 | 30 | 23 | Hart Field |
| 12 | 28 | 1999 | 362 | 2 | 24 | 21 | Hart Field |
| 12 | 29 | 1999 | 363 | 0 | 35 | 22 | Hart Field |
| 12 | 30 | 1999 | 364 | 0 | 49 | 35 | Hart Field |
| 12 | 31 | 1999 | 365 | 0 | 49 | 29 | Hart Field |
References
- McGill, W.B.; Hunt, H.W.; Woodmansee, R.G.; Reuss, J.O. PHONEX, a model of the dynamics of carbon and nitrogen in grassland soils. Ecol. Bull. 1981, 33, 49–115. [Google Scholar]
- Parton, W.J.; Schimel, D.S.; Cole, C.V.; Ojima, D.S. Analysis of Factors Controlling Soil Organic Matter Levels in Great Plains Grasslands. Soil Sci. Soc. Am. J. 1987, 51, 1173–1179. [Google Scholar] [CrossRef]
- Hanson, J.D.; Skiles, J.W.; Parton, W.J. A multi-species model for rangeland plant communities. Ecol. Model. 1988, 44, 89–123. [Google Scholar] [CrossRef]
- Hunt, H.W.; Trilica, M.J.; Redente, E.F.; Moore, J.C.; Detling, J.K.; Kittel, T.G.F.; Walter, D.E.; Fowler, M.C.; Klein, D.A.; Elliot, E.T. Simulation model for the effects of climate change on temperate grassland ecosystems. Ecol. Model. 1991, 53, 205–246. [Google Scholar] [CrossRef]
- Biondini, M. A three-dimensional spatial model for plant competition in an heterogeneous soil environment. Ecol. Model. 2001, 142, 189–225. [Google Scholar] [CrossRef]
- Johnson, I.R.; Chapman, D.F.; Snow, V.O.; Eckard, R.J.; Parsons, A.J.; Lambert, M.G.; Cullen, B.R. DairyMod and EcoMod: Biophysical pasture-simulation models for Australia and New Zealand. Aust. J. Exp. Agric. 2007, 48, 621–631. [Google Scholar] [CrossRef]
- Cobon, D.H.; Kouadio, L.; Mushtaq, S.; Jarvis, C.; Carter, J.; Stone, G.; Davis, P. Evaluating the shifts in rainfall and pasture-growth variabilities across the pastoral zone of Australia during 1910–2010. Crop. Pasture Sci. 2019, 70, 634–647. [Google Scholar] [CrossRef] [Green Version]
- Fick, G.W. A pasture production model for use in a whole farm simulator. Agric. Syst. 1980, 5, 137–161. [Google Scholar] [CrossRef]
- Pearson, C.J.; Ison, R.L. Agronomy of Grassland Systems, 2nd ed.; Cambridge University Press: New York, NY, USA, 1997; p. 222. [Google Scholar]
- Rayburn, E.B.; Hall, M.H.; Murphy, W.; Vough, L. Pasture production. In Pasture Management in the Northeast—Assessing Current Technologies, Research Directions and Educational Needs; Krueger, C.R., Pionke, H.B., Eds.; NRAES-113; Northeast Regional Agricultural Engineering Service: Ithaca, NY, USA, 1998; Volume 113, pp. 13–50. [Google Scholar]
- Hansen, D.J. Manure as a Nutrient Source. In The Mid-Atlantic Nutrient Management Handbook; Haering, K.C., Evanylo, G.K., Eds.; Mid-Atlantic Regional Water Program; MAWP 06-02: College Park, MD, USA, 2006; p. 215. Available online: https://extension.psu.edu/programs/nutrient-management/educational/nutrient-management-general/mid-atlantic-nutrient-management-handbook (accessed on 20 August 2021).
- Fribourg, H.A.; Reich, V.H. Soils differ in yield potential. Crop. Soils Mag. 1982, 35, 12–14. [Google Scholar]
- University of California, Davis. SoilWeb. Available online: https://casoilresource.lawr.ucdavis.edu/gmap/ (accessed on 20 August 2021).
- USDA/NRCS. Web Soil Survey. Available online: https://websoilsurvey.sc.egov.usda.gov/App/WebSoilSurvey.aspx (accessed on 20 August 2021).
- NOAA. National Oceanic and Atmospheric Administration. National Centers for Environmental Information. Available online: https://www.ncdc.noaa.gov/cdo-web/ (accessed on 20 August 2021).
- Weedfall, R.O.; Dickerson, W.H. The Climate of Bluestone Recreational Area, West. Virginia; Current Report; West Virginia University Agricultural Experiment Station: Morgantown, WV, USA, 1966; Volume 45, p. 15. [Google Scholar]
- Weedfall, R.O.; Dickerson, W.H.; Stirm, W.L. The Agroclimate of University Experiment Farm Kearneysville, West Virginia; Current Report; West Virginia University Agricultural Experiment Station: Morgantown, WV, USA, 1967; Volume 52, p. 19. [Google Scholar]
- Aronson, L.J.; Gold, A.J.; Hull, R.J.; Cisar, J.L. Evapotranspiration of Cool-Season Turfgrasses in the Humid Northeast. Agron. J. 1987, 79, 901–905. [Google Scholar] [CrossRef] [Green Version]
- Peck, N.H.; Vittum, M.T.; Gibbs, G.H. Evapotranspiration Rates for Irrigated Crops at Geneva, New York. Agron. J. 1968, 60, 23–26. [Google Scholar] [CrossRef]
- Lee, R.; Boyer, D.G.; Valli, V.J.; Dickerson, W.H. Global radiation in West Virginia. West Va. Agric. For. Exp. Stn. Bull. 1979, p. 665T. Available online: https://researchrepository.wvu.edu/wv_agricultural_and_forestry_experiment_station_bulletins/724/ (accessed on 20 August 2021).
- Smith, R.E. OPUS: An Integrated Simulation Model for Transport of Nonpoint-Source Pollutants at the Field Scale; Volume I Documentation USDA/ARS: Washington, DC, USA, 2000. [Google Scholar]
- Timlin, D.J.; Bryant, R.B.; Snyder, V.A.; Wagenet, R.J. Modeling corn grain yield in relation to soil erosion using a water budget approach. Soil Sci. Soc. Am. J. 1986, 50, 718–723. [Google Scholar] [CrossRef]
- Kowalenko, C.G.; Freyman, S.; Bates, D.L.; Holbek, N.E. An evaluation of the T-sum method for efficient timing of spring nitrogen applications on forage production in south coastal British Columbia. Can. J. Plant. Sci. 1989, 69, 1179–1192. [Google Scholar] [CrossRef] [Green Version]
- USDA/NRCS. Land Resource Regions and Major Land Resource Areas of the United States, the Caribbean, and the Pacific Basin; USDA Ag. Handbook 296; USDA: Washington, DC, USA, 2006; Volume 20250, p. 682.
- Rayburn, E.B.; Griggs, T.C. Light Interception and the Growth of Pastures under Ideal and Stressful Growing Conditions on the Allegheny Plateau. Plants 2020, 9, 734. [Google Scholar] [CrossRef] [PubMed]
- Rayburn, E.B.; Rayburn, S.B. A standardized plate meter for estimating pasture mass in on-farm research trials. Agron. J. 1998, 90, 238–241. [Google Scholar] [CrossRef]
- Macoon, B.; Schollenbereger, L.E.; Moore, J.E.; Staples, C.R.; Fike, J.H.; Portier, K.M. Comparison of three techniques for estimating the forage intake of lactating dairy cows on pasture. J. Anim. Sci. 2003, 81, 2357–2366. [Google Scholar] [CrossRef] [PubMed]
- Rayburn, E.B. Plate meter calibrations for forage mass follow a continuum of sward basal density. Crop. Forage Turfgrass Mgmt. 2020, 6, e20009. [Google Scholar] [CrossRef] [Green Version]
- NCSS. NCSS 11 Statistical Software; NCSS, LLC: Kaysville, UT, USA, 2016; Available online: ncss.com/software/ncss (accessed on 20 August 2021).
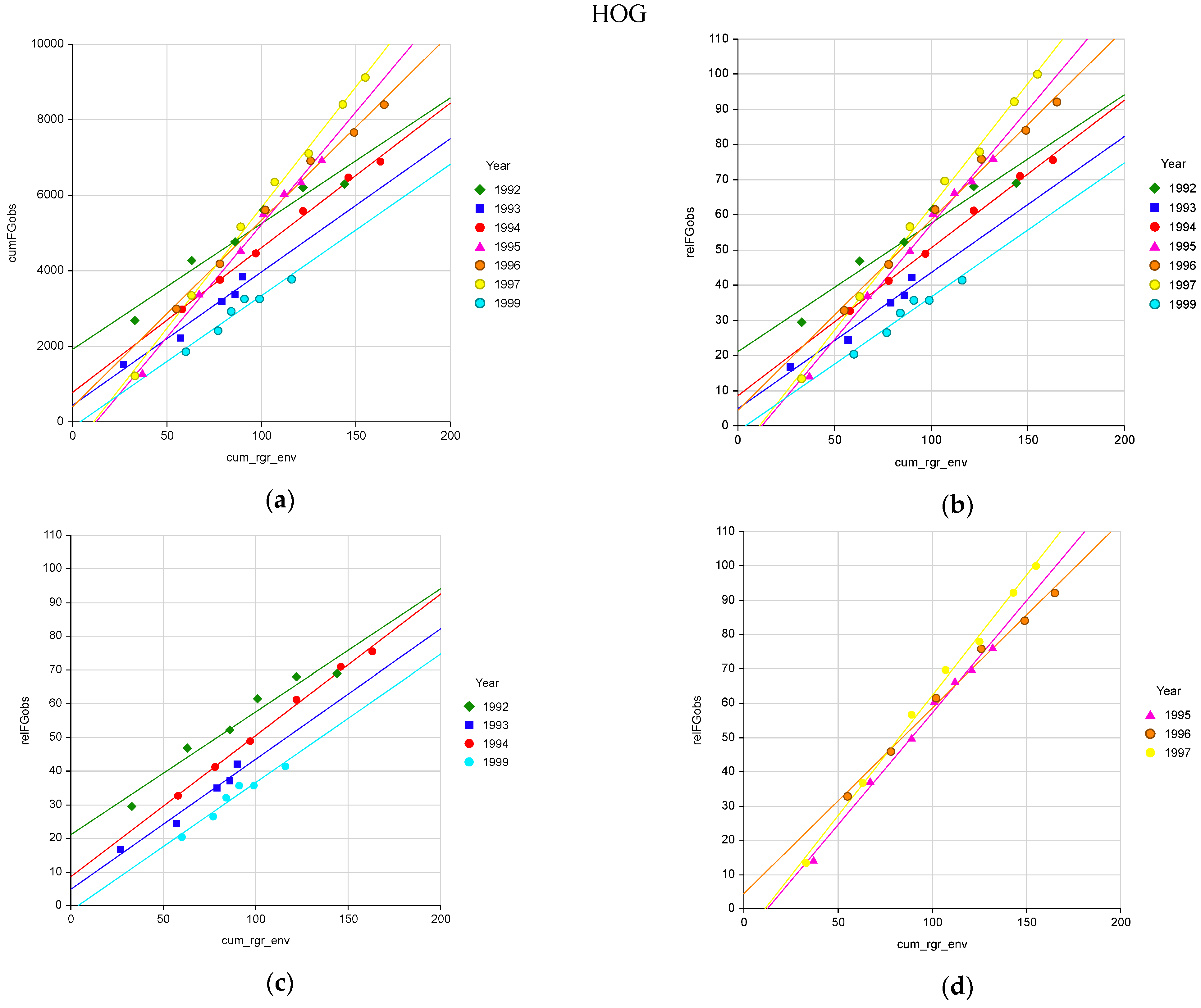

| Regression | R2 | SDreg ‡ | AAPE ‡‡ | N | |
|---|---|---|---|---|---|
| HOG | |||||
| A | cumFGobs = −232 + 51 cum_rgr_env | 0.83 | 849 | 18 | 43 |
| B | relFGobs = −3 †† + 0.56 cum_rgr_env | 0.83 | 9 | 18 | 43 |
| C | For years 1992, 1993, 1994, 1999 relFGobs = 19 + 0.39 cum_rgr_env + Year Year: 1992 = 0 1993 = −14 1994 = −7 1999 = −21 | 0.98 | 2 | 4 | 23 |
| D | For years 1995, 1996, 1997 relFGobs = −7 + 0.64 cum_rgr_env + Year Year: 1995 = 0 1996 = 0 1997 = 5 | 0.98 | 3 | 7 | 20 |
| WVU | |||||
| E | cumFGobs = 578 + 30 cum_rgr_env | 0.76 | 759 | 22 | 79 |
| F | relFGobs = 8 + 0.40 cum_rgr_env | 0.76 | 10 | 22 | 79 |
| G | relFGobs = -9 + 0.44 cum_rgr_env + 9 Litter + Year Year: 1997 = 0 1998 = 9 1999 = 14 | 0.87 | 7 | 17 | 79 |
| H | No-Litter Treatments relFGobs = 8 + 0.34 cum_rgr_env | 0.88 | 6 | 14 | 35 |
| I | Litter Treatments in 1997 relFGobs = −1 †† + 0.41 cum_rgr_env | 0.95 | 4 | 9 | 12 |
| J | Litter Treatments in 1998 and 1999 relFGobs = −2 †† + 0.60 cum_rgr_env + Year Year: 1998 = 0 1999 = 9 | 0.96 | 6 | 11 | 17 |
| Site | MLRA † | Elevation | Grazing Management | Treatments | Years | Growth Intervals |
|---|---|---|---|---|---|---|
| HOG | 126 | 305 m | Set stocked | Height of grazing | 7 | 43 |
| WVU | 127 | 610 m | Rotational stocked | Poultry litter applications | 3 | 79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rayburn, E.B. Validating a Simple Mechanistic Model That Describes Weather Impact on Pasture Growth. Plants 2021, 10, 1754. https://doi.org/10.3390/plants10091754
Rayburn EB. Validating a Simple Mechanistic Model That Describes Weather Impact on Pasture Growth. Plants. 2021; 10(9):1754. https://doi.org/10.3390/plants10091754
Chicago/Turabian StyleRayburn, Edward B. 2021. "Validating a Simple Mechanistic Model That Describes Weather Impact on Pasture Growth" Plants 10, no. 9: 1754. https://doi.org/10.3390/plants10091754
APA StyleRayburn, E. B. (2021). Validating a Simple Mechanistic Model That Describes Weather Impact on Pasture Growth. Plants, 10(9), 1754. https://doi.org/10.3390/plants10091754





