Hourly Relationship between Reference Evapotranspiration and Shoot Shrinkage in Walnut Trees and Pomegranate under Deficit Irrigation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Characterization of the Study Area
2.2. Treatments
2.3. Meteorological Variables
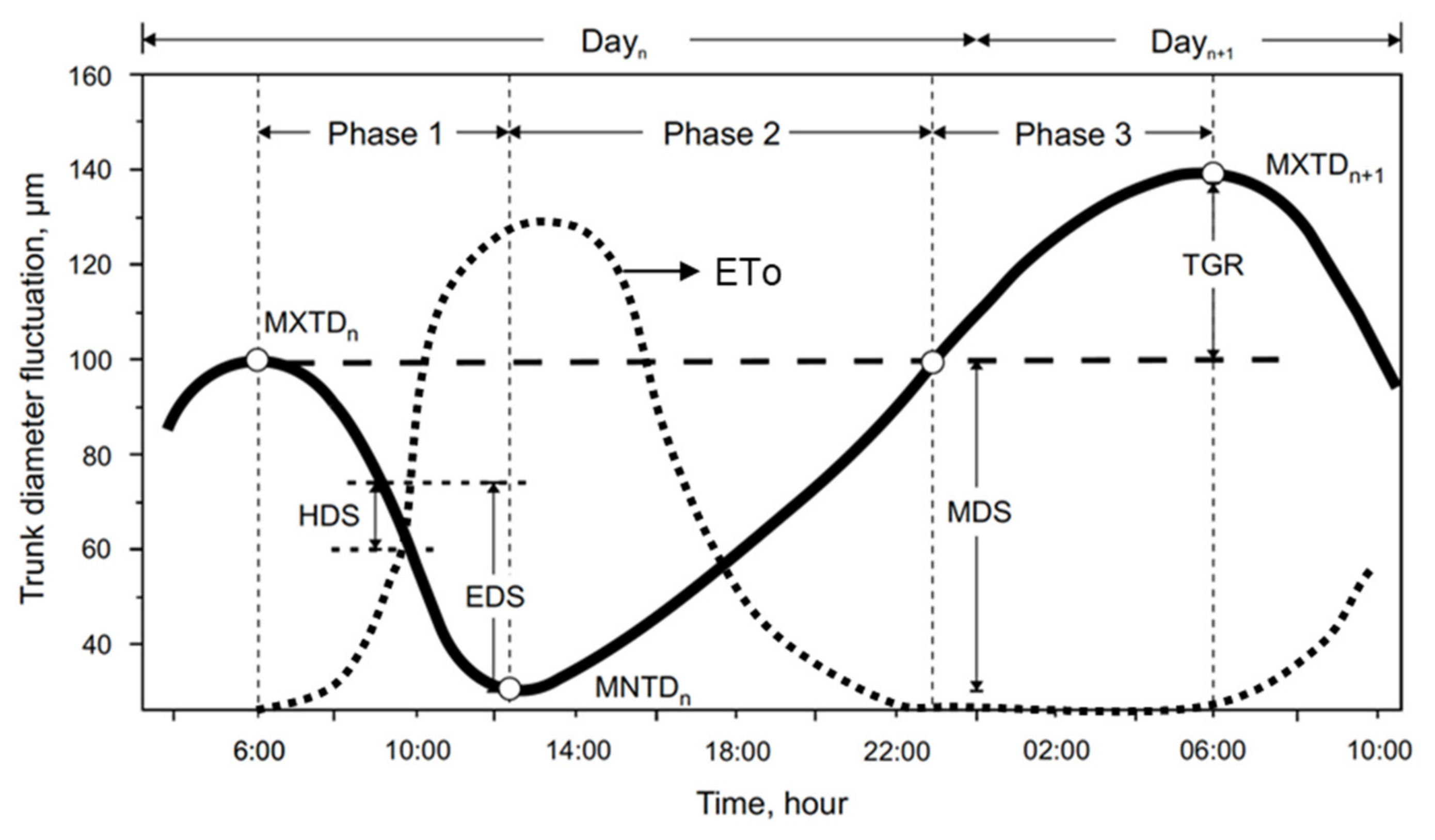
2.4. Dendrometry
2.5. Statistical Analysis
3. Results and Discussion
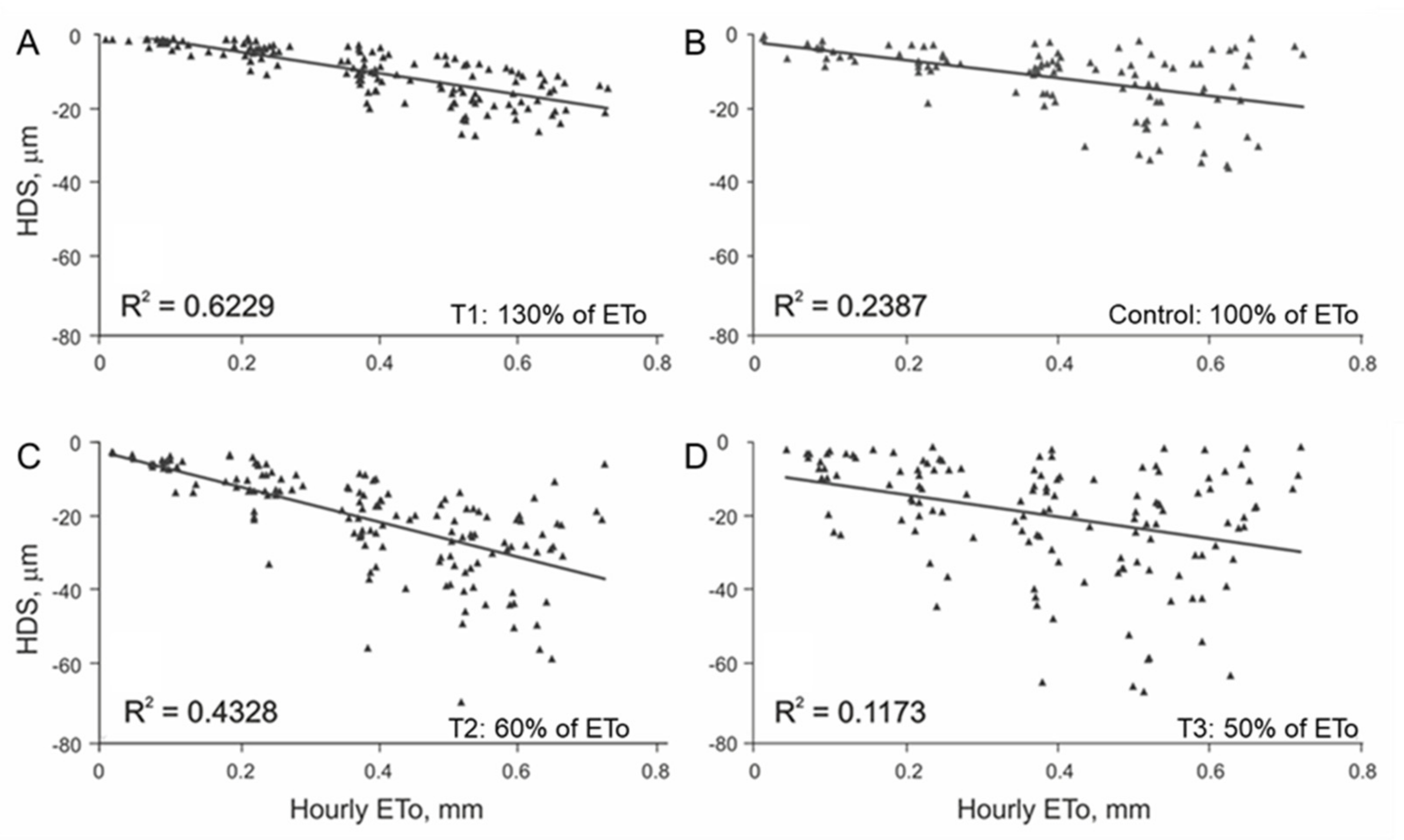
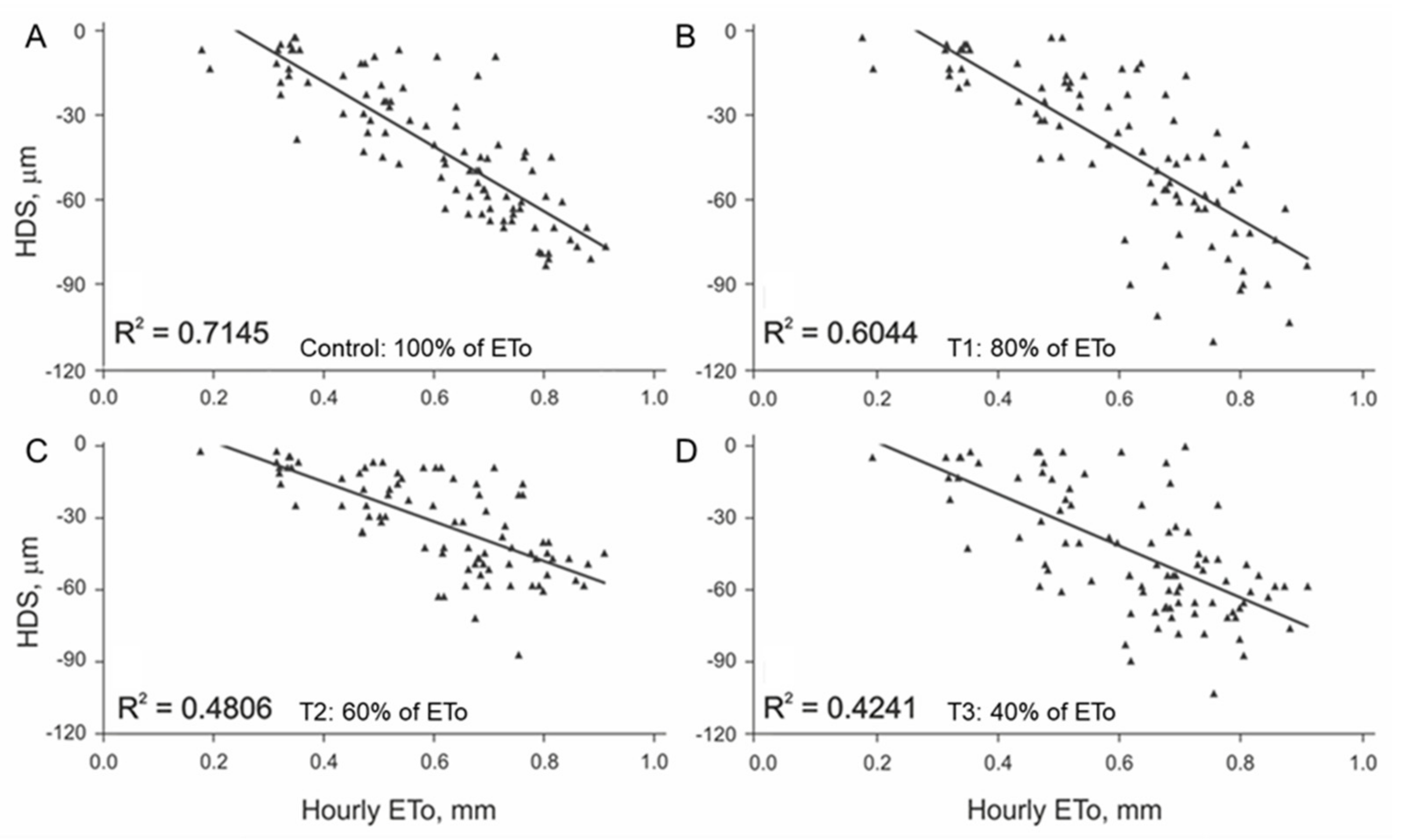
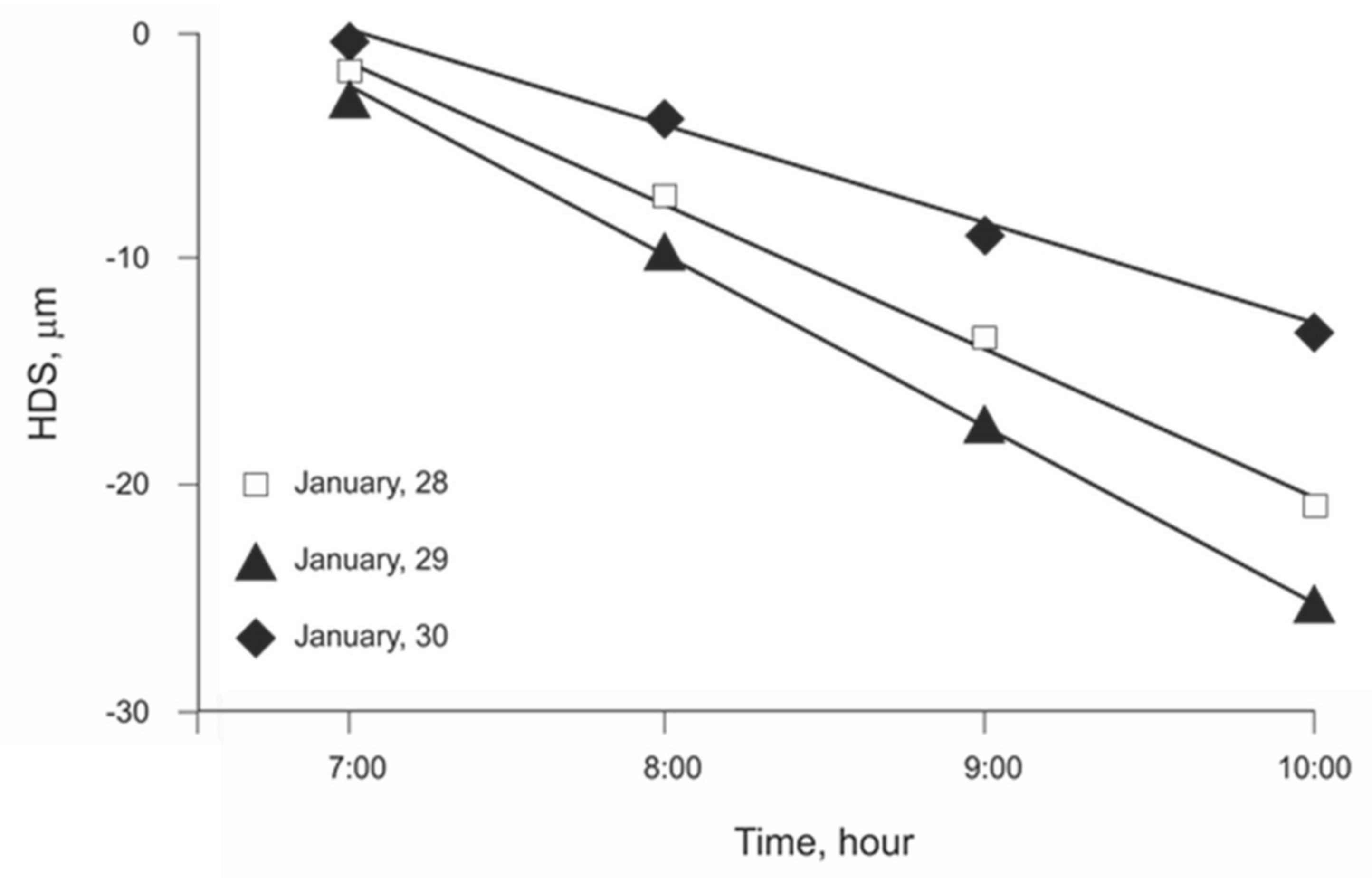
3.1. Initial Linear Relationship between HDS and EToh
3.2. Linear Regression Assumptions Analysis and Model Improvement
3.3. Daily ETo and MDS/EDS Relationship
3.4. Significance of Our Findings
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baver, L.; Gardner, W. Física de suelos. In Agencia Para el Desarrollo Internacional; Uteha: Ciudad de Mexico, Mexico, 1973; p. 529. [Google Scholar]
- Pfautsch, S.; Renard, J.; Tjoelker, M.; Salih, A. Phloem as capacitor: Radial transfer of water into xylem of tree stems occurs via symplastic transport in ray parenchyma. Plant Physiol. 2015, 167, 963–971. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knipfer, T.; Cuneo, I.F.; Earles, J.M.; Reyes, C.; Brodersen, C.; McElrone, A.J. Storage compartments for capillary water rarely refill in an intact woody plant. Plant Physiol. 2017, 175, 1649–1660. [Google Scholar] [CrossRef] [Green Version]
- Waring, R.H.; Whitehead, D.; Jarvis, P. The contribution of stored water to transpiration in Scots pine. Plant Cell Environ. 1979, 2, 309–317. [Google Scholar] [CrossRef]
- Cuneo, I.F.; Knipfer, T.; Mandal, P.; Brodersen, C.; McElrone, A. Water uptake can occur through woody portions of roots and facilitates localized embolism repair in grapevine. New Phytol. 2018, 218, 506–516. [Google Scholar] [CrossRef] [Green Version]
- Fernandez, J.; Cuevas, M. Irrigation scheduling from stem diameter variations: A review. Agric. For. Meteorol. 2010, 150, 135–151. [Google Scholar] [CrossRef]
- Goldhamer, D.; Fereres, E. Irrigation scheduling protocols using continuously recorded trunk diameter variations. Irrig. Sci. 2001, 20, 115–125. [Google Scholar] [CrossRef]
- Breitsprecher, A.; Hughes, W. A recording dendrometer for humid environments. Biotropica 1975, 7, 90–99. [Google Scholar] [CrossRef]
- Zweifel, R. Radial stem variations—A source of tree physiological information not fully exploited yet. Plant Cell Environ. 2016, 39, 231–232. [Google Scholar] [CrossRef]
- Steppe, K.; De Pauw, D.J.W.; Lemeur, R.; Vanrolleghem, P.A. A mathematical model linking tree sap flow dynamics to daily stem diameter fluctuations and radial stem growth. Tree Physiol. 2006, 26, 257–273. [Google Scholar] [CrossRef] [Green Version]
- Ježík, M.; Blaženec, M.; Střelcová, K.; Kovalčíková, D. Relations between potential evapotranspiration, sap flow and maximum daily stem shrinkage of spruce trees in growth stages of a pole- and trunk-mature forest during irrigation experiment. In Proceedings of the Bioclimate: Source and Limit of Social Development International Scientific Conference, Topoľčianky, Slovakia, 6–9 September 2011. [Google Scholar]
- Gallardo, M.; Thompson, R.; Valdés, L.; Fernandez, M. Response of stem diameter variations to water stress in greenhouse-grown vegetable crops. Hortic. Sci. Biotechnol. 2006, 81, 483–495. [Google Scholar] [CrossRef]
- Velez, J.; Intrigliolo, D.; Castel, J. Scheduling deficit irrigation of citrus trees with maximum daily trunk shrinkage. Agric. Water Manag. 2007, 90, 197–204. [Google Scholar] [CrossRef]
- Corell, M.; Martín-Palomo, M.; Pérez-López, D.; Centeno, A.; Girón, I.; Moreno, F.; Torrecillas, A.; Moriana, A. Approach for using trunk growth rate (TGR) in the irrigation scheduling of table olives orchards. Agric. Water Manag. 2017, 192, 12–20. [Google Scholar] [CrossRef]
- Nortes, P.; Pérez-Pastor, A.; Egea, G.; Conejero, W.; Domingo, R. Comparison of changes in stem diameter and water potential values for detecting water stress in young almond trees. Agric. Water Manag. 2005, 77, 296–307. [Google Scholar] [CrossRef]
- Intrigliolo, D.; Castel, J. Usefulness of diurnal trunk shrinkage as a water stress indicator in plum trees. Tree Physiol. 2006, 26, 303–311. [Google Scholar] [CrossRef]
- De Swaef, J.; Steppe, K.; Lemeur, R. Determining reference values for stem water potential and maximum daily trunk shrinkage in young apple trees based on plant responses to water deficit. Agric. Water Manag. 2009, 96, 541–550. [Google Scholar] [CrossRef]
- Ortuño, M.; Brito, J.; García-Orellana, Y.; Conejero, W.; Tordecillas, A. Maximum daily trunk shrinkage and stem water potential reference equations for irrigation scheduling of lemon trees. Irrig. Sci. 2009, 27, 121–127. [Google Scholar] [CrossRef]
- Spinelli, G.; Shackel, K.; Gilbert, M. A model exploring whether the coupled effects of plant water supply and demand affect the interpretation of water potentials and irrigation management. Agric. Water Manag. 2017, 192, 271–280. [Google Scholar] [CrossRef] [Green Version]
- Marsal, J.; Gelly, M.; Mata, M.; Arbonés, A.; Rufat, J.; Girona, J. Phenology and drought affect the relationship between daily trunk shrinkage and midday stem water potential of peach trees. J. Hortic. Sci. Biotechnol. 2002, 77, 411–417. [Google Scholar] [CrossRef]
- Cohen, M.; Luque, J.; Alvarez, I. Use of stem diameter variations for detecting the effects of ’pathogens on plant water status. Ann. Des Sci. For. INRA/EDP Sci. 1997, 54, 463–472. [Google Scholar] [CrossRef] [Green Version]
- Ameglio, T.; Cochard, H.; Ewers, W. Stem diameter variations and cold hardness in walnut trees. J. Exp. Bot. 2001, 52, 2135–2142. [Google Scholar] [CrossRef]
- Bugueño, F.; Livellara, N.; Varas, F.; Undurraga, P.; Castro, M.; Salgado, E. Responses of Young Punica granatum plants under four differents water regimes. Cienc. Investig. Agrar. 2016, 43, 49–56. [Google Scholar] [CrossRef] [Green Version]
- Silva-Contreras, C.; Sellés-Von Schouwen, G.; Ferreyra-Espada, R.; Silva-Robledo, H. Variation of water potential and trunk diameter answer as sensitivity to the water availability in table grapes. Chil. J. Agric. Res. 2012, 72, 459–469. [Google Scholar] [CrossRef] [Green Version]
- Livellara, N.; Saavedra, F.; Salgado, E. Plant based indicators for irrigation scheduling in young cherry trees. Agric. Water Manag. 2011, 98, 684–690. [Google Scholar] [CrossRef]
- Badal, E.; Buesa, I.; Guerra, D.; Bonet, L.; Ferrer, P.; Intrigliolo, D. Maximum diurnal trunk shrinkage is a sensitive indicator of plant water, stress in Diospyros kaki (Persimmon) trees. Agric. Water Manag. 2010, 98, 143–147. [Google Scholar] [CrossRef]
- Meng, Z.; Duan, A.; Chen, D.; Bandara Dassanayake, K.; Wang, X.; Liu, Z.; Gao, S. Suitable indicators using stem diameter variation-derived indices to monitor the water status of greenhouse tomato plants. PLoS ONE 2009, 12, e0171423. [Google Scholar] [CrossRef] [Green Version]
- Ortuño, M.; García-Orellana, Y.; Conejero, W.; Ruiz-Sánchez, M.; Mounzer, O.; Alarcón, J.; Torrecillas, A. Relationships between climatic variables and sap flow, stem water potential and maximum daily trunk shrinkage in lemon trees. Plant Soil 2006, 279, 229–242. [Google Scholar] [CrossRef]
- Moreno, F.; Conejero, W.; Martín-Palomo, M.J.; Girón, I.; Torrecillas, A. Maximum daily trunk shrinkage reference values for irrigation scheduling in olive trees. Agric. Water Manag. 2006, 84, 290–294. [Google Scholar] [CrossRef]
- Fereres, E.; Goldhamer, D. Suitability of stem diameter variations and water potential as indicators for irrigation scheduling of almond trees. Hortic. Sci. Biotechnol. 2003, 78, 139–144. [Google Scholar] [CrossRef]
- De la Rosa, J.; Dodd, I.; Domingo, R.; Pérez-Pastor, A. Early morning fluctuations in trunk diameter are highly sensitive to water stress in nectarine trees. Irrig. Sci. 2016, 34, 117–128. [Google Scholar] [CrossRef]
- Ortuño, M.; Conejero, W.; Moreno, F.; Moriana, A.; Intrigliolo, D.; Biel, C.; Mellisho, C.; Pérez-Pastor, A.; Domingo, R.; Ruiz-Sánchez, M.C.; et al. Could trunk diameter sensors be used in woody crops for irrigation scheduling? A review of current knowledge and future perspectives. Agric. Water Manag. 2010, 97, 1–11. [Google Scholar] [CrossRef]
- Zhang, L.; Lemeur, R. Evaluation of daily evapotranspiration estimates from instantaneous measurements. Agric. For. Meteorol. 1995, 74, 139–154. [Google Scholar] [CrossRef]
- Santibáñez, F.; Santibáñez, P.; Caroca, C.; González, P. Atlas Agroclimático de Chile. Estado Actual y Tendencias del Clima; Facultad de Ciencias Agronómicas. Universidad de Chile: Santiago, Chile, 2017; p. 40. [Google Scholar]
- FAO. Evapotranspiración del Cultivo. Guías para la Determinación de los Requerimientos de Agua de los Cultivos; Organización de las Naciones Unidas para la Agricultura y la Alimentación: Rome, Italy, 2006; p. 298. [Google Scholar]
- Intrigliolo, D.; Puerto, H.; Bonet, L.; Alarcón, J.; Nicolas, E.; Bartual, J. Usefulness of trunk diameter variations as continuous water stress indicators of pomegranate (Punica granatum) trees. Agric. Water Manag. 2011, 98, 1462–1468. [Google Scholar] [CrossRef]
- Fulton, A.; Salinas, M.; Montoro, A.; Goldhamer, D. Evaluation of Trunk or Scaffold Shrinkage in Walnut as an Indicator of Orchard Water Status; Walnut Research Reports. Water Management; California Walnut Board: Folsom, CA, USA, 2003; pp. 135–146. [Google Scholar]
| Walnut | Pomegranate | |
|---|---|---|
| Orchard age | 7 years | 1 year |
| Planting density | 7 × 7 m | 5 × 5 m |
| Average plant height | 5 m | 3.5 m |
| Stem type measured | Growing season stem | Growing season stem |
| Tree phenological stage | Fruit ripening | Young vegetative grow |
| Measuring period | Summer, 38 days | Summer 29 days |
| Irrigation method | Micro sprinkler | Drip |
| Understory vegetation | Clean soil with mechanical weed removal | |
| Category | Slope(HDS) | b | m | R2 | |
|---|---|---|---|---|---|
| Walnut | WS1 | MHDS > −4 | 2.5875 | −19.643 | 0.86 |
| Walnut | WS2 | −4 > MHDS > −5.5 | 2.6338 | −30.208 | 0.87 |
| Walnut | WS3 | −5.5 > MHDS > −6.5 | 3.9046 | −36.796 | 0.91 |
| Walnut | WS4 | −6.5 > MHDS | 3.4756 | −43.851 | 0.86 |
| Pomegranate | PS1 | MHDS > −14 | 11.0420 | −85.0200 | 0.65 |
| Pomegranate | PS2 | −14 > MHDS > −19 | 24.3540 | −109.8300 | 0.78 |
| Pomegranate | PS3 | −19 > MHDS > −22.5 | 40.8360 | −130.0000 | 0.69 |
| Pomegranate | PS4 | −22.5 > MHDS | 5.8220 | −156.8500 | 0.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salgado, E.; Livellara, N.; Chaigneau, E.; Varas, F.; Cuneo, I.F. Hourly Relationship between Reference Evapotranspiration and Shoot Shrinkage in Walnut Trees and Pomegranate under Deficit Irrigation. Plants 2022, 11, 31. https://doi.org/10.3390/plants11010031
Salgado E, Livellara N, Chaigneau E, Varas F, Cuneo IF. Hourly Relationship between Reference Evapotranspiration and Shoot Shrinkage in Walnut Trees and Pomegranate under Deficit Irrigation. Plants. 2022; 11(1):31. https://doi.org/10.3390/plants11010031
Chicago/Turabian StyleSalgado, Eduardo, Nieggiorba Livellara, Esteban Chaigneau, Fernando Varas, and Italo F. Cuneo. 2022. "Hourly Relationship between Reference Evapotranspiration and Shoot Shrinkage in Walnut Trees and Pomegranate under Deficit Irrigation" Plants 11, no. 1: 31. https://doi.org/10.3390/plants11010031
APA StyleSalgado, E., Livellara, N., Chaigneau, E., Varas, F., & Cuneo, I. F. (2022). Hourly Relationship between Reference Evapotranspiration and Shoot Shrinkage in Walnut Trees and Pomegranate under Deficit Irrigation. Plants, 11(1), 31. https://doi.org/10.3390/plants11010031






