Monitoring of Nitrogen Concentration in Soybean Leaves at Multiple Spatial Vertical Scales Based on Spectral Parameters
Abstract
:1. Introduction
2. Materials and Methods
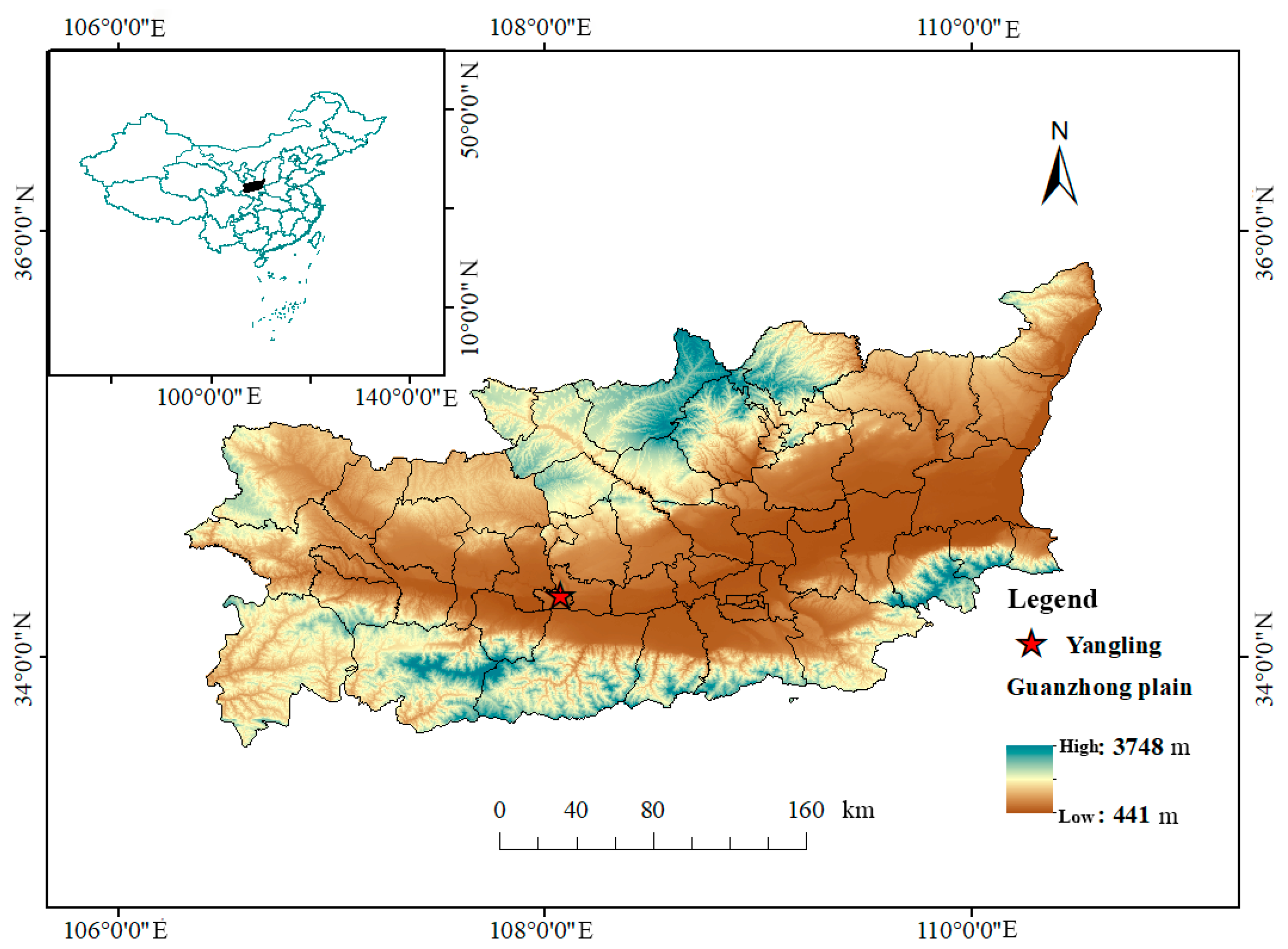
2.1. Research Area and Test Design
2.2. Data Collection
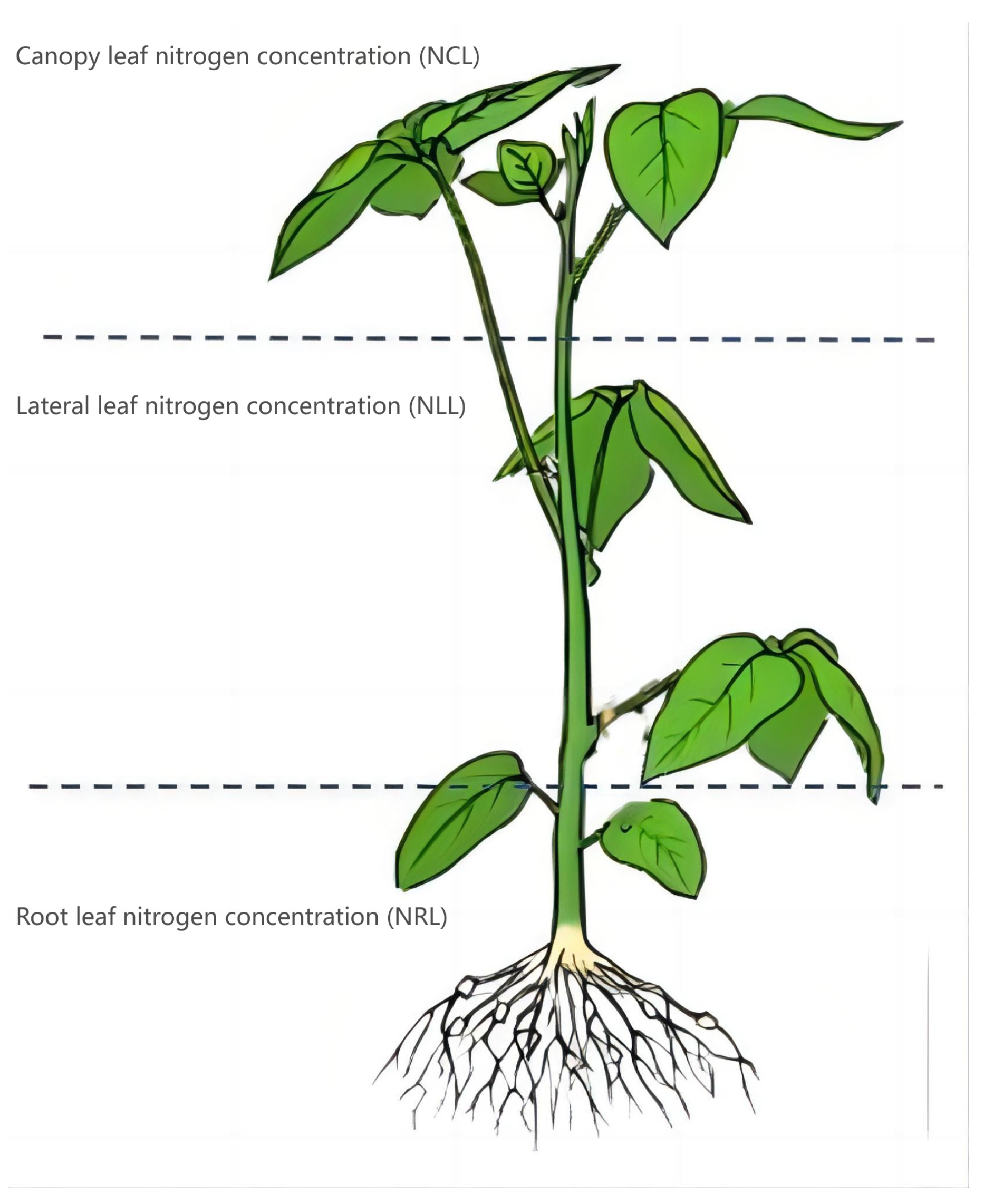
2.2.1. Measurement of Leaf Nitrogen Concentration
2.2.2. Acquisition of Hyperspectral Data
2.3. Techniques for Data Analysis
2.4. Techniques for Data Analysis
3. Results
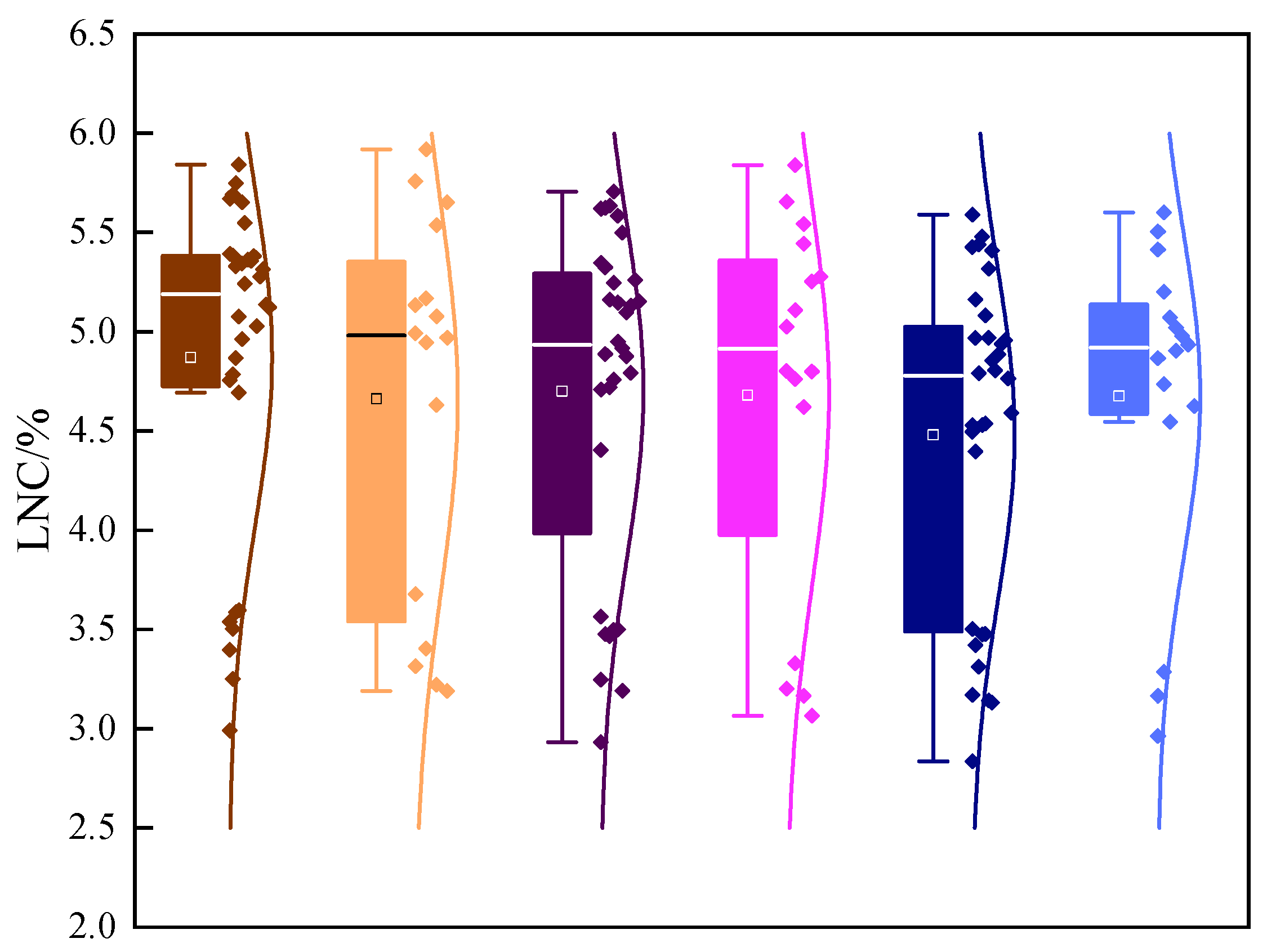
3.1. Comparison of LNCs in Different Leaf Layers of Soybean and Division of Sample Set
3.2. Correlation Analysis between Spectral Parameters and LNCs of Soybean Leaf Layers
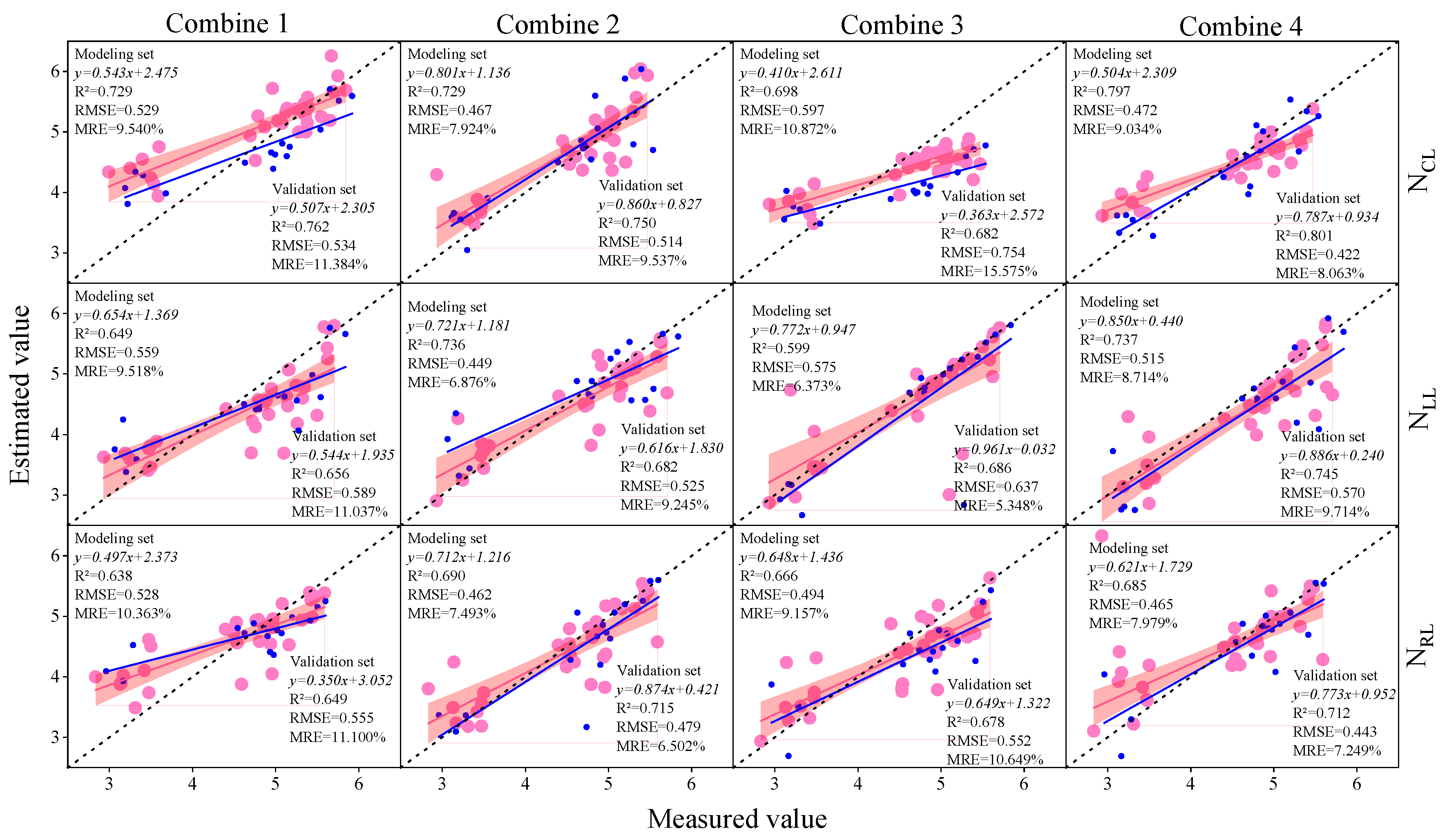
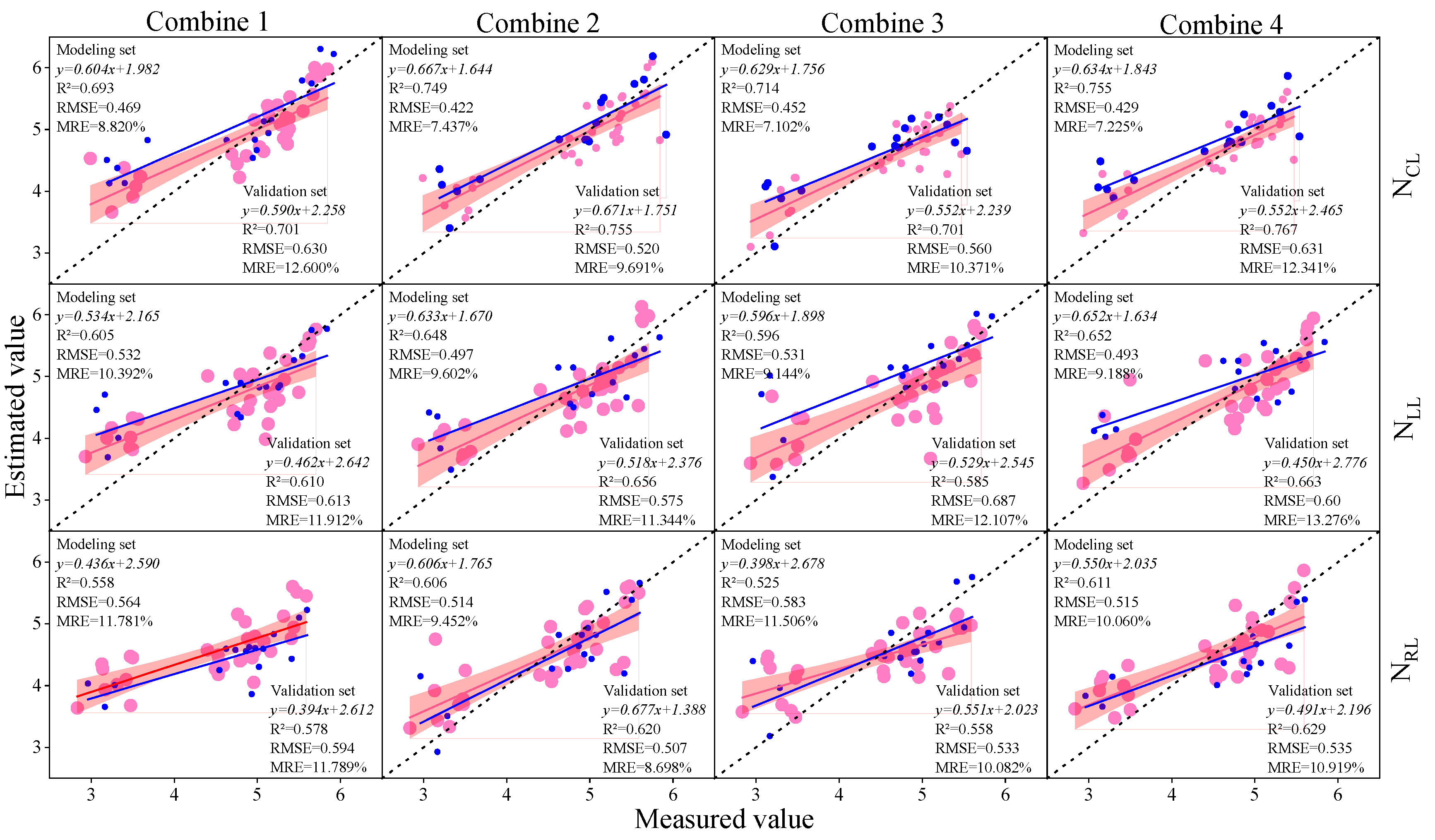
3.3. Construction of Soybean LNC Estimation Model at a Multi-Spatial Vertical Scale
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buezo, J.; Sanz-Saez, Á.; Moran, J.F.; Soba, D.; Aranjuelo, I.; Esteban, R. Drought tolerance response of high-yielding soybean varieties to mild drought: Physiological and photochemical adjustments. Physiol. Plant 2019, 166, 88–104. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Zhang, Z.; Guo, E.; Fu, Z.; Gong, J.; Yang, X. Historical and projected impacts of climate change and technology on soybean yield in China. Agric. Syst. 2022, 203, 103522. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, X.; Shan, J.; Xian, J.; Cao, D.; Luo, Y.; Yao, R.; Zhang, X. Nitrogen mitigates salt stress and promotes wheat growth in the Yellow River Delta, China. Water 2022, 14, 3819. [Google Scholar] [CrossRef]
- Sharma, S.K.; Sharma, P.K.; Mandeewal, R.L.; Sharma, V.; Chaudhary, R.; Pandey, R.; Gupta, S. Effect of foliar application of nano-urea under different nitrogen levels on growth and nutrient content of pearl millet (Pennisetum glaucum L.). Int. J. Plant Sci. 2022, 34, 149–155. [Google Scholar] [CrossRef]
- Olveira, A.L.; Rozas, H.S.; CastroFranco, M.; Carciochi, W.; Nieto, L.; Balzarini, M.; Ciampitti, I.; Reussi Calvo, N. Monitoring corn nitrogen concentration from radar (C-SAR), optical, and sensor satellite data fusion. Remote Sens. 2023, 15, 824. [Google Scholar] [CrossRef]
- Li, H.; Li, M.-R.; Guo, Y.-L.; Wei, Y.; Zhang, H.; Song, X.; Feng, W.; Guo, T. Angular effect of algorithms for monitoring leaf nitrogen concentration of wheat using multi-angle remote sensing data. Comput. Electron. Agric. 2022, 195, 106815. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; An, J.; Shi, H.; Tang, Z.; Zhao, X.; Guo, J.; Jin, L.; Xiang, Y.; Li, Z. Effects of Nitrogen Supply on Dry Matter Accumulation, Water-Nitrogen Use Efficiency and Grain Yield of Soybean (Glycine max L.) under Different Mulching Methods. Agronomy 2023, 13, 606. [Google Scholar] [CrossRef]
- Wang, X.; Xiang, Y.; Guo, J.; Tang, Z.; Zhao, S.; Wang, H.; Li, Z.; Zhang, F. Coupling effect analysis of drip irrigation and mixed slow-release nitrogen fertilizer on yield and physiological characteristics of winter wheat in Guanzhong area. Field Crop Res. 2023, 302, 109103. [Google Scholar] [CrossRef]
- Gao, W.; Shou, N.; Jiang, C.; Ma, R.; Yang, X. Optimizing N Application for Forage Sorghum to Maximize Yield, Quality, and N Use Efficiency While Reducing Environmental Costs. Agronomy 2022, 12, 2969. [Google Scholar] [CrossRef]
- Koppensteiner, L.J.; Kaul, H.P.; Piepho, H.P.; Barta, N.; Euteneuer, P.; Bernas, J.; Klimek-Kopyra, A.; Gronauer, A.; Neugschwandtner, R.W. Yield and yield components of facultative wheat are affected by sowing time, nitrogen fertilization and environment. Eur. J. Agron. 2022, 140, 126591. [Google Scholar] [CrossRef]
- Sun, J.; Shi, S.; Gong, W.; Yang, J.; Du, L.; Song, S.; Chen, B.; Zhang, Z. Evaluation of hyperspectral LiDAR for monitoring rice leaf nitrogen by comparison with multispectral LiDAR and passive spectrometer. Sci. Rep. 2017, 7, 40362. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Xu, D.; He, L.; Feng, W.; Wang, Y.; Wang, Z.; Coburn, C.A.; Guo, T. Using multi-angle hyperspectral data to monitor canopy leaf nitrogen content of wheat. Precis. Agric. 2016, 17, 721–736. [Google Scholar] [CrossRef]
- Cheng, M.; He, J.; Wang, H.; Fan, J.; Xiang, Y.; Liu, X.; Liao, Z.; Tang, Z.; Abdelghany, A.E.; Zhang, F. Establishing critical nitrogen dilution curves based on leaf area index and aboveground biomass for greenhouse cherry tomato: A Bayesian analysis. Eur. J. Agron. 2022, 141, 126615. [Google Scholar] [CrossRef]
- Guo, J.; Fan, J.; Xiang, Y.; Zhang, F.; Zheng, J.; Yan, S.; Yan, F.; Hou, X.; Li, Y.; Yang, L. Effects of nitrogen type on rainfed maize nutrient uptake and grain yield. Agron. J. 2021, 113, 5454–5471. [Google Scholar] [CrossRef]
- Li, D.; Chen, J.M.; Yan, Y.; Zheng, H.; Yao, X.; Zhu, Y.; Cao, W.; Cheng, T. Estimating leaf nitrogen content by coupling a nitrogen allocation model with canopy reflectance. Remote Sens. Environ. 2022, 283, 113314. [Google Scholar] [CrossRef]
- Schlemmer, M.; Gitelson, A.; Schepers, J.; Ferguson, R.; Peng, Y.; Shanahan, J.; Rundquist, D. Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels. Int. J. Appl. Earth Obs. 2013, 25, 47–54. [Google Scholar] [CrossRef]
- Moreno-Martínez, Á.; Camps-Valls, G.; Kattge, J.; Robinson, N.; Reichstein, M.; van Bodegom, P.; Kramer, K.; Cornelissen, J.H.C.; Reich, P.; Bahn, M.; et al. A methodology to derive global maps of leaf traits using remote sensing and climate data. Remote Sens. Environ. 2018, 218, 69–88. [Google Scholar] [CrossRef]
- Wang, Y.; Suarez, L.; Poblete, T.; Gonzalez-Dugo, V.; Ryu, D.; Zarco-Tejada, P.J. Evaluating the role of solar-induced fluorescence (SIF) and plant physiological traits for leaf nitrogen assessment in almond using airborne hyperspectral imagery. Remote Sens. Environ. 2022, 279, 113141. [Google Scholar] [CrossRef]
- Wan, L.; Zhou, W.; He, Y.; Wanger, T.C.; Cen, H. Combining transfer learning and hyperspectral reflectance analysis to assess leaf nitrogen concentration across different plant species datasets. Remote Sens. Environ. 2022, 269, 112826. [Google Scholar] [CrossRef]
- Raj, R.; Walker, J.P.; Pingale, R.; Banoth, B.N.; Jagarlapudi, A. Leaf nitrogen content estimation using top-of-canopy airborne hyperspectral data. Int. J. Appl. Earth Obs. 2021, 104, 102584. [Google Scholar] [CrossRef]
- Leo, S.; De Antoni Migliorati, M.; Nguyen, T.H.; Grace, P.R. Combining remote sensing-derived management zones and an auto-calibrated crop simulation model to determine optimal nitrogen fertilizer rates. Agric. Syst. 2023, 205, 103559. [Google Scholar] [CrossRef]
- Wang, D.; Li, R.; Liu, T.; Liu, S.; Sun, C.; Guo, W. Combining vegetation, color, and texture indices with hyperspectral parameters using machine-learning methods to estimate nitrogen concentration in rice stems and leaves. Field Crop Res. 2023, 304, 109175. [Google Scholar] [CrossRef]
- Fan, L.; Zhao, J.; Xu, X.; Liang, D.; Yang, G.; Feng, H.; Yang, H.; Wang, Y.; Chen, G.; Wei, P. Hyperspectral-Based Estimation of Leaf Nitrogen Content in Corn Using Optimal Selection of Multiple Spectral Variables. Sensors 2019, 19, 2898. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Wang, J.; Chen, L.; Fu, Y.; Zhu, H.; Feng, H.; Xu, X.; Li, Z. An entirely new approach based on remote sensing data to calculate the nitrogen nutrition index of winter wheat. J. Integr. Agric. 2021, 20, 2535–2551. [Google Scholar] [CrossRef]
- Shu, M.; Zhu, J.; Yang, X.; Gu, X.; Li, B.; Ma, Y. A spectral decomposition method for estimating the leaf nitrogen status of maize by UAV-based hyperspectral imaging. Comput. Electron. Agric. 2023, 212, 108100. [Google Scholar] [CrossRef]
- Tang, Z.; Guo, J.; Xiang, Y.; Lu, X.; Wang, Q.; Wang, H.; Cheng, M.; Wang, H.; Wang, X.; An, J.; et al. Estimation of Leaf Area Index and Above-Ground Biomass of Winter Wheat Based on Optimal Spectral Index. Agronomy 2022, 12, 1729. [Google Scholar] [CrossRef]
- Shi, H.; Guo, J.; An, J.; Tang, Z.; Wang, X.; Li, W.; Zhao, X.; Jin, L.; Xiang, Y.; Li, Z.; et al. Estimation of Chlorophyll Content in Soybean Crop at Different Growth Stages Based on Optimal Spectral Index. Agronomy 2023, 13, 663. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Pu, Y.; Zhang, Y.; Tang, Z.; Fu, J.; Xu, W.; Xiang, Y.; Zhang, F. Estimation of the Leaf Area Index of Winter Rapeseed Based on Hyperspectral and Machine Learning. Sustainability 2023, 15, 12930. [Google Scholar] [CrossRef]
- Ji, J.; Li, N.; Cui, H.; Li, Y.; Zhao, X.; Zhang, H.; Ma, H. Study on Monitoring SPAD Values for Multispatial Spatial Vertical Scales of Summer Maize Based on UAV Multispectral Remote Sensing. Agriculture 2023, 13, 1004. [Google Scholar] [CrossRef]
- GB20287-2006; Microbial Inoculants in Agriculture. Ministry of Agriculture: Beijing, China, 2006.
- Zhang, C.; Cai, H.; Li, Z. Estimation of Fraction of Absorbed Photosynthetically Active Radiation for Winter Wheat Based on Hyperspectral Characteristic Parameters. Spectrosc. Spectr. Anal. 2015, 35, 2644–2649. [Google Scholar]
- Zheng, J.; Li, F.; Du, X. Using Red Edge Position Shift to Monitor Grassland Grazing Intensity in Inner Mongolia. J. Indian Soc. Remote 2018, 46, 81–88. [Google Scholar] [CrossRef]
- Blackburn, G.A. Hyperspectral Remote Sensing of Plant Pigments. J. Exp. Bot. 2007, 58, 855–867. [Google Scholar] [CrossRef] [PubMed]
- Horler, D.N.H.; Barber, J.; Darch, J.P.; Ferns, D.C.; Barringer, A.R. Approaches to Detection of Geochemical Stress in Vegetation. Adv. Space Res. 1983, 3, 175–179. [Google Scholar] [CrossRef]
- Song, G.; Wang, Q. Coupling Effective Variable Selection with Machine Learning Techniques for Better Estimating Leaf Photosynthetic Capacity in a Tree Species (Fagus crenata Blume) from Hyperspectral Reflectance. Agric. For. Meteorol. 2023, 338, 109528. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Barnes, E.M.; Clarke, T.; Richards, S.E.; Colaizzi, P.D.; Haberland, J.; Kostrzewski, M.; Waller, P.M.; Choi, C.Y.; Riley, E.; Thompson, T.L.; et al. Coincident Detection of Crop Water Stress, Nitrogen Status and Canopy Density Using Ground-Based Multispectral Data. 2000. Available online: https://api.semanticscholar.org/CorpusID:128773162 (accessed on 19 July 2000).
- Ashburn, P. The vegetative index number and crop identification NASA. In Proceedings of the Technical description of the Large Area Crop Inventory Experiment, Houston, TX, USA, 23–26 October 1978; Volumes 1 and 2. [Google Scholar]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y.U. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plantarum. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Buschmann, C.; Nagel, E. In vivo spectroscopy and internal optics of leaves as basis for remote sensing of vegetation. Int. J. Remote Sens. 1993, 14, 711–722. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Shibayama, M.; Salli, A.; Häme, T.; Iso-Iivari, L.; Heino, S.; Alanen, M.; Morinaga, S.; Inoue, Y.; Akiyama, T. Detecting Phenophases of Subarctic Shrub Canopies by Using Automated Reflectance Measurements. Remote Sens. Environ. 1999, 67, 160–180. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A Review of Vegetation Indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. Isprs J. Photogramm. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Hong, Y.; Guo, L.; Chen, S.; Linderman, M.; Mouazen, A.M.; Yu, L.; Chen, Y.; Liu, Y.; Liu, Y.; Cheng, H.; et al. Exploring the potential of airborne hyperspectral image for estimating topsoil organic carbon: Effects of fractional-order derivative and optimal band combination algorithm. Geoderma 2020, 365, 114228. [Google Scholar] [CrossRef]
- Ren, K.; Dong, Y.; Huang, W.; Guo, A.; Jing, X. Monitoring of winter wheat stripe rust by collaborating canopy SIF with wavelet energy coefficients. Comput. Electron. Agric. 2023, 215, 108366. [Google Scholar] [CrossRef]
- Deng, J.; Zhang, X.; Yang, Z.; Zhou, C.; Wang, R.; Zhang, K.; Lv, X.; Yang, L.; Wang, Z.; Li, P.; et al. Pixel-level regression for UAV hyperspectral images: Deep learning-based quantitative inverse of wheat stripe rust disease index. Comput. Electron. Agric. 2023, 215, 108434. [Google Scholar] [CrossRef]
- Department of Plant Nutrition, China Agricultural University; Li, W.; Li, C. Comparison of N uptake and internal use efficiency in two tobacco varieties. Crop J. 2015, 3, 80–86. [Google Scholar] [CrossRef]
- Monadjemi, S.; El Roz, M.; Richard, C.; Ter Halle, A. Photoreduction of chlorothalonil fungicide on plant leaf models. Environ. Sci. Technol. 2011, 45, 9582–9589. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.; Ma, Y.; Xing, W.; Wu, Y.; Peng, S.; Mao, L.; Miao, Z. Inorganic Nitrogen-Containing Aerosol Deposition Caused “Excessive Photosynthesis” of Herbs, Resulting in Increased Nitrogen Demand. Plants 2022, 11, 2225. [Google Scholar] [CrossRef]
- Raza, M.A.; Feng, L.Y.; Khalid, M.H.B.; Iqbal, N.; Meraj, T.A.; Hassan, M.J.; Ahmed, S.; Chen, Y.K.; Feng, Y.; Yang, W. Optimum leaf excision increases the biomass accumulation and seed yield of maize plants under different planting patterns. Ann. Appl. Biol. 2019, 175, 54–68. [Google Scholar] [CrossRef]
- Su, Y.; Wang, Y.; Liu, G.; Zhang, Z.; Li, X.; Chen, G.; Guo, Z.; Gao, Q. Nitrogen (N) supplementation, slow release, and retention strategy improves N use efficiency via the synergistic effect of biochar, nitrogen-fixing bacteria, and dicyandiamide. Sci. Total Environ. 2023, 908, 168518. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, H.; Lu, X.; Wan, H.; Zhang, Y.; Zhang, J.; Jin, Z. Inversion of Leaf Water Content of Cinnamomum camphora Based on Preferred Spectral Index and Machine Learning Algorithm. Forests 2023, 14, 2285. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, X.; An, J.; Tang, Z.; Li, W.; Shi, H. Estimation of Leaf Area Index of Soybean Based on Fractional OrderDifferentiation and Optimal Spectral Index. Trans. Chin. Soc. Agric. Mach. 2023, 54, 329–342. [Google Scholar]
- Tang, Z.; Xiang, Y.; Wang, X.; An, J.; Guo, J.; Wang, H.; Li, Z.; Zhang, F. Comparison of SPAD Value and LAI Spectral Estimation of Soybean Leaves Based on Different Analysis Models. Soybean Sci. 2023, 42, 55–63. [Google Scholar]
- Wang, Q.; Lu, X.; Zhang, H.; Yang, B.; Gong, R.; Zhang, J.; Jin, Z.; Xie, R.; Xia, J.; Zhao, J. Comparison of Machine Learning Methods for Estimating Leaf Area Index and Aboveground Biomass of Cinnamomum camphora Based on UAV Multispectral Remote Sensing Data. Forests 2023, 14, 1688. [Google Scholar] [CrossRef]


| Selected Spectral Parameter | Calculation Formula | Reference |
|---|---|---|
| Maximum first-order derivative value in the blue edge (490–530 nm) Db | – | [31] |
| Maximum first-order derivative value in the yellow edge (462–642 nm) Dy | – | [31] |
| Maximum first-order derivative value in the red edge (670–760 nm) Dr | – | [32] |
| Maximum reflectivity of the green peak (510–560 nm) Rg | – | [33] |
| Minimum reflectivity of the red valley (650–690 nm) Rr | – | [33] |
| Blue edge (490–530 nm) area Sb | Sum of first-order derivatives within the blue edge wavelength range | [31] |
| Yellow edge (462–642 nm) area Sy | Sum of first-order derivatives within the yellow edge wavelength range | [31] |
| Red edge (670–760 nm) area Sr | Sum of first-order derivatives within the red edge wavelength range | [32] |
| Normalized red-blue amplitude difference (NDDr.b) | (Dr − Db)/(Dr + Db) | [34] |
| Normalized first-order red-blue amplitude difference (NDSDr.b) | (SDr − SDb)/(SDr + SDb) | [34] |
| Infrared percentage vegetation index (IPVI) | R800 × (R800 + R670) | [35] |
| Optimized soil-adjusted vegetation index (OSAVI) | [36] | |
| Normalized difference nitrogen index (NDNI) | [37] | |
| Ashburn vegetation index (AVI) | [38] | |
| Difference 678/500 (D678/500) | [39] | |
| Difference 800/550 (D800/550) | [40] | |
| Difference 800/680 (D800/680) | [41] | |
| Difference 833/658 (D833/658) | [42] | |
| Differenced vegetation index MSS (DVIMSS) | [43] | |
| Double difference index (DD) | [44] | |
| Ratio index (RI) | [27] | |
| Difference index (DI) | [27] | |
| Soil-adjusted vegetation index (SAVI) | [28] | |
| Normalized difference vegetation index (NDVI) | [28] | |
| Triangular vegetation index (TVI) | [28] | |
| Modified simple ratio (mSR) | [28] | |
| Modified normalized difference index (mNDI) | [28] | |
| Product index (PI) | [45] | |
| Sum index (SI) | [45] | |
| Reciprocal difference index (VI6) | [45] |
| 2021 | 2022 | |||||
|---|---|---|---|---|---|---|
| NCL | NLL | NRL | NCL | NLL | NRL | |
| RN3 | 5.81 a | 5.79 a | 5.59 a | 5.70 a | 5.62 a | 5.47 a |
| RN2 | 5.55 a | 5.38 a | 5.07 a | 5.33 b | 5.25 b | 4.98 bc |
| RN1 | 5.16 ab | 5.07 ab | 5.01 a | 4.97 d | 4.82 c | 4.59 d |
| RN0 | 4.09 bc | 3.95 bc | 3.82 b | 3.48 f | 3.41 e | 3.37 e |
| N3 | 4.96 abc | 4.88 abc | 4.66 ab | 5.44 b | 5.34 b | 5.19 b |
| N2 | 5.35 a | 5.19 a | 5.03 a | 5.13 c | 5.01 c | 4.88 c |
| N1 | 4.98 abc | 4.87 abc | 4.73 ab | 4.69 e | 4.58 d | 4.49 d |
| N0 | 3.84 c | 3.72 c | 3.64 b | 3.13 g | 3.06 f | 2.98 f |
| Significance level | ||||||
| N | * | ** | ** | ** | ** | ** |
| R | ns | * | ns | ** | * | ** |
| N*R | ns | * | ns | * | ns | * |
| Selected Spectral Parameter | Correlation Coefficient | ||
|---|---|---|---|
| NCL | NLL | NRL | |
| Maximum first-order derivative value in the blue edge (490–530 nm) Db | 0.601 * | 0.582 * | 0.514 * |
| Maximum first-order derivative value in the yellow edge (462–642 nm) Dy | 0.601 * | 0.582 * | 0.514 * |
| Maximum first-order derivative value in the red edge (670–760 nm) Dr | 0.660 * | 0.586 * | 0.526 * |
| Maximum reflectivity of the green peak (510–560 nm) Rg | 0.495 * | 0.501 * | 0.460 * |
| Minimum reflectivity of the red valley (650–690 nm) Rr | 0.208 | 0.259 | 0.258 |
| Blue edge (490–530 nm) area Sb | 0.483 * | 0.511 * | 0.476 * |
| Yellow edge (462–642 nm) area Sy | 0.176 | 0.255 | 0.260 |
| Red edge (670–760 nm) area Sr | 0.669 * | 0.604 * | 0.543 * |
| NDDr.b | 0.069 | 0.013 | 0.007 |
| NDSDr.b | 0.114 | 0.015 | 0.0004 |
| IPVI | 0.667 * | 0.630 * | 0.582 * |
| Optimized soil-adjusted vegetation index (OSAVI) | 0.512 * | 0.419 * | 0.369 * |
| Normalized difference nitrogen index (NDNI) | 0.550 * | 0.480 * | 0.441 * |
| Ashburn vegetation index (AVI) | 0.670 * | 0.631 * | 0.574 * |
| Difference 678/500 (D678/500) | 0.580 * | 0.510 * | 0.439 * |
| Difference 800/550 (D800/550) | 0.664 * | 0.603 * | 0.547 * |
| Difference 800/680 (D800/680) | 0.670 * | 0.605 * | 0.544 * |
| Difference 833/658 (D833/658) | 0.671 * | 0.609 * | 0.547 * |
| Differenced vegetation index MSS (DVIMSS) | 0.669 * | 0.631 * | 0.574 * |
| Double difference index (DDI) | 0.449 * | 0.363 * | 0.362 * |
| Selected Spectral Parameter | NCL | NLL | NRL | |||
|---|---|---|---|---|---|---|
| Correlation Coefficient | Wavelength Position (i,j) | Correlation Coefficient | Wavelength Position (i,j) | Correlation Coefficient | Wavelength Position (i,j) | |
| RI | 0.664 * | (840,843) | 0.567 * | (1043,1046) | 0.574 * | (839,844) |
| DI | 0.701 * | (1625,1637) | 0.684 * | (1221,1267) | 0.701 * | (1612,1611) |
| SAVI | 0.675 * | (413,934) | 0.662 * | (1358,1393) | 0.638 * | (1611,1612) |
| NDVI | 0.664 * | (840,843) | 0.599 * | (1043,1045) | 0.574 * | (844,839) |
| TVI | 0.689 * | (694,616) | 0.661 * | (1353,680) | 0.594 * | (1129,487) |
| mSR | 0.671 * | (840,843) | 0.597 * | (1043,1045) | 0.584 * | (844,839) |
| mNDI | 0.670 * | (840,841) | 0.597 * | (1043,1045) | 0.584 * | (844,839) |
| PI | 0.676 * | (856,854) | 0.642 * | (753,1356) | 0.593 * | (1046,1047) |
| SI | 0.686 * | (783,1368) | 0.663 * | (840,1368) | 0.579 * | (759,1129) |
| VI6 | 0.732 * | (841,842) | 0.658 * | (972,981) | 0.639 * | (840,843) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Li, Z.; Wang, Z.; Liu, Y.; Zhu, Z.; Zhao, Y.; Xie, W.; Cui, S.; Chen, G.; Yang, W.; et al. Monitoring of Nitrogen Concentration in Soybean Leaves at Multiple Spatial Vertical Scales Based on Spectral Parameters. Plants 2024, 13, 140. https://doi.org/10.3390/plants13010140
Sun T, Li Z, Wang Z, Liu Y, Zhu Z, Zhao Y, Xie W, Cui S, Chen G, Yang W, et al. Monitoring of Nitrogen Concentration in Soybean Leaves at Multiple Spatial Vertical Scales Based on Spectral Parameters. Plants. 2024; 13(1):140. https://doi.org/10.3390/plants13010140
Chicago/Turabian StyleSun, Tao, Zhijun Li, Zhangkai Wang, Yuchen Liu, Zhiheng Zhu, Yizheng Zhao, Weihao Xie, Shihao Cui, Guofu Chen, Wanli Yang, and et al. 2024. "Monitoring of Nitrogen Concentration in Soybean Leaves at Multiple Spatial Vertical Scales Based on Spectral Parameters" Plants 13, no. 1: 140. https://doi.org/10.3390/plants13010140
APA StyleSun, T., Li, Z., Wang, Z., Liu, Y., Zhu, Z., Zhao, Y., Xie, W., Cui, S., Chen, G., Yang, W., Zhang, Z., & Zhang, F. (2024). Monitoring of Nitrogen Concentration in Soybean Leaves at Multiple Spatial Vertical Scales Based on Spectral Parameters. Plants, 13(1), 140. https://doi.org/10.3390/plants13010140






