Parameterization of Four Models to Estimate Crop Evapotranspiration in a Solar Greenhouse
Abstract
:1. Introduction
2. Parameterization of Four Models
2.1. Penman–Monteith Model
2.2. Priestley–Taylor Model
2.3. Crop Coefficient Method
2.4. Shuttleworth–Wallace Model
2.5. Evaluation of Model Performance
3. Materials and Methods
3.1. Experiment Site and Description
3.2. Measurements
4. Results
4.1. Variations of Daytime Meteorological Factors, Leaf Area Index, and Soil Moisture in Five Study Years
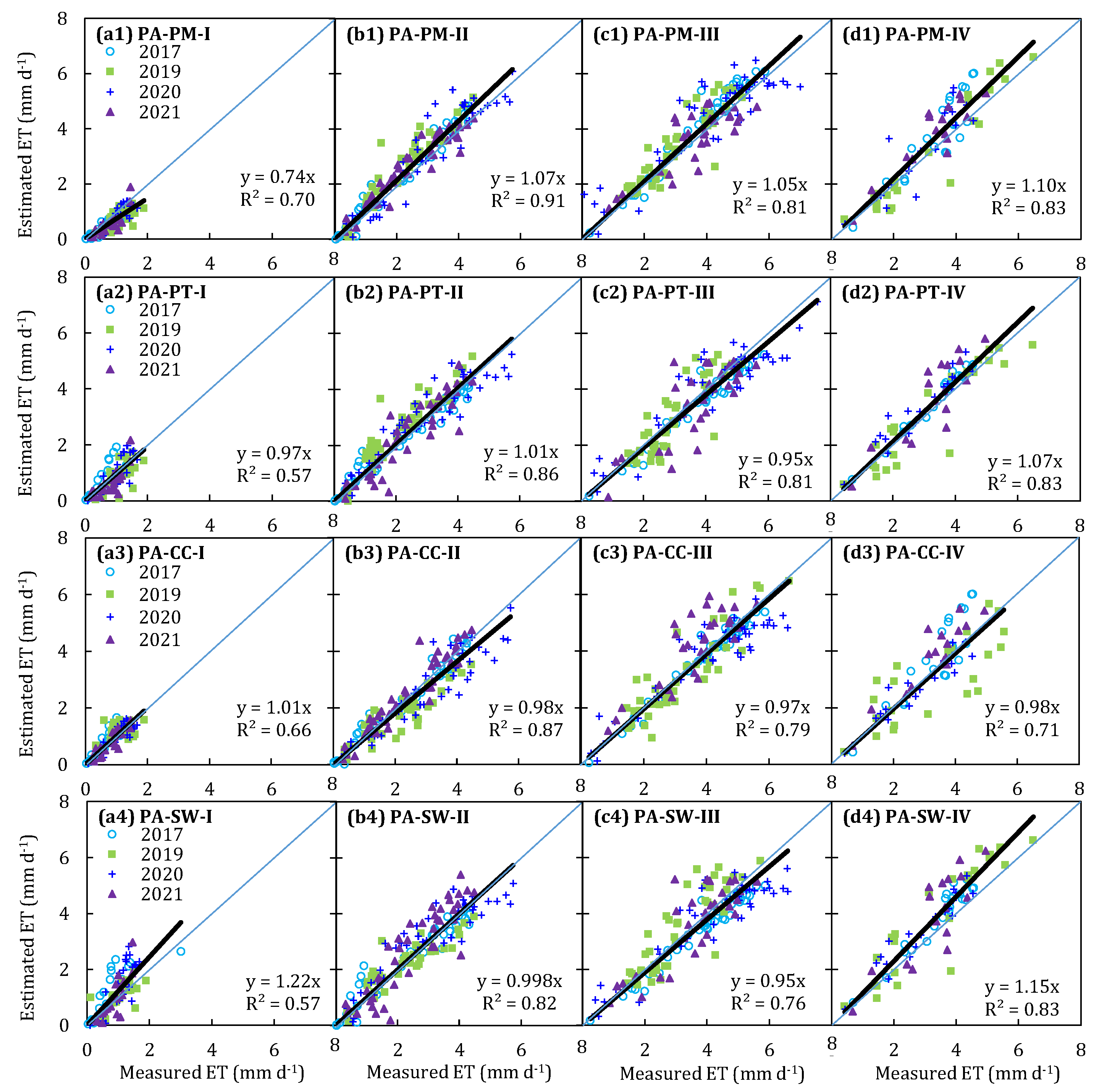
4.2. Performance of Parameterized Models for Simulating Daily ET at Four Growth Stages
4.3. Performance of Parameterized Models for Simulating Daily ET over the Whole Growth Stage
5. Discussion
5.1. Evaluation of Four Parameterized Models to Compute ET in Greenhouse
5.2. Advantages and Disadvantages of Four Parameterized Models
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of symbols | |
| A | Total available energy (W/m2) |
| As | Available energy to the soil surface (W/m2) |
| C | Extinction coefficient of light attenuation |
| Cs | Soil surface resistance coefficient |
| Cc | Canopy surface resistance coefficient |
| Cp | Specific heat of dry air at a constant pressure (J/(kg·K)) |
| ET | Evapotranspiration (mm) |
| ETo | Reference evapotranspiration (mm) |
| es | Saturation vapor pressure (kPa) |
| ea | Actual vapor pressure (kPa) |
| G | Surface soil heat flux (W/m2) |
| LAI | Leaf area index |
| Kc | Crop efficient |
| Rn | Net radiation (W/m2) |
| Rns | Net radiation reaching the soil surface (W/m2) |
| ra | Aerodynamic resistance (s/m) |
| rs | Surface resistance (s/m) |
| raa | Aerodynamic resistances from reference level to canopy source height (s/m) |
| rac | Boundary layer resistance of the crop in the canopy (s/m) |
| ras | Aerodynamic resistances from canopy source height to the soil surface (s/m) |
| rsc | Canopy surface resistance (s/m) |
| rss | Soil surface resistance (s/m) |
| VPD | Vapor pressure deficit (s/m) |
| αPT | Priestley–Taylor coefficient |
| ρ | Air density (kg/m3) |
| γ | Psychometric constant (kPa/K) |
| Δ | Slope of the saturation water vapor pressure versus temperature curve (kPa/°C) |
References
- Zhang, Q.; Zhang, X.Y.; Yang, Z.Q.; Huang, Q.Q.; Qiu, R.J. Characteristics of plastic greenhouse high-temperature and high-humidity events and their impacts on facility tomatoes growth. Front. Earth Sci. 2022, 10, 848924. [Google Scholar] [CrossRef]
- Wang, M.Y.; Li, J.P.; Li, J.J. Historical evolution, scale distribution and regional layout of facility vegetables in China. China Cucurbits Veg. 2020, 33, 86–89. [Google Scholar]
- Incrocci, L.; Thompson, R.B.; Fernandez-Fernandez, M.D.; Pascale, S.D.; Pardossi, A.; Stanghellini, C.; Rouphael, Y.; Gallardo, M. Irrigation management of European greenhouse vegetable crops. Agric. Water Manag. 2020, 242, 106393. [Google Scholar] [CrossRef]
- Nyolei, D.; Diels, J.; Mbilinyi, B.; Mbungu, W.; Griensven, A.V. Evapotranspiration simulation from a sparsely vegetated agricultural field in a semi-arid agro-ecosystem using Penman-Monteith models. Agric. For. Meteorol. 2021, 303, 108370. [Google Scholar] [CrossRef]
- Gong, X.W.; Qiu, R.J.; Zhang, B.Z.; Wang, S.S.; Ge, J.K.; Gao, S.K.; Yang, Z.Q. Energy budget for tomato plants grown in a greenhouse in northern China. Agric. Water Manag. 2021, 255, 107039. [Google Scholar] [CrossRef]
- Gong, X.W.; Qiu, R.J.; Sun, J.S.; Ge, J.K.; Li, Y.B.; Wang, S.S. Evapotranspiration and crop coefficient of tomato grown in a solar greenhouse under full and deficit irrigation. Agric. Water Manag. 2020, 235, 106154. [Google Scholar] [CrossRef]
- Katsoulas, N.; Stanghellini, C. Modelling crop transpiration in greenhouses: Different models for different applications. Agronomy 2019, 9, 392. [Google Scholar] [CrossRef]
- Kang, S.Z.; Su, X.L.; Tong, L.; Zhang, J.H.; Zhang, L.; Davies, W.J. A warning from an ancient oasis: Intensive human activities are leading to potential ecological and social catastrophe. Int. J. Sustain. Dev. World Ecol. 2008, 15, 440–447. [Google Scholar] [CrossRef] [PubMed]
- Moorhead, J.E.; Marek, G.W.; Colaizzi, P.D.; Gowda, P.H.; Evett, S.R.; Brauer, D.K.; Marek, T.H.; Porter, D.O. Evaluation of sensible heat flux and evapotranspiration estimates using a surface layer scintillometer and a large weighing lysimeter. Sensors 2017, 17, 2350. [Google Scholar] [CrossRef] [PubMed]
- Evett, S.R.; Schwartz, R.C.; Casanova, J.J.; Heng, L.K. Soil water sensing for water balance, ET, and WUE. Agric. Water Manag. 2012, 104, 1–9. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. In Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Qiu, R.J.; Du, T.S.; Kang, S.Z.; Chen, R.Q.; Wu, L.S. Assessing the SIMDualKc model for estimating evapotranspiration of hot pepper grown in a solar greenhouse in Northwest China. Agric. Syst. 2015, 138, 1–9. [Google Scholar] [CrossRef]
- Gong, X.W.; Liu, H.; Sun, J.S.; Gao, Y.; Zhang, H. Comparison of Shuttleworth-Wallace model and dual crop coefficient method for estimating evapotranspiration of tomato cultivated in a solar greenhouse. Agric. Water Manag. 2019, 217, 141–153. [Google Scholar] [CrossRef]
- Yan, H.F.; Zhang, C.; Gerrits, M.C.; Acquaha, S.J.; Zhang, H.N.; Wu, H.M.; Zhao, B.S.; Huang, S.; Fu, H.W. Parametrization of aerodynamic and canopy resistances for modeling evapotranspiration of greenhouse cucumber. Agric. For. Meteorol. 2018, 262, 370–378. [Google Scholar] [CrossRef]
- Modaberi, H.; Assari, M.; Ansari, S. Evaluation of common methods of reference evapotranspiration prediction in greenhouse by lysimeteric data. Agric. Sci. Dev. 2014, 3, 151–156. [Google Scholar]
- Li, B.; Shi, B.J.; Yao, Z.Z.; Shukla, M.K.; Du, T.S. Energy partitioning and microclimate of solar greenhouse under drip and furrow irrigation systems. Agric. Water Manag. 2020, 234, 106096. [Google Scholar] [CrossRef]
- Gong, X.W.; Liu, H.; Sun, J.S.; Gao, Y.; Zhang, X.X.; Jha, S.K.; Zhang, H.; Ma, X.J.; Wang, W.N. A proposed surface resistance model for the Penman-Monteith formula to estimate evapotranspiration in a solar greenhouse. J. Arid Land 2017, 9, 530–546. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.B.; Du, T.S.; Gong, D.Z.; Hu, X.T.; Zhang, L. Response of sap flux and evapotranspiration to deficit irrigation of greenhouse pear-jujube trees in semi-arid northwest China. Agric. Water Manag. 2017, 194, 1–12. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; López-Urrea, R.; Hunsaker, D.J.; Mota, M.; Mohammadi Shad, Z. Standard single and basal crop coefficients for vegetable crops, an update of FAO56 crop water requirements approach. Agric. Water Manag. 2021, 243, 106196. [Google Scholar] [CrossRef]
- Libardi, L.G.P.; Faria, R.T.; Dalri, A.B.; Rolim, G.S.; Palaretti, L.F.; Coelho, A.P.; Martins, I.P. Evapotranspiration and crop coefficient (Kc) of pre-sprouted sugarcane plantlets for greenhouse irrigation management. Agric. Water Manag. 2019, 212, 306–316. [Google Scholar] [CrossRef]
- Juhász, Á.; Hrotkó, K. Comparison of the transpiration part of two sources evapotranspiration model and the measurements of sap flow in the estimation of the transpiration of sweet cherry orchards. Agric. Water Manag. 2014, 143, 142–150. [Google Scholar] [CrossRef]
- Li, S.E.; Hao, X.M.; Du, T.S.; Tong, L.; Zhang, J.H.; Kang, S.Z. A coupled surface resistance model to estimate crop evapotranspiration in arid region of northwest China. Hydrol. Process. 2014, 28, 2312–2323. [Google Scholar] [CrossRef]
- Rajan, N.; Maas, S.J.; Kathilankal, J.C. Estimating crop water use of cotton in the Texas High Plains. Agron. J. 2010, 102, 1641–1651. [Google Scholar] [CrossRef]
- Iritza, Z.; Lindroth, A.; Heikinheimo, M.; Grelle, A.; Kellner, E. Test of a modified Shuttleworth-Wallace estimate of boreal forest evaporation. Agric. For. Meteorol. 1999, 98–99, 605–619. [Google Scholar] [CrossRef]
- Todorovic, M. Single-layer evapotranspiration model with variable canopy resistance. J. Irrig. Drain. Eng. 1999, 125, 235–245. [Google Scholar] [CrossRef]
- Stewart, J.B. Modelling surface conductance of pine forest. Agric. For. Meteorol. 1988, 43, 19–35. [Google Scholar] [CrossRef]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. B Biol. Sci. 1976, 273, 593–610. [Google Scholar]
- Li, X.J.; Kang, S.Z.; Li, F.S.; Jiang, X.L.; Tong, L.; Ding, R.S.; Du, T.S. Applying segmented Jarvis canopy resistance into Penman-Monteith model improves the accuracy of estimated evapotranspiration in maize for seed production with film-mulching in arid area. Agric. Water Manag. 2016, 178, 314–324. [Google Scholar] [CrossRef]
- Zhang, L.; Lemeur, R. Effect of aerodynamic resistance on energy balance and Penman-Monteith estimates of evapotranspiration in greenhouse conditions. Agric. For. Meteorol. 1992, 58, 209–228. [Google Scholar] [CrossRef]
- Fernández, M.D.; Bonachela, S.; Orgaz, F.; Thompson, R.B.; López, J.C.; Granados, M.R.; Gallardo, M.; Fereres, E. Measurement and estimation of plastic greenhouse reference evapotranspiration in a Mediterranean climate. Irrig. Sci. 2010, 28, 497–509, Erratum in Irrig. Sci. 2011, 29, 91–92. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Norman, J.M.; Colaizzi, P.D.; Howell, T.A.; Prueger, J.H.; Meyers, T.P.; Wilson, T.B. Application of the Priestley–Taylor approach in a two-source surface energy balance model. J. Hydrometeorol. 2010, 11, 185–198. [Google Scholar] [CrossRef]
- Utset, A.; Farré, I.; Martınez-Cob, A.; Cavero, J. Comparing Penman–Monteith and Priestley–Taylor approaches as reference-evapotranspiration inputs for modeling maize water-use under Mediterranean conditions. Agric. For. Meteorol. 2004, 66, 205–219. [Google Scholar] [CrossRef]
- Ai, Z.P.; Yang, Y.H. Modification and validation of Priestley–Taylor model for estimating cotton evapotranspiration under plastic mulch condition. J. Hydrometeorol. 2016, 17, 1281–1293. [Google Scholar] [CrossRef]
- Ding, R.S.; Kang, S.Z.; Li, F.S.; Zhang, Y.Q.; Tong, L. Evapotranspiration measurement and estimation using modified Priestley–Taylor model in an irrigated maize field with mulching. Agric. For. Meteorol. 2013, 168, 140–148. [Google Scholar] [CrossRef]
- Pereira, A.R. The Priestley–Taylor parameter and the decoupling factor for estimating reference evapotranspiration. Agric. For. Meteorol. 2004, 125, 305–313. [Google Scholar] [CrossRef]
- Pereira, A.R.; Villa Nova, N.A. Analysis of the Priestley–Taylor parameter. Agric. For. Meteorol. 1992, 61, 1–9. [Google Scholar] [CrossRef]
- Valdés-Gómez, H.; Ortega-Farías, S. and Argote, M. Evaluation of water requirements for a greenhouse tomato crop using the Priestley-Taylor method. Chil. J. Agric. Res. 2009, 69, 3–11. [Google Scholar]
- Lhomme, J.P. A theoretical basis for the Priestley–Taylor coefficient. Bound.-Layer Meteorol. 1997, 82, 179–191. [Google Scholar] [CrossRef]
- Gong, X.W.; Qiu, R.J.; Ge, J.K.; Bo, G.K.; Ping, Y.L.; Xin, Q.C.; Wang, S.S. Evapotranspiration partitioning of greenhouse grown tomato using a modified Priestley–Taylor model. Agric. Water Manag. 2021, 247, 106709. [Google Scholar] [CrossRef]
- Liu, B.; Cui, Y.L.; Luo, Y.F.; Shi, Y.Z.; Liu, M.; Liu, F.P. Energy partitioning and evapotranspiration over a rotated paddy field in Southern China. Agric. For. Meteorol. 2019, 276–277, 107626. [Google Scholar] [CrossRef]
- Qiu, R.J.; Liu, C.W.; Cui, N.B.; Wu, Y.J.; Wang, Z.C.; Li, G. Evapotranspiration estimation using a modified Priestley-Taylor model in a rice-wheat rotation system. Agric. Water Manag. 2019, 224, 105755. [Google Scholar] [CrossRef]
- Jiao, L.J.; Ding, R.S.; Kang, S.Z.; Du, T.S.; Tong, L.; Li, S.E. A comparison of energy partitioning and evapotranspiration over closed maize and sparse grapevine canopies in northwest China. Agric. Water Manag. 2018, 203, 251–260. [Google Scholar] [CrossRef]
- Allen, R.G. Using the FAO–56 dual crop coefficient method over an irrigated region as part of an evapotranspiration intercomparison study. J. Hydrol. 2000, 229, 27–41. [Google Scholar] [CrossRef]
- Suleiman, A.A.; Tojo Soler, C.M.; Hoogenboom, G. Evaluation of FAO-56 crop coefficient procedures for deficit irrigation management of cotton in a humid climate. Agric. Water Manag. 2007, 91, 33–42. [Google Scholar] [CrossRef]
- Kang, S.Z.; Gu, B.J.; Du, T.S.; Zhang, J.H. Crop coefficient and ratio of transpiration to evapotranspiration of winter wheat and maize in a semi-humid region. Agric. Water Manag. 2003, 59, 239–254. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Huang, S.; Yan, H.F.; Zhang, C.; Wang, G.Q.; Acquah, S.J.; Yu, J.J.; Li, L.L.; Ma, J.M.; Darko, R.O. Modeling evapotranspiration for cucumber plants based on the Shuttleworth-Wallace model in a Venlo-type greenhouse. Agric. Water Manag. 2019, 228, 105861. [Google Scholar] [CrossRef]
- Zhao, P.; Li, S.E.; Li, F.S.; Du, T.S.; Tong, L.; Kang, S.Z. Comparison of dual crop coefficient method and Shuttleworth–Wallace model in evapotranspiration partitioning in a vineyard of northwest China. Agric. Water Manag. 2015, 160, 41–56. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Fernando, R.M.; Alves, I.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software: 2. Model testing. Agric. Water Manag. 2012, 103, 62–77. [Google Scholar] [CrossRef]
- Palmer, A.R.; Ezenne, G.I.; Choruma, D.J.; Gwate, O.; Mantel, S.K.; Tanner, J.L. A comparison of three models used to determine water fluxes over the Albany Thicket, Eastern Cape, South Africa. Agric. For. Meteorol. 2020, 288–289, 107984. [Google Scholar] [CrossRef]
- Li, S.E.; Zhang, L.; Kang, S.Z.; Tong, L.; Du, T.; Hao, X.; Zhao, P. Comparison of several surface resistance models for estimating crop evapotranspiration over the entire growing season in arid regions. Agric. For. Meteorol. 2015, 208, 1–15. [Google Scholar] [CrossRef]
- Ortega-Farias, S.O.; Olioso, A.; Fuentes, S.; Valdes, H. Latent heat flux over a furrow-irrigated tomato crop using Penman–Monteith equation with a variable surface canopy resistance. Agric. Water Manag. 2006, 82, 421–432. [Google Scholar] [CrossRef]
- Li, S.E.; Kang, S.Z.; Zhang, L.; Ortega-Farias, S.; Li, F.S.; Du, T.S.; Tong, L.; Wang, S.F.; Ingman, M.; Guo, W.H. Measuring and modeling maize evapotranspiration under plastic film-mulching condition. J. Hydrol. 2013, 503, 153–168. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Carrasco, M.; Olioso, A.; Acevedo, C.; Poblete, C. Latent heat flux over Cabernet Sauvignon vineyard using the Shuttleworth and Wallace model. Irrig. Sci. 2007, 25, 161–170. [Google Scholar] [CrossRef]
- Gardiol, J.M.; Serio, L.A.; Maggiora, A.I.D. Modelling evapotranspiration of corn (Zea mays) under different plant densities. J. Hydrol. 2003, 271, 188–196. [Google Scholar] [CrossRef]
- Anadranistakis, M.; Liakatas, A.; Kerkides, P.; Rizos, S.; Gavanosis, J.; Poulovassilis, A. Crop water requirements model tested for crops grown in Greece. Agric. Water Manag. 2000, 45, 297–316. [Google Scholar] [CrossRef]
- Yan, H.F.; Deng, S.S.; Zhang, C.; Wang, G.Q.; Zhao, S.; Li, M.; Liang, S.W.; Jiang, J.H.; Zhou, Y.D. Determination of energy partition of a cucumber grown Venlo-type greenhouse in southeast China. Agric. Water Manag. 2023, 276, 108047. [Google Scholar] [CrossRef]
- Qiu, R.J.; Kang, S.Z.; Li, F.S.; Du, T.S.; Tong, L.; Wang, F.; Chen, R.Q.; Liu, J.Q.; Li, S.E. Energy partitioning and evapotranspiration of hot pepper grown in greenhouse with furrow and drip irrigation methods. Sci. Hortic. 2011, 129, 790–797. [Google Scholar] [CrossRef]
- Stanghellini, C. Transpiration of Solar Greenhouse Crops: An Aid to Climate Management; Agricultural University: Wageningen, The Netherlands, 1987; pp. 31–88. [Google Scholar]
- Hanson, B.R.; May, D.M. Crop evapotranspiration of processing tomato in the San Joaquin Valley of California, USA. Irrig. Sci. 2006, 24, 211–221. [Google Scholar] [CrossRef]
- Qiu, R.J.; Song, J.J.; Du, T.S.; Kang, S.Z.; Tong, L.; Chen, R.Q.; Wu, L.S. Response of evapotranspiration and yield to planting density of solar greenhouse grown tomato in northwest China. Agric. Water Manag. 2013, 130, 44–51. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics; Academic Press: New York, NY, USA, 2008; p. 418. [Google Scholar]
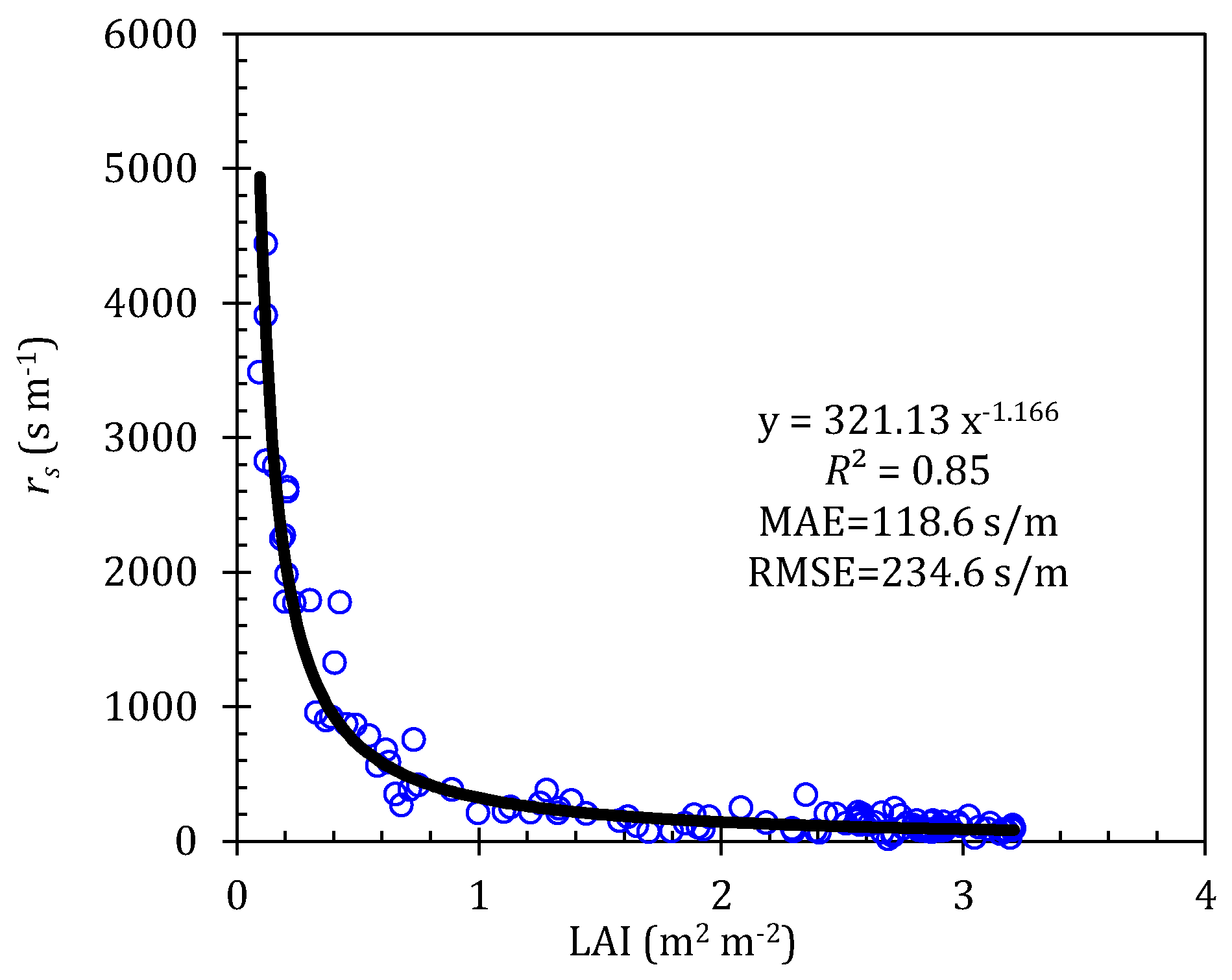
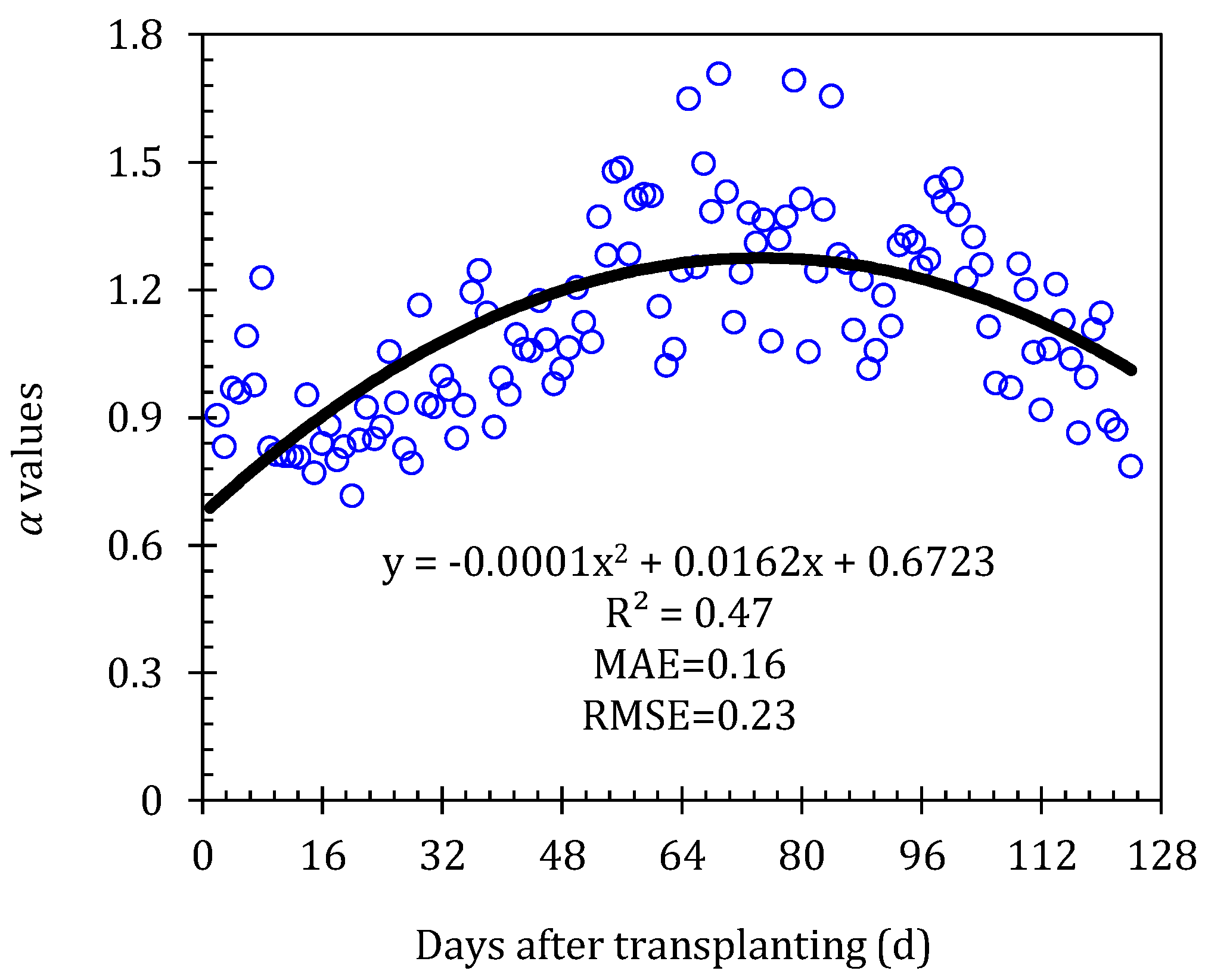
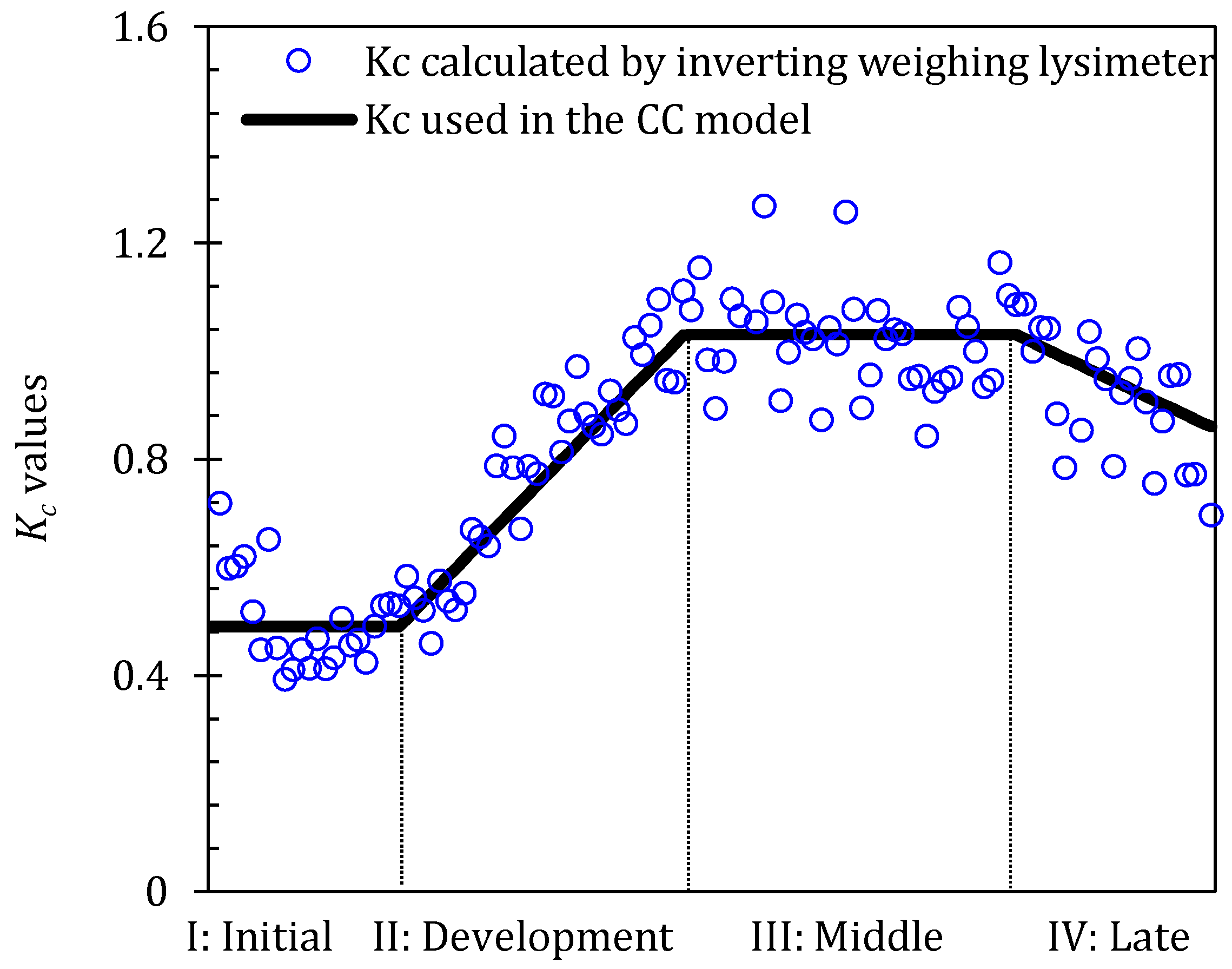
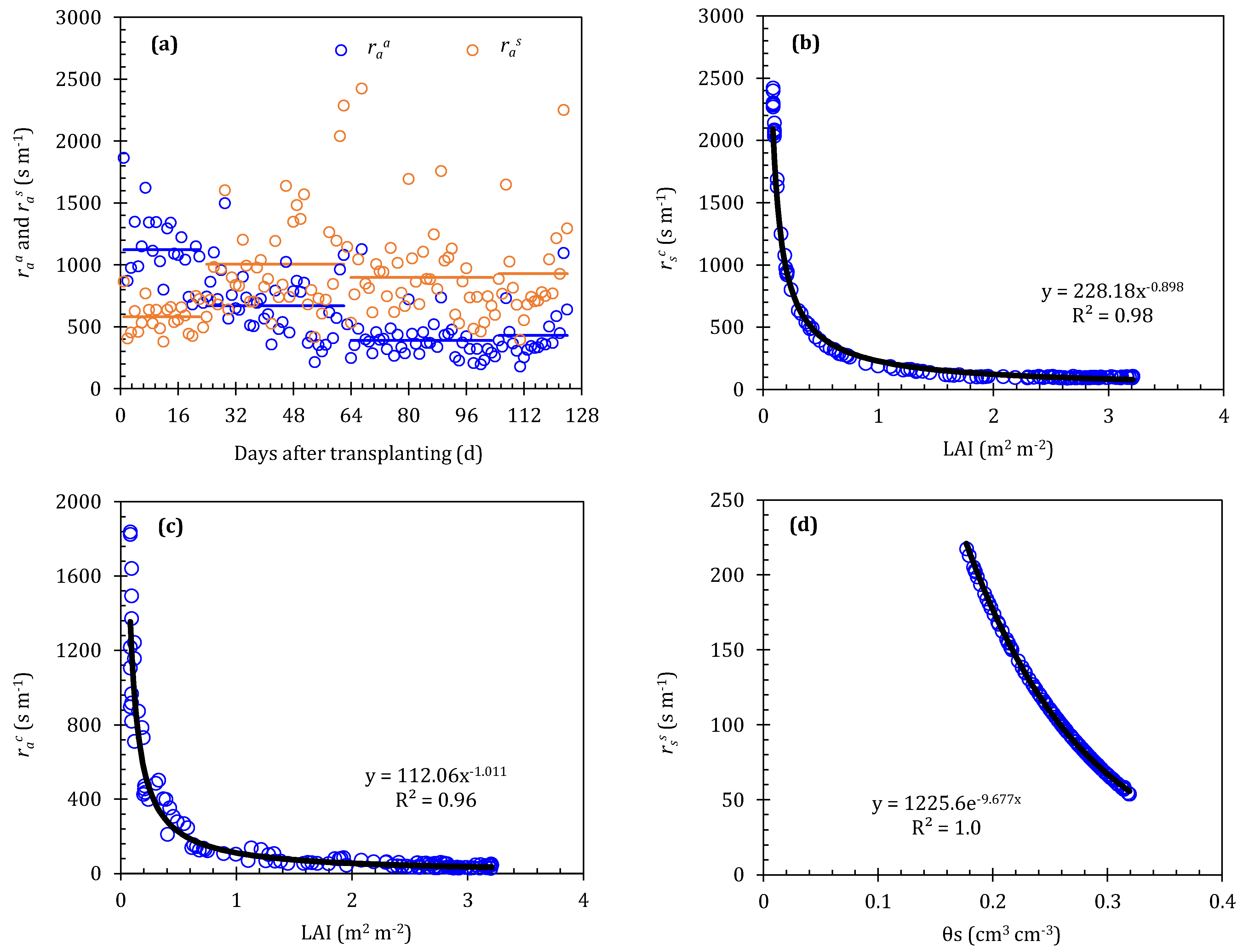
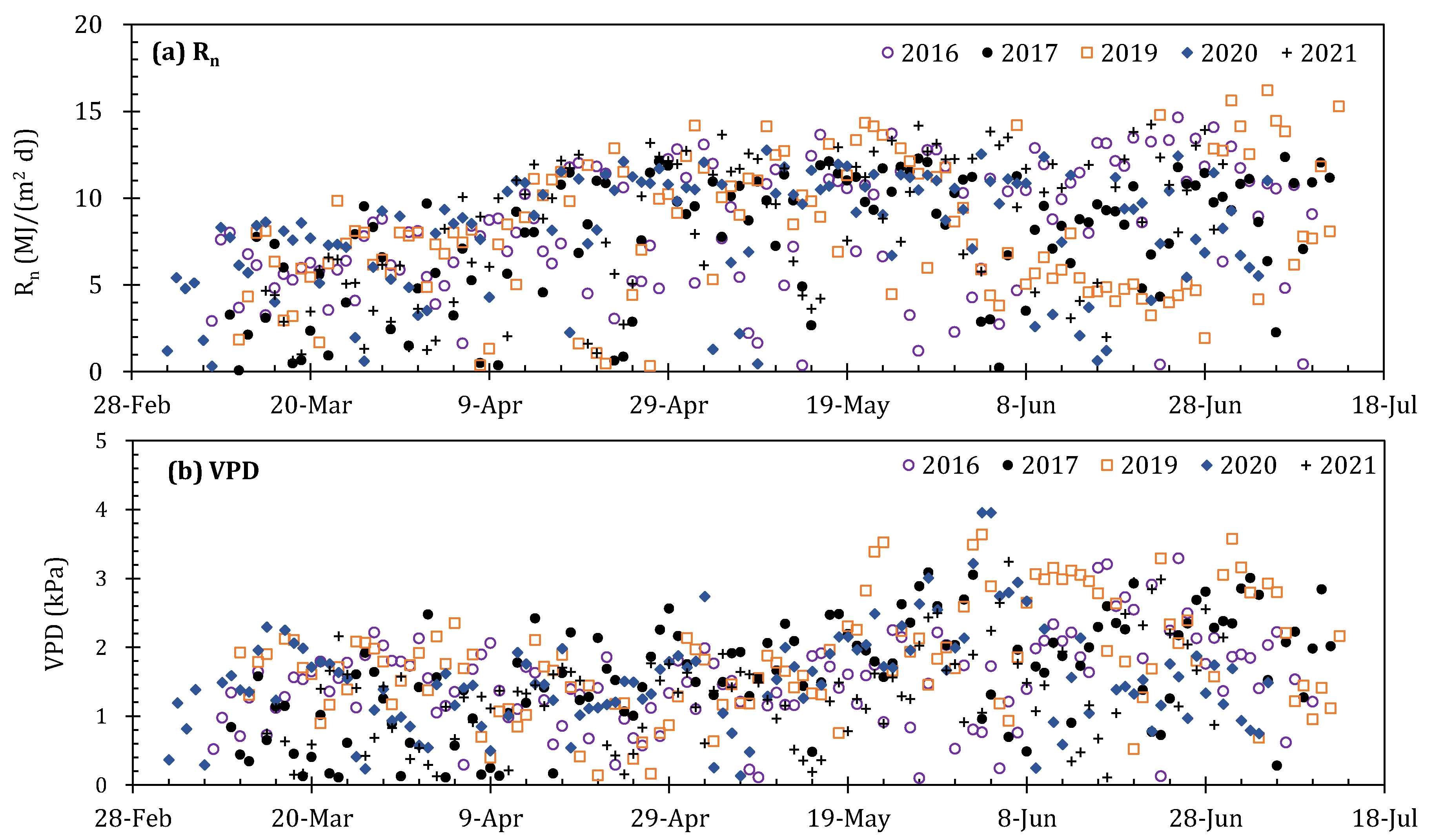


| Years | Growing Stages | Irrigation Number | Irrigation Amount (mm) | |||
|---|---|---|---|---|---|---|
| Initial | Development | Middle | Late | |||
| 2016 | 9–31 March | 1 April–10 May | 11 May–20 June | 21 June–10 July | 15 | 282.7 |
| 2017 | 1 March–11 April | 2 April–10 May | 11 May–21 June | 22 June–12 July | 15 | 308.2 |
| 2019 | 12 Mar–2 April | 3 April–11 May | 12 May–20 June | 21 June–13 July | 15 | 311.7 |
| 2020 | 4–25 March | 26 March–5 May | 6 May–16 June | 17 June–7 July | 14 | 270.5 |
| 2021 | 6–15 March | 7 April–16 May | 17 May–14 June | 15–30 June | 14 | 274.4 |
| Parameterized Models | Meteorological-Based Parameters | Crop Parameters | Soil Parameters |
|---|---|---|---|
| Penman–Monteith | Rn, Gs, RH, Ta, ρ, Cp, γ | LAI | / |
| Priestley–Taylor | Rn, Gs, Ta, γ | DAT | / |
| Crop coefficient method | Rn, Gs, RH, Ta, γ | DAT | / |
| Shuttleworth–Wallace | Rn, Gs, RH, Ta, ρ, Cp, γ | DAT, C, LAI | θs |
| Stages | Year | b0 | R2 | MAE | RMSE | RSR | AAE | ARE | PBIAS | EF | dIA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 2017 | 0.67 | 0.75 | 0.20 | 0.28 | 0.64 | 0.20 | 43.54 | 34.40 | 0.49 | 0.85 |
| 2019 | 0.69 | 0.24 | 0.35 | 0.45 | 0.93 | 0.35 | 28.99 | 29.03 | 0.46 | 0.64 | |
| 2020 | 0.82 | 0.71 | 0.28 | 0.30 | 0.67 | 0.23 | 24.13 | 18.13 | 0.44 | 0.87 | |
| 2021 | 0.73 | 0.66 | 0.28 | 0.33 | 0.69 | 0.28 | 37.79 | 31.03 | 0.20 | 0.83 | |
| 4 years | 0.74 | 0.70 | 0.27 | 0.35 | 0.68 | 0.27 | 33.66 | 27.04 | 0.40 | 0.85 | |
| Development | 2017 | 1.07 | 0.97 | 0.26 | 0.35 | 0.19 | 0.26 | 22.40 | −7.53 | 0.96 | 0.99 |
| 2019 | 1.19 | 0.90 | 0.48 | 0.62 | 0.45 | 0.48 | 30.28 | −19.73 | 0.78 | 0.96 | |
| 2020 | 1.05 | 0.87 | 0.48 | 0.63 | 0.35 | 0.48 | 21.76 | −4.29 | 0.87 | 0.97 | |
| 2021 | 1.03 | 0.89 | 0.32 | 0.40 | 0.33 | 0.32 | 18.03 | −6.01 | 0.90 | 0.98 | |
| 4 years | 1.07 | 0.91 | 0.39 | 0.51 | 0.36 | 0.39 | 23.07 | −8.64 | 0.86 | 0.97 | |
| Middle | 2017 | 1.09 | 0.96 | 0.39 | 0.49 | 0.32 | 0.39 | 9.99 | −8.78 | 0.87 | 0.97 |
| 2019 | 1.10 | 0.80 | 0.50 | 0.66 | 0.58 | 0.50 | 17.44 | −10.61 | 0.63 | 0.92 | |
| 2020 | 1.02 | 0.75 | 0.69 | 0.86 | 0.46 | 0.69 | 76.54 | −5.53 | 0.79 | 0.94 | |
| 2021 | 0.98 | 0.64 | 0.54 | 0.67 | 0.58 | 0.54 | 16.64 | 0.36 | 0.69 | 0.92 | |
| 4 years | 1.05 | 0.81 | 0.53 | 0.68 | 0.46 | 0.53 | 31.47 | −6.65 | 0.79 | 0.95 | |
| Late | 2017 | 1.14 | 0.79 | 0.66 | 0.82 | 0.77 | 0.66 | 19.43 | −12.90 | 0.28 | 0.88 |
| 2019 | 1.02 | 0.90 | 0.47 | 0.62 | 0.37 | 0.47 | 18.64 | −1.20 | 0.87 | 0.97 | |
| 2020 | 1.13 | 0.78 | 0.59 | 0.82 | 0.69 | 0.59 | 21.69 | −12.78 | 0.48 | 0.90 | |
| 2021 | 1.15 | 0.81 | 0.62 | 0.76 | 0.64 | 0.62 | 19.44 | −16.45 | 0.49 | 0.89 | |
| 4 years | 1.10 | 0.83 | 0.58 | 0.75 | 0.57 | 0.58 | 19.74 | −9.55 | 0.66 | 0.93 |
| Stages | Year | b0 | R2 | MAE | RMSE | RSR | AAE | ARE | PBIAS | EF | dIA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 2017 | 1.25 | 0.68 | 0.25 | 0.38 | 0.90 | 0.25 | 39.07 | −25.36 | 0.08 | 0.85 |
| 2019 | 0.83 | 0.35 | 0.33 | 0.43 | 1.05 | 0.33 | 31.34 | 16.13 | 0.41 | 0.72 | |
| 2020 | 1.09 | 0.61 | 0.33 | 0.39 | 0.97 | 0.33 | 33.38 | −7.42 | 0.08 | 0.84 | |
| 2021 | 0.83 | 0.60 | 0.24 | 0.32 | 0.74 | 0.24 | 31.04 | 20.11 | 0.23 | 0.84 | |
| 4 years | 0.97 | 0.57 | 0.29 | 0.38 | 0.85 | 0.29 | 33.68 | 3.40 | 0.28 | 0.85 | |
| Development | 2017 | 0.95 | 0.96 | 0.23 | 0.32 | 0.17 | 0.57 | 18.32 | 2.16 | 0.97 | 0.99 |
| 2019 | 1.18 | 0.88 | 0.48 | 0.63 | 0.54 | 0.48 | 30.05 | −20.37 | 0.76 | 0.95 | |
| 2020 | 0.98 | 0.83 | 0.47 | 0.57 | 0.30 | 0.47 | 21.32 | 1.94 | 0.92 | 0.98 | |
| 2021 | 0.99 | 0.84 | 0.40 | 0.54 | 0.43 | 0.40 | 21.03 | 1.61 | 0.83 | 0.96 | |
| 4 years | 1.01 | 0.86 | 0.40 | 0.53 | 0.37 | 0.40 | 22.65 | −3.92 | 0.86 | 0.96 | |
| Middle | 2017 | 0.93 | 0.95 | 0.34 | 0.40 | 0.31 | 0.33 | 9.86 | 7.29 | 0.91 | 0.98 |
| 2019 | 1.01 | 0.74 | 0.51 | 0.66 | 0.64 | 0.51 | 17.84 | −0.43 | 0.58 | 0.92 | |
| 2020 | 0.94 | 0.83 | 0.59 | 0.73 | 0.39 | 0.59 | 21.98 | 2.92 | 0.85 | 0.96 | |
| 2021 | 0.94 | 0.62 | 0.68 | 0.83 | 0.75 | 0.68 | 22.16 | 6.14 | 0.46 | 0.88 | |
| 4 years | 0.95 | 0.81 | 0.51 | 0.67 | 0.45 | 0.51 | 17.60 | 4.28 | 0.79 | 0.95 | |
| Late | 2017 | 1.08 | 0.97 | 0.28 | 0.33 | 0.34 | 0.28 | 8.05 | −7.76 | 0.88 | 0.97 |
| 2019 | 0.97 | 0.86 | 0.50 | 0.66 | 0.39 | 0.50 | 20.65 | 2.27 | 0.85 | 0.96 | |
| 2020 | 1.14 | 0.89 | 0.48 | 0.58 | 0.47 | 0.48 | 20.48 | −15.73 | 0.74 | 0.94 | |
| 2021 | 1.13 | 0.74 | 0.73 | 0.86 | 0.75 | 0.73 | 23.46 | −12.89 | 0.34 | 0.88 | |
| 4 years | 1.07 | 0.83 | 0.48 | 0.62 | 0.48 | 0.48 | 17.83 | −7.59 | 0.77 | 0.95 |
| Stages | Year | b0 | R2 | MAE | RMSE | RSR | AAE | ARE | PBIAS | EF | dIA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 2017 | 1.18 | 0.79 | 0.17 | 0.26 | 0.64 | 0.17 | 29.51 | −20.06 | 0.56 | 0.91 |
| 2019 | 1.00 | 0.35 | 0.32 | 0.39 | 1.05 | 0.32 | 34.14 | −7.28 | 0.62 | 0.60 | |
| 2020 | 0.97 | 0.71 | 0.21 | 0.23 | 0.58 | 0.21 | 20.49 | 1.54 | 0.67 | 0.92 | |
| 2021 | 0.96 | 0.79 | 0.15 | 0.19 | 0.52 | 0.15 | 23.35 | 4.58 | 0.73 | 0.94 | |
| 4 years | 1.01 | 0.66 | 0.21 | 0.28 | 0.62 | 0.21 | 26.83 | −3.98 | 0.62 | 0.90 | |
| Development | 2017 | 0.98 | 0.97 | 0.22 | 0.28 | 0.15 | 0.22 | 23.34 | 0.86 | 0.98 | 0.99 |
| 2019 | 0.78 | 0.82 | 0.53 | 0.64 | 0.49 | 0.53 | 27.02 | 19.36 | 0.75 | 0.91 | |
| 2020 | 0.85 | 0.87 | 0.55 | 0.72 | 0.32 | 0.55 | 17.96 | 14.99 | 0.87 | 0.96 | |
| 2021 | 1.03 | 0.91 | 0.29 | 0.40 | 0.29 | 0.29 | 15.89 | −3.12 | 0.91 | 0.98 | |
| 4 years | 0.91 | 0.87 | 0.40 | 0.54 | 0.38 | 0.40 | 20.98 | 8.19 | 0.87 | 0.97 | |
| Middle | 2017 | 0.96 | 0.96 | 0.24 | 0.29 | 0.22 | 0.24 | 8.19 | 4.03 | 0.95 | 0.99 |
| 2019 | 0.98 | 0.80 | 0.52 | 0.66 | 0.51 | 0.52 | 17.89 | 1.91 | 0.74 | 0.94 | |
| 2020 | 0.90 | 0.83 | 0.60 | 0.75 | 0.41 | 0.60 | 19.73 | 7.05 | 0.82 | 0.95 | |
| 2021 | 1.12 | 0.65 | 0.68 | 0.88 | 0.65 | 0.68 | 21.82 | −13.98 | 0.43 | 0.86 | |
| 4 years | 0.97 | 0.79 | 0.50 | 0.66 | 0.46 | 0.50 | 16.48 | 1.09 | 0.79 | 0.94 | |
| Late | 2017 | 0.99 | 0.97 | 0.14 | 0.99 | 0.19 | 0.14 | 3.84 | 1.64 | 0.96 | 0.99 |
| 2019 | 0.88 | 0.57 | 0.81 | 1.02 | 0.64 | 0.81 | 28.78 | 8.11 | 0.59 | 0.88 | |
| 2020 | 0.96 | 0.87 | 0.30 | 0.39 | 0.34 | 0.30 | 11.80 | 2.30 | 0.88 | 0.97 | |
| 2021 | 1.15 | 0.85 | 0.54 | 0.71 | 0.60 | 0.54 | 17.15 | −15.72 | 0.55 | 0.91 | |
| 4 years | 0.98 | 0.71 | 0.46 | 0.67 | 0.53 | 0.46 | 15.71 | 0.13 | 0.71 | 0.92 |
| Stages | Year | b0 | R2 | MAE | RMSE | RSR | AAE | ARE | PBIAS | EF | dIA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 2017 | 1.34 | 0.61 | 0.43 | 0.63 | 0.85 | 0.43 | 60.10 | −54.60 | 0.04 | 0.82 |
| 2019 | 0.98 | 0.30 | 0.26 | 0.36 | 0.85 | 0.26 | 57.02 | 2.17 | 0.28 | 0.80 | |
| 2020 | 1.42 | 0.61 | 0.59 | 0.72 | 1.29 | 0.59 | 57.02 | −38.53 | −2.17 | 0.70 | |
| 2021 | 1.19 | 0.63 | 0.28 | 0.46 | 1.24 | 0.28 | 31.10 | −10.42 | −0.53 | 0.81 | |
| 4 years | 1.22 | 0.57 | 0.39 | 0.56 | 1.01 | 0.39 | 51.07 | −24.26 | −0.21 | 0.80 | |
| Development | 2017 | 0.97 | 0.92 | 0.28 | 0.40 | 0.23 | 0.28 | 24.65 | 0.37 | 0.96 | 0.99 |
| 2019 | 0.93 | 0.77 | 0.38 | 0.49 | 0.40 | 0.38 | 22.43 | 1.06 | 0.86 | 0.96 | |
| 2020 | 0.98 | 0.77 | 0.53 | 0.64 | 0.35 | 0.53 | 24.83 | 2.81 | 0.90 | 0.97 | |
| 2021 | 1.11 | 0.81 | 0.62 | 0.73 | 0.61 | 0.62 | 31.50 | −9.40 | 0.68 | 0.94 | |
| 4 years | 1.00 | 0.82 | 0.46 | 0.58 | 0.41 | 0.46 | 25.87 | −3.10 | 0.87 | 0.96 | |
| Middle | 2017 | 0.89 | 0.95 | 0.45 | 0.50 | 0.39 | 0.45 | 12.79 | 10.65 | 0.85 | 0.97 |
| 2019 | 1.09 | 0.76 | 0.58 | 0.76 | 0.65 | 0.58 | 19.22 | −8.17 | 0.55 | 0.91 | |
| 2020 | 0.90 | 0.81 | 0.66 | 0.81 | 0.44 | 0.66 | 21.72 | 7.87 | 0.80 | 0.94 | |
| 2021 | 1.00 | 0.71 | 0.58 | 0.76 | 0.61 | 0.58 | 18.17 | −0.14 | 0.63 | 0.92 | |
| 4 years | 0.95 | 0.76 | 0.57 | 0.71 | 0.49 | 0.57 | 17.94 | 3.68 | 0.76 | 0.93 | |
| Late | 2017 | 1.13 | 0.93 | 0.45 | 0.55 | 0.54 | 0.45 | 13.03 | −12.74 | 0.68 | 0.94 |
| 2019 | 1.14 | 0.83 | 0.80 | 0.97 | 0.56 | 0.80 | 29.33 | −15.55 | 0.67 | 0.93 | |
| 2020 | 1.15 | 0.89 | 0.51 | 0.61 | 0.49 | 0.51 | 21.62 | −16.80 | 0.71 | 0.93 | |
| 2021 | 1.20 | 0.72 | 0.92 | 1.09 | 0.88 | 0.92 | 28.94 | −18.99 | 0.41 | 0.83 | |
| 4 years | 1.15 | 0.83 | 0.66 | 0.83 | 0.60 | 0.66 | 23.06 | −15.73 | 0.58 | 0.91 |
| Models | Year | b0 | R2 | MAE | RMSE | RSR | AAE | ARE | PBIAS | EF | dIA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PA-PM | 2017 | 1.09 | 0.96 | 0.36 | 0.50 | 0.29 | 0.36 | 21.44 | −7.73 | 0.92 | 0.98 |
| 2019 | 1.08 | 0.88 | 0.46 | 0.61 | 0.44 | 0.46 | 23.75 | −6.81 | 0.80 | 0.96 | |
| 2020 | 1.04 | 0.87 | 0.53 | 0.71 | 0.39 | 0.53 | 40.72 | −5.00 | 0.85 | 0.96 | |
| 2021 | 1.03 | 0.89 | 0.42 | 0.54 | 0.36 | 0.42 | 22.08 | −3.12 | 0.87 | 0.97 | |
| 4 years | 1.06 | 0.90 | 0.44 | 0.59 | 0.36 | 0.44 | 27.16 | −5.74 | 0.87 | 0.97 | |
| PA-PT | 2017 | 0.97 | 0.95 | 0.28 | 0.36 | 0.21 | 0.28 | 19.54 | 1.72 | 0.95 | 0.99 |
| 2019 | 0.97 | 0.95 | 0.28 | 0.36 | 0.21 | 0.28 | 18.10 | 1.77 | 0.95 | 0.99 | |
| 2020 | 0.98 | 0.87 | 0.49 | 0.68 | 0.47 | 0.49 | 23.56 | 0.17 | 0.78 | 0.95 | |
| 2021 | 0.99 | 0.84 | 0.49 | 0.66 | 0.45 | 0.49 | 23.82 | 1.80 | 0.80 | 0.95 | |
| 4 years | 0.98 | 0.91 | 0.38 | 0.51 | 0.30 | 0.38 | 21.18 | 0.69 | 0.91 | 0.98 | |
| PA-CC | 2017 | 0.97 | 0.98 | 0.20 | 0.27 | 0.16 | 0.20 | 16.00 | 1.79 | 0.98 | 0.99 |
| 2019 | 0.91 | 0.79 | 0.54 | 0.70 | 0.48 | 0.54 | 25.67 | 7.19 | 0.77 | 0.94 | |
| 2020 | 0.89 | 0.89 | 0.47 | 0.63 | 0.35 | 0.47 | 18.07 | 8.65 | 0.87 | 0.96 | |
| 2021 | 1.10 | 0.91 | 0.40 | 0.59 | 0.40 | 0.40 | 19.26 | −9.27 | 0.84 | 0.96 | |
| 4 years | 0.96 | 0.88 | 0.41 | 0.57 | 0.35 | 0.41 | 19.77 | 2.73 | 0.88 | 0.97 | |
| PA-SW | 2017 | 0.97 | 0.90 | 0.40 | 0.51 | 0.30 | 0.40 | 25.17 | 0.08 | 0.91 | 0.98 |
| 2019 | 1.07 | 0.85 | 0.50 | 0.67 | 0.47 | 0.50 | 28.93 | −7.23 | 0.78 | 0.95 | |
| 2020 | 0.96 | 0.79 | 0.58 | 0.71 | 0.40 | 0.58 | 28.56 | 2.44 | 0.84 | 0.95 | |
| 2021 | 1.08 | 0.83 | 0.58 | 0.76 | 0.51 | 0.58 | 27.46 | −7.80 | 0.74 | 0.94 | |
| 4 years | 1.01 | 0.83 | 0.51 | 0.67 | 0.41 | 0.51 | 27.54 | −4.03 | 0.83 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Li, Y.; Gong, X.; Li, Y. Parameterization of Four Models to Estimate Crop Evapotranspiration in a Solar Greenhouse. Plants 2024, 13, 1579. https://doi.org/10.3390/plants13111579
Gao S, Li Y, Gong X, Li Y. Parameterization of Four Models to Estimate Crop Evapotranspiration in a Solar Greenhouse. Plants. 2024; 13(11):1579. https://doi.org/10.3390/plants13111579
Chicago/Turabian StyleGao, Shikai, Yu Li, Xuewen Gong, and Yanbin Li. 2024. "Parameterization of Four Models to Estimate Crop Evapotranspiration in a Solar Greenhouse" Plants 13, no. 11: 1579. https://doi.org/10.3390/plants13111579
APA StyleGao, S., Li, Y., Gong, X., & Li, Y. (2024). Parameterization of Four Models to Estimate Crop Evapotranspiration in a Solar Greenhouse. Plants, 13(11), 1579. https://doi.org/10.3390/plants13111579








