Multiscale Mathematical Modeling in Systems Biology: A Framework to Boost Plant Synthetic Biology
Abstract
:1. Introduction
2. Model Building
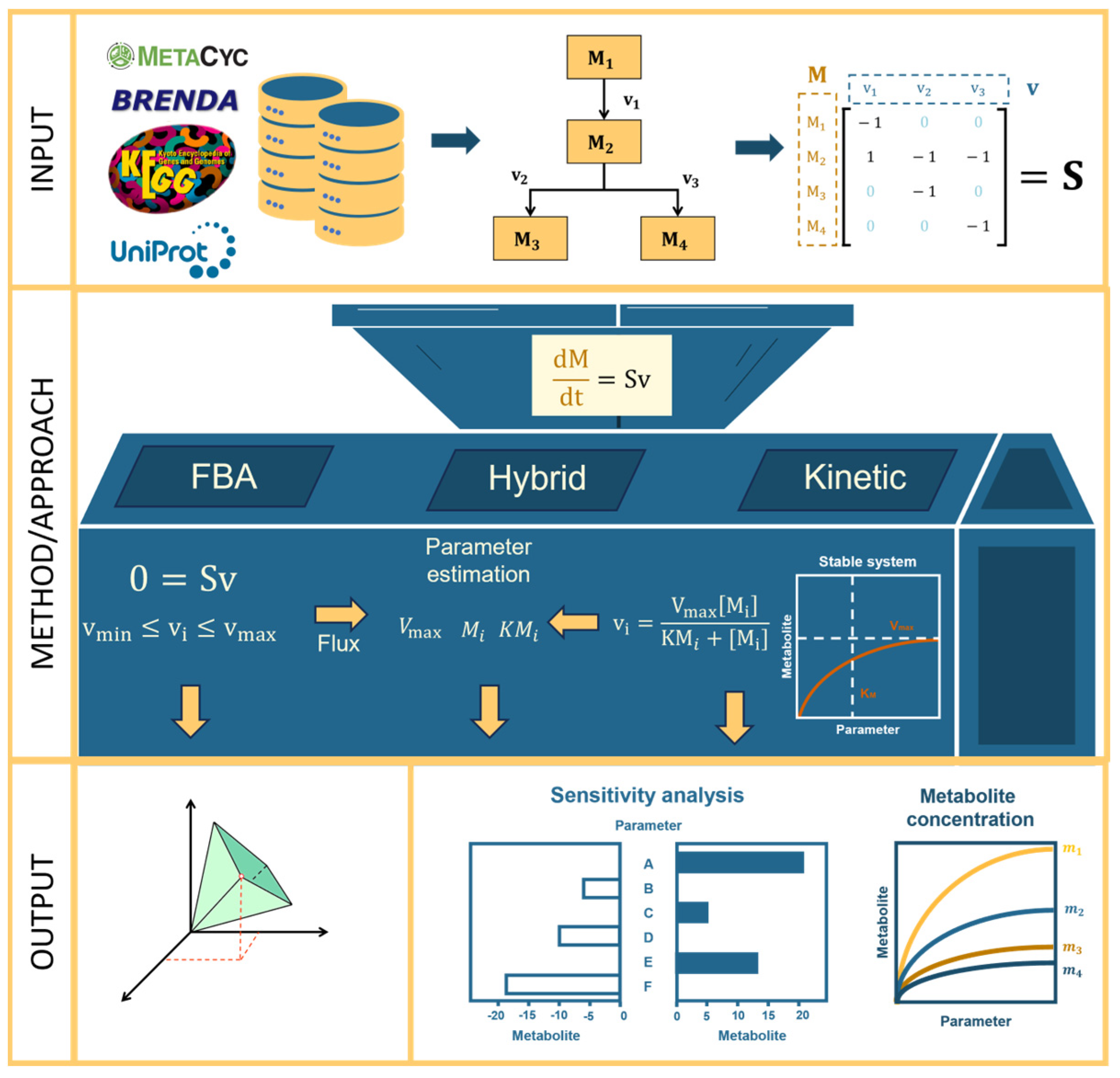
2.1. Metabolic Modeling with FBA, Kinetic, or Hybrid Approaches
2.1.1. Applications
2.1.2. Creating a Metabolic Model
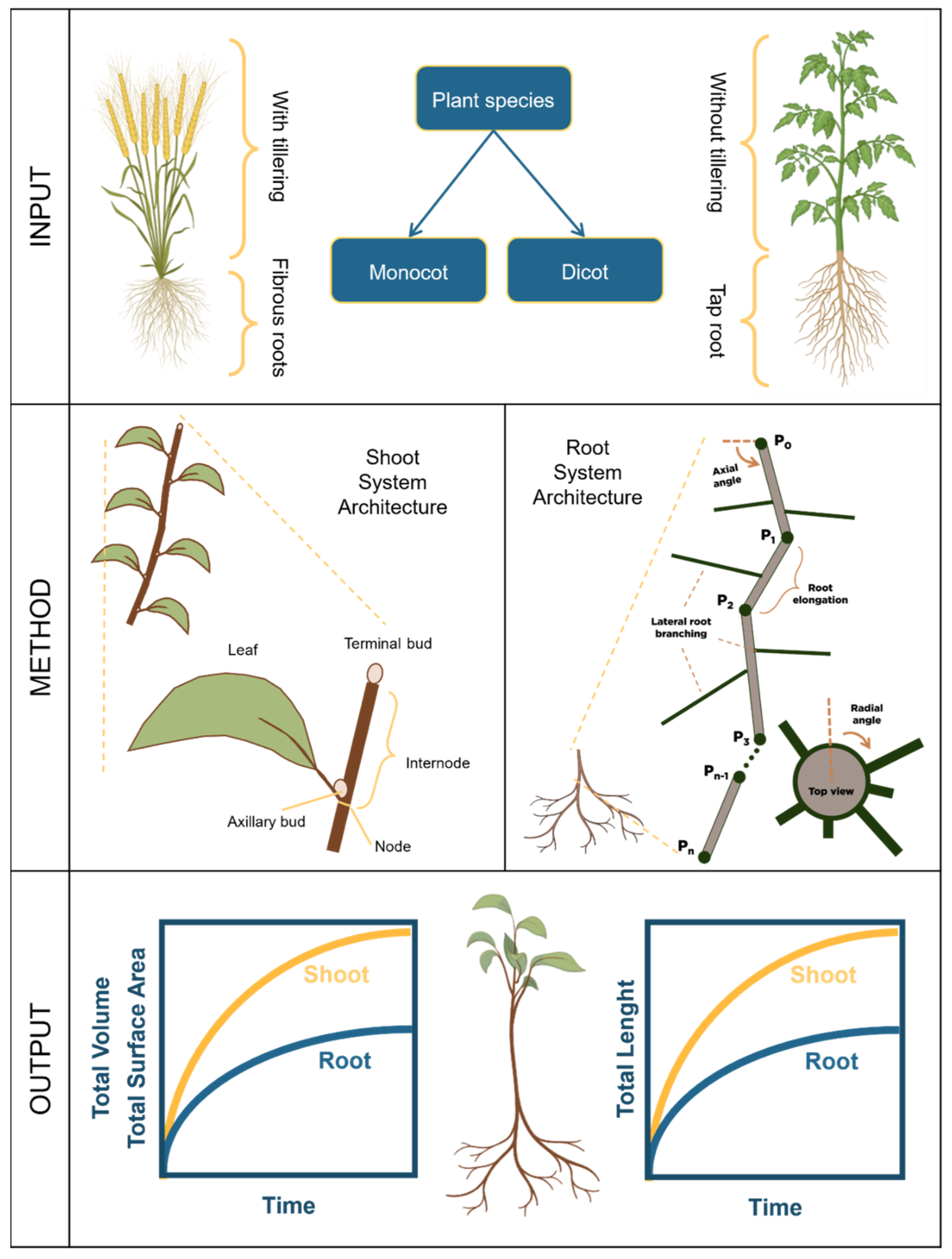
2.2. Shoot and Root System Architecture
2.2.1. Shoot System Architecture
Applications
Creating a Shoot System Architecture
2.2.2. Root System Architecture
Applications
Creating a Root System Architecture
2.3. Resource Acquisition
2.3.1. Photosynthesis
Applications
Creating a Photosynthesis Model
2.3.2. Nutrient Uptake Model
Applications
Creating a Root Nutrient Uptake Model
2.4. Shoot–Root Interaction
2.4.1. Applications
2.4.2. Creating a Shoot-Interaction Model
3. Discussion
3.1. The Potential of Multiscale Mathematical Modeling
3.2. Limitations of Multiscale Mathematical Modeling
3.3. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations. Save and Grow in Practice: Maize, Rice, Wheat. In A Guide to Sustainable Cereal Production; Food and Agriculture Organization of the United Nations: Rome, Italy, 2016; ISBN 978-92-5-108519-6. [Google Scholar]
- Pingali, P.L. Green Revolution: Impacts, Limits, and the Path Ahead. Proc. Natl. Acad. Sci. USA 2012, 109, 12302–12308. [Google Scholar] [CrossRef] [PubMed]
- John, D.A.; Babu, G.R. Lessons from the Aftermaths of Green Revolution on Food System and Health. Front. Sustain. Food Syst. 2021, 5, 644559. [Google Scholar] [CrossRef] [PubMed]
- Venkatappa, M.; Sasaki, N.; Han, P.; Abe, I. Impacts of Droughts and Floods on Croplands and Crop Production in Southeast Asia–An Application of Google Earth Engine. Sci. Total Environ. 2021, 795, 148829. [Google Scholar] [CrossRef] [PubMed]
- Yacoubou, A.-M.; Zoumarou Wallis, N.; Menkir, A.; Zinsou, V.A.; Onzo, A.; Garcia-Oliveira, A.L.; Meseka, S.; Wende, M.; Gedil, M.; Agre, P. Breeding Maize (Zea mays) for Striga Resistance: Past, Current and Prospects in Sub-Saharan Africa. Plant Breed. 2021, 140, 195–210. [Google Scholar] [CrossRef]
- Glauber, J.W.; Laborde Debucquet, D.; Swinnen, J. The Russia-Ukraine War’s Impact on Global Food Markets: A Historical Perspective; International Food Policy Research Institute: Washington, DC, USA, 2023. [Google Scholar]
- Martyshev, P.; Nivievskyi, O.; Bogonos, M. Regional War, Global Consequences: Mounting Damages to Ukraine’s Agriculture and Growing Challenges for Global Food Security. Available online: https://ebrary.ifpri.org/digital/collection/p15738coll2/id/136766 (accessed on 4 October 2023).
- OECD; Food and Agriculture Organization of the United Nations. OECD-FAO Agricultural Outlook 2021–2030; OECD-FAO Agricultural Outlook; OECD: Paris, France, 2021; ISBN 978-92-64-43607-7. [Google Scholar]
- Lynch, J.P. Roots of the Second Green Revolution. Aust. J. Bot. 2007, 55, 493–512. [Google Scholar] [CrossRef]
- Liu, W.; Stewart, C.N. Plant Synthetic Biology. Trends Plant Sci. 2015, 20, 309–317. [Google Scholar] [CrossRef]
- Petzold, C.; Chan, L.J.; Nhan, M.; Adams, P. Analytics for Metabolic Engineering. Front. Bioeng. Biotechnol. 2015, 3, 135. [Google Scholar] [CrossRef]
- Varadan, R.; Solomatin, S.; Holz-Schietinger, C.; Cohn, E.; Klapholz-Brown, A.; Shiu, J.W.-Y.; Kale, A.; Karr, J.; Fraser, R. Ground Meat Replicas. Br. Patent WO2015153666A1, 8 October 2015. [Google Scholar]
- Shankar, S.; Hoyt, M.A. Expression Constructs and Methods of Genetically Engineering Methylotrophic Yeast. U.S. Patent 20170349906A1, 7 December 2017. [Google Scholar]
- Mcnamara, J.; Harvey, J.D.; Graham, M.J.; Scherger, C. Optically Transparent Polyimides. Br. Patent WO2019156717A2, 15 August 2019. [Google Scholar]
- Temme, K.; Tamsir, A.; Bloch, S.; Clark, R.; Tung, E. Methods and Compositions for Improving Plant Traits. Br. Patent WO2017011602A1, 19 January 2017. [Google Scholar]
- Haun, W.; Coffman, A.; Clasen, B.M.; Demorest, Z.L.; Lowy, A.; Ray, E.; Retterath, A.; Stoddard, T.; Juillerat, A.; Cedrone, F.; et al. Improved Soybean Oil Quality by Targeted Mutagenesis of the Fatty Acid Desaturase 2 Gene Family. Plant Biotechnol. J. 2014, 12, 934–940. [Google Scholar] [CrossRef]
- Voigt, C.A. Synthetic Biology 2020–2030: Six Commercially-Available Products That Are Changing Our World. Nat. Commun. 2020, 11, 6379. [Google Scholar] [CrossRef]
- Nowacka, M.; Trusinska, M.; Chraniuk, P.; Piatkowska, J.; Pakulska, A.; Wisniewska, K.; Wierzbicka, A.; Rybak, K.; Pobiega, K. Plant-Based Fish Analogs—A Review. Appl. Sci. 2023, 13, 4509. [Google Scholar] [CrossRef]
- Sun, T.; Song, J.; Wang, M.; Zhao, C.; Zhang, W. Challenges and Recent Progress in the Governance of Biosecurity Risks in the Era of Synthetic Biology. J. Biosaf. Biosecurity 2022, 4, 59–67. [Google Scholar] [CrossRef]
- Bohua, L.; Yuexin, W.; Yakun, O.; Kunlan, Z.; Huan, L.; Ruipeng, L. Ethical Framework on Risk Governance of Synthetic Biology. J. Biosaf. Biosecurity 2023, 5, 45–56. [Google Scholar] [CrossRef]
- Haseltine, E.L.; Arnold, F.H. Synthetic Gene Circuits: Design with Directed Evolution. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Chandran, D.; Copeland, W.B.; Sleight, S.C.; Sauro, H.M. Mathematical Modeling and Synthetic Biology. Drug Discov. Today Dis. Models 2008, 5, 299–309. [Google Scholar] [CrossRef]
- Henkel, J.; Maurer, S.M. The Economics of Synthetic Biology. Mol. Syst. Biol. 2007, 3, 117. [Google Scholar] [CrossRef]
- Douglas, T.; Savulescu, J. Synthetic Biology and the Ethics of Knowledge. J. Med. Ethics 2010, 36, 687–693. [Google Scholar] [CrossRef]
- Kurtoğlu, A.; Yıldız, A.; Arda, B. The View of Synthetic Biology in the Field of Ethics: A Thematic Systematic Review. Front. Bioeng. Biotechnol. 2024, 12, 1397796. [Google Scholar] [CrossRef]
- Chew, Y.H.; Wenden, B.; Flis, A.; Mengin, V.; Taylor, J.; Davey, C.L.; Tindal, C.; Thomas, H.; Ougham, H.J.; de Reffye, P.; et al. Multiscale Digital Arabidopsis Predicts Individual Organ and Whole-Organism Growth. Proc. Natl. Acad. Sci. USA 2014, 111, E4127–E4136. [Google Scholar] [CrossRef]
- Karr, J.R.; Sanghvi, J.C.; Macklin, D.N.; Gutschow, M.V.; Jacobs, J.M.; Bolival, B.; Assad-Garcia, N.; Glass, J.I.; Covert, M.W. A Whole-Cell Computational Model Predicts Phenotype from Genotype. Cell 2012, 150, 389–401. [Google Scholar] [CrossRef]
- Carrera, J.; Estrela, R.; Luo, J.; Rai, N.; Tsoukalas, A.; Tagkopoulos, I. An Integrative, Multi-scale, Genome-wide Model Reveals the Phenotypic Landscape of Escherichia Coli. Mol. Syst. Biol. 2014, 10, 735. [Google Scholar] [CrossRef]
- Ye, C.; Xu, N.; Gao, C.; Liu, G.; Xu, J.; Zhang, W.; Chen, X.; Nielsen, J.; Liu, L. Comprehensive Understanding of Saccharomyces Cerevisiae Phenotypes with Whole-Cell Model WM_S288C. Biotechnol. Bioeng. 2020, 117, 1562–1574. [Google Scholar] [CrossRef] [PubMed]
- Matthews, M.L.; Marshall-Colón, A. Multiscale Plant Modeling: From Genome to Phenome and Beyond. Emerg. Top. Life Sci. 2021, 5, 231–237. [Google Scholar] [CrossRef] [PubMed]
- Benes, B.; Guan, K.; Lang, M.; Long, S.P.; Lynch, J.P.; Marshall-Colón, A.; Peng, B.; Schnable, J.; Sweetlove, L.J.; Turk, M.J. Multiscale Computational Models Can Guide Experimentation and Targeted Measurements for Crop Improvement. Plant J. 2020, 103, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Messina, C.D.; Technow, F.; Tang, T.; Totir, R.; Gho, C.; Cooper, M. Leveraging Biological Insight and Environmental Variation to Improve Phenotypic Prediction: Integrating Crop Growth Models (CGM) with Whole Genome Prediction (WGP). Eur. J. Agron. 2018, 100, 151–162. [Google Scholar] [CrossRef]
- De Falco, B.; Giannino, F.; Carteni, F.; Mazzoleni, S.; Kim, D.-H. Metabolic Flux Analysis: A Comprehensive Review on Sample Preparation, Analytical Techniques, Data Analysis, Computational Modelling, and Main Application Areas. RSC Adv. 2022, 12, 25528–25548. [Google Scholar] [CrossRef]
- Clark, T.J.; Guo, L.; Morgan, J.; Schwender, J. Modeling Plant Metabolism: From Network Reconstruction to Mechanistic Models. Annu. Rev. Plant Biol. 2020, 71, 303–326. [Google Scholar] [CrossRef]
- Foster, C.J.; Wang, L.; Dinh, H.V.; Suthers, P.F.; Maranas, C.D. Building Kinetic Models for Metabolic Engineering. Curr. Opin. Biotechnol. 2021, 67, 35–41. [Google Scholar] [CrossRef]
- Gudmundsson, S.; Nogales, J. Recent Advances in Model-Assisted Metabolic Engineering. Curr. Opin. Syst. Biol. 2021, 28, 100392. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What Is Flux Balance Analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Poolman, M.G.; Miguet, L.; Sweetlove, L.J.; Fell, D.A. A Genome-Scale Metabolic Model of Arabidopsis and Some of Its Properties. Plant Physiol. 2009, 151, 1570–1581. [Google Scholar] [CrossRef]
- Poolman, M.G.; Kundu, S.; Shaw, R.; Fell, D.A. Responses to Light Intensity in a Genome-Scale Model of Rice Metabolism. Plant Physiol. 2013, 162, 1060–1072. [Google Scholar] [CrossRef] [PubMed]
- de O Dal’Molin, C.G.; Quek, L.-E.; Palfreyman, R.W.; Brumbley, S.M.; Nielsen, L.K. AraGEM, a Genome-Scale Reconstruction of the Primary Metabolic Network in Arabidopsis. Plant Physiol. 2010, 152, 579–589. [Google Scholar] [CrossRef]
- Williams, T.C.R.; Poolman, M.G.; Howden, A.J.M.; Schwarzlander, M.; Fell, D.A.; Ratcliffe, R.G.; Sweetlove, L.J. A Genome-Scale Metabolic Model Accurately Predicts Fluxes in Central Carbon Metabolism under Stress Conditions. Plant Physiol. 2010, 154, 311–323. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Suthers, P.F.; Maranas, C.D. Zea Mays iRS1563: A Comprehensive Genome-Scale Metabolic Reconstruction of Maize Metabolism. PLoS ONE 2011, 6, e21784. [Google Scholar] [CrossRef]
- Mintz-Oron, S.; Meir, S.; Malitsky, S.; Ruppin, E.; Aharoni, A.; Shlomi, T. Reconstruction of Arabidopsis Metabolic Network Models Accounting for Subcellular Compartmentalization and Tissue-Specificity. Proc. Natl. Acad. Sci. USA 2012, 109, 339–344. [Google Scholar] [CrossRef]
- Cheung, C.Y.M.; Williams, T.C.R.; Poolman, M.G.; Fell, D.A.; Ratcliffe, R.G.; Sweetlove, L.J. A Method for Accounting for Maintenance Costs in Flux Balance Analysis Improves the Prediction of Plant Cell Metabolic Phenotypes under Stress Conditions. Plant J. 2013, 75, 1050–1061. [Google Scholar] [CrossRef]
- Yen, J.Y.; Nazem-Bokaee, H.; Freedman, B.G.; Athamneh, A.I.M.; Senger, R.S. Deriving Metabolic Engineering Strategies from Genome-Scale Modeling with Flux Ratio Constraints. Biotechnol. J. 2013, 8, 581–594. [Google Scholar] [CrossRef]
- Simons, M.; Saha, R.; Amiour, N.; Kumar, A.; Guillard, L.; Clément, G.; Miquel, M.; Li, Z.; Mouille, G.; Lea, P.J.; et al. Assessing the Metabolic Impact of Nitrogen Availability Using a Compartmentalized Maize Leaf Genome-Scale Model. Plant Physiol. 2014, 166, 1659–1674. [Google Scholar] [CrossRef]
- Yuan, H.; Cheung, C.Y.M.; Poolman, M.G.; Hilbers, P.A.J.; Riel, N.A.W. van A Genome-Scale Metabolic Network Reconstruction of Tomato (Solanum Lycopersicum L.) and Its Application to Photorespiratory Metabolism. Plant J. 2016, 85, 289–304. [Google Scholar] [CrossRef]
- Wanichthanarak, K.; Boonchai, C.; Kojonna, T.; Chadchawan, S.; Sangwongchai, W.; Thitisaksakul, M. Deciphering Rice Metabolic Flux Reprograming under Salinity Stress via in Silico Metabolic Modeling. Comput. Struct. Biotechnol. J. 2020, 18, 3555–3566. [Google Scholar] [CrossRef]
- Sugimoto, K.; Zager, J.J.; Aubin, B.S.; Lange, B.M.; Howe, G.A. Flavonoid Deficiency Disrupts Redox Homeostasis and Terpenoid Biosynthesis in Glandular Trichomes of Tomato. Plant Physiol. 2022, 188, 1450–1468. [Google Scholar] [CrossRef] [PubMed]
- Savageau, M.A. Biochemical Systems Analysis. In A Study of Function and Design in Molecular Biology; Addison Wesley Publishing: Reading, MA, USA, 1976. [Google Scholar]
- Comas, J.; Benfeitas, R.; Vilaprinyo, E.; Sorribas, A.; Solsona, F.; Farré, G.; Berman, J.; Zorrilla, U.; Capell, T.; Sandmann, G.; et al. Identification of Line-Specific Strategies for Improving Carotenoid Production in Synthetic Maize through Data-Driven Mathematical Modeling. Plant J. 2016, 87, 455–471. [Google Scholar] [CrossRef] [PubMed]
- Basallo, O.; Perez, L.; Lucido, A.; Sorribas, A.; Marin-Saguino, A.; Vilaprinyo, E.; Perez-Fons, L.; Albacete, A.; Martínez-Andújar, C.; Fraser, P.D.; et al. Changing Biosynthesis of Terpenoid Percursors in Rice through Synthetic Biology. Front Plant Sci. 2023, 14, 1133299. [Google Scholar] [CrossRef]
- Yang, Z.; Midmore, D.J. A Model for the Circadian Oscillations in Expression and Activity of Nitrate Reductase in Higher Plants. Ann. Bot. 2005, 96, 1019–1026. [Google Scholar] [CrossRef] [PubMed]
- Curien, G.; Bastien, O.; Robert-Genthon, M.; Cornish-Bowden, A.; Cárdenas, M.L.; Dumas, R. Understanding the Regulation of Aspartate Metabolism Using a Model Based on Measured Kinetic Parameters. Mol. Syst. Biol. 2009, 5, 271. [Google Scholar] [CrossRef]
- Colón, A.M.; Sengupta, N.; Rhodes, D.; Dudareva, N.; Morgan, J. A Kinetic Model Describes Metabolic Response to Perturbations and Distribution of Flux Control in the Benzenoid Network of Petunia Hybrida. Plant J. 2010, 62, 64–76. [Google Scholar] [CrossRef]
- Nägele, T.; Henkel, S.; Hörmiller, I.; Sauter, T.; Sawodny, O.; Ederer, M.; Heyer, A.G. Mathematical Modeling of the Central Carbohydrate Metabolism in Arabidopsis Reveals a Substantial Regulatory Influence of Vacuolar Invertase on Whole Plant Carbon Metabolism. Plant Physiol. 2010, 153, 260–272. [Google Scholar] [CrossRef]
- Groenenboom, M.; Gomez-Roldan, V.; Stigter, H.; Astola, L.; van Daelen, R.; Beekwilder, J.; Bovy, A.; Hall, R.; Molenaar, J. The Flavonoid Pathway in Tomato Seedlings: Transcript Abundance and the Modeling of Metabolite Dynamics. PLoS ONE 2013, 8, e68960. [Google Scholar] [CrossRef]
- Valancin, A.; Srinivasan, B.; Rivoal, J.; Jolicoeur, M. Analyzing the Effect of Decreasing Cytosolic Triosephosphate Isomerase on Solanum Tuberosum Hairy Root Cells Using a Kinetic–Metabolic Model. Biotechnol. Bioeng. 2013, 110, 924–935. [Google Scholar] [CrossRef]
- Pokhilko, A.; Bou-Torrent, J.; Pulido, P.; Rodríguez-Concepción, M.; Ebenhöh, O. Mathematical Modelling of the Diurnal Regulation of the MEP Pathway in Arabidopsis. New Phytol. 2015, 206, 1075–1085. [Google Scholar] [CrossRef]
- Lucido, A.; Basallo, O.; Sorribas, A.; Marin-Sanguino, A.; Vilaprinyo, E.; Alves, R. A Mathematical Model for Strigolactone Biosynthesis in Plants. Front. Plant Sci. 2022, 13, 979162. [Google Scholar] [CrossRef] [PubMed]
- Olsen, K.M.; Slimestad, R.; Lea, U.S.; Brede, C.; Løvdal, T.; Ruoff, P.; Verheul, M.; Lillo, C. Temperature and Nitrogen Effects on Regulators and Products of the Flavonoid Pathway: Experimental and Kinetic Model Studies. Plant Cell Environ. 2009, 32, 286–299. [Google Scholar] [CrossRef] [PubMed]
- Sorribas, A.; Hernández-Bermejo, B.; Vilaprinyo, E.; Alves, R. Cooperativity and Saturation in Biochemical Networks: A Saturable Formalism Using Taylor Series Approximations. Biotechnol. Bioeng. 2007, 97, 1259–1277. [Google Scholar] [CrossRef] [PubMed]
- Alves, R.; Vilaprinyo, E.; Hernádez-Bermejo, B.; Sorribas, A. Mathematical Formalisms Based on Approximated Kinetic Representations for Modeling Genetic and Metabolic Pathways. Biotechnol. Genet. Eng. Rev. 2008, 25, 1–40. [Google Scholar] [CrossRef]
- Faraji, M.; Fonseca, L.L.; Escamilla-Treviño, L.; Barros-Rios, J.; Engle, N.L.; Yang, Z.K.; Tschaplinski, T.J.; Dixon, R.A.; Voit, E.O. A Dynamic Model of Lignin Biosynthesis in Brachypodium Distachyon. Biotechnol. Biofuels 2018, 11, 253. [Google Scholar] [CrossRef]
- Lee, Y.; Voit, E.O. Mathematical Modeling of Monolignol Biosynthesis in Populus Xylem. Math. Biosci. 2010, 228, 78–89. [Google Scholar] [CrossRef]
- Tran, L.M.; Rizk, M.L.; Liao, J.C. Ensemble Modeling of Metabolic Networks. Biophys. J. 2008, 95, 5606–5617. [Google Scholar] [CrossRef]
- Reder, C. Metabolic Control Theory: A Structural Approach. J. Theor. Biol. 1988, 135, 175–201. [Google Scholar] [CrossRef]
- Savageau, M.A. Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2010; ISBN 978-1-4495-9076-5. [Google Scholar]
- Voit, E. A First Course in Systems Biology; Garland Science: New York, NY, USA, 2012; ISBN 978-0-8153-4467-4. [Google Scholar]
- Resendis-Antonio, O. Stoichiometric Matrix. In Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.-H., Yokota, H., Eds.; Springer: New York, NY, USA, 2013; p. 2014. ISBN 978-1-4419-9863-7. [Google Scholar]
- Paez-Garcia, A.; Motes, C.M.; Scheible, W.-R.; Chen, R.; Blancaflor, E.B.; Monteros, M.J. Root Traits and Phenotyping Strategies for Plant Improvement. Plants 2015, 4, 334–355. [Google Scholar] [CrossRef]
- Tajima, R. Importance of Individual Root Traits to Understand Crop Root System in Agronomic and Environmental Contexts. Breed. Sci. 2021, 71, 13–19. [Google Scholar] [CrossRef]
- Vergauwen, D.; De Smet, I. From Early Farmers to Norman Borlaug—the Making of Modern Wheat. Curr. Biol. 2017, 27, R858–R862. [Google Scholar] [CrossRef]
- Reynolds, M.P.; Braun, H.-J. Wheat Improvement. In Wheat Improvement: Food Security in a Changing Climate; Reynolds, M.P., Braun, H.-J., Eds.; Springer International Publishing: Cham, Switzerland, 2022; ISBN 978-3-030-90673-3. [Google Scholar]
- Ramstein, G.P.; Jensen, S.E.; Buckler, E.S. Breaking the Curse of Dimensionality to Identify Causal Variants in Breeding 4. Theor. Appl. Genet. 2019, 132, 559–567. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Kang, M.Z.; de Reffye, P.; Dingkuhn, M. A Dynamic, Architectural Plant Model Simulating Resource-dependent Growth. Ann. Bot. 2004, 93, 591–602. [Google Scholar] [CrossRef] [PubMed]
- McSteen, P.; Leyser, O. Shoot Branching. Annu. Rev. Plant Biol. 2005, 56, 353–374. [Google Scholar] [CrossRef] [PubMed]
- Evers, J.B.; Vos, J. Modeling Branching in Cereals. Front. Plant Sci. 2013, 4, 399. [Google Scholar] [CrossRef]
- Wen, W.; Wang, Y.; Wu, S.; Liu, K.; Gu, S.; Guo, X. 3D Phytomer-Based Geometric Modelling Method for Plants—The Case of Maize. AoB PLANTS 2021, 13, plab055. [Google Scholar] [CrossRef]
- Buck-Sorlin, G.H.; Kniemeyer, O.; Kurth, W. Barley Morphology, Genetics and Hormonal Regulation of Internode Elongation Modelled by a Relational Growth Grammar. New Phytol. 2005, 166, 859–867. [Google Scholar] [CrossRef]
- Buck-Sorlin, G.; de Visser, P.H.B.; Henke, M.; Sarlikioti, V.; van der Heijden, G.W.A.M.; Marcelis, L.F.M.; Vos, J. Towards a Functional–Structural Plant Model of Cut-Rose: Simulation of Light Environment, Light Absorption, Photosynthesis and Interference with the Plant Structure. Ann. Bot. 2011, 108, 1121–1134. [Google Scholar] [CrossRef]
- Groer, C.; Kniemeyer, O.; Hemmerling, R.; Kurth, W.; Becker, H.; Buck-Sorlin, G. A Dynamic 3D Model of Rape (Brassica Napus L.) Computing Yield Components under Variable Nitrogen Fertilization Regimes. In Proceedings of the 5th International Workshop on Functional-Structural Plant Models, Napier, New Zealand, 4–9 November 2007. [Google Scholar]
- Thornby, D.; Spencer, D.; Hanan, J.; Sher, A. L-DONAX, a Growth Model of the Invasive Weed Species, Arundo Donax L. Aquat. Bot. 2007, 87, 275–284. [Google Scholar] [CrossRef]
- Barczi, J.-F.; Rey, H.; Caraglio, Y.; de Reffye, P.; Barthélémy, D.; Dong, Q.X.; Fourcaud, T. AmapSim: A Structural Whole-Plant Simulator Based on Botanical Knowledge and Designed to Host External Functional Models. Ann. Bot. 2008, 101, 1125–1138. [Google Scholar] [CrossRef]
- Kahlen, K.; Wiechers, D.; Stützel, H. Modelling Leaf Phototropism in a Cucumber Canopy. Funct. Plant Biol. 2008, 35, 876–884. [Google Scholar] [CrossRef] [PubMed]
- Jallas, E.; Sequeira, R.; Martin, P.; Turner, S.; Papajorgji, P. Mechanistic Virtual Modeling: Coupling a Plant Simulation Model with a Three-Dimensional Plant Architecture Component. Env. Model Assess 2009, 14, 29–45. [Google Scholar] [CrossRef]
- Chen, T.-W.; Nguyen, T.M.N.; Kahlen, K.; Stützel, H. Quantification of the Effects of Architectural Traits on Dry Mass Production and Light Interception of Tomato Canopy under Different Temperature Regimes Using a Dynamic Functional–Structural Plant Model. J. Exp. Bot. 2014, 65, 6399–6410. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Evers, J.B.; Zhang, L.; Mao, L.; Zhang, S.; Zhao, X.; Liu, S.; van der Werf, W.; Li, Z. Modelling the Structural Response of Cotton Plants to Mepiquat Chloride and Population Density. Ann. Bot. 2014, 114, 877–887. [Google Scholar] [CrossRef]
- Henke, M.; Kurth, W.; Buck-Sorlin, G.H. FSPM-P: Towards a General Functional-Structural Plant Model for Robust and Comprehensive Model Development. Front. Comput. Sci. 2016, 10, 1103–1117. [Google Scholar] [CrossRef]
- Boudon, F.; Persello, S.; Jestin, A.; Briand, A.-S.; Grechi, I.; Fernique, P.; Guédon, Y.; Léchaudel, M.; Lauri, P.-É.; Normand, F. V-Mango: A Functional–Structural Model of Mango Tree Growth, Development and Fruit Production. Ann. Bot. 2020, 126, 745–763. [Google Scholar] [CrossRef]
- Prusinkiewicz, P. A Look at the Visual Modeling of Plants Using L-Systems. In Proceedings of the Bioinformatics; Hofestädt, R., Lengauer, T., Löffler, M., Schomburg, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 11–29. [Google Scholar]
- Lobet, G.; Draye, X.; Périlleux, C. An Online Database for Plant Image Analysis Software Tools. Plant Methods 2013, 9, 38. [Google Scholar] [CrossRef]
- Teichmann, T.; Muhr, M. Shaping Plant Architecture. Front. Plant Sci. 2015, 6, 233. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, G.; Han, J.; Li, F.; Zhang, Q.; Doonan, J. A Functional-Structural Model for Alfalfa That Accurately Integrates Shoot and Root Growth and Development. In Proceedings of the 2018 6th International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications (PMA), Hefei, China, 4–8 November 2018; IEEE Press: New York, NY, USA, 2018; pp. 134–140. [Google Scholar]
- Trachsel, S.; Kaeppler, S.M.; Brown, K.M.; Lynch, J.P. Shovelomics: High Throughput Phenotyping of Maize (Zea mays L.) Root Architecture in the Field. Plant Soil 2011, 341, 75–87. [Google Scholar] [CrossRef]
- Teramoto, S.; Kitomi, Y.; Nishijima, R.; Takayasu, S.; Maruyama, N.; Uga, Y. Backhoe-Assisted Monolith Method for Plant Root Phenotyping under Upland Conditions. Breed. Sci. 2019, 69, 508–513. [Google Scholar] [CrossRef]
- Teramoto, S.; Takayasu, S.; Kitomi, Y.; Arai-Sanoh, Y.; Tanabata, T.; Uga, Y. High-Throughput Three-Dimensional Visualization of Root System Architecture of Rice Using X-Ray Computed Tomography. Plant Methods 2020, 16, 66. [Google Scholar] [CrossRef] [PubMed]
- Leitner, D.; Klepsch, S.; Bodner, G.; Schnepf, A. A Dynamic Root System Growth Model Based on L-Systems. Plant Soil 2010, 332, 177–192. [Google Scholar] [CrossRef]
- Stützel, H.; Kahlen, K. Editorial: Virtual Plants: Modeling Plant Architecture in Changing Environments. Front. Plant Sci. 2016, 7, 1734. [Google Scholar] [CrossRef] [PubMed]
- Lungley, D.R. The Growth of Root Systems—A Numerical Computer Simulation Model. Plant Soil 1973, 38, 145–159. [Google Scholar] [CrossRef]
- Hackett, C.; Rose, D.A. A Model of The Extension and Branching of a Seminal Root of Barley, and Its Use in Studying Relations Between Root Dimensions. Aust. J. Biol. Sci. 1972, 25, 669–680. [Google Scholar] [CrossRef]
- Diggle, A.J. ROOTMAP—A Model in Three-Dimensional Coordinates of the Growth and Structure of Fibrous Root Systems. Plant Soil 1988, 105, 169–178. [Google Scholar] [CrossRef]
- Pagès, L.; Jordan, M.O.; Picard, D. A Simulation Model of the Three-Dimensional Architecture of the Maize Root System. Plant Soil 1989, 119, 147–154. [Google Scholar] [CrossRef]
- Pagès, L.; Vercambre, G.; Drouet, J.-L.; Lecompte, F.; Collet, C.; Le Bot, J. Root Typ: A Generic Model to Depict and Analyse the Root System Architecture. Plant Soil 2004, 258, 103–119. [Google Scholar] [CrossRef]
- Barczi, J.-F.; Rey, H.; Griffon, S.; Jourdan, C. DigR: A Generic Model and Its Open Source Simulation Software to Mimic Three-Dimensional Root-System Architecture Diversity. Ann. Bot. 2018, 121, 1089–1104. [Google Scholar] [CrossRef]
- Wu, L.; McGechan, M.B.; McRoberts, N.; Baddeley, J.A.; Watson, C.A. SPACSYS: Integration of a 3D Root Architecture Component to Carbon, Nitrogen and Water Cycling—Model Description. Ecol. Model. 2007, 200, 343–359. [Google Scholar] [CrossRef]
- Lynch, J.P.; Nielsen, K.L.; Davis, R.D.; Jablokow, A.G. SimRoot: Modelling and Visualization of Root Systems. Plant Soil 1997, 188, 139–151. [Google Scholar] [CrossRef]
- Postma, J.A.; Kuppe, C.; Owen, M.R.; Mellor, N.; Griffiths, M.; Bennett, M.J.; Lynch, J.P.; Watt, M. OpenSimRoot: Widening the Scope and Application of Root Architectural Models. New Phytol. 2017, 215, 1274–1286. [Google Scholar] [CrossRef] [PubMed]
- Schnepf, A.; Leitner, D.; Landl, M.; Lobet, G.; Mai, T.H.; Morandage, S.; Sheng, C.; Zörner, M.; Vanderborght, J.; Vereecken, H. CRootBox: A Structural–Functional Modelling Framework for Root Systems. Ann. Bot. 2018, 121, 1033–1053. [Google Scholar] [CrossRef] [PubMed]
- Lucido, A.; Andrade, F.; Basallo, O.; Eleiwa, A.; Marin-Sanguino, A.; Vilaprinyo, E.; Sorribas, A.; Alves, R. Modeling the Effects of Strigolactone Levels on Maize Root System Architecture. Front. Plant Sci. 2024, 14, 1329556. [Google Scholar] [CrossRef] [PubMed]
- Niinemets, Ü.; Tenhunen, J.D. A Model Separating Leaf Structural and Physiological Effects on Carbon Gain along Light Gradients for the Shade-Tolerant Species Acer Saccharum. Plant Cell Environ. 1997, 20, 845–866. [Google Scholar] [CrossRef]
- Hinojo-Hinojo, C.; Castellanos, A.E.; Llano-Sotelo, J.; Peñuelas, J.; Vargas, R.; Romo-Leon, J.R. High Vcmax, Jmax and Photosynthetic Rates of Sonoran Desert Species: Using Nitrogen and Specific Leaf Area Traits as Predictors in Biochemical Models. J. Arid Environ. 2018, 156, 1–8. [Google Scholar] [CrossRef]
- Liu, Q.; Xie, L.; Li, F. Dynamic Simulation of the Crown Net Photosynthetic Rate for Young Larix Olgensis Henry Trees. Forests 2019, 10, 321. [Google Scholar] [CrossRef]
- Barley, K.P. The Configuration of the Root System in Relation to Nutrient Uptake. In Advances in Agronomy; Brady, N.C., Ed.; Academic Press: Cambridge, MA, USA, 1970; Volume 22, pp. 159–201. [Google Scholar]
- Johnson, M.P. Photosynthesis. Essays Biochem. 2016, 60, 255–273. [Google Scholar] [CrossRef]
- Del García-Rodríguez, L.C.; Prado-Olivarez, J.; Guzmán-Cruz, R.; Rodríguez-Licea, M.A.; Barranco-Gutiérrez, A.I.; Perez-Pinal, F.J.; Espinosa-Calderon, A. Mathematical Modeling to Estimate Photosynthesis: A State of the Art. Appl. Sci. 2022, 12, 5537. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A Biochemical Model of Photosynthetic CO2 Assimilation in Leaves of C 3 Species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef]
- Von Caemmerer, S. Updating the Steady-State Model of C4 Photosynthesis. J. Exp. Bot. 2021, 72, 6003–6017. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Struik, P.C. C3 and C4 Photosynthesis Models: An Overview from the Perspective of Crop Modelling. NJAS Wagening. J. Life Sci. 2009, 57, 27–38. [Google Scholar] [CrossRef]
- Sage, R.F. The Evolution of C4 Photosynthesis. New Phytol. 2004, 161, 341–370. [Google Scholar] [CrossRef] [PubMed]
- Burgos, A.; Miranda, E.; Vilaprinyo, E.; Meza-Canales, I.D.; Alves, R. CAM Models: Lessons and Implications for CAM Evolution. Front. Plant Sci. 2022, 13, 893095. [Google Scholar] [CrossRef]
- Nungesser, D.; Kluge, M.; Tolle, H.; Oppelt, W. A Dynamic Computer Model of the Metabolic and Regulatory Processes in Crassulacean Acid Metabolism. Planta 1984, 162, 204–214. [Google Scholar] [CrossRef]
- Lüttge, U.; Beck, F. Endogenous Rhythms and Chaos in Crassulacean Acid Metabolism. Planta 1992, 188, 28–38. [Google Scholar] [CrossRef]
- Blasius, B.; Neif, R.; Beck, F.; Lüttge, U. Oscillatory Model of Crassulacean Acid Metabolism with a Dynamic Hysteresis Switch. Proc. R. Soc. London. Ser. B Biol. Sci. 1999, 266, 93–101. [Google Scholar] [CrossRef]
- Cheung, C.Y.M.; Poolman, M.G.; Fell, D.A.; Ratcliffe, R.G.; Sweetlove, L.J. A Diel Flux Balance Model Captures Interactions between Light and Dark Metabolism during Day-Night Cycles in C3 and Crassulacean Acid Metabolism Leaves. Plant Physiol. 2014, 165, 917–929. [Google Scholar] [CrossRef]
- Javaux, M.; Schröder, T.; Vanderborght, J.; Vereecken, H. Use of a Three-Dimensional Detailed Modeling Approach for Predicting Root Water Uptake. Vadose Zone J. 2008, 7, 1079–1088. [Google Scholar] [CrossRef]
- Lacointe, A.; Minchin, P.E.H. A Mechanistic Model to Predict Distribution of Carbon Among Multiple Sinks. In Phloem: Methods and Protocols; Liesche, J., Ed.; Springer: New York, NY, USA, 2019; pp. 371–386. ISBN 978-1-4939-9562-2. [Google Scholar]
- Rengel, Z. Mechanistic Simulation Models of Nutrient Uptake: A Review. Plant Soil 1993, 152, 161–173. [Google Scholar] [CrossRef]
- De Willigen, P.; Noordwijk, M. van Modelling Nutrient Uptake: From Single Roots to Complete Root Systems. In Simulation and Systems Analysis for Rice Production (SARP) Selected Papers Presented at Workshops on Crop Simulation of a Network of National and International Research Centres of Several Asian Countries and The Netherlands, 1990–1991; Pudoc: Wageningen, The Netherlands, 1991; pp. 277–295. [Google Scholar]
- Nye, P.H. The Effect of the Nutrient Intensity and Buffering Power of a Soil, and the Absorbing Power, Size and Root Hairs of a Root, on Nutrient Absorption by Diffusion. Plant Soil 1966, 25, 81–105. [Google Scholar] [CrossRef]
- Nye, P.H.; Marriott, F.H.C. A Theoretical Study of the Distribution of Substances around Roots Resulting from Simultaneous Diffusion and Mass Flow. Plant Soil 1969, 30, 459–472. [Google Scholar] [CrossRef]
- Baldwin, J.P.; Nye, P.H.; Tinker, P.B. Uptake of Solutes by Multiple Root Systems from Soil: Iii—a Model for Calculating the Solute Uptake by a Randomly Dispersed Root System Developing in a Finite Volume of Soil. Plant Soil 1973, 38, 621–635. [Google Scholar] [CrossRef]
- Baldwin, J.P.; Nye, P.H. A Model to Calculate the Uptake by a Developing Root System or Root Hair System of Solutes with Concentration Variable Diffusion Coefficients. Plant Soil 1974, 40, 703–706. [Google Scholar] [CrossRef]
- Bhat, K.K.S.; Nye, P.H.; Baldwin, J.P. Diffusion of Phosphate to Plant Roots in Soil. Plant Soil 1976, 44, 63–72. [Google Scholar] [CrossRef]
- Itoh, S.; Barber, S.A. A Numerical Solution of Whole Plant Nutrient Uptake for Soil-Root Systems with Root Hairs. Plant Soil 1983, 70, 403–413. [Google Scholar] [CrossRef]
- Barber, S.A. Soil Nutrient Bioavailability: A Mechanistic Approach; John Wiley & Sons: Hoboken, NJ, USA, 1995; ISBN 978-0-471-58747-7. [Google Scholar]
- Tinker, P.B.; Nye, P.H. Solute Movement in the Rhizosphere, 2nd ed.; Oxford University Press: New York, NY, USA, 2000; ISBN 978-0-19-512492-7. [Google Scholar]
- Roose, T.; Fowler, A.C.; Darrah, P.R. A Mathematical Model of Plant Nutrient Uptake. J. Math. Biol. 2001, 42, 347–360. [Google Scholar] [CrossRef]
- Roose, T.; Fowler, A.C. A Mathematical Model for Water and Nutrient Uptake by Plant Root Systems. J. Theor. Biol. 2004, 228, 173–184. [Google Scholar] [CrossRef]
- Roose, T.; Fowler, A.C. A Model for Water Uptake by Plant Roots. J. Theor. Biol. 2004, 228, 155–171. [Google Scholar] [CrossRef]
- Roose, T.; Kirk, G.J.D. The Solution of Convection–Diffusion Equations for Solute Transport to Plant Roots. Plant Soil 2009, 316, 257–264. [Google Scholar] [CrossRef]
- Ou, Z. Approximate Nutrient Flux and Concentration Solutions of the Nye–Tinker–Barber Model by the Perturbation Expansion Method. J. Theor. Biol. 2019, 476, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lin, W.; Ou, Z. Analytical Solution of Nye–Tinker–Barber Model by Laplace Transform. Biosystems 2023, 225, 104845. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.B. (Ed.) Plant Nutrition and Soil Fertility Manual, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-0-429-13081-6. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology. In Classics in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005; ISBN 978-0-89871-554-5. [Google Scholar]
- Kuppe, C.W.; Schnepf, A.; von Lieres, E.; Watt, M.; Postma, J.A. Rhizosphere Models: Their Concepts and Application to Plant-Soil Ecosystems. Plant Soil 2022, 474, 17–55. [Google Scholar] [CrossRef]
- Conejo, A.N. Non-Dimensionalization of Differential Equations. In Fundamentals of Dimensional Analysis; Springer: Singapore, Singapore, 2021; pp. 347–378. ISBN 9789811616013. [Google Scholar]
- Kuppe, C.W.; Huber, G.; Postma, J.A. Comparison of Numerical Methods for Radial Solute Transport to Simulate Uptake by Plant Roots. Rhizosphere 2021, 18, 100352. [Google Scholar] [CrossRef]
- Sultan, S.E. Phenotypic Plasticity for Plant Development, Function and Life History. Trends Plant Sci. 2000, 5, 537–542. [Google Scholar] [CrossRef]
- Thornley, J.H.M. A Balanced Quantitative Model for Root: Shoot Ratios in Vegetative Plants. Ann. Bot. 1972, 36, 431–441. [Google Scholar] [CrossRef]
- Thornley, J.H.M. Shoot: Root Allocation with Respect to C, N and P: An Investigation and Comparison of Resistance and Teleonomic Models. Ann. Bot. 1995, 75, 391–405. [Google Scholar] [CrossRef]
- Thornley, J.H.M. Modelling Shoot [Ratio] Root Relations: The Only Way Forward? Ann. Bot. 1998, 81, 165–171. [Google Scholar] [CrossRef]
- Dewar, R.C. A Root-Shoot Partitioning Model Based on Carbon-Nitrogen-Water Interactions and Munch Phloem Flow. Funct. Ecol. 1993, 7, 356–368. [Google Scholar] [CrossRef]
- Feller, C.; Favre, P.; Janka, A.; Zeeman, S.C.; Gabriel, J.-P.; Reinhardt, D. Mathematical Modeling of the Dynamics of Shoot-Root Interactions and Resource Partitioning in Plant Growth. PLoS ONE 2015, 10, e0127905. [Google Scholar] [CrossRef]
- Zhou, X.-R.; Schnepf, A.; Vanderborght, J.; Leitner, D.; Lacointe, A.; Vereecken, H.; Lobet, G. CPlantBox, a Whole-Plant Modelling Framework for the Simulation of Water- and Carbon-Related Processes. In Silico Plants 2020, 2, diaa001. [Google Scholar] [CrossRef]
- Lacointe, A.; Minchin, P.E.H. Modelling Phloem and Xylem Transport within a Complex Architecture. Funct. Plant Biol. 2008, 35, 772–780. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.B. A Review of Evidence on the Control of Shoot: Root Ratio, in Relation to Models. Ann. Bot. 1988, 61, 433–449. [Google Scholar] [CrossRef]
- Reynolds, J.F.; Thornley, J.H.M. A Shoot: Root Partitioning Model. Ann. Bot. 1982, 49, 585–597. [Google Scholar] [CrossRef]
- Li, X.; Feng, Y.; Boersma, L. Partition of Photosynthates between Shoot and Root in Spring Wheat (Triticum Aestivum L.) as a Function of Soil Water Potential and Root Temperature. Plant Soil 1994, 164, 43–50. [Google Scholar] [CrossRef]
- Bertheloot, J.; Cournède, P.-H.; Andrieu, B. NEMA, a Functional–Structural Model of Nitrogen Economy within Wheat Culms after Flowering. I. Model Description. Ann. Bot. 2011, 108, 1085–1096. [Google Scholar] [CrossRef]
- Gupta, D.; Sharma, G.; Saraswat, P.; Ranjan, R. Synthetic Biology in Plants, a Boon for Coming Decades. Mol. Biotechnol. 2021, 63, 1138–1154. [Google Scholar] [CrossRef]
- Deneer, A.; Fleck, C. Mathematical Modelling in Plant Synthetic Biology. Methods Mol. Biol. 2022, 2379, 209–251. [Google Scholar]
- Roell, M.-S.; Zurbriggen, M.D. The Impact of Synthetic Biology for Future Agriculture and Nutrition. Curr. Opin. Biotechnol. 2020, 61, 102–109. [Google Scholar] [CrossRef]
- Andres, J.; Blomeier, T.; Zurbriggen, M.D. Synthetic Switches and Regulatory Circuits in Plants. Plant Physiol. 2019, 179, 862–884. [Google Scholar] [CrossRef]
- Scheible, W.-R.; Lauerer, M.; Schulze, E.-D.; Caboche, M.; Stitt, M. Accumulation of Nitrate in the Shoot Acts as a Signal to Regulate Shoot-Root Allocation in Tobacco. Plant J. 1997, 11, 671–691. [Google Scholar] [CrossRef]
- Lemoine, R.; La Camera, S.; Atanassova, R.; Dédaldéchamp, F.; Allario, T.; Pourtau, N.; Bonnemain, J.-L.; Laloi, M.; Coutos-Thévenot, P.; Maurousset, L.; et al. Source-to-Sink Transport of Sugar and Regulation by Environmental Factors. Front. Plant Sci. 2013, 4, 272. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Ruan, Y.-L. Shoot–Root Carbon Allocation, Sugar Signalling and Their Coupling with Nitrogen Uptake and Assimilation. Funct. Plant Biol. 2015, 43, 105–113. [Google Scholar] [CrossRef] [PubMed]
- Alves, R.; Savageau, M.A. Effect of Overall Feedback Inhibition in Unbranched Biosynthetic Pathways. Biophys. J. 2000, 79, 2290–2304. [Google Scholar] [CrossRef]
- Vazquez-Vilar, M.; Selma, S.; Orzaez, D. The Design of Synthetic Gene Circuits in Plants: New Components, Old Challenges. J. Exp. Bot. 2023, 74, 3791–3805. [Google Scholar] [CrossRef]
- Marshall-Colon, A.; Long, S.P.; Allen, D.K.; Allen, G.; Beard, D.A.; Benes, B.; von Caemmerer, S.; Christensen, A.J.; Cox, D.J.; Hart, J.C.; et al. Crops in Silico: Generating Virtual Crops Using an Integrative and Multi-Scale Modeling Platform. Front. Plant Sci. 2017, 8, 786. [Google Scholar] [CrossRef]
- Baldazzi, V.; Bertin, N.; de Jong, H.; Génard, M. Towards Multiscale Plant Models: Integrating Cellular Networks. Trends Plant Sci. 2012, 17, 728–736. [Google Scholar] [CrossRef]
- Herrero-Huerta, M.; Meline, V.; Iyer-Pascuzzi, A.S.; Souza, A.M.; Tuinstra, M.R.; Yang, Y. 4D Structural Root Architecture Modeling from Digital Twins by X-Ray Computed Tomography. Plant Methods 2021, 17, 123. [Google Scholar] [CrossRef]
- York, L.M. Functional Phenomics: An Emerging Field Integrating High-Throughput Phenotyping, Physiology, and Bioinformatics. J. Exp. Bot. 2019, 70, 379–386. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucido, A.; Basallo, O.; Marin-Sanguino, A.; Eleiwa, A.; Martinez, E.S.; Vilaprinyo, E.; Sorribas, A.; Alves, R. Multiscale Mathematical Modeling in Systems Biology: A Framework to Boost Plant Synthetic Biology. Plants 2025, 14, 470. https://doi.org/10.3390/plants14030470
Lucido A, Basallo O, Marin-Sanguino A, Eleiwa A, Martinez ES, Vilaprinyo E, Sorribas A, Alves R. Multiscale Mathematical Modeling in Systems Biology: A Framework to Boost Plant Synthetic Biology. Plants. 2025; 14(3):470. https://doi.org/10.3390/plants14030470
Chicago/Turabian StyleLucido, Abel, Oriol Basallo, Alberto Marin-Sanguino, Abderrahmane Eleiwa, Emilce Soledad Martinez, Ester Vilaprinyo, Albert Sorribas, and Rui Alves. 2025. "Multiscale Mathematical Modeling in Systems Biology: A Framework to Boost Plant Synthetic Biology" Plants 14, no. 3: 470. https://doi.org/10.3390/plants14030470
APA StyleLucido, A., Basallo, O., Marin-Sanguino, A., Eleiwa, A., Martinez, E. S., Vilaprinyo, E., Sorribas, A., & Alves, R. (2025). Multiscale Mathematical Modeling in Systems Biology: A Framework to Boost Plant Synthetic Biology. Plants, 14(3), 470. https://doi.org/10.3390/plants14030470








